Deep-Time Demographic Inference Suggests Ecological Release as Driver of Neoavian Adaptive Radiation
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
4.1. Estimates of Ne
4.2. Caveats in the Estimation of Ne
4.2.1. Accuracy of Ne Estimates
4.2.2. Homoplasy and Sequence Alignment
4.2.3. Biases Associated with Relaxed Clock Analyses
4.2.4. Generation Length
4.2.5. Taxon Sampling Bias
4.2.6. Other Potential Biases
4.3. Ecological Theory of Adaptive Radiation
4.4. Comparison to Extant Birds
5. Conclusions and Future Directions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eldredge, N. Punctuated equilibria: An alternative to phyletic gradualism. In Models in Paleobiology; Schopf, T.J., Ed.; Freeman, Cooper and Company: San Fransisco, IL, USA, 1972; pp. 82–115. [Google Scholar]
- Gould, S.J. Tempo and mode in the macroevolutionary reconstruction of Darwinism. Proc. Natl. Acad. Sci. USA 1994, 91, 6764–6771. [Google Scholar] [CrossRef] [PubMed]
- Penny, D. Charles Darwin, Gradualism and Punctuated Equilibria. Syst. Zool. 1983, 32, 72. [Google Scholar] [CrossRef]
- Rhodes, F.H.T. Darwinian gradualism and its limits: The development of Darwin’s views on the rate and pattern of evolutionary change. J. Hist. Biol. 1987, 20, 139–157. [Google Scholar] [CrossRef]
- Gillham, N.W. Evolution by jumps: Francis Galton and William Bateson and the mechanism of evolutionary change. Genetics 2001, 159, 1383–1392. [Google Scholar] [PubMed]
- Simpson, G.G. Tempo and Mode in Evolution; Columbia Biological Series, No. 15; Columbia University Press: New York, NY, USA, 1944. [Google Scholar]
- Mooers, A.Ø.; Heard, S.B. Inferring Evolutionary Process from Phylogenetic Tree Shape. Q. Rev. Boil. 1997, 72, 31–54. [Google Scholar] [CrossRef]
- Ricklefs, R.E. Estimating diversification rates from phylogenetic information. Trends Ecol. Evol. 2007, 22, 601–610. [Google Scholar] [CrossRef] [PubMed]
- Alfaro, M.E.; Santini, F.; Brock, C.; Alamillo, H.; Dornburg, A.; Rabosky, D.L.; Carnevale, G.; Harmon, L.J. Nine exceptional radiations plus high turnover explain species diversity in jawed vertebrates. Proc. Natl. Acad. Sci. USA 2009, 106, 13410–13414. [Google Scholar] [CrossRef] [PubMed]
- Schluter, L. Ecological Causes of Adaptive Radiation. Am. Nat. 1996, 148, S40–S64. [Google Scholar] [CrossRef]
- Glor, R.E. Phylogenetic Insights on Adaptive Radiation. Annu. Rev. Ecol. Evol. Syst. 2010, 41, 251–270. [Google Scholar] [CrossRef]
- Feduccia, A. ‘Big bang’ for tertiary birds? Trends Ecol. Evol. 2003, 18, 172–176. [Google Scholar] [CrossRef]
- Feduccia, A. Avian extinction at the end of the Cretaceous: Assessing the magnitude and subsequent explosive radiation. Cretac. Res. 2014, 50, 1–15. [Google Scholar] [CrossRef]
- Ksepka, D.; Stidham, T.A.; Williamson, T.E. Early Paleocene landbird supports rapid phylogenetic and morphological diversification of crown birds after the K–Pg mass extinction. Proc. Natl. Acad. Sci. USA 2017, 114, 8047–8052. [Google Scholar] [CrossRef] [PubMed]
- Field, D.J.; Bercovici, A.; Berv, J.S.; Dunn, R.; Fastovsky, D.E.; Lyson, T.R.; Vajda, V.; Gauthier, J.A. Early Evolution of Modern Birds Structured by Global Forest Collapse at the End-Cretaceous Mass Extinction. Curr. Boil. 2018, 28, 1825–1831.e2. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Penny, D. Mass Survival of Birds Across the Cretaceous-Tertiary Boundary: Molecular Evidence. Science 1997, 275, 1109–1113. [Google Scholar] [CrossRef] [PubMed]
- Van Tuinen, M.; Hedges, S.B. Calibration of avian molecular clocks. Mol. Boil. Evol. 2001, 18, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.W.; Rest, J.; García-Moreno, J.; Sorenson, M.D.; Mindell, D.P. Strong mitochondrial DNA support for a Cretaceous origin of modern avian lineages. BMC Boil. 2008, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Cracraft, J. Avian evolution, Gondwana biogeography and the Cretaceous–Tertiary mass extinction event. Proc. R. Soc. B Boil. Sci. 2001, 268, 459–469. [Google Scholar] [CrossRef]
- Paton, T.; Haddrath, O.; Baker, A.J. Complete mitochondrial DNA genome sequences show that modern birds are not descended from transitional shorebirds. Proc. R. Soc. B Boil. Sci. 2002, 269, 839–846. [Google Scholar] [CrossRef]
- Wright, T.; Schirtzinger, E.E.; Matsumoto, T.; Eberhard, J.R.; Graves, G.R.; Sanchez, J.J.; Capelli, S.; Müller, H.; Scharpegge, J.; Chambers, G.; et al. A Multilocus Molecular Phylogeny of the Parrots (Psittaciformes): Support for a Gondwanan Origin during the Cretaceous. Mol. Boil. Evol. 2008, 25, 2141–2156. [Google Scholar] [CrossRef]
- Blokland, J.C.; Reid, C.M.; Worthy, T.H.; Tennyson, A.; Clarke, J.A.; Scofield, R.P. Chatham Island Paleocene fossils provide insight into the palaeobiology, evolution, and diversity of early penguins (Aves, Sphenisciformes). Palaeontol. Electron. 2019, 22, 1–92. [Google Scholar] [CrossRef]
- Mitchell, K.J.; Cooper, A.; Phillips, M.J. Comment on “Whole-genome analyses resolve early branches in the tree of life of modern birds”. Science 2015, 349, 1460. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, E.; Mirarab, S.; Aberer, A.J.; Li, B.; Houde, P.; Li, C.; Ho, S.Y.W.; Faircloth, B.C.; Nabholz, B.; Howard, J.T.; et al. Whole-genome analyses resolve early branches in the tree of life of modern birds. Science 2014, 346, 1320–1331. [Google Scholar] [CrossRef] [PubMed]
- Prum, R.O.; Berv, J.S.; Dornburg, A.; Field, D.J.; Townsend, J.P.; Lemmon, E.M.; Lemmon, A.R. A comprehensive phylogeny of birds (Aves) using targeted next-generation DNA sequencing. Nature 2015, 526, 569–573. [Google Scholar] [CrossRef] [PubMed]
- Cracraft, J.; Houde, P.; Ho, S.Y.W.; Mindell, D.P.; Fjeldså, J.; Lindow, B.; Edwards, S.V.; Rahbek, C.; Mirarab, S.; Warnow, T.; et al. Response to Comment on “Whole-genome analyses resolve early branches in the tree of life of modern birds”. Science 2015, 349, 1460. [Google Scholar] [CrossRef] [PubMed]
- Claramunt, S.; Cracraft, J. A new time tree reveals Earth history’s imprint on the evolution of modern birds. Sci. Adv. 2015, 1, e1501005. [Google Scholar] [CrossRef]
- Kimball, R.T.; Oliveros, C.H.; Wang, N.; White, N.; Barker, F.K.; Field, D.J.; Ksepka, D.; Chesser, R.T.; Moyle, R.G.; Braun, M.J.; et al. A Phylogenomic Supertree of Birds. Diversity 2019, 11, 109. [Google Scholar] [CrossRef]
- Oliveros, C.H.; Field, D.J.; Ksepka, D.T.; Barker, K.; Aleixo, A.; Andersen, M.J.; Alström, P.; Benz, B.W.; Braun, E.L.; Braun, M.J.; et al. Earth history and the passerine superradiation. Proc. Natl. Acad. Sci. USA 2019, 116, 7916–7925. [Google Scholar] [CrossRef]
- Moyle, R.G.; Filardi, C.E.; Smith, C.E.; Diamond, J. Explosive Pleistocene diversification and hemispheric expansion of a “great speciator”. Proc. Natl. Acad. Sci. USA 2009, 106, 1863–1868. [Google Scholar] [CrossRef]
- Bourdon, E.; Bouya, B.; Iarochène, M. Earliest African neornithine bird: A new species of Prophaethontidae (Aves) from the Paleocene of Morocco. J. Vertebr. Paléontol. 2005, 25, 157–170. [Google Scholar] [CrossRef]
- Bourdon, E.; Mourer-Chauviré, C.; Amaghzaz, M.; Bouya, B. New specimens of Lithoptila abdounensis (Aves, Prophaethontidae) from the lower Paleogene of Morocco. J. Vertebr. Paléontol. 2008, 28, 751–761. [Google Scholar] [CrossRef]
- Zelenkov, N.V.; Dyke, G. The Fossil Record and Evolution of Mousebirds (Aves: Coliiformes). Palaeontol. 2008, 51, 1403–1418. [Google Scholar] [CrossRef]
- Rich, P.V.; Bohaska, D.J. The world’s oldest owl: A new strigiform from the Paleocene of southwestern Colorado. Smithson. Contrib. Paleobiol. 1976, 27, 87–94. [Google Scholar]
- Kurochkin, E.N.; Dyke, G. The first fossil owls (Aves: Strigiformes) from the Paleogene of Asia and a review of the fossil record of Strigiformes. Paléontol. J. 2011, 45, 445–458. [Google Scholar] [CrossRef]
- Mayr, G. Paleogene Fossil Birds; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Berv, J.S.; Field, D.J. Genomic Signature of an Avian Lilliput Effect across the K-Pg Extinction. Syst. Boil. 2017, 67, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Field, D.J.; Berv, J.S.; Hsiang, A.Y.; Lanfear, R.; Landis, M.J.; Dornburg, A. Timing the extant avian radiation: The rise of modern birds, and the importance of modeling molecular rate variation. PeerJ Prepr. 2019. [Google Scholar] [CrossRef]
- Hackett, S.J.; Kimball, R.T.; Reddy, S.; Bowie, R.C.K.; Braun, E.L.; Braun, M.J.; Chojnowski, J.L.; Cox, W.; Han, K.-L.; Harshman, J.; et al. A Phylogenomic Study of Birds Reveals Their Evolutionary History. Science 2008, 320, 1763–1768. [Google Scholar] [CrossRef]
- Reddy, S.; Kimball, R.T.; Pandey, A.; Hosner, P.A.; Braun, M.J.; Hackett, S.J.; Han, K.-L.; Harshman, J.; Huddleston, C.J.; Kingston, S.; et al. Why Do Phylogenomic Data Sets Yield Conflicting Trees? Data Type Influences the Avian Tree of Life more than Taxon Sampling. Syst. Boil. 2017, 66, 857–879. [Google Scholar] [CrossRef]
- Hedges, S.B.; Marin, J.; Suleski, M.; Paymer, M.; Kumar, S. Tree of life reveals clock-like speciation and diversification. Mol. Boil. Evol. 2015, 32, 835–845. [Google Scholar] [CrossRef]
- Matzke, A.; Churakov, G.; Berkes, P.; Arms, E.M.; Kelsey, D.; Brosius, J.; Kriegs, J.O.; Schmitz, J. Retroposon Insertion Patterns of Neoavian Birds: Strong Evidence for an Extensive Incomplete Lineage Sorting Era. Mol. Boil. Evol. 2012, 29, 1497–1501. [Google Scholar] [CrossRef]
- Suh, A.; Smeds, L.; Ellegren, H. The Dynamics of Incomplete Lineage Sorting across the Ancient Adaptive Radiation of Neoavian Birds. PLoS Boil. 2015, 13, e1002224. [Google Scholar] [CrossRef]
- Suh, A. The phylogenomic forest of bird trees contains a hard polytomy at the root of Neoaves. Zool. Scr. 2016, 45, 50–62. [Google Scholar] [CrossRef]
- Han, K.-L.; Braun, E.L.; Kimball, R.T.; Reddy, S.; Bowie, R.C.K.; Braun, M.J.; Chojnowski, J.L.; Hackett, S.J.; Harshman, J.; Huddleston, C.J.; et al. Are Transposable Element Insertions Homoplasy Free: An Examination Using the Avian Tree of Life. Syst. Boil. 2011, 60, 375–386. [Google Scholar] [CrossRef] [PubMed]
- Poe, S.; Chubb, A.L. Birds in A Bush: Five Genes Indicate Explosive Evolution of Avian Orders. Evolution 2004, 58, 404–415. [Google Scholar] [CrossRef]
- Chojnowski, J.L.; Kimball, R.T.; Braun, E.L. Introns outperform exons in analyses of basal avian phylogeny using clathrin heavy chain genes. Gene 2008, 410, 89–96. [Google Scholar] [CrossRef]
- Kimball, R.T.; Wang, N.; Heimer-McGinn, V.; Ferguson, C.; Braun, E.L. Identifying localized biases in large datasets: A case study using the avian tree of life. Mol. Phylogenet. Evol. 2013, 69, 1021–1032. [Google Scholar] [CrossRef]
- Braun, E.L.; Cracraft, J.; Houde, P. Resolving the Avian Tree of Life from Top to Bottom: The Promise and Potential Boundaries of the Phylogenomic Era. In Avian Genomics in Ecology and Evolution; Springer: Cham, Switzerland, 2019; pp. 151–210. ISBN 978-3-030-16476-8. [Google Scholar]
- Pamilo, P.; Nei, M. Relationships between gene trees and species trees. Mol. Boil. Evol. 1988, 5, 568–583. [Google Scholar] [CrossRef]
- International Union for Conservation of Nature. 2006 IUCN Red List of Threatened Species, 2006. Available online: http://www.iucnredlist.org/ (accessed on 1 March 2008).
- Nadachowska-Brzyska, K.; Li, C.; Smeds, L.; Zhang, G.; Ellegren, H. Temporal Dynamics of Avian Populations during Pleistocene Revealed by Whole-Genome Sequences. Curr. Boil. 2015, 25, 1375–1380. [Google Scholar] [CrossRef]
- Simpson, G.G. The Major Features of Evolution; Columbia University Press: New York, NY, USA, 1953. [Google Scholar]
- Schluter, D. The Ecology of Adaptive Radiation; Oxford University Press: Oxford UK, 2000; ISBN 9780198505228. [Google Scholar]
- Gavrilets, S.; Losos, J.B.; Rowland, J.M.; Emlen, D.J. Adaptive Radiation: Contrasting Theory with Data. Science 2009, 323, 732–737. [Google Scholar] [CrossRef]
- Yoder, J.; Clancey, E.; Roches, S.D.; Eastman, J.M.; Gentry, L.; Godsoe, W.; Hagey, T.J.; Jochimsen, D.; Oswald, B.P.; Robertson, J.; et al. Ecological opportunity and the origin of adaptive radiations. J. Evol. Boil. 2010, 23, 1581–1596. [Google Scholar] [CrossRef]
- Stroud, J.T.; Losos, J.B. Ecological Opportunity and Adaptive Radiation. Annu. Rev. Ecol. Evol. Syst. 2016, 47, 507–532. [Google Scholar] [CrossRef]
- Gillespie, R.; Bennett, G.M.; De Meester, L.; Feder, J.L.; Fleischer, R.C.; Harmon, L.J.; Hendry, A.P.; Knope, M.L.; Mallet, J.; Martin, C.H.; et al. Comparing Adaptive Radiations Across Space, Time, and Taxa. J. Hered. 2020, 111, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Kassen, R. Toward a General Theory of Adaptive Radiation. Ann. N. Y. Acad. Sci. 2009, 1168, 3–22. [Google Scholar] [CrossRef] [PubMed]
- Roches, S.D.; Robertson, J.M.; Harmon, L.J.; Rosenblum, E.B. Ecological release in White Sands lizards. Ecol. Evol. 2011, 1, 571–578. [Google Scholar] [CrossRef] [PubMed]
- Losos, J.B.; De Queiroz, K. Evolutionary consequences of ecological release in Caribbean Anolis lizards. Boil. J. Linn. Soc. 1997, 61, 459–483. [Google Scholar] [CrossRef]
- Mahler, D.L.; Revell, L.J.; Glor, R.E.; Losos, J.B. Ecological Opportunity and The Rate of Morphological Evolution in the Diversification of Greater Antillean Anoles. Evolution 2010, 64, 2731–2745. [Google Scholar] [CrossRef]
- Meyer, A.; Kocher, T.D.; Basasibwaki, P.; Wilson, A.C. Monophyletic origin of Lake Victoria cichlid fishes suggested by mitochondrial DNA sequences. Nature 1990, 347, 550–553. [Google Scholar] [CrossRef]
- Cox, G.W.; Ricklefs, R.E. Species Diversity and Ecological Release in Caribbean Land Bird Faunas. Oikos 1977, 28, 113. [Google Scholar] [CrossRef]
- Lovette, I.J.; Bermingham, E.; Ricklefs, R.E. Clade-specific morphological diversification and adaptive radiation in Hawaiian songbirds. Proc. R. Soc. B Boil. Sci. 2002, 269, 37–42. [Google Scholar] [CrossRef]
- Grant, P.R.; Grant, B.R. How and Why Species Multiply: The Radiation of Darwin’s Finches (princeton Series In Evolutionary Biology), 1st ed.; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 978-0-691-13360-7. [Google Scholar]
- Jønsson, K.A.; Fabre, P.-H.; Fritz, S.A.; Etienne, R.S.; Ricklefs, R.E.; Jørgensen, T.B.; Fjeldså, J.; Rahbek, C.; Ericson, P.G.P.; Woog, F.; et al. Ecological and evolutionary determinants for the adaptive radiation of the Madagascan vangas. Proc. Natl. Acad. Sci. USA 2012, 109, 6620–6625. [Google Scholar] [CrossRef]
- Weir, J.T.; Mursleen, S. Diversity-Dependent Cladogenesis and Trait Evolution in the Adaptive Radiation of The Auks (Aves: Alcidae). Evolution 2012, 67, 403–416. [Google Scholar] [CrossRef]
- Sepkoski, J.J. A factor analytic description of the Phanerozoic marine fossil record. Paleobiology 1981, 7, 36–53. [Google Scholar] [CrossRef]
- Neige, P.; Dera, G.; Dommergues, J.-L. Adaptive radiation in the fossil record: A case study among Jurassic ammonoids. Palaeontology 2013, 56, 1247–1261. [Google Scholar] [CrossRef]
- Boivin, S.; Saucede, T.; Laffont, R.; Steimetz, E.; Neige, P. Diversification rates indicate an early role of adaptive radiations at the origin of modern echinoid fauna. PLoS ONE 2018, 13, e0194575. [Google Scholar] [CrossRef]
- Niklas, K.J.; Tiffney, B.H.; Knoll, A.H. Patterns in vascular land plant diversification. Nature 1983, 303, 614–616. [Google Scholar] [CrossRef]
- López-Fernández, H.; Arbour, J.H.; Winemiller, K.O.; Honeycutt, R.L. Testing for Ancient Adaptive Radiations in Neotropical Cichlid Fishes. Evolution 2013, 67, 1321–1337. [Google Scholar] [CrossRef] [PubMed]
- Rauhut, O.W.M.; Pol, D. Probable basal allosauroid from the early Middle Jurassic Cañadón Asfalto Formation of Argentina highlights phylogenetic uncertainty in tetanuran theropod dinosaurs. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Magallón, S.; Sanderson, M.J. Absolute Diversification Rates in Angiosperm Clades. Evolution 2001, 55, 1762–1780. [Google Scholar] [CrossRef]
- Jetz, W.; Thomas, G.; Joy, J.B.; Hartmann, K.; Mooers, A.O. The global diversity of birds in space and time. Nature 2012, 491, 444–448. [Google Scholar] [CrossRef]
- Claramunt, S. Discovering Exceptional Diversifications at Continental Scales: The Case of the Endemic Families of Neotropical Suboscine Passerines. Evolution 2010, 64, 2004–2019. [Google Scholar] [CrossRef]
- Moyle, R.G.; Oliveros, C.H.; Andersen, M.J.; Hosner, P.A.; Benz, B.W.; Manthey, J.; Travers, S.L.; Brown, R.M.; Faircloth, B.C. Tectonic collision and uplift of Wallacea triggered the global songbird radiation. Nat. Commun. 2016, 7, 12709. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Diamond, J.M.; Karr, J.R. Density Compensation in Island Faunas. Ecology 1972, 53, 330–342. [Google Scholar] [CrossRef]
- Wright, S.J. Density compensation in island avifaunas. Oecologia 1980, 45, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Springer, M.S.; Molloy, E.K.; Sloan, D.B.; Simmons, M.P.; Gatesy, J. ILS-Aware Analysis of Low-Homoplasy Retroelement Insertions: Inference of Species Trees and Introgression Using Quartets. J. Hered. 2019, 111, 147–168. [Google Scholar] [CrossRef]
- Springer, M.S.; Gatesy, J. Retroposon Insertions within a Multispecies Coalescent Framework Suggest that Ratite Phylogeny is not in the ‘Anomaly Zone’. BioRxiv 2019, 643296. [Google Scholar] [CrossRef]
- Tiley, G.P.; Pandey, A.; Kimball, R.T.; Braun, E.L.; Burleigh, J.G. Whole genome phylogeny of Gallus: Introgression and data-type effects. Avian Res. 2020, 11, 7. [Google Scholar] [CrossRef]
- Zhang, C.; Rabiee, M.; Sayyari, E.; Mirarab, S. ASTRAL-III: Polynomial time species tree reconstruction from partially resolved gene trees. BMC Bioinform. 2018, 19, 153. [Google Scholar] [CrossRef] [PubMed]
- Mirarab, S. Species Tree Estimation Using ASTRAL: Practical Considerations. arXiv 2019, arXiv:1904.03826. [Google Scholar]
- Jarvis, E.; Mirarab, S.; Aberer, A.J.; Li, B.; Houde, P.; Li, C.; Ho, S.Y.W.; Faircloth, B.C.; Nabholz, B.; Howard, J.T.; et al. Phylogenomic analyses data of the avian phylogenomics project. GigaScience 2015, 4, 4–9. [Google Scholar] [CrossRef]
- Salinas, N.R.; Little, D.P. 2matrix: A utility for indel coding and phylogenetic matrix concatenation1. Appl. Plant Sci. 2014, 2, 1300083. [Google Scholar] [CrossRef]
- Simmons, M.P.; Ochoterena, H. Gaps as characters in sequence-based phylogenetic analyses. Syst. Boil. 2000, 49, 369–381. [Google Scholar] [CrossRef]
- Houde, P.; Braun, E.L.; Narula, N.; Minjares, U.; Mirarab, S. Phylogenetic Signal of Indels and the Neoavian Radiation. Diversity 2019, 11, 108. [Google Scholar] [CrossRef]
- Maddison, D.R.; Swofford, D.L.; Maddison, W.P.; Cannatella, D. Nexus: An Extensible File Format for Systematic Information. Syst. Boil. 1997, 46, 590–621. [Google Scholar] [CrossRef] [PubMed]
- GitHub—Smirarab/ASTRAL: Accurate Species TRee Algorithm. Available online: https://github.com/smirarab/ASTRAL (accessed on 21 February 2020).
- Mirarab, S.; Bayzid, M.S.; Boussau, B.; Warnow, T. Statistical binning enables an accurate coalescent-based estimation of the avian tree. Science 2014, 346, 1250463. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yu, L.; Edwards, S.V. A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Boil. 2010, 10, 302. [Google Scholar] [CrossRef]
- Avise, J.C.; Robinson, T. Hemiplasy: A New Term in the Lexicon of Phylogenetics. Syst. Boil. 2008, 57, 503–507. [Google Scholar] [CrossRef]
- Revell, L.J. phytools: An R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2011, 3, 217–223. [Google Scholar] [CrossRef]
- Cracraft, J.C. Avian higher-level relationships and classification: Nonpasseriforms. In The Howard and Moore Complete Checklist of the Birds of the World, 4th ed.; Dickinson, E.C., Remsen, J.V., Jr., Eds.; Aves Press: Northhampton, UK, 2013; Volume 1. [Google Scholar]
- Felsenstein, J. Cases in which Parsimony or Compatibility Methods will be Positively Misleading. Syst. Boil. 1978, 27, 401–410. [Google Scholar] [CrossRef]
- Morgan-Richards, M.; Trewick, S.A.; Bartosch-Härlid, A.; Kardailsky, O.; Phillips, M.J.; McLenachan, P.A.; Penny, D. Bird evolution: Testing the Metaves clade with six new mitochondrial genomes. BMC Evol. Boil. 2008, 8, 20. [Google Scholar] [CrossRef] [PubMed]
- Saurabh, K.; Holland, B.; Gibb, G.; Penny, D. Gaps: An Elusive Source of Phylogenetic Information. Syst. Boil. 2012, 61, 1075–1082. [Google Scholar] [CrossRef]
- Korlach, J.; Gedman, G.; Kingan, S.B.; Chin, C.-S.; Howard, J.T.; Audet, J.-N.; Cantin, L.; Jarvis, E.D. De novo PacBio long-read and phased avian genome assemblies correct and add to reference genes generated with intermediate and short reads. GigaScience 2017, 6, 1–16. [Google Scholar] [CrossRef]
- Swofford, D.L. PAUP*. Phylogenetic Analysis Using Parsimony (*and Other Methods); Sinauer Associates: Sunderland, MA, USA, 2003. [Google Scholar]
- Lloyd, G.T.; Davis, K.E.; Pisani, D.; Tarver, J.E.; Ruta, M.; Sakamoto, M.; Hone, D.W.E.; Jennings, R.; Benton, M.J. Dinosaurs and the cretaceous terrestrial revolution. Proc. Biol. Sci. 2008, 275, 2483–2490. [Google Scholar] [CrossRef] [PubMed]
- Barba-Montoya, J.; Dos Reis, M.; Schneider, H.; Donoghue, P.C.J.; Yang, Z. Constraining uncertainty in the timescale of angiosperm evolution and the veracity of a Cretaceous Terrestrial Revolution. New Phytol. 2018, 218, 819–834. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Rannala, B. Bayesian Estimation of Species Divergence Times Under a Molecular Clock Using Multiple Fossil Calibrations with Soft Bounds. Mol. Boil. Evol. 2005, 23, 212–226. [Google Scholar] [CrossRef] [PubMed]
- Rannala, B. Conceptual issues in Bayesian divergence time estimation. Philos. Trans. R. Soc. B Boil. Sci. 2016, 371, 20150134. [Google Scholar] [CrossRef]
- Ho, S.Y.W. The changing face of the molecular evolutionary clock. Trends Ecol. Evol. 2014, 29, 496–503. [Google Scholar] [CrossRef]
- Ronquist, F.; Lartillot, N.; Phillips, M.J. Closing the gap between rocks and clocks using total-evidence dating. Philos. Trans. R. Soc. B Boil. Sci. 2016, 371, 20150136. [Google Scholar] [CrossRef]
- Zhang, C.; Stadler, T.; Klopfstein, S.; Heath, T.A.; Ronquist, F. Total-Evidence Dating under the Fossilized Birth-Death Process. Syst. Boil. 2015, 65, 228–249. [Google Scholar] [CrossRef]
- Lee, M.S.; Cau, A.; Naish, D.; Dyke, G. Morphological Clocks in Paleontology, and a Mid-Cretaceous Origin of Crown Aves. Syst. Boil. 2014, 63, 442–449. [Google Scholar] [CrossRef]
- Arbogast, B.S.; Edwards, S.V.; Wakeley, J.; Beerli, P.; Slowinski, J.B. Estimating divergence times from molecular data on phylogenetic and population genetic timescales. Annu. Rev. Ecol. Syst. 2002, 33, 707–740. [Google Scholar] [CrossRef]
- Edwards, S.V.; Beerli, P. Perspective: Gene Divergence, Population Divergence, And the Variance in Coalescence Time in Phylogeographic Studies. Evolution 2000, 54, 1839–1854. [Google Scholar] [CrossRef]
- Mendes, F.K.; Hahn, M.W. Gene Tree Discordance Causes Apparent Substitution Rate Variation. Syst. Boil. 2016, 65, 711–721. [Google Scholar] [CrossRef] [PubMed]
- Ogilvie, H.A.; Bouckaert, R.R.; Drummond, A.J. Starbeast2 brings faster species tree inference and accurate estimates of substitution rates. Mol. Biol. Evol. 2017, 34, 2101–2114. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.V.; Cloutier, A.; Baker, A.J. Conserved nonexonic elements: A novel class of marker for phylogenomics. Syst. Biol. 2017, 66, 1028–1044. [Google Scholar] [CrossRef]
- Hill, W.G.; Robertson, A. The effect of linkage on limits to artificial selection. Genet. Res. 1966, 8, 269. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Inference of human population history from individual whole-genome sequences. Nature 2011, 475, 493–496. [Google Scholar] [CrossRef]
- Olson, S.L.; Parris, D.C. The Cretaceous Birds of New Jersey. Smithson. Contrib. Paleobiol. 1987, 63, 1–22. [Google Scholar] [CrossRef]
- Chen, A.; White, N.; Benson, R.B.J.; Braun, M.J.; Field, D.J. Total-Evidence Framework Reveals Complex Morphological Evolution in Nightbirds (Strisores). Diversity 2019, 11, 143. [Google Scholar] [CrossRef]
- Ksepka, D.; Clarke, J.A. Phylogenetically vetted and stratigraphically constrained fossil calibrations within Aves. Palaeontol. Electron. 2015. [Google Scholar] [CrossRef]
- Harmon, L.J.; Braude, S. Conservation of Small Populations: In An Introduction to Methods and Models in Ecology, Evolution, and Conservation Biology; JSTOR: New York, NY, USA, 2010; pp. 125–138. [Google Scholar]
- Ebersberger, I.; Galgoczy, P.; Taudien, S.; Taenzer, S.; Von Haeseler, A.; Platzer, M. Mapping Human Genetic Ancestry. Mol. Boil. Evol. 2007, 24, 2266–2276. [Google Scholar] [CrossRef]
- Hudson, R.R.; Coyne, J.A. Mathematical Consequences of the Genealogical Species Concept. Evolution 2002, 56, 1557–1565. [Google Scholar] [CrossRef]
- Springer, M.S.; Gatesy, J. The gene tree delusion. Mol. Phylogenet. Evol. 2016, 94, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Stiller, J.; Zhang, G. Comparative Phylogenomics, a Stepping Stone for Bird Biodiversity Studies. Diversity 2019, 11, 115. [Google Scholar] [CrossRef]
- Louca, S.; Pennell, M.W. Extant timetrees are consistent with a myriad of diversification histories. Nature 2020, 1–4. [Google Scholar] [CrossRef]
- Alvarez, L.W.; Asaro, F.; Michel, H.V.; Alvarez, W. Extraterrestrial Cause for the Cretaceous-Tertiary Extinction. Science 1980, 208, 1095–1108. [Google Scholar] [CrossRef]
- Schulte, P.; Alegret, L.; Arenillas, I.; Arz, J.A.; Barton, P.J.; Bown, P.R.; Bralower, T.J.; Christeson, G.L.; Claeys, P.; Cockell, C.S.; et al. The Chicxulub Asteroid Impact and Mass Extinction at the Cretaceous-Paleogene Boundary. Science 2010, 327, 1214–1218. [Google Scholar] [CrossRef]
- Mayr, G. The origins of crown group birds: Molecules and fossils. Palaeontology 2014, 57, 231–242. [Google Scholar] [CrossRef]
- Wright, S.J. Extinction-Mediated Competition: The Anolis Lizards and Insectivorous Birds of the West Indies. Am. Nat. 1981, 117, 181–192. [Google Scholar] [CrossRef]
- Buckley, L.B.; Jetz, W. Insularity and the determinants of lizard population density. Ecol. Lett. 2007, 10, 481–489. [Google Scholar] [CrossRef]
- Gattepaille, L.; Günther, T.; Jakobsson, M. Inferring Past Effective Population Size from Distributions of Coalescent Times. Genetics 2016, 204, 1191–1206. [Google Scholar] [CrossRef]
- Ho, S.Y.W.; Shapiro, B. Skyline-plot methods for estimating demographic history from nucleotide sequences. Mol. Ecol. Resour. 2011, 11, 423–434. [Google Scholar] [CrossRef]
- Schiffels, S.; Durbin, R. Inferring human population size and separation history from multiple genome sequences. Nat. Genet. 2014, 46, 919–925. [Google Scholar] [CrossRef] [PubMed]
- Sheehan, S.; Harris, K.; Song, Y.S. Estimating Variable Effective Population Sizes from Multiple Genomes: A Sequentially Markov Conditional Sampling Distribution Approach. Genetics 2013, 194, 647–662. [Google Scholar] [CrossRef] [PubMed]
- Barbato, M.; Orozco-Terwengel, P.; Tapio, M.; Bruford, M.W. SNeP: A tool to estimate trends in recent effective population size trajectories using genome-wide SNP data. Front. Genet. 2015, 6, 109. [Google Scholar] [CrossRef] [PubMed]
- Palacios, J.A.; Wakeley, J.; Ramachandran, S. Bayesian Nonparametric Inference of Population Size Changes from Sequential Genealogies. Genetics 2015, 201, 281–304. [Google Scholar] [CrossRef]
- Longrich, N.R.; Tokaryk, T.; Field, D.J. Mass extinction of birds at the Cretaceous–Paleogene (K–Pg) boundary. Proc. Natl. Acad. Sci. USA 2011, 108, 15253–15257. [Google Scholar] [CrossRef]
- Janzen, D.H. Who Survived the Cretaceous? Science 1995, 268, 785. [Google Scholar] [CrossRef]
- Rabosky, D.L.; Lovette, I.J. Explosive Evolutionary Radiations: Decreasing Speciation or Increasing Extinction Through Time? Evolution 2008, 62, 1866–1875. [Google Scholar] [CrossRef]
- Cracraft, J.; Claramunt, S. Conceptual and analytical worldviews shape differences about global avian biogeography. J. Biogeogr. 2017, 44, 958–960. [Google Scholar] [CrossRef]
- Wang, J. Estimation of effective population sizes from data on genetic markers. Philos. Trans. R. Soc. B Boil. Sci. 2005, 360, 1395–1409. [Google Scholar] [CrossRef]
- Charlesworth, B. Effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 2009, 10, 195–205. [Google Scholar] [CrossRef]
- Wang, J.; Santiago-Rubio, E.; Caballero, A. Prediction and estimation of effective population size. Heredity 2016, 117, 193–206. [Google Scholar] [CrossRef]
- Alò, D.; Turner, T.F. Effects of Habitat Fragmentation on Effective Population Size in the Endangered Rio Grande Silvery Minnow. Conserv. Boil. 2005, 19, 1138–1148. [Google Scholar] [CrossRef]
- Turner, T.F.; Osborne, M.J.; Moyer, G.R.; Benavides, M.A.; Alò, D. Life history and environmental variation interact to determine effective population to census size ratio. Proc. R. Soc. B Boil. Sci. 2006, 273, 3065–3073. [Google Scholar] [CrossRef]
- Nielsen, R.; Beaumont, M. Statistical inferences in phylogeography. Mol. Ecol. 2009, 18, 1034–1047. [Google Scholar] [CrossRef]
- Mazet, O.; Rodríguez, W.; Chikhi, L. Demographic inference using genetic data from a single individual: Separating population size variation from population structure. Theor. Popul. Boil. 2015, 104, 46–58. [Google Scholar] [CrossRef]
- Mazet, O.; Rodríguez, W.; Grusea, S.; Boitard, S.; Chikhi, L. On the importance of being structured: Instantaneous coalescence rates and human evolution—lessons for ancestral population size inference? Heredity 2015, 116, 362–371. [Google Scholar] [CrossRef]
- Moyer, G.R.; Winemeller, K.O.; McPhee, M.V.; Turner, T.F. Historical Demography, Selection, And Coalescence of Mitochondrial and Nuclear Genes in Prochilodus Species of Northern South America. Evolution 2005, 59, 599–610. [Google Scholar] [CrossRef]
- Khatri, B.; Burt, A. Robust Estimation of Recent Effective Population Size from Number of Independent Origins in Soft Sweeps. Mol. Boil. Evol. 2019, 36, 2040–2052. [Google Scholar] [CrossRef]
- Lessa, E.P.; Cook, J.A.; Patton, J.L. Genetic footprints of demographic expansion in North America, but not Amazonia, during the Late Quaternary. Proc. Natl. Acad. Sci. USA 2003, 100, 10331–10334. [Google Scholar] [CrossRef] [PubMed]
- Braasch, J.; Barker, B.S.; Dlugosch, K.M. Expansion history and environmental suitability shape effective population size in a plant invasion. Mol. Ecol. 2019, 28, 2546–2558. [Google Scholar] [CrossRef] [PubMed]
- Kraus, R.; Kerstens, H.H.D.; Van Hooft, P.; Megens, H.-J.; Elmberg, J.; Tsvey, A.; Sartakov, D.; Soloviev, S.; Crooijmans, R.P.M.A.; Groenen, M.; et al. Widespread horizontal genomic exchange does not erode species barriers among sympatric ducks. BMC Evol. Boil. 2012, 12, 45. [Google Scholar] [CrossRef] [PubMed]
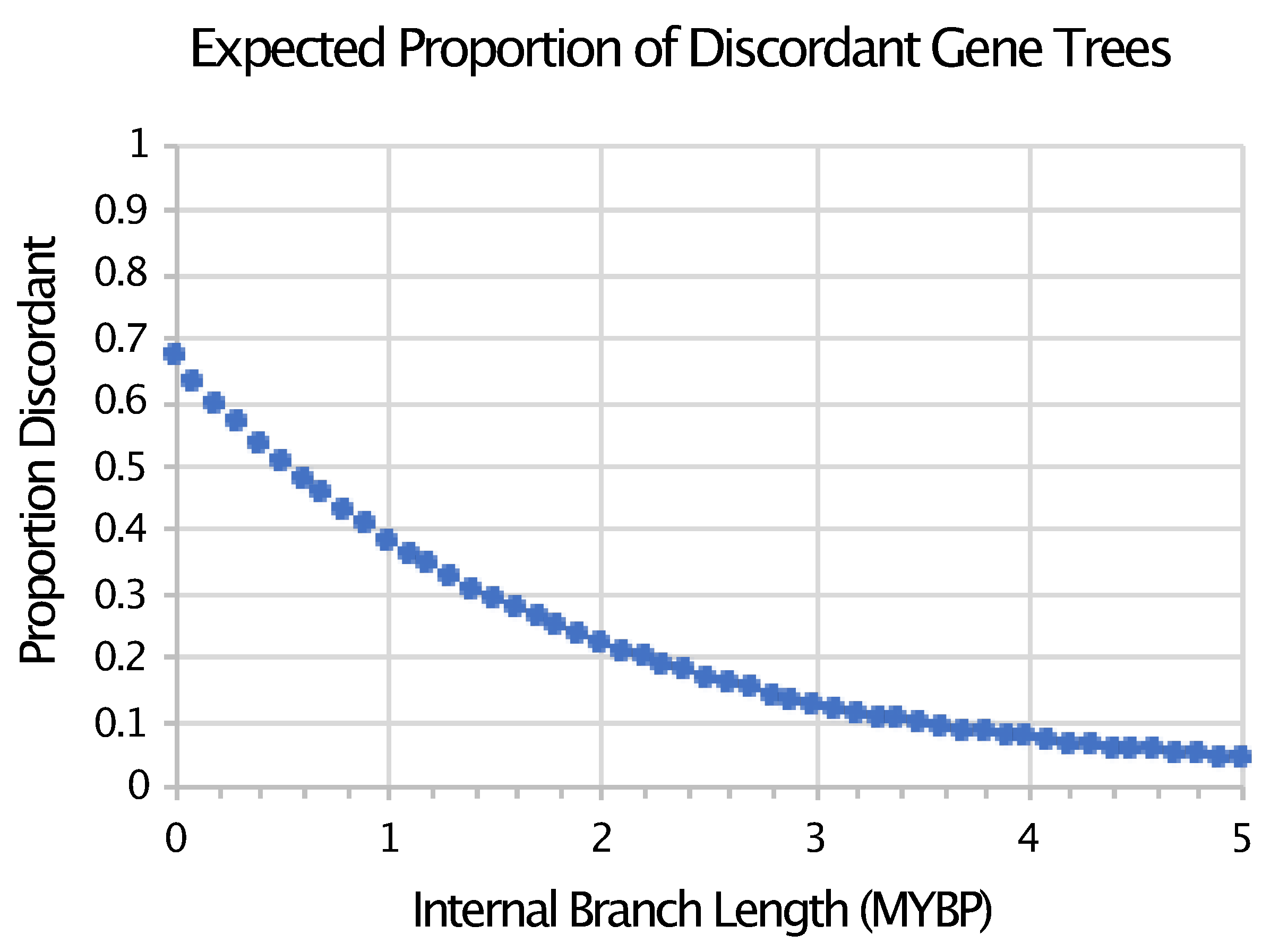

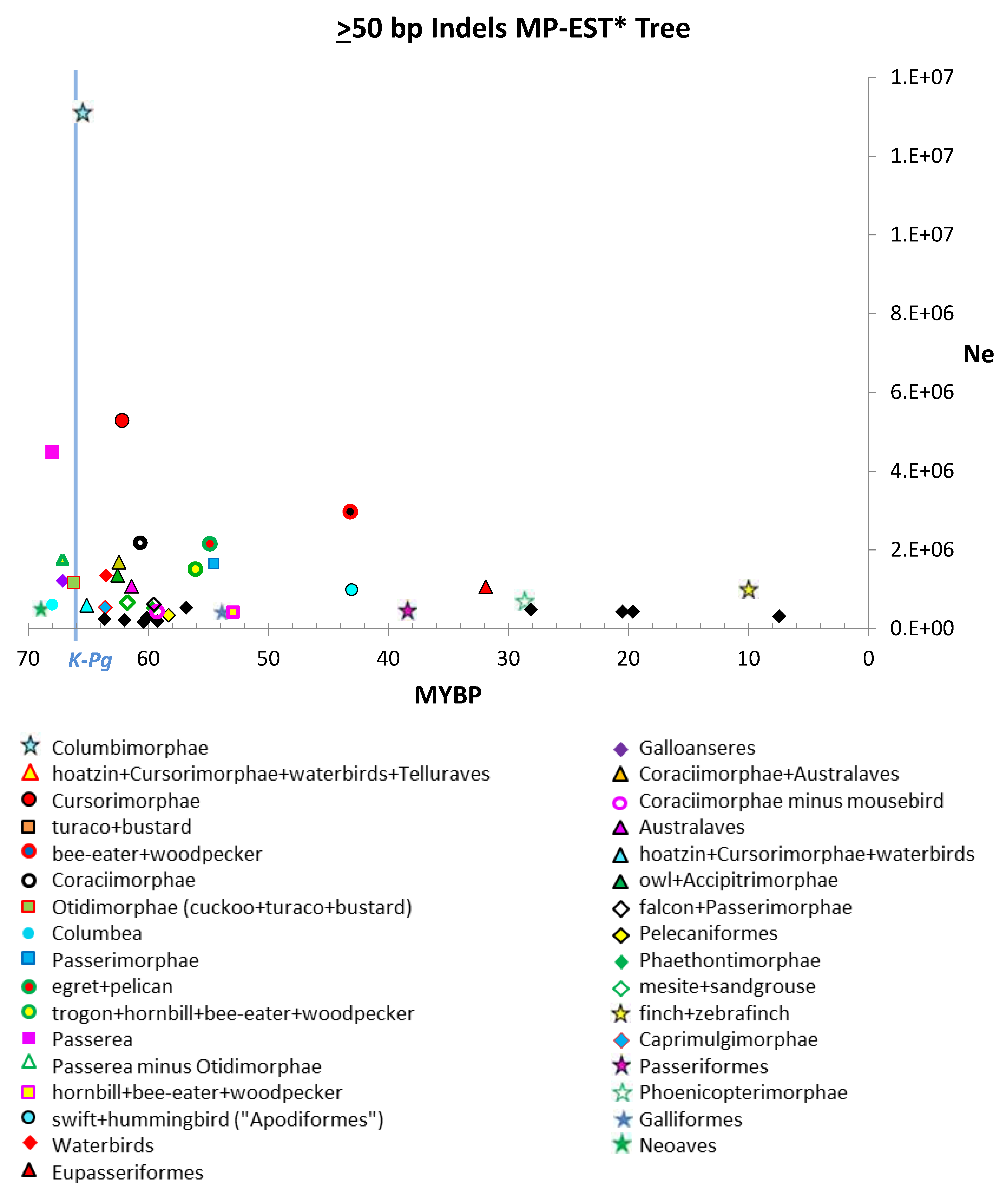
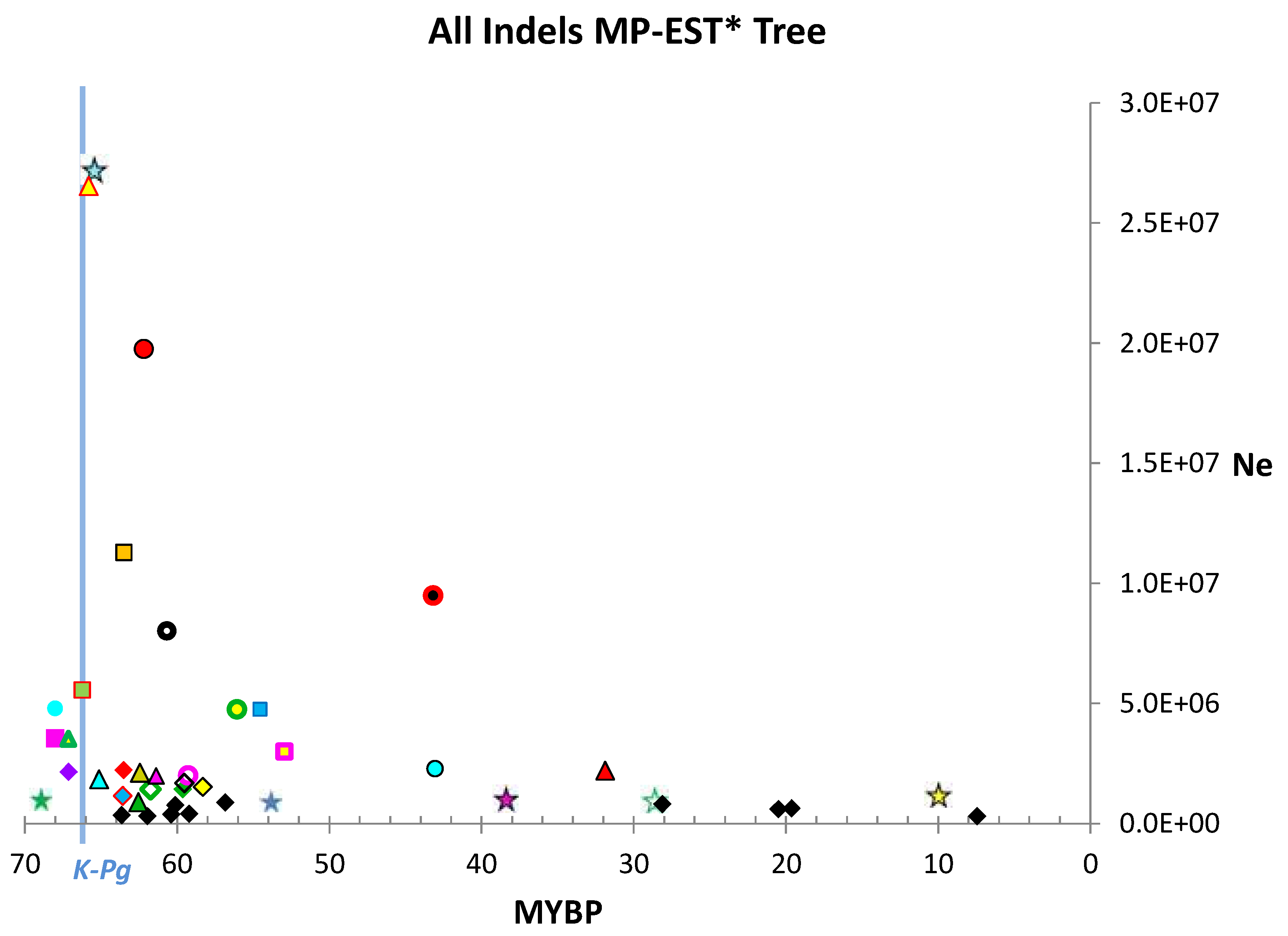
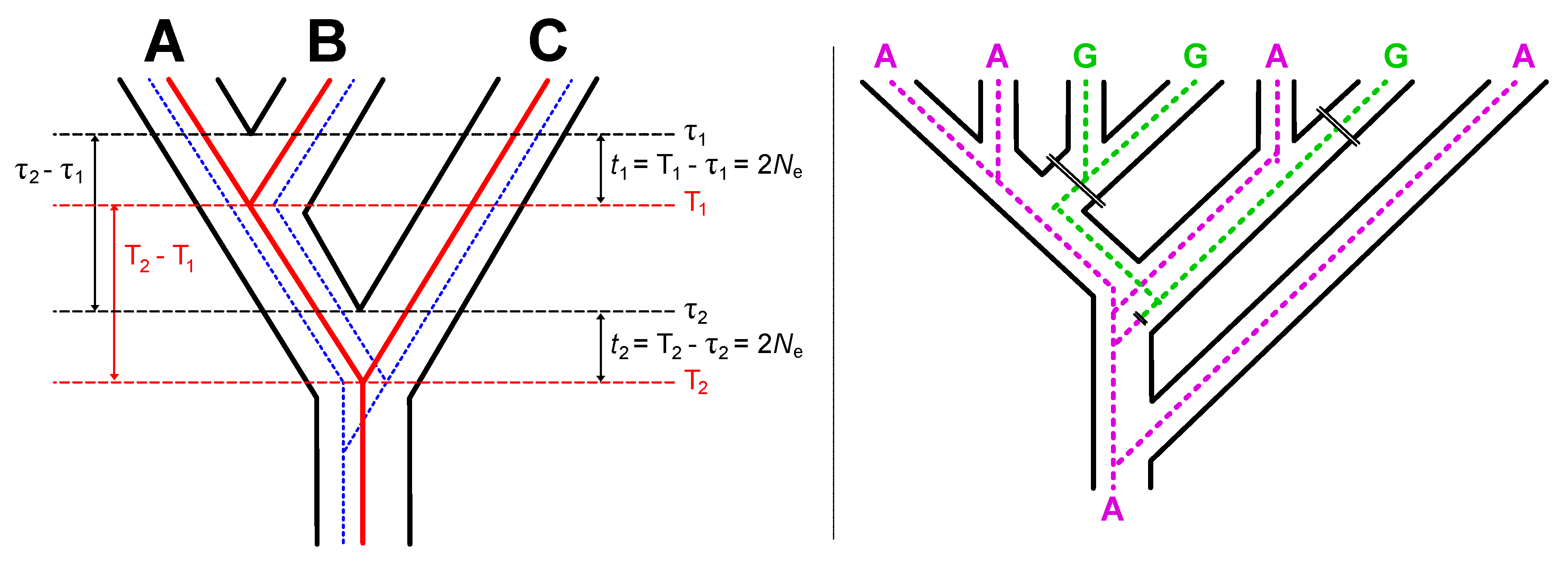
| Data Type 1 | MP-EST* | TENT |
|---|---|---|
| Indels | ||
| >100 bp indels | 0.8326 | 0.8323 |
| >50 bp indels | 0.807 | 0.8061 |
| >10 bp indels | 0.6703 | 0.6685 |
| >2 bp indels | 0.6129 | 0.6111 |
| all indels | 0.617 | 0.6152 |
| Gene trees | ||
| 1938 loci | ||
| nucleotides | 0.6300 | 0.6286 |
| unweighted indels | 0.5613 | 0.5592 |
| weighted indels | 0.5550 | 0.5528 |
| nucleotides + unweighted indels | 0.6274 | 0.6253 |
| nucleotides + weighted indels | 0.6248 | 0.6230 |
| 2515 loci | ||
| nucleotides | 0.6109 | 0.6091 |
| unweighted indels | 0.5476 | 0.5453 |
| nucleotides + unweighted indels | 0.6090 | 0.6063 |
| Indels | |||||
| ≥100 bp | ≥50 bp | ≥10 bp | ≥2 bp | all | |
| Median | 646,358 | 613,876 | 1,397,245 | 1,703,268 | 1,763,134 |
| Upper Quartile | 1,203,937 | 1,354,148 | 3,205,650 | 4,135,471 | 3,547,585 |
| Gene Trees | |||||
| 1938 loci | |||||
| nts | unwt indels | wt25 indels | nts + unwt indels | nts + wt25 indels | |
| Median | 421,623 | 992,529 | 1,034,323 | 406,267 | 447,136 |
| Upper Quartile | 1,262,357 | 2,293,435 | 2,480,454 | 1,107,612 | 1,139,726 |
| 2515 loci | |||||
| Median | 493,796 | 1,125,470 | — 1 | 499,080 | — 1 |
| Upper Quartile | 1,431,494 | 2,631,364 | — 1 | 1,244,437 | — 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Houde, P.; Braun, E.L.; Zhou, L. Deep-Time Demographic Inference Suggests Ecological Release as Driver of Neoavian Adaptive Radiation. Diversity 2020, 12, 164. https://doi.org/10.3390/d12040164
Houde P, Braun EL, Zhou L. Deep-Time Demographic Inference Suggests Ecological Release as Driver of Neoavian Adaptive Radiation. Diversity. 2020; 12(4):164. https://doi.org/10.3390/d12040164
Chicago/Turabian StyleHoude, Peter, Edward L. Braun, and Lawrence Zhou. 2020. "Deep-Time Demographic Inference Suggests Ecological Release as Driver of Neoavian Adaptive Radiation" Diversity 12, no. 4: 164. https://doi.org/10.3390/d12040164
APA StyleHoude, P., Braun, E. L., & Zhou, L. (2020). Deep-Time Demographic Inference Suggests Ecological Release as Driver of Neoavian Adaptive Radiation. Diversity, 12(4), 164. https://doi.org/10.3390/d12040164







