Structure–Property Relationships in Zwitterionic Pyridinium–Triazole Ligands: Insights from Crystal Engineering and Hirshfeld Surface Analysis
Abstract
1. Introduction
2. Results and Discussion
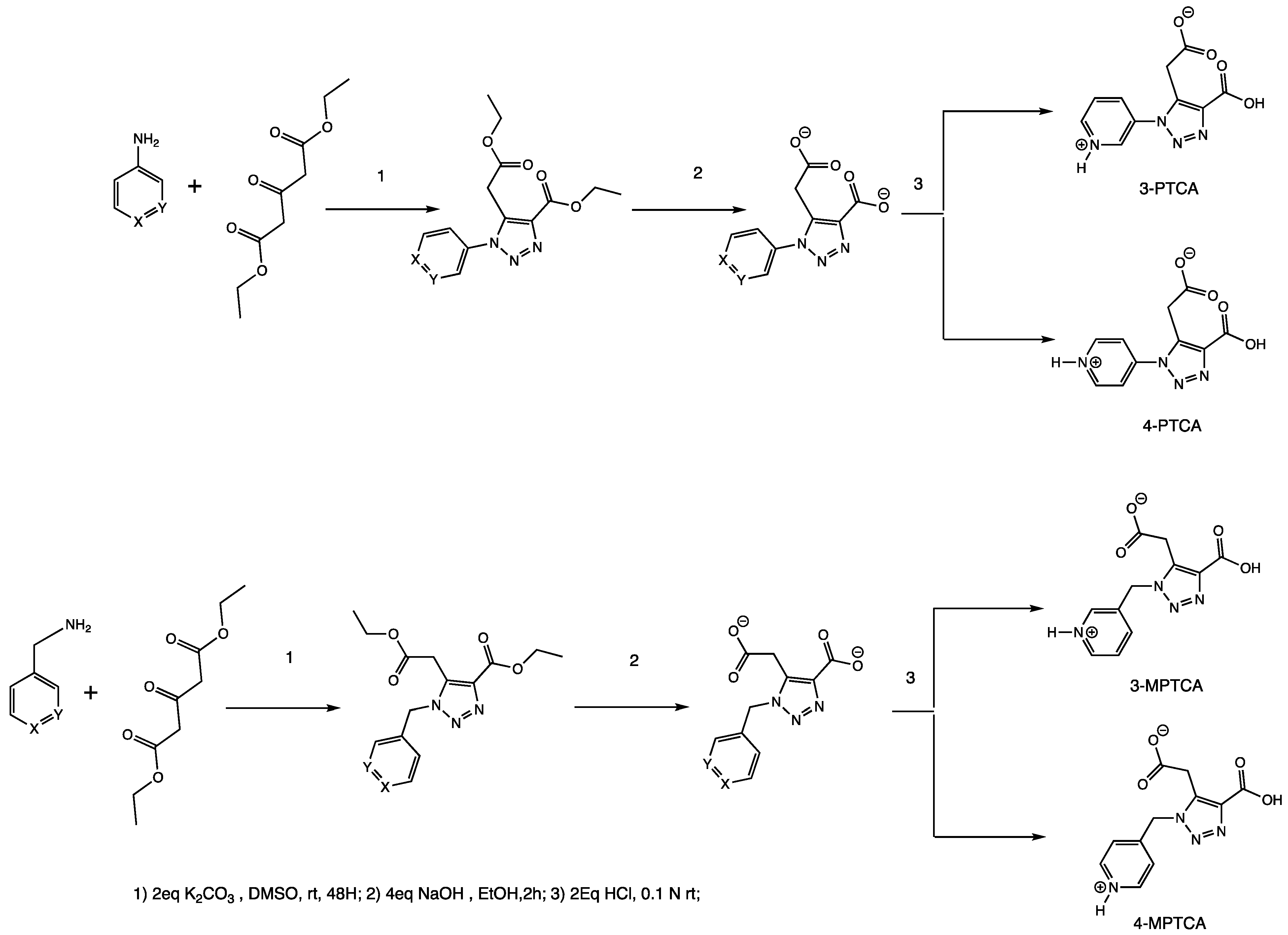
2.1. Syntheses
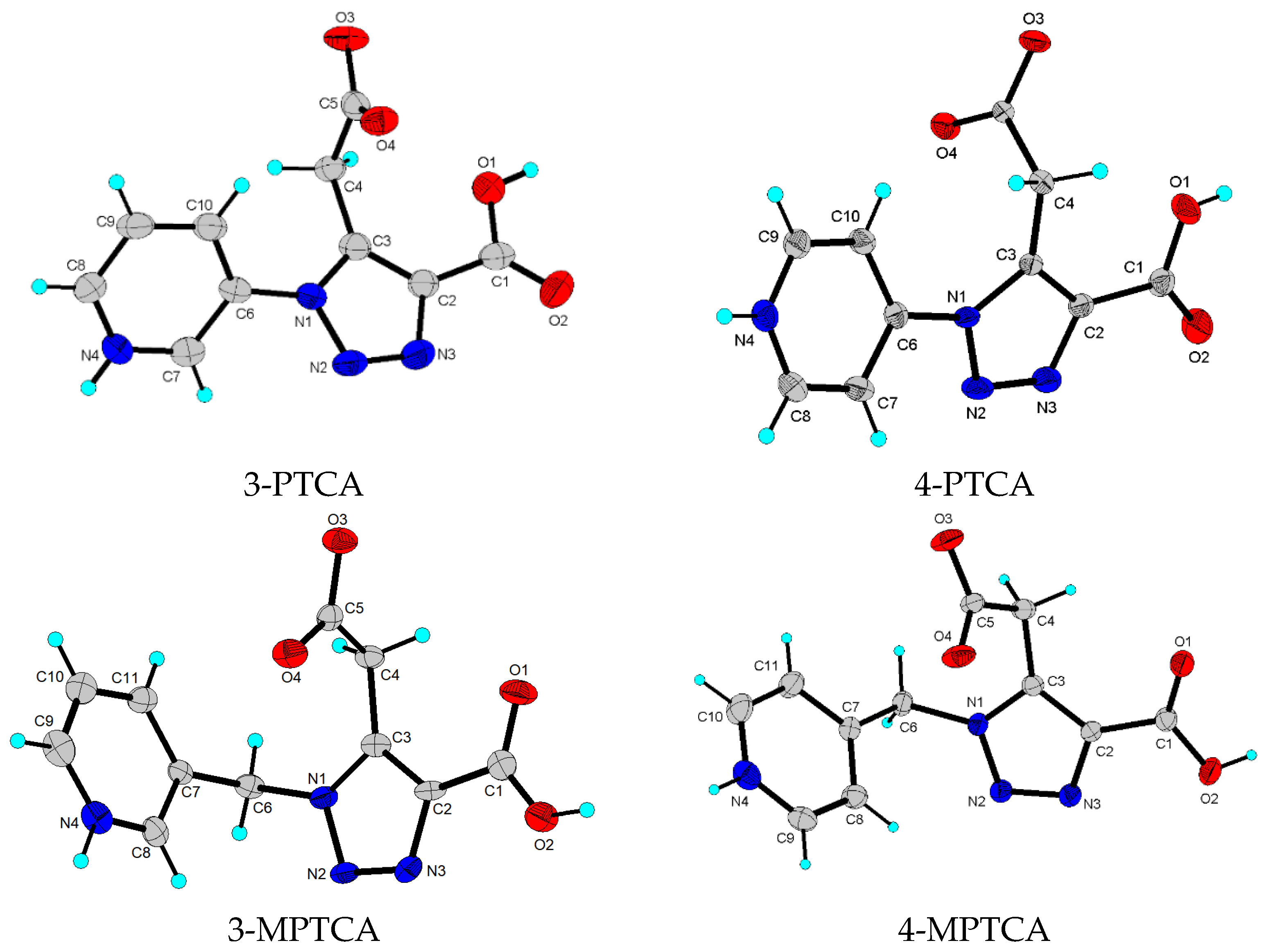
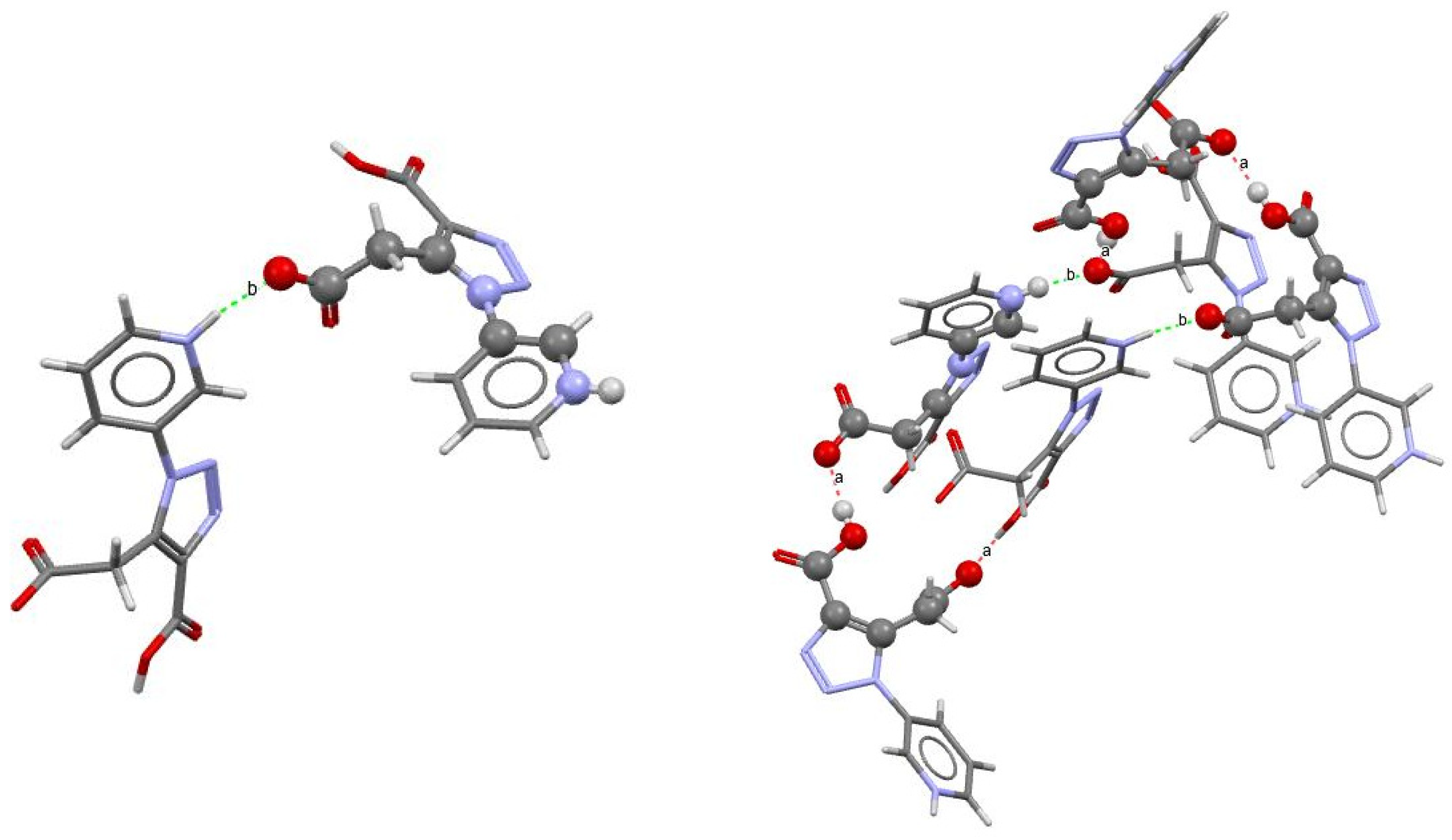
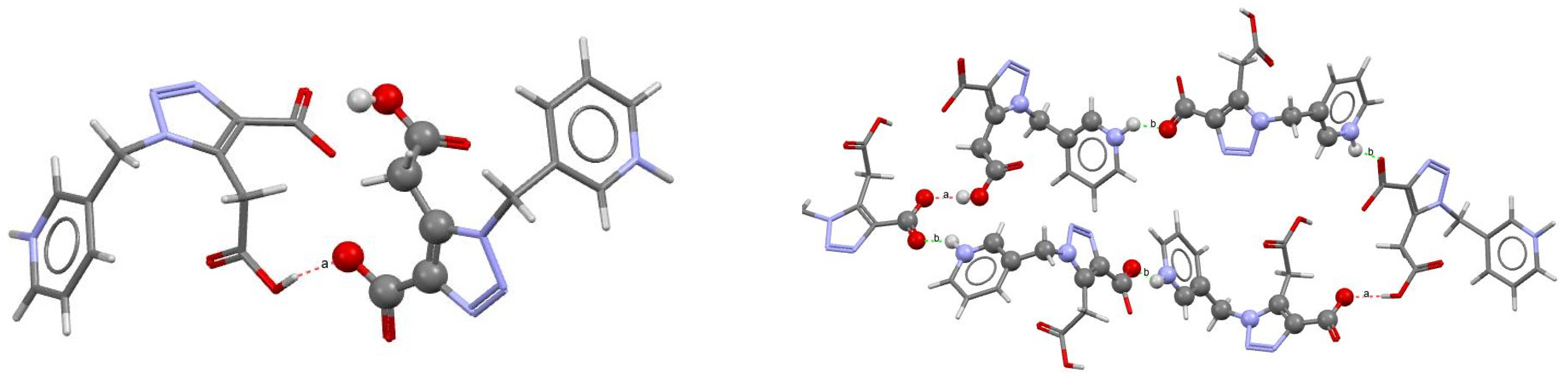
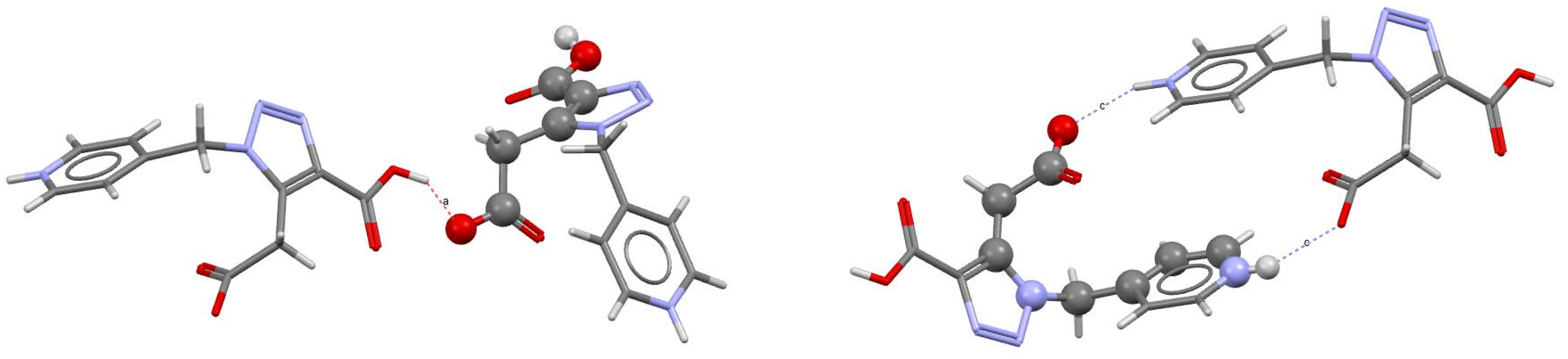
2.2. Crystal Structure
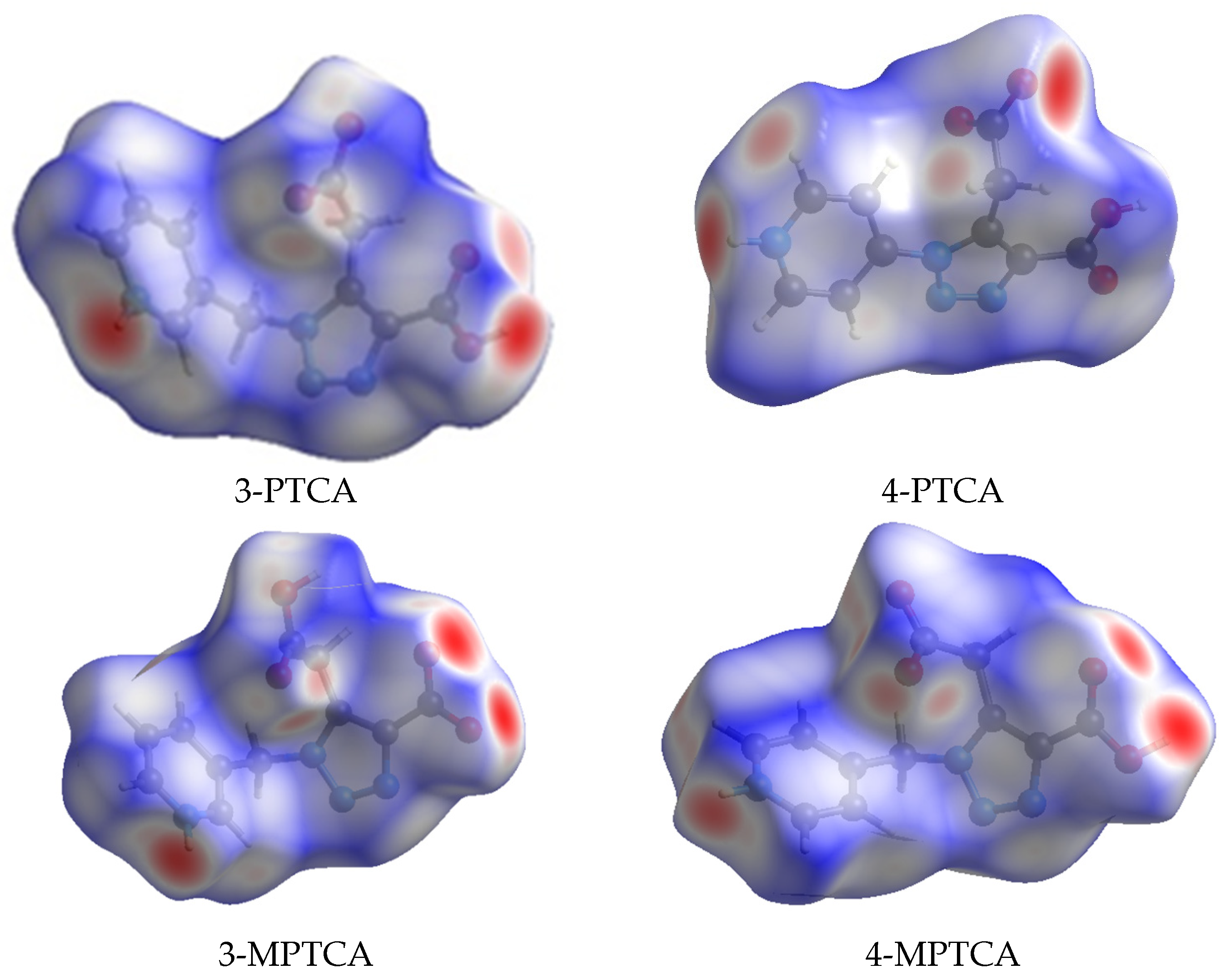
2.3. Hirshfeld Surface and Topological Studies
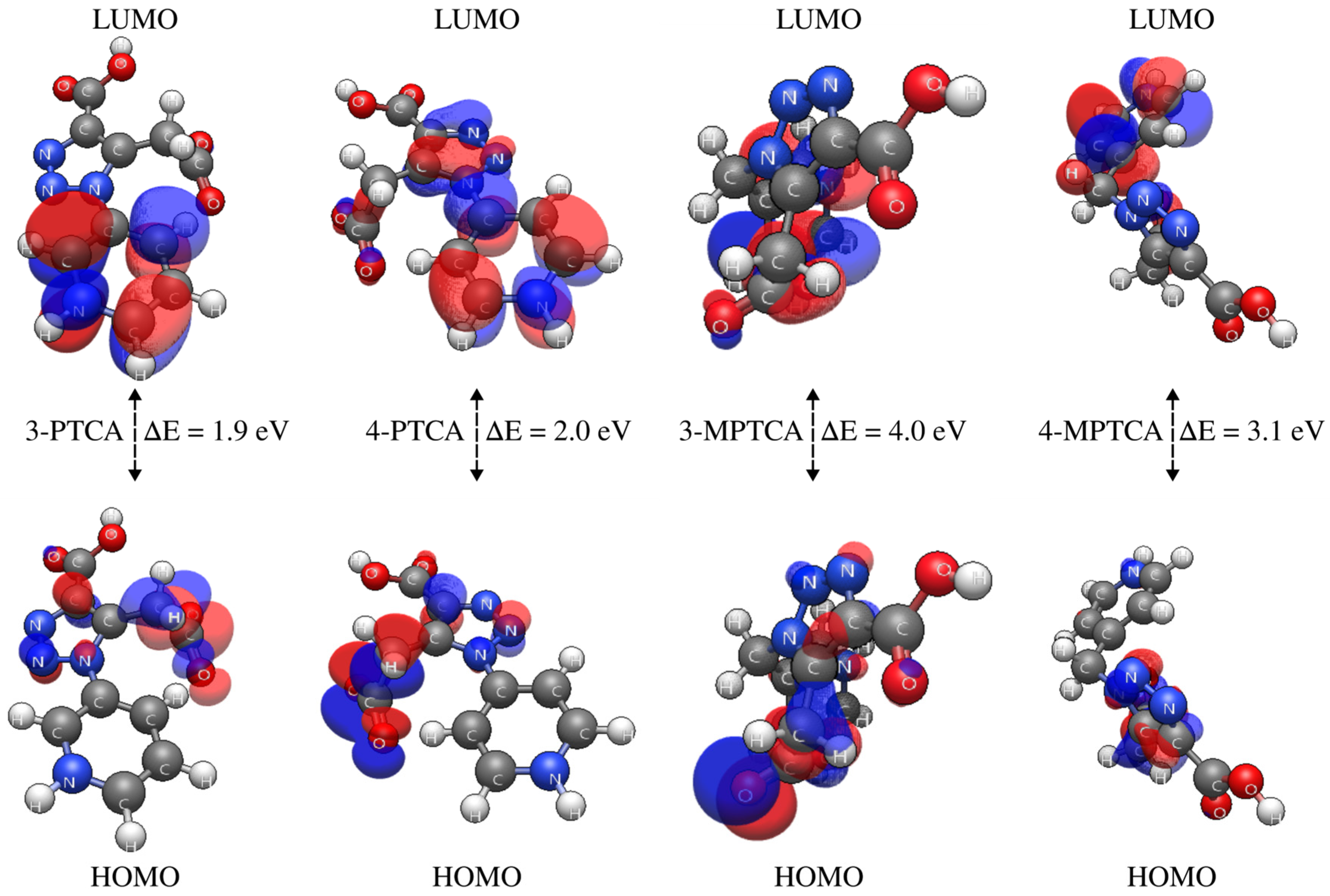
2.4. Density Functional Theory (DFT) Calculations
3. Materials and Methods
3.1. Chemicals
3.2. Characterization
3.3. Hirshfeld Surface and Topological Analysis
3.4. Density Functional Theory Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kanupriya; Mittal, R.K.; Sharma, V.; Biswas, T.; Mishra, I. Recent Advances in Nitrogen-Containing Heterocyclic Scaffolds as Antiviral Agents. Med. Chem. 2024, 20, 487–502. [Google Scholar] [CrossRef]
- Egbujor, M.C.; Tucci, P.; Onyeije, U.C.; Emeruwa, C.N.; Saso, L. NRF2 Activation by Nitrogen Heterocycles: A Review. Molecules 2023, 28, 2751. [Google Scholar] [CrossRef]
- Juríček, M.; Kouwer, P.H.J.; Rowan, A.E. Triazole: A Unique Building Block for the Construction of Functional Materials. Chem. Commun. 2011, 47, 8740. [Google Scholar] [CrossRef]
- Fantoni, N.Z.; El-Sagheer, A.H.; Brown, T. A Hitchhiker’s Guide to Click-Chemistry with Nucleic Acids. Chem. Rev. 2021, 121, 7122–7154. [Google Scholar] [CrossRef]
- Jankovič, D.; Virant, M.; Gazvoda, M. Copper-Catalyzed Azide–Alkyne Cycloaddition of Hydrazoic Acid Formed In Situ from Sodium Azide Affords 4-Monosubstituted-1,2,3-Triazoles. J. Org. Chem. 2022, 87, 4018–4028. [Google Scholar] [CrossRef]
- Esposito, M.R.; Newar, R.; Kim, M.; Cohen, S.M. Incorporation of Low-Valent Metal Ions in Metal-Organic Frameworks and Coordination Polymers. Coord. Chem. Rev. 2025, 531, 216491. [Google Scholar] [CrossRef]
- Naik, A.D.; Dîrtu, M.M.; Railliet, A.P.; Marchand-Brynaert, J.; Garcia, Y. Coordination Polymers and Metal Organic Frameworks Derived from 1,2,4-Triazole Amino Acid Linkers. Polymers 2011, 3, 1750–1775. [Google Scholar] [CrossRef]
- Narea, P.; Cisterna, J.; Cárdenas, A.; Amo-Ochoa, P.; Zamora, F.; Climent, C.; Alemany, P.; Conejeros, S.; Llanos, J.; Brito, I. Crystallization Induced Enhanced Emission in Two New Zn(II) and Cd(II) Supramolecular Coordination Complexes with the 1-(3,4-Dimethylphenyl)-5-Methyl-1H-1,2,3-Triazole-4-Carboxylate Ligand. Polymers 2020, 12, 1756. [Google Scholar] [CrossRef]
- Bezerra Morais, P.A.; Javarini, C.L.; Valim, T.C.; Francisco, C.S.; de Freitas Ferreira, L.C.; Trancoso Bottocim, R.R.; Neto, Á.C.; Júnior, V.L. Triazole: A New Perspective in Medicinal Chemistry and Material Science. Curr. Org. Chem. 2022, 26, 1691–1702. [Google Scholar] [CrossRef]
- Kantheti, S.; Narayan, R.; Raju, K.V.S.N. The Impact of 1,2,3-Triazoles in the Design of Functional Coatings. RSC Adv. 2015, 5, 3687–3708. [Google Scholar] [CrossRef]
- Sehrawat, R.; Vashishth, P.; Bairagi, H.; Shukla, S.K.; Kumar, H.; Ji, G.; Mangla, B. Coordination Bonding and Corrosion Inhibition Characteristics of Chalcone Compounds for Metals: An Inclusive Review Based on Experimental as Well as Theoretical Perspectives. Coord. Chem. Rev. 2024, 514, 215820. [Google Scholar] [CrossRef]
- Sun, J.-K.; Zhang, J. Functional Metal–Bipyridinium Frameworks: Self-Assembly and Applications. Dalton Trans. 2015, 44, 19041–19055. [Google Scholar] [CrossRef]
- Huang, Y.; Cohen, T.A.; Sperry, B.M.; Larson, H.; Nguyen, H.A.; Homer, M.K.; Dou, F.Y.; Jacoby, L.M.; Cossairt, B.M.; Gamelin, D.R.; et al. Organic Building Blocks at Inorganic Nanomaterial Interfaces. Mater. Horiz. 2022, 9, 61–87. [Google Scholar] [CrossRef]
- Cameron, J.M.; Guillemot, G.; Galambos, T.; Amin, S.S.; Hampson, E.; Mall Haidaraly, K.; Newton, G.N.; Izzet, G. Supramolecular Assemblies of Organo-Functionalised Hybrid Polyoxometalates: From Functional Building Blocks to Hierarchical Nanomaterials. Chem. Soc. Rev. 2022, 51, 293–328. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Zhao, L.; Zhang, Y.; Li, Z.-T.; Huang, F. Multiple Hydrogen Bonding Driven Supramolecular Architectures and Their Biomedical Applications. Chem. Soc. Rev. 2024, 53, 1592–1623. [Google Scholar] [CrossRef]
- Rehm, T.H.; Schmuck, C. Ion-Pair Induced Self-Assembly in Aqueous Solvents. Chem. Soc. Rev. 2010, 39, 3597. [Google Scholar] [CrossRef]
- Miao, Z.; Zhou, J. Multiscale Modeling and Simulation of Zwitterionic Anti-Fouling Materials. Langmuir 2025, 41, 7980–7995. [Google Scholar] [CrossRef]
- Anthony, A.; Desiraju, G.R.; Jetti, R.K.R.; Kuduva, S.S.; Madhavi, N.N.L.; Nangia, A.; Thaimattam, R.; Thalladi, V.R. Crystal Engineering: Some Further Strategies. Cryst. Eng. 1998, 1, 1–18. [Google Scholar] [CrossRef]
- Disa, A.S.; Nova, T.F.; Cavalleri, A. Engineering Crystal Structures with Light. Nat. Phys. 2021, 17, 1087–1092. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, L.; Liu, C.; Li, Z.; Zou, Y.; Zhang, X.; Zhang, Y.; Zhang, Z.; Wei, G.; Yu, C. Crystal Engineering Enables Cobalt-Based Metal–Organic Frameworks as High-Performance Electrocatalysts for H 2 O 2 Production. J. Am. Chem. Soc. 2023, 145, 7791–7799. [Google Scholar] [CrossRef]
- Yuan, Y.; Patel, R.K.; Banik, S.; Reta, T.B.; Bisht, R.S.; Fong, D.D.; Sankaranarayanan, S.K.R.S.; Ramanathan, S. Proton Conducting Neuromorphic Materials and Devices. Chem. Rev. 2024, 124, 9733–9784. [Google Scholar] [CrossRef]
- Mukherjee, D.; Saha, A.; Moni, S.; Volkmer, D.; Das, M.C. Anhydrous Solid-State Proton Conduction in Crystalline MOFs, COFs, HOFs, and POMs. J. Am. Chem. Soc. 2025, 147, 5515–5553. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, N.; Lei, L.; Yu, C.; Ding, J.; Li, P.; Chen, J.; Li, M.; Ling, S.; Zhuang, X.; et al. Supramolecular Proton Conductors Self-Assembled by Organic Cages. JACS Au 2022, 2, 819–826. [Google Scholar] [CrossRef]
- Shi, C.-Y.; Qin, W.-Y.; Qu, D.-H. Semi-Crystalline Polymers with Supramolecular Synergistic Interactions: From Mechanical Toughening to Dynamic Smart Materials. Chem. Sci. 2024, 15, 8295–8310. [Google Scholar] [CrossRef]
- Lugger, S.J.D.; Houben, S.J.A.; Foelen, Y.; Debije, M.G.; Schenning, A.P.H.J.; Mulder, D.J. Hydrogen-Bonded Supramolecular Liquid Crystal Polymers: Smart Materials with Stimuli-Responsive, Self-Healing, and Recyclable Properties. Chem. Rev. 2022, 122, 4946–4975. [Google Scholar] [CrossRef]
- Ying, Y.P.; Kamarudin, S.K.; Masdar, M.S. Silica-Related Membranes in Fuel Cell Applications: An Overview. Int. J. Hydrogen Energy 2018, 43, 16068–16084. [Google Scholar] [CrossRef]
- Chu, D.; Huang, C.-C.; Tsen, W.-C.; Gong, C. Biomass Composite Proton Exchange Membranes with High Mechanical Strength and Proton Conductivity Based on Chitosan and Zwitterion-Modified Palygorskite. Appl. Clay Sci. 2024, 253, 107367. [Google Scholar] [CrossRef]
- Chen, L.; Ren, Y.; Fan, F.; Wu, T.; Wang, Z.; Zhang, Y.; Zhao, J.; Cui, G. Artificial Frameworks towards Ion-Channel Construction in Proton Exchange Membranes. J. Power Sources 2023, 574, 233081. [Google Scholar] [CrossRef]
- Li, Q.; Wen, C.; Yang, J.; Zhou, X.; Zhu, Y.; Zheng, J.; Cheng, G.; Bai, J.; Xu, T.; Ji, J.; et al. Zwitterionic Biomaterials. Chem. Rev. 2022, 122, 17073–17154. [Google Scholar] [CrossRef]
- Qu, K.; Yuan, Z.; Wang, Y.; Song, Z.; Gong, X.; Zhao, Y.; Mu, Q.; Zhan, Q.; Xu, W.; Wang, L. Structures, Properties, and Applications of Zwitterionic Polymers. ChemPhysMater 2022, 1, 294–309. [Google Scholar] [CrossRef]
- He, G.; Li, Z.; Li, Y.; Li, Z.; Wu, H.; Yang, X.; Jiang, Z. Zwitterionic Microcapsules as Water Reservoirs and Proton Carriers within a Nafion Membrane To Confer High Proton Conductivity under Low Humidity. ACS Appl. Mater. Interfaces 2014, 6, 5362–5366. [Google Scholar] [CrossRef] [PubMed]
- Doobi, F.A.; Mir, F.Q. Exploring the Development of Natural Biopolymer (Chitosan)-Based Proton Exchange Membranes for Fuel Cells: A Review. Results Surf. Interfaces 2024, 15, 100218. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next Generation of Proton-Exchange Membrane Fuel Cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Nagao, Y. Proton-Conducting Polymers: Key to Next-Generation Fuel Cells, Electrolyzers, Batteries, Actuators, and Sensors. ChemElectroChem 2024, 11, e202300846. [Google Scholar] [CrossRef]
- Narea, P.; Hernández, B.; Cisterna, J.; Cárdenas, A.; Llanos, J.; Amo-Ochoa, P.; Zamora, F.; Priego, J.L.; Cortijo, M.; Delgado, G.E.; et al. Heterobimetallic Three-Dimensional 4d-4f Coordination Polymers Based on 5-Methyl-1-(Pyridyn-4-Ylmethyl)-1H-1,2,3-Triazole-3,4-Dicarboxylate. J. Solid. State Chem. 2022, 310, 123027. [Google Scholar] [CrossRef]
- Hernández, B.; Narea, P.; Espinoza, D.; Navarrete, A.; Aguirre, G.; Delgado, G.E.; Cárdenas, A.; Brito, I.; Cisterna, J. Novel Zn(II) and Cd(II) Coordination Polymers Derived from 1,2,3-Triazole-1,3-Diketone Ligand. Syntheses and Structural, Thermal, Computational, and Luminescent Studies. J. Solid. State Chem. 2022, 312, 123156. [Google Scholar] [CrossRef]
- Kamalraj, V.R.; Senthil, S.; Kannan, P. One-Pot Synthesis and the Fluorescent Behavior of 4-Acetyl-5-Methyl-1,2,3-Triazole Regioisomers. J. Mol. Struct. 2008, 892, 210–215. [Google Scholar] [CrossRef]
- Cisterna, J.; Araneda, C.; Narea, P.; Cárdenas, A.; Llanos, J.; Brito, I. The Positional Isomeric Effect on the Structural Diversity of Cd(II) Coordination Polymers, Using Flexible Positional Isomeric Ligands Containing Pyridyl, Triazole, and Carboxylate Fragments. Molecules 2018, 23, 2634. [Google Scholar] [CrossRef]
- Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of Bond Lengths Determined by X-Ray and Neutron-Diffraction. 1. Bond Lengths in Organic-Compounds. J. Chem. Soc. Perkin Trans. 1987, 2, S1–S19. [Google Scholar] [CrossRef]
- Groom, C.R.; Allen, F.H. The Cambridge Structural Database in Retrospect and Prospect. Angew. Chem. Int. Ed. 2014, 53, 662–671. [Google Scholar] [CrossRef]
- Etter, M.C.; MacDonald, J.C.; Bernstein, J. Graph-Set Analysis of Hydrogen-Bond Patterns in Organic Crystals. Acta Crystallogr. B 1990, 46, 256–262. [Google Scholar] [CrossRef] [PubMed]
- Fábián, L.; Kálmán, A. Volumetric Measure of Isostructurality. Acta Crystallogr. B 1999, 55, 1099–1108. [Google Scholar] [CrossRef]
- Wolff, S.K.; Grimwood, D.J.; McKinnon, J.J.; Turner, M.J.; Jayatilaka, D.; Spackman, M.A. Crystal Explorer, version 17.5; Crystal Explorer 17.5; The University of Western Australia: Perth, Australia, 2012. [Google Scholar]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld Surface Analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting Intermolecular Interactions in Molecular Crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer Model Energies and Energy Frameworks: Extension to Metal Coordination Compounds, Organic Salts, Solvates and Open-Shell Systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef] [PubMed]
- Bruker AXS INC. APEX4 Package. APEX4, SAINT and SADABS; Bruker AXS INC: Madison, WI, USA, 2020. [Google Scholar]
- Sheldrick, G.M. SADABS, Software for Empirical Absorption Correction; University of Göttingen: Göttingen, Germany, 2000. [Google Scholar]
- Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Spek, A.L. Single-Crystal Structure Validation with the Program. PLATON J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A Program for Hirshfeld Surface Analysis, Visualization and Quantitative Analysis of Molecular Crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Bondi, A. Van Der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Batsanov, S.S. Van Der Waals Radii of Elements. Inorg. Mater. Transl. Neorg. Mater. Orig. Russ. Text. 2001, 37, 871–885. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J.; Jayatilaka, D. Electrostatic Potentials Mapped on Hirshfeld Surfaces Provide Direct Insight into Intermolecular Interactions in Crystals. CrystEngComm 2008, 10, 377–388. [Google Scholar] [CrossRef]
- Jayatilaka, D.; Grimwood, D.J. Tonto: A Fortran Based Object-Oriented System for Quantum Chemistry and Crystallography. In Proceedings of the Computational Science—ICCS 2003, Melbourne, Australia, 2–4 June 2003; pp. 142–151. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef]
- Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied Topological Analysis of Crystal Structures with the Program Package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Peskov, M.A.; Ramsden, S.J.; Yaghi, O.M. The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets. Acc. Chem. Res. 2008, 41, 1782–1789. [Google Scholar] [CrossRef]
- Alexandrov, E.V.; Blatov, V.A.; Kochetkov, A.V.; Proserpio, D.M. Underlying Nets in Three-Periodic Coordination Polymers: Topology, Taxonomy and Prediction from a Computer-Aided Analysis of the Cambridge Structural Database. CrystEngComm 2011, 13, 3947. [Google Scholar] [CrossRef]
- Shevchenko, A.P.; Blatov, V.A. Simplify to Understand: How to Elucidate Crystal Structures? Struct. Chem. 2021, 32, 507–519. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]

| 3-PTCA | 4-PTCA | |
| CCDC number | 2317647 | 2317648 |
| Empirical formula | C10H8N4O4 | C10H8N4O4 |
| Formula weight | 248.20 | 248.20 |
| Temperature/K | 297 | 297 |
| Crystal system | orthorhombic | orthorhombic |
| Space group | Pna21 (No 33) | Pna21 (No 33) |
| a/Å | 12.0311(14) | 13.962(5) |
| b/Å | 17.673(2) | 17.017(6) |
| c/Å | 5.0309(4) | 4.4663(17) |
| Volume/Å3 | 1069.7(2) | 1061.2(7) |
| Z’ | 1 | 1 |
| Z | 4 | 4 |
| ρcalcg/cm3 | 1.541 | 1.554 |
| μ/mm−1 | 1.052 | 0.124 |
| F (000) | 512 | 512 |
| Crystal size/mm3 | 0.11 × 0.21 × 0.30 | 0.15 × 0.20 × 0.38 |
| Radiation | CuKα (λ = 1.54178) | MoKα (λ = 0.71073) |
| 2Θ range for data collection/° | 4.4 to 59.2 | 2.8 to 26.5 |
| Index ranges | −10 ≤ h ≤ 13, −17 ≤ k ≤ 19, −5 ≤ l ≤ 5 | −17 ≤ h ≤ 17, −20 ≤ k ≤ 21, −5 ≤ l ≤ 5 |
| Reflections collected | 11,775 | 7489 |
| Independent reflections | 1462 [Rint = 0.177] | 1916 [Rint = 0.047] |
| Data/restraints/parameters | 1462/0/166 | 1916/0/165 |
| Goodness-of-fit on F2 | 1.00 | 1.30 |
| Flack parameter (x) | 0.6(1) | 0(3) |
| Final R indexes [all data] | R1 = 0.0693, wR2 = 0.1904 | R1 = 0.0432, wR2 = 0.1719 |
| Largest diff. peak/hole/e Å−3 | 0.25/-0.25 | 0.68/−0.65 |
| 3-MPTCA | 4-MPTCA | |
| CCDC number | 2317645 | 2317646 |
| Empirical formula | C11H10N4O4 | C11H10N4O4 |
| Formula weight | 262.23 | 262.23 |
| Temperature/K | 297 | 297 |
| Crystal system | orthorhombic | monoclinic |
| Space group | P212121 (No 19) | P21/c (No 14) |
| a/Å | 4.748(12) | 4.9510(7) |
| b/Å | 12.88(4) | 19.019(3) |
| c/Å | 18.02(5) | 11.9930(16) |
| β/° | - | 93.526(7) |
| Volume/Å3 | 1102(5) | 1127.2(3) |
| Z’ | 1 | 1 |
| Z | 4 | 4 |
| ρcalcg/cm3 | 1.581 | 1.545 |
| μ/mm−1 | 0.124 | 1.030 |
| F(000) | 544 | 544 |
| Crystal size/mm3 | 0.18 × 0.08 × 0.07 | 0.19 × 0.06 × 0.05 |
| Radiation | MoKα (λ = 0.71073) | MoKα (λ = 0.71073) |
| 2Θ range for data collection/° | 2.8 to 25.0 | 4.4 to 6.4 |
| Index ranges | −5 ≤ h ≤ 3, −15 ≤ k ≤ 15, −21 ≤ l ≤ 21 | −5 ≤ h ≤ 5, −22 ≤ k ≤ 19, −14 ≤ l ≤ 14 |
| Reflections collected | 6439 | 13612 |
| Independent reflections | 1902 [Rint = 0.211] | 1921 [Rint = 0.315] |
| Data/restraints/parameters | 1902/0/174 | 1921/0/173 |
| Goodness-of-fit on F2 | 0.97 | 1.07 |
| Final R indexes [all data] | R1 = 0.0712, wR2 = 0.1830 | R1 = 0.0554, wR2 = 0.1139 |
| Largest diff. peak/hole/e Å−3 | 0.24/−0.29 | 0.33/−0.25 |
| 3-PTCA | 4-PTCA | |
| C3-N1-C6-C10 | −44 (2) | 26.7 (8) |
| C3-C4-C5-O4 | −1.4 (1) | 26.7 (6) |
| C3-C2-C1-O1 | −7 (2) | −2.0 (8) |
| 3-MPTCA | 4-MPTCA | |
| N1-C6-C7-C8 | −66 (1) | −39.8 (3) |
| C3-C2-C1-O1 | −4.0 (2) | 4.6 (3) |
| C3-C4-C5-O4 | −17 (1) | −19.4 (3) |
| Sample | D−H∙∙∙A * | Symmetry Code | D∙∙∙A (Å) | D−H∙∙∙A (°) |
|---|---|---|---|---|
| 3-PTCA | O1−H1∙∙∙O3 | [1 − x, 1 − y, −1/2 + z] | 2.519 (12) | 173 |
| N4−H4∙∙∙O3 | [−1/2 + x, 1/2 − y, 1 + z] | 2.565 (13) | 170 | |
| H1∙∙ O3-C5 | [1 − x,1 − y, 1/2 + z] | 2.519 (12) | 173 | |
| H4∙∙∙O3−C5 | [1/2 + x, 1/2 − y, −1 + z] | 2.565 (13) | 170 | |
| 4-PTCA | O1−H1∙∙∙O3 | [−x, −y, 1/2 + z] | 2.551 (5) | 162 |
| N4−H4∙∙∙O3 | [1/2 + x, −1/2 − y,1 + z] | 2.640 (6) | 179 | |
| H1∙∙∙O3−C5 | [−x, −y, 1/2 + z] | 2.551 (5) | 163 | |
| H4∙∙∙O3−C5 | [−1/2 + x, −1/2 − y, −1 + z] | 2.640 (6) | 179 | |
| 3-MPTCA | O3−H3∙∙∙O1 | [−1/2 + x, 1/2 − y, 1 − z] | 2.434 (9) | 165 |
| N4−H4∙∙∙O2 | [3/2 − x, 1 − y, −1/2 + z] | 2.628 (15) | 145 | |
| 4-MPTCA | O2−H2∙∙∙O3 | [1 + x, 1/2 − y, ½ − z] | 2.450 (3) | 133 |
| N4−H4∙∙∙O1 | [1 − x, 1/2 + y, ½ − z] | 2.757 (3) | 142 | |
| (N)H∙∙∙O1−C1 | [1 − x, −1/2 + y,1/2 + z] | 2.757 (3) | 142 | |
| H2∙∙∙O3−C5 | [−1 + x, 1/2 − y, −1/2 + z] | 2.449 (3) | 133 |
| Parameter | 3-PTCA | 4-PTCA | 3-MPTCA | 4-MPTCA |
|---|---|---|---|---|
| EHOMO | −5.5285 | −5.6125 | −6.3038 | −5.7310 |
| ELUMO | −3.6468 | −3.5904 | −2.2618 | −2.6355 |
| EGap | 1.8817 | 2.0221 | 4.0420 | 3.0955 |
| IP | 5.5285 | 5.6125 | 6.3038 | 5.7310 |
| EA | 3.6468 | 3.5904 | 2.2618 | 2.6355 |
| Hardness (η) | 0.9409 | 1.0111 | 2.0210 | 1.5477 |
| Electronegativity (X) | 4.5877 | 4.6014 | 4.2828 | 4.1833 |
| Chemical Potential (μ) | −4.5877 | −4.6014 | −4.2828 | −4.1833 |
| Electrophilicity (ω) | 11.1849 | 10.4710 | 4.5379 | 5.6532 |
| Softness (σ) | 0.5314 | 0.4945 | 0.2474 | 0.3230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, G.E.; Cisterna, J.; Llanos, J.; Pulido, R.; Naveas, N.; Narea, P.; Amo-Ochoa, P.; Zamora, F.; León, Y.; Brito, I. Structure–Property Relationships in Zwitterionic Pyridinium–Triazole Ligands: Insights from Crystal Engineering and Hirshfeld Surface Analysis. Int. J. Mol. Sci. 2025, 26, 5123. https://doi.org/10.3390/ijms26115123
Delgado GE, Cisterna J, Llanos J, Pulido R, Naveas N, Narea P, Amo-Ochoa P, Zamora F, León Y, Brito I. Structure–Property Relationships in Zwitterionic Pyridinium–Triazole Ligands: Insights from Crystal Engineering and Hirshfeld Surface Analysis. International Journal of Molecular Sciences. 2025; 26(11):5123. https://doi.org/10.3390/ijms26115123
Chicago/Turabian StyleDelgado, Gerzon E., Jonathan Cisterna, Jaime Llanos, Ruth Pulido, Nelson Naveas, Pilar Narea, Pilar Amo-Ochoa, Félix Zamora, Yasna León, and Iván Brito. 2025. "Structure–Property Relationships in Zwitterionic Pyridinium–Triazole Ligands: Insights from Crystal Engineering and Hirshfeld Surface Analysis" International Journal of Molecular Sciences 26, no. 11: 5123. https://doi.org/10.3390/ijms26115123
APA StyleDelgado, G. E., Cisterna, J., Llanos, J., Pulido, R., Naveas, N., Narea, P., Amo-Ochoa, P., Zamora, F., León, Y., & Brito, I. (2025). Structure–Property Relationships in Zwitterionic Pyridinium–Triazole Ligands: Insights from Crystal Engineering and Hirshfeld Surface Analysis. International Journal of Molecular Sciences, 26(11), 5123. https://doi.org/10.3390/ijms26115123









