Structure-Directing Interplay between Tetrel and Halogen Bonding in Co-Crystal of Lead(II) Diethyldithiocarbamate with Tetraiodoethylene
Abstract
1. Introduction
2. Results
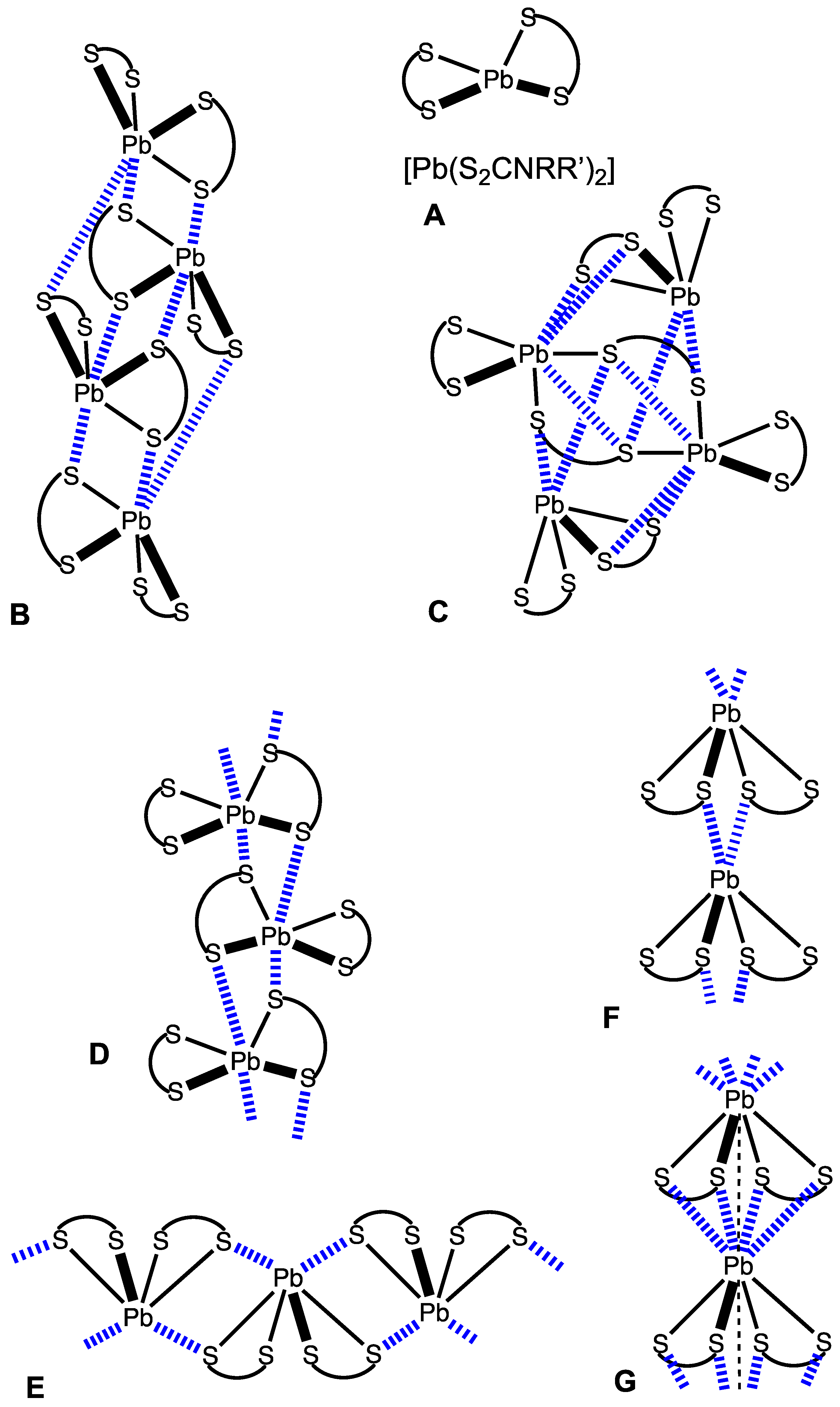
2.1. CSD Search: Structural Features of Homoleptic Lead(II) Dithiocarbamates
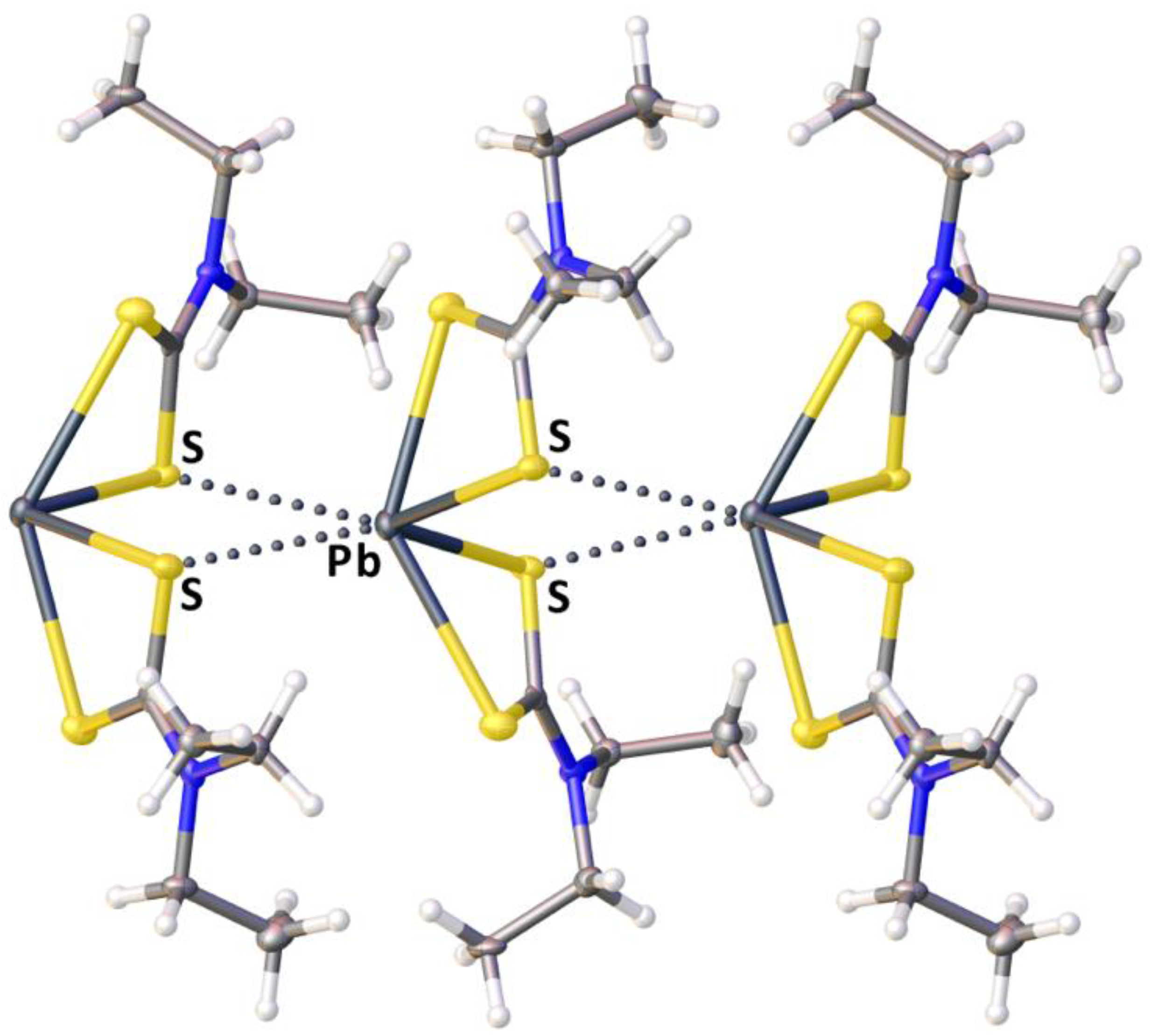
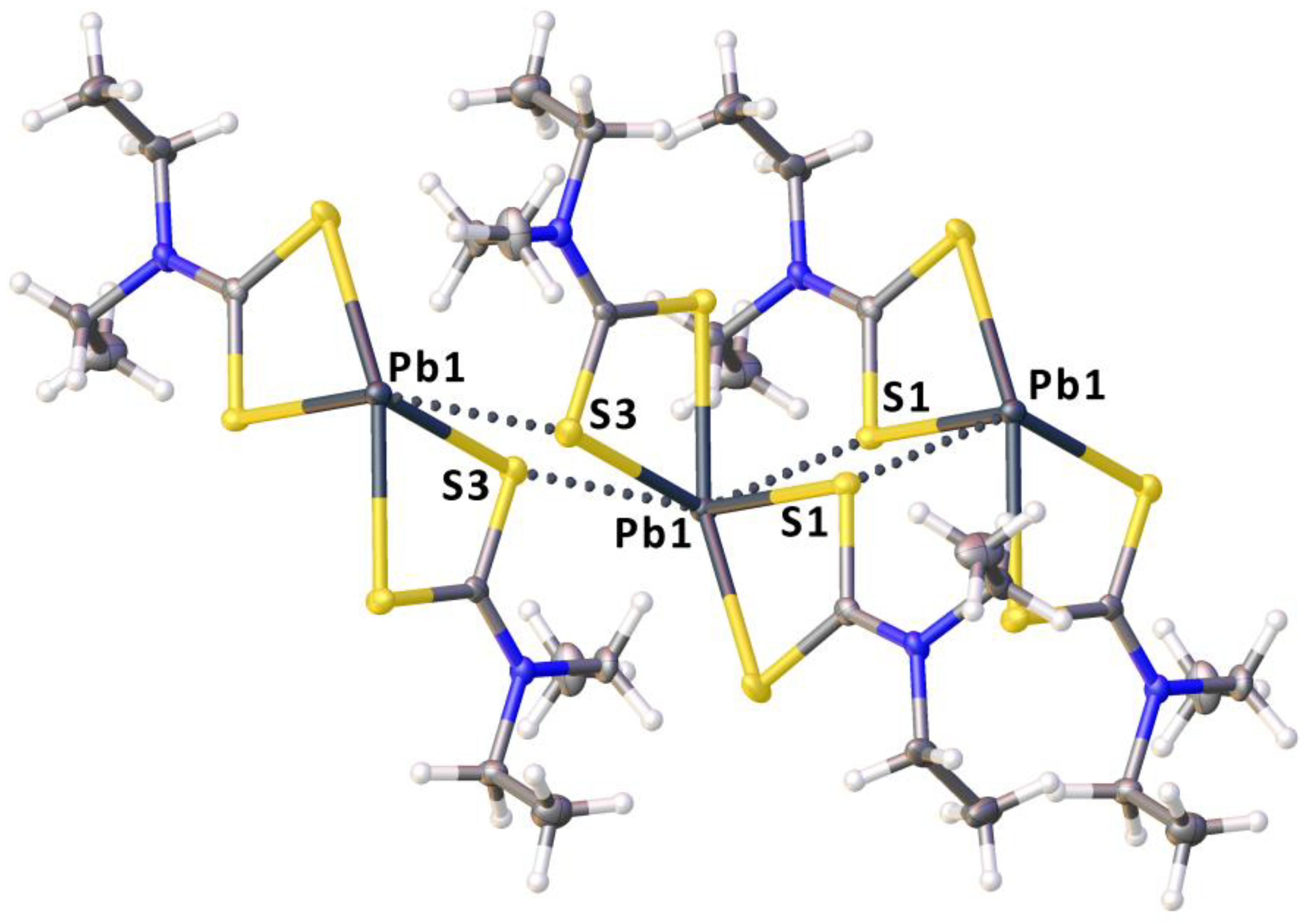
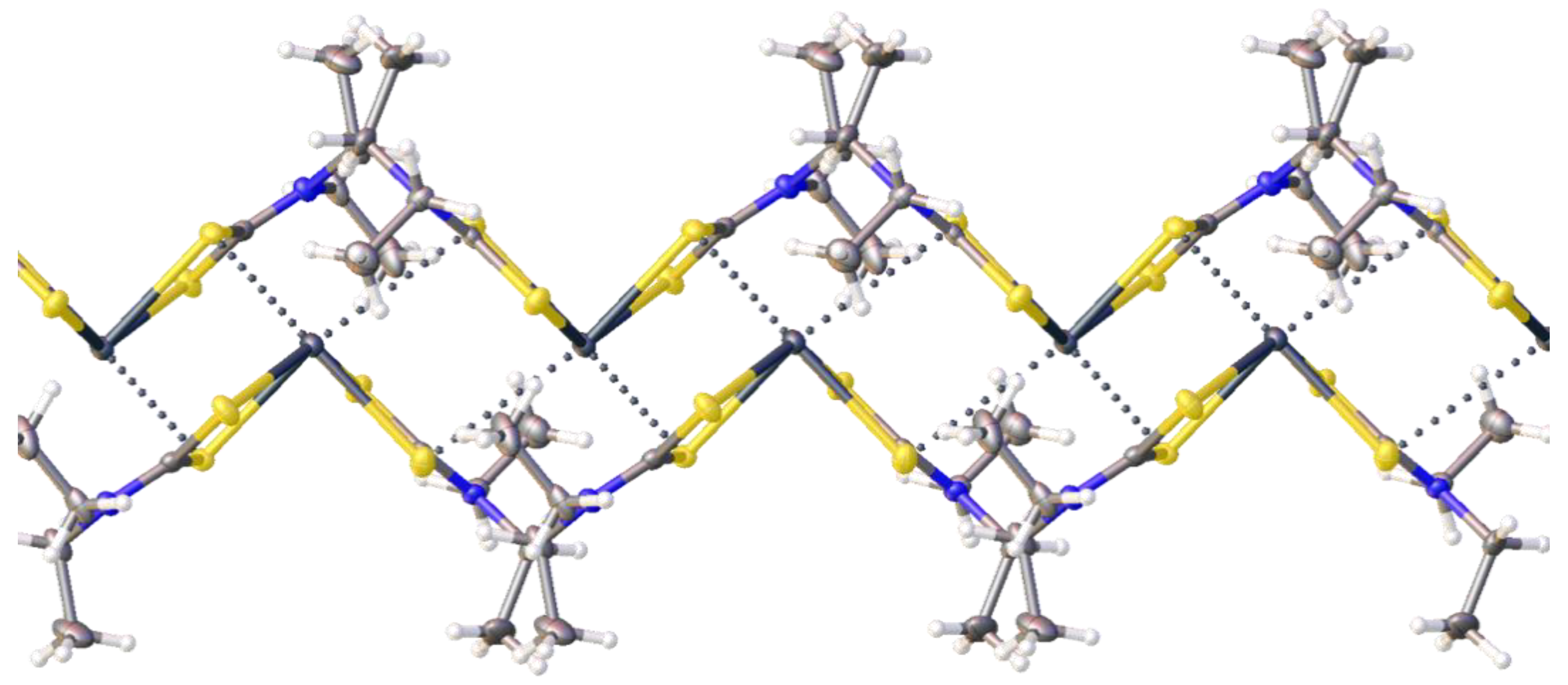
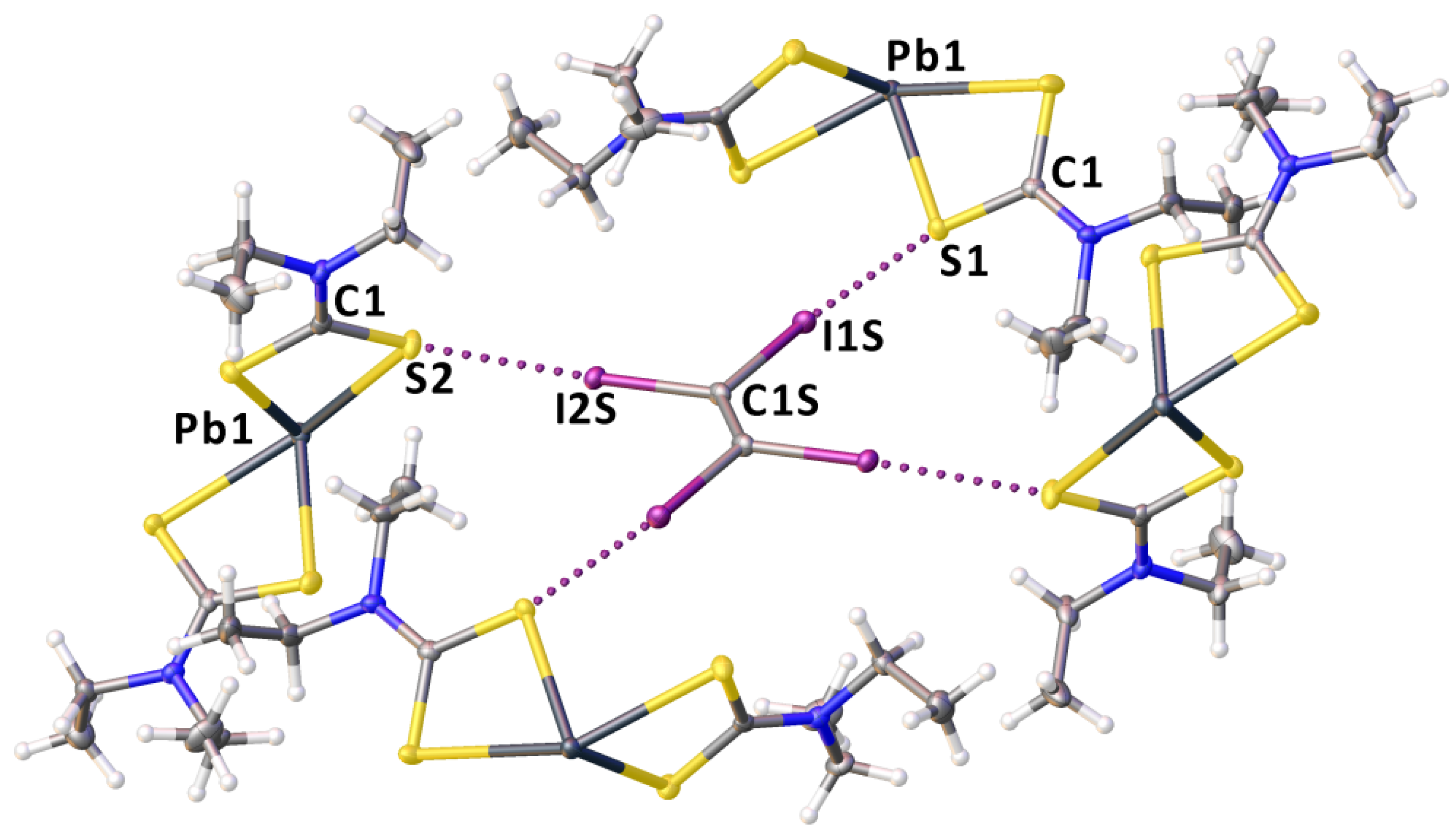
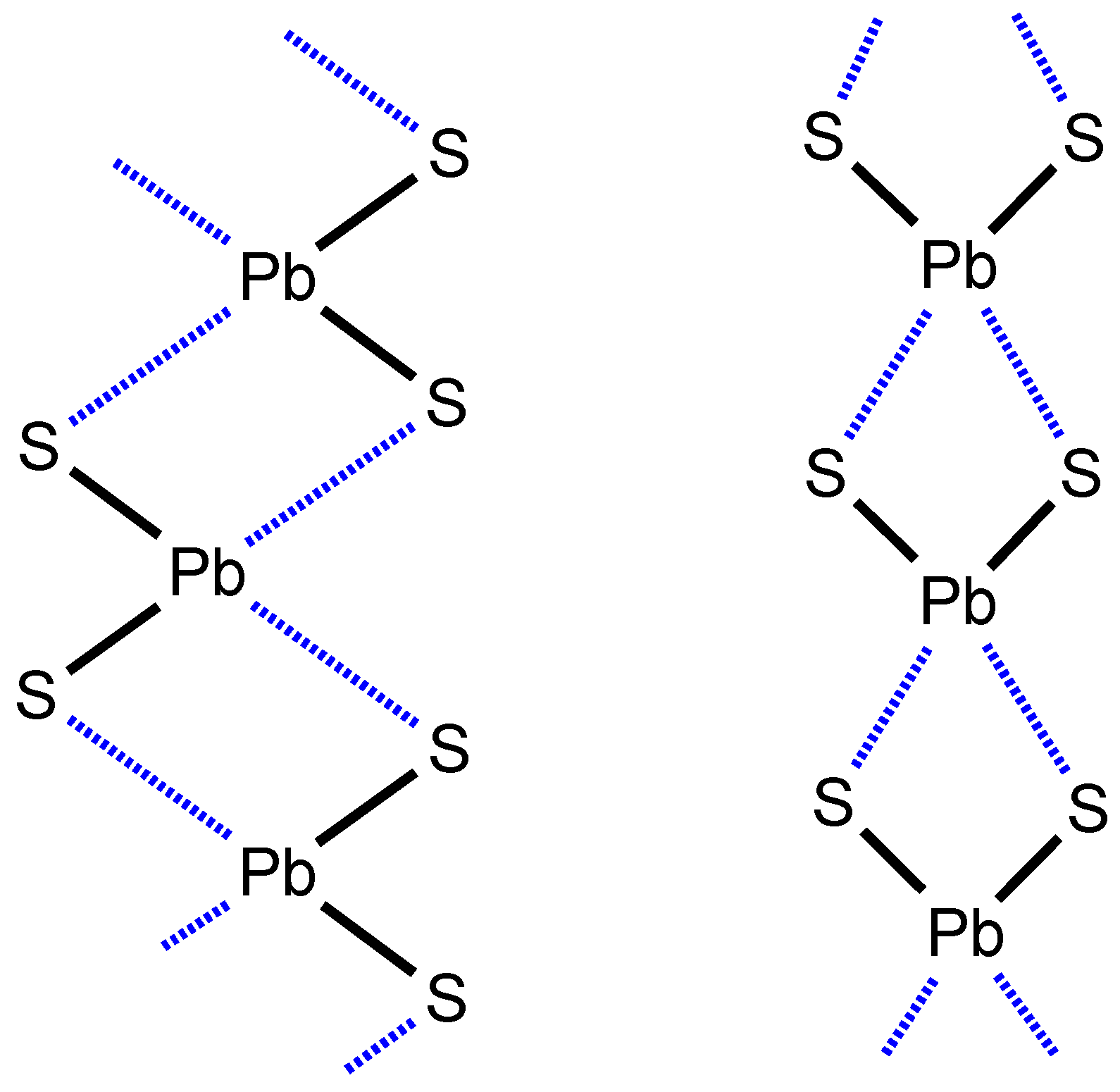
2.2. Crystallizations and Structural Motifs of the XRD Structures
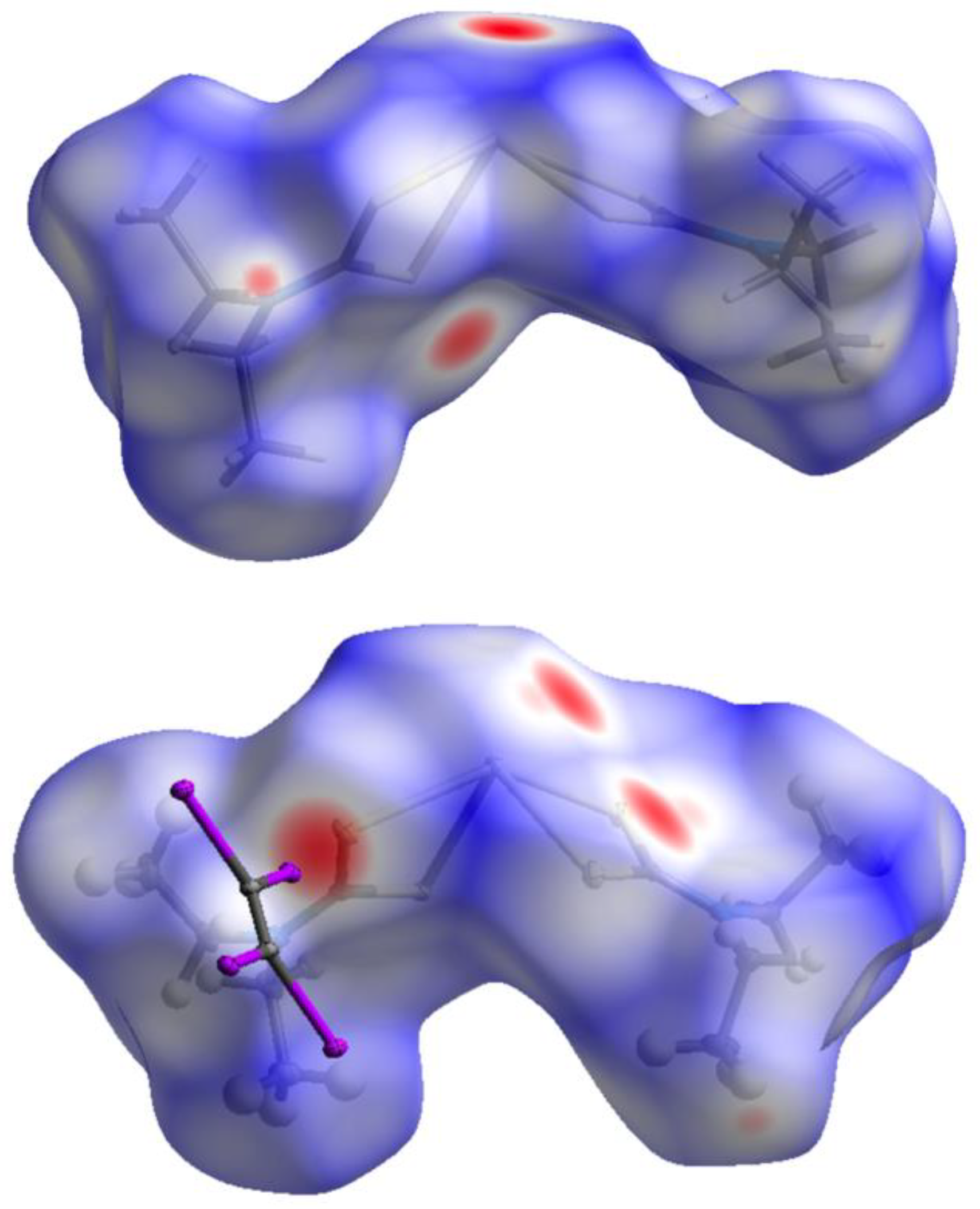
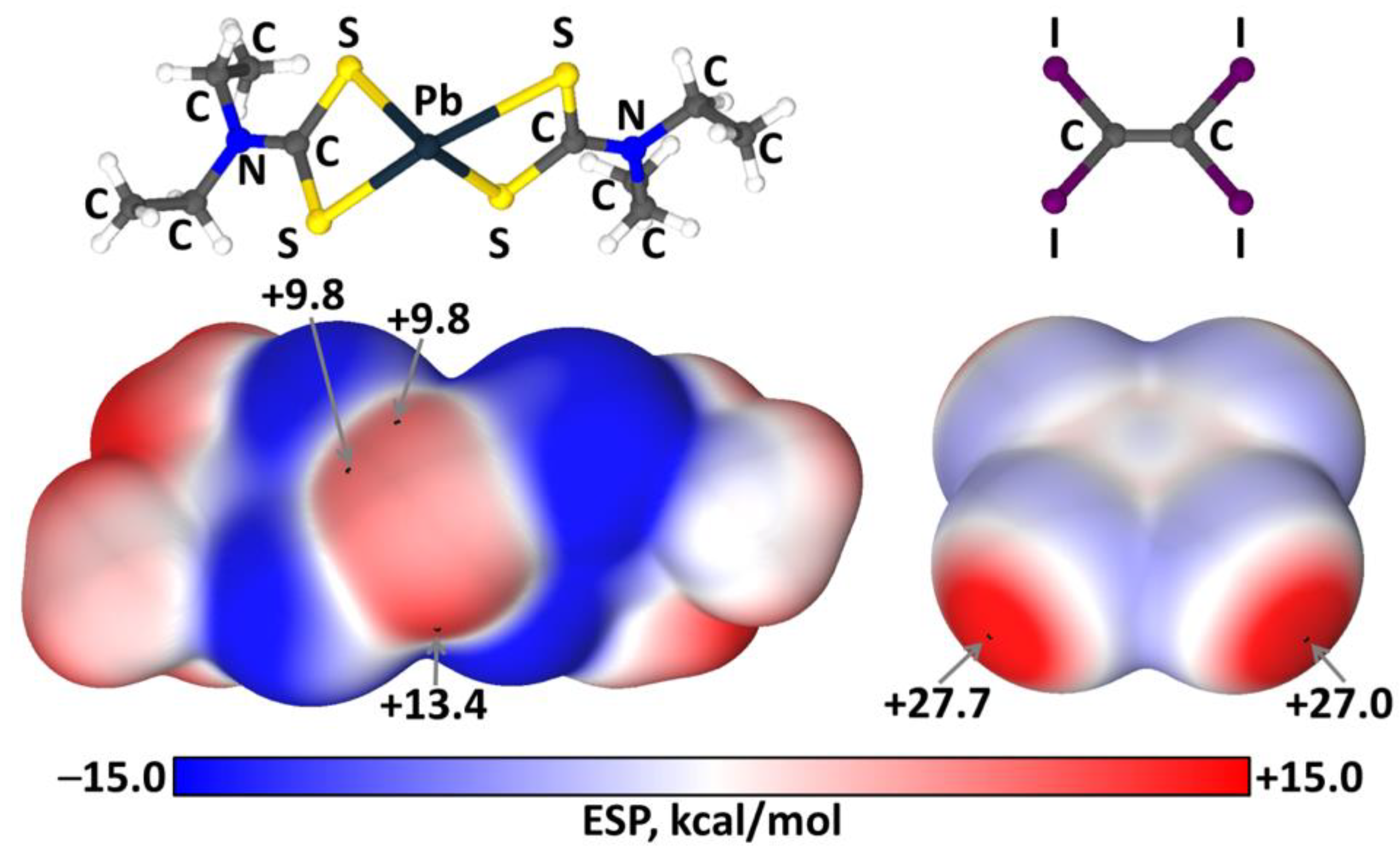
2.3. Theoretical Calculations
3. Discussion
4. Materials and Methods
4.1. Materials and Instrumentation
4.2. Co-Crystallization
4.3. X-ray Structure Determination
4.4. Computational Details
4.5. Details of the Hirshfeld Surface Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shukla, R.; Chopra, D. Chalcogen and pnictogen bonds: Insights and relevance. Curr. Sci. 2021, 120, 1848–1853. [Google Scholar] [CrossRef]
- Selvakumar, K.; Singh, H.B. Adaptive responses of sterically confined intramolecular chalcogen bonds. Chem. Sci. 2018, 9, 7027–7042. [Google Scholar] [CrossRef]
- Cornaton, Y.; Djukic, J.-P. Noncovalent Interactions in Organometallic Chemistry: From Cohesion to Reactivity, a New Chapter. Acc. Chem. Res. 2021, 54, 3828–3840. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
- Frontera, A.; Bauzá, A. On the Importance of σ–Hole Interactions in Crystal Structures. Crystals 2021, 11, 1205. [Google Scholar] [CrossRef]
- Miller, D.K.; Chernyshov, I.Y.; Torubaev, Y.V.; Rosokha, S.V. From weak to strong interactions: Structural and electron topology analysis of the continuum from the supramolecular chalcogen bonding to covalent bonds. Phys. Chem. Chem. Phys. 2022, 24, 8251–8259. [Google Scholar] [CrossRef]
- Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Discuss 2017, 203, 485–507. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Li, B.; Zang, S.-Q.; Wang, L.-Y.; Mak, T.C.W. Halogen bonding: A powerful, emerging tool for constructing high-dimensional metal-containing supramolecular networks. Coord. Chem. Rev. 2016, 308, 1–21. [Google Scholar] [CrossRef]
- Maharramov, A.M.; Mahmudov, K.T.; Kopylovich, M.N.; Pombeiro, A.J. Non-Covalent Interactions in the Synthesis and Design of New Compounds; Wiley Online Library: Hoboken, NJ, USA, 2016. [Google Scholar]
- Tepper, R.; Schubert, U.S. Halogen Bonding in Solution: Anion Recognition, Templated Self-Assembly, and Organocatalysis. Angew. Chem. Int. Ed. 2018, 57, 6004–6016. [Google Scholar] [CrossRef]
- Lim, J.Y.C.; Beer, P.D. Sigma-Hole Interactions in Anion Recognition. Chem 2018, 4, 731–783. [Google Scholar] [CrossRef]
- Scheiner, S.; Michalczyk, M.; Zierkiewicz, W. Coordination of anions by noncovalently bonded σ-hole ligands. Coord. Chem. Rev. 2020, 405, 213136. [Google Scholar] [CrossRef]
- Lisac, K.; Topić, F.; Arhangelskis, M.; Cepić, S.; Julien, P.A.; Nickels, C.W.; Morris, A.J.; Friščić, T.; Cinčić, D. Halogen-bonded cocrystallization with phosphorus, arsenic and antimony acceptors. Nat. Commun. 2019, 10, 61. [Google Scholar] [CrossRef] [PubMed]
- McNaughton, D.A.; Fares, M.; Picci, G.; Gale, P.A.; Caltagirone, C. Advances in fluorescent and colorimetric sensors for anionic species. Coord. Chem. Rev. 2021, 427, 213573. [Google Scholar] [CrossRef]
- Nemec, V.; Lisac, K.; Bedekovic, N.; Fotovic, L.; Stilinovic, V.; Cincic, D. Crystal engineering strategies towards halogen-bonded metal-organic multi-component solids: Salts, cocrystals and salt cocrystals. Crystengcomm 2021, 23, 3063–3083. [Google Scholar] [CrossRef]
- Pancholi, J.; Beer, P.D. Halogen bonding motifs for anion recognition. Coord. Chem. Rev. 2020, 416, 213281. [Google Scholar] [CrossRef]
- Taylor, M.S. Anion recognition based on halogen, chalcogen, pnictogen and tetrel bonding. Coord. Chem. Rev. 2020, 413, 213270. [Google Scholar] [CrossRef]
- Kowalik, M.; Brzeski, J.; Gawrońska, M.; Kazimierczuk, K.; Makowski, M. Experimental and theoretical investigation of conformational states and noncovalent interactions in crystalline sulfonamides with a methoxyphenyl moiety. CrystEngComm 2021, 23, 6137–6162. [Google Scholar] [CrossRef]
- Zhu, M.Z.; Li, C.W.; Li, B.Y.; Zhang, J.K.; Sun, Y.Q.; Guo, W.S.; Zhou, Z.M.; Pang, S.P.; Yan, Y.F. Interaction engineering in organic-inorganic hybrid perovskite solar cells. Mater. Horiz. 2020, 7, 2208–2236. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; da Silva, M. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
- Breugst, M.; Koenig, J.J. sigma-Hole Interactions in Catalysis. Eur. J. Org. Chem. 2020, 2020, 5473–5487. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Arimitsu, S.; Saá, J.M.; Sarazin, Y.; Frontera, A.; Yamada, S.; Caminade, A.-M.; Chikkali, S.H.; Mal, P.; Momiyama, N. Noncovalent Interactions in Catalysis; Royal Society of Chemistry: London, UK, 2019. [Google Scholar]
- Nagorny, P.; Sun, Z.K. New approaches to organocatalysis based on C-H and C-X bonding for electrophilic substrate activation. Beilstein J. Org. Chem. 2016, 12, 2834–2848. [Google Scholar] [CrossRef] [PubMed]
- Bulfield, D.; Huber, S.M. Halogen Bonding in Organic Synthesis and Organocatalysis. Chem. Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef]
- Benz, S.; Poblador-Bahamonde, A.I.; Low-Ders, N.; Matile, S. Catalysis with Pnictogen, Chalcogen, and Halogen Bonds. Angew. Chem. Int. Ed. 2018, 57, 5408–5412. [Google Scholar] [CrossRef]
- Breugst, M.; von der Heiden, D.; Schmauck, J. Novel Noncovalent Interactions in Catalysis: A Focus on Halogen, Chalcogen, and Anion-pi Bonding. Synth. Stuttg. 2017, 49, 3224–3236. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Kopylovich, M.N.; da Silva, M.; Pombeiro, A.J.L. Non-covalent interactions in the synthesis of coordination compounds: Recent advances. Coord. Chem. Rev. 2017, 345, 54–72. [Google Scholar] [CrossRef]
- Scheiner, S. Participation of S and Se in hydrogen and chalcogen bonds. CrystEngComm 2021, 23, 6821–6837. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Defining the hydrogen bond: An account (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 1619–1636. [Google Scholar] [CrossRef]
- Mulliken, R.S. Structures of Complexes Formed by Halogen Molecules with Aromatic and with Oxygenated Solvents1. J. Am. Chem. Soc. 1950, 72, 600–608. [Google Scholar] [CrossRef]
- Hassel, O.; Hvoslef, J. The Structure of Bromine 1,4-Dioxanate. Acta Chem. Scand. 1954, 8, 873. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
- Scheiner, S. Origins and properties of the tetrel bond. Phys. Chem. Chem. Phys. 2021, 23, 5702–5717. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Seth, S.K.; Frontera, A. Tetrel bonding interactions at work: Impact on tin and lead coordination compounds. Coord. Chem. Rev. 2019, 384, 107–125. [Google Scholar] [CrossRef]
- Daolio, A.; Scilabra, P.; Terraneo, G.; Resnati, G. C(sp3) atoms as tetrel bond donors: A crystallographic survey. Coord. Chem. Rev. 2020, 413, 213265. [Google Scholar] [CrossRef]
- Grabowski, S.J. Pnicogen and tetrel bonds—Tetrahedral Lewis acid centres. Struct. Chem. 2019, 30, 1141–1152. [Google Scholar] [CrossRef]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef]
- Khera, M.; Goel, N. Cooperative Effect of Noncovalent Interactions on Tetrel Bonding in Halogenated Silanes. ChemPhysChem 2022, 23, e202100776. [Google Scholar] [CrossRef]
- Bhattarai, S.; Sutradhar, D.; Chandra, A.K. Strongly Bound π-Hole Tetrel Bonded Complexes between H2SiO and Substituted Pyridines. Influence of Substituents. ChemPhysChem 2022, 23, e202200146. [Google Scholar] [CrossRef]
- Southern, S.A.; Nag, T.; Kumar, V.; Triglav, M.; Levin, K.; Bryce, D.L. NMR Response of the Tetrel Bond Donor. J. Phys. Chem. C 2022, 126, 851–865. [Google Scholar] [CrossRef]
- Barszcz, B.; Masternak, J.; Kowalik, M. Structural insights into coordination polymers based on 6s2 Pb(II) and Bi(III) centres connected via heteroaromatic carboxylate linkers and their potential applications. Coord. Chem. Rev. 2021, 443, 213935. [Google Scholar] [CrossRef]
- Araujo, V.O.; Casagrande, G.A.; Tirloni, B.; Schwade, V.D. Lead(II) compounds with neutral coordination of semicarbazones: Synthesis and characterization. Inorg. Chim. Acta 2022, 533, 120785. [Google Scholar] [CrossRef]
- Kowalik, M.; Masternak, J.; Brzeski, J.; Daszkiewicz, M.; Barszcz, B. Effect of a lone electron pair and tetrel interactions on the structure of Pb(II) CPs constructed from pyrimidine carboxylates and auxiliary inorganic ions. Polyhedron 2022, 219, 115818. [Google Scholar] [CrossRef]
- Majumdar, D.; Frontera, A.; Gomila, R.M.; Das, S.; Bankura, K. Synthesis, spectroscopic findings and crystal engineering of Pb(ii)–Salen coordination polymers, and supramolecular architectures engineered by σ-hole/spodium/tetrel bonds: A combined experimental and theoretical investigation. RSC Adv. 2022, 12, 6352–6363. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, G.; García-Santos, I.; Pittelkow, M.; Kamounah, F.S.; Zangrando, E.; Babashkina, M.G.; Frontera, A.; Safin, D.A. The tetrel bonding role in supramolecular aggregation of lead(II) acetate and a thiosemicarbazide derivative. Acta Crystallogr. Sect. B 2022, 78, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Bikbaeva, Z.M.; Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Bokach, N.A.; Kukushkin, V.Y. Electrophilic-Nucleophilic Dualism of Nickel(II) toward Ni center dot center dot center dot l Noncovalent Interactions: Semicoordination of Iodine Centers via Electron Belt and Halogen Bonding via sigma-Hole. Inorg. Chem. 2017, 56, 13562–13578. [Google Scholar] [CrossRef]
- Bairagi, K.M.; Ingle, K.S.; Bhowal, R.; Mohurle, S.A.; Hasija, A.; Alwassil, O.I.; Venugopala, K.N.; Chopra, D.; Nayak, S.K. Interplay of Halogen and Hydrogen Bonding through Co–Crystallization in Pharmacologically Active Dihydropyrimidines: Insights from Crystal Structure and Energy Framework. ChemPlusChem 2021, 86, 1167–1176. [Google Scholar] [CrossRef]
- Bertram, C.; Miller, D.P.; Schunke, C.; Kemeny, I.; Kimura, M.; Bovensiepen, U.; Zurek, E.; Morgenstern, K. Interplay of Halogen and Weak Hydrogen Bonds in the Formation of Magic Nanoclusters on Surfaces. J. Phys. Chem. C 2022, 126, 588–596. [Google Scholar] [CrossRef]
- Dehaven, B.A.; Chen, A.L.; Shimizu, E.A.; Salpage, S.R.; Smith, M.D.; Shimizu, L.S. Interplay between Hydrogen and Halogen Bonding in Cocrystals of Dipyridinylmethyl Oxalamides and Tetrafluorodiiodobenzenes. Cryst. Growth Des. 2019, 19, 5776–5783. [Google Scholar] [CrossRef]
- Díaz-Torres, R.; Echeverría, J.; Loveday, O.; Harding, P.; Harding, D.J. Interplay of halogen and hydrogen bonding in a series of heteroleptic iron(iii) complexes. CrystEngComm 2021, 23, 4069–4076. [Google Scholar] [CrossRef]
- Goswami, A.; Garai, M.; Biradha, K. Interplay of Halogen Bonding and Hydrogen Bonding in the Cocrystals and Salts of Dihalogens and Trihalides with N, N′-Bis(3-pyridylacrylamido) Derivatives: Phosphorescent Organic Salts. Cryst. Growth Des. 2019, 19, 2175–2188. [Google Scholar] [CrossRef]
- La Manna, P.; De Rosa, M.; Talotta, C.; Rescifina, A.; Floresta, G.; Soriente, A.; Gaeta, C.; Neri, P. Synergic Interplay Between Halogen Bonding and Hydrogen Bonding in the Activation of a Neutral Substrate in a Nanoconfined Space. Angew. Chem. Int. Ed. 2020, 59, 811–818. [Google Scholar] [CrossRef] [PubMed]
- Pinfold, H.; Sacchi, M.; Pattison, G.; Costantini, G. Determining the Relative Structural Relevance of Halogen and Hydrogen Bonds in Self-Assembled Monolayers. J. Phys. Chem. C 2021, 125, 27784–27792. [Google Scholar] [CrossRef]
- Guo, X.; Li, Q. Dual functions of Lewis acid and base of Se in F2C=Se and their interplay in F2CSe•••NH3•••HX. J. Mol. Model. 2015, 21, 157. [Google Scholar] [CrossRef] [PubMed]
- Otilia, M.; Montero-Campillo, M.M.; Alkorta, I.; Elguero, J.; Yáñez, M. Ternary Complexes Stabilized by Chalcogen and Alkaline-Earth Bonds: Crucial Role of Cooperativity and Secondary Noncovalent Interactions. Chem. A Eur. J. 2019, 25, 11688–11695. [Google Scholar] [CrossRef]
- Bamberger, J.; Ostler, F.; Mancheño, O.G. Frontiers in Halogen and Chalcogen-Bond Donor Organocatalysis. ChemCatChem 2019, 11, 5198–5211. [Google Scholar] [CrossRef]
- Schwade, V.D.; Tirloni, B.; Burrow, R.A.; Lang, E.S. Lead(II) thiocyanate reaction behaviour with hydrazones. Polyhedron 2020, 188, 114707. [Google Scholar] [CrossRef]
- García-Santos, I.; Castiñeiras, A.; Mahmoudi, G.; Babashkina, M.G.; Zangrando, E.; Gomila, R.M.; Frontera, A.; Safin, D.A. Lead(ii) supramolecular structures formed through a cooperative influence of the hydrazinecarbothioamide derived and ancillary ligands. CrystEngComm 2022, 24, 368–378. [Google Scholar] [CrossRef]
- Kowalik, M.; Masternak, J.; Kazimierczuk, K.; Kupcewicz, B.; Khavryuchenko, O.V.; Barszcz, B. Exploring thiophene-2-acetate and thiophene-3-acetate binding modes towards the molecular and supramolecular structures and photoluminescence properties of Pb(ii) polymers. CrystEngComm 2020, 22, 7025–7035. [Google Scholar] [CrossRef]
- Mahmoudi, G.; Zangrando, E.; Mitoraj, M.P.; Gurbanov, A.V.; Zubkov, F.I.; Moosavifar, M.; Konyaeva, I.A.; Kirillov, A.M.; Safin, D.A. Extended lead(II) architectures engineered: Via tetrel bonding interactions. New J. Chem. 2018, 42, 4959–4971. [Google Scholar] [CrossRef]
- Zhao, Q. Mutual influence of tetrel and halogen bonds between XCN (X=Cl, Br) and 4-TF3-pyridine (T=C, Si, Ge). J. Mol. Model. 2020, 26, 329. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Competition between a Tetrel and Halogen Bond to a Common Lewis Acid. J. Phys. Chem. A 2021, 125, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Zelenkov, L.E.; Eliseeva, A.A.; Baykov, S.V.; Suslonov, V.V.; Galmés, B.; Frontera, A.; Kukushkin, V.Y.; Ivanov, D.M.; Bokach, N.A. Electron belt-to-σ-hole switch of noncovalently bound iodine(i) atoms in dithiocarbamate metal complexes. Inorg. Chem. Front. 2021, 8, 2505–2517. [Google Scholar] [CrossRef]
- Zelenkov, L.E.; Ivanov, D.M.; Sadykov, E.K.; Bokach, N.A.; Galmés, B.; Frontera, A.; Kukushkin, V.Y. Semicoordination Bond Breaking and Halogen Bond Making Change the Supramolecular Architecture of Metal-Containing Aggregates. Cryst. Growth Des. 2020, 20, 6956–6965. [Google Scholar] [CrossRef]
- Zelenkov, L.E.; Eliseeva, A.A.; Baykov, S.; Ivanov, D.M.; Sumina, A.I.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y.; Bokach, N.A. Inorganic–Organic {dz2-MIIS4}···π-Hole Stacking in Reverse Sandwich Structures. The Case of Cocrystals of Group 10 Metal Dithiocarbamates with Electron-deficient Arenes. Inorg. Chem. Front. 2022, 9, 2869–2879. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii of Metals in Covalent Compounds. J. Phys. Chem. 1966, 70, 3006–3007. [Google Scholar] [CrossRef]
- Trindade, T.; O’Brien, P.; Zhang, X.-m.; Motevalli, M. Synthesis of PbS nanocrystallites using a novel single molecule precursors approach: X-ray single-crystal structure of Pb(S2CNEtPri)2. J. Mater. Chem. 1997, 7, 1011–1016. [Google Scholar] [CrossRef]
- Caruso, F.; Chan, M.-L.; Rossi, M. A Short Pb···Pb Separation in the Polymeric Compound Bis(pyrrolidinecarbodithioato)lead(II) and a Conformational Pathway Interconversion for the “PbIIS4” Framework. Inorg. Chem. 1997, 36, 3609–3615. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Scrocco, E.; Tomasi, J. Electronic Molecular Structure, Reactivity and Intermolecular Forces: An Euristic Interpretation by Means of Electrostatic Molecular Potentials. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press: Cambridge, MA, USA, 1978; Volume 11, pp. 115–193. [Google Scholar]
- Scrocco, E.; Tomasi, J. The electrostatic molecular potential as a tool for the interpretation of molecular properties. In New Concepts II. Topics in Current Chemistry Fortschritte der Chemischen Forschung; Springer: Berlin/Heidelberg, Germany, 1973; pp. 95–170. [Google Scholar]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface electrostatic potentials of halogenated methanes as indicators of directional intermolecular interactions. Int. J. Quantum Chem. 1992, 44, 57–64. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Borštnik, U.; VandeVondele, J.; Weber, V.; Hutter, J. Sparse matrix multiplication: The distributed block-compressed sparse row library. Parallel Comput. 2014, 40, 47–58. [Google Scholar] [CrossRef]
- Schütt, O.; Messmer, P.; Hutter, J.; VandeVondele, J. GPU-Accelerated Sparse Matrix–Matrix Multiplication for Linear Scaling Density Functional Theory. In Electronic Structure Calculations on Graphics Processing Units; John, Willey and Sons: Hoboken, NJ, USA, 2016; pp. 173–190. [Google Scholar]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.D.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Jorge, F.E.; Canal Neto, A.; Camiletti, G.G.; Machado, S.F. Contracted Gaussian basis sets for Douglas–Kroll–Hess calculations: Estimating scalar relativistic effects of some atomic and molecular properties. J. Chem. Phys. 2009, 130, 064108. [Google Scholar] [CrossRef] [PubMed]
- Barros, C.L.; de Oliveira, P.J.P.; Jorge, F.E.; Canal Neto, A.; Campos, M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010, 108, 1965–1972. [Google Scholar] [CrossRef]
- de Berrêdo, R.C.; Jorge, F.E. All-electron double zeta basis sets for platinum: Estimating scalar relativistic effects on platinum(II) anticancer drugs. J. Mol. Struct. THEOCHEM 2010, 961, 107–112. [Google Scholar] [CrossRef]
- Jorge, F.E.; Martins, L.S.C.; Franco, M.L. All-electron double zeta basis sets for the lanthanides: Application in atomic and molecular property calculations. Chem. Phys. Lett. 2016, 643, 84–88. [Google Scholar] [CrossRef]
- Barysz, M.; Sadlej, A.J. Two-component methods of relativistic quantum chemistry: From the Douglas–Kroll approximation to the exact two-component formalism. J. Mol. Struct. THEOCHEM 2001, 573, 181–200. [Google Scholar] [CrossRef]
- Reiher, M. Relativistic Douglas–Kroll–Hess theory. WIREs Comput. Mol. Sci. 2012, 2, 139–149. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09W; Gaussian, Inc.: Wallingford, UK, 2009. [Google Scholar]
- Bader, R.F.W.; Nguyen-Dang, T.T. Quantum Theory of Atoms in Molecules–Dalton Revisited. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press: Cambridge, MA, USA, 1981; Volume 14, pp. 63–124. [Google Scholar]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Trindle, C. Bond index description of delocalization. J. Am. Chem. Soc. 1969, 91, 219–220. [Google Scholar] [CrossRef]
- Trindle, C.; Sinanoglu, O. Local orbital and bond index characterization of hybridization. J. Am. Chem. Soc. 1969, 91, 853–858. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Natural Bond Orbitals and Extensions of Localized Bonding Concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Nguyen, J.H.; Swidan, A.a.; Macdonald, C.L.B. Water and Ammonia Complexes of Germanium(II) Dications. Angew. Chem. Int. Ed. 2013, 52, 3469–3472. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, D.C.; Butler, P.; Browne, E.C.; Wilson, D.J.D.; Dutton, J.L. On the Bonding in Bis-pyridine Iodonium Cations *. Aust. J. Chem. 2013, 66, 1179–1188. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. Engl. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
- Suslonov, V.V.; Eliseeva, A.A.; Novikov, A.S.; Ivanov, D.M.; Dubovtsev, A.Y.; Bokach, N.A.; Kukushkin, V.Y. Tetrachloroplatinate(ii) anion as a square-planar tecton for crystal engineering involving halogen bonding. CrystEngComm 2020, 22, 4180–4189. [Google Scholar] [CrossRef]
- Mertsalov, D.F.; Gomila, R.M.; Zaytsev, V.P.; Grigoriev, M.S.; Nikitina, E.V.; Zubkov, F.I.; Frontera, A. On the Importance of Halogen Bonding Interactions in Two X-ray Structures Containing All Four (F, Cl, Br, I) Halogen Atoms. Crystals 2021, 11, 1406. [Google Scholar] [CrossRef]
- Usoltsev, A.N.; Novikov, A.S.; Sokolov, M.N.; Adonin, S.A. Neutral heteroleptic complexes of bis(2-halopyridine)dihalocopper(II) family: How the nature of halogen atom affects supramolecular motifs and energies of halogen bonding in solid state? Solid State Sci. 2020, 109, 106441. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Naming Interactions from the Electrophilic Site. Cryst. Growth Des. 2014, 14, 2697–2702. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Bruno, I.J.; Cole, J.C.; Edgington, P.R.; Kessler, M.; Macrae, C.F.; McCabe, P.; Pearson, J.; Taylor, R. New software for searching the Cambridge Structural Database and visualizing crystal structures. Acta Crystallogr. Sect. B 2002, 58, 389–397. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G. SHELXT-Integrated space-group and crystal-structure determination. Acta Cryst. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G. Crystal structure refinement with SHELXL. Acta Cryst. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Lippert, G.; Hutter, J.; Parrinello, M. The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations. Theor. Chem. Acc. 1999, 103, 124–140. [Google Scholar] [CrossRef]
- Kinzhalov, M.A.; Ivanov, D.M.; Melekhova, A.A.; Bokach, N.A.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y. Chameleonic metal-bound isocyanides: A π-donating CuI-center imparts nucleophilicity to the isocyanide carbon toward halogen bonding. Inorg. Chem. Front. 2022, 9, 1655–1665. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Aliyarova, I.S.; Tupikina, E.Y.; Soldatova, N.S.; Ivanov, D.M.; Postnikov, P.S.; Yusubov, M.; Kukushkin, V.Y. Halogen Bonding Involving Gold Nucleophiles in Different Oxidation States. Inorg. Chem. 2022, 61, 15398–15407. [Google Scholar] [CrossRef] [PubMed]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- CrystalExplorer. Available online: http://crystalexplorer.scb.uwa.edu.au (accessed on 7 September 2022).
- McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 37, 3814–3816. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
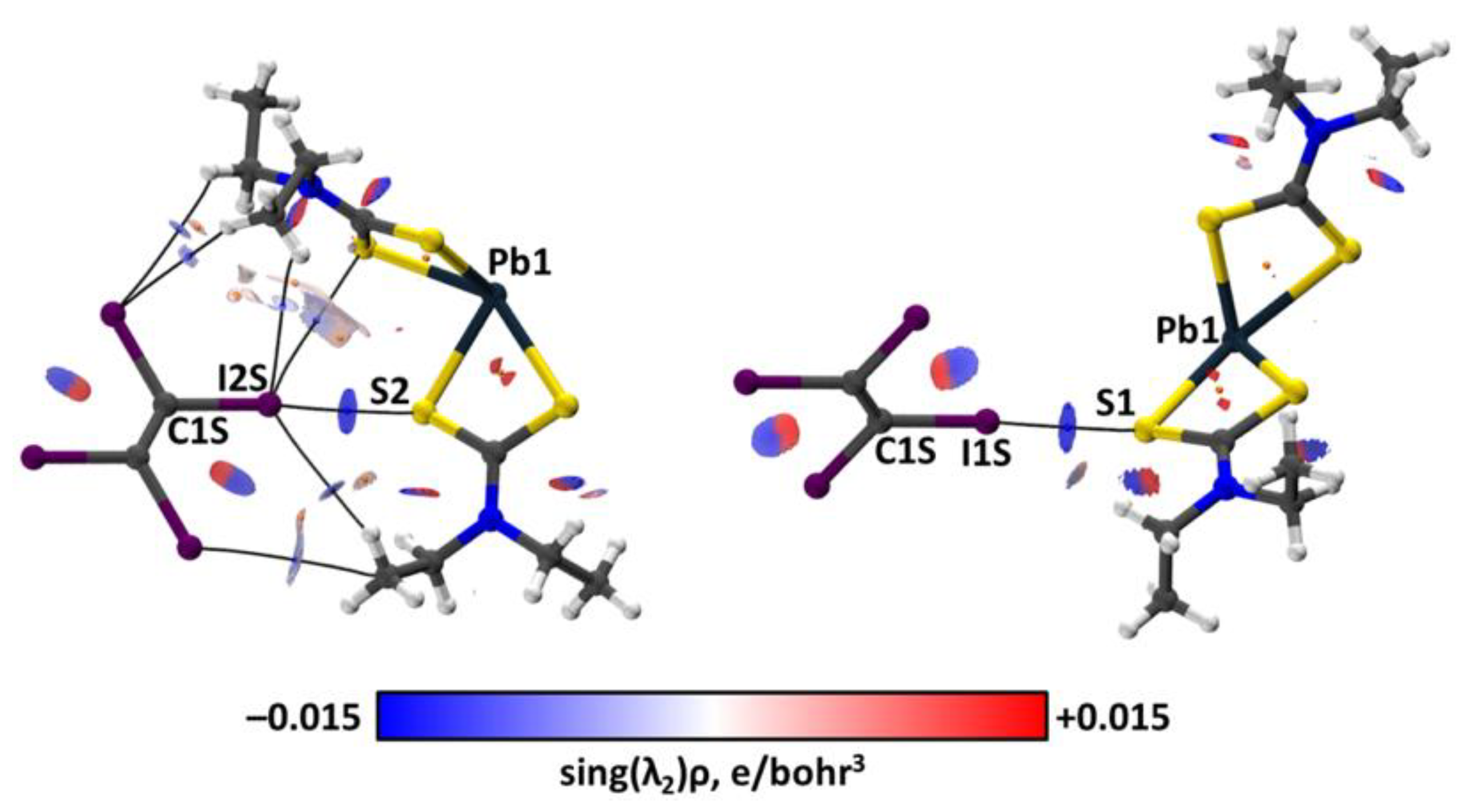
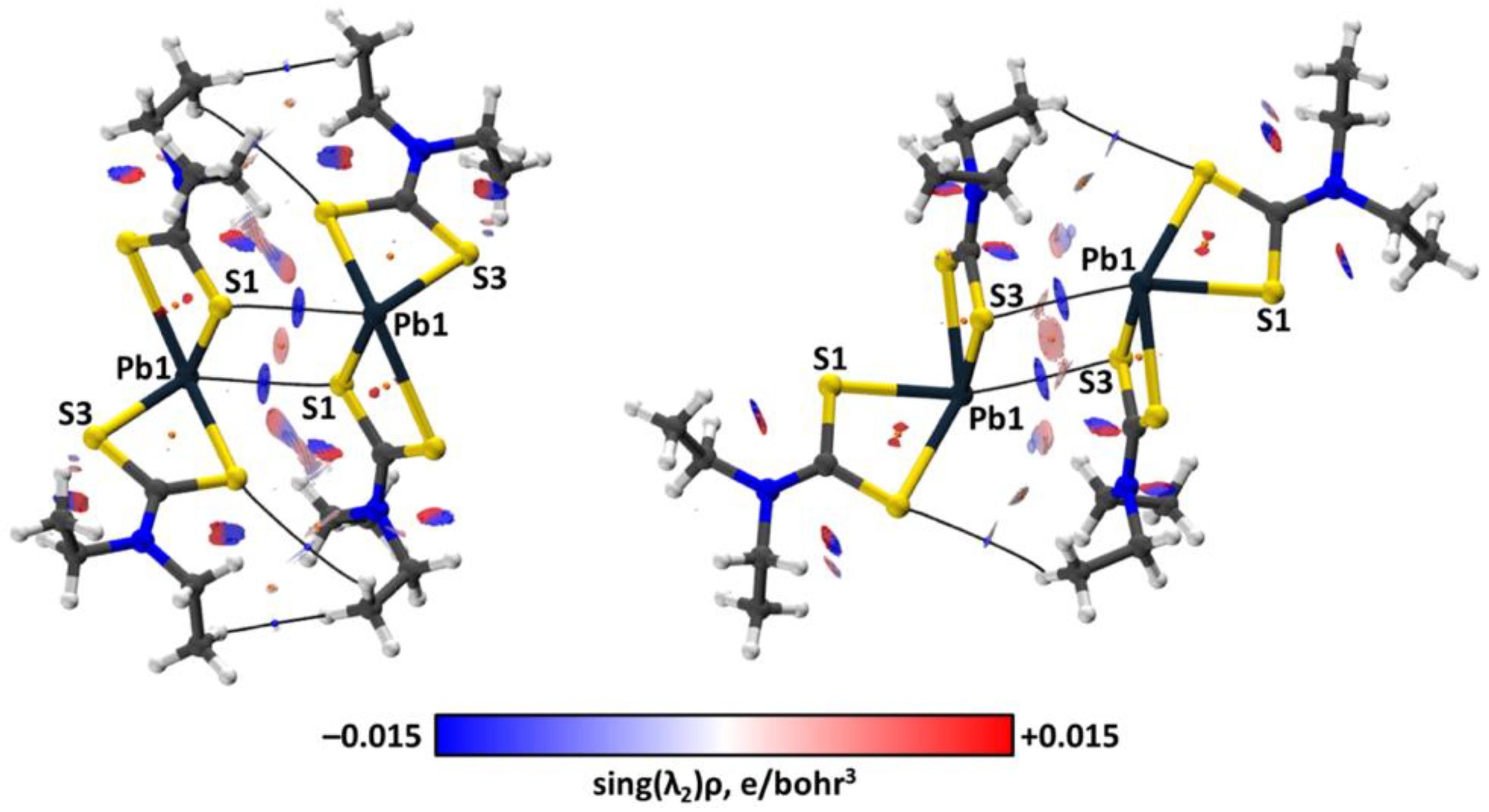
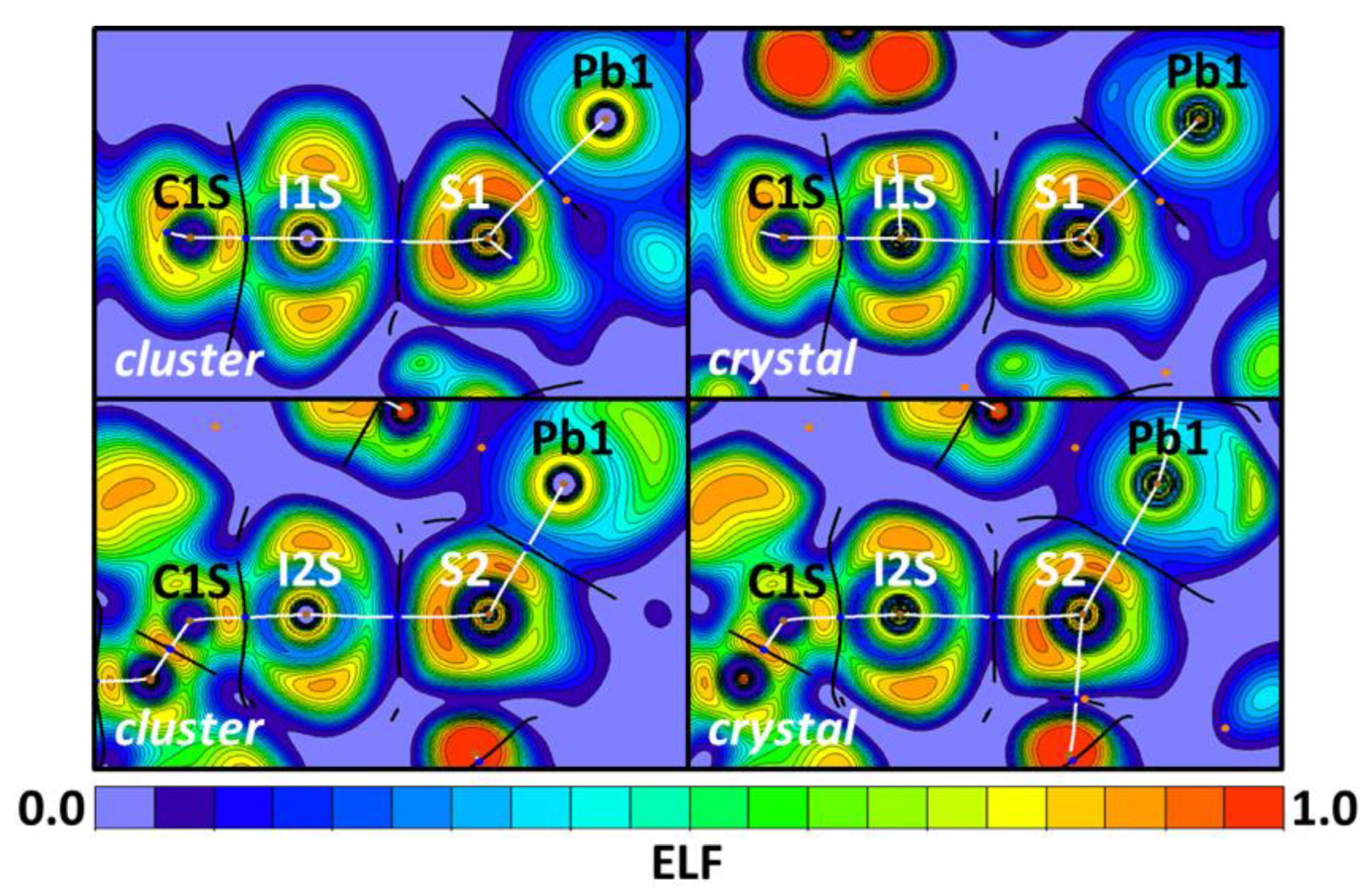
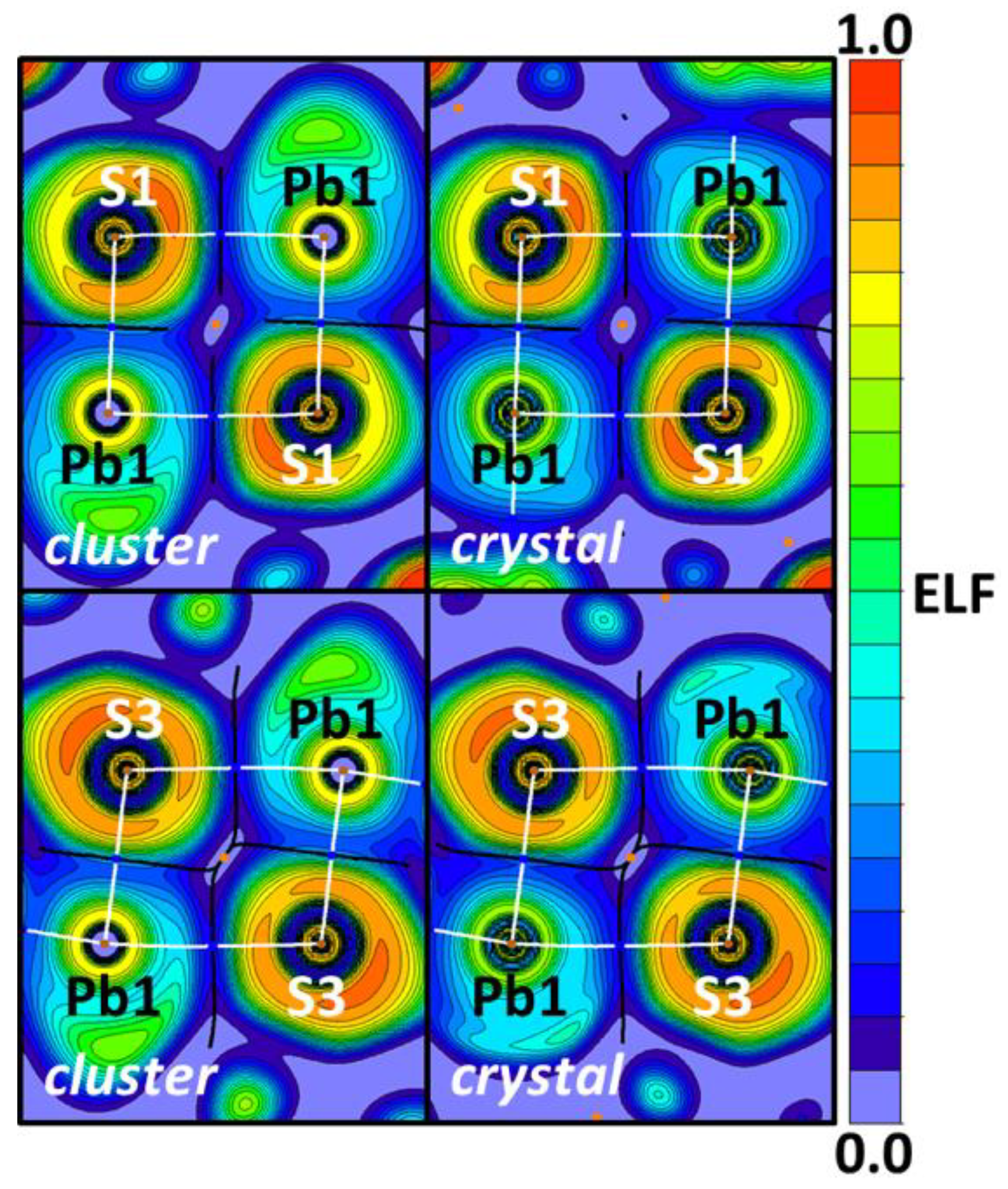
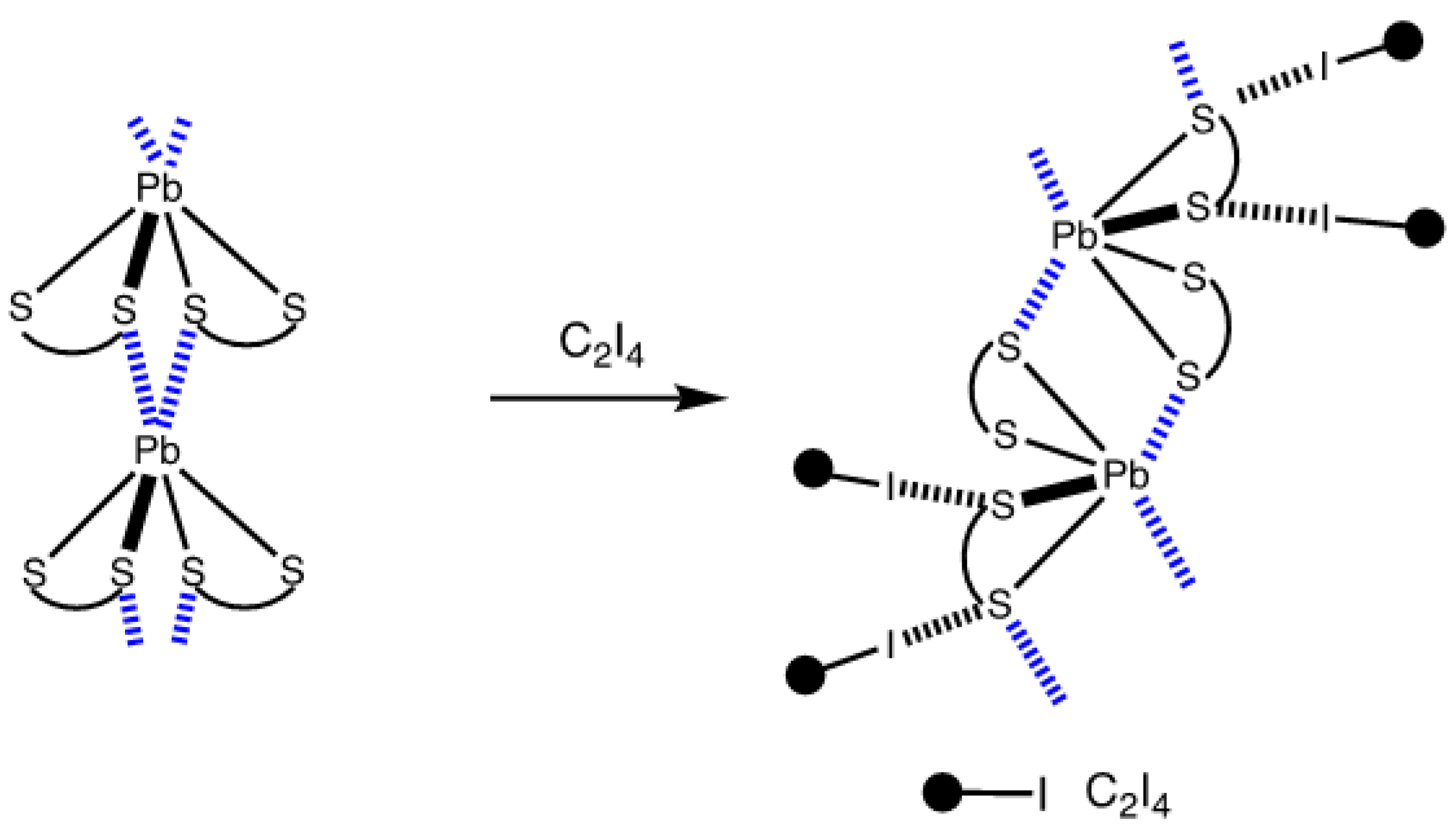
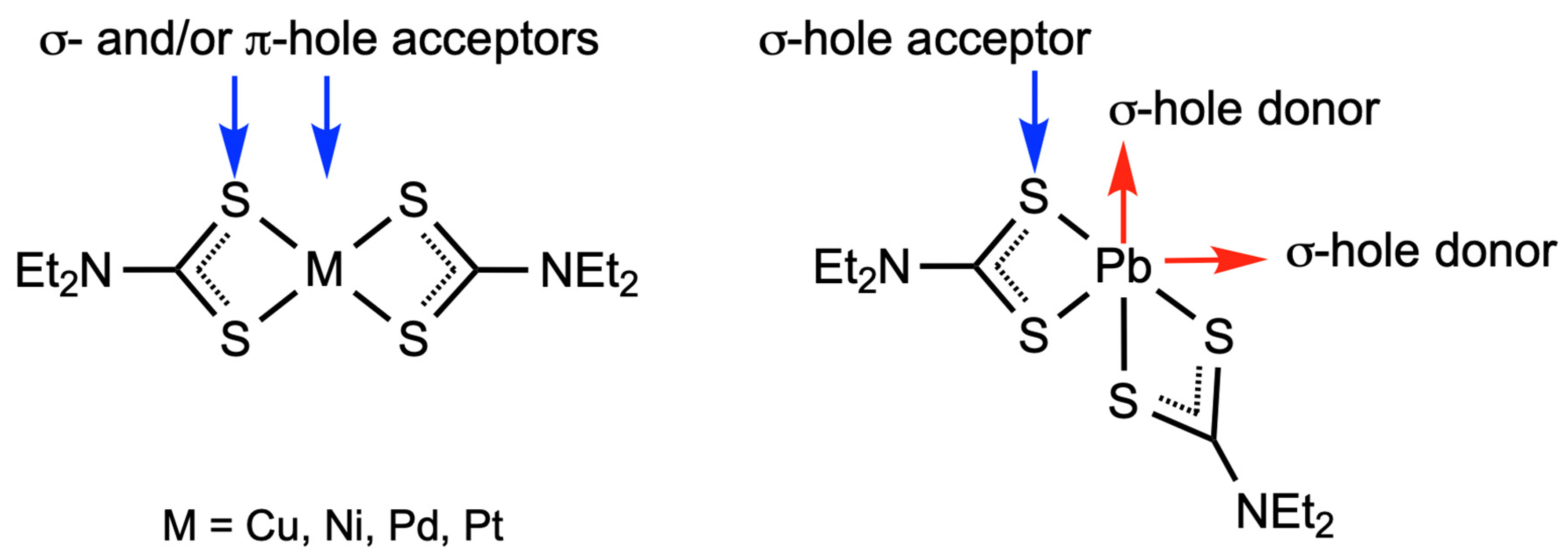
| Bond | Model | sign(λ2)ρ(r) | ▽2ρ(r) | G(r) | V(r) | Hb | WBI |
|---|---|---|---|---|---|---|---|
| C1S–I1S⋯S1 | crystal | −0.016 | 0.043 | 0.010 | −0.009 | 0.001 | |
| cluster | −0.016 | 0.038 | 0.009 | −0.008 | 0.001 | 0.08 | |
| C1S–I2S⋯S2 | crystal | −0.019 | 0.046 | 0.011 | −0.011 | 0.000 | |
| cluster | −0.018 | 0.042 | 0.010 | −0.009 | 0.001 | 0.10 | |
| S3–Pb1⋯S1 | crystal | −0.019 | 0.039 | 0.010 | −0.009 | 0.001 | |
| cluster | −0.019 | 0.038 | 0.010 | −0.010 | 0.000 | 0.14 | |
| S1–Pb1⋯S3 | crystal | −0.016 | 0.032 | 0.008 | −0.007 | 0.001 | |
| cluster | −0.016 | 0.032 | 0.008 | −0.008 | 0.000 | 0.09 |
| Cluster Type | Bond | ΔE |
|---|---|---|
| (1)∙(C2I4) | I1S⋯S1 | −11.37 |
| I2S⋯S2 | −7.26 | |
| (1)2 | Pb1⋯S1 | −7.78 a |
| Pb1⋯S3 | −5.41 a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelenkov, L.E.; Ivanov, D.M.; Tyumentsev, I.A.; Izotova, Y.A.; Kukushkin, V.Y.; Bokach, N.A. Structure-Directing Interplay between Tetrel and Halogen Bonding in Co-Crystal of Lead(II) Diethyldithiocarbamate with Tetraiodoethylene. Int. J. Mol. Sci. 2022, 23, 11870. https://doi.org/10.3390/ijms231911870
Zelenkov LE, Ivanov DM, Tyumentsev IA, Izotova YA, Kukushkin VY, Bokach NA. Structure-Directing Interplay between Tetrel and Halogen Bonding in Co-Crystal of Lead(II) Diethyldithiocarbamate with Tetraiodoethylene. International Journal of Molecular Sciences. 2022; 23(19):11870. https://doi.org/10.3390/ijms231911870
Chicago/Turabian StyleZelenkov, Lev E., Daniil M. Ivanov, Ilya A. Tyumentsev, Yulia A. Izotova, Vadim Yu. Kukushkin, and Nadezhda A. Bokach. 2022. "Structure-Directing Interplay between Tetrel and Halogen Bonding in Co-Crystal of Lead(II) Diethyldithiocarbamate with Tetraiodoethylene" International Journal of Molecular Sciences 23, no. 19: 11870. https://doi.org/10.3390/ijms231911870
APA StyleZelenkov, L. E., Ivanov, D. M., Tyumentsev, I. A., Izotova, Y. A., Kukushkin, V. Y., & Bokach, N. A. (2022). Structure-Directing Interplay between Tetrel and Halogen Bonding in Co-Crystal of Lead(II) Diethyldithiocarbamate with Tetraiodoethylene. International Journal of Molecular Sciences, 23(19), 11870. https://doi.org/10.3390/ijms231911870









