Mechanical Properties of Human Bronchial Epithelial Cells Expressing Wt- and Mutant CFTR
Abstract
1. Introduction
2. Results
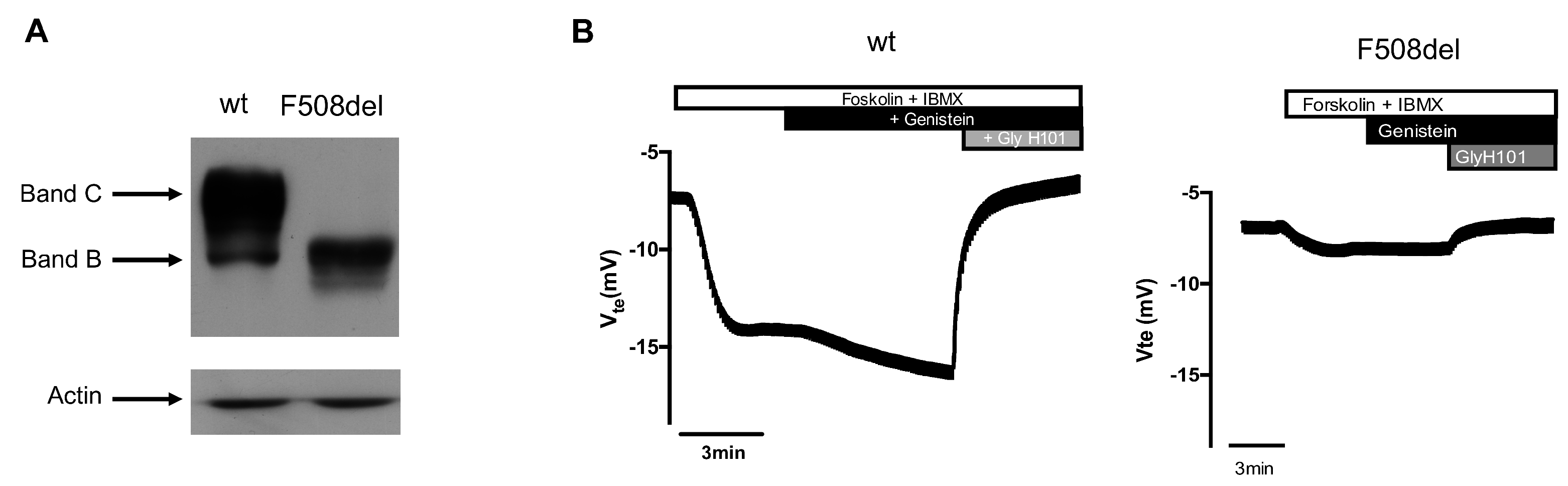
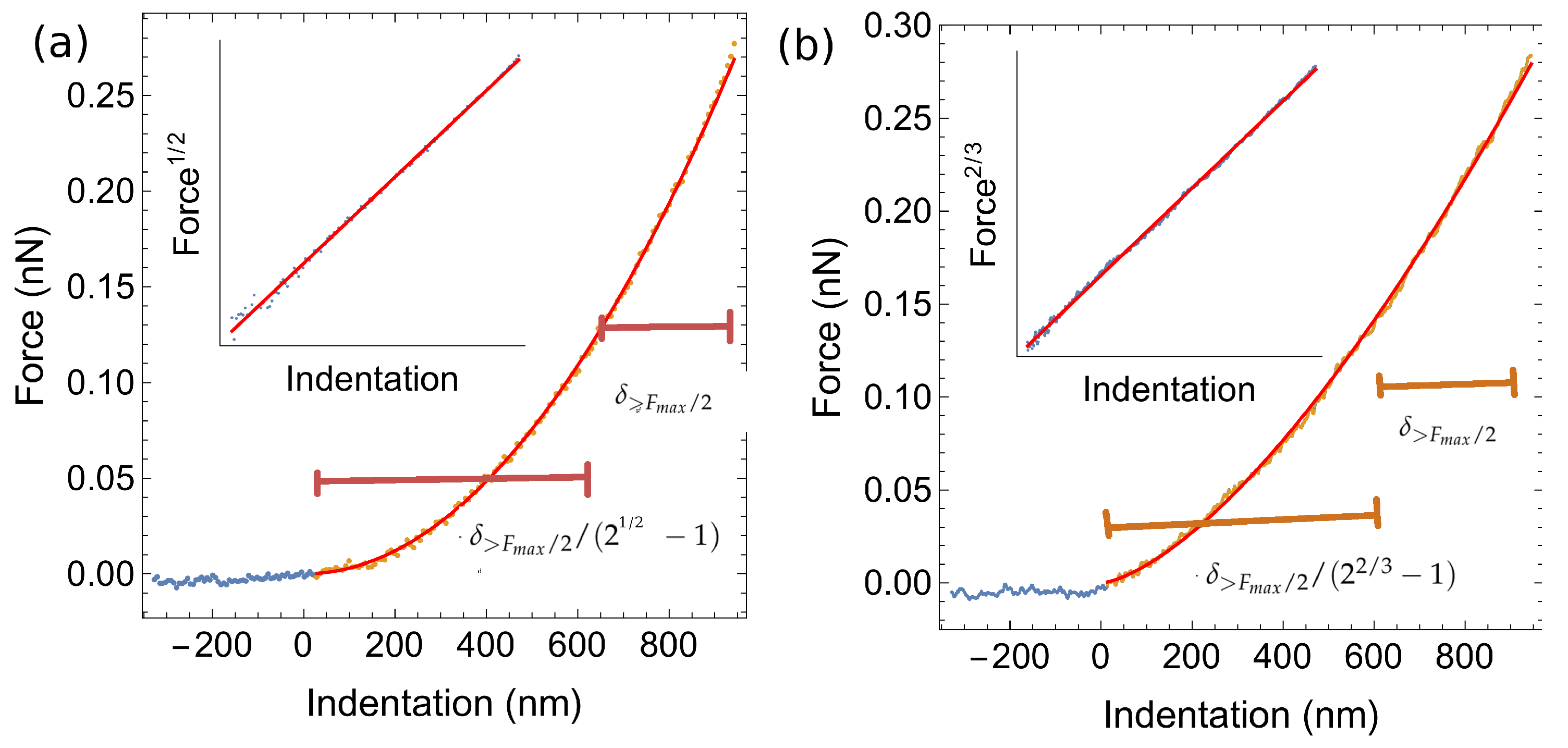
2.1. Atomic Force Microscopy Indentation Tests
2.2. Force Feedback Microscopy Indentation Tests
3. Discussion
4. Materials and Methods
4.1. Cell Culture
4.2. Atomic Force Microscopy
4.3. Force Feedback Microscopy
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| FFM | Force Feedback Microscopy |
| CF | Cystic fibrosis |
| CFBE | Cystic Fibrosis Bronchial Epithelial Cells |
| CFTR | Cystic fibrosis transmembrane conductance regulator |
| LD | linear dichroism |
References
- Stutts, M.J.; Canessa, C.M.; Olsen, J.C.; Hamrick, M.; Cohn, J.A.; Rossier, B.C.; Boucher, R.C. CFTR as a cAMP-dependent regulator of sodium channels. Science 1995, 269, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Boucher, R. New concepts of the pathogenesis of cystic fibrosis lung disease. Eur. Respir. J. 2004, 23, 146–158. [Google Scholar] [CrossRef]
- Li, C.; Naren, A.P. Macromolecular complexes of cystic fibrosis transmembrane conductance regulator and its interacting partners. Pharmacol. Ther. 2005, 108, 208–223. [Google Scholar] [CrossRef] [PubMed]
- Cheung, J.C.; Deber, C.M. Misfolding of the cystic fibrosis transmembrane conductance regulator and disease. Biochemistry 2008, 47, 1465–1473. [Google Scholar] [CrossRef] [PubMed]
- Riordan, J.R. CFTR function and prospects for therapy. Annu. Rev. Biochem. 2008, 77, 701–726. [Google Scholar] [CrossRef] [PubMed]
- Farinha, C.M. CFTR and Cystic Fibrosis. In CFTR and Cystic Fibrosis; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–56. [Google Scholar]
- Voltz, J.W.; Weinman, E.J.; Shenolikar, S. Expanding the role of NHERF, a PDZ-domain containing protein adapter, to growth regulation. Oncogene 2001, 20, 6309. [Google Scholar] [CrossRef]
- Lobo, M.J.; Amaral, M.D.; Zaccolo, M.; Farinha, C.M. EPAC1 activation by cAMP stabilizes CFTR at the membrane by promoting its interaction with NHERF1. J. Cell Sci. 2016, 129, 2599–2612. [Google Scholar] [CrossRef]
- Ganeshan, R.; Nowotarski, K.; Di, A.; Nelson, D.J.; Kirk, K.L. CFTR surface expression and chloride currents are decreased by inhibitors of N-WASP and actin polymerization. Biochim. Et Biophys. Acta (BBA) Mol. Cell Res. 2007, 1773, 192–200. [Google Scholar] [CrossRef]
- Okiyoneda, T.; Lukacs, G.L. Cell surface dynamics of CFTR: The ins and outs. Biochim. Et Biophys. Acta (BBA) Mol. Cell Res. 2007, 1773, 476–479. [Google Scholar] [CrossRef]
- Favia, M.; Guerra, L.; Fanelli, T.; Cardone, R.A.; Monterisi, S.; Di Sole, F.; Castellani, S.; Chen, M.; Seidler, U.; Reshkin, S.J.; et al. Na+/H+ exchanger regulatory factor 1 overexpression-dependent increase of cytoskeleton organization is fundamental in the rescue of F508del cystic fibrosis transmembrane conductance regulator in human airway CFBE41o-cells. Mol. Biol. Cell 2010, 21, 73–86. [Google Scholar] [CrossRef]
- Krieg, M.; Fläschner, G.; Alsteens, D.; Gaub, B.M.; Roos, W.H.; Wuite, G.J.; Gaub, H.E.; Gerber, C.; Dufrêne, Y.F.; Müller, D.J. Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 2018, 1, 41–57. [Google Scholar] [CrossRef]
- Kuznetsova, T.G.; Starodubtseva, M.N.; Yegorenkov, N.I.; Chizhik, S.A.; Zhdanov, R.I. Atomic force microscopy probing of cell elasticity. Micron 2007, 38, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Haase, K.; Pelling, A.E. Investigating cell mechanics with atomic force microscopy. J. R. Soc. Interface 2015, 12, 20140970. [Google Scholar] [CrossRef] [PubMed]
- Hertz, H. MiSCellane0us PaperS; Jones, D.E.; Schott, G.A., Translators; MaCimillan: New York, NY, USA, 1896; pp. 146–162. [Google Scholar]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Rodrigues, M.S.; Costa, L.; Chevrier, J.; Comin, F. Why do atomic force microscopy force curves still exhibit jump to contact? Appl. Phys. Lett. 2012, 101, 203105. [Google Scholar] [CrossRef]
- Bebok, Z.; Collawn, J.F.; Wakefield, J.; Parker, W.; Li, Y.; Varga, K.; Sorscher, E.J.; Clancy, J. Failure of cAMP agonists to activate rescued ΔF508 CFTR in CFBE41o–airway epithelial monolayers. J. Physiol. 2005, 569, 601–615. [Google Scholar] [CrossRef]
- Rodrigues, M.S.; Costa, L.; Chevrier, J.; Comin, F. System analysis of force feedback microscopy. J. Appl. Phys. 2014, 115, 054309. [Google Scholar] [CrossRef]
- Vitorino, M.V.; Vieira, A.; Marques, C.A.; Rodrigues, M.S. Direct measurement of the capillary condensation time of a water nanobridge. Sci. Rep. 2018, 8, 13848. [Google Scholar] [CrossRef]
- Kim, S.O.; Kim, J.; Okajima, T.; Cho, N.J. Mechanical properties of paraformaldehyde-treated individual cells investigated by atomic force microscopy and scanning ion conductance microscopy. Nano Converg. 2017, 4, 5. [Google Scholar] [CrossRef]
- van Helvert, S.; Friedl, P. Strain Stiffening of Fibrillar Collagen during Individual and Collective Cell Migration Identified by AFM Nanoindentation. ACS Appl. Mater. Interfaces 2016, 8, 21946–21955. [Google Scholar] [CrossRef]
- Yang, C.; DelRio, F.W.; Ma, H.; Killaars, A.R.; Basta, L.P.; Kyburz, K.A.; Anseth, K.S. Spatially patterned matrix elasticity directs stem cell fate. Proc. Natl. Acad. Sci. USA 2016, 113, E4439–E4445. [Google Scholar] [CrossRef] [PubMed]
- Pyka-Fościak, G.; Zemła, J.; Lis, G.; Litwin, J.; Lekka, M. Changes in spinal cord stiffness in the course of experimental autoimmune encephalomyelitis, a mouse model of multiple sclerosis. Arch. Biochem. Biophys. 2020, 680, 108221. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.A.; Vitorino, M.V.; Robalo, T.; Rodrigues, M.S.; Sá-Correia, I. Variation of Burkholderia cenocepacia cell wall morphology and mechanical properties during cystic fibrosis lung infection, assessed by atomic force microscopy. Sci. Rep. 2019, 9, 16118. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.; Lekka, M.; Stylianopoulos, T. AFM assessing of nanomechanical fingerprints for cancer early diagnosis and classification: From single cell to tissue level. Nanoscale 2018, 10, 20930–20945. [Google Scholar] [CrossRef]
- Guedes, A.F.; Carvalho, F.A.; Malho, I.; Lousada, N.; Sargento, L.; Santos, N.C. Atomic force microscopy as a tool to evaluate the risk of cardiovascular diseases in patients. Nat. Nanotechnol. 2016, 11, 687–692. [Google Scholar] [CrossRef]
- Lasalvia, M.; Castellani, S.; D’Antonio, P.; Perna, G.; Carbone, A.; Colia, A.L.; Maffione, A.B.; Capozzi, V.; Conese, M. Human airway epithelial cells investigated by atomic force microscopy: A hint to cystic fibrosis epithelial pathology. Exp. Cell Res. 2016, 348, 46–55. [Google Scholar] [CrossRef]
- Takahashi, A.; Watanabe, T.; Mondal, A.; Suzuki, K.; Kurusu-Kanno, M.; Li, Z.; Yamazaki, T.; Fujiki, H.; Suganuma, M. Mechanism-based inhibition of cancer metastasis with (-)-epigallocatechin gallate. Biochem. Biophys. Res. Commun. 2014, 443, 1–6. [Google Scholar] [CrossRef]
- Luo, Q.; Kuang, D.; Zhang, B.; Song, G. Cell stiffness determined by atomic force microscopy and its correlation with cell motility. Biochim. Et Biophys. Acta (BBA) Gen. Subj. 2016, 1860, 1953–1960. [Google Scholar] [CrossRef]
- Carl, P.; Schillers, H. Elasticity measurement of living cells with an atomic force microscope: Data acquisition and processing. Pflügers Arch. Eur. J. Physiol. 2008, 457, 551. [Google Scholar] [CrossRef]
- Sader, J.E.; Chon, J.W.; Mulvaney, P. Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instruments 1999, 70, 3967–3969. [Google Scholar] [CrossRef]
- Schillers, H.; Rianna, C.; Schäpe, J.; Luque, T.; Doschke, H.; Wälte, M.; Uriarte, J.J.; Campillo, N.; Michanetzis, G.P.; et al. Standardized nanomechanical atomic force microscopy procedure (SNAP) for measuring soft and biological samples. Sci. Rep. 2017, 7, 5117. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carapeto, A.P.; Vitorino, M.V.; Santos, J.D.; Ramalho, S.S.; Robalo, T.; Rodrigues, M.S.; Farinha, C.M. Mechanical Properties of Human Bronchial Epithelial Cells Expressing Wt- and Mutant CFTR. Int. J. Mol. Sci. 2020, 21, 2916. https://doi.org/10.3390/ijms21082916
Carapeto AP, Vitorino MV, Santos JD, Ramalho SS, Robalo T, Rodrigues MS, Farinha CM. Mechanical Properties of Human Bronchial Epithelial Cells Expressing Wt- and Mutant CFTR. International Journal of Molecular Sciences. 2020; 21(8):2916. https://doi.org/10.3390/ijms21082916
Chicago/Turabian StyleCarapeto, Ana P., Miguel V. Vitorino, João D. Santos, Sofia S. Ramalho, Tiago Robalo, Mário S. Rodrigues, and Carlos M. Farinha. 2020. "Mechanical Properties of Human Bronchial Epithelial Cells Expressing Wt- and Mutant CFTR" International Journal of Molecular Sciences 21, no. 8: 2916. https://doi.org/10.3390/ijms21082916
APA StyleCarapeto, A. P., Vitorino, M. V., Santos, J. D., Ramalho, S. S., Robalo, T., Rodrigues, M. S., & Farinha, C. M. (2020). Mechanical Properties of Human Bronchial Epithelial Cells Expressing Wt- and Mutant CFTR. International Journal of Molecular Sciences, 21(8), 2916. https://doi.org/10.3390/ijms21082916





