Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface
Abstract
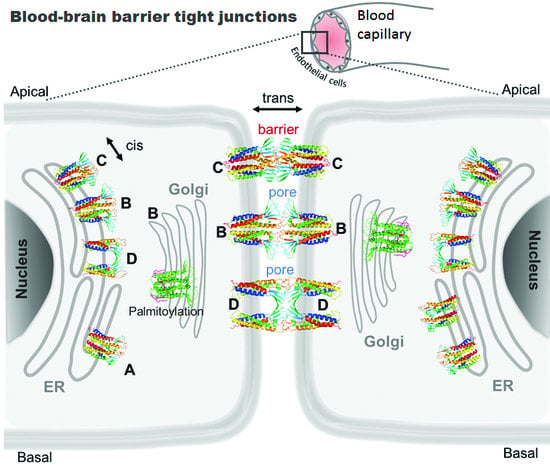
1. The Blood–Brain Barrier
2. Tight Junctions: Role of Claudin-5 in the BBB
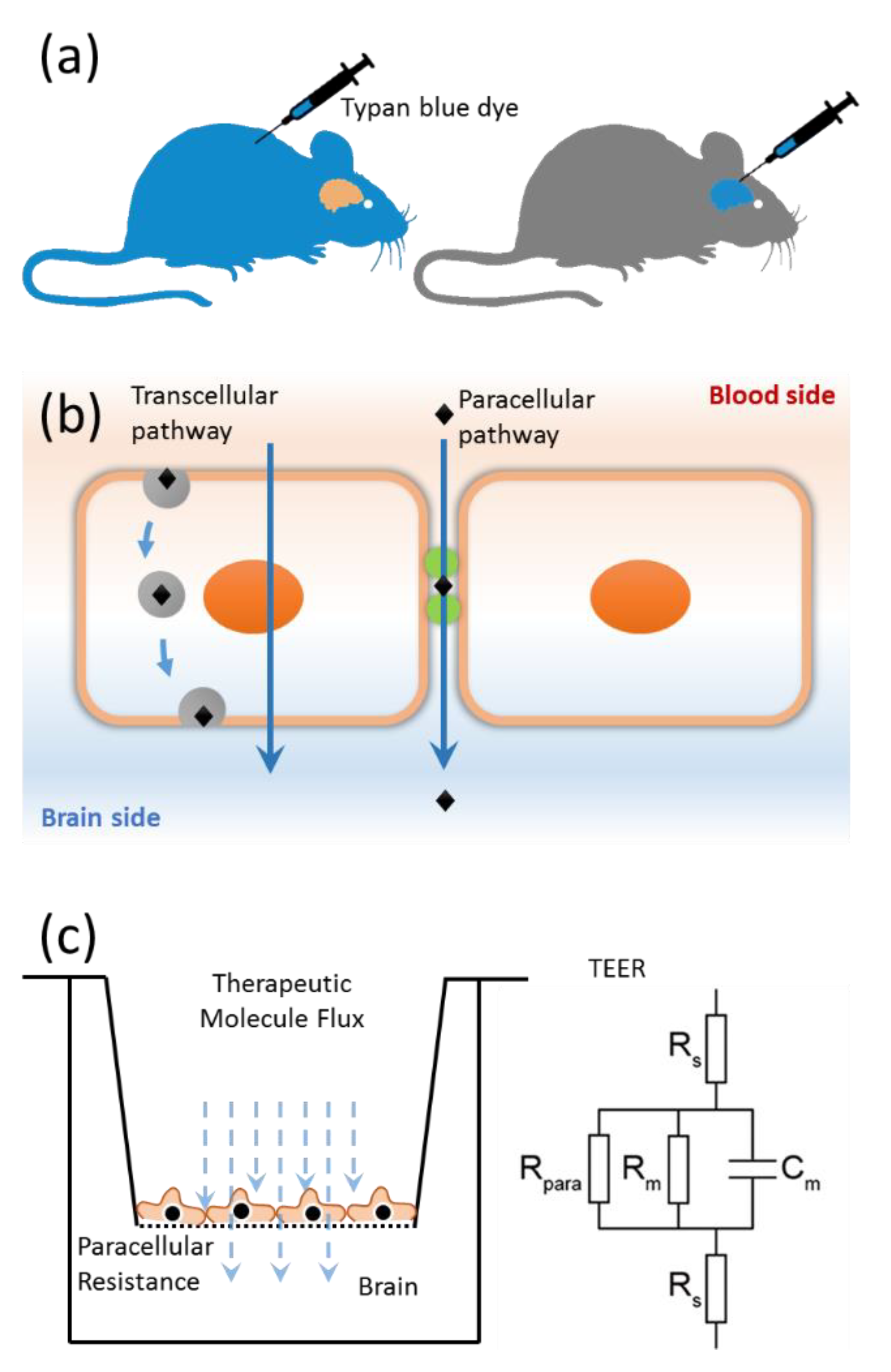
3. Need for Computational Modeling
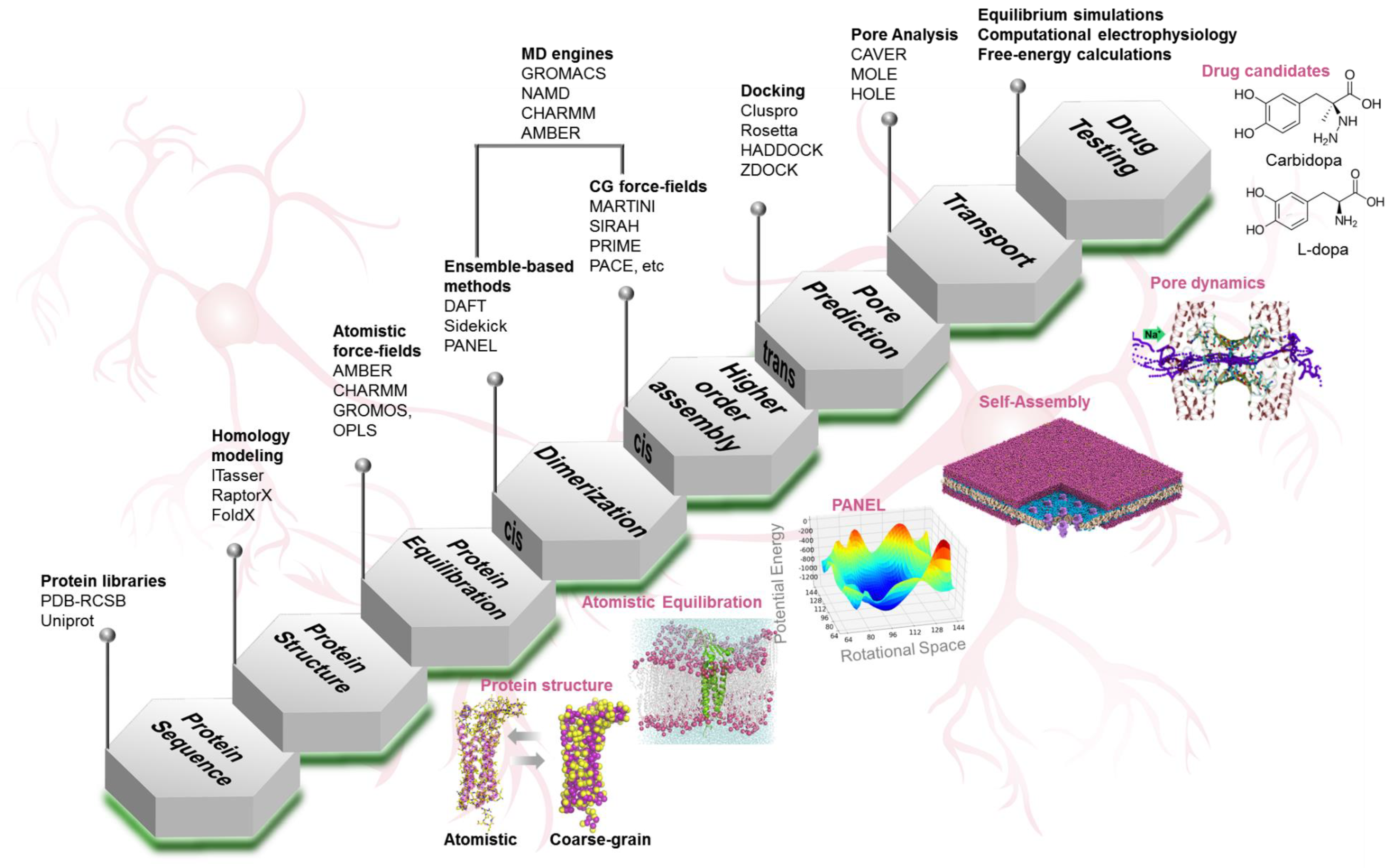
4. Computational Toolkit
4.1. Protein Structure Prediction
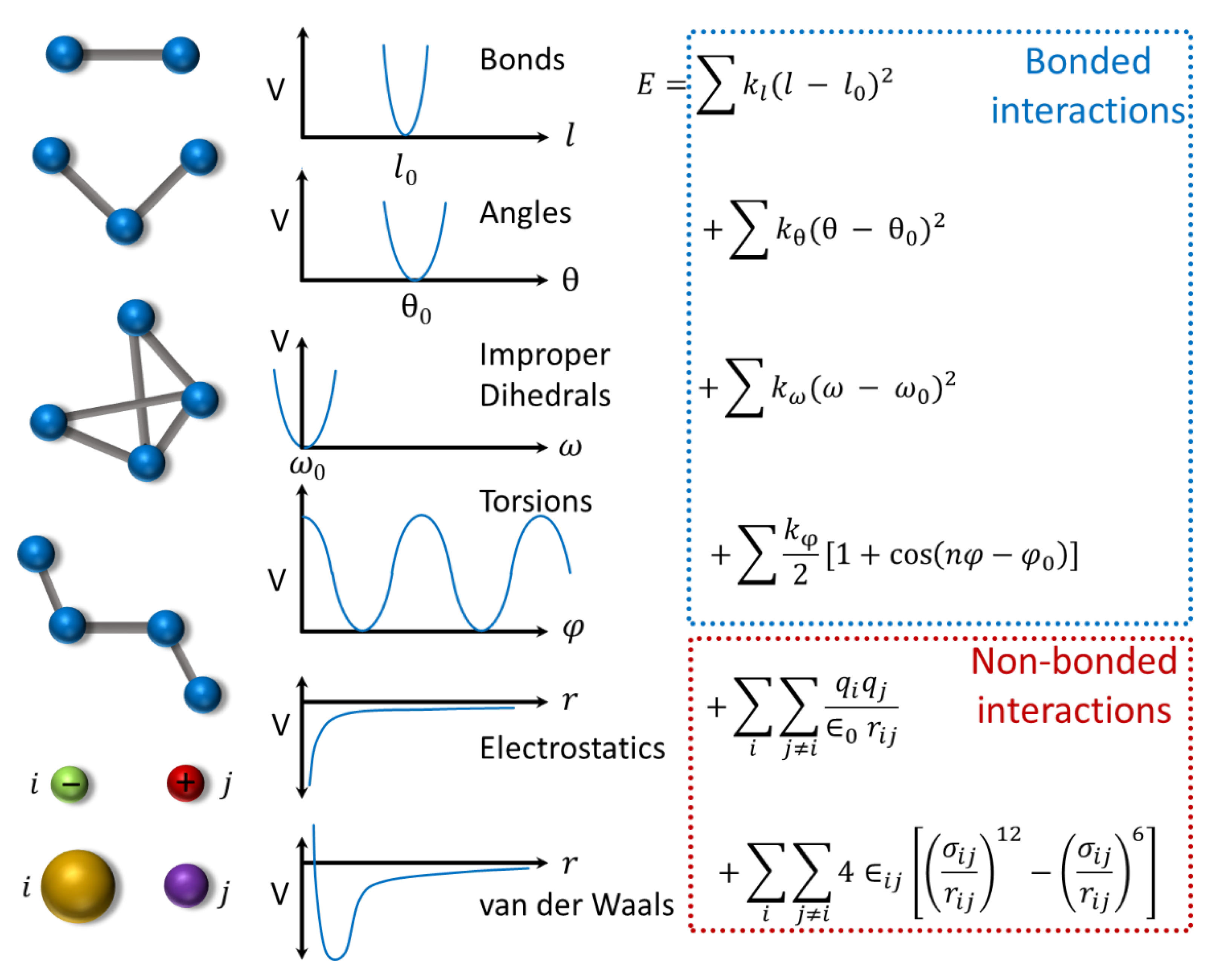
4.2. Protein Dynamics
4.3. Protein–Protein Interactions
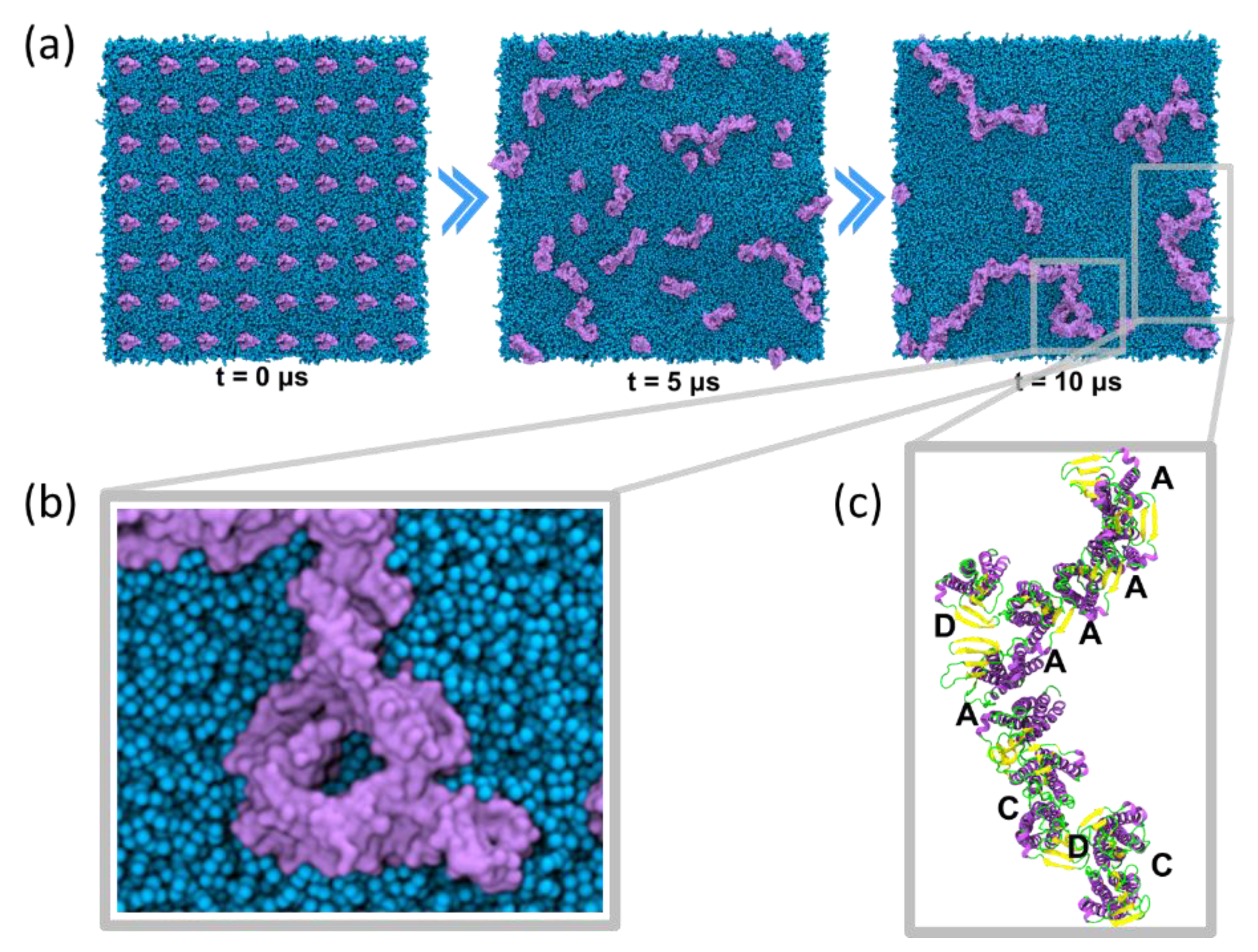
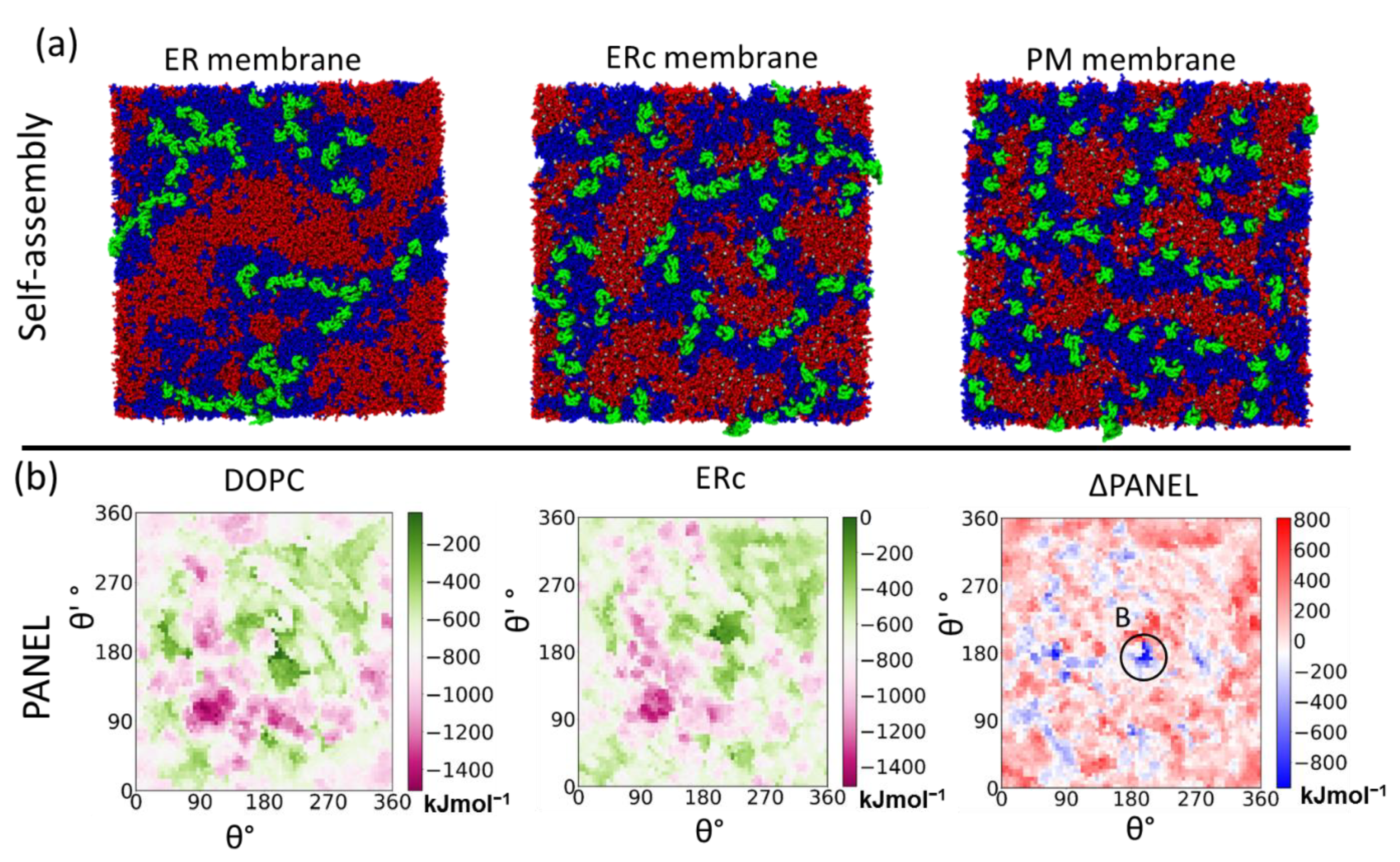
4.3.1. Self-Assembly Simulations
4.3.2. Molecular Docking
4.3.3. Protein Association Energy Landscape
4.4. Pore Characterization and Paracellular Transport
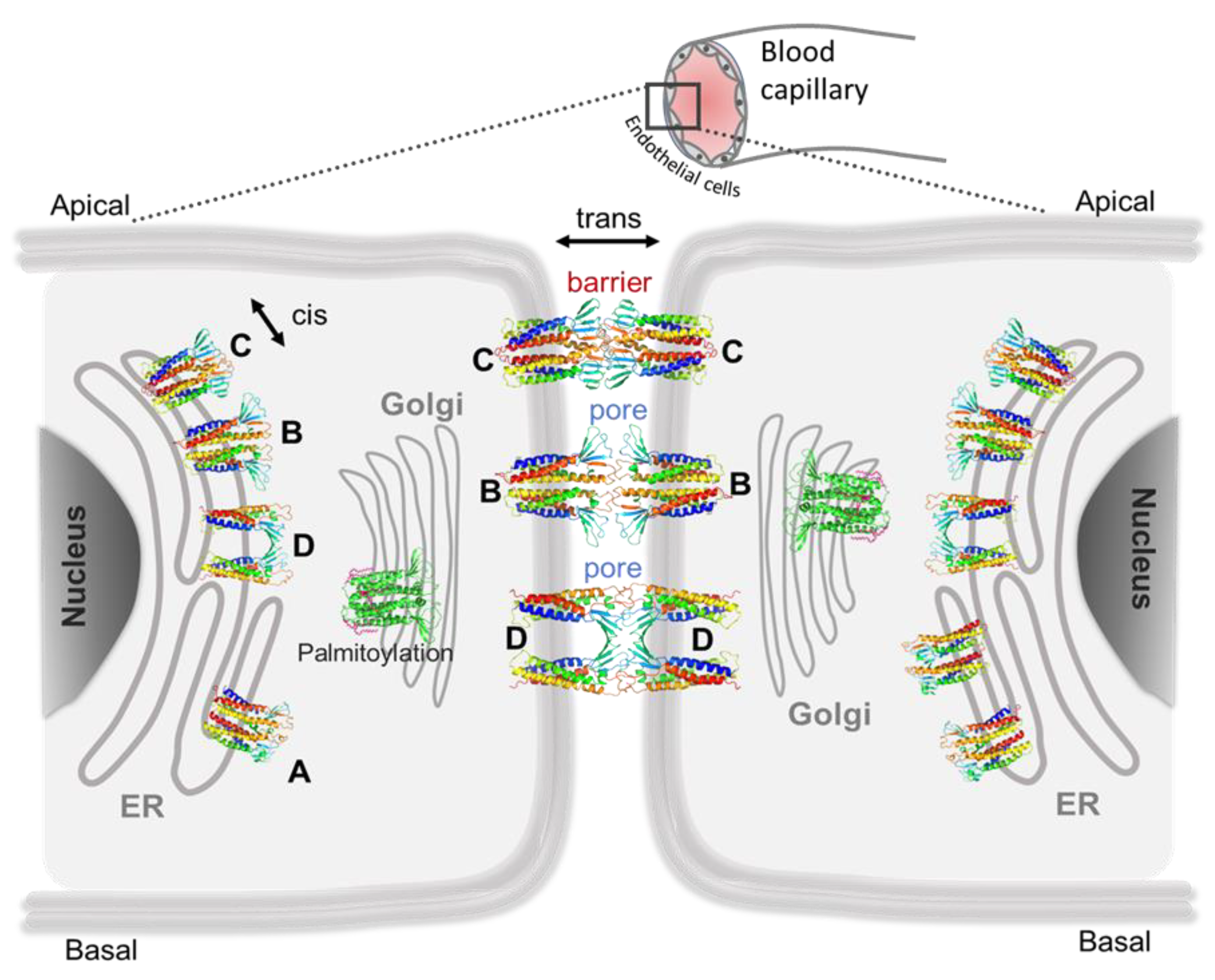
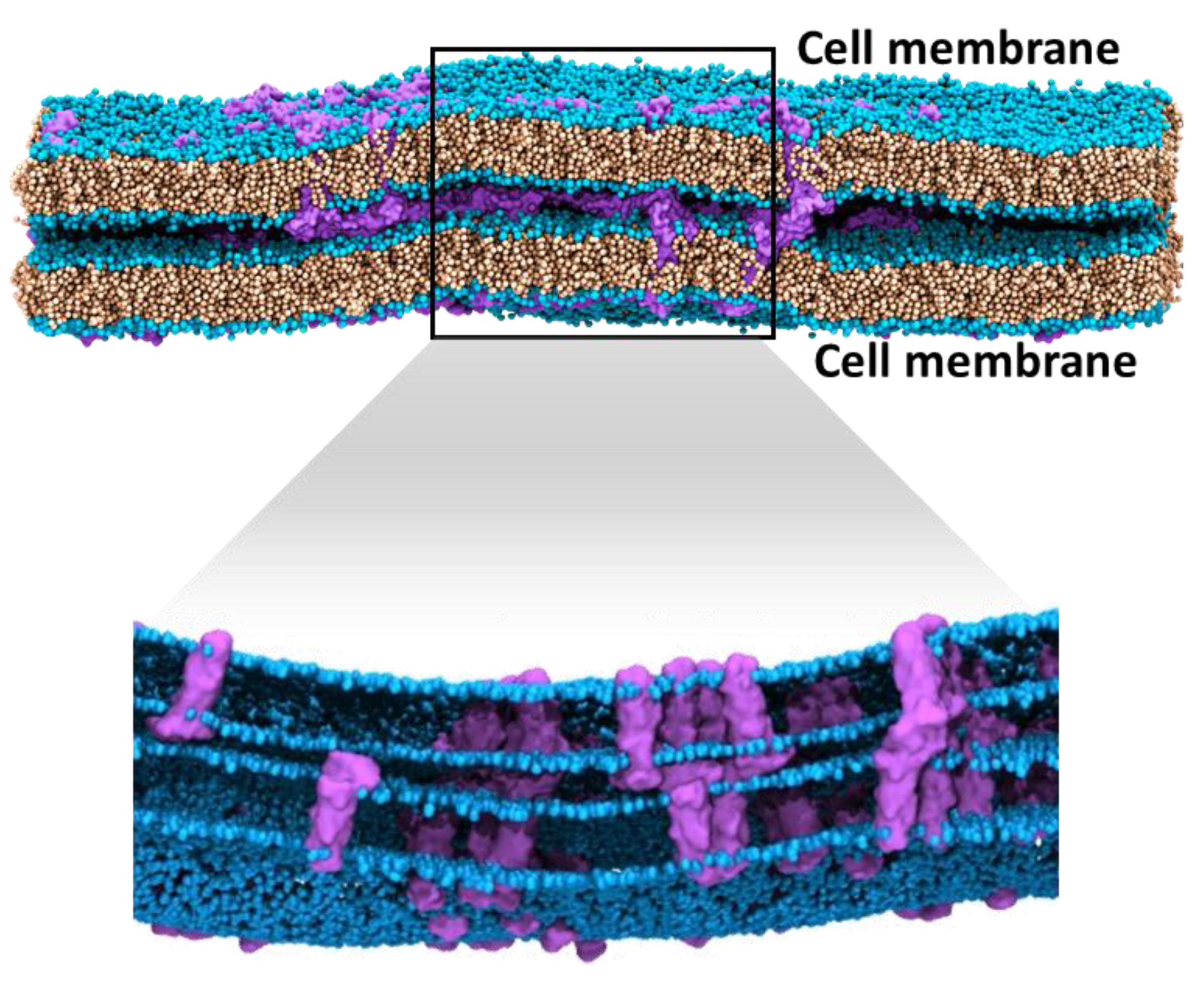
5. Computational Nanoscopy of Claudin-5 in BBB Tight Junction Architecture
- (1)
- How do claudin proteins form contiguous strands? Do the claudin proteins have preferred cis conformations?
- (2)
- Where along the secretory pathway do claudin-5 proteins undergo cis assembly?
- (3)
- How do posttranslational modifications of claudin-5 influence the cis interactions?
- (4)
- How are TJ pores and barriers formed?
- (5)
- How do BBB TJs get their size and change selectivity?
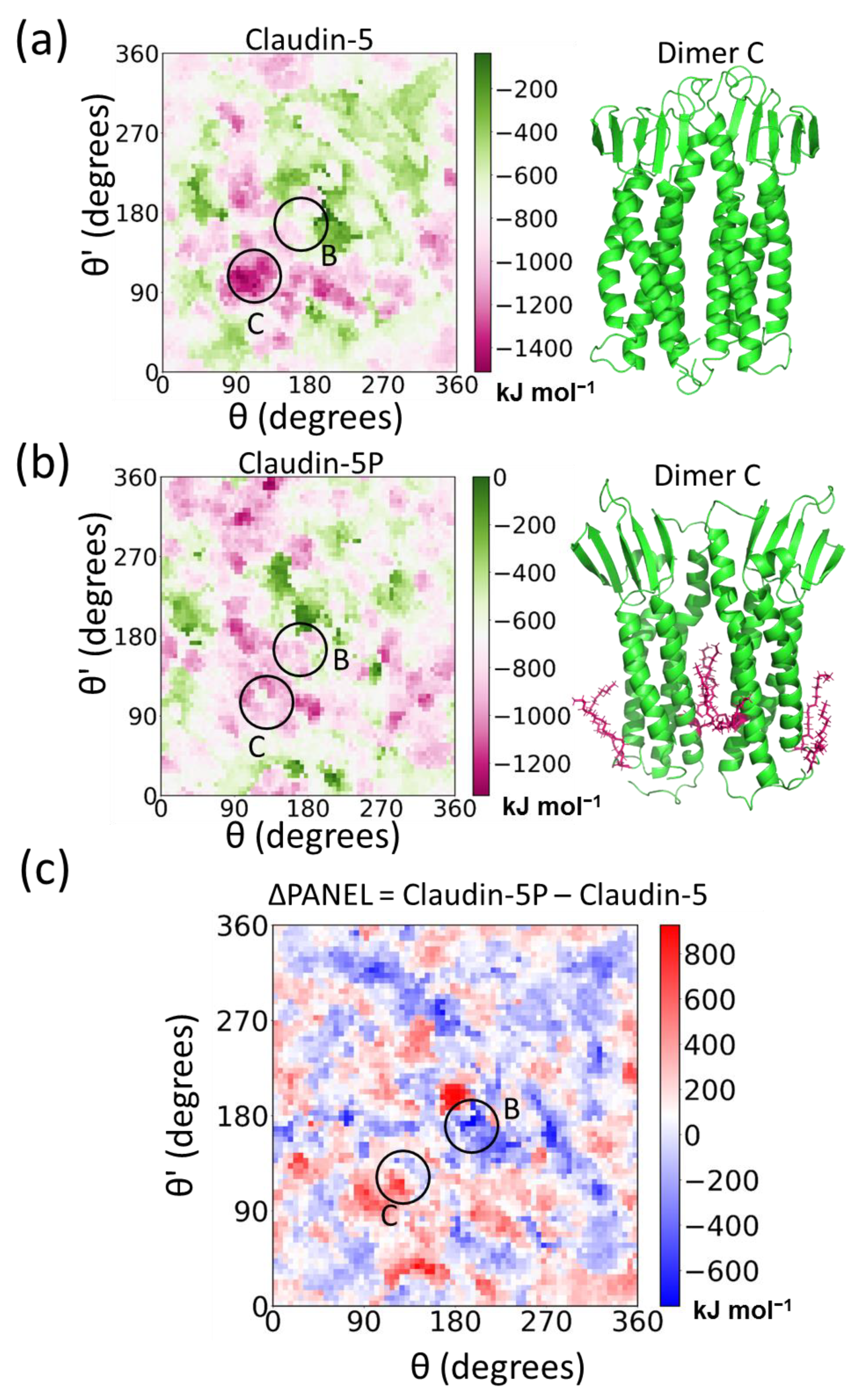
5.1. Claudin-5 Forms Symmetric and Asymmetric Dimer Conformations that Form Contiguous Strands
5.2. Primary Cis Interactions Occur Early in the Secretory Pathway
5.3. Posttranslational Modifications Alter Relative Stability of cis Dimers
5.4. Cis Dimers Act as Precursors to Form Trans Interfaces
5.5. Sub-Nanometer Wide Claudin-5 TJ Pores, Lined by Charged Residue Determine Pore Selectivity
6. Additional Factors that Influence Tight Junctions
6.1. Higher Order Claudin Aggregates
6.2. Involvement of Other TJ Proteins: Key to TJ Structural Stability
6.3. Cytoskeletal Involvement
7. Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BBB | Blood–brain barrier |
| CG | Coarse grained |
| Claudin-5P | Palmitoylated claudin |
| DAFT | Docking assay for transmembrane |
| DHHC | Aspartate-Histidine-Histidine-Cysteine |
| DOPC | 1,2-dioleoyl-sn-glycero-3-phosphocholine |
| ECL | Extracellular loop |
| ER | Endoplasmic Reticulum |
| ERc | Cholesterol enriched Endoplasmic Reticulum |
| ICL | Intracellular loop |
| JAMS | Junctional adhesion molecules |
| MD | Molecular dynamics |
| PANEL | Protein Association Energy Landscape |
| TEER | Transendothelial/epithelial electrical resistance |
| TJ | Tight junction |
| TM | Transmembrane loop |
| ZO | Zonula Occuldens |
References
- Abbott, N.J. Comparative Physiology of the Blood-Brain Barrier. In Physiology and Pharmacology of the Blood-Brain Barrier; Bradbury, M.W.B., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 371–396. [Google Scholar]
- Bauer, H.C.; Krizbai, I.A.; Bauer, H.; Traweger, A. “You Shall Not Pass”-tight junctions of the blood brain barrier. Front. Neurosci. 2014, 8, 392. [Google Scholar] [CrossRef] [PubMed]
- Begley, D.J.; Brightman, M.W. Structural and functional aspects of the blood-brain barrier. In Peptide Transport and Delivery into the Central Nervous System; Prokai, L., Prokai-Tatrai, K., Eds.; Birkhäuser Basel: Basel, Switzerland, 2003; pp. 39–78. [Google Scholar]
- Daneman, R.; Prat, A. The blood-brain barrier. Cold Spring Harb. Perspect. Biol. 2015, 7, a020412. [Google Scholar] [CrossRef] [PubMed]
- Saunders, N.R.; Dreifuss, J.-J.; Dziegielewska, K.M.; Johansson, P.A.; Habgood, M.D.; Møllgård, K.; Bauer, H.-C. The rights and wrongs of blood-brain barrier permeability studies: A walk through 100 years of history. Front. Neurosci. 2014, 8, 404. [Google Scholar] [CrossRef] [PubMed]
- Lewandowsky, M. Zur Lehre von der Cerebrospinalflüssgkeit. Z. Clin. Med. 1900, 40, 480–494. [Google Scholar]
- Goldmann, E.E. Die äussere und innere Sekretion des gesunden und kranken Organismus im Lichte der ‘vitalen Färbung. Beiträg Klin. Chir. 1909, 64, 192–265. [Google Scholar]
- Goldmann, E.E. Vitalfärbung am Zentralnervensyatem. Beitrag zur Physio-Pathologie des plexus chorioideus und der Hirnhäute. Abh. Preuss Akad. Wiss. Phys. Math. Kl. 1913, 1, 1–60. [Google Scholar]
- Ehrlich, P. The Relations Existing between Chemical Constitution, Distribution and Pharmacological Action; Collected Studies on Immunity New York: John Wiley & Sons, translated by C Bolduana from Ch XXXIV of Gesammelte Arbeiten zur Immunitätsforschung; Ehrlich, P., Ed.; Hirschwald: Berlin, Germany, 1906. [Google Scholar]
- Ehrlich, P. Das Sauerstoffbedürfnis des Organismus. In Eine Farbenanalytische Studie; Hirschwald: Berlin, Germany, 1885. [Google Scholar]
- Stern, L.; Gautier, R. II.—Les Rapports Entre Le Liquide Céphalo-Rachidien Et Les éléments Nerveux De L’axe Cerebrospinal. Arch. Int. Physiol. 1922, 17, 391–448. [Google Scholar] [CrossRef]
- Stern, L.; Gautier, R. III.—Rapports Entre Le Liquide Céphalo-Rachidien Des Espaces Ventriculaires Et Celui Des Espaces Sous-Arachnoïdiens. Arch. Int. Physiol. 1923, 20, 403–436. [Google Scholar] [CrossRef]
- Stern, L.; Gautier, R. Passage simultané des substances dans le liquide céphalo-rachidien et dans les centres nerveux. Rcr D. Ia Soc. De Phys. Et D’hist. Natur. De Genève 1918, 35, 58–60. [Google Scholar]
- Stern, L.; Gautier, R. Le passage dans le liquide céphalo-rachidien de substances introduites dans la circulation et leur action sur le système nerveux central chez les différentes espèces animales. Rcr D. Ia Soc. De Phys. Et D’hist. Natur. De Genève 1918, 35, 91–94. [Google Scholar]
- Stern, L.; Gautier, R. Recherches sur le liquide céphalo-rachidien. 1. Les rapports entre le liquide céphalo-rachidien et la circulation sanguine. Arch. Int. Physiol. 1921, 17, 138–192. [Google Scholar] [CrossRef]
- Roux, E.; Borrel, A. Tétanos cérébral et immunité contre le tétanus. Ann. Inst. Pasteur 1898, 12, 225–239. [Google Scholar]
- Bouffard, G. Injection des couleurs de benzidine aux animaux normaux. Ann. D. L’lnst. Pasteur. Paris 1906, 20, 539–548. [Google Scholar]
- Weed, L.H. An anatomical consideration of the cerebro-spinal fluid. Anat. Res. 1917, 461–496. [Google Scholar] [CrossRef]
- Weed, L.H. The development of the cerebrospinal fluid spaces in pig and in man. Contrib. Embryol. Carnegie Inst. 1917, 5, 3–116. [Google Scholar]
- Wislocki, G.B. Experimental studies on fetal absorption. I. The vitality stained fetus. Embryol. Carnegie Inst. 1920, 11, 45–60. [Google Scholar]
- Cohen, H.; Davies, S. The Morphology and Permeability of the Roof of the Fourth Ventricle in some Mammalian Embryos. J. Anat. 1938, 72, 430–455. [Google Scholar]
- Friedemann, U. Blood-brain barrier. Physiol. Rev. 1942, 22, 125–145. [Google Scholar] [CrossRef]
- Wolburg, H.; Lippoldt, A. Tight junctions of the blood–brain barrier: Development, composition and regulation. Vasc. Pharmacol. 2002, 38, 323–337. [Google Scholar] [CrossRef]
- Duelli, R.; Kuschinsky, W. Brain Glucose Transporters: Relationship to Local Energy Demand. Physiology 2001, 16, 71–76. [Google Scholar] [CrossRef]
- Howarth, C.; Gleeson, P.; Attwell, D. Updated energy budgets for neural computation in the neocortex and cerebellum. J. Cereb. Blood Flow Metab. 2012, 32, 1222–1232. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.; Jolivet, R.; Attwell, D. Synaptic Energy Use and Supply. Neuron 2012, 75, 762–777. [Google Scholar] [CrossRef] [PubMed]
- Mergenthaler, P.; Lindauer, U.; Dienel, G.A.; Meisel, A. Sugar for the brain: The role of glucose in physiological and pathological brain function. Trends Neurosci. 2013, 36, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Patching, S.G. Glucose Transporters at the Blood-Brain Barrier: Function, Regulation and Gateways for Drug Delivery. Mol. Neurobiol. 2017, 54, 1046–1077. [Google Scholar] [CrossRef]
- Abbott, N.J. Inflammatory Mediators and Modulation of Blood–Brain Barrier Permeability. Cell. Mol. Neurobiol. 2000, 20, 131–147. [Google Scholar] [CrossRef]
- Huber, J.D.; Egleton, R.D.; Davis, T.P. Molecular physiology and pathophysiology of tight junctions in the blood–brain barrier. Trends Neurosci. 2001, 24, 719–725. [Google Scholar] [CrossRef]
- Pardridge, W.M. Drug and Gene Delivery to the Brain: The Vascular Route. Neuron 2002, 36, 555–558. [Google Scholar] [CrossRef]
- Ballabh, P.; Braun, A.; Nedergaard, M. The blood–brain barrier: An overview: Structure, regulation, and clinical implications. Neurobiol. Dis. 2004, 16, 1–13. [Google Scholar] [CrossRef]
- Hawkins, B.T.; Davis, T.P. The Blood-Brain Barrier/Neurovascular Unit in Health and Disease. Pharmacol. Rev. 2005, 57, 173. [Google Scholar] [CrossRef]
- Kniesel, U.; Wolburg, H. Tight Junctions of the Blood–Brain Barrier. Cell. Mol. Neurobiol. 2000, 20, 57–76. [Google Scholar] [CrossRef]
- Luissint, A.-C.; Artus, C.; Glacial, F.; Ganeshamoorthy, K.; Couraud, P.-O. Tight junctions at the blood brain barrier: Physiological architecture and disease-associated dysregulation. Fluids Barriers CNS 2012, 9, 23. [Google Scholar] [CrossRef] [PubMed]
- Greene, C.; Campbell, M. Tight junction modulation of the blood brain barrier: CNS delivery of small molecules. Tissue Barriers 2016, 4, e1138017. [Google Scholar] [CrossRef] [PubMed]
- Butt, A.M.; Jones, H.C.; Abbott, N.J. Electrical resistance across the blood-brain barrier in anaesthetized rats: A developmental study. J. Physiol. 1990, 429, 47–62. [Google Scholar] [CrossRef] [PubMed]
- Abbott, N.J.; Patabendige, A.A.K.; Dolman, D.E.M.; Yusof, S.R.; Begley, D.J. Structure and function of the blood–brain barrier. Neurobiol. Dis. 2010, 37, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Pardridge, W.M. The blood-brain barrier: Bottleneck in brain drug development. NeuroRX 2005, 2, 3–14. [Google Scholar] [CrossRef]
- Pardridge, W.M. Blood–brain barrier delivery. Drug Discov. Today 2007, 12, 54–61. [Google Scholar] [CrossRef]
- Pardridge, W.M. Drug Transport across the Blood–Brain Barrier. J. Cereb. Blood Flow Metab. 2012, 32, 1959–1972. [Google Scholar] [CrossRef]
- Cucullo, L.; Bennani-Baiti, B.; Rapp, E.; Janigro, D. Drug delivery and in vitro models of the blood–brain barrier. Curr. Opin. Drug Discov. Dev. 2005, 8, 89–99. [Google Scholar]
- Wilhelm, I.; Krizbai, I. In Vitro Models of the Blood-Brain Barrier for the Study of Drug Delivery to the Brain. Mol. Pharm. 2014, 11, 1949–1963. [Google Scholar] [CrossRef]
- Heymans, M.; Sevin, E.; Gosselet, F.; Lundquist, S.; Culot, M. Mimicking brain tissue binding in an in vitro model of the blood-brain barrier illustrates differences between in vitro and in vivo methods for assessing the rate of brain penetration. Eur. J. Pharm. Biopharm. 2018, 127, 453–461. [Google Scholar] [CrossRef]
- Srinivasan, B.; Kolli, A.R.; Esch, M.B.; Abaci, H.E.; Shuler, M.L.; Hickman, J.J. TEER Measurement Techniques for In Vitro Barrier Model Systems. J. Lab. Autom. 2015, 20, 107–126. [Google Scholar] [CrossRef] [PubMed]
- Santaguida, S.; Janigro, D.; Hossain, M.; Oby, E.; Rapp, E.; Cucullo, L. Side by side comparison between dynamic versus static models of blood–brain barrier in vitro: A permeability study. Brain Res. 2006, 1109, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Achyuta, A.K.H.; Conway, A.J.; Crouse, R.B.; Bannister, E.C.; Lee, R.N.; Katnik, C.P.; Behensky, A.A.; Cuevas, J.; Sundaram, S.S. A modular approach to create a neurovascular unit-on-a-chip. Lab. A Chip 2013, 13, 542–553. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.I.; Abaci, H.E.; Shuler, M.L. Microfluidic blood-brain barrier model provides in vivo-like barrier properties for drug permeability screening. Biotechnol. Bioeng. 2017, 114, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Bennion, B.J.; Be, N.A.; McNerney, M.W.; Lao, V.; Carlson, E.M.; Valdez, C.A.; Malfatti, M.A.; Enright, H.A.; Nguyen, T.H.; Lightstone, F.C.; et al. Predicting a Drug’s Membrane Permeability: A Computational Model Validated With in Vitro Permeability Assay Data. J. Phys. Chem. B 2017, 121, 5228–5237. [Google Scholar] [CrossRef] [PubMed]
- Dickson, C.J.; Hornak, V.; Pearlstein, R.A.; Duca, J.S. Structure–Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling. J. Am. Chem. Soc. 2017, 139, 442–452. [Google Scholar] [CrossRef]
- Carpenter, T.S.; Kirshner, D.A.; Lau, E.Y.; Wong, S.E.; Nilmeier, J.P.; Lightstone, F.C. A method to predict blood-brain barrier permeability of drug-like compounds using molecular dynamics simulations. Biophys. J. 2014, 107, 630–641. [Google Scholar] [CrossRef]
- Geldenhuys, W.J.; Mohammad, A.S.; Adkins, C.E.; Lockman, P.R. Molecular determinants of blood-brain barrier permeation. Ther. Deliv. 2015, 6, 961–971. [Google Scholar] [CrossRef]
- González-Mariscal, L.; Betanzos, A.; Nava, P.; Jaramillo, B.E. Tight junction proteins. Prog. Biophys. Mol. Biol. 2003, 81, 1–44. [Google Scholar] [CrossRef]
- Tsukita, S.; Furuse, M.; Itoh, M. Multifunctional strands in tight junctions. Nat. Rev. Mol. Cell Biol. 2001, 2, 285–293. [Google Scholar] [CrossRef]
- Morita, K.; Furuse, M.; Fujimoto, K.; Tsukita, S. Claudin multigene family encoding four-transmembrane domain protein components of tight junction strands. Proc. Natl. Acad. Sci. USA 1999, 96, 511. [Google Scholar] [CrossRef] [PubMed]
- Schulzke, J.D.; Ploeger, S.; Amasheh, M.; Fromm, A.; Zeissig, S.; Troeger, H.; Richter, J.; Bojarski, C.; Schumann, M.; Fromm, M. Epithelial Tight Junctions in Intestinal Inflammation. Ann. N. Y. Acad. Sci. 2009, 1165, 294–300. [Google Scholar] [CrossRef] [PubMed]
- Morita, K.; Sasaki, H.; Furuse, M.; Tsukita, S. Endothelial Claudin. J. Cell Biol. 1999, 147, 185. [Google Scholar] [CrossRef] [PubMed]
- Furuse, M.; Hata, M.; Furuse, K.; Yoshida, Y.; Haratake, A.; Sugitani, Y.; Noda, T.; Kubo, A.; Tsukita, S. Claudin-based tight junctions are crucial for the mammalian epidermal barrier. J. Cell Biol. 2002, 156, 1099. [Google Scholar] [CrossRef]
- Günzel, D.; Yu, A.S.L. Claudins and the Modulation of Tight Junction Permeability. Physiol. Rev. 2013, 93, 525–569. [Google Scholar] [CrossRef]
- Günzel, D.; Fromm, M. Claudins and Other Tight Junction Proteins. Compr. Physiol. 2012, 2, 1819–1852. [Google Scholar]
- Van Itallie, C.M.; Anderson, J.M. Claudin interactions in and out of the tight junction. Tissue Barriers 2013, 1, e25247. [Google Scholar] [CrossRef]
- Krause, G.; Winkler, L.; Mueller, S.L.; Haseloff, R.F.; Piontek, J.; Blasig, I.E. Structure and function of claudins. Biochim. Biophys. Acta (BBA) Biomembr. 2008, 1778, 631–645. [Google Scholar] [CrossRef]
- Buckley, A.; Turner, J.R. Cell Biology of Tight Junction Barrier Regulation and Mucosal Disease. Cold Spring Harb. Perspect. Biol. 2018, 10, a029314. [Google Scholar] [CrossRef]
- Garcia-Hernandez, V.; Quiros, M.; Nusrat, A. Intestinal epithelial claudins: Expression and regulation in homeostasis and inflammation. Ann. N. Y. Acad. Sci. 2017, 1397, 66–79. [Google Scholar] [CrossRef]
- Hou, J.; Rajagopal, M.; Yu, A.S.L. Claudins and the kidney. Annu. Rev. Physiol. 2013, 75, 479–501. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, K.J.; Agarwal, R.; Morin, P.J. The claudin gene family: Expression in normal and neoplastic tissues. BMC Cancer 2006, 6, 186. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yang, X. The expression patterns of tight junction protein claudin-1, -3, and -4 in human gastric neoplasms and adjacent non-neoplastic tissues. Int. J. Clin. Exp. Pathol. 2015, 8, 881–887. [Google Scholar] [PubMed]
- Suzuki, H.; Nishizawa, T.; Tani, K.; Yamazaki, Y.; Tamura, A.; Ishitani, R.; Dohmae, N.; Tsukita, S.; Nureki, O.; Fujiyoshi, Y. Crystal Structure of a Claudin Provides Insight into the Architecture of Tight Junctions. Science 2014, 344, 304. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, S.; Yamaguchi, H.; Katsukura, Y.; Asashima, T.; Terasaki, T. mRNA expression levels of tight junction protein genes in mouse brain capillary endothelial cells highly purified by magnetic cell sorting. J. Neurochem. 2008, 104, 147–154. [Google Scholar] [CrossRef]
- Daneman, R.; Zhou, L.; Agalliu, D.; Cahoy, J.D.; Kaushal, A.; Barres, B.A. The Mouse Blood-Brain Barrier Transcriptome: A New Resource for Understanding the Development and Function of Brain Endothelial Cells. PLoS ONE 2010, 5, e13741. [Google Scholar] [CrossRef]
- Nitta, T.; Hata, M.; Gotoh, S.; Seo, Y.; Sasaki, H.; Hashimoto, N.; Furuse, M.; Tsukita, S. Size-selective loosening of the blood-brain barrier in claudin-5-deficient mice. J. Cell Biol. 2003, 161, 653–660. [Google Scholar] [CrossRef]
- Krause, G.; Winkler, L.; Piehl, C.; Blasig, I.; Piontek, J.; Müller, S.L. Structure and Function of Extracellular Claudin Domains. Mol. Biol. Cell 2009, 1165, 4333–4346. [Google Scholar] [CrossRef]
- Rossa, J.; Ploeger, C.; Vorreiter, F.; Saleh, T.; Protze, J.; Günzel, D.; Wolburg, H.; Krause, G.; Piontek, J. Claudin-3 and Claudin-5 Protein Folding and Assembly into the Tight Junction Are Controlled by Non-conserved Residues in the Transmembrane 3 (TM3) and Extracellular Loop 2 (ECL2) Segments. J. Biol. Chem. 2014, 289, 7641–7653. [Google Scholar] [CrossRef]
- Piehl, C.; Piontek, J.; Cording, J.; Wolburg, H.; Blasig, I.E. Participation of the second extracellular loop of claudin-5 in paracellular tightening against ions, small and large molecules. Cell. Mol. Life Sci. 2010, 67, 2131–2140. [Google Scholar] [CrossRef]
- Keaney, J.; Walsh, D.M.; O’Malley, T.; Hudson, N.; Crosbie, D.E.; Loftus, T.; Sheehan, F.; McDaid, J.; Humphries, M.M.; Callanan, J.J.; et al. Autoregulated paracellular clearance of amyloid-β across the blood-brain barrier. Sci. Adv. 2015, 1, e1500472. [Google Scholar] [CrossRef] [PubMed]
- Greene, C.; Hanley, N.; Campbell, M. Claudin-5: Gatekeeper of neurological function. Fluids Barriers CNS 2019, 16, 3. [Google Scholar] [CrossRef] [PubMed]
- Di Ventura, B.; Lemerle, C.; Michalodimitrakis, K.; Serrano, L. From in vivo to in silico biology and back. Nature 2006, 443, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Ekins, S.; Mestres, J.; Testa, B. In silico pharmacology for drug discovery: Methods for virtual ligand screening and profiling. Br. J. Pharmacol. 2007, 152, 9–20. [Google Scholar] [CrossRef]
- McInnes, C. Virtual screening strategies in drug discovery. Curr. Opin. Chem. Biol. 2007, 11, 494–502. [Google Scholar] [CrossRef]
- Huggins, D.J.; Biggin, P.C.; Dämgen, M.A.; Essex, J.W.; Harris, S.A.; Henchman, R.H.; Khalid, S.; Kuzmanic, A.; Laughton, C.A.; Michel, J.; et al. Biomolecular simulations: From dynamics and mechanisms to computational assays of biological activity. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1393. [Google Scholar] [CrossRef]
- Hope, H. Crystallography of Biological Macromolecules at Ultra-Low Temperature. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 107–126. [Google Scholar] [CrossRef]
- Smyth, M.S.; Martin, J.H. x ray crystallography. Mol. Pathol. 2000, 53, 8–14. [Google Scholar] [CrossRef]
- Carpenter, E.P.; Beis, K.; Cameron, A.D.; Iwata, S. Overcoming the challenges of membrane protein crystallography. Curr. Opin. Struct. Biol. 2008, 18, 581–586. [Google Scholar] [CrossRef]
- Caffrey, M. Crystallizing Membrane Proteins for Structure Determination: Use of Lipidic Mesophases. Annu. Rev. Biophys. 2009, 38, 29–51. [Google Scholar] [CrossRef]
- Seddon, A.M.; Curnow, P.; Booth, P.J. Membrane proteins, lipids and detergents: Not just a soap opera. Biochim. Biophys. Acta (BBA) Biomembr. 2004, 1666, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Dimmic, M.W.; Hubisz, M.J.; Bustamante, C.D.; Nielsen, R. Detecting coevolving amino acid sites using Bayesian mutational mapping. Bioinformatics 2005, 21, i126–i135. [Google Scholar] [CrossRef] [PubMed]
- Lui, S.; Tiana, G. The network of stabilizing contacts in proteins studied by coevolutionary data. J. Chem. Phys. 2013, 139, 155103. [Google Scholar] [CrossRef] [PubMed]
- Jana, B.; Morcos, F.; Onuchic, J.N. From structure to function: The convergence of structure based models and co-evolutionary information. Phys. Chem. Chem. Phys. 2014, 16, 6496–6507. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Barth, P. Evolutionary-guided de novo structure prediction of self-associated transmembrane helical proteins with near-atomic accuracy. Nat. Commun. 2015, 6, 7196. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, P.L.; Mendenhall, J.L.; Heinze, S.; Weiner, B.; Skwark, M.J.; Meiler, J. Membrane protein contact and structure prediction using co-evolution in conjunction with machine learning. PLoS ONE 2017, 12, e0177866. [Google Scholar] [CrossRef]
- Rajagopal, N.; Irudayanathan, F.J.; Nangia, S. Palmitoylation of Claudin-5 Proteins Influences Their Lipid Domain Affinity and Tight Junction Assembly at the Blood–Brain Barrier Interface. J. Phys. Chem. B 2019, 123, 983–993. [Google Scholar] [CrossRef]
- Murthy, A.C.; Dignon, G.L.; Kan, Y.; Zerze, G.H.; Parekh, S.H.; Mittal, J.; Fawzi, N.L. Molecular interactions underlying liquid−liquid phase separation of the FUS low-complexity domain. Nat. Struct. Mol. Biol. 2019, 26, 637–648. [Google Scholar] [CrossRef]
- Zheng, M.; Zhao, J.; Cui, C.; Fu, Z.; Li, X.; Liu, X.; Ding, X.; Tan, X.; Li, F.; Luo, X.; et al. Computational chemical biology and drug design: Facilitating protein structure, function, and modulation studies. Med. Res. Rev. 2018, 38, 914–950. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, X.; Wang, N.; Willsey, S.R.; Seddon, I.A.; Nangia, S. Self-Assembly Simulations of Classic Claudins—Insights into the Pore Structure, Selectivity, and Higher Order Complexes. J. Phys. Chem. B 2018, 122, 7463–7474. [Google Scholar] [CrossRef]
- Ibsen, K.N.; Ma, H.; Banerjee, A.; Tanner, E.E.L.; Nangia, S.; Mitragotri, S. Mechanism of Antibacterial Activity of Choline-Based Ionic Liquids (CAGE). ACS Biomater. Sci. Eng. 2018, 4, 2370–2379. [Google Scholar] [CrossRef]
- Sengupta, D.; Prasanna, X.; Mohole, M.; Chattopadhyay, A. Exploring GPCR–Lipid Interactions by Molecular Dynamics Simulations: Excitements, Challenges, and the Way Forward. J. Phys. Chem. B 2018, 122, 5727–5737. [Google Scholar] [CrossRef] [PubMed]
- Irudayanathan, F.J.; Wang, N.; Wang, X.; Nangia, S. Architecture of the paracellular channels formed by claudins of the blood–brain barrier tight junctions. Ann. N. Y. Acad. Sci. 2017, 1405, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Grime, J.M.A.; Dama, J.F.; Ganser-Pornillos, B.K.; Woodward, C.L.; Jensen, G.J.; Yeager, M.; Voth, G.A. Coarse-grained simulation reveals key features of HIV-1 capsid self-assembly. Nat. Commun. 2016, 7, 11568. [Google Scholar] [CrossRef] [PubMed]
- Ingólfsson, H.I.; Arnarez, C.; Periole, X.; Marrink, S.J. Computational ‘microscopy’ of cellular membranes. J. Cell Sci. 2016, 129, 257. [Google Scholar] [CrossRef] [PubMed]
- Reddy, T.; Sansom, M.S. The Role of the Membrane in the Structure and Biophysical Robustness of the Dengue Virion Envelope. Structure 2016, 24, 375–382. [Google Scholar] [CrossRef]
- Arnarez, C.; Marrink, S.J.; Periole, X. Molecular mechanism of cardiolipin-mediated assembly of respiratory chain supercomplexes. Chem. Sci. 2016, 7, 4435–4443. [Google Scholar] [CrossRef]
- Holdbrook, D.A.; Huber, R.G.; Piggot, T.J.; Bond, P.J.; Khalid, S. Dynamics of Crowded Vesicles: Local and Global Responses to Membrane Composition. PLoS ONE 2016, 11, e0156963. [Google Scholar] [CrossRef]
- Castillo, N.; Monticelli, L.; Barnoud, J.; Tieleman, D.P. Free energy of WALP23 dimer association in DMPC, DPPC, and DOPC bilayers. Chem. Phys. Lipids 2013, 169, 95–105. [Google Scholar] [CrossRef]
- Bennett, W.F.D.; MacCallum, J.L.; Hinner, M.J.; Marrink, S.J.; Tieleman, D.P. Molecular View of Cholesterol Flip-Flop and Chemical Potential in Different Membrane Environments. J. Am. Chem. Soc. 2009, 131, 12714–12720. [Google Scholar] [CrossRef]
- Periole, X.; Knepp, A.M.; Sakmar, T.P.; Marrink, S.J.; Huber, T. Structural Determinants of the Supramolecular Organization of G Protein-Coupled Receptors in Bilayers. J. Am. Chem. Soc. 2012, 134, 10959–10965. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, L.V.; de Jong, D.H.; Holt, A.; Rzepiela, A.J.; de Vries, A.H.; Poolman, B.; Killian, J.A.; Marrink, S.J. Lipid packing drives the segregation of transmembrane helices into disordered lipid domains in model membranes. Proc. Natl. Acad. Sci. USA 2011, 108, 1343. [Google Scholar] [CrossRef] [PubMed]
- Duncan, A.L.; Reddy, T.; Koldsø, H.; Hélie, J.; Fowler, P.W.; Chavent, M.; Sansom, M.S.P. Protein crowding and lipid complexity influence the nanoscale dynamic organization of ion channels in cell membranes. Sci. Rep. 2017, 7, 16647. [Google Scholar] [CrossRef] [PubMed]
- Koldsø, H.; Sansom, M.S.P. Organization and Dynamics of Receptor Proteins in a Plasma Membrane. J. Am. Chem. Soc. 2015, 137, 14694–14704. [Google Scholar] [CrossRef]
- Shorthouse, D.; Hedger, G.; Koldsø, H.; Sansom, M.S.P. Molecular simulations of glycolipids: Towards mammalian cell membrane models. Biochimie 2016, 120, 105–109. [Google Scholar] [CrossRef]
- Koldsø, H.; Reddy, T.; Fowler, P.W.; Duncan, A.L.; Sansom, M.S.P. Membrane Compartmentalization Reducing the Mobility of Lipids and Proteins within a Model Plasma Membrane. J. Phys. Chem. B 2016, 120, 8873–8881. [Google Scholar] [CrossRef]
- Duncan, A.L.; Song, W.; Sansom, M.S.P. Lipid-Dependent Regulation of Ion Channels and G Protein–Coupled Receptors: Insights from Structures and Simulations. Annu. Rev. Pharmacol. Toxicol. 2019. [Google Scholar] [CrossRef]
- Koldsø, H.; Shorthouse, D.; Hélie, J.; Sansom, M.S.P. Lipid Clustering Correlates with Membrane Curvature as Revealed by Molecular Simulations of Complex Lipid Bilayers. PLoS Comput. Biol. 2014, 10, e1003911. [Google Scholar] [CrossRef]
- Duncan, A.L.; Bandurka, M.A.R.; Chavent, M.G.; Rassam, P.; Song, W.; Birkholz, O.; Helie, J.; Reddy, T.; Beliaev, D.; Hambly, B.; et al. How Nanoscale Protein Interactions Determine the Mesoscale Dynamic Organisation of Membrane Proteins. Biophys. J. 2019, 116, 365a. [Google Scholar] [CrossRef]
- Lin, X.; Gorfe, A.A.; Levental, I. Protein Partitioning into Ordered Membrane Domains: Insights from Simulations. Biophys. J. 2018, 114, 1936–1944. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Trasatti, J.P.; Karande, P.; Nangia, S. Molecular Architecture of the Blood Brain Barrier Tight Junction Proteins–A Synergistic Computational and In Vitro Approach. J. Phys. Chem. B 2016, 120, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Irudayanathan, F.J.; Jiang, W.; Nangia, S. Simulating Gram-Negative Bacterial Outer Membrane: A Coarse Grain Model. J. Phys. Chem. B 2015, 119, 14668–14682. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, Y.; Suzuki, H.; Tani, K.; Nishikawa, K.; Irie, K.; Ogura, Y.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Structural insight into tight junction disassembly by Clostridium perfringens enterotoxin. Science 2015, 347, 775. [Google Scholar] [CrossRef] [PubMed]
- Shinoda, T.; Shinya, N.; Ito, K.; Ohsawa, N.; Terada, T.; Hirata, K.; Kawano, Y.; Yamamoto, M.; Kimura-Someya, T.; Yokoyama, S.; et al. Structural basis for disruption of claudin assembly in tight junctions by an enterotoxin. Sci. Rep. 2016, 6, 33632. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, S.; Irie, K.; Tanaka, H.; Nishikawa, K.; Suzuki, H.; Saitoh, Y.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Morphologic determinant of tight junctions revealed by claudin-3 structures. Nat. Commun. 2019, 10, 816. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Z. Advances in homology protein structure modeling. Curr. Protein Pept. Sci. 2006, 7, 217–227. [Google Scholar] [CrossRef]
- Shen, M.-y.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef]
- Kopp, J.; Schwede, T. Automated protein structure homology modeling: A progress report. Pharmacogenomics 2004, 5, 405–416. [Google Scholar] [CrossRef]
- Fiser, A. Template-based protein structure modeling. Methods Mol. Biol. 2010, 673, 73–94. [Google Scholar]
- Mineta, K.; Yamamoto, Y.; Yamazaki, Y.; Tanaka, H.; Tada, Y.; Saito, K.; Tamura, A.; Igarashi, M.; Endo, T.; Takeuchi, K.; et al. Predicted expansion of the claudin multigene family. FEBS Lett. 2011, 585, 606–612. [Google Scholar] [CrossRef]
- Kelley, L.A.; Mezulis, S.; Yates, C.M.; Wass, M.N.; Sternberg, M.J.E. The Phyre2 web portal for protein modeling, prediction and analysis. Nat. Protoc. 2015, 10, 845. [Google Scholar] [CrossRef] [PubMed]
- Schwede, T.; Kopp, J.; Guex, N.; Peitsch, M.C. SWISS-MODEL: An automated protein homology-modeling server. Nucleic Acids Res. 2003, 31, 3381–3385. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Kucukural, A.; Zhang, Y. I-TASSER: A unified platform for automated protein structure and function prediction. Nat. Protoc. 2010, 5, 725–738. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yan, R.; Roy, A.; Xu, D.; Poisson, J.; Zhang, Y. The I-TASSER Suite: Protein structure and function prediction. Nat. Methods 2014, 12, 7. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhang, Y. I-TASSER server: New development for protein structure and function predictions. Nucleic Acids Res. 2015, 43, W174–W181. [Google Scholar] [CrossRef]
- Källberg, M.; Wang, H.; Wang, S.; Peng, J.; Wang, Z.; Lu, H.; Xu, J. Template-based protein structure modeling using the RaptorX web server. Nat. Protoc. 2012, 7, 1511–1522. [Google Scholar] [CrossRef]
- Peng, J.; Xu, J. RaptorX: Exploiting structure information for protein alignment by statistical inference. Proteins 2011, 79 (Suppl. 10), 161–171. [Google Scholar] [CrossRef]
- Fiser, A.; Do, R.K.G.; Šali, A. Modeling of loops in protein structures. Protein Sci. 2000, 9, 1753–1773. [Google Scholar] [CrossRef]
- Baker, D.; Sali, A. Protein Structure Prediction and Structural Genomics. Science 2001, 294, 93. [Google Scholar] [CrossRef]
- Wiltgen, M. Algorithms for Structure Comparison and Analysis: Homology Modelling of Proteins. In Encyclopedia of Bioinformatics and Computational Biology; Ranganathan, S., Gribskov, M., Nakai, K., Schönbach, C., Eds.; Academic Press: Oxford, UK, 2019; pp. 38–61. [Google Scholar] [CrossRef]
- Schymkowitz, J.; Borg, J.; Stricher, F.; Nys, R.; Rousseau, F.; Serrano, L. The FoldX web server: An online force field. Nucleic Acids Res. 2005, 33, W382–W388. [Google Scholar] [CrossRef]
- Fiser, A.; Sali, A. ModLoop: Automated modeling of loops in protein structures. Bioinformatics 2003, 19, 2500–2501. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Junghans, C.; Kremer, K. Comparative atomistic and coarse-grained study of water: What do we lose by coarse-graining? Eur. Phys. J. E 2009, 28, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, A.; Freddolino, P.L.; Imada, K.; Namba, K.; Schulten, K. Coarse-Grained Molecular Dynamics Simulations of a Rotating Bacterial Flagellum. Biophys. J. 2006, 91, 4589–4597. [Google Scholar] [CrossRef]
- Shih, A.Y.; Arkhipov, A.; Freddolino, P.L.; Schulten, K. Coarse Grained Protein−Lipid Model with Application to Lipoprotein Particles. J. Phys. Chem. B 2006, 110, 3674–3684. [Google Scholar] [CrossRef]
- Akhmatskaya, E.; Reich, S. Meso-GSHMC: A stochastic algorithm for meso-scale constant temperature simulations. Procedia Comput. Sci. 2011, 4, 1353–1362. [Google Scholar] [CrossRef]
- de Jong, D.H.; Periole, X.; Marrink, S.J. Dimerization of Amino Acid Side Chains: Lessons from the Comparison of Different Force Fields. J. Chem. Theory Comput. 2012, 8, 1003–1014. [Google Scholar] [CrossRef]
- Ayton, G.S.; Voth, G.A. Systematic multiscale simulation of membrane protein systems. Curr. Opin. Struct. Biol. 2009, 19, 138–144. [Google Scholar] [CrossRef]
- Yuan, C.; Li, S.; Zou, Q.; Ren, Y.; Yan, X. Multiscale simulations for understanding the evolution and mechanism of hierarchical peptide self-assembly. Phys. Chem. Chem. Phys. 2017, 19, 23614–23631. [Google Scholar] [CrossRef]
- Singh, N.; Li, W. Recent Advances in Coarse-Grained Models for Biomolecules and Their Applications. Int. J. Mol. Sci. 2019, 20, 3774. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Luo, J.; Nangia, S. Multiscale Approach to Investigate Self-Assembly of Telodendrimer Based Nanocarriers for Anticancer Drug Delivery. Langmuir 2015, 31, 4270–4280. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Wang, X.; Guo, D.; Luo, J.; Nangia, S. Drug-Specific Design of Telodendrimer Architecture for Effective Doxorubicin Encapsulation. J. Phys. Chem. B 2016, 120, 9766–9777. [Google Scholar] [CrossRef] [PubMed]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Grindon, C.; Harris, S.; Evans, T.; Novik, K.; Coveney, P.; Laughton, C. Large-scale molecular dynamics simulation of DNA: Implementation and validation of the AMBER98 force field in LAMMPS. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 1373–1386. [Google Scholar]
- Case, D.A.; Cheatham Iii, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.L.; Cheng, X.; Jo, S.; Rui, H.; Song, K.C.; Dávila-Contreras, E.M.; Qi, Y.; Lee, J.; Monje-Galvan, V.; Venable, R.M.; et al. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 2014, 35, 1997–2004. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks Iii, C.L.; Mackerell Jr, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- The PyMOL Molecular Graphics System; Version 2.0; Schrödinger, LLC: New York, NY, USA, 2015.
- Land, H.; Humble, M.S. YASARA: A Tool to Obtain Structural Guidance in Biocatalytic Investigations. In Protein Engineering: Methods and Protocols; Bornscheuer, U.T., Höhne, M., Eds.; Springer New York: New York, NY, USA, 2018; pp. 43–67. [Google Scholar] [CrossRef]
- Krieger, E.; Vriend, G. YASARA View—molecular graphics for all devices—From smartphones to workstations. Bioinformatics 2014, 30, 2981–2982. [Google Scholar] [CrossRef] [PubMed]
- Krieger, E.; Koraimann, G.; Vriend, G. Increasing the precision of comparative models with YASARA NOVA—A self-parameterizing force field. Proteins Struct. Funct. Bioinform. 2002, 47, 393–402. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.-J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef]
- Periole, X.; Marrink, S.-J. The Martini Coarse-Grained Force Field. In Biomolecular Simulations: Methods and Protocols; Monticelli, L., Salonen, E., Eds.; Humana Press: Totowa, NJ, USA, 2013; pp. 533–565. [Google Scholar]
- de Jong, D.H.; Singh, G.; Bennett, W.F.D.; Arnarez, C.; Wassenaar, T.A.; Schäfer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef] [PubMed]
- Darré, L.; Machado, M.R.; Brandner, A.F.; González, H.C.; Ferreira, S.; Pantano, S. SIRAH: A Structurally Unbiased Coarse-Grained Force Field for Proteins with Aqueous Solvation and Long-Range Electrostatics. J. Chem. Theory Comput. 2015, 11, 723–739. [Google Scholar] [CrossRef] [PubMed]
- Machado, M.R.; Pantano, S. SIRAH tools: Mapping, backmapping and visualization of coarse-grained models. Bioinformatics 2016, 32, 1568–1570. [Google Scholar] [CrossRef] [PubMed]
- Kar, P.; Gopal, S.M.; Cheng, Y.-M.; Predeus, A.; Feig, M. PRIMO: A Transferable Coarse-grained Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 3769–3788. [Google Scholar] [CrossRef] [PubMed]
- Cheon, M.; Chang, I.; Hall, C.K. Extending the PRIME model for protein aggregation to all 20 amino acids. Proteins 2010, 78, 2950–2960. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Wan, C.-K.; Wu, Y.-D. PACE Force Field for Protein Simulations. 2. Folding Simulations of Peptides. J. Chem. Theory Comput. 2010, 6, 3390–3402. [Google Scholar] [CrossRef]
- Han, W.; Wan, C.-K.; Jiang, F.; Wu, Y.-D. PACE Force Field for Protein Simulations. 1. Full Parameterization of Version 1 and Verification. J. Chem. Theory Comput. 2010, 6, 3373–3389. [Google Scholar] [CrossRef]
- Uusitalo, J.J.; Ingólfsson, H.I.; Marrink, S.J.; Faustino, I. Martini Coarse-Grained Force Field: Extension to RNA. Biophys. J. 2017, 113, 246–256. [Google Scholar] [CrossRef]
- Bernardi, R.C.; Melo, M.C.R.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Et Biophys. Acta (BBA) Gen. Subj. 2015, 1850, 872–877. [Google Scholar] [CrossRef]
- Perilla, J.R.; Goh, B.C.; Cassidy, C.K.; Liu, B.; Bernardi, R.C.; Rudack, T.; Yu, H.; Wu, Z.; Schulten, K. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 2015, 31, 64–74. [Google Scholar] [CrossRef]
- Perilla, J.R.; Schulten, K. Physical properties of the HIV-1 capsid from all-atom molecular dynamics simulations. Nat. Commun. 2017, 8, 15959. [Google Scholar] [CrossRef] [PubMed]
- Xiao, G.; Ren, M.; Hong, H. 50 million atoms scale molecular dynamics modelling on a single consumer graphics card. Adv. Eng. Softw. 2018, 124, 66–72. [Google Scholar] [CrossRef]
- Orsi, M. 15-Molecular simulation of self-assembly. In Self-Assembling Biomaterials; Azevedo, H.S., da Silva, R.M.P., Eds.; Woodhead Publishing: Cambridge, MA, USA, 2018; pp. 305–318. [Google Scholar] [CrossRef]
- Ben-Nissan, G.; Sharon, M. Capturing protein structural kinetics by mass spectrometry. Chem. Soc. Rev. 2011, 40, 3627–3637. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, A.; Vallurupalli, P.; Kay, L.E. Defining a length scale for millisecond-timescale protein conformational exchange. Proc. Natl. Acad. Sci. USA 2013, 110, 11391. [Google Scholar] [CrossRef]
- Agrawal, P.; Singh, H.; Srivastava, H.K.; Singh, S.; Kishore, G.; Raghava, G.P.S. Benchmarking of different molecular docking methods for protein-peptide docking. BMC Bioinform. 2019, 19, 426. [Google Scholar] [CrossRef]
- Pagadala, N.S.; Syed, K.; Tuszynski, J. Software for molecular docking: A review. Biophys. Rev. 2017, 9, 91–102. [Google Scholar] [CrossRef]
- Kozakov, D.; Hall, D.R.; Xia, B.; Porter, K.A.; Padhorny, D.; Yueh, C.; Beglov, D.; Vajda, S. The ClusPro web server for protein–protein docking. Nat. Protoc. 2017, 12, 255. [Google Scholar] [CrossRef]
- Comeau, S.R.; Gatchell, D.W.; Vajda, S.; Camacho, C.J. ClusPro: A fully automated algorithm for protein–protein docking. Nucleic Acids Res. 2004, 32, W96–W99. [Google Scholar] [CrossRef]
- Lyskov, S.; Gray, J.J. The RosettaDock server for local protein-protein docking. Nucleic Acids Res. 2008, 36, W233–W238. [Google Scholar] [CrossRef]
- de Vries, S.J.; van Dijk, M.; Bonvin, A.M.J.J. The HADDOCK web server for data-driven biomolecular docking. Nat. Protoc. 2010, 5, 883. [Google Scholar] [CrossRef]
- Dominguez, C.; Boelens, R.; Bonvin, A.M.J.J. HADDOCK: A Protein−Protein Docking Approach Based on Biochemical or Biophysical Information. J. Am. Chem. Soc. 2003, 125, 1731–1737. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Li, L.; Weng, Z. ZDOCK: An initial-stage protein-docking algorithm. Proteins Struct. Funct. Bioinform. 2003, 52, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, L.; Li, W.; Zhao, D.; Song, M.; Yang, Y. FIPSDock: A new molecular docking technique driven by fully informed swarm optimization algorithm. J. Comput. Chem. 2013, 34, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, J.K.; Law, S.M.; Brooks Iii, C.L. Flexible CDOCKER: Development and application of a pseudo-explicit structure-based docking method within CHARMM. J. Comput. Chem. 2016, 37, 753–762. [Google Scholar] [CrossRef] [PubMed]
- Pons, C.; Garzon, J.I.; Lopéz-Blanco, J.R.; Fernandez-Recio, J.; Kovacs, J.; Chacon, P.; Abagyan, R. FRODOCK: A new approach for fast rotational protein–protein docking. Bioinformatics 2009, 25, 2544–2551. [Google Scholar]
- Liu, M.; Wang, S. MCDOCK: A Monte Carlo simulation approach to the molecular docking problem. J. Comput. Aided Mol. Des. 1999, 13, 435–451. [Google Scholar] [CrossRef]
- Yellapu, N.K. Molecular Modelling, Dynamics, and Docking of Membrane Proteins: Still a Challenge. In Applied Case Studies and Solutions in Molecular Docking-Based Drug Design; IGI Global: Hershey, PA, USA, 2016; pp. 186–208. [Google Scholar]
- Burke, K.A.; Yates, E.A.; Legleiter, J. Biophysical insights into how surfaces, including lipid membranes, modulate protein aggregation related to neurodegeneration. Front. Neurol 2013, 4, 17. [Google Scholar] [CrossRef]
- Bogdanov, M.; Dowhan, W.; Vitrac, H. Lipids and topological rules governing membrane protein assembly. Biochim. Biophys. Acta 2014, 1843, 1475–1488. [Google Scholar] [CrossRef]
- Bogdanov, M.; Mileykovskaya, E.; Dowhan, W. Lipids in the assembly of membrane proteins and organization of protein supercomplexes: Implications for lipid-linked disorders. Subcell. Biochem. 2008, 49, 197–239. [Google Scholar]
- Ho, C.-C. Chapter 7—Membranes for Bioseparations. In Bioprocessing for Value-Added Products from Renewable Resources; Yang, S.-T., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 163–183. [Google Scholar] [CrossRef]
- Page, R.C.; Li, C.; Hu, J.; Gao, F.P.; Cross, T.A. Lipid bilayers: An essential environment for the understanding of membrane proteins. Magn. Reson. Chem. 2007, 45, S2–S11. [Google Scholar] [CrossRef]
- Sengupta, D.; Marrink, S.J. Lipid-mediated interactions tune the association of glycophorin A helix and its disruptive mutants in membranes. Phys. Chem. Chem. Phys. 2010, 12, 12987–12996. [Google Scholar] [CrossRef] [PubMed]
- Wassenaar, T.A.; Pluhackova, K.; Moussatova, A.; Sengupta, D.; Marrink, S.J.; Tieleman, D.P.; Böckmann, R.A. High-Throughput Simulations of Dimer and Trimer Assembly of Membrane Proteins. The DAFT Approach. J. Chem. Theory Comput. 2015, 11, 2278–2291. [Google Scholar] [CrossRef] [PubMed]
- Altwaijry, N.A.; Baron, M.; Wright, D.W.; Coveney, P.V.; Townsend-Nicholson, A. An Ensemble-Based Protocol for the Computational Prediction of Helix–Helix Interactions in G Protein-Coupled Receptors using Coarse-Grained Molecular Dynamics. J. Chem. Theory Comput. 2017, 13, 2254–2270. [Google Scholar] [CrossRef] [PubMed]
- Hall, B.A.; Halim, K.B.A.; Buyan, A.; Emmanouil, B.; Sansom, M.S.P. Sidekick for Membrane Simulations: Automated Ensemble Molecular Dynamics Simulations of Transmembrane Helices. J. Chem. Theory Comput. 2014, 10, 2165–2175. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, N.; Nangia, S. Obtaining Protein Association Energy Landscape (PANEL) for Integral Membrane Proteins. J. Chem. Theory Comput. 2019. [Google Scholar] [CrossRef] [PubMed]
- Petrek, M.; Otyepka, M.; Banás, P.; Kosinová, P.; Koca, J.; Damborský, J. CAVER: A new tool to explore routes from protein clefts, pockets and cavities. BMC Bioinform. 2006, 7, 316. [Google Scholar] [CrossRef]
- Petřek, M.; Košinová, P.; Koča, J.; Otyepka, M. MOLE: A Voronoi Diagram-Based Explorer of Molecular Channels, Pores, and Tunnels. Structure 2007, 15, 1357–1363. [Google Scholar] [CrossRef]
- Smart, O.S.; Neduvelil, J.G.; Wang, X.; Wallace, B.A.; Sansom, M.S. HOLE: A program for the analysis of the pore dimensions of ion channel structural models. J. Mol Graph. 1996, 14, 354–360. [Google Scholar] [CrossRef]
- Yaffe, E.; Fishelovitch, D.; Wolfson, H.J.; Halperin, D.; Nussinov, R. MolAxis: A server for identification of channels in macromolecules. Nucleic Acids Res. 2008, 36, W210–W215. [Google Scholar] [CrossRef]
- Yaffe, E.; Fishelovitch, D.; Wolfson, H.J.; Halperin, D.; Nussinov, R. MolAxis: Efficient and accurate identification of channels in macromolecules. Proteins 2008, 73, 72–86. [Google Scholar] [CrossRef]
- Pellegrini-Calace, M.; Maiwald, T.; Thornton, J.M. PoreWalker: A Novel Tool for the Identification and Characterization of Channels in Transmembrane Proteins from Their Three-Dimensional Structure. PLoS Comput. Biol. 2009, 5, e1000440. [Google Scholar] [CrossRef] [PubMed]
- Peter, C.; Hummer, G. Ion Transport through Membrane-Spanning Nanopores Studied by Molecular Dynamics Simulations and Continuum Electrostatics Calculations. Biophys. J. 2005, 89, 2222–2234. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G.; Pratt, L.R.; García, A.E. Molecular Theories and Simulation of Ions and Polar Molecules in Water. J. Phys. Chem. A 1998, 102, 7885–7895. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Kutzner, C.; Grubmüller, H.; de Groot, B.L.; Zachariae, U. Computational electrophysiology: The molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 2011, 101, 809–817. [Google Scholar] [CrossRef]
- Kutzner, C.; Köpfer, D.A.; Machtens, J.-P.; de Groot, B.L.; Song, C.; Zachariae, U. Insights into the function of ion channels by computational electrophysiology simulations. Biochim. Biophys. Acta (BBA) Biomembr. 2016, 1858, 1741–1752. [Google Scholar] [CrossRef]
- Epand, R.M. Lipid polymorphism and protein–lipid interactions. Biochim. Biophys. Acta (BBA) Rev. Biomembr. 1998, 1376, 353–368. [Google Scholar] [CrossRef]
- Killian, J.A. Hydrophobic mismatch between proteins and lipids in membranes. Biochim. Biophys. Acta (BBA) Rev. Biomembr. 1998, 1376, 401–416. [Google Scholar] [CrossRef]
- de Jesus, A.J.; Allen, T.W. The determinants of hydrophobic mismatch response for transmembrane helices. Biochim. Biophys. Acta (BBA) Biomembr. 2013, 1828, 851–863. [Google Scholar] [CrossRef] [PubMed]
- Parton, D.L.; Klingelhoefer, J.W.; Sansom, M.S.P. Aggregation of model membrane proteins, modulated by hydrophobic mismatch, membrane curvature, and protein class. Biophys. J. 2011, 101, 691–699. [Google Scholar] [CrossRef] [PubMed]
- Bavi, O.; Vossoughi, M.; Naghdabadi, R.; Jamali, Y. The Combined Effect of Hydrophobic Mismatch and Bilayer Local Bending on the Regulation of Mechanosensitive Ion Channels. PLoS ONE 2016, 11, e0150578. [Google Scholar] [CrossRef] [PubMed]
- Webb, R.J.; East, J.M.; Sharma, R.P.; Lee, A.G. Hydrophobic Mismatch and the Incorporation of Peptides into Lipid Bilayers: A Possible Mechanism for Retention in the Golgi. Biochemistry 1998, 37, 673–679. [Google Scholar] [CrossRef]
- Milovanovic, D.; Honigmann, A.; Koike, S.; Göttfert, F.; Pähler, G.; Junius, M.; Müllar, S.; Diederichsen, U.; Janshoff, A.; Grubmüller, H.; et al. Hydrophobic mismatch sorts SNARE proteins into distinct membrane domains. Nat. Commun. 2015, 6, 5984. [Google Scholar] [CrossRef]
- Fowler, P.W.; Williamson, J.J.; Sansom, M.S.P.; Olmsted, P.D. Roles of Interleaflet Coupling and Hydrophobic Mismatch in Lipid Membrane Phase-Separation Kinetics. J. Am. Chem. Soc. 2016, 138, 11633–11642. [Google Scholar] [CrossRef]
- Koval, M. Differential pathways of claudin oligomerization and integration into tight junctions. Tissue Barriers 2013, 1, e24518. [Google Scholar] [CrossRef]
- Koval, M. Claudins—Key Pieces in the Tight Junction Puzzle. Cell Commun. Adhes. 2006, 13, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Heiler, S.; Mu, W.; Zöller, M.; Thuma, F. The importance of claudin-7 palmitoylation on membrane subdomain localization and metastasis-promoting activities. Cell Commun. Signal. 2015, 13. [Google Scholar] [CrossRef] [PubMed]
- Van Itallie, C.M.; Gambling, T.M.; Carson, J.L.; Anderson, J.M. Palmitoylation of claudins is required for efficient tight-junction localization. J. Cell Sci. 2005, 118, 1427–1436. [Google Scholar] [CrossRef]
- Fukata, Y.; Bredt, D.S.; Fukata, M. Protein Palmitoylation by DHHC Protein Family, the Dynamic Synapse: Molecular Methods in Ionotropic Receptor Biology; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Gorleku, O.A.; Barns, A.-M.; Prescott, G.R.; Greaves, J.; Chamberlain, L.H. Endoplasmic Reticulum Localization of DHHC Palmitoyltransferases Mediated by Lysine-based Sorting Signals. J. Biol. Chem. 2011, 286, 39573–39584. [Google Scholar] [CrossRef] [PubMed]
- Chamberlain, L.H.; Shipston, M.J. The Physiology of Protein S-acylation. Physiol. Rev. 2015, 95, 341–376. [Google Scholar] [CrossRef]
- Hou, J. Chapter 2—Paracellular Channel Formation. In The Paracellular Channel; Hou, J., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 9–27. [Google Scholar] [CrossRef]
- Hou, J.; Renigunta, A.; Konrad, M.; Gomes, A.S.; Schneeberger, E.E.; Paul, D.L.; Waldegger, S.; Goodenough, D.A. Claudin-16 and claudin-19 interact and form a cation-selective tight junction complex. J. Clin. Investig. 2008, 118, 619–628. [Google Scholar] [CrossRef]
- Mitic, L.L.; Unger, V.M.; Anderson, J.M. Expression, solubilization, and biochemical characterization of the tight junction transmembrane protein claudin-4. Protein Sci. 2003, 12, 218–227. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Mitic, L.L.; Anderson, J.M. Claudin-2 Forms Homodimers and Is a Component of a High Molecular Weight Protein Complex. J. Biol. Chem. 2011, 286, 3442–3450. [Google Scholar] [CrossRef]
- Suzuki, H.; Tani, K.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Model for the architecture of claudin-based paracellular ion channels through tight junctions. J. Mol. Biol. 2015, 427, 291–297. [Google Scholar] [CrossRef]
- Coyne, C.B.; Gambling, T.M.; Boucher, R.C.; Carson, J.L.; Johnson, L.G. Role of claudin interactions in airway tight junctional permeability. Am. J. Physiol. Lung Cell. Mol. Physiol. 2003, 285, L1166–L1178. [Google Scholar] [CrossRef]
- Angelow, S.; Yu, A.S.L. Structure-Function Studies of Claudin Extracellular Domains by Cysteine-scanning Mutagenesis. J. Biol. Chem. 2009, 284, 29205–29217. [Google Scholar] [CrossRef] [PubMed]
- Anbazhagan, V.; Schneider, D. The membrane environment modulates self-association of the human GpA TM domain—Implications for membrane protein folding and transmembrane signaling. Biochim. Biophys. Acta (BBA) Biomembr. 2010, 1798, 1899–1907. [Google Scholar] [CrossRef] [PubMed]
- van Meer, G.; Voelker, D.R.; Feigenson, G.W. Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9, 112. [Google Scholar] [CrossRef] [PubMed]
- Von Heijne, G. The membrane protein universe: What’s out there and why bother? J. Intern. Med. 2007, 261, 543–557. [Google Scholar] [CrossRef]
- Blaskovic, S.; Blanc, M.; Goot, F.G. What does S-palmitoylation do to membrane proteins? FEBS J. 2013, 280, 2766–2774. [Google Scholar] [CrossRef]
- Linder, M.E.; Deschenes, R.J. Palmitoylation: Policing protein stability and traffic. Nat. Rev. Mol. Cell Biol. 2007, 8, 74–84. [Google Scholar] [CrossRef]
- Rossa, J.; Lorenz, D.; Ringling, M.; Veshnyakova, A.; Piontek, J. Overexpression of claudin-5 but not claudin-3 induces formation of trans-interaction–dependent multilamellar bodies. Ann. N. Y. Acad. Sci. 2012, 1257, 59–66. [Google Scholar] [CrossRef]
- Piontek, J.; Winkler, L.; Wolburg, H.; Müller, S.L.; Zuleger, N.; Piehl, C.; Wiesner, B.; Krause, G.; Blasig, I.E. Formation of tight junction: Determinants of homophilic interaction between classic claudins. FASEB J. 2007, 22, 146–158. [Google Scholar] [CrossRef]
- Kausalya, P.J.; Amasheh, S.; Günzel, D.; Wurps, H.; Müller, D.; Fromm, M.; Hunziker, W. Disease-associated mutations affect intracellular traffic and paracellular Mg2+ transport function of Claudin-16. J. Clin Investig. 2006, 116, 878–891. [Google Scholar] [CrossRef]
- Galochkina, T.; Ng Fuk Chong, M.; Challali, L.; Abbar, S.; Etchebest, C. New insights into GluT1 mechanics during glucose transfer. Sci. Rep. 2019, 9, 998. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, Y.; Gongpan, P.; Zhang, Q.; Huang, S.; Wang, B.; Xu, B.; Shan, Y.; Xiong, W.; Li, G.; et al. Single glucose molecule transport process revealed by force tracing and molecular dynamics simulations. Nanoscale Horiz. 2018, 3, 517–524. [Google Scholar] [CrossRef]
- Samanta, P.; Wang, Y.; Fuladi, S.; Zou, J.; Li, Y.; Shen, L.; Weber, C.; Khalili-Araghi, F. Molecular determination of claudin-15 organization and channel selectivity. J. Gen. Physiol. 2018, 150, 949. [Google Scholar] [CrossRef] [PubMed]
- Alberini, G.; Benfenati, F.; Maragliano, L. Molecular Dynamics Simulations of Ion Selectivity in a Claudin-15 Paracellular Channel. J. Phys. Chem. B 2018, 122, 10783–10792. [Google Scholar] [CrossRef] [PubMed]
- Alberini, G.; Benfenati, F.; Maragliano, L. A refined model of claudin-15 tight junction paracellular architecture by molecular dynamics simulations. PLoS ONE 2017, 12, e0184190. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.R.; Turner, J.R. Dynamic modeling of the tight junction pore pathway. Ann. N. Y. Acad. Sci. 2017, 1397, 209–218. [Google Scholar] [CrossRef]
- Shen, L.; Weber, C.R.; Turner, J.R. The tight junction protein complex undergoes rapid and continuous molecular remodeling at steady state. J. Cell Biol. 2008, 181, 683. [Google Scholar] [CrossRef]
- Krystofiak, E.S.; Heymann, J.B.; Kachar, B. Carbon replicas reveal double stranded structure of tight junctions in phase-contrast electron microscopy. Commun. Biol. 2019, 2, 98. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajagopal, N.; Irudayanathan, F.J.; Nangia, S. Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface. Int. J. Mol. Sci. 2019, 20, 5583. https://doi.org/10.3390/ijms20225583
Rajagopal N, Irudayanathan FJ, Nangia S. Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface. International Journal of Molecular Sciences. 2019; 20(22):5583. https://doi.org/10.3390/ijms20225583
Chicago/Turabian StyleRajagopal, Nandhini, Flaviyan Jerome Irudayanathan, and Shikha Nangia. 2019. "Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface" International Journal of Molecular Sciences 20, no. 22: 5583. https://doi.org/10.3390/ijms20225583
APA StyleRajagopal, N., Irudayanathan, F. J., & Nangia, S. (2019). Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface. International Journal of Molecular Sciences, 20(22), 5583. https://doi.org/10.3390/ijms20225583