Tuning the Energy Levels of Adamantane by Boron Substitution
Abstract
1. Introduction
2. Results and Discussion
2.1. Structure Modelling
2.2. Structural Properties
2.3. Electronic Properties
2.3.1. Analysis of Neutral, Anionic and Cationic Energies
2.3.2. Analysis of HOMO and LUMO Orbitals
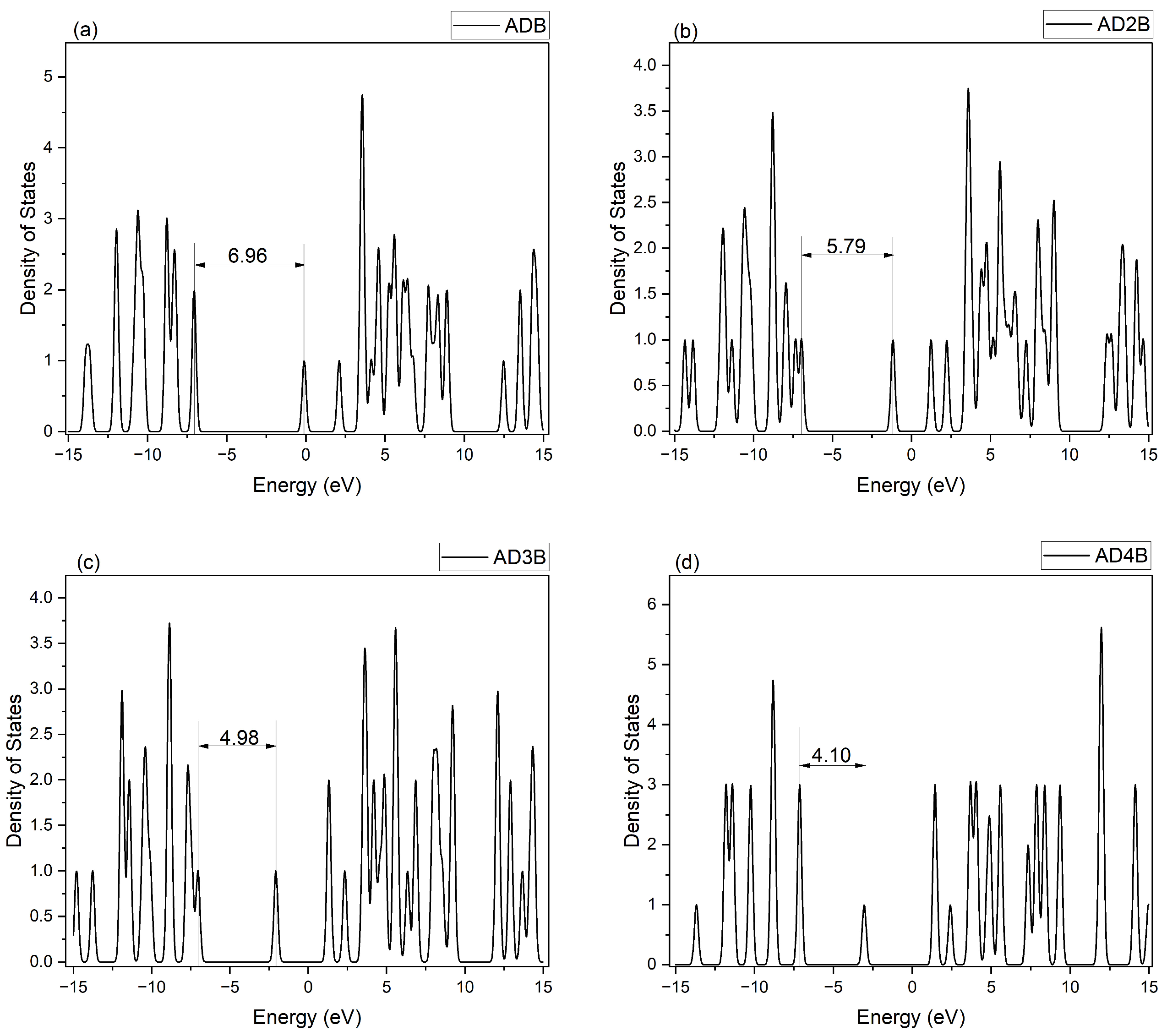
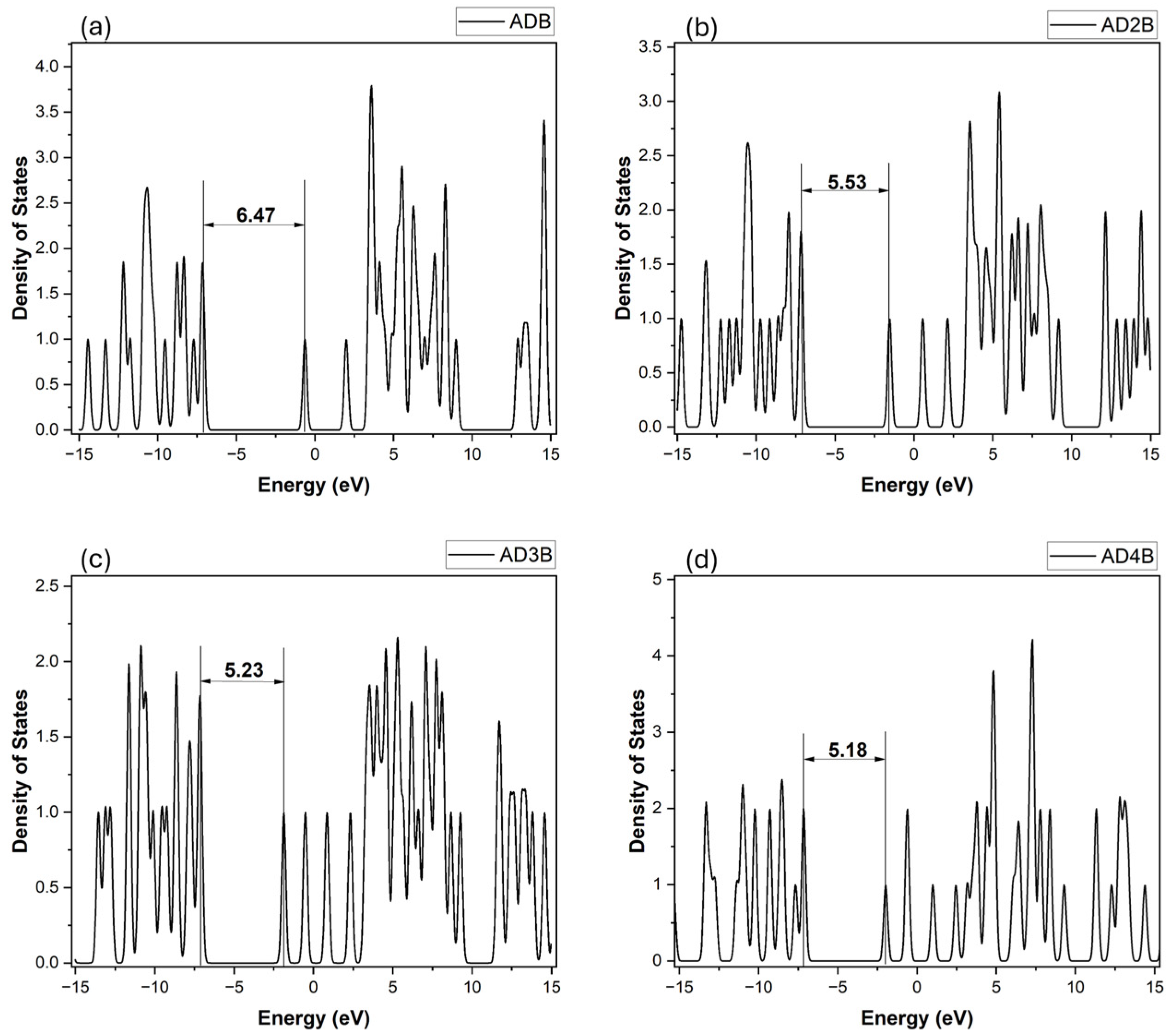
2.3.3. Density of States Analysis
2.4. Optical Properties and Transition Character
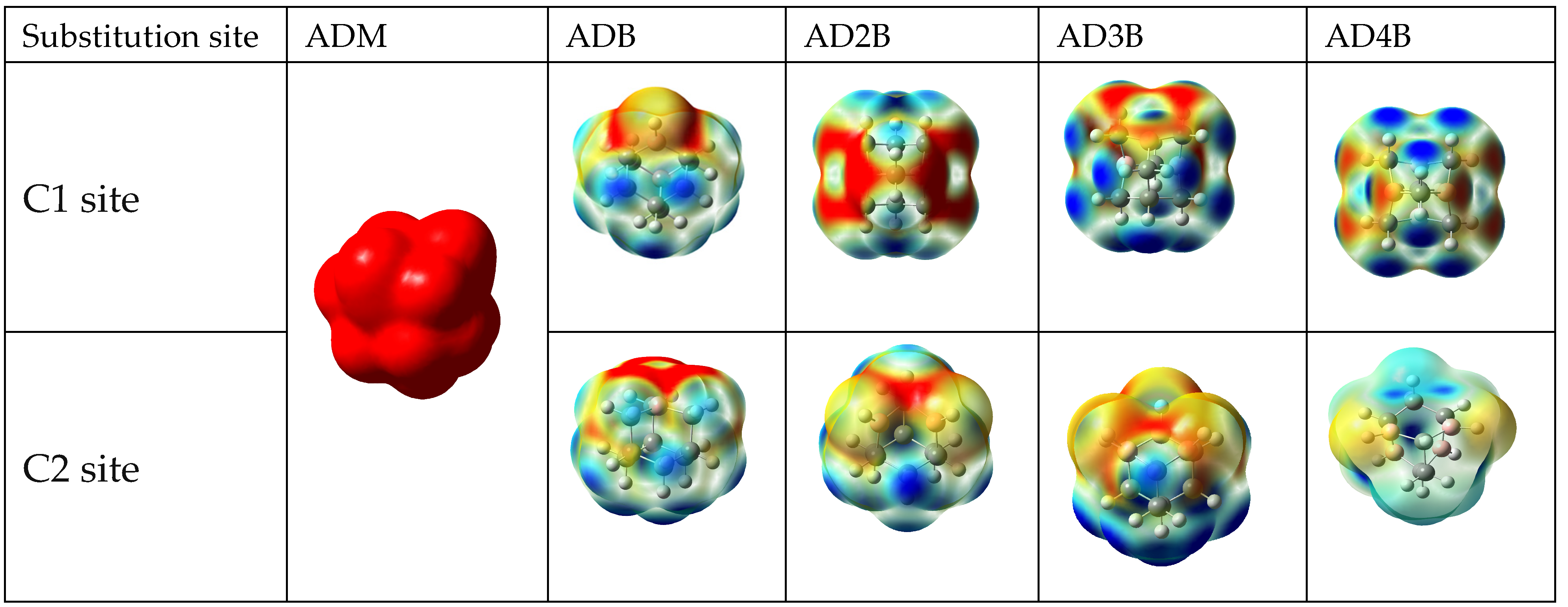
2.5. Electrostatic Potential Surface
3. Computational Methods
4. Potential Applications and Future Prospects
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwertfeger, H.; Fokin, A.A.; Schreiner, P.R. Diamonds are a chemist’s best friend: Diamondoid chemistry beyond adamantane. Angew. Chem. Int. Ed. 2008, 47, 1022–1036. [Google Scholar] [CrossRef]
- Richardson, S.L.; Baruah, T.; Mehl, M.J.; Pederson, M.R. Theoretical confirmation of the experimental Raman spectra of the lower order diamondoid molecule: Cyclohexamantane (C26H30). Chem. Phys. Lett. 2005, 403, 83–88. [Google Scholar] [CrossRef]
- Schoell, M.; Carlson, R.M. Diamondoids and oil are not forever. Nature 1999, 399, 15–16. [Google Scholar] [CrossRef]
- Hála, S.; Landa, S.; Hanuš, V. Isolation of Tetracyclo dodecane and Pentacyclo (Diamantane) from Petroleum. Angew. Chem 1966, 5, 1045–1046. [Google Scholar] [CrossRef]
- Lin, R.; Wilk, Z.A. Natural occurrence of tetramantane (C22H28), pentamantane (C26H32) and hexamantane (C30H36) in a deep petroleum reservoir. Fuel 1995, 74, 1512–1521. [Google Scholar] [CrossRef]
- Lee, S.; Seo, M.H. Synthesis and electro-optical properties of adamantane-based host and hole-transporting material for thermal stable blue phosphorescent OLEDs. J. Nanosci. Nanotech. 2017, 17, 7292–7296. [Google Scholar] [CrossRef]
- Mansoori, G.A. Diamondoid molecules. Adv. Chem. Phys. 2007, 136, 207–258. [Google Scholar]
- Lu, A.J.; Pan, B.C.; Han, J.G. Erratum: Electronic and vibrational properties of diamondlike hydrocarbons. Phys. Rev. B 2005, 72, 209901. [Google Scholar] [CrossRef]
- McIntosh, G.C.; Yoon, M.; Berber, S.; Tománek, D. Diamond fragments as building blocks of functional nanostructures. Phys. Rev. B 2004, 70, 045401. [Google Scholar] [CrossRef]
- Sasagawa, T.; Shen, Z.-x. A route to tunable direct band-gap diamond devices: Electronic structures of nanodiamond crystals. J. Appl. Phys. 2008, 104, 073704. [Google Scholar] [CrossRef]
- Drummond, N.D.; Williamson, A.J.; Needs, R.J.; Galli, G. Electron Emission from Diamondoids: A Diffusion Quantum Monte Carlo Study. Phys. Rev. Lett. 2005, 95, 096801. [Google Scholar] [CrossRef] [PubMed]
- Fokin, A.A.; Schreiner, P.R. Band gap tuning in nanodiamonds: First principle computational studies. Mol. Phys. 2009, 107, 823–830. [Google Scholar] [CrossRef]
- Weigel, W.; Dang, H.; Feceu, A.; Martin, D. Direct radical functionalization methods to access substituted adamantanes and diamondoids. Org. Biomol. Chem. 2021, 20, 10–36. [Google Scholar] [CrossRef]
- Teunissen, J.L.; De Proft, F.; De Vleeschouwer, F. Tuning the HOMO–LUMO energy gap of small diamondoids using inverse molecular design. J. Chem. Theory Comput. 2017, 13, 1351–1365. [Google Scholar] [CrossRef]
- Fokin, A.A.; Zhuk, T.S.; Pashenko, A.E.; Dral, P.O.; Gunchenko, P.A.; Dahl, J.E.P.; Carlson, R.M.K.; Koso, T.V.; Serafin, M.; Schreiner, P.R. Oxygen-Doped Nanodiamonds: Synthesis and Functionalization. Org. Lett. 2009, 11, 3068–3071. [Google Scholar] [CrossRef]
- Rander, T.; Staiger, M.; Richter, R.; Zimmermann, T.; Landt, L.; Wolter, D.; Dahl, J.E.; Carlson, R.M.K.; Tkachenko, B.A.; Fokina, N.A.; et al. Electronic structure tuning of diamondoids through functionalization. J. Chem. Phys. 2013, 138, 024310. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Flores, J.; Ramos, E.; Sansores Cuevas, L.E.; García-Cruz, I.; Salcedo, R. Diamondoid metallic complexes as an alternative to capture N2: A DFT study. J. Comput. Theo. Chem. 2017, 1110, 8–13. [Google Scholar] [CrossRef]
- Matsuura, Y. Tunnel magnetoresistance of diamondoids. Chem. Phys. Lett. 2016, 663, 21–26. [Google Scholar] [CrossRef]
- Mansoori, G.A.; George, T.F.; Zhang, G.P.; Assoufid, L. Structure and opto-electronic behaviour of diamondoids, with applications as mems and at the nanoscale level. In Progress in Nanotechnology Research; Nova Science: Hauppauge, NY, USA, 2007; pp. 1–19. [Google Scholar]
- Ranjbar, A.; Khazaei, M.; Venkataramanan, N.S.; Lee, H.; Kawazoe, Y. Chemical engineering of adamantane by lithium functionalization: A first-principles density functional theory study. Phys. Rev. B 2011, 83, 115401. [Google Scholar] [CrossRef]
- Štimac, A.; Šekutor, M.; Mlinarić-Majerski, K.; Frkanec, L.; Frkanec, R. Adamantane in Drug Delivery Systems and Surface Recognition. Molecules 2017, 22, 297. [Google Scholar] [CrossRef]
- Miranda, W.D.A.; Moreira, E.; Tavares, M.S.; Coutinho, S.S.; Gargano, R.; Azevedo, D.L. BN adamantane isomers: An optical absorption spectrum study. Appl. Phys. A 2021, 127, 32. [Google Scholar] [CrossRef]
- Garcia, J.C.; Justo, J.F.; Machado, W.V.M.; Assali, L.V.C. Boron and nitrogen functionalized diamondoids: A first principles investigation. Diamond Relat. Mater. 2010, 19, 837–840. [Google Scholar] [CrossRef]
- Marsusi, F.; Mirabbaszadeh, K.; Mansoori, G.A. Opto-electronic properties of adamantane and hydrogen-terminated sila-and germa-adamantane: A comparative study. Physica E 2009, 41, 1151–1156. [Google Scholar] [CrossRef]
- Hamadanian, M.; Khoshnevisan, B.; Fotooh, F.K. Structure and electronic properties of Na-doped adamantane crystals. J. Mol. Struct. 2010, 961, 48–54. [Google Scholar] [CrossRef]
- Krongsuk, S.; Shinsuphan, N.; Amornkitbumrung, V. Effect of the alkali metal (Li, Na, K) substitution on the geometric, electronic and optical properties of the smallest diamondoid: First principles calculations. Chin. J. Chem. Eng. 2019, 27, 476–482. [Google Scholar] [CrossRef]
- Song, Y.-D.; Wang, L.; Wu, L.-M. The structures and nonlinear optical responses of Li/Na doped adamantane: A density functional study. Optik 2016, 127, 10825–10837. [Google Scholar] [CrossRef]
- Wu, H.-Q.; Zhong, R.-L.; Sun, S.-L.; Xu, H.-L.; Su, Z.-M. Alkali Metals-Substituted Adamantanes Lead to Visible Light Absorption: Large First Hyperpolarizability. J. Phys. Chem. C 2014, 118, 6952–6958. [Google Scholar] [CrossRef]
- Santos, A.; Moreira, E.; Meiyazhagan, A.; Azevedo, D. Bond order effects on the optoelectronic properties of oxygen/sulphur functionalized adamantanes. J. Mol. Graphics Modell. 2021, 105, 107869. [Google Scholar] [CrossRef]
- Elavarasi, S.B.; Mariam, D.; Momeen, M.U.; Hu, J.; Guin, M. Effect of fluorination on bandgap, first and second order hyperpolarizabilities in lithium substituted adamantane: A time dependent density functional theory. Chem. Phys. Lett. 2019, 715, 310–316. [Google Scholar] [CrossRef]
- Aravindhan, R.; Momeen, M.U.; Hu, J. Halogenation effects on the bridgehead position of the adamantane molecule. Chem. Phys. Lett. 2023, 829, 140746. [Google Scholar] [CrossRef]
- Adhikari, B.; Fyta, M. Towards double-functionalized small diamondoids: Selective electronic band-gap tuning. Nanotechnology 2015, 26, 035701. [Google Scholar] [CrossRef]
- Sarap, C.S.; Adhikari, B.; Meng, S.; Uhlig, F.; Fyta, M. Optical properties of single-and double-functionalized small diamondoids. J. Phys. Chem. A 2018, 122, 3583–3593. [Google Scholar] [CrossRef] [PubMed]
- Rander, T.; Bischoff, T.; Knecht, A.; Wolter, D.; Richter, R.; Merli, A.; Möller, T. Electronic and Optical Properties f Methylated Adamantanes. J. Am. Chem. Soc. 2017, 139, 11132–11137. [Google Scholar] [CrossRef] [PubMed]
- Jariwala, D.; Sangwan, V.K.; Lauhon, L.J.; Marks, T.J.; Hersam, M.C. Carbon nanomaterials for electronics, optoelectronics, photovoltaics, and sensing. Chem. Soc. Rev. 2013, 42, 2824–2860. [Google Scholar] [CrossRef] [PubMed]
- Chesnokov, V.V.; Prosvirin, I.P.; Gerasimov, E.Y.; Chichkan, A.S. Synthesis of Boron-Doped Carbon Nanomaterial. Materials 2023, 16, 1986. [Google Scholar] [CrossRef]
- Ekimov, E.; Sidorov, V.; Rakhmanina, A.; Mel’nik, N.; Timofeev, M.; Sadykov, R. Synthesis, structure, and physical properties of boron-doped diamond. Inorg. Mater. 2006, 42, 1198–1204. [Google Scholar] [CrossRef]
- Fyta, M. Stable boron nitride diamondoids as nanoscale materials. Nanotechnology 2014, 25, 365601. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView 6.0. 16; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Garcia, J.C.; Justo, J.F.; Machado, W.V.M.; Assali, L.V. Functionalized adamantane: Building blocks for nanostructure self-assembly. Phys. Rev. B 2009, 80, 125421. [Google Scholar] [CrossRef]
- Kuchitsu, K.; Cyvin, S.J. Molecular Structures and Vibrations. In SJ Cyvin; Elsevier: Amsterdam, The Netherlands, 1972; p. 183. [Google Scholar]
- Vijayakumar, V.; Alka, B.G.; Godwal, B.K.; Sikka, S.K. Pressure induced phase transitions and equation of state of adamantane. J. Phys. Condens. Matt. 2001, 13, 1961. [Google Scholar] [CrossRef]
- Wade, K.; Wade, K. Carboranes. In Electron Deficient Compounds; Nelson: London, UK, 1971; pp. 150–175. [Google Scholar]
- Goss, J.; Briddon, P. Theory of boron aggregates in diamond: First-principles calculations. Phys. Rev. B 2006, 73, 085204. [Google Scholar] [CrossRef]
- Koretsune, T.; Saito, S. Electronic structure of boron-doped carbon nanotubes. Phys. Rev. B 2008, 77, 165417. [Google Scholar] [CrossRef]
- Wu, X.; Radovic, L.R. Ab initio molecular orbital study on the electronic structures and reactivity of boron-substituted carbon. J. Phys. Chem. A 2004, 108, 9180–9187. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Stanton, J.F. Applications of Post-Hartree—Fock Methods: A Tutorial. Rev. Comput. Chem. 1994, 5, 65–169. [Google Scholar]
- Tozer, D.J.; De Proft, F. Computation of the hardness and the problem of negative electron affinities in density functional theory. J. Phys. Chem. A 2005, 109, 8923–8929. [Google Scholar] [CrossRef]
- Wheeler, J.C. Electron affinities of the alkaline earth metals and the sign convention for electron affinity. J. Chem. Edu. 1997, 74, 123. [Google Scholar] [CrossRef]
- Li, Q.-S.; Feng, X.-J.; Xie, Y.; Schaefer, H.F. Perfluoroadamantane and its negative ion. J. Phys. Chem. A 2005, 109, 1454–1457. [Google Scholar] [CrossRef]
- Bartlett, R.J. Coupled-cluster approach to molecular structure and spectra: A step toward predictive quantum chemistry. J. Phys. Chem. 1989, 93, 1697–1708. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Partridge, H. The sensitivity of B3LYP atomization energies to the basis set and a comparison of basis set requirements for CCSD (T) and B3LYP. Chem. Phys. Lett. 1995, 240, 533–540. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Yu, J.; Su, N.Q.; Yang, W. Describing chemical reactivity with frontier molecular orbitalets. JACS Au 2022, 2, 1383–1394. [Google Scholar] [CrossRef]
- O’boyle, N.M.; Tenderholt, A.L.; Langner, K.M. Cclib: A library for package-independent computational chemistry algorithms. J. Comp. Chem. 2008, 29, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Ralph, C.M. Molecular building blocks and development strategies for molecular nanotechnology. Nanotechnology 2000, 11, 89. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C. 01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phy. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* basis set for third-row atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Goerigk, L.; Casanova-Paéz, M. The trip to the density functional theory zoo continues: Making a case for time-dependent double hybrids for excited-state problems. Aust. J. Chem. 2020, 74, 3–15. [Google Scholar] [CrossRef]
- Elliott, P.; Furche, F.; Burke, K. Excited states from time-dependent density functional theory. Rev. Comput. Chem. 2008, 26, 91–165. [Google Scholar]
- Wong, M.W.; Gill, P.M.; Nobes, R.H.; Radom, L. 6-311G (MC)(d, p): A second-row analogue of the 6-311G (d, p) basis set: Calculated heats of formation for second-row hydrides. J. Phy. Chem. 1998, 92, 4875–4880. [Google Scholar] [CrossRef]
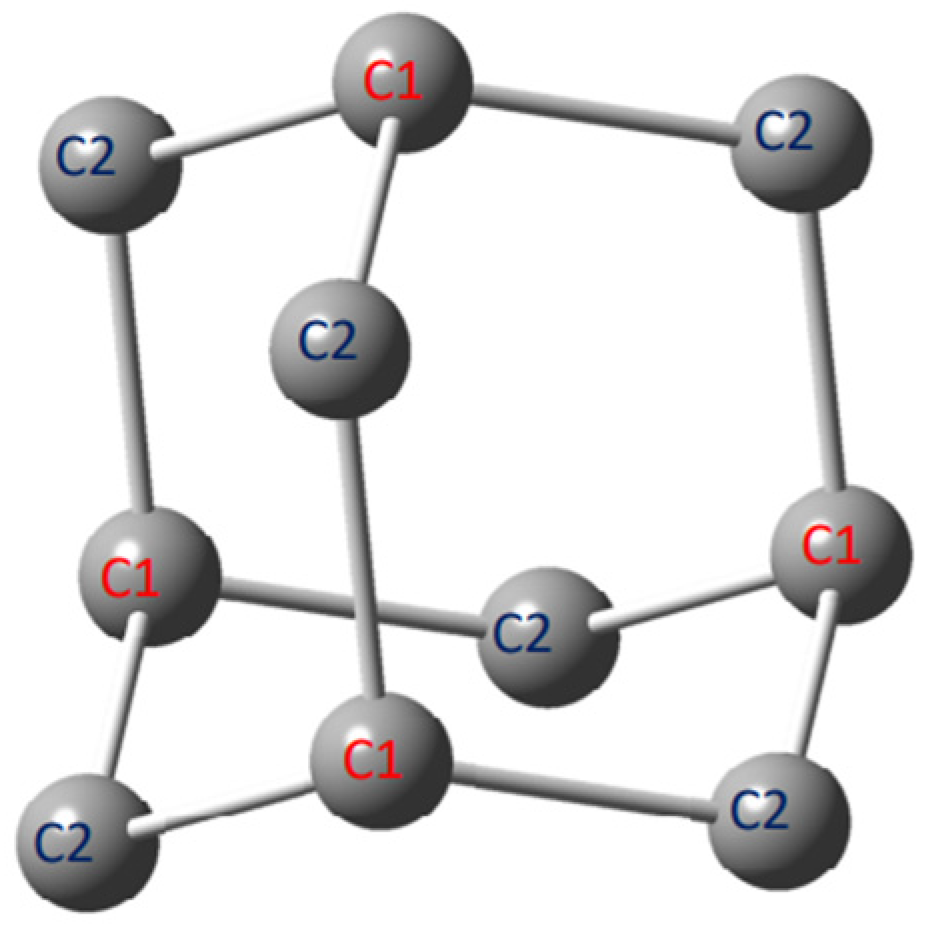

 —C1-type substitution,
—C1-type substitution,  —C2-type substitution, and
—C2-type substitution, and  —pristine adamantane).
—pristine adamantane).
 —C1-type substitution,
—C1-type substitution,  —C2-type substitution, and
—C2-type substitution, and  —pristine adamantane).
—pristine adamantane).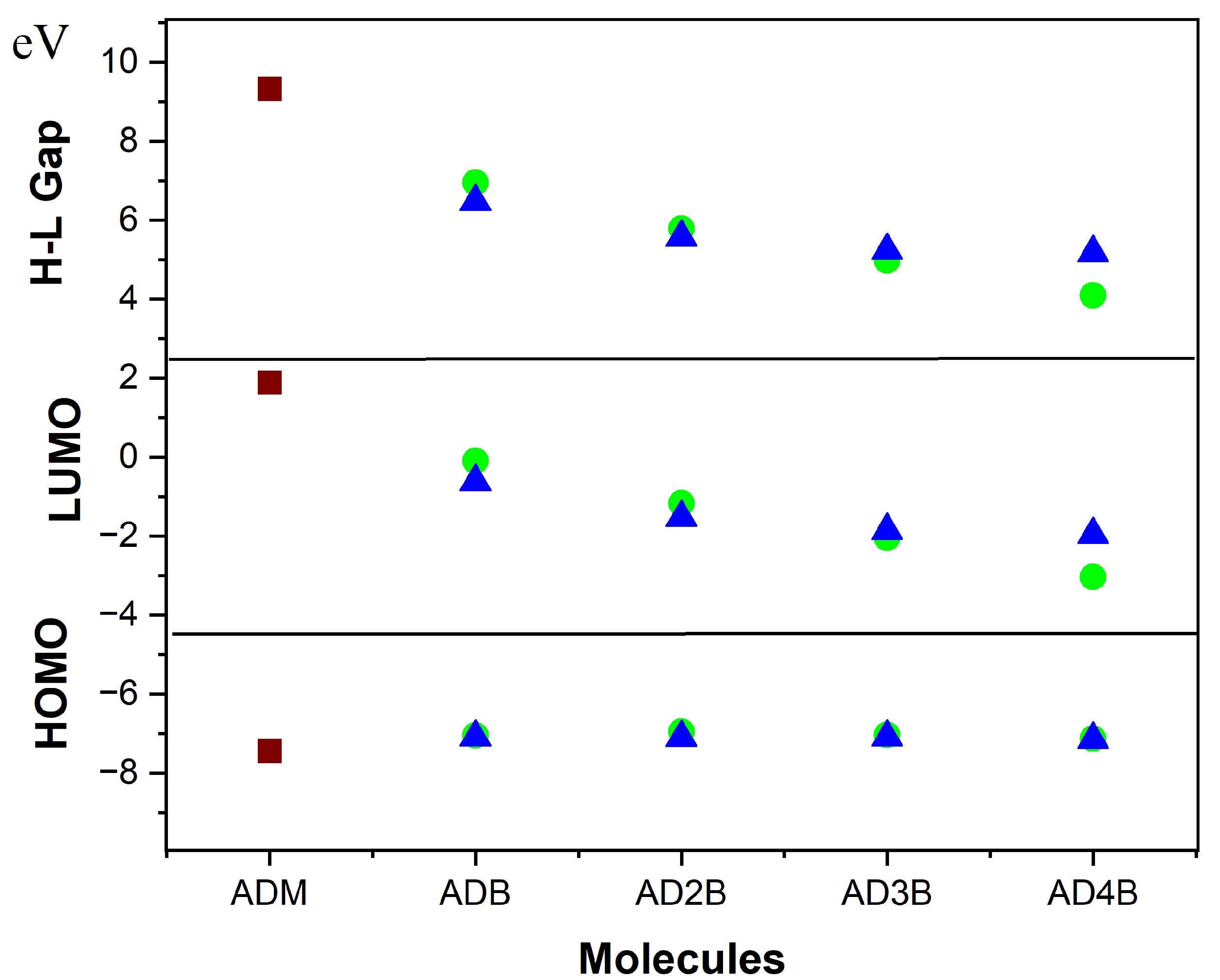

| # | # Boron | Molecular Formula | Naming | Configuration of Different Atom Types a |
|---|---|---|---|---|
| 1 | None | C10H16 | Adamantane | (C1)4(C2)6 |
| 2 | B | C9H15B | 1-bora-adamantane | (C1)3(B1)1(C2)6 |
| 3 | C9H15B | 2-bora-adamantane | (C1)4(C2)5(B2)1 | |
| 4 | 2B | C8H14B2 | 1,3-di-bora-adamantane | (C1)2(B1)2(C2)6 |
| 5 | C8H14B2 | 2,4-di-bora-adamantane | (C1)4(C2)4(B2)2 | |
| 6 | 3B | C7H13B3 | 1,3,5-tri-bora-adamantane | (C1)1(B1)3(C2)6 |
| 7 | C7H13B3 | 2,4,6-tri-bora-adamantane | (C1)4(C2)3(B2)3 | |
| 8 | 4B | C6H12B4 | 1,3,5,7-tetra-bora-adamantane | (B1)4(C2)6 |
| 9 | C6H12B4 | 2,4,6,8-tetra-bora-adamantane | (C1)4(C2)2(B2)4 | |
| 10 | 5B | C5H11B5 | 1,2,3,5,7-penta-bora-adamantane | (B1)4(C2)5(B2)1 |
| 11 | C5H11B5 | 2,4,6,8,9-penta-bora-adamantne | (C1)4(C2)1(B2)5 | |
| 12 | 6B | C4H10B6 | 1,2,3,5,6,7-hexa-bora-adamantane | (B1)4(C2)4(B2)2 |
| 13 | C4H10B6 | 2,4,6,8,9,10-hexa-bora-adamantane | (C1)4(B2)6 |
| Molecule | E0 | E+ | E− | ΔE1 | ΔE2 |
|---|---|---|---|---|---|
| Adamantane | −10,632.18 | −10,623.09 | −10,628.82 | 9.10 | −3.36 |
| C1 Substitution | |||||
| 1-bora | −10,254.77 | −10,246.21 | −10,253.60 | 8.56 | −1.17 |
| 1,3-di-bora | −9877.73 | −9869.16 | −9877.38 | 8.57 | −0.35 |
| 1,3,5-tri-bora | −9500.93 | −9491.88 | −9501.44 | 9.05 | 0.51 |
| 1,3,5,7-tetra-bora | −9124.18 | −9115.40 | −9125.45 | 8.78 | 1.27 |
| C2 Substitution | |||||
| 2-bora | −10,254.56 | −10,246.02 | −10,253.45 | 8.54 | −1.11 |
| 2,4-dibora | −9877.23 | −9868.22 | −9876.98 | 9.02 | −0.25 |
| 2,4,6-tribora | −9499.90 | −9491.19 | −9500.50 | 8.71 | 0.60 |
| 2,4,6,8-tetrabora | −9122.80 | −9114.07 | −9123.36 | 8.73 | 0.56 |
| 2,4,6,8,9-pentabora | −8746.72 | −8737.79 | −8747.82 | 8.93 | 0.14 |
| 2,4,6,8,9,10-hexabora | −8370.50 | −8361.30 | −8371.43 | 9.20 | 0.93 |
| Molecule | E0 | E+ | E− | ΔE1 | ΔE2 |
|---|---|---|---|---|---|
| Adamantane | −10,601.81 | −10,591.98 | −10,598.63 | 9.83 | −3.18 |
| C1 Substitution | |||||
| 1-bora | −10,228.62 | −10,219.14 | −10,277.10 | 9.48 | −1.52 |
| 1,3-di-bora | −9852.07 | −9842.73 | −9851.60 | 9.33 | −0.47 |
| 1,3,5-tri-bora | −9475.77 | −9466.36 | −9476.20 | 9.41 | 0.43 |
| 1,3,5,7-tetra-bora | −9099.50 | −9089.97 | −9100.97 | 9.52 | 1.47 |
| C2 Substitution | |||||
| 2-bora | −10,228.36 | −10,218.85 | −10,227.31 | 9.51 | −1.05 |
| 2,4-dibora | −9848.10 | −9838.64 | −9847.97 | 9.46 | −0.13 |
| 2,4,6-tribora | −9471.33 | −9461.97 | −9471.58 | 9.36 | 0.25 |
| 2,4,6,8-tetrabora | −9094.81 | 9085.36 | −9095.11 | 9.45 | 0.29 |
| 2,4,6,8,9-pentabora | −8719.38 | −8709.72 | −8719.66 | 9.66 | 0.27 |
| 2,4,6,8,9,10-hexabora | −8343.50 | −8333.85 | −8343.43 | 9.65 | 0.30 |
| Molecules | Absorption Wavelength (nm) | Excitation Energy (eV) | Oscillator Strength | Transition State |
|---|---|---|---|---|
| Adamantane | 147 | 8.44 | 0.0034 | HOMO(A)→LUMO(A) (48%), HOMO(B)→LUMO(B) (48%) |
| 147 | 8.44 | 0.0034 | H-1(A)→LUMO(A) (48%), H-2(B)→LUMO(B) (48%) | |
| C1 Substitution | ||||
| 1-bora-adamantane | 213 | 5.82 | 0.0034 | H-1(A)→LUMO(A) (46%), HOMO(B)→LUMO(B) (46%) |
| 153 | 8.10 | 0.0952 | H-4(A)→LUMO(A) (48%), H-4(B)→LUMO(B) (48%) | |
| 1,3-dibora-adamantane | 235 | 5.28 | 0.0105 | H-1(A)→LUMO(A) (48%), H-1(B)→LUMO(B) (48%) |
| 174 | 7.13 | 0.0269 | H-6(A)→LUMO(A) (37%), H-3(A)→LUMO(A) (10%) | |
| 1,3,5-tribora-adamantane | 258 | 4.81 | 0.0127 | H-1(A)→LUMO(A) (49%), H-1(B)→LUMO(B) (49%) |
| 250 | 4.96 | 0.0101 | H-3(A)→LUMO(A) (37%), H-2(B)→LUMO(B) (45%) | |
| 1,3,5,7-tetrabora-adamantane | 423 | 2.93 | 0.0000 | H-1(A)→LUMO(A) (48%), H-1(B)→LUMO(B) (48%) |
| 238 | 5.21 | 0.0006 | H-5(A)→LUMO(A) (48%), H-5(B)→LUMO(B) (48%) | |
| C2 Substitution | ||||
| 2-bora-adamantane | 184 | 6.74 | 0.0085 | H-2→LUMO (98%) |
| 127 | 9.76 | 0.1442 | H-3→L+1 (16%), H-1→L+2 (59%) | |
| 2,4-dibora-adamantane | 267 | 4.64 | 0.0071 | H-1(A)→LUMO(A) (46%), H-1(B)→LUMO(B) (46%) |
| 219 | 5.66 | 0.0137 | H-2(A)→LUMO(A) (39%), H-2(B)→LUMO(B) (39%) | |
| 2,4,6-tribora-adamantane | 293 | 4.23 | 0.0095 | HOMO(A)→LUMO(A) (46%), HOMO(B)→LUMO(B) (46%) |
| 191 | 6.49 | 0.0171 | H-5(A)→LUMO(A) (14%), H-2(A)→L+1(A) (21%) | |
| 2,4,6,8-tetrabora-adamantane | 279 | 4.47 | 0.0084 | H-1(A)→LUMO(A) (44%), H-1(B)→LUMO(B) (44%) |
| 206 | 6.02 | 0.0296 | H-4(A)→LUMO(A) (30%), H-4(B)→LUMO(B) (30%) | |
| 2,4,6,8,9-pentabora-adamantane | 252 | 4.92 | 0.0233 | H-1(A)→LUMO(A) (33%), HOMO(A)→L+1(A) (14%) |
| 201 | 6.17 | 0.0501 | H-4(A)→LUMO(A) (16%), H-3(A)→L+1(A) (22%) | |
| 2,4,6,8,9,10-hexabora-adamantane | 252 | 4.92 | 0.0000 | HOMO(A)→L+2(A) (41%), HOMO(B)→L+2(B) (41%) |
| 217 | 5.71 | 0.0331 | H-1(A)→L+2(A) (48%), H-1(B)→L+2(B) (48%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusuf, A.H.; Golovko, V.B.; Masters, S.L. Tuning the Energy Levels of Adamantane by Boron Substitution. Molecules 2025, 30, 1976. https://doi.org/10.3390/molecules30091976
Yusuf AH, Golovko VB, Masters SL. Tuning the Energy Levels of Adamantane by Boron Substitution. Molecules. 2025; 30(9):1976. https://doi.org/10.3390/molecules30091976
Chicago/Turabian StyleYusuf, Aminu H., Vladimir B. Golovko, and Sarah L. Masters. 2025. "Tuning the Energy Levels of Adamantane by Boron Substitution" Molecules 30, no. 9: 1976. https://doi.org/10.3390/molecules30091976
APA StyleYusuf, A. H., Golovko, V. B., & Masters, S. L. (2025). Tuning the Energy Levels of Adamantane by Boron Substitution. Molecules, 30(9), 1976. https://doi.org/10.3390/molecules30091976






