The Common Concept of Anticooperativity Among Molecules Is Fundamentally Flawed, Based on Novel and Unified Molecular-Wide and Electron Density (MOWeD) Concept of Chemical Bonding
Abstract
1. Introduction
- 1.
- Three-dimensional six-water clusters discussed in this work are more stable than two-dimensional cyclic homodromic water hexamer, and the latter is restricted to ad configurations showing only positive, non-additivity in the strength of H-bonds, i.e., classical cooperativity;
- 2.
- Prism, being the most stable 3D six-water hexamer, does not have water molecules of ad configurations (there are three aad and three add waters),
- i.
- are more stable than the six-water cyclic hexamer; notably, they are the smallest 3D clusters that are more stable than their cyclic counterparts;
- ii.
- have water molecules with aad and add configurations, and these motifs are observed in each of the ice polymorphs [2].
- i.
- ii.
- The Fragment Attributed Molecular System Energy Change (FAMSEC) family of methods [54,55] is used to identify molecular fragments that either drive or obstruct a chemical change the most. FAMSEC also meets the all-body requirements, as the quantified energy contributions made by fragments are harvested from the entire space occupied by a system.
2. Theoretical Background
2.1. The FALDI Density Decomposition Scheme
2.2. A Fragment Attributed Molecular System Energy Change (FAMSEC) Protocol
3. Results and Discussion
3.1. Validation of B3LYP-Computed Relative Stabilities of Water Hexamers
3.2. A Cooperativity-Driven Decrease in E(hexamer) Relative to E(6H2O)
3.3. Quantifying Cooperativity
- (i)
- The number of delocalized electrons by ad waters in 3D hexamers examined is the same as found for the cyclic hexamer for which intermolNdeloc = 1.557 ± 0.001e [47].
- (ii)
- The difference in intermolNdeloc between aad and add waters in 3D hexamers is insignificant.
- (iii)
- Most importantly, there is a very significant difference in the number of delocalized electrons between ad and double-acceptor aad and double-donor add waters, with ad delocalizing about 0.45e less.
3.4. Quantifying Individual Water’s Contribution to the Cluster’s Stability
3.5. Quantifying Individual Intermolecular H-Bond Contributions to the Cluster’s Stability
4. Computational Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Frank, H.S.; Wen, W.-Y. III. Ion-Solvent Interaction. Structural Aspects of Ion-Solvent Interaction in Aaqueous Solutions: A Suggested Picture of Water Structure. Discuss. Faraday Soc. 1957, 24, 133–140. [Google Scholar] [CrossRef]
- Hankins, D.; Moskowitz, J.W.; Stillinger, F.H. Water Molecule Interactions. J. Chem. Phys. 1970, 53, 4544–4554. [Google Scholar] [CrossRef]
- White, J.C.; Davidson, E.R. An Analysis of the Hydrogen Bond in Ice. J. Chem. Phys. 1990, 93, 8029–8035. [Google Scholar] [CrossRef]
- Xantheas, S.S.; Dunning, T.H., Jr. The Structure of the Water Trimer From ab Initio Calculations. J. Chem. Phys. 1993, 98, 8037–8040. [Google Scholar] [CrossRef]
- Xantheas, S.S.; Dunning, T.H., Jr. Ab Initio Studies of Cyclic Water Clusters (H2O)n, n = 1–6. I. Optimal Structures and Vibrational Spectra. J. Chem. Phys. 1993, 99, 8774–8792. [Google Scholar] [CrossRef]
- Xantheas, S.S. Ab Initio Studies of Cyclic Water Clusters (H2O)n, n = 1–6. II. Analysis of Many-Body Interactions. J. Chem. Phys. 1994, 100, 7523–7534. [Google Scholar] [CrossRef]
- Luck, W.A.P. The importance of cooperativity for the properties of liquid water. J. Mol. Struct. 1998, 448, 131–142. [Google Scholar] [CrossRef]
- Ugalde, J.M.; Alkorta, I.; Elguero, J. Water Clusters: Towards an Understanding Based on First Principles of Their Static and Dynamic Properties. Angew. Chem. Int. Ed. 2000, 39, 717–721. [Google Scholar] [CrossRef]
- Ludwig, R. Water: From Clusters to the Bulk. Angew. Chem. Int. Ed. 2001, 40, 1808–1827. [Google Scholar] [CrossRef]
- Keutsch, F.N.; Cruzan, J.D.; Saykally, R.J. The Water Trimer. Chem. Rev. 2003, 103, 2533–2577. [Google Scholar] [CrossRef]
- Ohno, K.; Okimura, M.; Akaib, N.; Katsumotoa, Y. The effect of cooperative hydrogen bonding on the OH stretching-band shift for water clusters studied by matrix-isolation infrared spectroscopy and density functional theory. Phys. Chem. Chem. Phys. 2005, 7, 3005–3014. [Google Scholar] [CrossRef] [PubMed]
- Neela, Y.I.; Mahadevi, A.S.; Sastry, G.N. Hydrogen Bonding in Water Clusters and Their Ionized Counterparts. J. Phys. Chem. B 2010, 114, 17162–17171. [Google Scholar] [CrossRef] [PubMed]
- Pérez, C.; Muckle, M.T.; Zaleski, D.P.; Seifert, N.A.; Temelso, B.; Shields, G.C.; Kisiel, Z.; Pate, B.H. Structures of Cage, Prism, and Book Isomers of Water Hexamer from Broadband Rotational Spectroscopy. Science 2012, 336, 897–901. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, L.; Boyd, R.J. Visualizing Internal Stabilization in Weakly Bound Systems Using Atomic Energies: Hydrogen Bonding in Small Water Clusters. J. Phys. Chem. A 2012, 116, 3946–3951. [Google Scholar] [CrossRef]
- Guevara-Vela, J.M.; Chávez-Calvillo, R.; García-Revilla, M.; Hernández-Trujillo, J.; Christiansen, O.; Francisco, E.; Martín Pendás, Á.; Rocha-Rinza, T. Hydrogen-Bond Cooperative Effects in Small Cyclic Water Clusters as Revealed by the Interacting Quantum Atoms Approach. Chem. Eur. J. 2013, 19, 14304–14315. [Google Scholar] [CrossRef]
- Albrecht, L.; Chowdhury, S.; Boyd, R.J. Hydrogen Bond Cooperativity in Water Hexamers: Atomic Energy Perspective of Local Stabilities. J. Phys. Chem. A 2013, 117, 10790–10799. [Google Scholar] [CrossRef]
- Howard, J.C.; Tschumper, G.S. Wavefunction Methods for the Accurate Characterization of Water Clusters. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 199–224. [Google Scholar] [CrossRef]
- Marshall, B.D. A Second Order Thermodynamic Perturbation Theory for Hydrogen Bond Cooperativity in Water. J. Chem. Phys. 2017, 146, 174104. [Google Scholar] [CrossRef]
- Rakshit, A.; Bandyopadhyay, P.; Heindel, J.P.; Xantheas, S.S. Atlas of Putative Minima and Low-Lying Energy Networks of Water Clusters n = 3–25. J. Chem. Phys. 2019, 151, 214307. [Google Scholar] [CrossRef]
- Simon, A.; Rapacioli, M.; Michoulier, E.; Zheng, L.; Korchagina, K.; Cuny, J. Contribution of the Density-Functional-Based Tight-Binding Scheme to the Description of Water Clusters: Methods, Applications and Extension to Bulk Systems. Mol. Simul. 2019, 45, 249–268. [Google Scholar] [CrossRef]
- Ahirwar, M.B.; Gadre, S.R.; Deshmukh, M.M. Direct and Reliable Method for Estimating the Hydrogen Bond Energies and Cooperativity in Water Clusters, Wn, n = 3 to 8. J. Phys. Chem. A 2020, 124, 6699–6706. [Google Scholar] [CrossRef] [PubMed]
- Bilbrey, J.A.; Heindel, J.P.; Schram, M.; Bandyopadhyay, P.; Xantheas, S.S.; Choudhury, S. A Look Inside the Black Box: Using Graph Theoretical Descriptors to Interpret a Continuous-Filter Convolutional Neural Network (CF-CNN) Trained on the Global and Local Minimum Energy Structures of Neutral Water Clusters. J. Chem. Phys. 2020, 153, 024302. [Google Scholar] [CrossRef] [PubMed]
- Ben-Amotz, D. Electric Buzz in a Glass of Pure Water. Hydrogen Bond Charge Transfer in Water May Have Far-Reaching Chemical Iimplications. Science 2022, 376, 800–801. [Google Scholar] [CrossRef]
- Seijas, L.E.; Zambrano, C.H.; Almeida, R.; Alí-Torres, J.; Rincón, L.; Torres, F.J. Exploring the Non-Covalent Bonding in Water Clusters. Int. J. Mol. Sci. 2023, 24, 5271. [Google Scholar] [CrossRef]
- Santis, G.D.; Herman, K.M.; Heindel, J.P.; Xantheas, S.S. Descriptors of Water Aggregation. J. Chem. Phys. 2024, 160, 054306. [Google Scholar] [CrossRef]
- Ojamäe, L.; Hermansson, K. Ab Initio Study of Cooperativity in Water Chains: Binding Energies and Anharmonic Frequencies. J. Phys. Chem. 1994, 98, 4271–4282. [Google Scholar] [CrossRef]
- Luck, W.A.P.; Klein, D.; Rangsriwatananon, K. Anti-Cooperativity of the Two Water OH Groups. J. Mol. Struct. 1997, 416, 287–296. [Google Scholar] [CrossRef]
- Huš, M.; Urbic, T. Strength of Hydrogen Bonds of Water Depends on Local Environment. J. Chem. Phys. 2012, 136, 144305. [Google Scholar] [CrossRef]
- Albrecht, L.; Boyd, R.J. Atomic energy analysis of cooperativity, anti-cooperativity, and non-cooperativity in small clusters of methanol, water, and formaldehyde. Comput. Theor. Chem. 2015, 1053, 328–336. [Google Scholar] [CrossRef]
- Saha, S.; Sastry, G.N. Quantifying cooperativity in water clusters: An attempt towards obtaining a generalised equation. Mol. Phys. 2015, 113, 3031–3041. [Google Scholar] [CrossRef]
- Guevara-Vela, J.M.; Romero-Montalvo, E.; Gómez, V.A.M.; Chávez-Calvillo, R.; García-Revilla, M.; Francisco, E.; Martín Pendás, Á.; Rocha-Rinza, T. Hydrogen Bond Cooperativity and Anticooperativity Within the Water Hexamer. Phys. Chem. Chem. Phys. 2016, 18, 19557–19566. [Google Scholar] [CrossRef] [PubMed]
- Mahadevi, A.S.; Sastry, G.N. Cooperativity in Noncovalent Interactions. Chem. Rev. 2016, 116, 2775–2825. [Google Scholar] [CrossRef] [PubMed]
- Silvestrelli, P.L. Hydrogen bonding characterization in water and small molecules. J. Chem. Phys. 2017, 146, 244315. [Google Scholar] [CrossRef] [PubMed]
- Castor-Villegas, V.M.; Guevara-Vela, J.M.; Vallejo Narváez, W.E.; Martín Pendás, Á.; Rocha-Rinza, T.; Fernández-Alarcón, A. On the Strength of Hydrogen Bonding Within Water Clusters on the Coordination Limit. J. Comput. Chem. 2020, 41, 2266–2277. [Google Scholar] [CrossRef]
- Sauza-de la Vega, A.; Rocha-Rinza, T.; Guevara-Vela, J.M. Cooperativity and Anticooperativity in Ion-Water Interactions: Implications for the Aqueous Solvation of Ions. ChemPhysChem 2021, 22, 1269–1285. [Google Scholar] [CrossRef]
- Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Hakala, M.; Nygård, K.; Manninen, S.; Pettersson, L.G.M.; Hämäläinen, K. Intra-and Intermolecular Effects in the Compton Profile of Water. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 035432. [Google Scholar] [CrossRef]
- Ignatov, I.; Mosin, O. Mathematical Models Describing Water Clusters as Interaction Among Water Molecules. Distributions of Energies of Hydrogen Bonds. J. Med. Physiol. Biophys. 2014, 3, 48–70. [Google Scholar]
- Weimann, M.; Fárník, M.; Suhm, M.A.; Alikhani, M.E.; Sadlej, J. Cooperative and Anticooperative Mixed Trimers of HCl and Methanol. J. Mol. Struct. 2006, 790, 18–26. [Google Scholar] [CrossRef]
- Zabardasti, A.; Kakanejadi, A.; Ghenaatian, F.; Bigleri, Z. A Theoretical Study of Cooperative and Anticooperative Effects on Hydrogen-Bonded Clusters of Water and the Cyanuric Acid. Mol. Simul. 2010, 36, 960–968. [Google Scholar] [CrossRef]
- Zabardasti, A.; Kakanejadi, A.; Moosavi, S.; Bigleri, Z.; Solimannejad, M. Anticooperativity in Dihydrogen Bonded Clusters of Ammonia and BeH42–. J. Mol. Struct. THEOCHEM 2010, 945, 97–100. [Google Scholar] [CrossRef]
- Han, G.; Ding, Y.; Qian, P.; Zhang, C.; Song, W. Theoretical Investigation of Gas Phase Ethanol–(Water)n (n = 1–5) Clusters and Comparison with Gas Phase Pure Water Clusters (Water)n (n = 2–6). Int. J. Quantum Chem. 2013, 113, 1511–1521. [Google Scholar] [CrossRef]
- Romero-Montalvo, E.; Guevara-Vela, J.M.; Costales, A.; Martín Pendás, Á.; Rocha-Rinza, T. Cooperative and Aticooperative Effects in Resonance Assisted Hydrogen Bonds in Merged Structures of Malondialdehyde. Phys. Chem. Chem. Phys. 2017, 19, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Monu; Oram, B.K.; Bandyopadhyay, B. Simultaneous Exhibition of Positive and Negative Cooperativity by Purely C H⋅⋅⋅O H-bonded (1,3-cyclohexanedione)n (n = 2–6) Clusters: A Density Functional Theoretical Investigation. Int. J. Quantum Chem. 2021, 121, 26581. [Google Scholar] [CrossRef]
- Guo, S.; Zhu, C.; Chen, G.; Gu, J.; Ma, C.; Gao, H.; Li, L.; Zhang, Y.; ·Li, X.; Wang, Z.; et al. A Theoretical Study on Intermolecular Hydrogen Bonds of Isopropanol-Water Clusters. Theor. Chem. Acc. 2022, 141, 6. [Google Scholar] [CrossRef]
- Patkar, D.; Ahirwar, M.B.; Deshmukh, M.M. Energetic Ordering of Hydrogen Bond Strengths in Methanol-Water Clusters: Insights via Molecular Tailoring Approach. ChemPhysChem 2022, 23, 202200143. [Google Scholar] [CrossRef]
- The Oxford Reference. Anticooperativity. In Oxford Dictionary of Biochemistry and Molecular Biology, 2nd ed.; Oxford University Press: Oxford, UK, 2008; Available online: https://www.oxfordreference.com/search?q=Anticooperativity&searchBtn=Search&isQuickSearch=true (accessed on 24 March 2025).
- Cukrowski, I.; Zaaiman, S.; Hussain, S.; de Lange, J.H. All-Body Concept and Quantified Limits of Cooperativity and Related Effects in Homodromic Cyclic Water Clusters from a Molecular-Wide and Electron Density (MOWeD)-Based Approach. J. Comput. Chem. 2024, 45, 2812–2824. [Google Scholar] [CrossRef]
- Cukrowski, I. A Unified Molecular-Wide and Electron Density Based Concept of Chemical Bonding. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, 1579. [Google Scholar] [CrossRef]
- Bader, R.F.W. Bond Paths are not Chemical Bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef]
- de Lange, J.H.; Cukrowski, I. Toward Deformation Densities for Intramolecular Interactions without Radical Reference States Using the Fragment, Atom, Localized, Delocalized, and Interatomic (FALDI) Charge Density Decomposition Scheme. J. Comput. Chem. 2017, 38, 981–997. [Google Scholar] [CrossRef]
- de Lange, J.H.; van Niekerk, D.M.; Cukrowski, I. FALDI-Based Decomposition of an Atomic Interaction Line Leads to 3D Representation of the Multicenter Nature of Interactions. J. Comput. Chem. 2018, 39, 973–985. [Google Scholar] [CrossRef] [PubMed]
- de Lange, J.H.; Cukrowski, I. Exact and Exclusive Electron Localization Indices Within QTAIM Atomic Basins. J. Comput. Chem. 2018, 39, 1517–1530. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, I. IQA-Embedded Fragment Attributed Molecular System Energy Change in Exploring Intramolecular Interactions. Comput. Theor. Chem. 2015, 1066, 62–75. [Google Scholar] [CrossRef]
- Cukrowski, I.; Dhimba, G.; Riley, D.L. A Reaction Energy Profile and Fragment Attributed Molecular System Energy Change (FAMSEC)-Based Protocol Designed to Uncover Reaction Mechanisms: A Case Study of the Proline-Catalysed Aldol Reaction. Phys. Chem. Chem. Phys. 2019, 21, 16694–16705. [Google Scholar] [CrossRef]
- Cooper, D.L.; de Lange, J.H.; Ponec, R. Comparison of DAFH and FALDI-like approaches. Theor. Chem. Acc. 2020, 139, 179. [Google Scholar] [CrossRef]
- Bates, T.G.; de Lange, J.H.; Cukrowski, I. The CH⋅⋅⋅HC interaction in biphenyl is a delocalized, molecular-wide and entirely non-classical interaction: Results from FALDI analysis. J. Comput. Chem. 2021, 42, 706–718. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Cukrowski, I.; Dhimba, G.; Riley, D.L. A Molecular-Wide and Electron Density-Based Approach in Exploring Chemical Reactivity and Explicit Dimethyl Sulfoxide (DMSO) Solvent Molecule Effects in the Proline Catalyzed Aldol Reaction. Molecules 2022, 27, 962. [Google Scholar] [CrossRef]
- Mangondo, P.; Cukrowski, I. On the Origin of the Relative Stability of ZnIINTA and ZnIINTPA Metal Complexes. An Insight From the IQA, IQF, and π-FARMS methods. Int. J. Quantum Chem. 2017, 117, 25321. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Sagan, F.; Szczepanik, D.W.; de Lange, J.H.; Ptaszek, A.L.; van Niekerk, D.M.E.; Cukrowski, I. Origin of Hydrocarbons Stability from a Computational Perspective: A Case Study of Ortho-Xylene Isomers. ChemPhysChem 2020, 21, 494–502. [Google Scholar] [CrossRef]
- Blanco, M.A.; Martín Pendás, Á.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef]
- Francisco, E.; Martín Pendás, Á.; Blanco, M.A. A Molecular Energy Decomposition Scheme for Atoms in Molecules. J. Chem. Theory Comput. 2006, 2, 90–102. [Google Scholar] [CrossRef] [PubMed]
- Bates, D.M.; Tschumper, G.S. CCSD(T) Complete Basis Set Limit Relative Energies for Low-Lying Water Hexamer Structures. J. Phys. Chem. A 2009, 113, 3555–3559. [Google Scholar] [CrossRef] [PubMed]
- Kryachko, E.S. Ab Initio Studies of the Conformations of Water Hexamer: Modelling the Penta-Coordinated Hydrogen-Bonded Pattern in liquid water. Chem. Phys. Lett. 1999, 314, 353–363. [Google Scholar] [CrossRef]
- Olson, R.M.; Bentz, J.L.; Kendall, R.A.; Schmidt, M.W.; Gordon, M.S. A Novel Approach to Parallel Coupled Cluster Calculations: Combining Distributed and Shared Memory Techniques for Modern Cluster Based Systems. J. Chem. Theory Comput. 2007, 3, 1312–1328. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Koch, D.; Pavanello, M.; Shao, X.; Ihara, M.; Ayers, P.W.; Matta, C.F.; Jenkins, S.; Manzhos, S. The Analysis of Electron Densities: From Basics to Emergent Applications. Chem. Rev. 2024, 124, 12661–12737. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian 09, Revision, D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll (Version 19.02.13); TK Gristmill Software: Overland Park, KS, USA, 2019; Available online: https://aim.tkgristmill.com (accessed on 24 March 2019).
- Cukrowski, I. Reliability of HF/IQA, B3LYP/IQA, and MP2/IQA data in interpreting the nature and strength of interactions. Phys. Chem. Chem. Phys. 2019, 21, 10244–10260. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Cukrowski, I.; de Lange, J.H.; Hussain, S. MOWeD-LAC (Molecular-Wide Electron (de)Localization Atomic Counts) and MOWeD-LFC (Molecular-Wide Electron (de)Localization Fragment Counts) Software Applications. 2023. Available online: https://bit.ly/link-to-mowed-software (accessed on 24 March 2025).
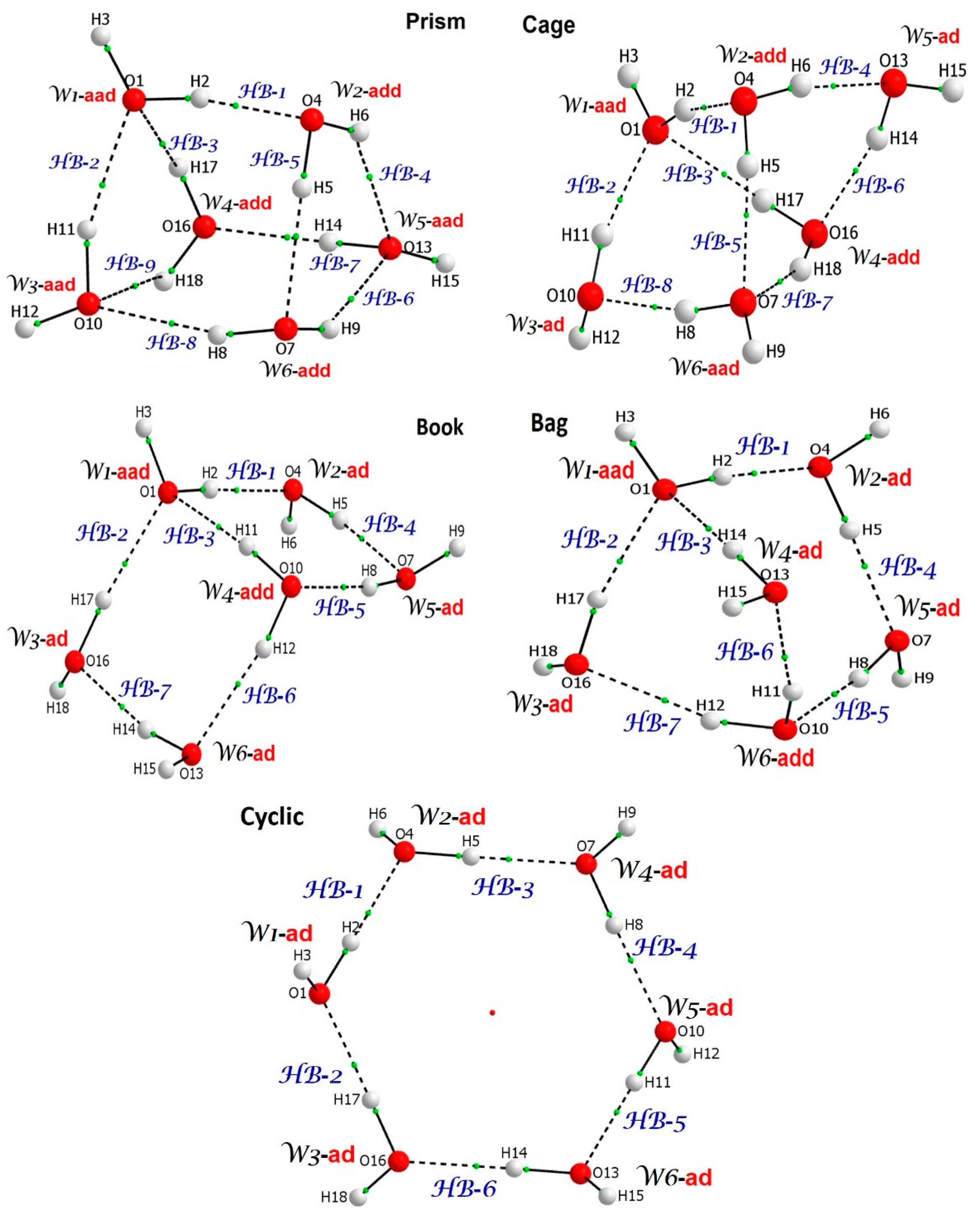
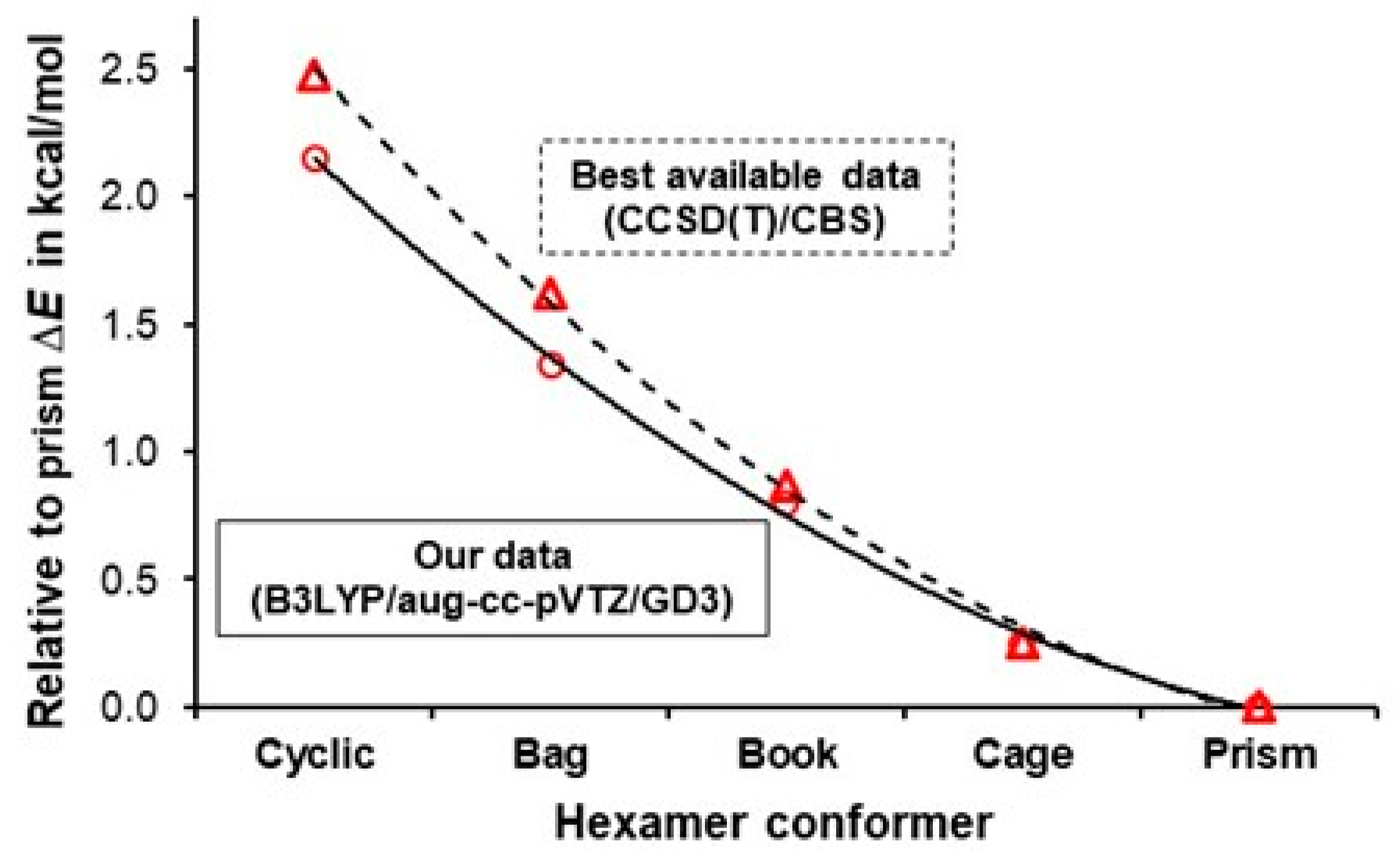
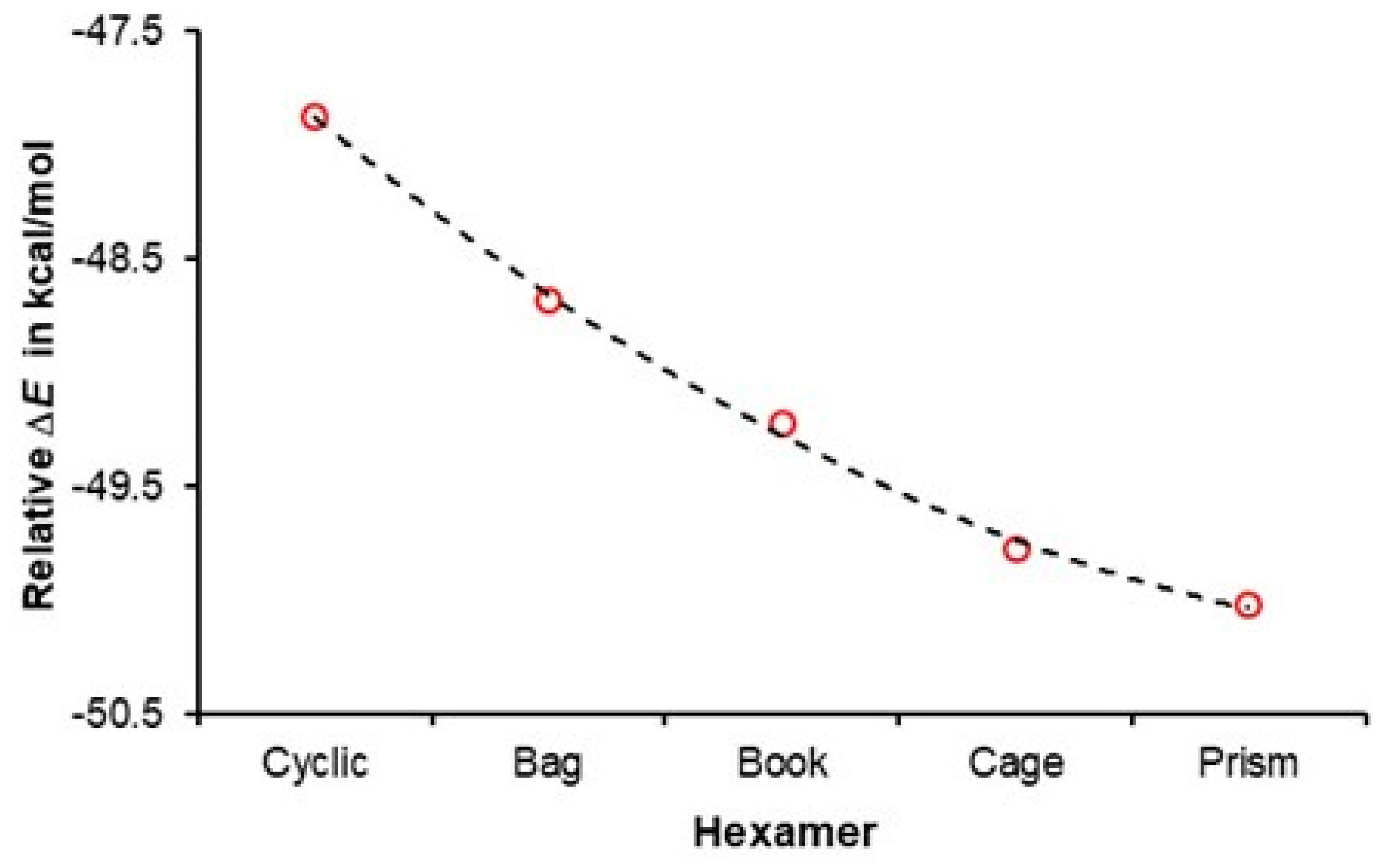
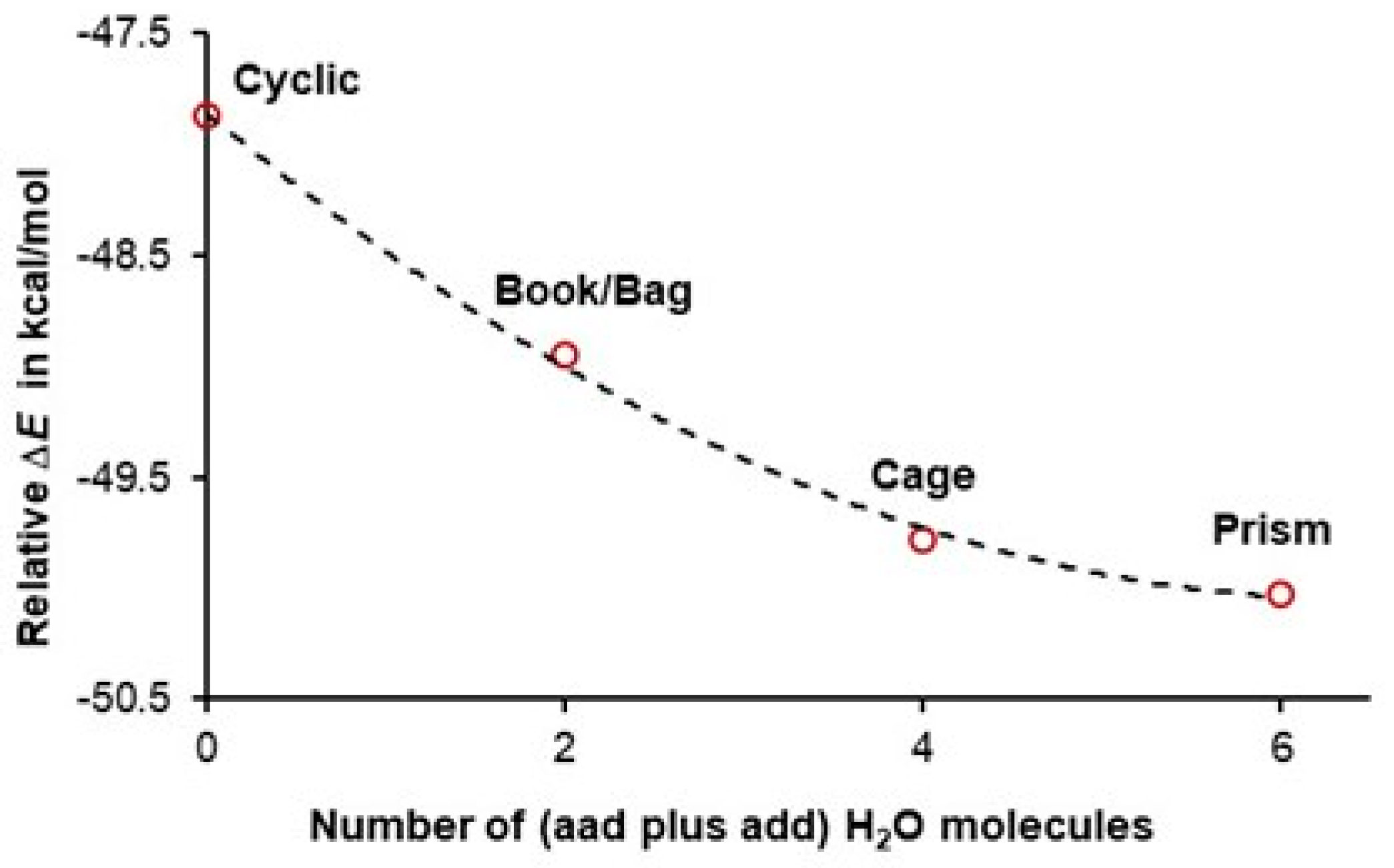
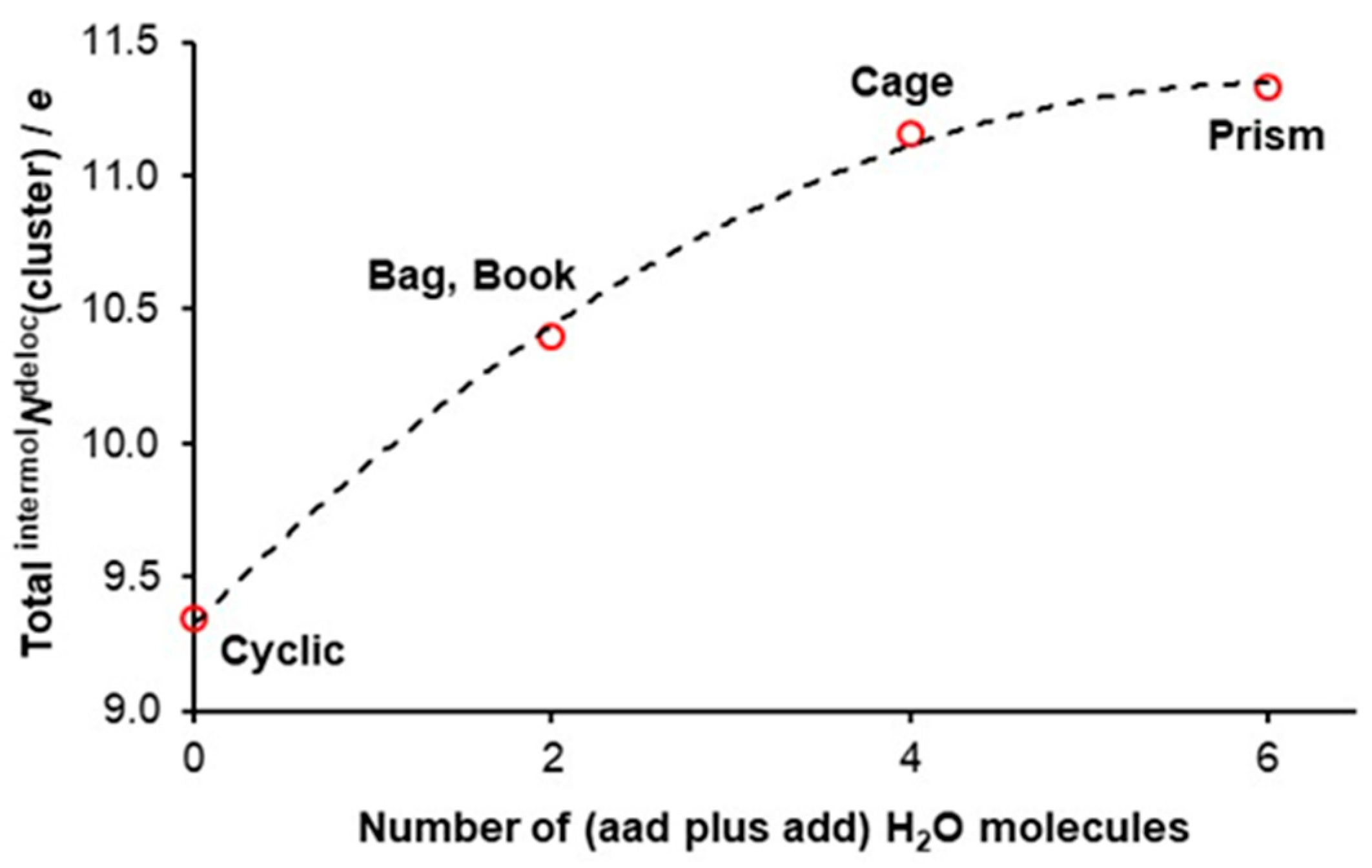
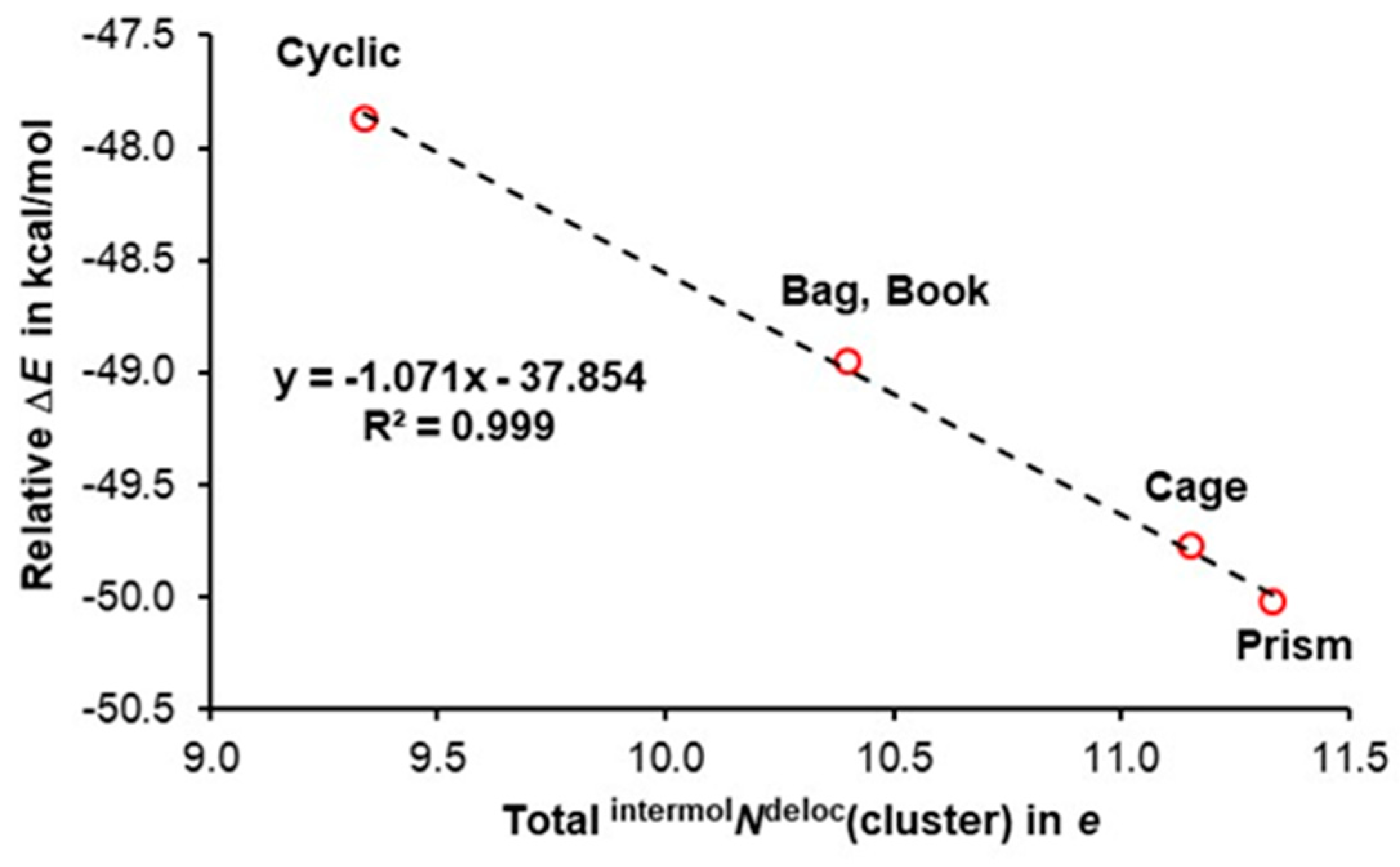
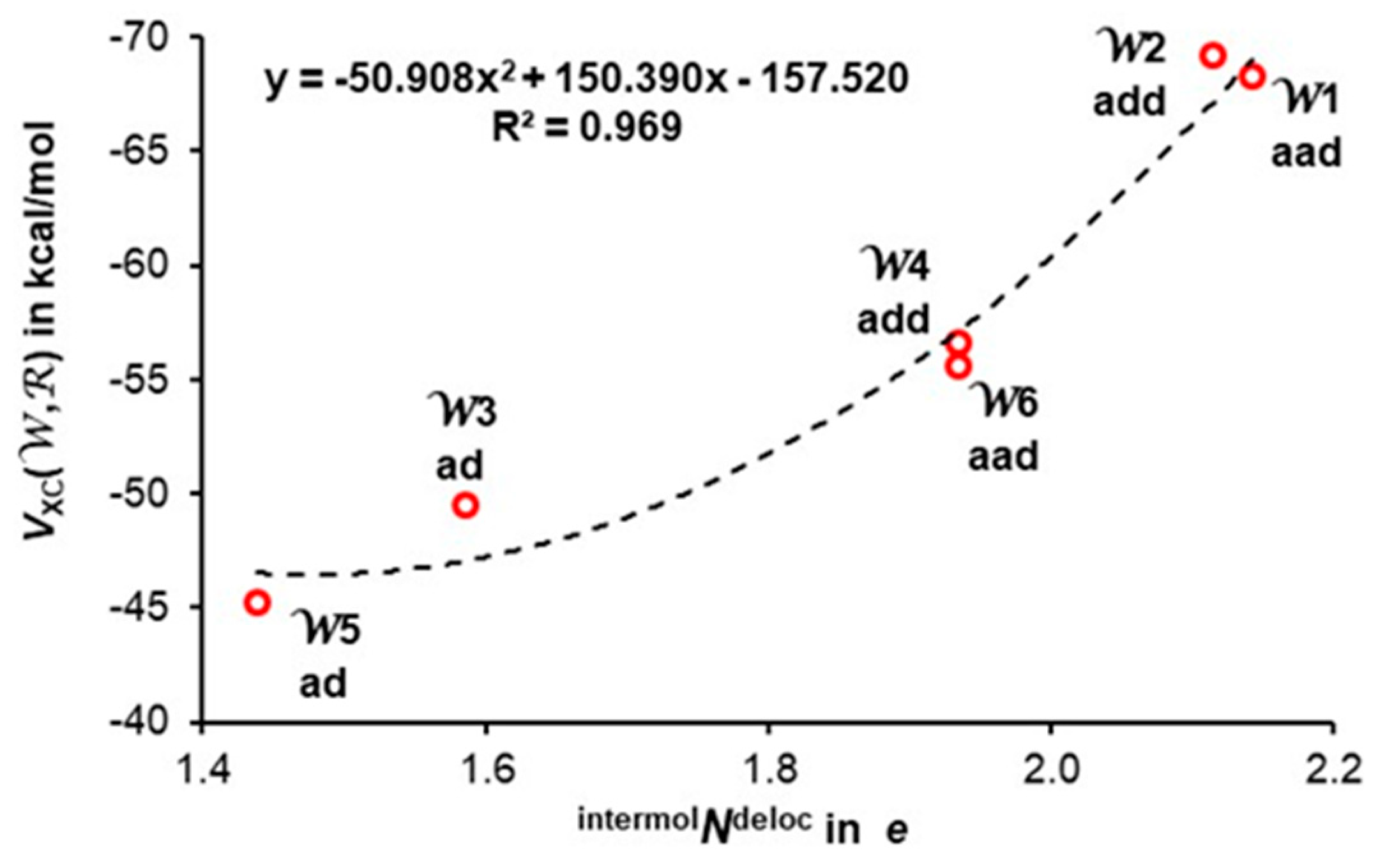


| ΔE = E(hexamer) − E(prism) in kcal/mol | ||||||
|---|---|---|---|---|---|---|
| Source | Level of Theory | Cyclic | Bag | Book | Cage | Prism |
| Our data | B3LYP/aug-cc-pVTZ/GD3 | 2.15 | 1.34 | 0.80 | 0.25 | 0 |
| Bates et al. [64] | CCSD(T)/CBS | 2.48 | 1.62 | 0.87 | 0.25 | 0 |
| Kryachko [65] | MP2(full)/aug-cc-pVDZ | 2.06 | N/A | 1.16 | 0.25 | 0 |
| Olson et al. [66] | CCSD(T)/aug-cc-pVTZ | 2.10 | N/A | 1.20 | 0.30 | 0 |
| Prism | Cage | Book | Bag | ||||
|---|---|---|---|---|---|---|---|
| Water | Ndeloc | Water | Ndeloc | Water | Ndeloc | Water | Ndeloc |
| aad 1 | 2.112 | aad 1 | 2.142 | aad 1 | 2.100 | aad 1 | 2.188 |
| add 2 | 2.027 | add 2 | 2.116 | add 4 | 2.048 | add 6 | 2.074 |
| aad 3 | 1.771 | add 4 | 1.935 | ad 2 | 1.647 | ad 2 | 1.719 |
| add 4 | 1.861 | aad 6 | 1.935 | ad 3 | 1.484 | ad 3 | 1.433 |
| aad 5 | 1.778 | ad 3 | 1.587 | ad 5 | 1.603 | ad 4 | 1.411 |
| add 6 | 1.786 | ad 5 | 1.439 | ad 6 | 1.412 | ad 5 | 1.677 |
| Energy Terms in kcal/mol | |||
|---|---|---|---|
| Water | Eint() | VXC() | mol-FAMSEC |
| aad 1 | −100.03 | −70.22 | −57.81 |
| add 6 | −95.36 | −69.20 | −56.58 |
| ad 2 | −86.34 | −59.52 | −50.39 |
| ad 5 | −85.31 | −59.23 | −50.07 |
| ad 3 | −54.68 | −40.56 | −32.69 |
| ad 4 | −52.42 | −39.20 | −31.12 |
| Average: | −79.0 | −56.3 | −46.4 |
| St. Dev.: | 20.5 | 13.6 | 11.7 |
| Water cluster | |||||
|---|---|---|---|---|---|
| Prism | Cage | Book | Bag | Cyclic | |
| H-Bond | mol-FAMSEC in kcal/mol | ||||
| -1 | –141.0 | –139.3 | –139.5 | –142.1 | –115.2 |
| -2 | –157.3 | –145.1 | –167.7 | –142.7 | |
| -3 | –163.0 | –161.0 | –143.4 | –143.7 | |
| -4 | –126.4 | –133.0 | –119.4 | –121.8 | |
| -5 | –156.9 | –161.5 | –118.8 | –119.2 | |
| -6 | –139.1 | –150.1 | –119.4 | –122.4 | |
| -7 | –124.4 | –109.8 | –109.2 | –125.5 | – |
| -8 | –138.1 | –126.3 | – | – | – |
| -9 | –158.5 | – | – | – | – |
| Average: | –145.0 | –140.8 | –131.1 | –131.1 | –115.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cukrowski, I.; Zaaiman, S.; Hussain, S. The Common Concept of Anticooperativity Among Molecules Is Fundamentally Flawed, Based on Novel and Unified Molecular-Wide and Electron Density (MOWeD) Concept of Chemical Bonding. Molecules 2025, 30, 1944. https://doi.org/10.3390/molecules30091944
Cukrowski I, Zaaiman S, Hussain S. The Common Concept of Anticooperativity Among Molecules Is Fundamentally Flawed, Based on Novel and Unified Molecular-Wide and Electron Density (MOWeD) Concept of Chemical Bonding. Molecules. 2025; 30(9):1944. https://doi.org/10.3390/molecules30091944
Chicago/Turabian StyleCukrowski, Ignacy, Stéfan Zaaiman, and Shahnawaz Hussain. 2025. "The Common Concept of Anticooperativity Among Molecules Is Fundamentally Flawed, Based on Novel and Unified Molecular-Wide and Electron Density (MOWeD) Concept of Chemical Bonding" Molecules 30, no. 9: 1944. https://doi.org/10.3390/molecules30091944
APA StyleCukrowski, I., Zaaiman, S., & Hussain, S. (2025). The Common Concept of Anticooperativity Among Molecules Is Fundamentally Flawed, Based on Novel and Unified Molecular-Wide and Electron Density (MOWeD) Concept of Chemical Bonding. Molecules, 30(9), 1944. https://doi.org/10.3390/molecules30091944








