Decrypting the Unusual Structure and σ-Hole Interactions of the XC(NO2)3 (X=F, Cl, Br, and I) Compounds Using Quasi-Atomic Orbitals
Abstract
1. Introduction
2. Evaluation of Covalent and Non-Covalent Interactions
2.1. QUAO Analysis
- The symbol of the atom the QUAO is localized on is indicated with an upper-case letter. The symbol of the atom it is oriented towards is indicated with a lower-case letter. The type of bonding interaction is given next. For instance, the label Cn refers to a QUAO localized on atom C oriented towards atom N, via a σ bond.
- For atoms containing p lone pairs, the symbol of the atom where the lone pair is located is followed by the label lp. It is noted that s lone pairs are also present on the oxygen and halogen atoms but, since they do not contribute to the bonding interactions in these systems, they are not discussed further.
2.2. Analysis of the Intermolecular Forces
2.3. Energy Landscape Exploration
3. Results
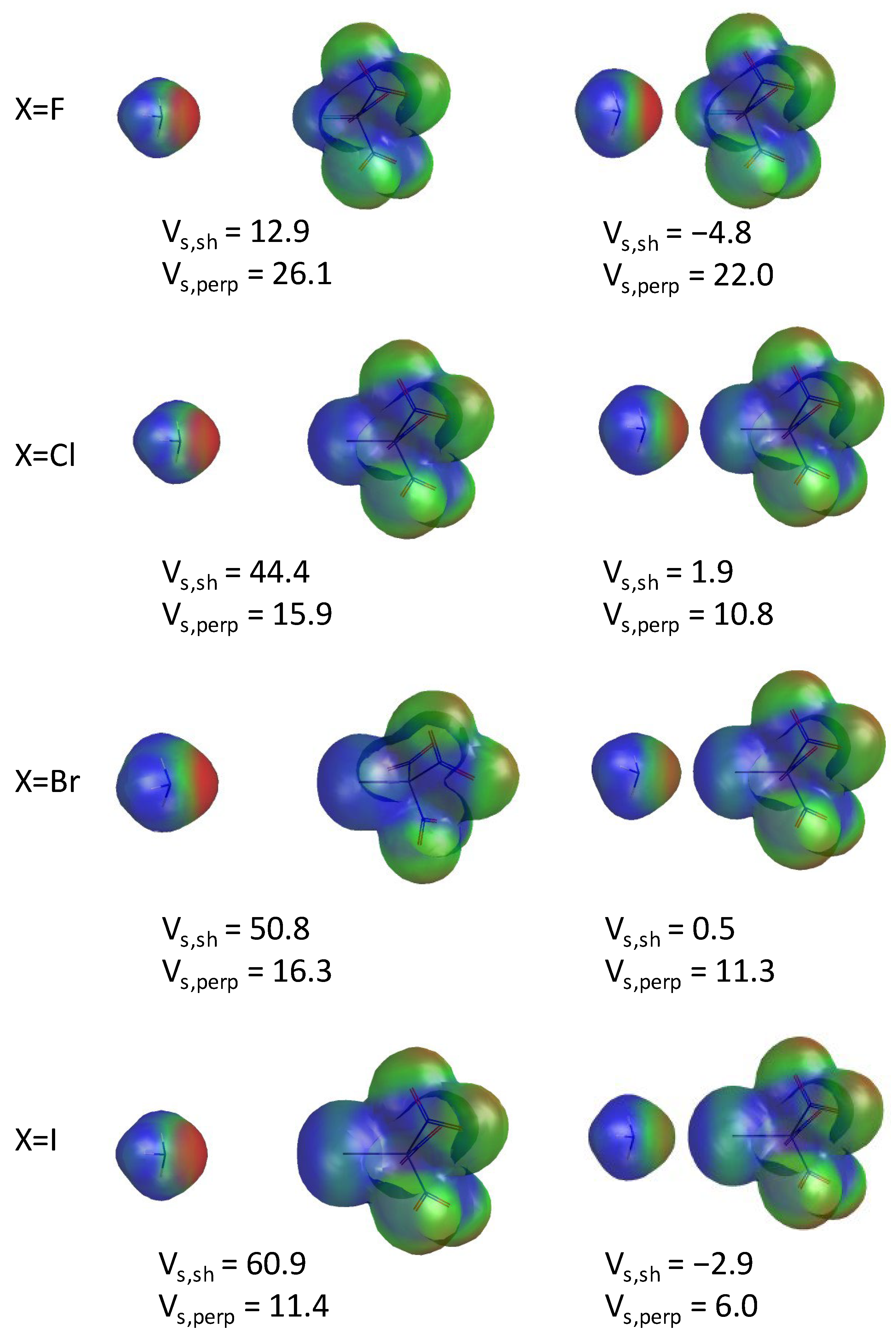
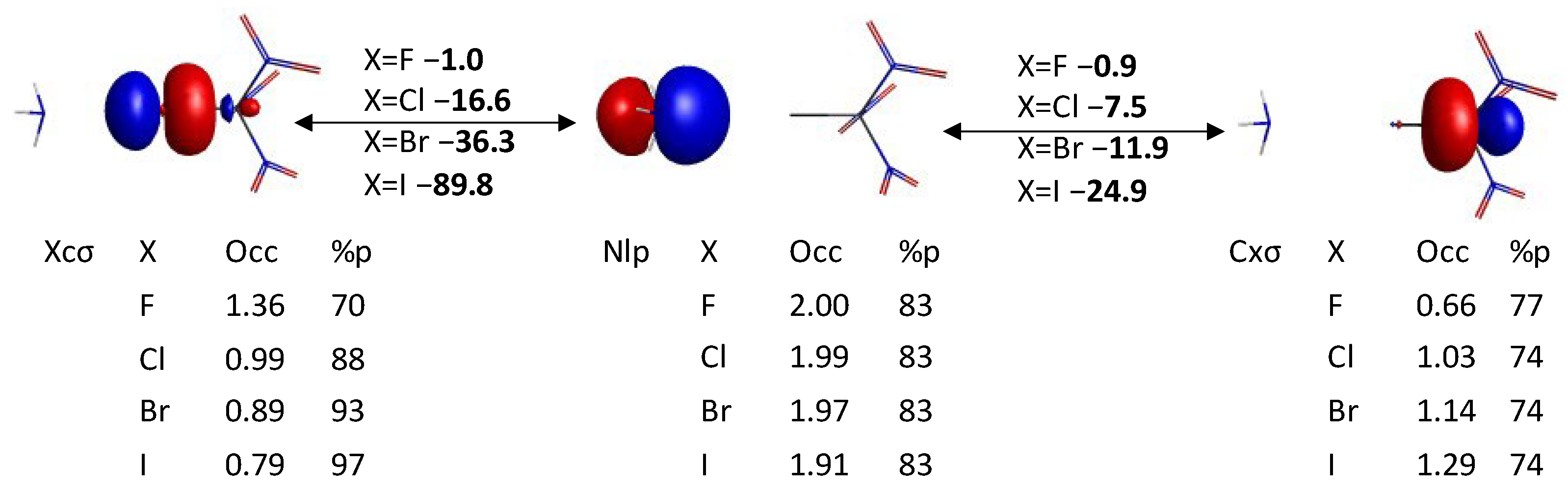
3.1. Geometry, Electrostatic Potential, and QUAO Analysis of XC(NO2)3
3.2. Geometry, Electrostatic Potential, and QUAO Analysis of the Dimer NH3--XC(NO2)3
3.2.1. Geometries and Electrostatic Potentials
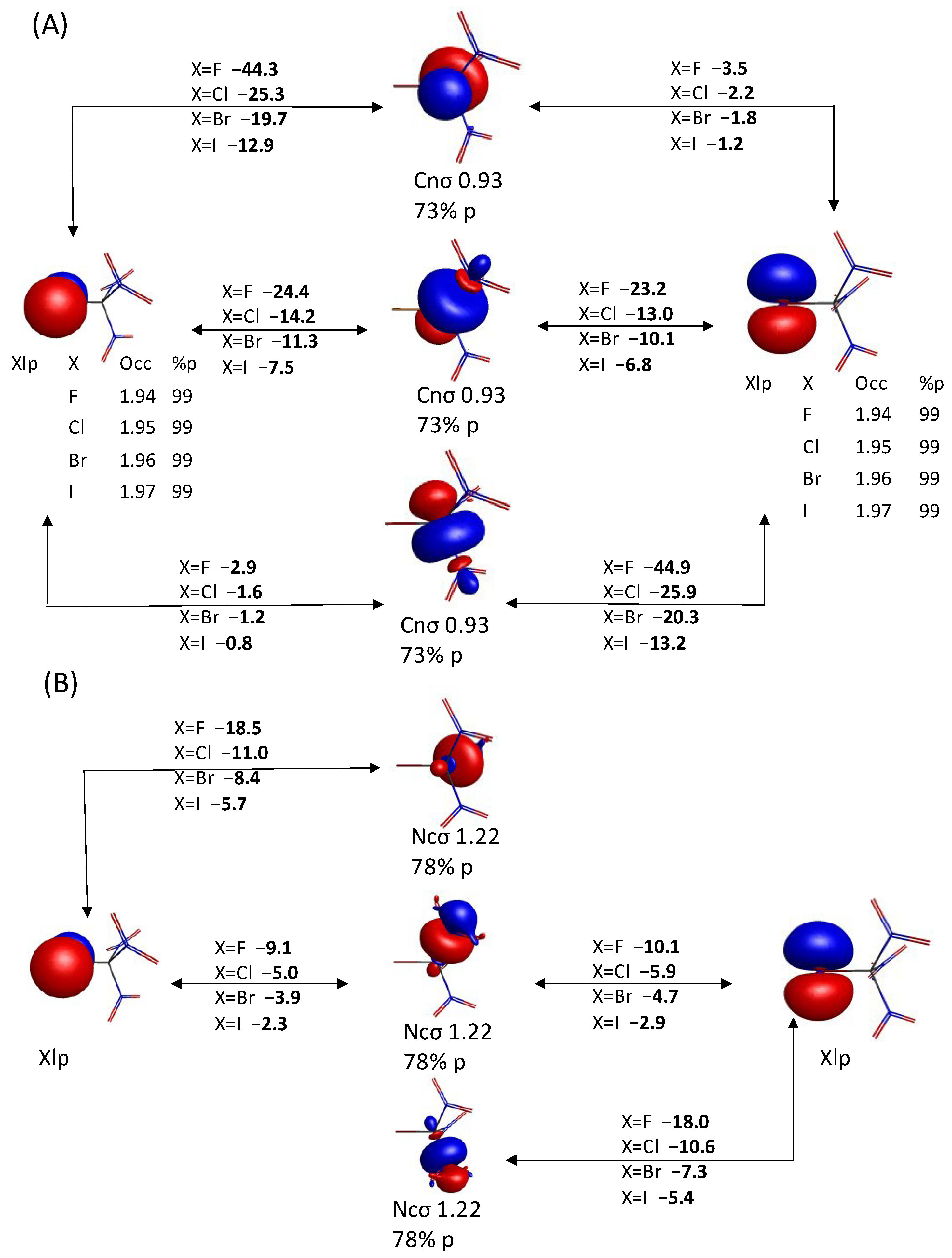
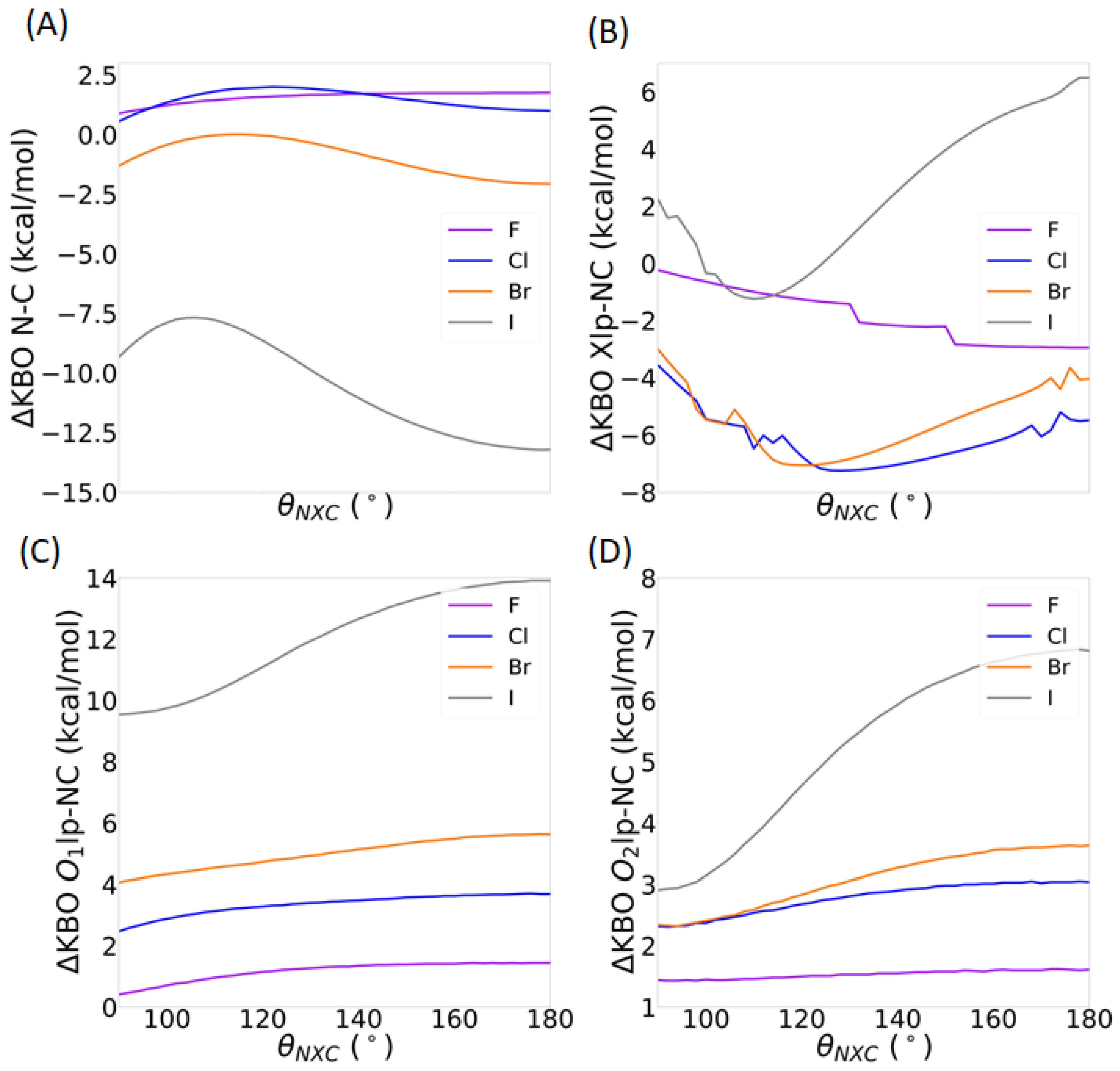
3.2.2. QUAO Analysis
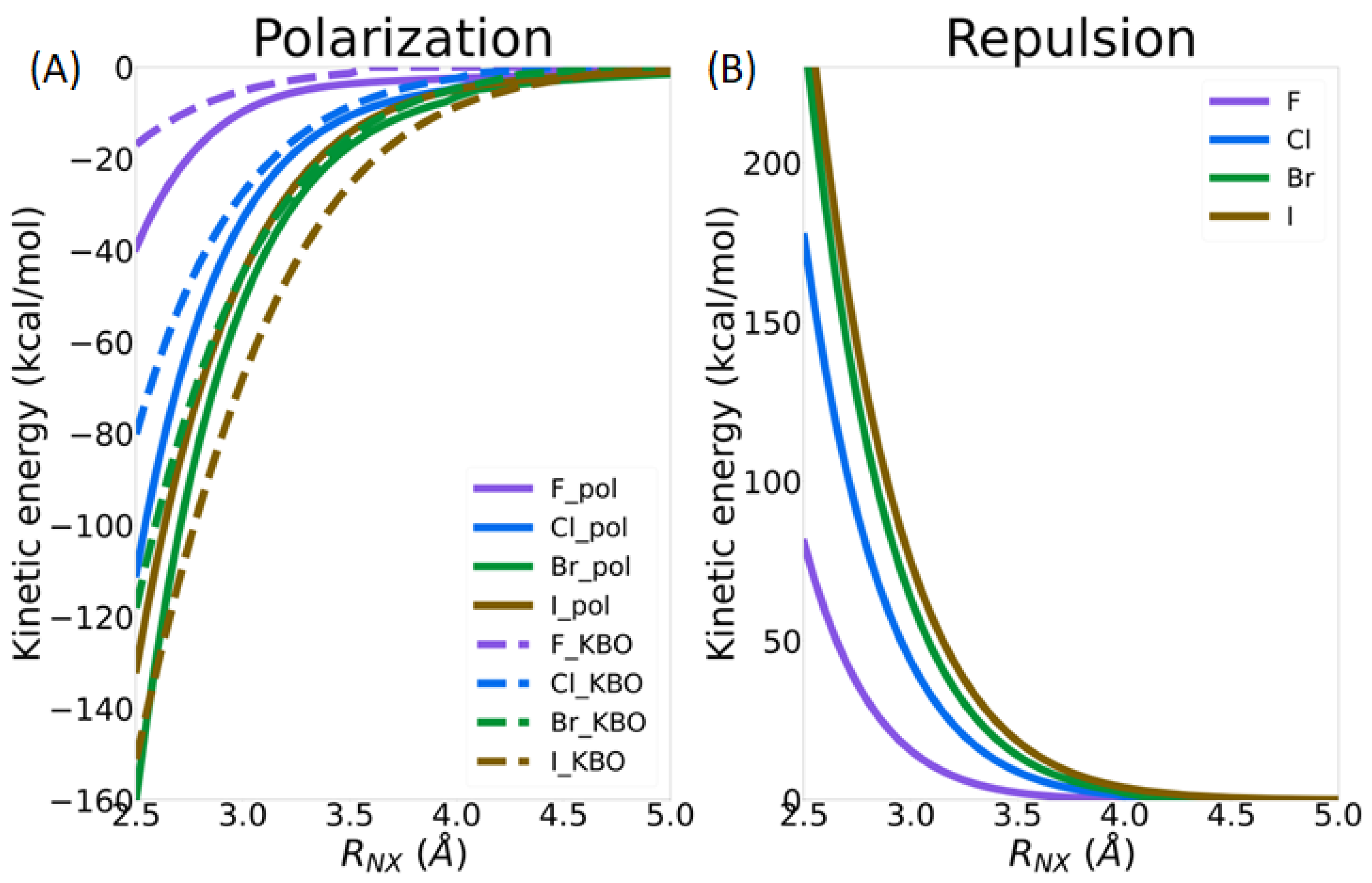
3.2.3. Intermolecular Forces
3.3. NH3--XC(NO2)3 Energy Landscape Exploration
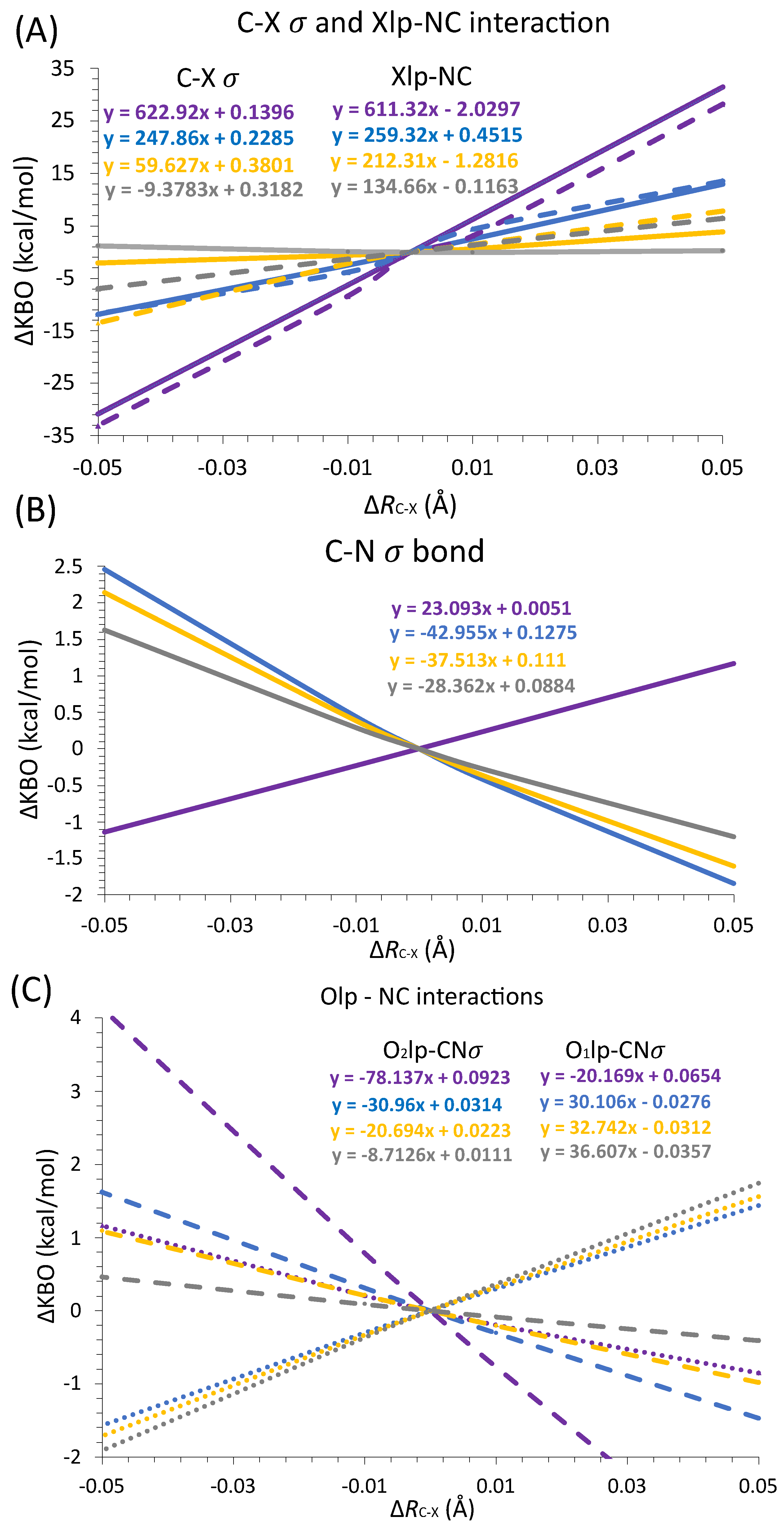
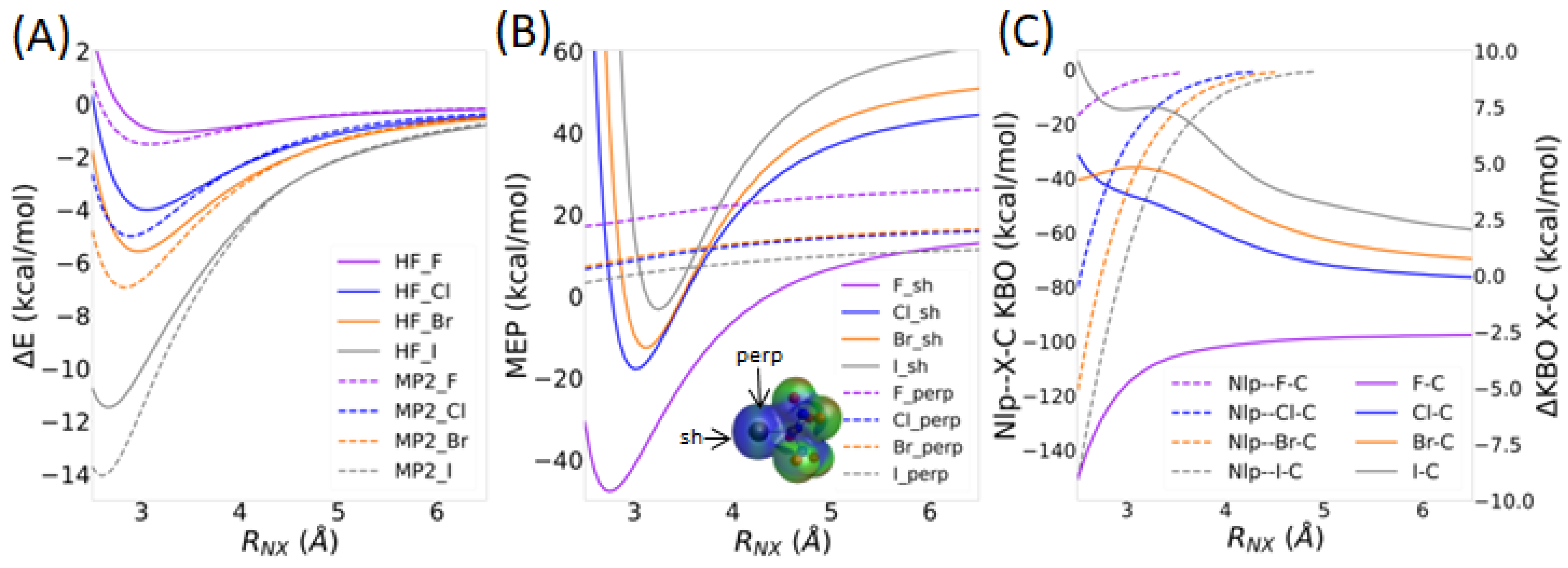
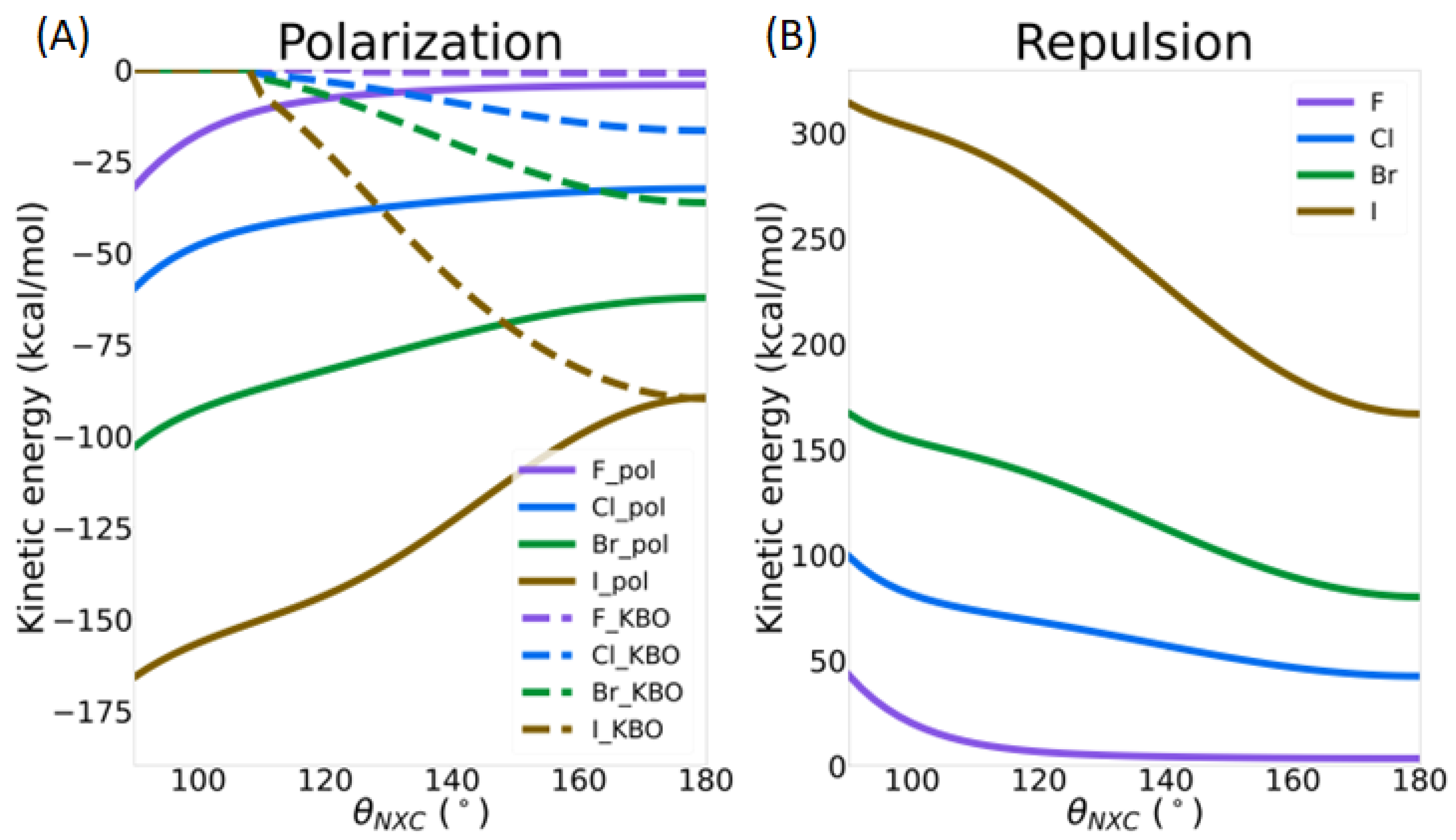
3.3.1. Intermolecular Distance
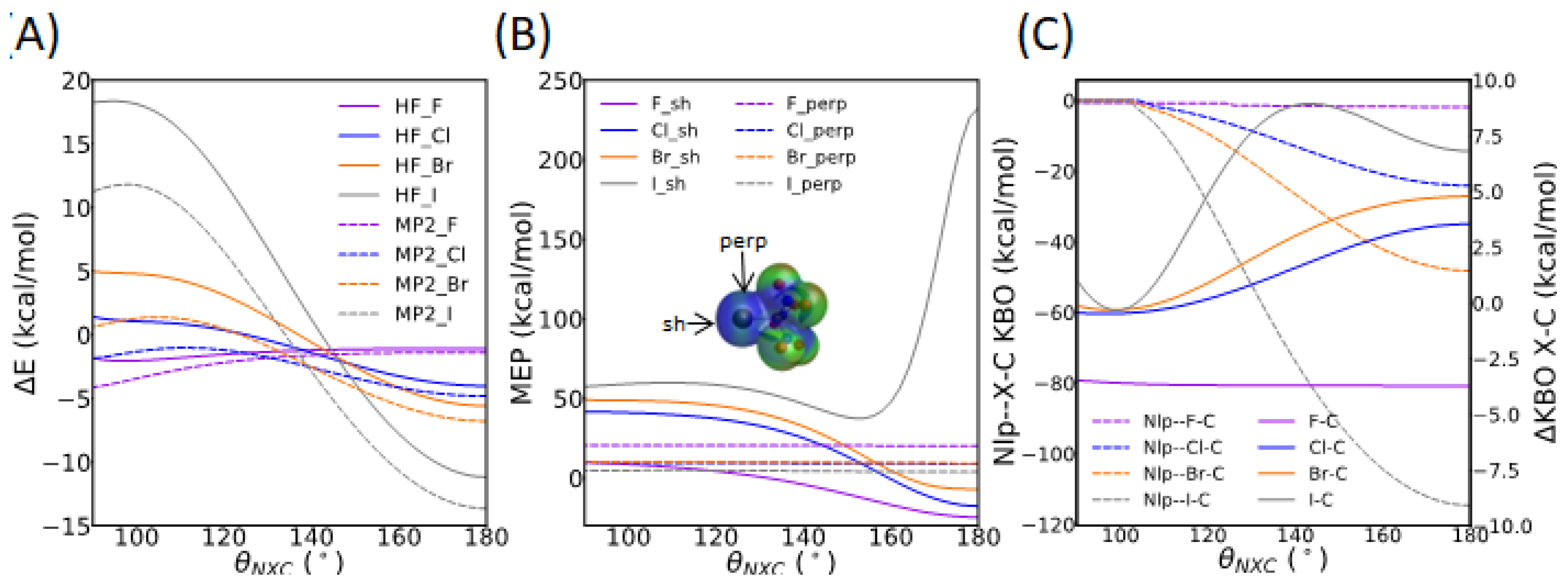
3.3.2. Directionality of the σ-Hole Interaction
4. Computational Methods
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brammer, L.; Peuronen, A.; Roseveare, T.M. Halogen bonds, chalcogen bonds, pnictogen bonds, tetrel bonds and other σ-hole interactions: A snapshot of current progress. Acta Crystallogr. Sect. C Struct. Chem. 2023, 79, 204–216. [Google Scholar] [CrossRef] [PubMed]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms. Inorganics 2019, 7, 71. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T.; Wakisaka, A.; Ono, T.; Sonoda, T. CCSD(T) level interaction energy for halogen bond between pyridine and substituted iodobenzenes: Origin and additivity of substituent effects. Phys. Chem. Chem. Phys. 2013, 15, 6088–6096. [Google Scholar] [CrossRef]
- Donald, K.J.; Pham, N.; Ravichandran, P. Sigma Hole Potentials as Tools: Quantifying and Partitioning Substituent Effects. J. Phys. Chem. A 2023, 127, 10147–10158. [Google Scholar] [CrossRef]
- Zurita, J.; Rodriguez, V.; Zambrano, C.; Mora, J.R.; Rincón, L.; Torres, F.J. Theoretical Description of R–X⋯NH3 Halogen Bond Complexes: Effect of the R Group on the Complex Stability and Sigma-Hole Electron Depletion. Molecules 2020, 25, 530. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Lane, P. σ-Hole bonding and hydrogen bonding: Competitive interactions. Int. J. Quantum Chem. 2007, 107, 3046–3052. [Google Scholar] [CrossRef]
- Metrangolo, P.; Neukirch, H.; Pilati, T.; Resnati, G. Halogen Bonding Based Recognition Processes: A World Parallel to Hydrogen Bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar] [CrossRef]
- Siddiqui, R.; Rani, J.; Titi, H.M.; Patra, R. Unravelling the potential of sigma hole-assisted co-crystallization: Highlighting recent developments. Coord. Chem. Rev. 2024, 517, 215994. [Google Scholar] [CrossRef]
- Voth, A.R.; Hays, F.A.; Ho, P.S. Directing macromolecular conformation through halogen bonds. Proc. Natl. Acad. Sci. USA 2007, 104, 6188–6193. [Google Scholar] [CrossRef] [PubMed]
- Nunes, R.S.; Vila-Viçosa, D.; Costa, P.J. Halogen Bonding: An Underestimated Player in Membrane–Ligand Interactions. J. Am. Chem. Soc. 2021, 143, 4253–4267. [Google Scholar] [CrossRef] [PubMed]
- Parisini, E.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen bonding in halocarbon–protein complexes: A structural survey. Chem. Soc. Rev. 2011, 40, 2267–2278. [Google Scholar] [CrossRef]
- Piña, M.d.l.N.; Frontera, A.; Bauzá, A. Quantifying Intramolecular Halogen Bonds in Nucleic Acids: A Combined Protein Data Bank and Theoretical Study. ACS Chem. Biol. 2020, 15, 1942–1948. [Google Scholar] [CrossRef]
- Berger, G.; Frangville, P.; Meyer, F. Halogen bonding for molecular recognition: New developments in materials and biological sciences. Chem. Commun. 2020, 56, 4970–4981. [Google Scholar] [CrossRef]
- Mendez, L.; Henriquez, G.; Sirimulla, S.; Narayan, M. Looking Back, Looking Forward at Halogen Bonding in Drug Discovery. Molecules 2017, 22, 1397. [Google Scholar] [CrossRef]
- Heidrich, J.; Sperl, L.E.; Boeckler, F.M. Embracing the Diversity of Halogen Bonding Motifs in Fragment-Based Drug Discovery—Construction of a Diversity-Optimized Halogen-Enriched Fragment Library. Front. Chem. 2019, 7, 9. [Google Scholar] [CrossRef]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. WIREs Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Costa, P.J. The halogen bond: Nature and applications. Phys. Sci. Rev. 2017, 2, 20170136. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef]
- Thirman, J.; Engelage, E.; Huber, S.M.; Head-Gordon, M. Characterizing the interplay of Pauli repulsion, electrostatics, dispersion and charge transfer in halogen bonding with energy decomposition analysis. Phys. Chem. Chem. Phys. 2018, 20, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M.; Palusiak, M. Nature of a Hydride–Halogen Bond. A SAPT-, QTAIM-, and NBO-Based Study. J. Phys. Chem. A 2012, 116, 2322–2332. [Google Scholar] [CrossRef]
- Murray, J.S. The Formation of σ-Hole Bonds: A Physical Interpretation. Molecules 2024, 29, 600. [Google Scholar] [CrossRef]
- Szczęśniak, M.M.; Chałasinski, G. Reassessing the Role of σ Holes in Noncovalent Interactions: It is Pauli Repulsion that Counts. Front. Chem. 2022, 10, 858946. [Google Scholar] [CrossRef]
- Panikkattu, V.V.; Tran, A.; Sinha, A.S.; Reinheimer, E.W.; Guidez, E.B.; Aakeröy, C.B. Traversing the Tightrope between Halogen and Chalcogen Bonds Using Structural Chemistry and Theory. Cryst. Growth Des. 2021, 21, 7168–7178. [Google Scholar] [CrossRef]
- Anderson, L.N.; Aquino, F.W.; Raeber, A.E.; Chen, X.; Wong, B.M. Halogen Bonding Interactions: Revised Benchmarks and a New Assessment of Exchange vs Dispersion. J. Chem. Theory Comput. 2018, 14, 180–190. [Google Scholar] [CrossRef]
- Huber, S.M.; Scanlon, J.D.; Jimenez-Izal, E.; Ugalde, J.M.; Infante, I. On the directionality of halogen bonding. Phys. Chem. Chem. Phys. 2013, 15, 10350–10357. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. The intrinsic strength of the halogen bond: Electrostatic and covalent contributions described by coupled cluster theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef]
- Li, D.; Xia, T.; Feng, W.; Cheng, L. Revisiting the covalent nature of halogen bonding: A polarized three-center four-electron bond. RSC Adv. 2021, 11, 32852–32860. [Google Scholar] [CrossRef] [PubMed]
- Kellett, C.W.; Kennepohl, P.; Berlinguette, C.P. π covalency in the halogen bond. Nat. Commun. 2020, 11, 3310. [Google Scholar] [CrossRef] [PubMed]
- Guidez, E.B. Quasi-atomic orbital analysis of halogen bonding interactions. J. Chem. Phys. 2023, 159, 194307. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef]
- Roos, G.; Murray, J.S. Probing intramolecular interactions using molecular electrostatic potentials: Changing electron density contours to unveil both attractive and repulsive interactions. Phys. Chem. Chem. Phys. 2024, 26, 7592–7601. [Google Scholar] [CrossRef]
- Göbel, M.; Tchitchanov, B.H.; Murray, J.S.; Politzer, P.; Klapötke, T.M. Chlorotrinitromethane and its exceptionally short carbon–chlorine bond. Nat. Chem. 2009, 1, 229–235. [Google Scholar] [CrossRef]
- Levchenkov, D.V.; Kharitonkin, A.B.; Shlyapochnikov, V.A. Molecular structures of trinitromethane derivatives. Russ. Chem. Bull. 2001, 50, 385–389. [Google Scholar] [CrossRef]
- Sadova, N.I.; Popik, N.I.; Vilkov, L.V.; Pankrushev, A.; Shlyapochnikov, V.A. Electron diffraction study of gaseous CH(NO2)3 and CCl(NO2)3. J. Chem. Soc. Chem. Commun. 1973, 19, 708–709. [Google Scholar] [CrossRef]
- Witt, J.R.; Britton, D.; Mahon, C. The crystal structures of BrC(CN)3, ClC(CN)3, and CH3C(CN)3. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 950–955. [Google Scholar] [CrossRef]
- Fo, H.P.M.; de Oliveira, J.B.L.; Guadagnini, P.H.; Bruns, R.E. Infrared Vibrational Intensities and Polar Tensors of the Fluorochloromethanes. J. Phys. Chem. 1995, 99, 11357–11364. [Google Scholar] [CrossRef]
- Klapötke, T.M.; Krumm, B.; Moll, R.; Rest, S.F.; Vishnevskiy, Y.V.; Reuter, C.; Stammler, H.-G.; Mitzel, N.W. Halogenotrinitromethanes: A Combined Study in the Crystalline and Gaseous Phase and Using Quantum Chemical Methods. Chem. A Eur. J. 2014, 20, 12962–12973. [Google Scholar] [CrossRef] [PubMed]
- Macaveiu, L.; Göbel, M.; Klapötke, T.M.; Murray, J.S.; Politzer, P. The unique role of the nitro group in intramolecular interactions: Chloronitromethanes. Struct. Chem. 2010, 21, 139–146. [Google Scholar] [CrossRef]
- Bartashevich, E.V.; Pendás, Á.M.; Tsirelson, V.G. An anatomy of intramolecular atomic interactions in halogen-substituted trinitromethanes. Phys. Chem. Chem. Phys. 2014, 16, 16780–16789. [Google Scholar] [CrossRef]
- West, A.C.; Schmidt, M.W.; Gordon, M.S.; Ruedenberg, K. A comprehensive analysis of molecule-intrinsic quasi-atomic, bonding, and correlating orbitals. I. Hartree-Fock wave functions. J. Chem. Phys. 2013, 139, 234107. [Google Scholar] [CrossRef]
- West, A.C.; Schmidt, M.W.; Gordon, M.S.; Ruedenberg, K. Intrinsic Resolution of Molecular Electronic Wave Functions and Energies in Terms of Quasi-atoms and Their Interactions. J. Phys. Chem. A 2017, 121, 1086–1105. [Google Scholar] [CrossRef]
- Guidez, E.B.; Gordon, M.S.; Ruedenberg, K. Why is Si2H2 Not Linear? An Intrinsic Quasi-Atomic Bonding Analysis. J. Am. Chem. Soc. 2020, 142, 13729–13742. [Google Scholar] [CrossRef]
- Duchimaza Heredia, J.J.; Sadow, A.D.; Gordon, M.S. A Quasi-Atomic Analysis of Three-Center Two-Electron Zr–H–Si Interactions. J. Phys. Chem. A 2018, 122, 9653–9669. [Google Scholar] [CrossRef]
- Harville, T.; Gordon, M.S. Intramolecular hydrogen bonding analysis. J. Chem. Phys. 2022, 156, 174302. [Google Scholar] [CrossRef]
- Ferreras, K.N.; Harville, T.; Del Angel Cruz, D.; Gordon, M.S. Analysis of bonding motifs in unusual molecules II: Infinitene. Phys. Chem. Chem. Phys. 2024, 26, 21407–21418. [Google Scholar] [CrossRef]
- Del Angel Cruz, D.; Ferreras, K.N.; Harville, T.; Schoendorff, G.; Gordon, M.S. Analysis of bonding motifs in unusual molecules I: Planar hexacoordinated carbon atoms. Phys. Chem. Chem. Phys. 2024, 26, 21395–21406. [Google Scholar] [CrossRef]
- Duchimaza Heredia, J.J.; Ruedenberg, K.; Gordon, M.S. Quasi-Atomic Bonding Analysis of Xe-Containing Compounds. J. Phys. Chem. A 2018, 122, 3442–3454. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys. 2009, 131, 014102. [Google Scholar] [CrossRef] [PubMed]
- West, A.C.; Duchimaza-Heredia, J.J.; Gordon, M.S.; Ruedenberg, K. Identification and Characterization of Molecular Bonding Structures by ab initio Quasi-Atomic Orbital Analyses. J. Phys. Chem. A 2017, 121, 8884–8898. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.; Hull, E.A.; Windus, T.L. Valence Virtual Orbitals: An Unambiguous ab Initio Quantification of the LUMO Concept. J. Phys. Chem. A 2015, 119, 10408–10427. [Google Scholar] [CrossRef]
- Lu, W.C.; Wang, C.Z.; Schmidt, M.W.; Bytautas, L.; Ho, K.M.; Ruedenberg, K. Molecule intrinsic minimal basis sets. I. Exact resolution of ab initio optimized molecular orbitals in terms of deformed atomic minimal-basis orbitals. J. Chem. Phys. 2004, 120, 2629–2637. [Google Scholar] [CrossRef]
- Lu, W.C.; Wang, C.Z.; Schmidt, M.W.; Bytautas, L.; Ho, K.M.; Ruedenberg, K. Molecule intrinsic minimal basis sets. II. Bonding analyses for Si4H6 and Si2 to Si10. J. Chem. Phys. 2004, 120, 2638–2651. [Google Scholar] [CrossRef]
- Ivanic, J.; Atchity, G.J.; Ruedenberg, K. Intrinsic local constituents of molecular electronic wave functions. I. Exact representation of the density matrix in terms of chemically deformed and oriented atomic minimal basis set orbitals. Theor. Chem. Acc. 2008, 120, 281–294. [Google Scholar] [CrossRef]
- Ruedenberg, K. Atoms and interatomic bonding synergism inherent in molecular electronic wave functions. J. Chem. Phys. 2022, 157, 024111. [Google Scholar] [CrossRef]
- Kuchitsu, K. Structure of Free Polyatomic Molecules: Basic Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hargittai, M.; Schultz, G.; Schwerdtfeger, P.; Seth, M. The Structure of Gaseous Carbon Tetraiodide from Electron Diffraction and All Carbon Iodides, CIn (n = 1–4), and Their Dimers, C2I2n (n = 1–3) from High-Level Computation. Any Other Carbon-Iodide Species in the Vapor? Struct. Chem. 2001, 12, 377–391. [Google Scholar] [CrossRef]
- Stone, A.J. Are Halogen Bonded Structures Electrostatically Driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef]
- Ai-Guo, Z. Dissecting the nature of halogen bonding interactions from energy decomposition and wavefunction analysis. Monatshefte Für Chem. Chem. Mon. 2017, 148, 1259–1267. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1167–1189. [Google Scholar]
- Zahariev, F.; Xu, P.; Westheimer, B.M.; Webb, S.; Galvez Vallejo, J.; Tiwari, A.; Sundriyal, V.; Sosonkina, M.; Shen, J.; Schoendorff, G.; et al. The General Atomic and Molecular Electronic Structure System (GAMESS): Novel Methods on Novel Architectures. J. Chem. Theory Comput. 2023, 19, 7031–7055. [Google Scholar] [CrossRef] [PubMed]
- Jorge, F.E.; Canal Neto, A.; Camiletti, G.G.; Machado, S.F. Contracted Gaussian basis sets for Douglas–Kroll–Hess calculations: Estimating scalar relativistic effects of some atomic and molecular properties. J. Chem. Phys. 2009, 130, 064108. [Google Scholar] [CrossRef]
- Campos, C.T.; Jorge, F.E. Triple zeta quality basis sets for atoms Rb through Xe: Application in CCSD(T) atomic and molecular property calculations. Mol. Phys. 2013, 111, 167–173. [Google Scholar] [CrossRef]
- Jansen, G.; Hess, B.A. Revision of the Douglas-Kroll transformation. Phys. Rev. A 1989, 39, 6016–6017. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Bode, B.M.; Gordon, M.S. Macmolplt: A graphical user interface for GAMESS. J. Mol. Graph. Model. 1998, 16, 133–138. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Peterson, K.A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements. J. Chem. Phys. 2003, 119, 11113–11123. [Google Scholar] [CrossRef]
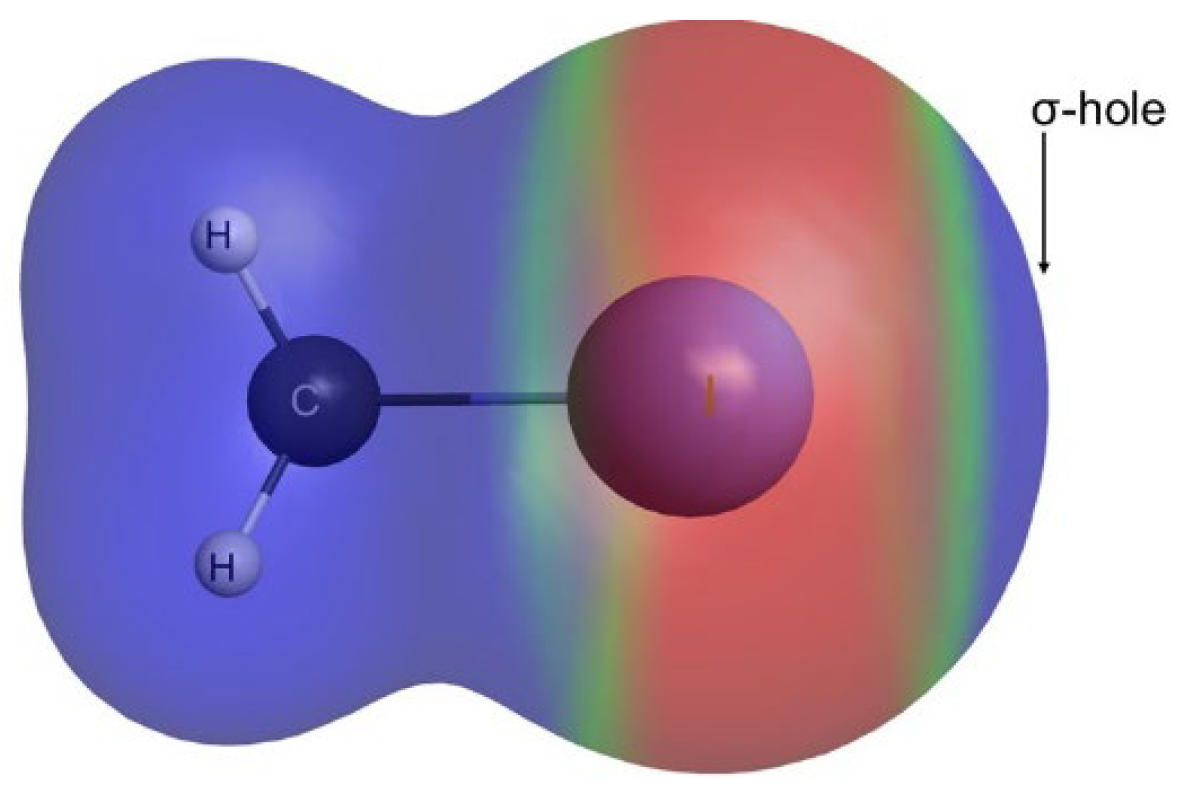

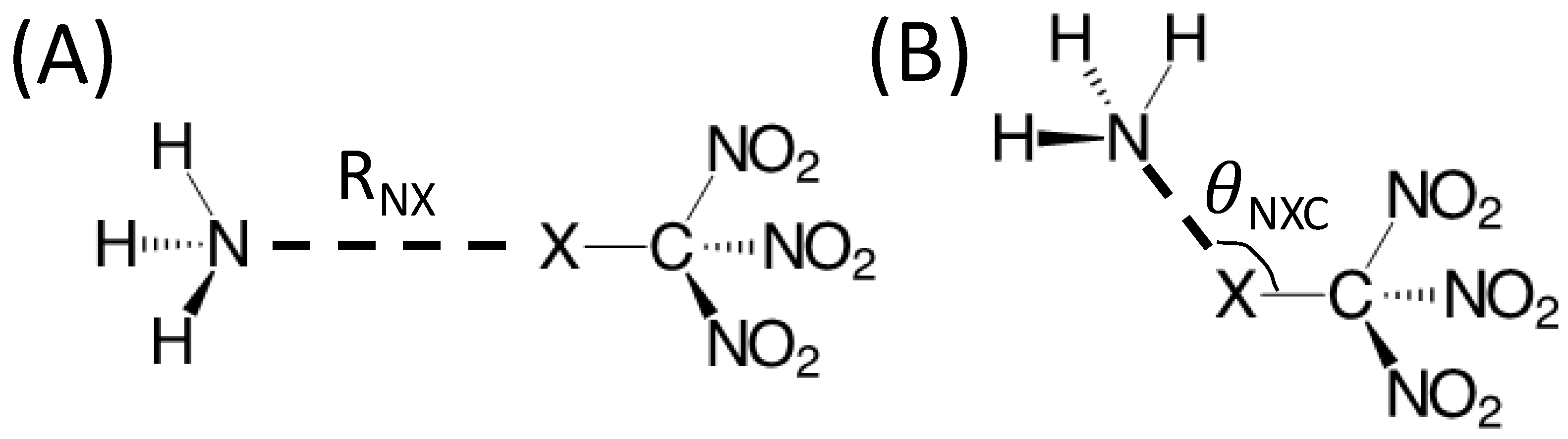
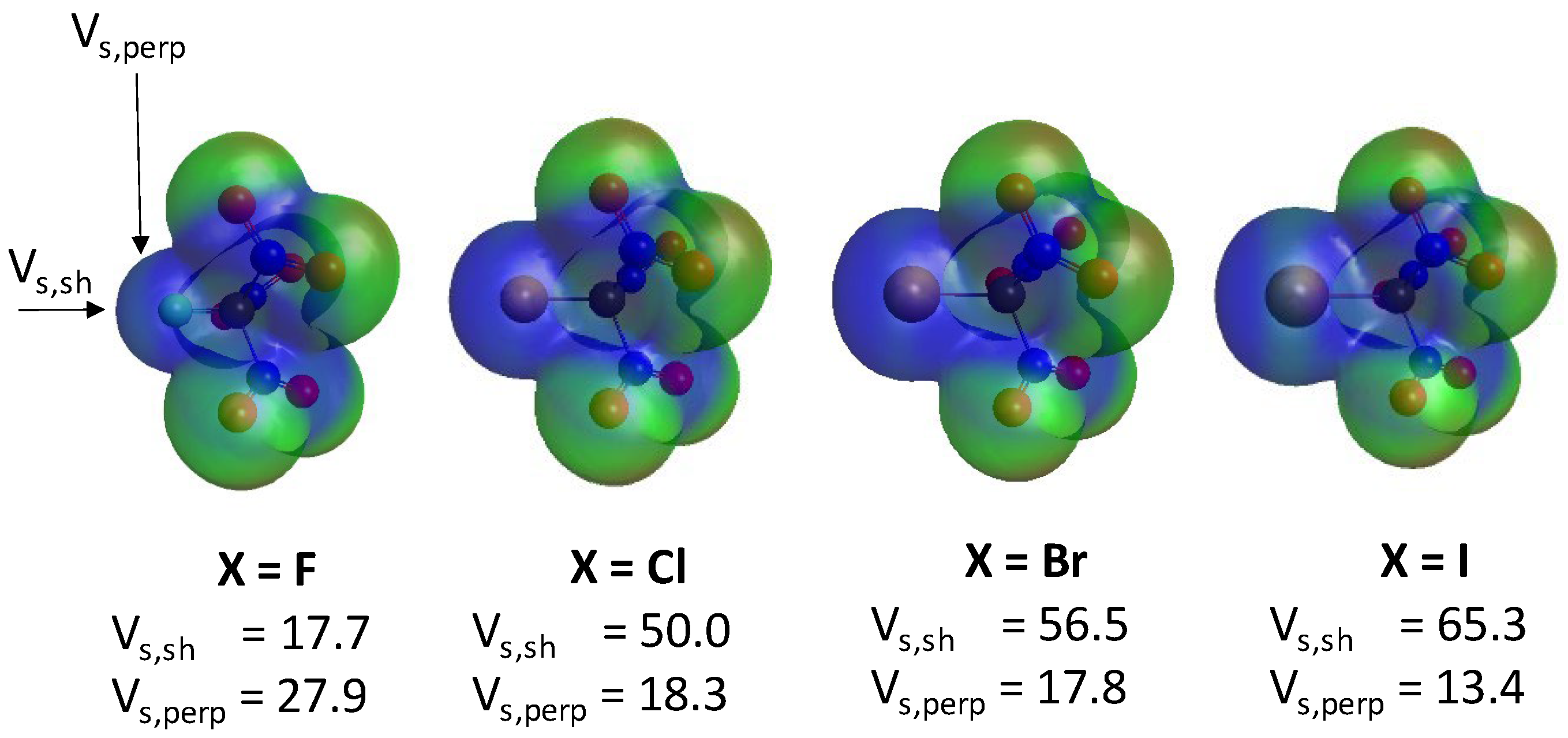
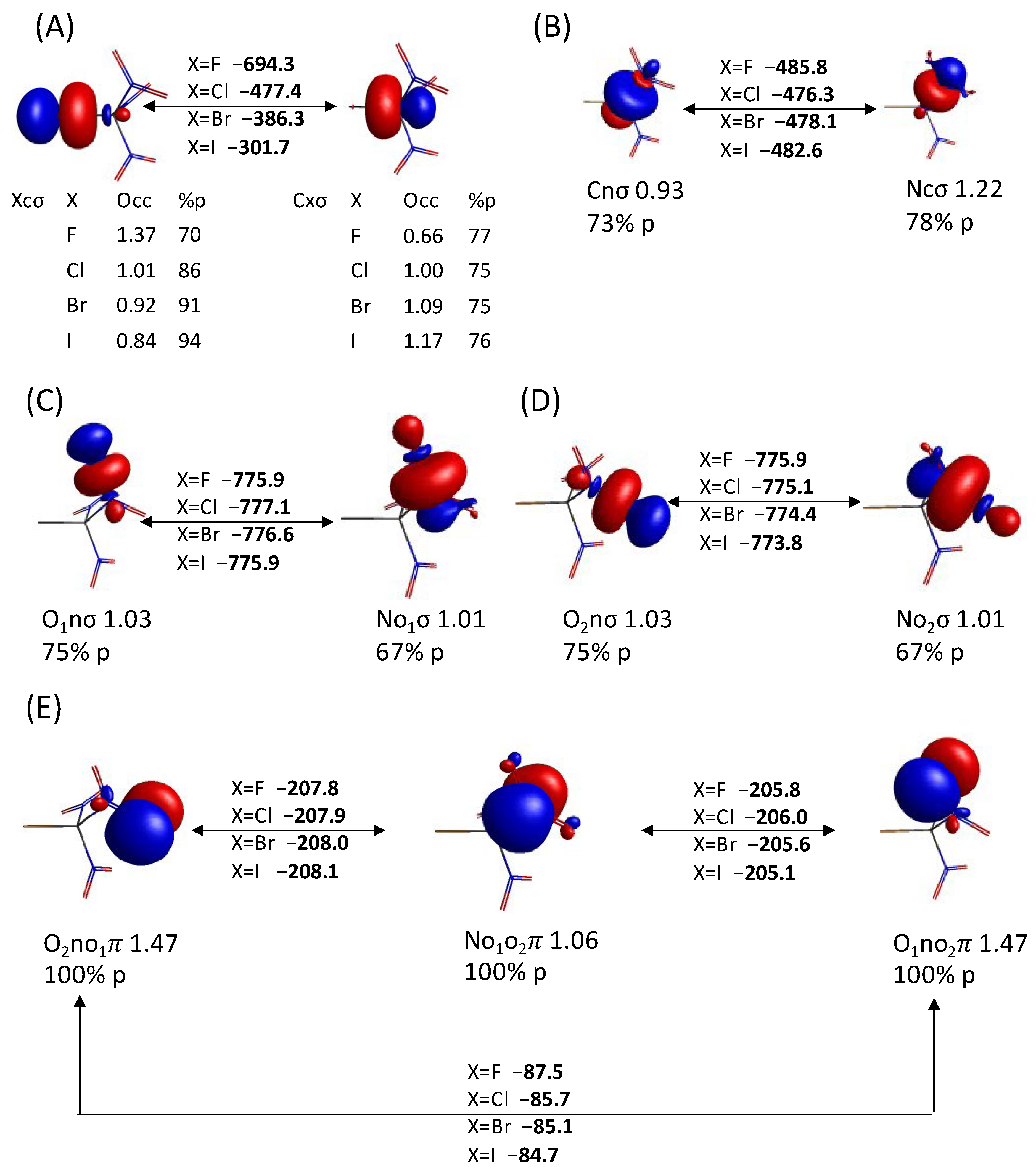




| X=F | X=Cl | X=Br | X=I | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HF | MP2 | Exp a | HF | MP2 | Exp b | HF | MP2 | Exp a | HF | MP2 | Exp a | |
| C-X | 1.277 | 1.303 | 1.297 | 1.711 | 1.701 | 1.694 | 1.879 | 1.839 | 1.853 | 2.104 | 2.074 | 2.097 |
| C-N | 1.509 | 1.516 | 1.525 | 1.520 | 1.533 | 1.542 | 1.519 | 1.532 | 1.532 | 1.513 | 1.526 | 1.535 |
| N-O1 | 1.171 | 1.219 | 1.206 | 1.171 | 1.217 | 1.210 | 1.171 | 1.217 | 1.198 | 1.172 | 1.217 | 1.207 |
| N-O2 | 1.172 | 1.220 | 1.215 | 1.172 | 1.220 | 1.213 | 1.172 | 1.220 | 1.219 | 1.173 | 1.221 | 1.209 |
| X-C-N | 109.98 | 110.48 | 110.4 | 111.68 | 112.19 | 112.5 | 111.86 | 112.74 | 112.6 | 111.61 | 112.34 | 112.8 |
| X-C-N-O1 | −39.54 | −40.20 | −36.3 | −43.31 | −43.19 | −42.2 | −44.40 | −44.74 | −42.2 | −45.67 | −45.91 | −44.8 |
| X=F | X=Cl | X=Br | X=I | |
|---|---|---|---|---|
| C | 0.566 | 0.203 | 0.136 | 0.08 |
| X | −0.249 | 0.088 | 0.159 | 0.214 |
| N | 0.686 | 0.702 | 0.704 | 0.706 |
| O1 | −0.396 | −0.401 | −0.403 | −0.405 |
| O2 | −0.396 | −0.399 | −0.399 | −0.399 |
| QUAO Pair | X=F | X=Cl | X=Br | X=I |
|---|---|---|---|---|
| Xcσ-Cxσ | −3.8 | +3.6 | +4.8 | +6.9 |
| Cnσ-Ncσ | +1.8 | +1.0 | −2.1 | −13.2 |
| O1nσ-No1σ | −0.9 | +0.2 | +1.4 | +5.6 |
| O2nσ-No2σ | +1.4 | +1.6 | +1.6 | +2.4 |
| O-N-O π bond | +0.3 | +0.9 | +1.5 | +4.1 |
| O1lp-NC a | +1.4 | +3.7 | +5.6 | +13.9 |
| O2lp-NC a | +1.6 | +3.1 | +3.6 | +6.8 |
| Xlp-NC a | −6.1 | −4.5 | −3.3 | +6.5 |
| IMF | X=F | X=Cl | X=Br | X=I |
|---|---|---|---|---|
| Electrostatic | −1.20 (−1.29) | −6.64 (−6.80) | −10.55 (−10.59) | −27.32 (−26.00) |
| Polarization | −0.19 (−0.15) | −1.46 (−1.58) | −2.82 (−3.17) | −11.22 (−12.84) |
| Dispersion | −0.33 (−0.20) | −0.86 (−0.52) | −1.46 (−0.94) | −2.39 (−1.28) |
| Exchange | −0.38 (−0.59) | −5.74 (−5.87) | −10.59 (−10.78) | −35.73 (−35.88) |
| Repulsion | 0.70 (1.05) | 9.80 (10.39) | 18.45 (19.40) | 65.90 (67.00) |
| ΔEHF | −1.07 (−0.97) | −4.05 (−3.86) | −5.50 (−5.14) | −8.36 (−7.72) |
| ΔEMP2 | −1.39 (−1.17) | −4.91 (−4.38) | −6.96 (−6.08) | −10.75 (−9.01) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guidez, E.B. Decrypting the Unusual Structure and σ-Hole Interactions of the XC(NO2)3 (X=F, Cl, Br, and I) Compounds Using Quasi-Atomic Orbitals. Molecules 2025, 30, 1986. https://doi.org/10.3390/molecules30091986
Guidez EB. Decrypting the Unusual Structure and σ-Hole Interactions of the XC(NO2)3 (X=F, Cl, Br, and I) Compounds Using Quasi-Atomic Orbitals. Molecules. 2025; 30(9):1986. https://doi.org/10.3390/molecules30091986
Chicago/Turabian StyleGuidez, Emilie B. 2025. "Decrypting the Unusual Structure and σ-Hole Interactions of the XC(NO2)3 (X=F, Cl, Br, and I) Compounds Using Quasi-Atomic Orbitals" Molecules 30, no. 9: 1986. https://doi.org/10.3390/molecules30091986
APA StyleGuidez, E. B. (2025). Decrypting the Unusual Structure and σ-Hole Interactions of the XC(NO2)3 (X=F, Cl, Br, and I) Compounds Using Quasi-Atomic Orbitals. Molecules, 30(9), 1986. https://doi.org/10.3390/molecules30091986







