High-Accuracy and High-Resolution Calorimetry Revealing New Correlations of Phase Change Enthalpy, Entropy, and Number of Carbon Atoms n in n-Alkanes
Abstract
1. Introduction
- The uncertainty of the individual measurement with respect to enthalpy change and temperature values. Often no uncertainty is presented, and even if it is present, it is often estimated too optimistically.
- The way enthalpy and temperature values were determined from measurement data.For example, if DSC was used, a value for the phase change enthalpy can refer to the whole enthalpy change or only an integral above the peak baseline, and it can depend on the temperature range used for integration; similarly, the phase change temperature could be read from the peak onset or other points. A more detailed discussion can be found in [8,9]. The methods of determination are often not described in the literature, and different sources might also have used different methods.
- The correct identification of the phase transition that the enthalpy change and temperature values refer to. For example, if DSC was used, high heating rates can cause a solid–solid and a solid–liquid phase change to overlap and look like a single phase change.
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Calorimetric Method to Determine H(T)
2.2.2. Determination of Transition Temperatures and Transition Heats
2.2.3. Calculation of the Data Basis
- The phase transitions (solid–solid and solid–liquid) were identified, and the corresponding enthalpy change (in J/g) and temperature (in K) for each transition were determined.
- The enthalpy change values were then converted from J/g to J/mol, using molar mass values.
- The entropy change was then calculated using Equation (3).
- For total values, enthalpy changes in solid–solid and solid–liquid transitions were added; the same was applied for entropy changes.
3. Results
3.1. Data Basis
3.2. Graphical Evaluation of Enthalpy Change vs. Entropy Change
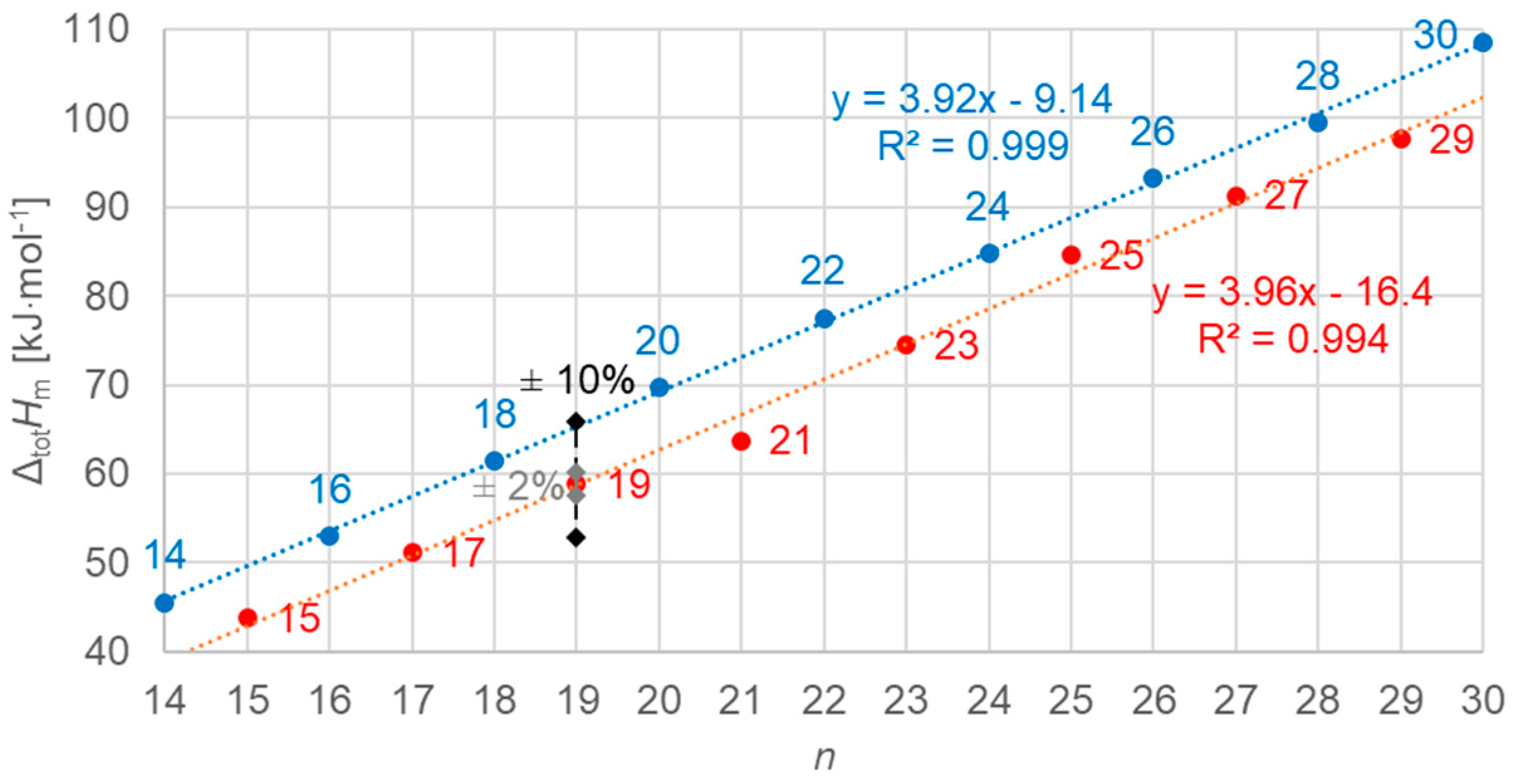
3.2.1. Total Values
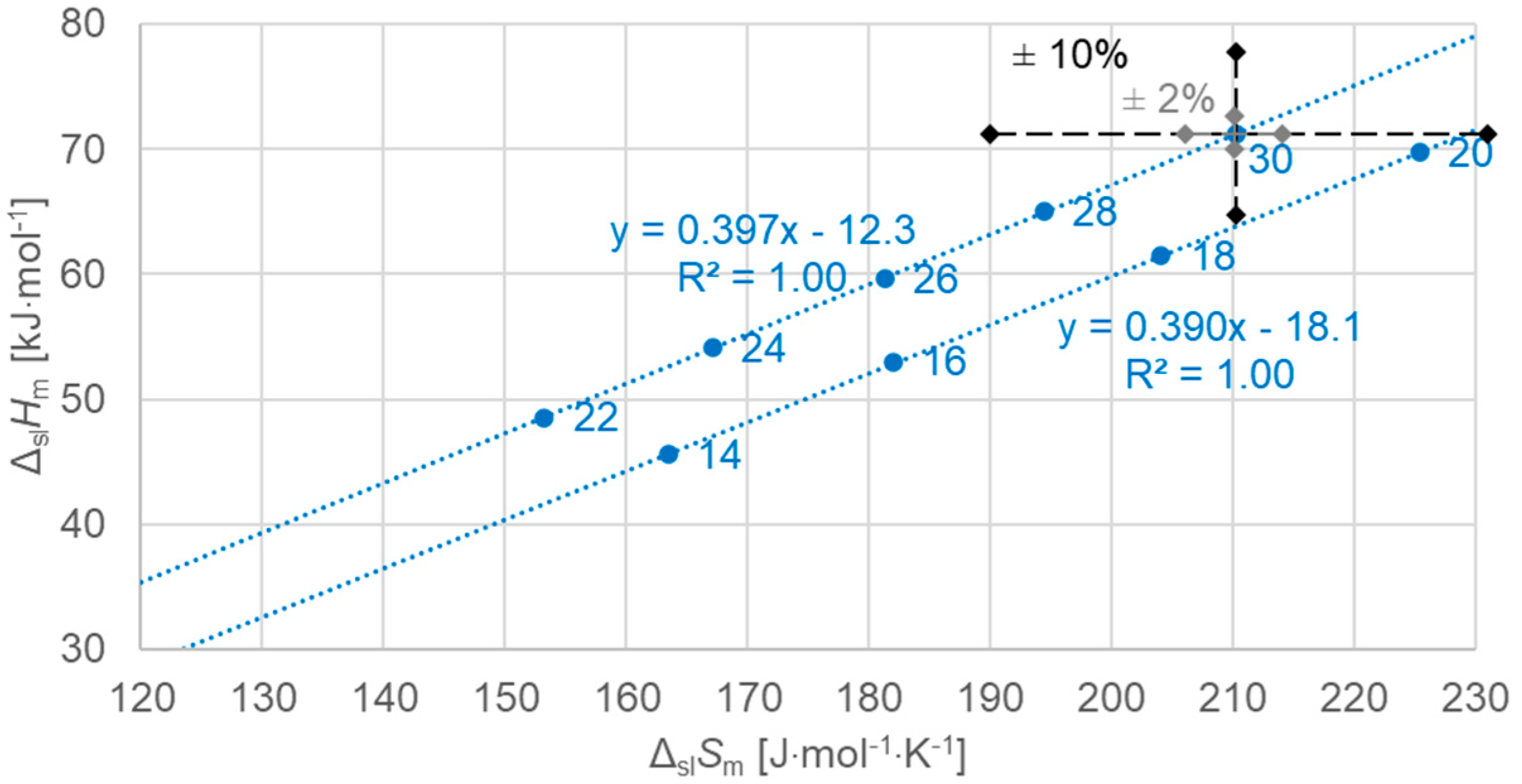
3.2.2. Solid–Liquid Values
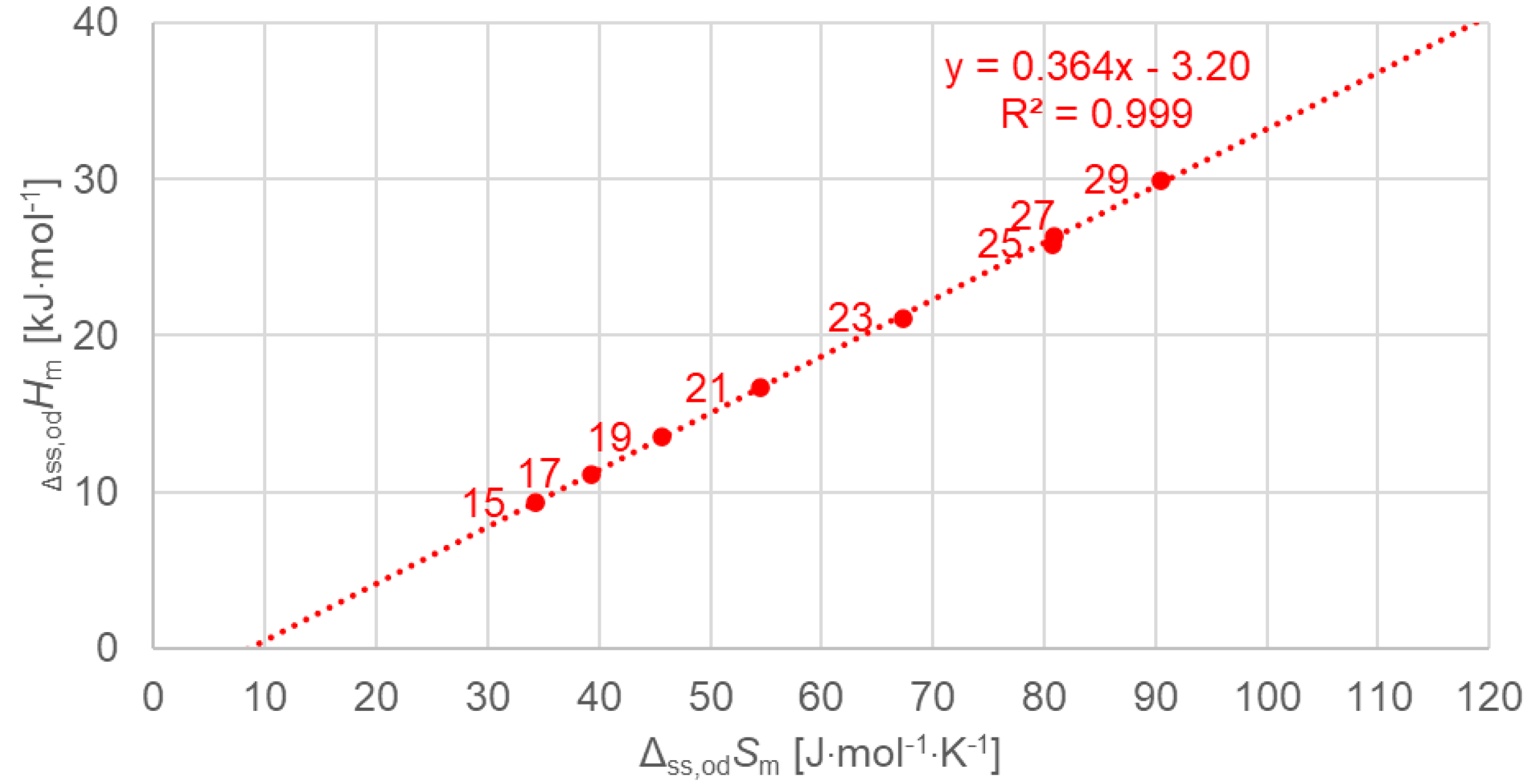
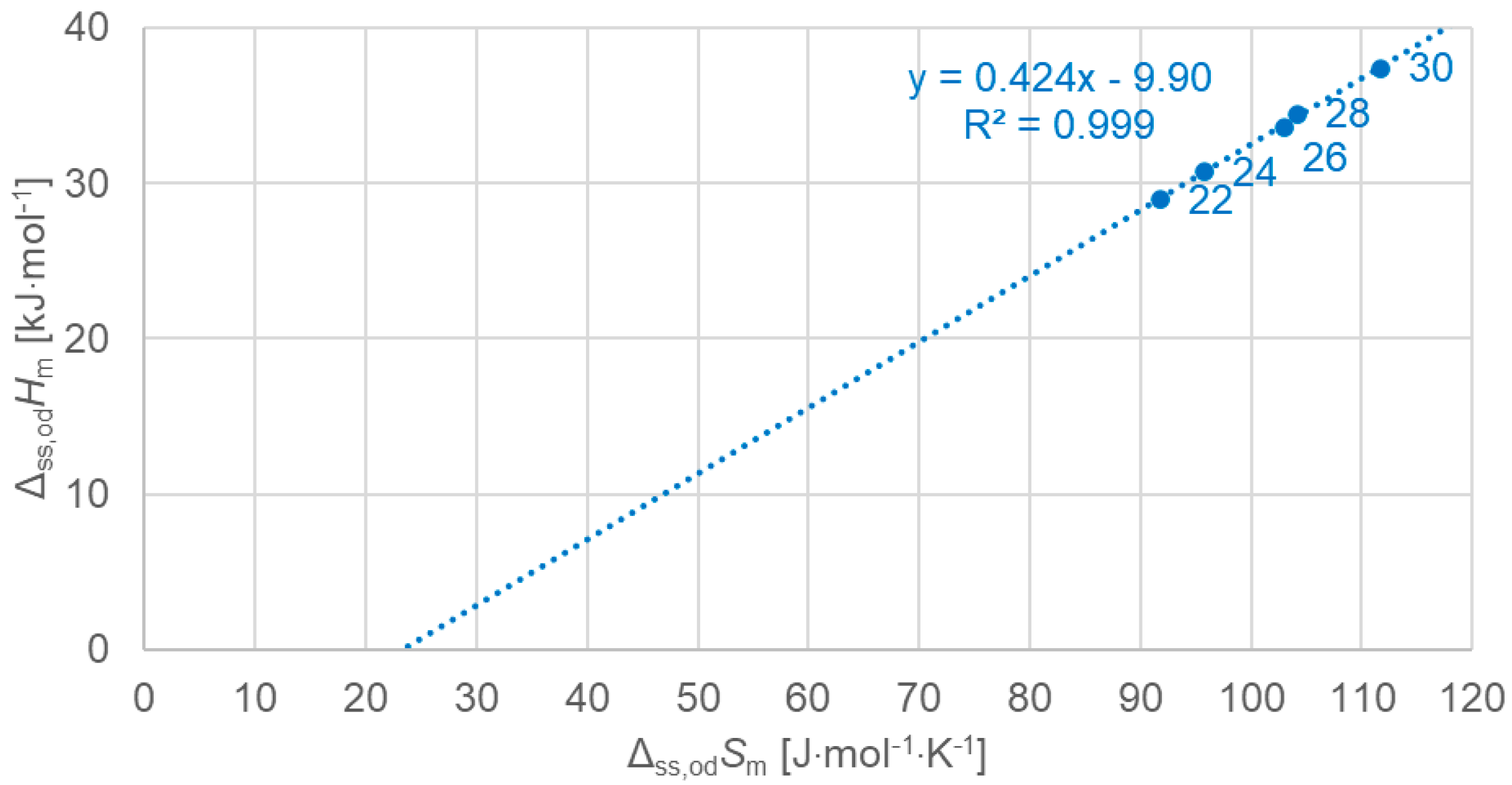
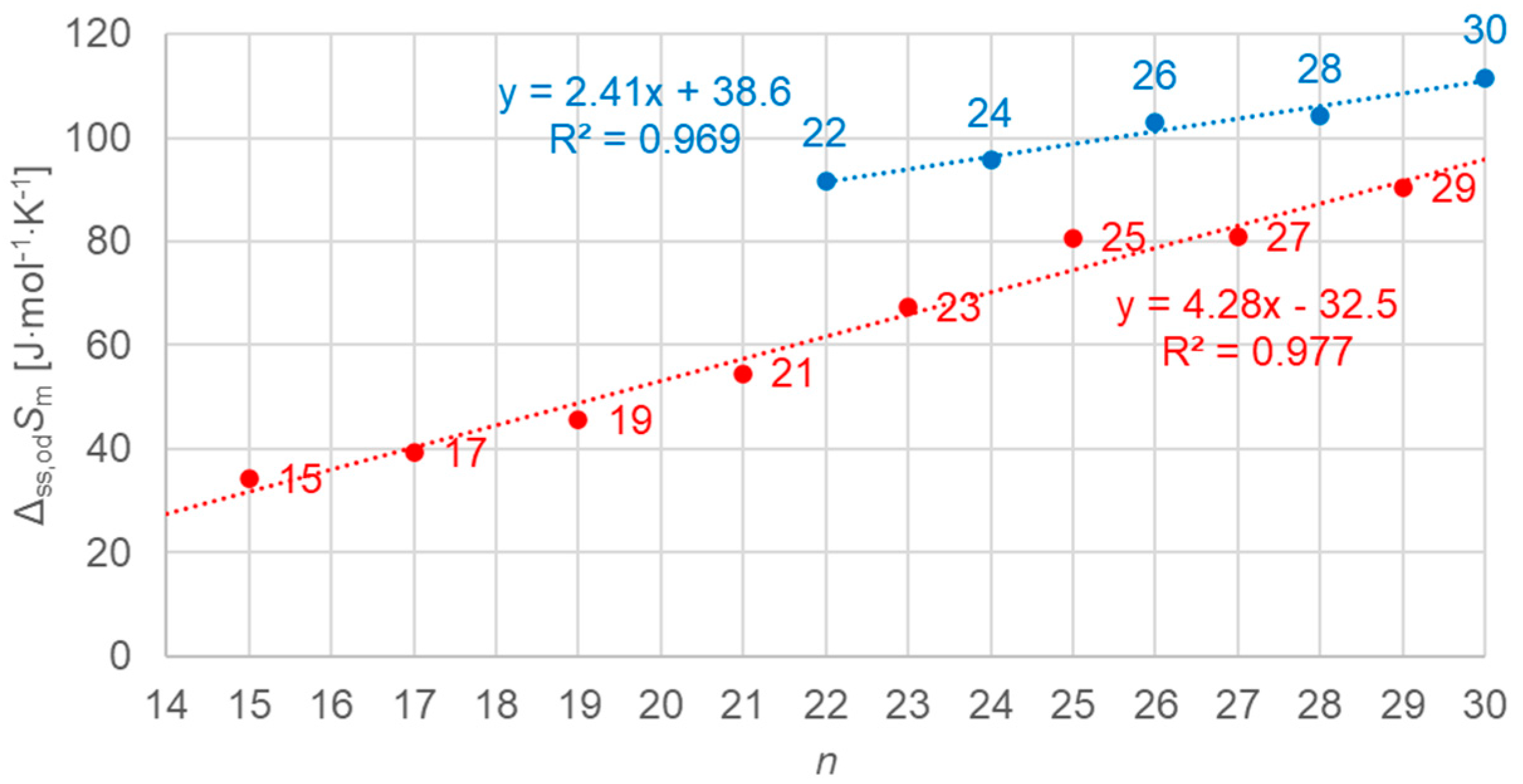
3.2.3. Solid–Solid Values (Plots Only for Order–Disorder Transitions [od], Meaning Ordered Crystal to Rotator Phase)
3.3. Graphical Evaluation of Enthalpy vs. n and Entropy vs. n
3.3.1. Total Values
3.3.2. Solid–Liquid Values
3.3.3. Solid–Solid Values
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mehling, H.; Brütting, M.; Haussmann, T. PCM products and their fields of application—An overview of the state in 2020/2021. J. Energy Storage 2022, 51, 104354. [Google Scholar] [CrossRef]
- Mehling, H. Enthalpy and temperature of the phase change solid–liquid—An analysis of data of the elements using information on their structure. Sol. Energy 2013, 88, 71–79. [Google Scholar] [CrossRef]
- Mehling, H. Enthalpy and temperature of the phase change solid–liquid—An analysis of data of compounds employing entropy. Sol. Energy 2013, 95, 290–299. [Google Scholar] [CrossRef]
- Mehling, H. Enthalpy, entropy, and temperature of the phase change liquid-gas—An analysis of data of 719 materials regarding systematic correlations. High Temp. High Press. 2019, 48, 233–251. [Google Scholar] [CrossRef]
- Dall’Acqua, L.; Gatta, G.D.; Nowicka, B.; Ferloni, P. Enthalpies and entropies of fusion of ten alkane-α, ω-diamines H2N–(CH2)n–NH2 where 3 ≤ n ≤ 12. J. Chem. Thermodyn. 2002, 34, 1–12. [Google Scholar] [CrossRef]
- Badea, E.; Gatta, G.D.; D’Angelo, D.; Brunetti, B.; Rečková, Z. Odd–even effect in melting properties of 12 alkane-α,ω-diamides. J. Chem. Thermodyn. 2006, 38, 1546–1552. [Google Scholar] [CrossRef]
- Mehling, H.; White, M.A. Analysis of trends in phase change enthalpy, entropy and temperature for alkanes, alcohols and fatty acids. Chem. Phys. Impact 2023, 6, 100222. [Google Scholar] [CrossRef]
- Mehling, H.; Leys, J.; Glorieux, C.; Thoen, J. Potential new reference materials for caloric measurements on PCM. SN Appl. Sci. 2021, 3, 202. [Google Scholar] [CrossRef]
- Kahwaji, S.; Johnson, M.B.; White, M.A. Thermal property determination for phase change materials. J. Chem. Thermodyn. 2021, 160, 1–8. [Google Scholar] [CrossRef]
- Thoen, J. High Resolution Adiabatic Scanning Calorimetry and Heat Capacities. In Heat Capacities; Wilhelm, E., Letcher, T.M., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2010; Chapter 13; pp. 287–306. [Google Scholar] [CrossRef]
- Thoen, J.; Leys, J.; Losada-Pérez, P.; Glorieux, C. Enthalpy Measurements of Condensed Matter by Peltier-element-based Adiabatic Scanning Calorimetry (pASC). In Enthalpy and Internal Energy: Liquids, Solutions and Vapours; Wilhelm, E., Letcher, T., Eds.; The Royal Society of Chemistry: London, UK, 2017; Chapter 3; pp. 77–95. [Google Scholar] [CrossRef]
- Cohen, E.R.; Cvitas, T.; Frey, J.G.; Holmstrom, B.; Kuchitsu, K.; Marquardt, R.; Mills, I.; Pavese, F.; Quack, M.; Stohner, J.; et al. Quantities, Units, and Symbols in Physical Chemistry, IUPAC Green Book, 3rd ed.; RSC Publishing: Croydon, UK, 2007; ISBN 0-85404-433-7. [Google Scholar]
- Thoen, J.; Cordoyiannis, G.; Glorieux, C. High-resolution and high-accuracy calorimetry of order–disorder and melting transitions in the n-alkanes n-pentadecane, n-hexadecane, n-heptadecane, n-octadecane, n-nonadecane and n-eicosane. J. Chem. Thermodyn. 2024, 194, 1072853. [Google Scholar] [CrossRef]
- Leys, J.; Losada-Pérez, P.; Glorieux, C.; Thoen, J. Temperature Dependence of the Enthalpy of Alkanes and Related Phase Change Materials (PCMs). In Enthalpy and Internal Energy: Liquids, Solutions and Vapours; Wilhelm, E., Letcher, T.M., Eds.; The Royal Society of Chemistry: London, UK, 2018. [Google Scholar]
- Dirand, M.; Bouroukba, M.; Briard, A.-J.; Chevallier, V.; Petitjean, D.; Corriou, J.-P. Temperatures and enthalpies of (solid + solid) and (solid + liquid) transitions of n-alkanes. J. Chem. Thermodyn. 2002, 34, 1255–1277. [Google Scholar] [CrossRef]
- Kahwaji, S.; Johnson, M.B.; Kheirabadi, A.C.; Groulx, D.; White, M.A. A comprehensive study of properties of paraffin phase change materials for solar thermal energy storage and thermal management applications. Energy 2018, 162, 1169–1182. [Google Scholar] [CrossRef]
- Briard, A.-J.; Bouroukba, M.; Petitjean, D.; Hubert, N.; Dirand, M. Experimental Enthalpy Increments from the Solid Phases to the Liquid Phase of Homologous n-Alkane Series (C18 to C38 and C41, C44, C46, C50, C54, and C60). J. Chem. Eng. Data 2003, 48, 497–513. [Google Scholar] [CrossRef]
- Faden, M.; Höhlein, S.; Wanner, J.; König-Haagen, A.; Brüggemann, D. Review of Thermophysical Property Data of Octadecane for Phase-Change Studies. Materials 2019, 12, 2974. [Google Scholar] [CrossRef] [PubMed]
- Thoen, J.; Leys, J.; Glorieux, C. Adiabatic Scanning Calorimeter, European Patent EP 2 91328 B1 (22 September 2015). U.S. Patent No 9,310,263 B2, 12 April 2016. [Google Scholar]
- Leys, J.; Losada-Pérez, P.; Glorieux, C.; Thoen, J. Application of a novel type of adiabatic scanning calorimeter for high-resolution thermal data near the melting point of gallium. J. Therm. Anal. Calorim. 2014, 117, 173. [Google Scholar] [CrossRef]
- Leys, J.; Losada- Pérez, P.; Slenders, E.; Glorieux, C.; Thoen, J. Investigation of the melting behavior of the reference materials biphenyl and phenyl salicylate by a new type adiabatic scanning calorimeter. Thermochim. Acta 2014, 582, 68–76. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook, SRD 69. Available online: https://webbook.nist.gov/chemistry/name-ser/ (accessed on 30 August 2024).
- VWR. Available online: https://de.vwr.com/store/product/738725/n-triacontan-99 (accessed on 30 August 2024).


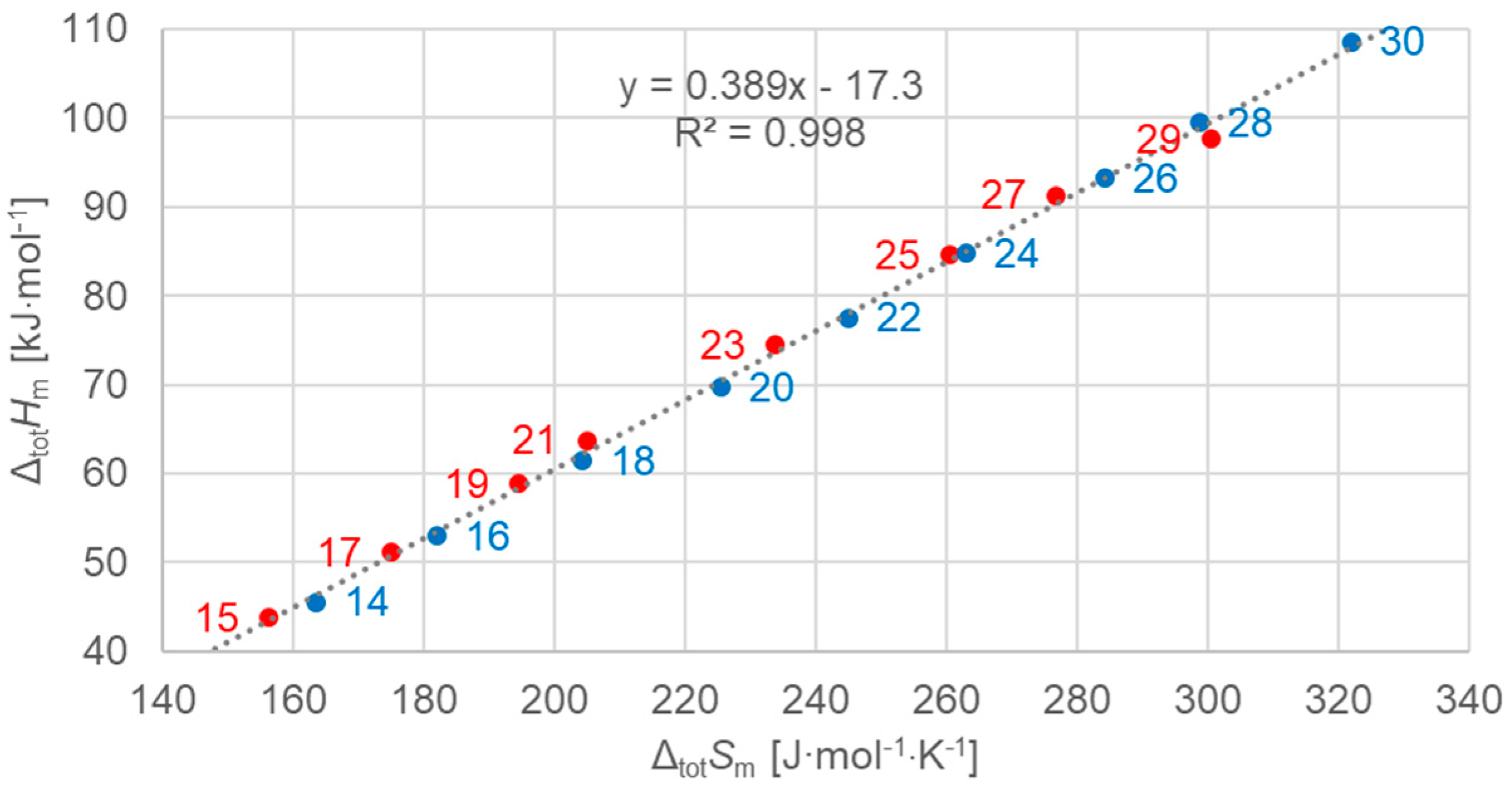
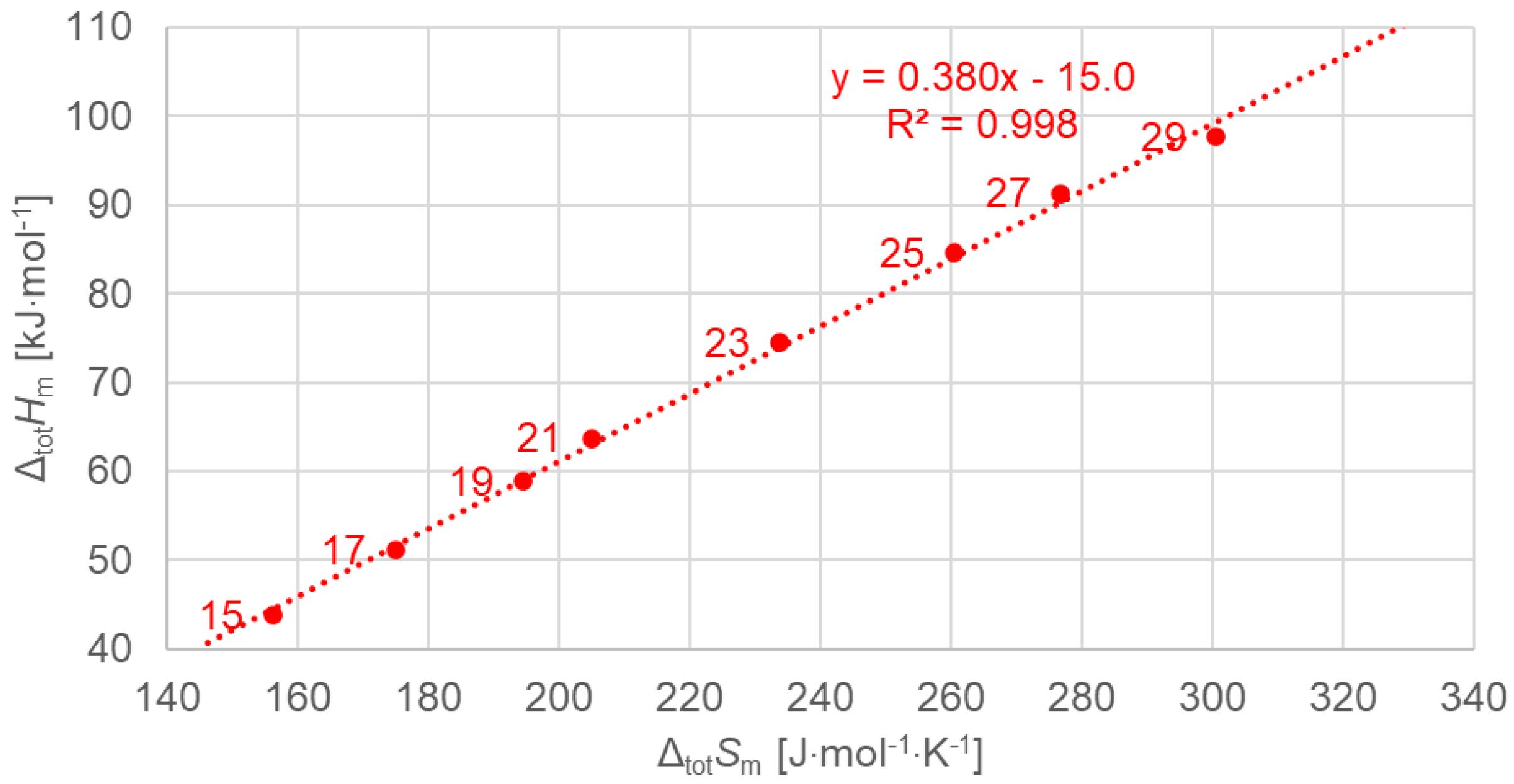
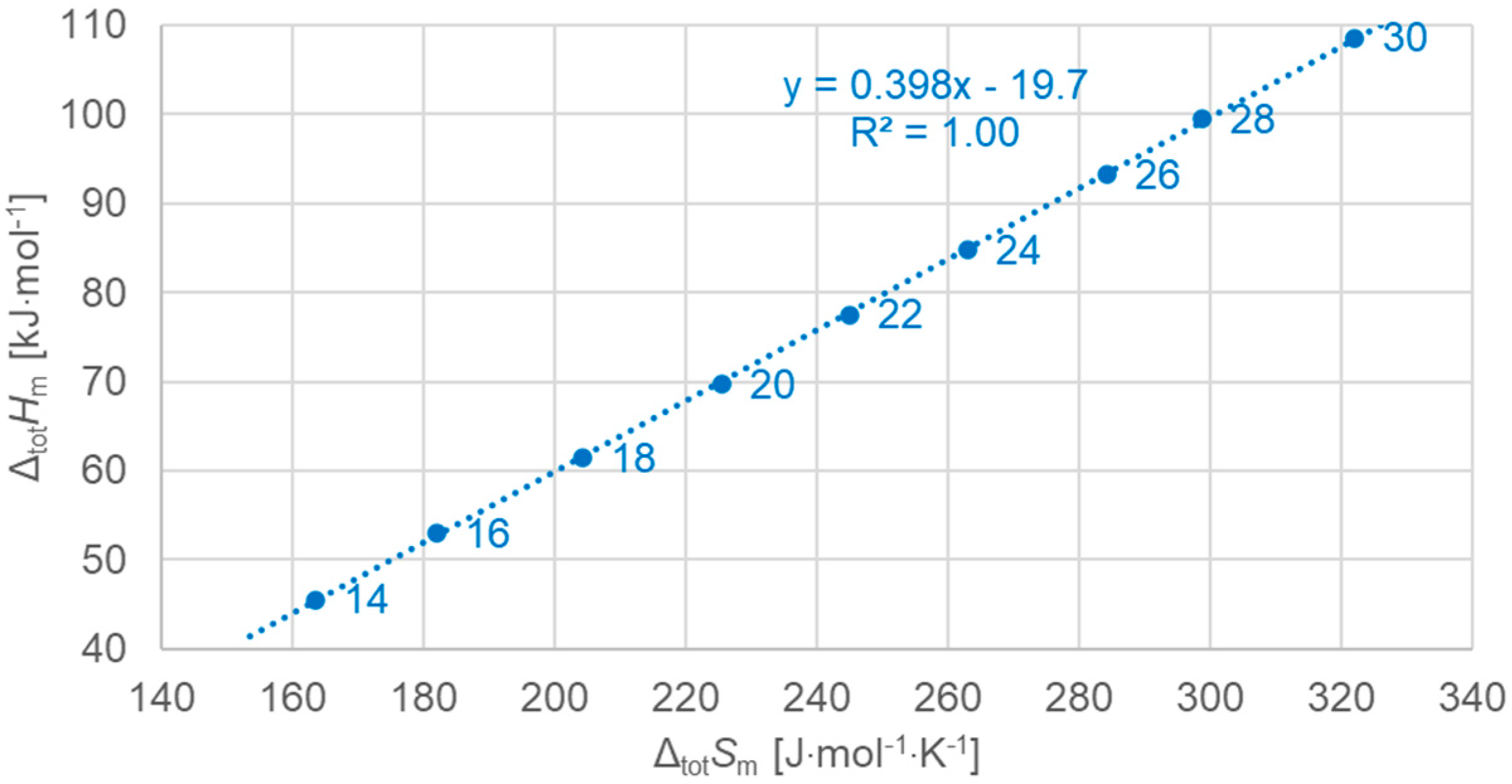

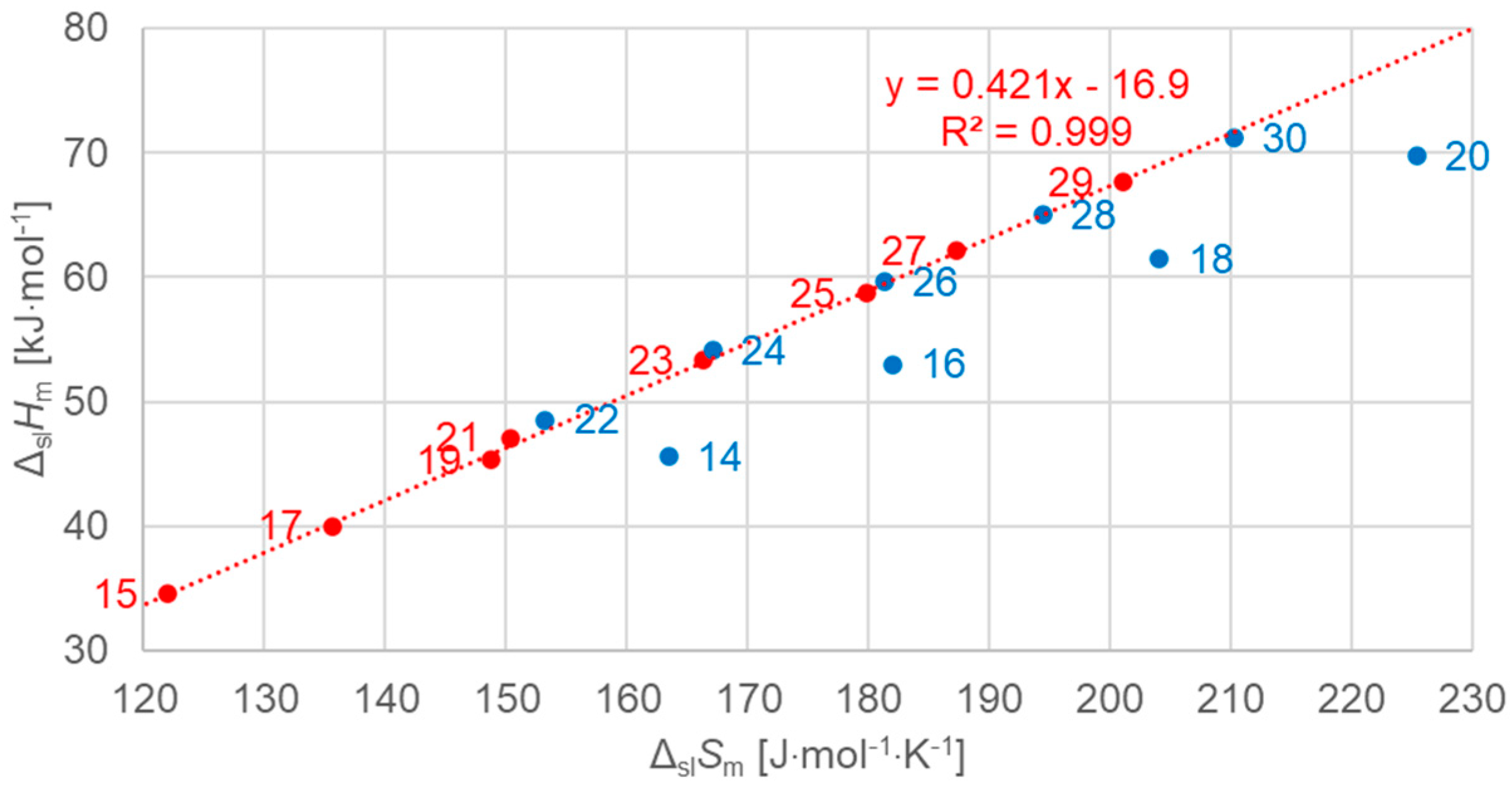





| Solid–Solid cc (Crystal–Crystal) | Solid–Solid od (Crystal–Rotator) | Solid–Liquid (Fusion) | Total (Sum of All) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Odd/Even | n (C…) | Name | Molar Mass [g∙mol−1] | Tss [K] | ΔssHm [kJ∙mol−1] | ΔssSm [J∙mol−1∙K−1] | Tss [K] | ΔssHm [kJ∙mol−1] | ΔssSm [J∙mol−1∙K−1] | Tsl [K] | ΔslHm [kJ∙mol−1] | ΔslSm [J∙mol−1∙K−1] | ΔtotHm [kJ∙mol−1] | ΔtotSm [J∙mol−1∙K−1] |
| even | 14 | n-tetradecane | 198.39 | 278.8 | 45.6 | 163 | 45.6 | 163 | ||||||
| even | 16 | n-hexadecane | 226.44 | 291.1 | 53.0 | 182 | 53.0 | 182 | ||||||
| even | 18 | n-octadecane | 254.49 | 301.2 | 61.5 | 204 | 61.5 | 204 | ||||||
| even | 20 | n-eicosane | 282.55 | 309.5 | 69.7 | 225 | 69.7 | 225 | ||||||
| even | 22 | n-docosane | 310.60 | 315.9 | 29.0 | 91.7 | 316.8 | 48.5 | 153 | 77.5 | 245 | |||
| even | 24 | n-tetracosane | 338.65 | 321.2 | 30.7 | 95.7 | 323.7 | 54.1 | 167 | 84.8 | 263 | |||
| even | 26 | n-hexacosane | 366.71 | 326.2 | 33.6 | 103 | 329.1 | 59.7 | 181 | 93.3 | 284 | |||
| even | 28 | n-octacosane | 394.76 | 330.7 | 34.5 | 104 | 334.3 | 65.0 | 194 | 99.4 | 299 | |||
| even | 30 | n-triacotane | 422.82 | 335.2 | 37.4 | 112 | 338.5 | 71.2 | 210 | 109 | 322 | |||
| odd | 15 | n-pentadecane | 212.41 | 270.8 | 9.3 | 34.3 | 283.0 | 34.5 | 122 | 43.8 | 156 | |||
| odd | 17 | n-heptadecane | 240.47 | 284.1 | 11.2 | 39.3 | 294.9 | 40.0 | 136 | 51.1 | 175 | |||
| odd | 19 | n-nonadecane | 268.52 | 295.8 | 13.5 | 45.7 | 304.9 | 45.4 | 149 | 58.9 | 194 | |||
| odd | 21 | n-heneicosane | 296.57 | 305.2 | 16.6 | 54.5 | 313.1 | 47.1 | 150 | 63.7 | 205 | |||
| odd | 23 | n-tricosane | 324.63 | 313.7 | 21.1 | 67.4 | 320.6 | 53.3 | 166 | 74.4 | 234 | |||
| odd | 25 | n-pentacosane | 352.68 | 320.4 | 25.9 | 80.7 | 326.7 | 58.7 | 180 | 84.6 | 260 | |||
| odd | 27 | n-heptacosane | 380.73 | 323.1 | 2.78 | 8.60 | 326.3 | 26.4 | 80.9 | 331.9 | 62.1 | 187 | 91.3 | 277 |
| odd | 29 | n-nonacosane | 408.79 | 326.0 | 2.90 | 8.90 | 331.4 | 30.0 | 90.4 | 336.5 | 67.7 | 201 | 97.6 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehling, H.; Thoen, J.; Glorieux, C.; White, M.A. High-Accuracy and High-Resolution Calorimetry Revealing New Correlations of Phase Change Enthalpy, Entropy, and Number of Carbon Atoms n in n-Alkanes. Molecules 2025, 30, 1300. https://doi.org/10.3390/molecules30061300
Mehling H, Thoen J, Glorieux C, White MA. High-Accuracy and High-Resolution Calorimetry Revealing New Correlations of Phase Change Enthalpy, Entropy, and Number of Carbon Atoms n in n-Alkanes. Molecules. 2025; 30(6):1300. https://doi.org/10.3390/molecules30061300
Chicago/Turabian StyleMehling, Harald, Jan Thoen, Christ Glorieux, and Mary Anne White. 2025. "High-Accuracy and High-Resolution Calorimetry Revealing New Correlations of Phase Change Enthalpy, Entropy, and Number of Carbon Atoms n in n-Alkanes" Molecules 30, no. 6: 1300. https://doi.org/10.3390/molecules30061300
APA StyleMehling, H., Thoen, J., Glorieux, C., & White, M. A. (2025). High-Accuracy and High-Resolution Calorimetry Revealing New Correlations of Phase Change Enthalpy, Entropy, and Number of Carbon Atoms n in n-Alkanes. Molecules, 30(6), 1300. https://doi.org/10.3390/molecules30061300






