Integrating Explicit and Implicit Fullerene Models into UNRES Force Field for Protein Interaction Studies
Abstract
1. Introduction
1.1. Fullerene-Protein Interactions
1.2. Theoretical Methods of Studying Nanoparticles
2. Methods
2.1. UNRES Model
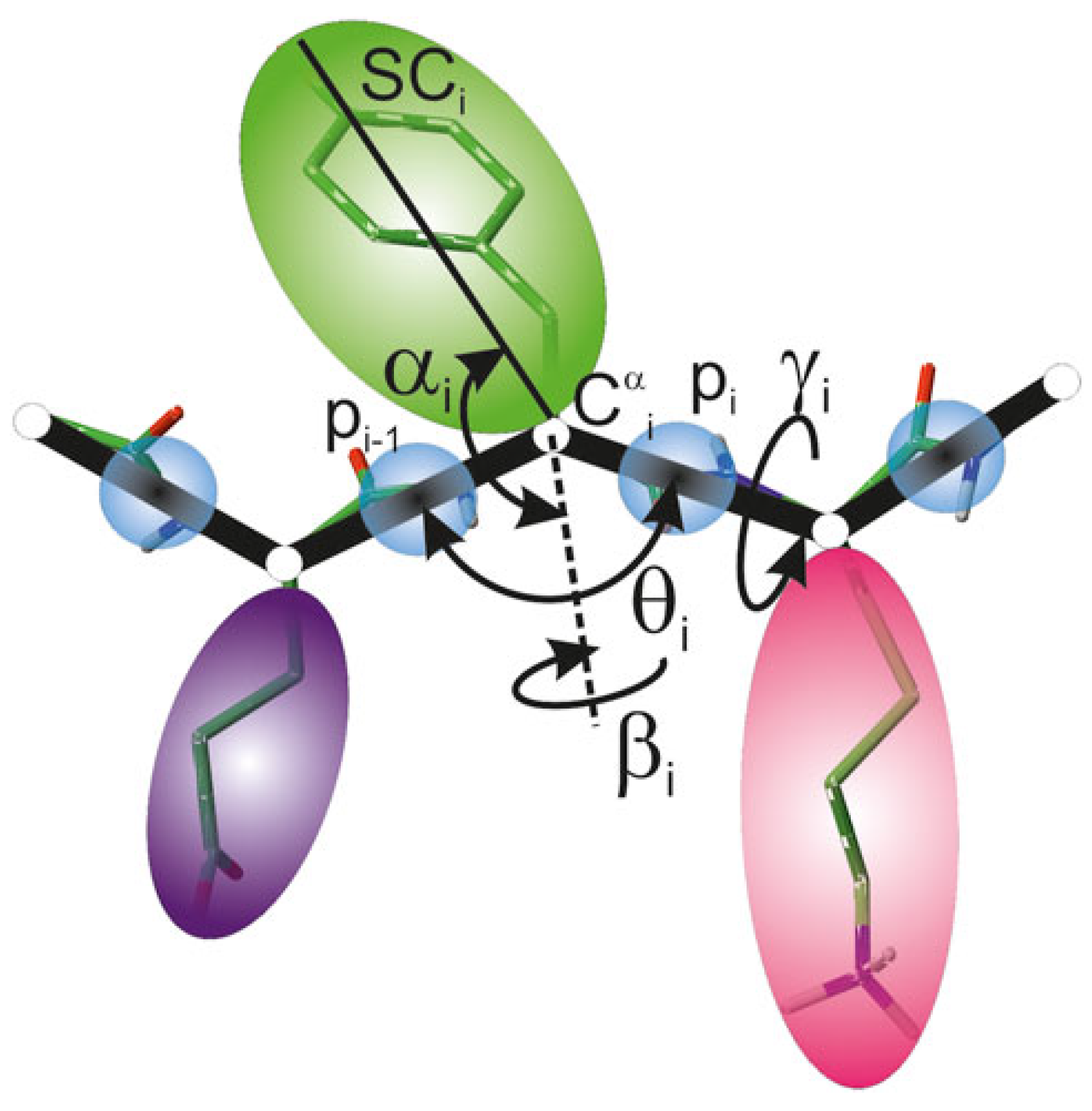
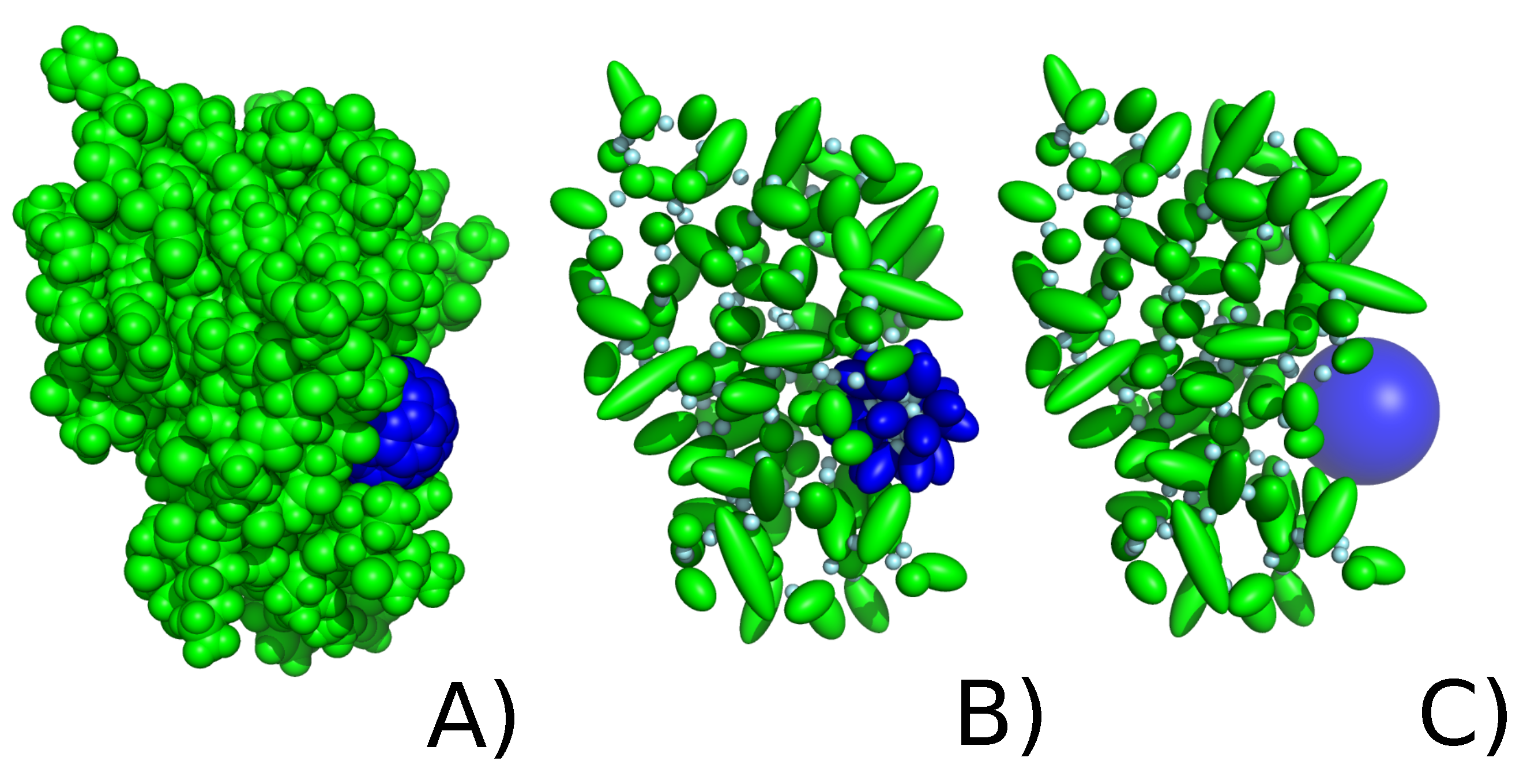
2.2. C60 Model in UNRES Force Field
2.2.1. Explicit Model
2.2.2. Implicit Model of Nanoparticle Representation
2.3. Protein Selection
2.4. MD Simulation Details
2.4.1. Coarse-Grained UNRES Simulations
- Without fullerene nanoparticle (to assess protein stability);
- With implicit model of fullerene nanoparticle;
- With explicit model of fullerene nanoparticle.
2.4.2. All-Atom Amber Simulations
2.5. Analysis
2.5.1. Binding Energy Estimation
2.5.2. All-Atom Structure Reconstruction
2.5.3. CPPTRAJ Analysis
2.5.4. Contact Probability
3. Results
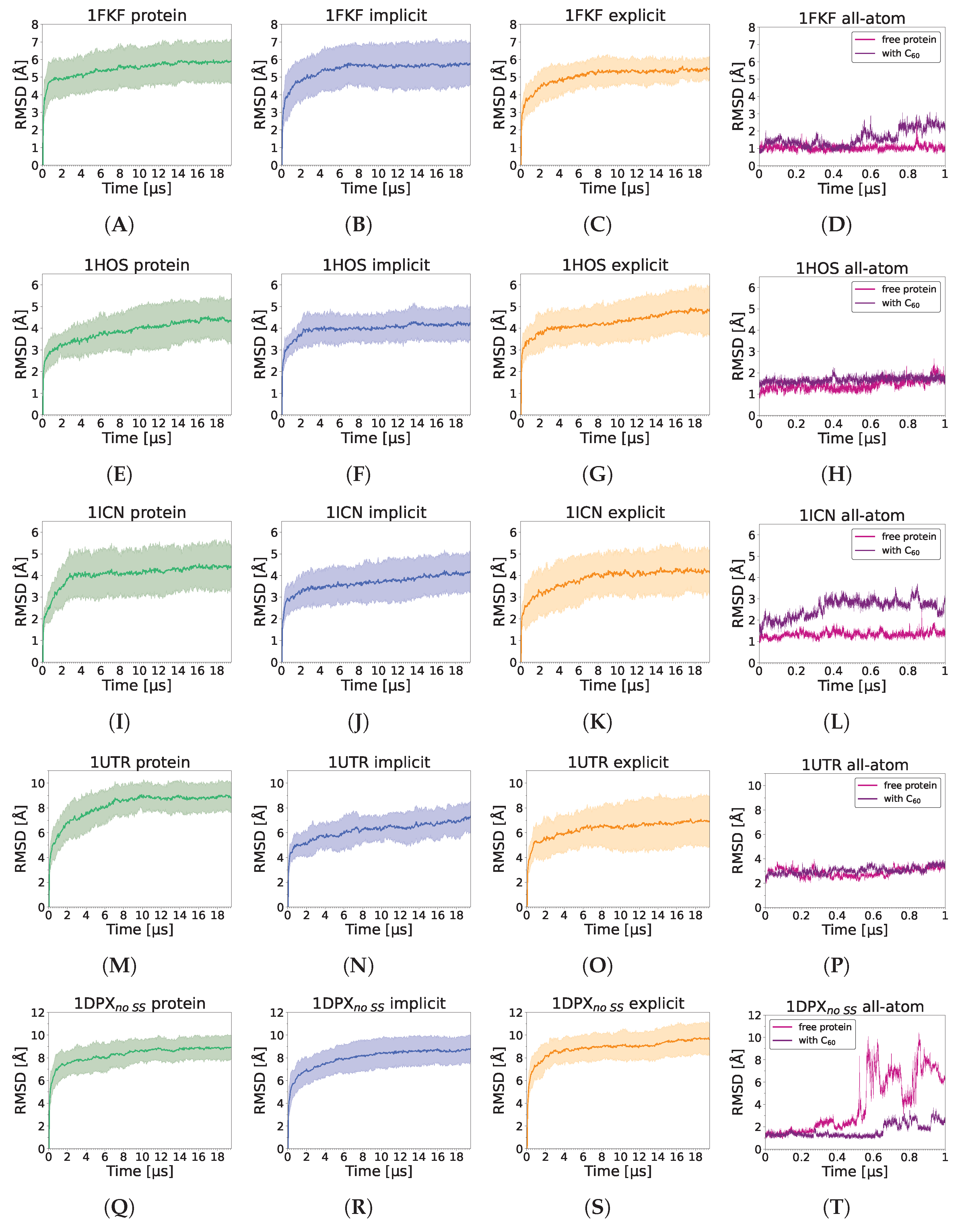
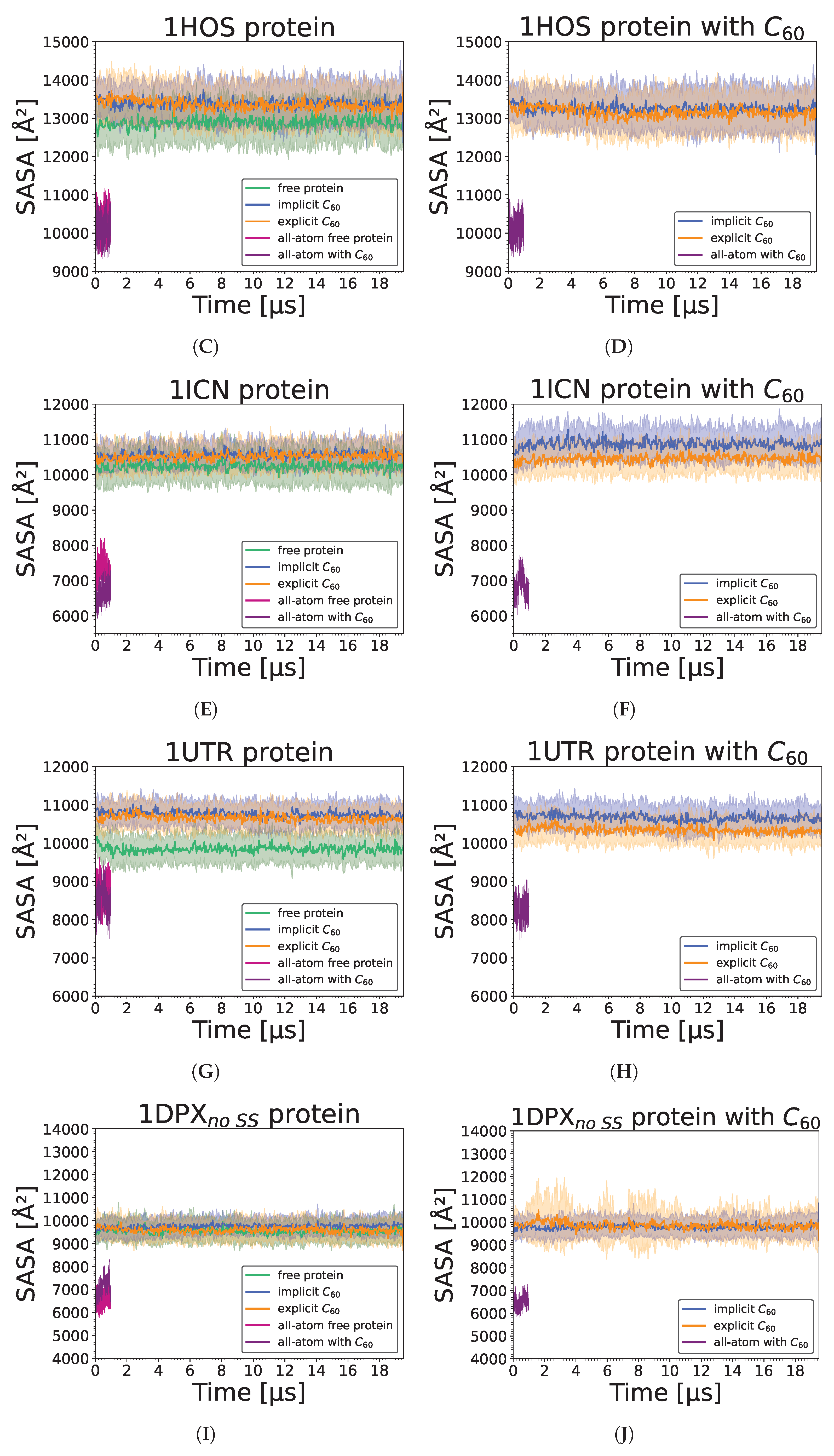
3.1. Stability of a Nanoparticle in a Complex
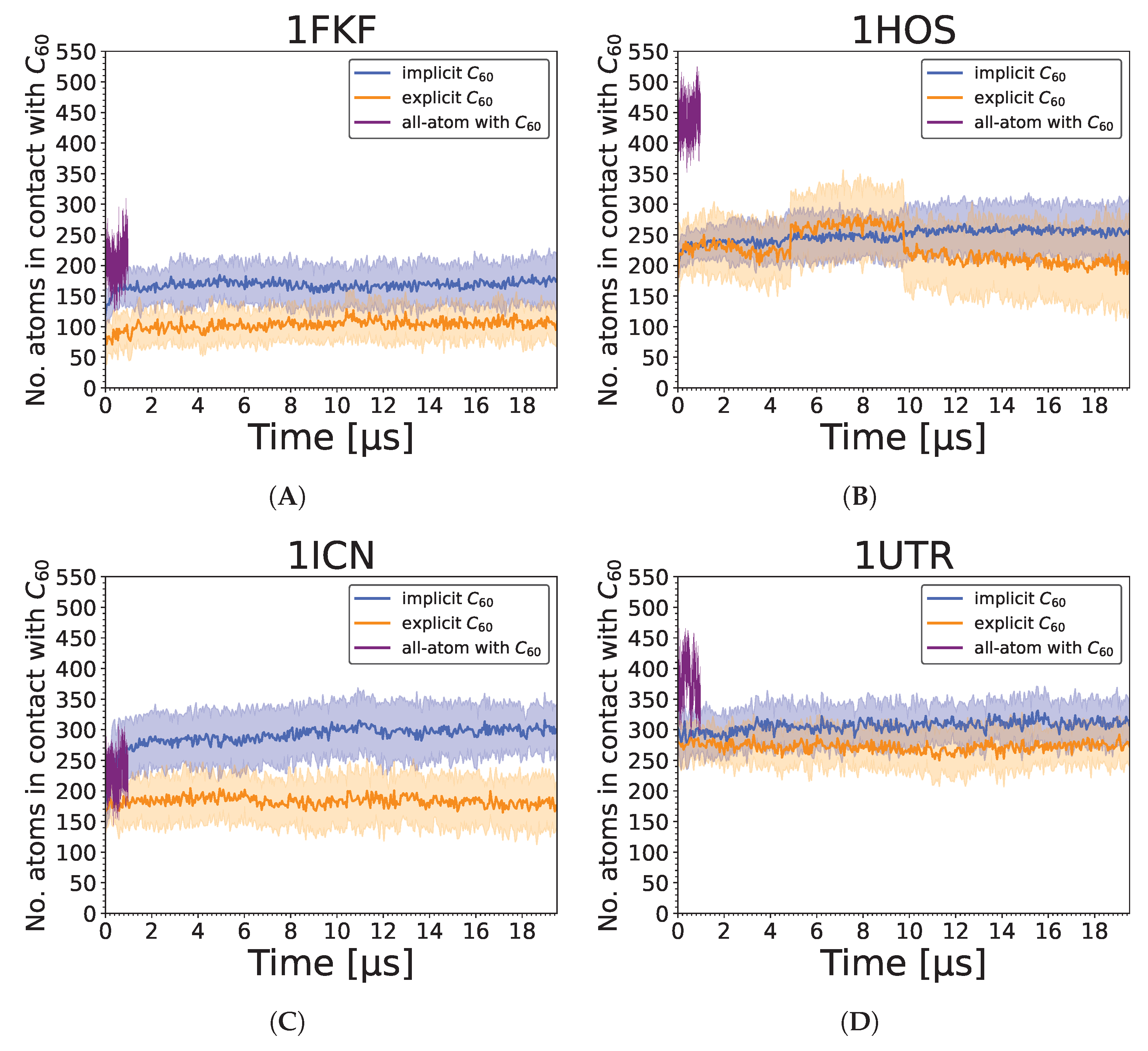
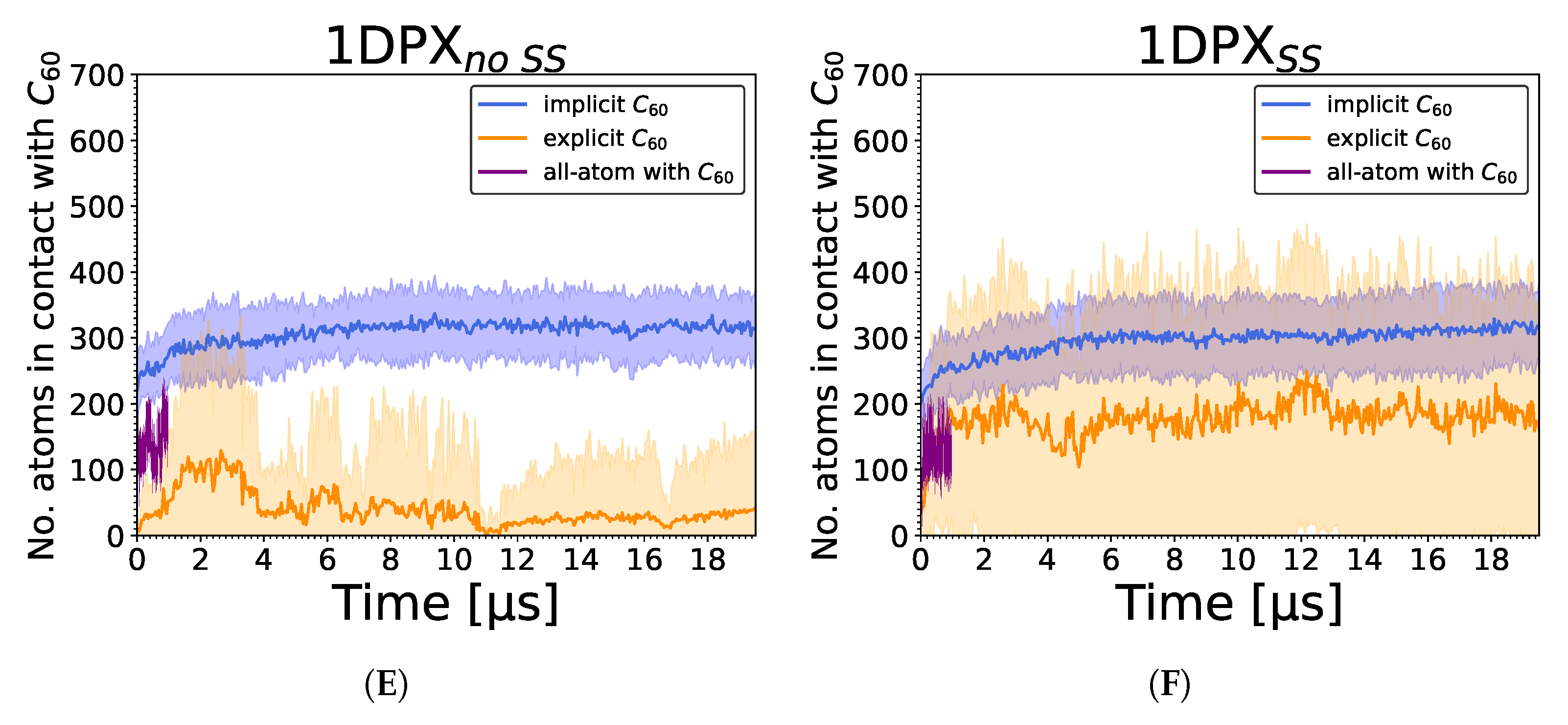
3.2. Strength of the Protein–Nanoparticle Interaction
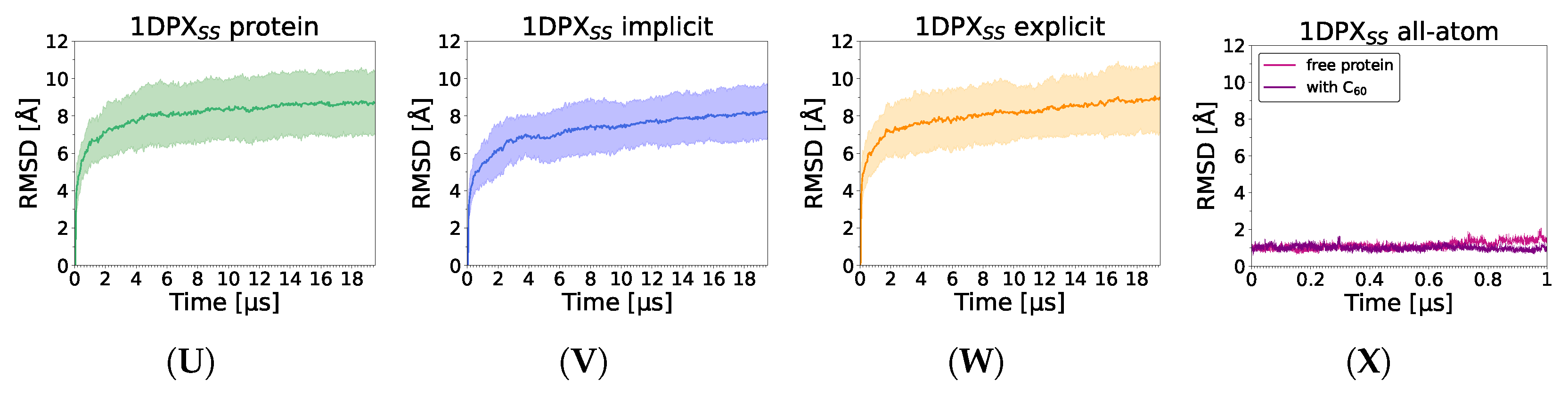
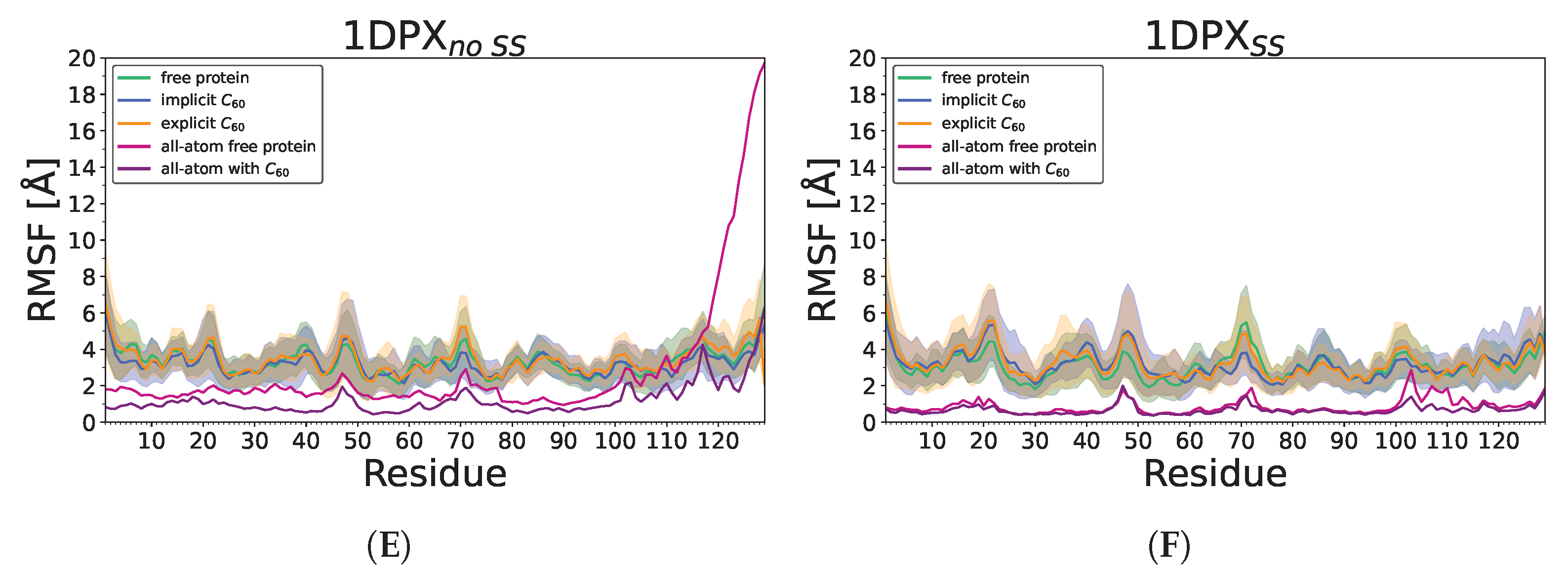
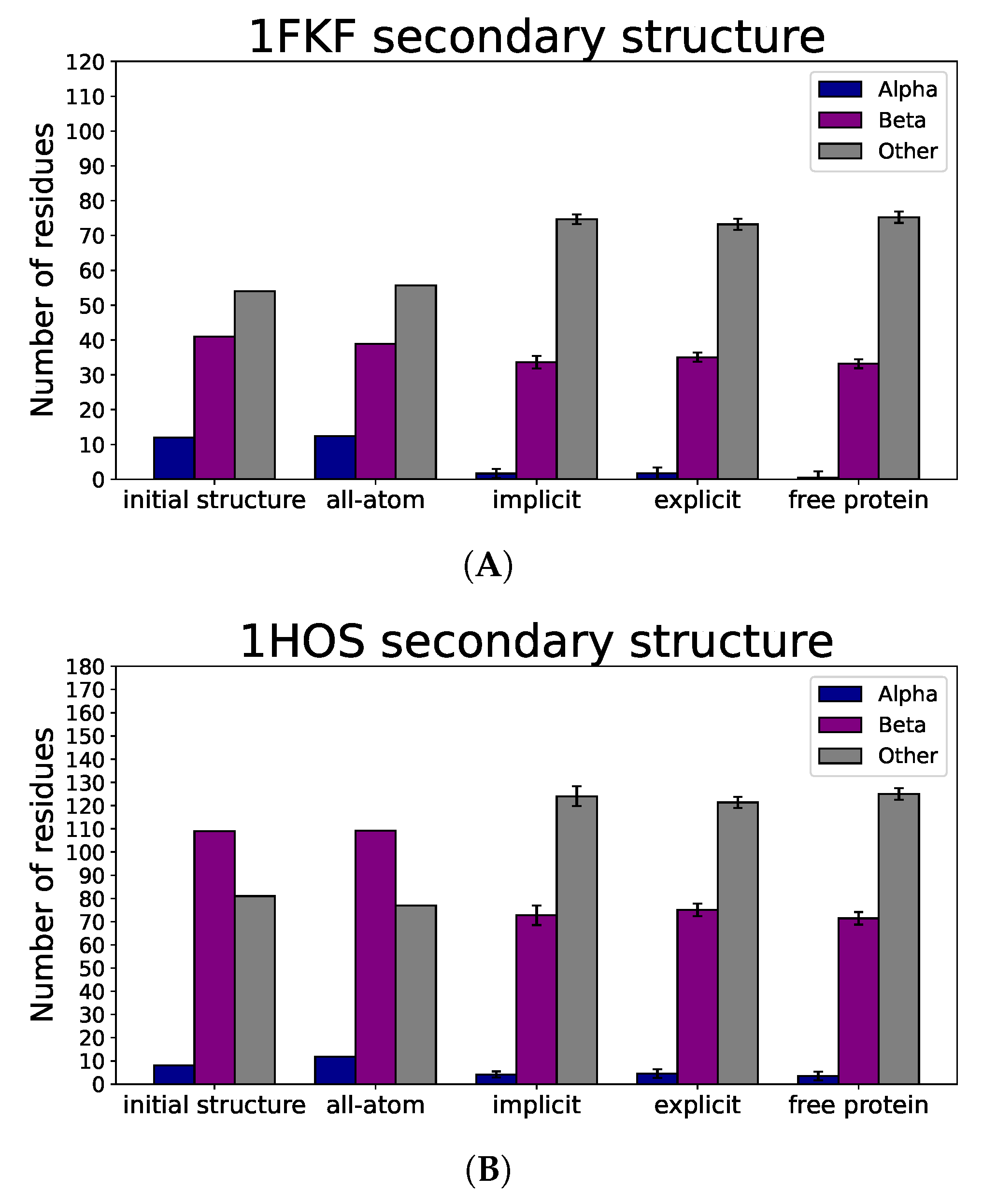
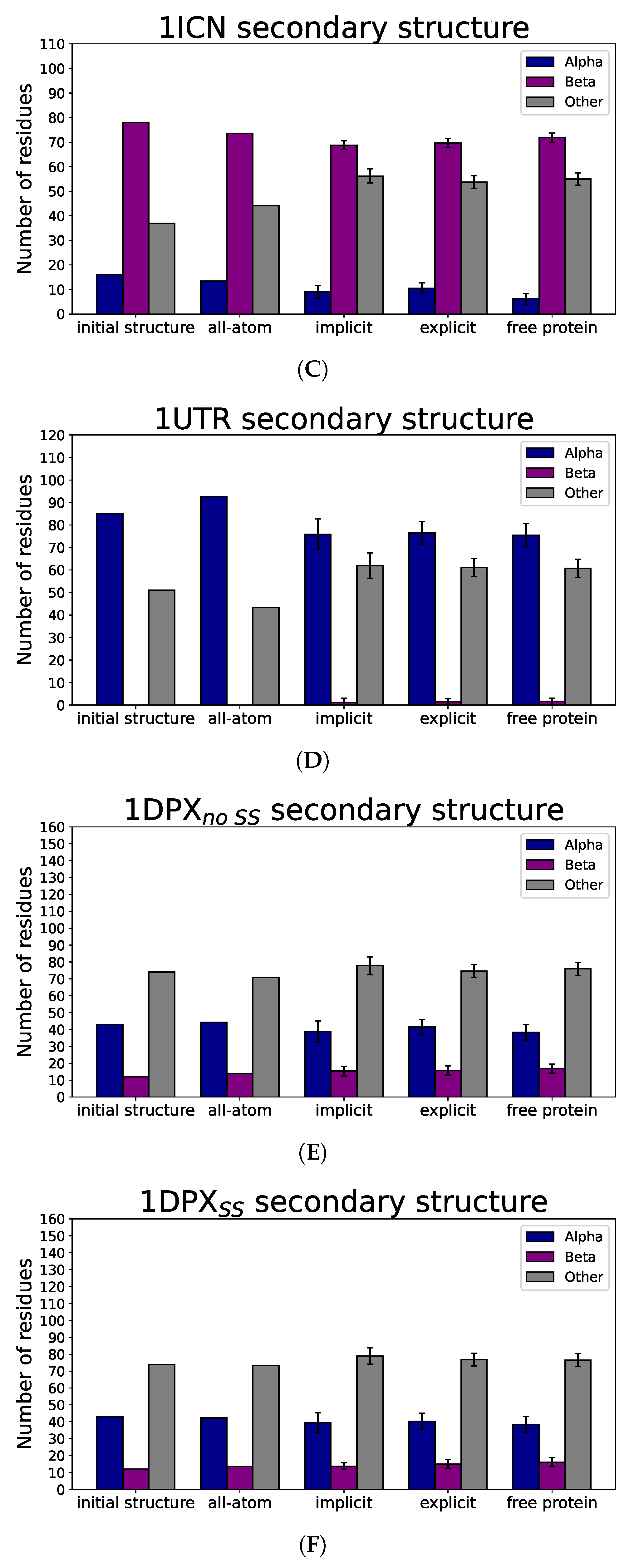
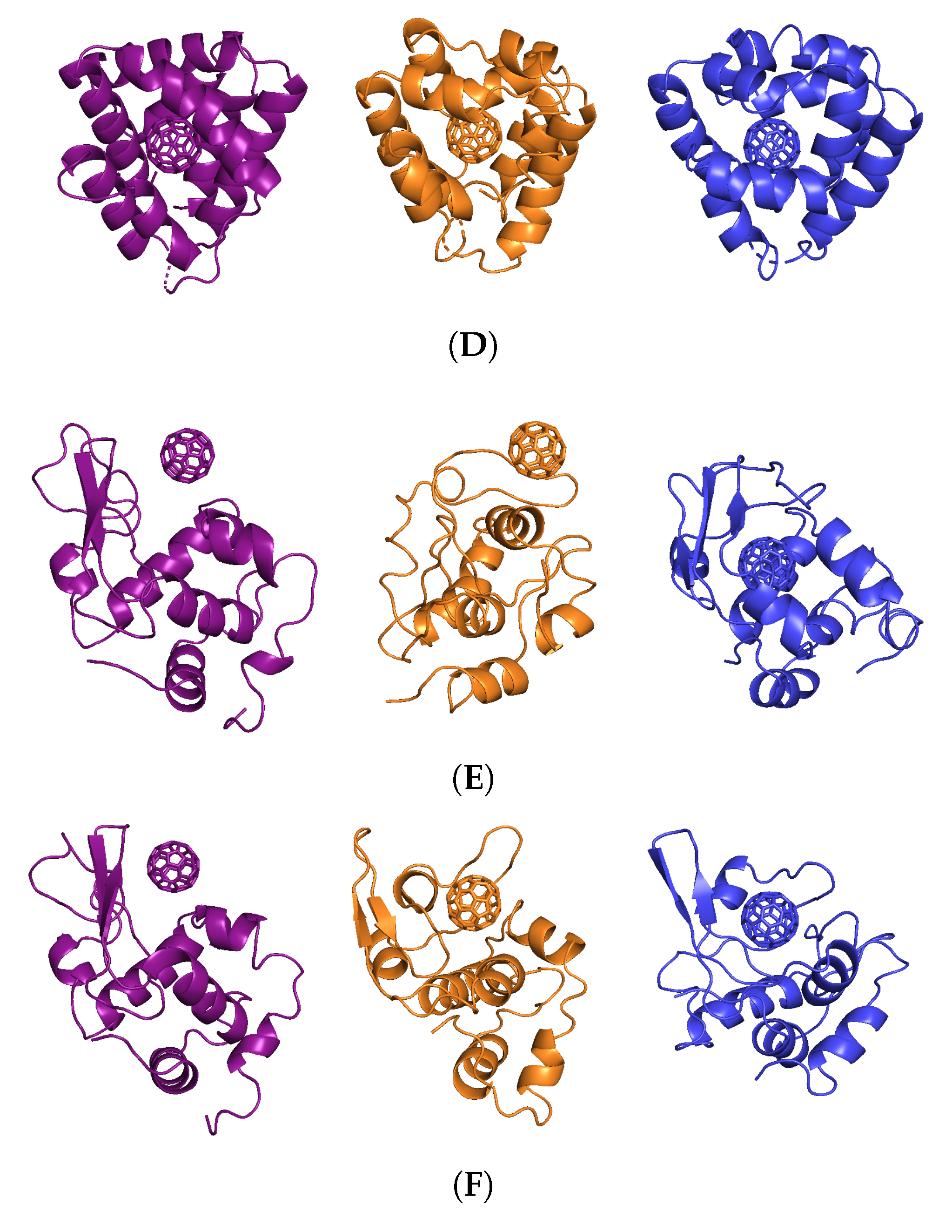
3.3. Nanoparticle Impact on Protein Structure
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baig, N.; Kammakakam, I.; Falath, W. Nanomaterials: A review of synthesis methods, properties, recent progress, and challenges. Mater. Adv. 2021, 2, 1821–1871. [Google Scholar] [CrossRef]
- Bayda, S.; Adeel, M.; Tuccinardi, T.; Cordani, M.; Rizzolio, F. The History of Nanoscience and Nanotechnology: From Chemical–Physical Applications to Nanomedicine. Molecules 2020, 25, 112. [Google Scholar] [CrossRef] [PubMed]
- Mauter, M.S.; Elimelech, M. Environmental Applications of Carbon-Based Nanomaterials. Environ. Sci. Technol. 2008, 42, 5843–5859. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, A. The Chemistry of the Fullerenes: An Overview. Angew. Chem. 1993, 32, 1138–1141. [Google Scholar] [CrossRef]
- Prato, M. [60]Fullerene chemistry for materials science applications. J. Mater. Chem. 1997, 7, 1097–1109. [Google Scholar] [CrossRef]
- Kroto, H.; Heath, J.; O’Brien, S. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Cui, F.; Luo, C.; Dong, J. Dimerization of C60 molecules within the single-walled carbon nanotube. Phys. Lett. A 2004, 327, 55–60. [Google Scholar] [CrossRef]
- Baker, G.; Gupta, A.; Clark, M.; Valenzuela, B.; Staska, L.; Harbo, S.; Pierce, J.; Dill, J. Inhalation toxicity and lung toxicokinetics of C60 fullerene nanoparticles and microparticles. Toxicol. Sci. 2008, 101, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Buseck, P.R. Geological fullerenes: Review and analysis. Earth Planet. Sci. Lett. 2002, 203, 781–792. [Google Scholar] [CrossRef]
- Sayers, B.C.; Walker, N.J.; Roycroft, J.H.; Germolec, D.R.; Baker, G.L.; Clark, M.L.; Hayden, B.K.; DeFord, H.; Dill, J.A.; Gupta, A.; et al. Lung deposition and clearance of microparticle and nanoparticle C60 fullerene aggregates in B6C3F1 mice and Wistar Han rats following nose-only inhalation for 13 weeks. Toxicology 2016, 339, 87–96. [Google Scholar] [CrossRef]
- Hendren, C.O.; Mesnard, X.; Dröge, J.; Wiesner, M.R. Estimating Production Data for Five Engineered Nanomaterials As a Basis for Exposure Assessment. Environ. Sci. Technol. 2011, 45, 2562–2569. [Google Scholar] [CrossRef] [PubMed]
- Junaid, M.; Almuqri, E.; Liu, J.; Zhang, H. Analyses of the Binding between Water Soluble C60 Derivatives and Potential Drug Targets through a Molecular Docking Approach. PLoS ONE 2016, 11, e0147761. [Google Scholar] [CrossRef] [PubMed]
- Thompson, B.C.; Fréchet, J.M.J. Polymer-fullerene composite solar cells. Angew. Chem. 2008, 47, 58–77. [Google Scholar] [CrossRef] [PubMed]
- Shetti, N.P.; Mishra, A.; Basu, S.; Aminabhavi, T.M. Versatile fullerenes as sensor materials. Mater. Today Chem. 2021, 20, 100454. [Google Scholar] [CrossRef]
- Panwar, N.; Soehartono, A.M.; Chan, K.K.; Zeng, S.; Xu, G.; Qu, J.; Coquet, P.; Yong, K.T.; Chen, X. Nanocarbons for Biology and Medicine: Sensing, Imaging, and Drug Delivery. Chem. Rev. 2019, 119, 9559–9656. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.Z.; Nafisi, S.; Maibach, H.I. Fullerene nanoparticle in dermatological and cosmetic applications. Nanomed. Nanotechnol. Biol. Med. 2017, 13, 1071–1087. [Google Scholar] [CrossRef] [PubMed]
- Kazemzadeh, H.; Mozafari, M. Fullerene-based delivery systems. Drug Discov. Today 2019, 24, 898–905. [Google Scholar] [CrossRef]
- Dellinger, A.; Zhou, Z.; Connor, J.; Madhankumar, A.; Pamujula, S.; Sayes, C.M.; Kepley, C.L. Application of fullerenes in nanomedicine: An update. Nanomed. 2013, 8, 1191–1208. [Google Scholar] [CrossRef] [PubMed]
- Utsunomiya, S.; Jensen, K.A.; Keeler, G.J.; Ewing, R.C. Uraninite and Fullerene in Atmospheric Particulates. Environ. Sci. Technol. 2002, 36, 4943–4947. [Google Scholar] [CrossRef]
- Aschberger, K.; Johnston, H.J.; Stone, V.; Aitken, R.J.; Tran, C.L.; Hankin, S.M.; Peters, S.A.; Christensen, F.M. Review of fullerene toxicity and exposure—Appraisal of a human health risk assessment, based on open literature. Regul. Toxicol. Pharmacol. 2010, 58, 455–473. [Google Scholar] [CrossRef]
- Johnston, H.J.; Hutchison, G.R.; Christensen, F.M.; Aschberger, K.; Stone, V. The biological mechanisms and physicochemical characteristics responsible for driving fullerene toxicity. Toxicol. Sci. 2010, 114, 162–182. [Google Scholar] [CrossRef] [PubMed]
- Ha, Y.; Wang, X.; Liljestr, H.M.; Maynard, J.A.; Katz, L.E. Elucidating the mechanism of cellular uptake of fullerene nanoparticles. Environ. Eng. Res. 2022, 27, 200658. [Google Scholar] [CrossRef]
- Friedman, S.H.; DeCamp, D.L.; Sijbesma, R.P.; Srdanov, G.; Wudl, F.; Kenyon, G.L. Inhibition of the HIV-1 protease by fullerene derivatives: Model building studies and experimental verification. J. Am. Chem. Soc. 1993, 115, 6506–6509. [Google Scholar] [CrossRef]
- Chen, B.; Wilson, S.; Das, M.; Coughlin, D.; Erlanger, B. Antigenicity of fullerenes: Antibodies specific for fullerenes and their characteristics. Proc. Nat. Acad. Sci. USA 1998, 95, 10809–10813. [Google Scholar] [CrossRef] [PubMed]
- Ueng, T.H.; Kang, J.J.; Wang, H.W.; Cheng, Y.W.; Chiang, L.Y. Suppression of microsomal cytochrome P450-dependent monooxygenases and mitochondrial oxidative phosphorylation by fullerenol, a polyhydroxylated fullerene C60. Toxicol. Lett. 1997, 93, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Simic-Krstic, J. Effects of C60(OH)24 on Microtubule Assembly. Arch. Oncol. 1997, 5, 143–147. [Google Scholar]
- Jin, H.; Chen, W.; Tang, X.; Chiang, L.; Yang, C.; Schloss, J.; Wu, J. Polyhydroxylated C60, fullerenols, as glutamate receptor antagonists and neuroprotective agents. J. Neurosci. Res. 2000, 62, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.T.; Wang, H.; Guo, L.; Gao, Y.; Liu, Y.; Cao, A. Interaction of fullerenol with lysozyme investigated by experimental and computational approaches. Nanotechnology 2008, 19, 395101. [Google Scholar] [CrossRef]
- Tokuyama, H.; Yamago, S.; Nakamura, E.; Shiraki, T.; Sugiura, Y. Photoinduced biochemical activity of fullerene carboxylic acid. J. Am. Chem. Soc. 1993, 115, 7918–7919. [Google Scholar] [CrossRef]
- Nakamura, E.; Tokuyama, H.; Yamago, S.; Shiraki, T.; Sugiura, Y. Biological Activity of Water-Soluble Fullerenes. Structural Dependence of DNA Cleavage, Cytotoxicity, and Enzyme Inhibitory Activities Including HIV-Protease Inhibition. Bull. Chem. Soc. Jpn. 1996, 69, 2143–2151. [Google Scholar] [CrossRef]
- Wolff, D.J.; Mialkowski, K.; Richardson, C.F.; Wilson, S.R. C60-Fullerene monomalonate adducts selectively inactivate neuronal nitric oxide synthase by uncoupling the formation of reactive oxygen intermediates from nitric oxide production. Biochemistry 2001, 40, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Park, K.H.; Chhowalla, M.; Iqbal, Z.; Sesti, F. Single-walled Carbon Nanotubes Are a New Class of Ion Channel Blockers. J. Biol. Chem. 2003, 278, 50212–50216. [Google Scholar] [CrossRef]
- Belgorodsky, B.; Fadeev, L.; Ittah, V.; Benyamini, H.; Zelner, S.; Huppert, D.; Kotlyar, A.B.; Gozin, M. Formation and Characterization of Stable Human Serum Albumin-Tris-malonic Acid [C60]Fullerene Complex. Bioconj. Chem. 2005, 16, 1058–1062. [Google Scholar] [CrossRef] [PubMed]
- Belgorodsky, B.; Fadeev, L.; Kolsenik, J.; Gozin, M. Formation of a Soluble Stable Complex between Pristine C60-Fullerene and a Native Blood Protein. ChemBioChem 2006, 7, 1783–1789. [Google Scholar] [CrossRef]
- Pastorin, G.; Marchesan, S.; Hoebeke, J.; Da Ros, T.; Ehret-Sabatier, L.; Briand, J.P.; Prato, M.; Bianco, A. Design and activity of cationic fullerene derivatives as inhibitors of acetylcholinesterase. Org. Biomol. Chem. 2006, 4, 2556–2562. [Google Scholar] [CrossRef] [PubMed]
- Calvaresi, M.; Zerbetto, F. Baiting Proteins with C60. ACS Nano 2010, 4, 2283–2299. [Google Scholar] [CrossRef]
- Ahmed, L.; Rasulev, B.; Kar, S.; Krupa, P.; Mozolewska, M.A.; Leszczynski, J. Inhibitors or toxins? Large library target-specific screening of fullerene-based nanoparticles for drug design purpose. Nanoscale 2017, 9, 10263–10276. [Google Scholar] [CrossRef]
- Sayes, C.M.; Fortner, J.D.; Guo, W.; Lyon, D.A.; Boyd, A.M.; Ausman, K.D.; Colvin, V.L. The Differential Cytotoxicity of Water-Soluble Fullerenes. Nano Lett. 2004, 4, 1881–1887. [Google Scholar] [CrossRef]
- Sayes, C.M.; Marchione, A.A.; Reed, K.L.; Warheit, D.B. Comparative Pulmonary Toxicity Assessments of C60Water Suspensions in Rats: Few Differences in Fullerene Toxicity in Vivo in Contrast to in Vitro Profiles. Nano Lett. 2007, 7, 2399–2406. [Google Scholar] [CrossRef] [PubMed]
- Caldeira, D.A.; Mesquita, F.M.; Pinheiro, F.G.; Oliveira, D.F.; Oliveira, L.F.; Nascimento, J.H.; Takiya, C.M.; Maciel, L.; Zin, W.A. Acute exposure to C60 fullerene damages pulmonary mitochondrial function and mechanics. Nanotoxicology 2021, 15, 352–365. [Google Scholar] [CrossRef] [PubMed]
- Ghavanloo, E.; Rafii-Tabar, H.; Kausar, A.; Giannopoulos, G.I.; Fazelzadeh, S.A. Experimental and computational physics of fullerenes and their nanocomposites: Synthesis, thermo-mechanical characteristics and nanomedicine applications. Phys. Rep. 2023, 996, 1–116. [Google Scholar] [CrossRef]
- Nasraoui, S.; Ben Brahim, N.; Bel Haj Mohamed, N.; Ben Chaabane, R.; Allouche, A. Theoretical and experimental investigation on ligands-CdS clusters interactions: Influence of solvent. J. Mol. Struct. 2018, 1173, 894–902. [Google Scholar] [CrossRef]
- Lin, P.C.; Lin, S.; Wang, P.C.; Sridhar, R. Techniques for physicochemical characterization of nanomaterials. Biotech. Adv. 2014, 32, 711–726. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Castillo, M.; Lugo-Preciado, G.; Laurencin, D.; Tielens, F.; van der Lee, A.; Clément, S.; Guari, Y.; López-de Luzuriaga, J.M.; Monge, M.; Remacle, F.; et al. Experimental and Theoretical Study of the Reactivity of Gold Nanoparticles Towards Benzimidazole-2-ylidene Ligands. Chem. Eur. J. 2016, 22, 10446–10458. [Google Scholar] [CrossRef] [PubMed]
- Nisoh, N.; Jarerattanachat, V.; Karttunen, M.; Wong-ekkabut, J. Fullerenes’ Interactions with Plasma Membranes: Insight from the MD Simulations. Biomolecules 2022, 12, 639. [Google Scholar] [CrossRef] [PubMed]
- Tavanti, F.; Pedone, A.; Menziani, M.C. Multiscale Molecular Dynamics Simulation of Multiple Protein Adsorption on Gold Nanoparticles. Int. J. Mol. Sci. 2019, 20, 3539. [Google Scholar] [CrossRef] [PubMed]
- Wallace, E.J.; Sansom, M.S.P. Carbon nanotube self-assembly with lipids and detergent: A molecular dynamics study. Nanotechnology 2008, 20, 045101. [Google Scholar] [CrossRef] [PubMed]
- D’Rozario, R.S.G.; Wee, C.L.; Wallace, E.J.; Sansom, M.S.P. The interaction of C60 and its derivatives with a lipid bilayer via molecular dynamics simulations. Nanotechnology 2009, 20, 115102. [Google Scholar] [CrossRef] [PubMed]
- Lai, K.; Wang, B.; Zhang, Y.; Zheng, Y. Computer simulation study of nanoparticle interaction with a lipid membrane under mechanical stress. Phys. Chem. Chem. Phys. 2013, 15, 270–278. [Google Scholar] [CrossRef]
- Lin, J.Q.; Zheng, Y.G.; Zhang, H.W.; Chen, Z. A Simulation Study on Nanoscale Holes Generated by Gold Nanoparticles on Negative Lipid Bilayers. Langmuir 2011, 27, 8323–8332. [Google Scholar] [CrossRef]
- Alessandri, R.; Thallmair, S.; Herrero, C.G.; Mera-Adasme, R.; Marrink, S.J.; Souza, P.C.T. A Practical Introduction to Martini 3 and its Application to Protein-Ligand Binding Simulations. In A Practical Guide to Recent Advances in Multiscale Modeling and Simulation of Biomolecules; AIP Publishing LLC: Melville, NY, USA, 2023. [Google Scholar] [CrossRef]
- Borges-Araújo, L.; Patmanidis, I.; Singh, A.P.; Santos, L.H.S.; Sieradzan, A.K.; Vanni, S.; Czaplewski, C.; Pantano, S.; Shinoda, W.; Monticelli, L.; et al. Pragmatic Coarse-Graining of Proteins: Models and Applications. J. Chem. Theory Comput. 2023, 19, 7112–7135. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Monticelli, L.; Melo, M.N.; Alessandri, R.; Tieleman, D.P.; Souza, P.C.T. Two decades of Martini: Better beads, broader scope. WIREs Comput. Mol. Sci. 2023, 13, e1620. [Google Scholar] [CrossRef]
- Periole, X.; Cavalli, M.; Marrink, S.J.; Ceruso, M.A. Combining an elastic network with a coarse-grained molecular force field: Structure, dynamics, and intermolecular recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543. [Google Scholar] [CrossRef] [PubMed]
- Poma, A.B.; Cieplak, M.; Theodorakis, P.E. Combining the MARTINI and structure-based coarse-grained approaches for the molecular dynamics studies of conformational transitions in proteins. J. Chem. Theory Comput. 2017, 13, 1366–1374. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Baranowski, M.; Czaplewski, C.; Gołaś, E.; He, Y.; Jagieła, D.; Krupa, P.; Maciejczyk, M.; Makowski, M.; Mozolewska, M.A.; et al. A unified coarse-grained model of biological macromolecules based on mean-field multipole-multipole interactions. J. Mol. Model. 2014, 20, 2306. [Google Scholar] [CrossRef]
- Sieradzan, A.K.; Czaplewski, C.; Krupa, P.; Mozolewska, M.A.; Karczyńska, A.S.; Lipska, A.G.; Lubecka, E.A.; Gołąś, E.; Wirecki, T.; Makowski, M.; et al. Modeling the Structure, Dynamics, and Transformations of Proteins with the UNRES Force Field. In Protein Folding: Methods and Protocols; Muñoz, V., Ed.; Springer: New York, NY, USA, 2022; pp. 399–416. [Google Scholar] [CrossRef]
- Chinchio, M.; Czaplewski, C.; Liwo, A.; Ołdziej, S.; Scheraga, H.A. Dynamic Formation and Breaking of Disulfide Bonds in Molecular Dynamics Simulations with the UNRES Force Field. J. Chem. Theory Comput. 2007, 3, 1236–1248. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Czaplewski, C.; Pillardy, J.; Scheraga, H.A. Cumulant-based expressions for the multibody terms for the correlation between local and electrostatic interactions in the united-residue force field. J. Chem. Phys. 2001, 115, 2323–2347. [Google Scholar] [CrossRef]
- Krupa, P.; Hałabis, A.; Żmudzińska, W.; Ołdziej, S.; Scheraga, H.A.; Liwo, A. Maximum Likelihood Calibration of the UNRES Force Field for Simulation of Protein Structure and Dynamics. J. Chem. Inf. Model. 2017, 57, 2364–2377. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Khalili, M.; Czaplewski, C.; Kalinowski, S.; Ołdziej, S.; Wachucik, K.; Scheraga, H.A. Modification and Optimization of the United-Residue (UNRES) Potential Energy Function for Canonical Simulations. I. Temperature Dependence of the Effective Energy Function and Tests of the Optimization Method with Single Training Proteins. J. Phys. Chem. B 2007, 111, 260–285. [Google Scholar] [CrossRef]
- He, Y.; Mozolewska, M.A.; Krupa, P.; Sieradzan, A.K.; Wirecki, T.K.; Liwo, A.; Kachlishvili, K.; Rackovsky, S.; Jagieła, D.; Scheraga, H.A.; et al. Lessons from application of the UNRES force field to predictions of structures of CASP10 targets. Proc. Nat. Acad. Sci. USA 2013, 110, 14936–14941. [Google Scholar] [CrossRef]
- Krupa, P.; Mozolewska, M.A.; Wiśniewska, M.; Yin, Y.; He, Y.; Sieradzan, A.K.; Ganzynkowicz, R.; Lipska, A.G.; Karczyńska, A.; Ślusarz, M.; et al. Performance of protein-structure predictions with the physics-based UNRES force field in CASP11. Bioinformatics 2016, 32, 3270–3278. [Google Scholar] [CrossRef]
- Lubecka, E.A.; Karczyńska, A.S.; Lipska, A.G.; Sieradzan, A.K.; Zieba, K.; Sikorska, C.; Uciechowska, U.; Samsonov, S.A.; Krupa, P.; Mozolewska, M.A.; et al. Evaluation of the scale-consistent UNRES force field in template-free prediction of protein structures in the CASP13 experiment. J. Mol. Graph. Modell. 2019, 92, 154–166. [Google Scholar] [CrossRef]
- Karczyńska, A.S.; Zieba, K.; Uciechowska, U.; Mozolewska, M.A.; Krupa, P.; Lubecka, E.A.; Lipska, A.G.; Sikorska, C.; Samsonov, S.A.; Sieradzan, A.K.; et al. Improved Consensus-Fragment Selection in Template-Assisted Prediction of Protein Structures with the UNRES Force Field in CASP13. J. Chem. Inf. Model. 2020, 60, 1844–1864. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Maisuradze, G.G.; Suñol, D.; Liwo, A.; Scheraga, H.A. Folding kinetics of WW domains with the united residue force field for bridging microscopic motions and experimental measurements. Proc. Nat. Acad. Sci. USA 2014, 111, 18243–18248. [Google Scholar] [CrossRef] [PubMed]
- Maisuradze, G.G.; Senet, P.; Czaplewski, C.; Liwo, A.; Scheraga, H.A. Investigation of Protein Folding by Coarse-Grained Molecular Dynamics with the UNRES Force Field. J. Phys. Chem. A 2010, 114, 4471–4485. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.L.; Krupa, P.; Hai, N.M.; Linh, H.Q.; Li, M.S. Structure and Physicochemical Properties of the Aβ42 Tetramer: Multiscale Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 7253–7269. [Google Scholar] [CrossRef] [PubMed]
- Lipska, A.G.; Sieradzan, A.K.; Czaplewski, C.; Lipińska, A.D.; Ocetkiewicz, K.M.; Proficz, J.; Czarnul, P.; Krawczyk, H.; Liwo, A. Long-time scale simulations of virus-like particles from three human-norovirus strains. J. Comput. Chem. 2023, 44, 1470–1483. [Google Scholar] [CrossRef] [PubMed]
- Sieradzan, A.K.; Mozolewska, M.A. Extension of coarse-grained UNRES force field to treat carbon nanotubes. J. Mol. Model. 2018, 24, 121. [Google Scholar] [CrossRef] [PubMed]
- Zaborowski, B.; Jagieła, D.; Czaplewski, C.; Hałabis, A.; Lewandowska, A.; Żmudzińska, W.; Liwo, A. A Maximum-Likelihood Approach to Force-Field Calibration. J. Chem. Inf. Model. 2015, 55, 2050–2070. [Google Scholar] [CrossRef]
- Makowski, M.; Liwo, A.; Scheraga, H.A. Simple physics-based analytical formulas for the potentials of mean force of the interaction of amino acid side chains in water. VII. Charged–hydrophobic/polar and polar–hydrophobic/polar side chains. J. Phys. Chem. B 2017, 121, 379–390. [Google Scholar] [CrossRef]
- Kihara, T. The second virial coefficient of non-spherical molecules. J. Phys. Soc. Jpn. 1951, 6, 289–296. [Google Scholar] [CrossRef]
- Giełdoń, A.; Witt, M.M.; Gajewicz, A.; Puzyn, T. Rapid insight into C60 influence on biological functions of proteins. Struct. Chem. 2017, 28, 1775–1788. [Google Scholar] [CrossRef]
- Krupa, P.; Sieradzan, A.K.; Mozolewska, M.A.; Li, H.; Liwo, A.; Scheraga, H.A. Dynamics of Disulfide-Bond Disruption and Formation in the Thermal Unfolding of Ribonuclease A. J. Chem. Theory Comput. 2017, 13, 5721–5730. [Google Scholar] [CrossRef] [PubMed]
- Gay, D.M. Algorithm 611: Subroutines for Unconstrained Minimization Using a Model/Trust-Region Approach. ACM Trans. Math. Softw. 1983, 9, 503–524. [Google Scholar] [CrossRef]
- Antoniak, A.; Biskupek, I.; Bojarski, K.K.; Czaplewski, C.; Giełdoń, A.; Kogut, M.; Kogut, M.M.; Krupa, P.; Lipska, A.G.; Liwo, A.; et al. Modeling protein structures with the coarse-grained UNRES force field in the CASP14 experiment. J. Mol. Graph. Modell. 2021, 108, 108008. [Google Scholar] [CrossRef]
- Case, D.; Aktulga, H.; Belfon, K.; Ben-Shalom, I.; Berryman, J.; Brozell, S.; Cerutti, D.; Cheatham, T.I.; Cisneros, G.; Cruzeiro, V.; et al. Amber 2023; University of California, San Francisco: San Francisco, CA, USA, 2023. [Google Scholar]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Izadi, S.; Anandakrishnan, R.; Onufriev, A.V. Building Water Models: A Different Approach. J. Phys. Chem. Lett. 2014, 5, 3863–3871. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef]
- Nguyen, H.; Roe, D.R.; Simmerling, C. Improved Generalized Born Solvent Model Parameters for Protein Simulations. J. Chem. Theory Comput. 2013, 9, 2020–2034. [Google Scholar] [CrossRef]
- Rotkiewicz, P.; Skolnick, J. Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem. 2008, 29, 1460–1465. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E.I. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Duyne, G.D.V.; Standaert, R.F.; Karplus, P.A.; Schreiber, S.L.; Clardy, J. Atomic Structure of FKBP-FK506, an Immunophilin-Immunosuppressant Complex. Science 1991, 252, 839–842. [Google Scholar] [CrossRef]
- Badaya, A.; Sasidhar, Y.U. Inhibition of the activity of HIV-1 protease through antibody binding and mutations probed by molecular dynamics simulations. Sci. Rep. 2020, 10, 5501. [Google Scholar] [CrossRef]
- Miller, M.; Schneider, J.; Sathyanarayana, B.K.; Toth, M.V.; Marshall, G.R.; Clawson, L.; Selk, L.; Kent, S.B.; Wlodawer, A. Structure of complex of synthetic HIV-1 protease with a substrate-based inhibitor at 2.3 A resolution. Science 1989, 246, 1149–1152. [Google Scholar] [CrossRef]
- Likić, V.A.; Prendergast, F.G. Structure and dynamics of the fatty acid binding cavity in apo rat intestinal fatty acid binding protein. Protein Sci. 1999, 8, 1649–1657. [Google Scholar] [CrossRef]
- Härd, T.; Barnes, H.J.; Larsson, C.; Gustafsson, J.Å.; Lund, J. Solution structure of a mammalian PCB-binding protein in complex with a PCB. Nat. Struct. Mol. Biol. 1995, 2, 983–989. [Google Scholar] [CrossRef]
- Lipska, A.G.; Sieradzan, A.K.; Krupa, P.; Mozolewska, M.A.; D’Auria, S.; Liwo, A. Studies of conformational changes of an arginine-binding protein from Thermotoga maritima in the presence and absence of ligand via molecular dynamics simulations with the coarse-grained UNRES force field. J. Mol. Model. 2015, 21, 64. [Google Scholar] [CrossRef]
- Krupa, P.; Karczyńska, A.S.; Mozolewska, M.A.; Liwo, A.; Czaplewski, C. UNRES-Dock—Protein–protein and peptide–protein docking by coarse-grained replica-exchange MD simulations. Bioinformatics 2020, 37, 1613–1615. [Google Scholar] [CrossRef] [PubMed]
- Ocetkiewicz, K.M.; Czaplewski, C.; Krawczyk, H.; Lipska, A.G.; Liwo, A.; Proficz, J.; Sieradzan, A.K.; Czarnul, P. UNRES-GPU for physics-based coarse-grained simulations of protein systems at biological time- and size-scales. Bioinformatics 2023, 39, btad391. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jiao, Q.; Wang, J.; Cai, X.; Zhao, W.; Cui, X. Prediction of protein-ligand binding affinity with deep learning. Comput. Struct. Biotechnol. J. 2023, 21, 5796–5806. [Google Scholar] [CrossRef]
- Hoogeboom, E.; Satorras, V.G.; Vignac, C.; Welling, M. Equivariant Diffusion for Molecule Generation in 3D. arXiv 2022, arXiv:2203.17003. [Google Scholar]
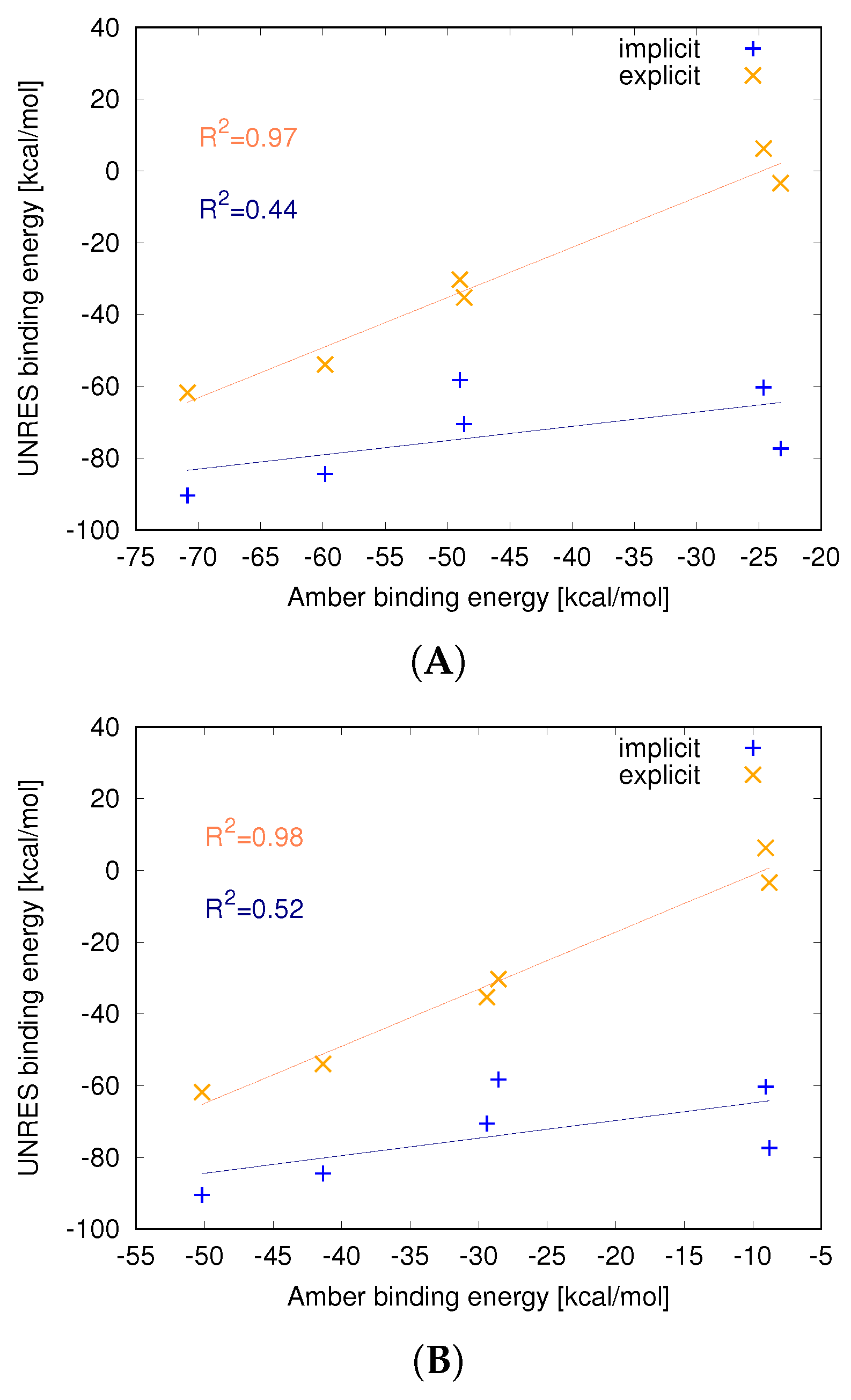





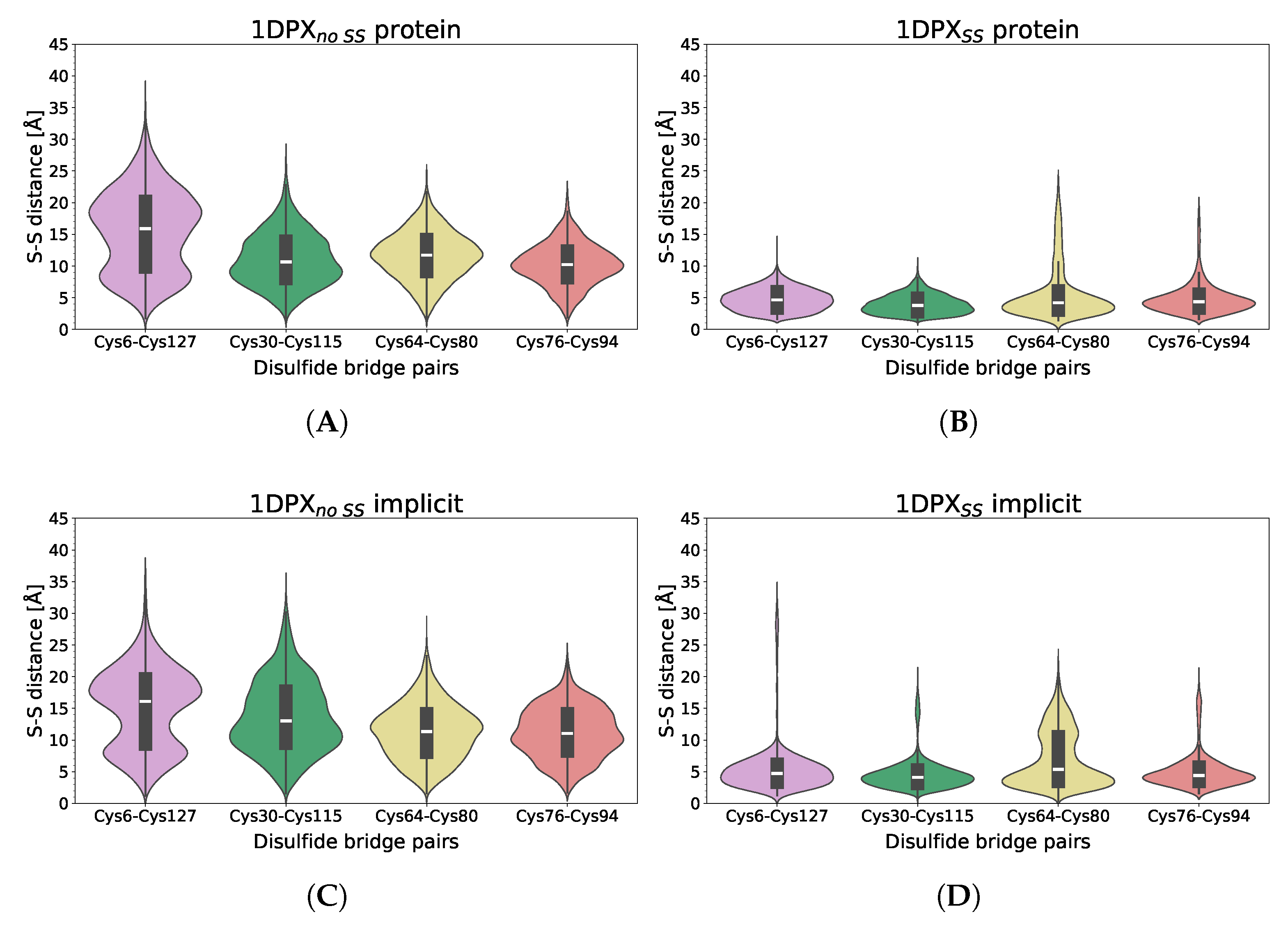
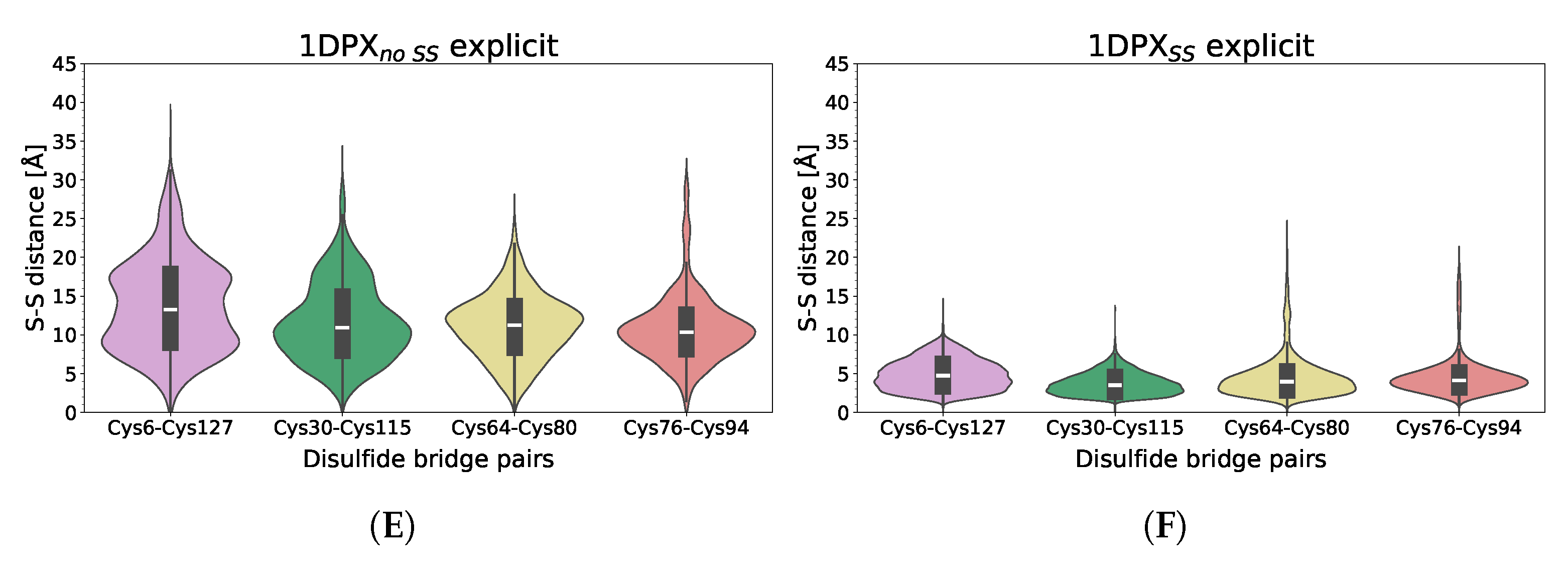
| Protein | Energy [kcal/mol] | |||
|---|---|---|---|---|
| UNRES | Amber | |||
| Implicit C60 | Explicit C60 | |||
| 1FKF | −58.29 ± 3.67 | −30.33 ± 4.82 | −49.02 ± 3.95 | −28.55± 5.40 |
| 1HOS | −70.58 ± 3.67 | −35.28 ± 6.23 | −48.66 ± 2.99 | −29.40± 6.16 |
| 1ICN | −84.48 ± 3.62 | −53.96 ± 4.75 | −59.83 ± 2.78 | −41.36 ± 3.50 |
| 1UTR | −90.48 ± 4.15 | −61.81 ± 6.22 | −70.87 ± 3.81 | −50.18 ±.6.27 |
| 1DPXno SS | −73.00 ± 10.45 | −3.46 ± 5.56 * | −24.63 ± 2.15 | −8.79 ± 3.67 |
| 1DPXSS | −60.32 ± 7.85 | 6.24 ± 5.59 * | −23.26 ± 3.29 | −9.06 ± 2.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogoża, N.H.; Krupa, M.A.; Krupa, P.; Sieradzan, A.K. Integrating Explicit and Implicit Fullerene Models into UNRES Force Field for Protein Interaction Studies. Molecules 2024, 29, 1919. https://doi.org/10.3390/molecules29091919
Rogoża NH, Krupa MA, Krupa P, Sieradzan AK. Integrating Explicit and Implicit Fullerene Models into UNRES Force Field for Protein Interaction Studies. Molecules. 2024; 29(9):1919. https://doi.org/10.3390/molecules29091919
Chicago/Turabian StyleRogoża, Natalia H., Magdalena A. Krupa, Pawel Krupa, and Adam K. Sieradzan. 2024. "Integrating Explicit and Implicit Fullerene Models into UNRES Force Field for Protein Interaction Studies" Molecules 29, no. 9: 1919. https://doi.org/10.3390/molecules29091919
APA StyleRogoża, N. H., Krupa, M. A., Krupa, P., & Sieradzan, A. K. (2024). Integrating Explicit and Implicit Fullerene Models into UNRES Force Field for Protein Interaction Studies. Molecules, 29(9), 1919. https://doi.org/10.3390/molecules29091919








