Synergistic Charge Transfer Effect in Ferrous Heme–CO Bonding within Cytochrome P450
Abstract
1. Introduction
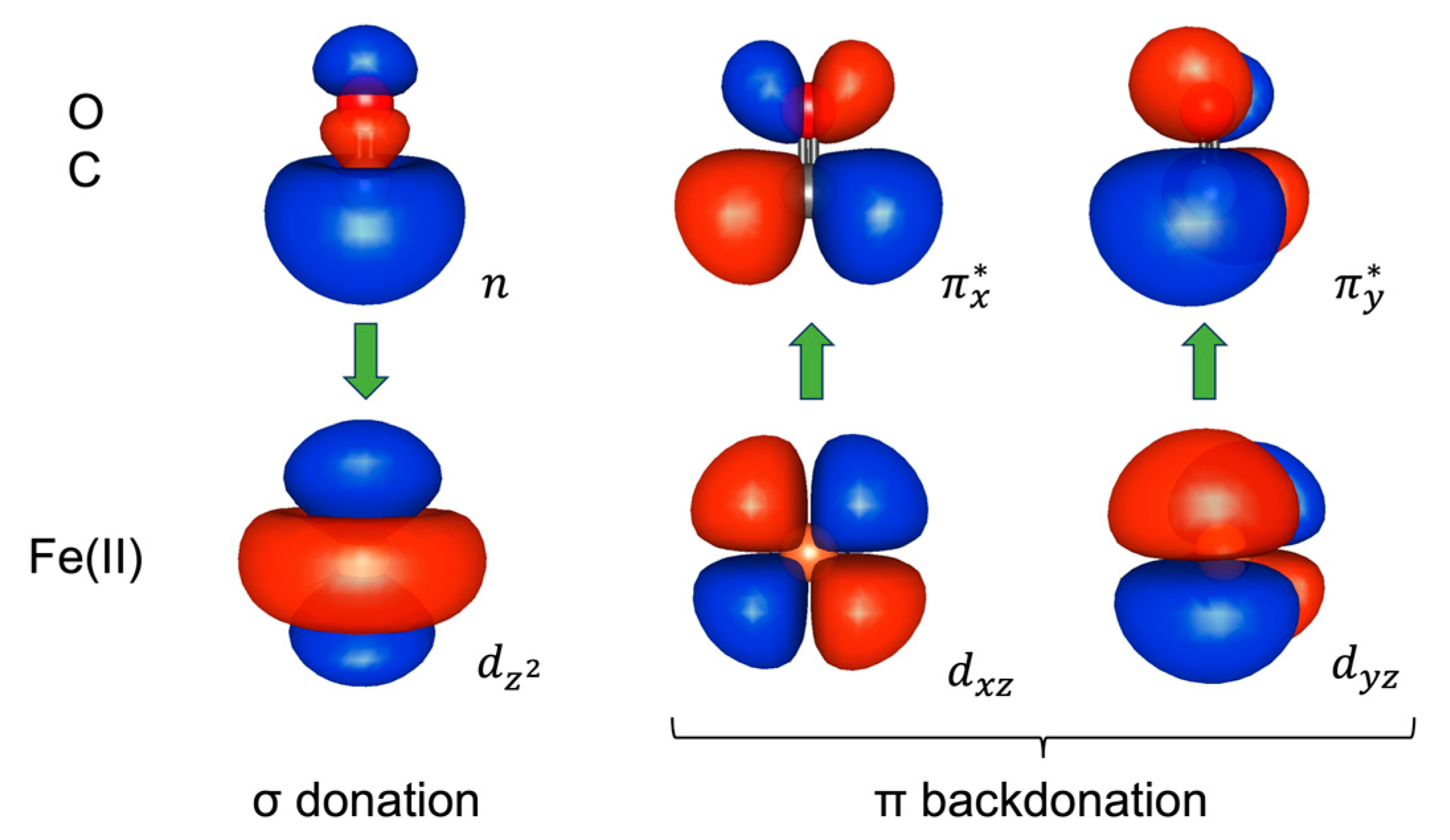
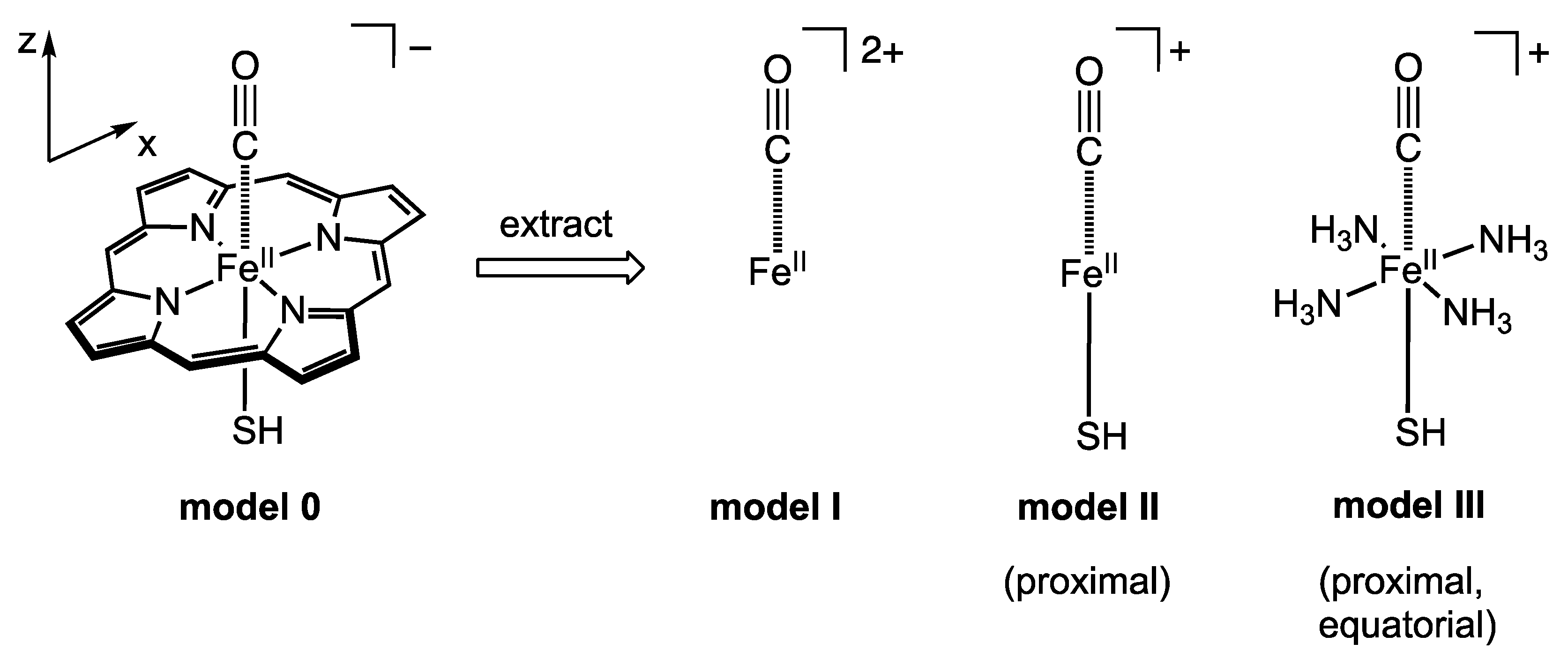
2. Results and Discussion
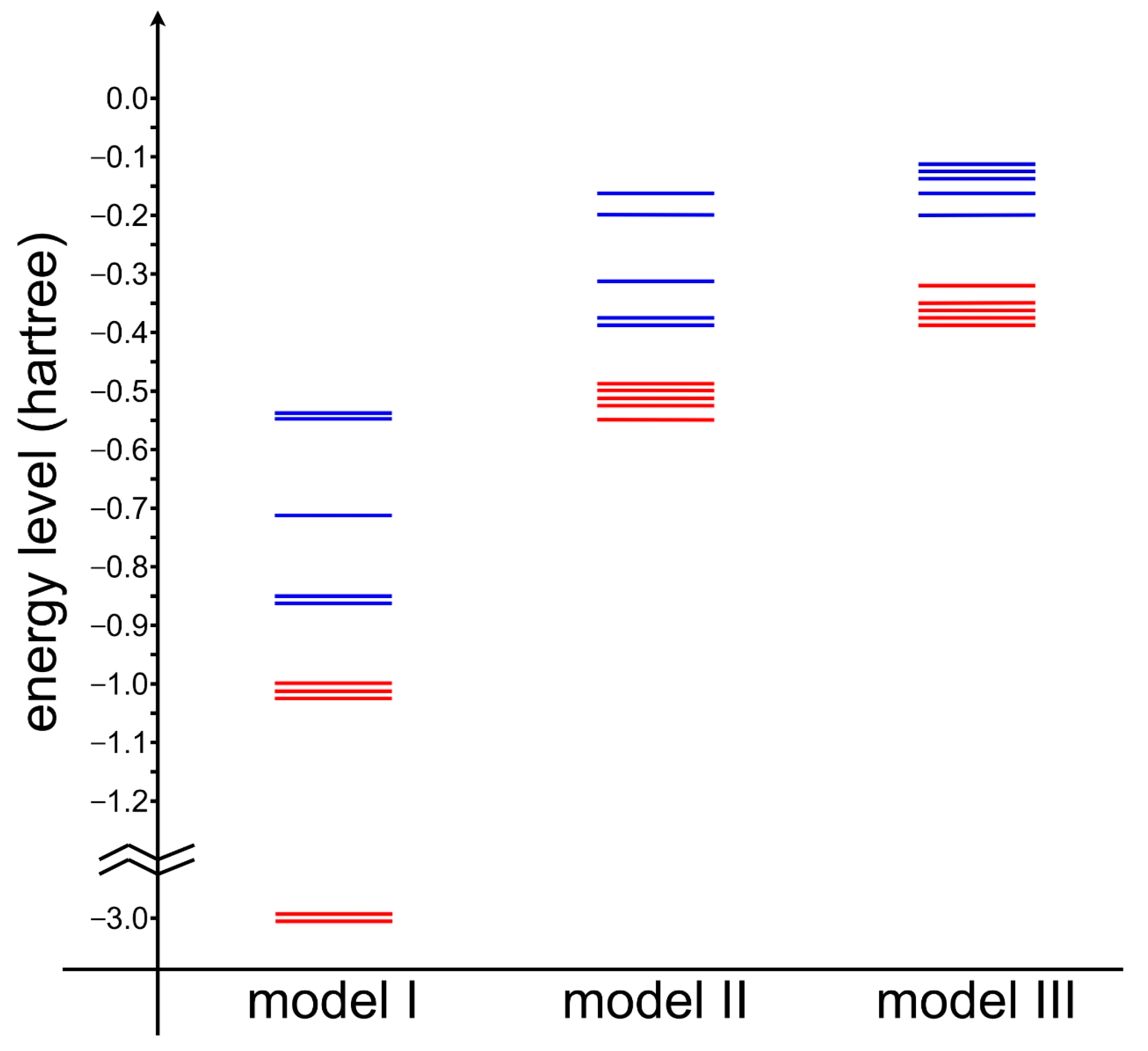
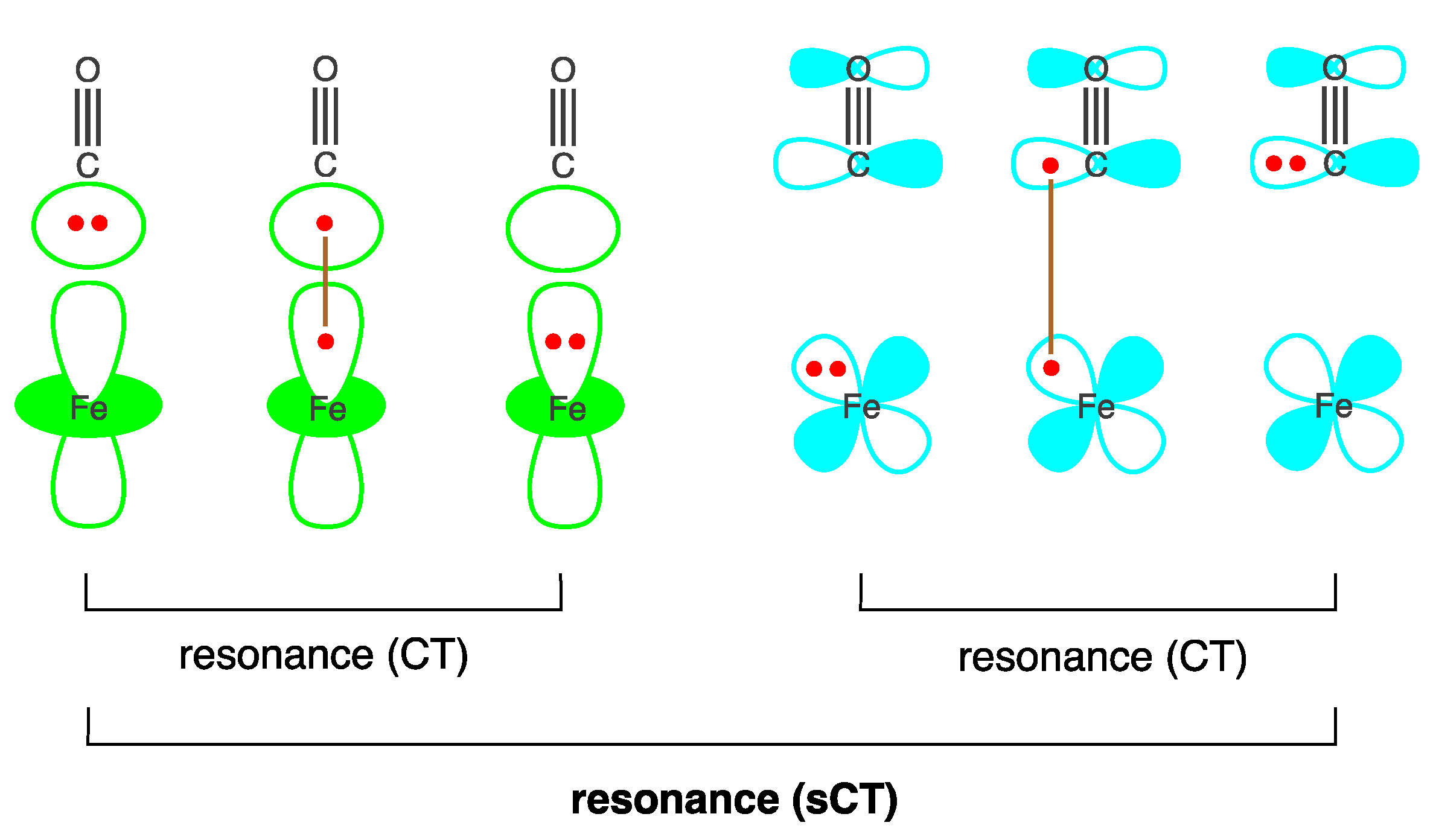
2.1. Wave Function Analysis: Relative Significance of Different VB Structures
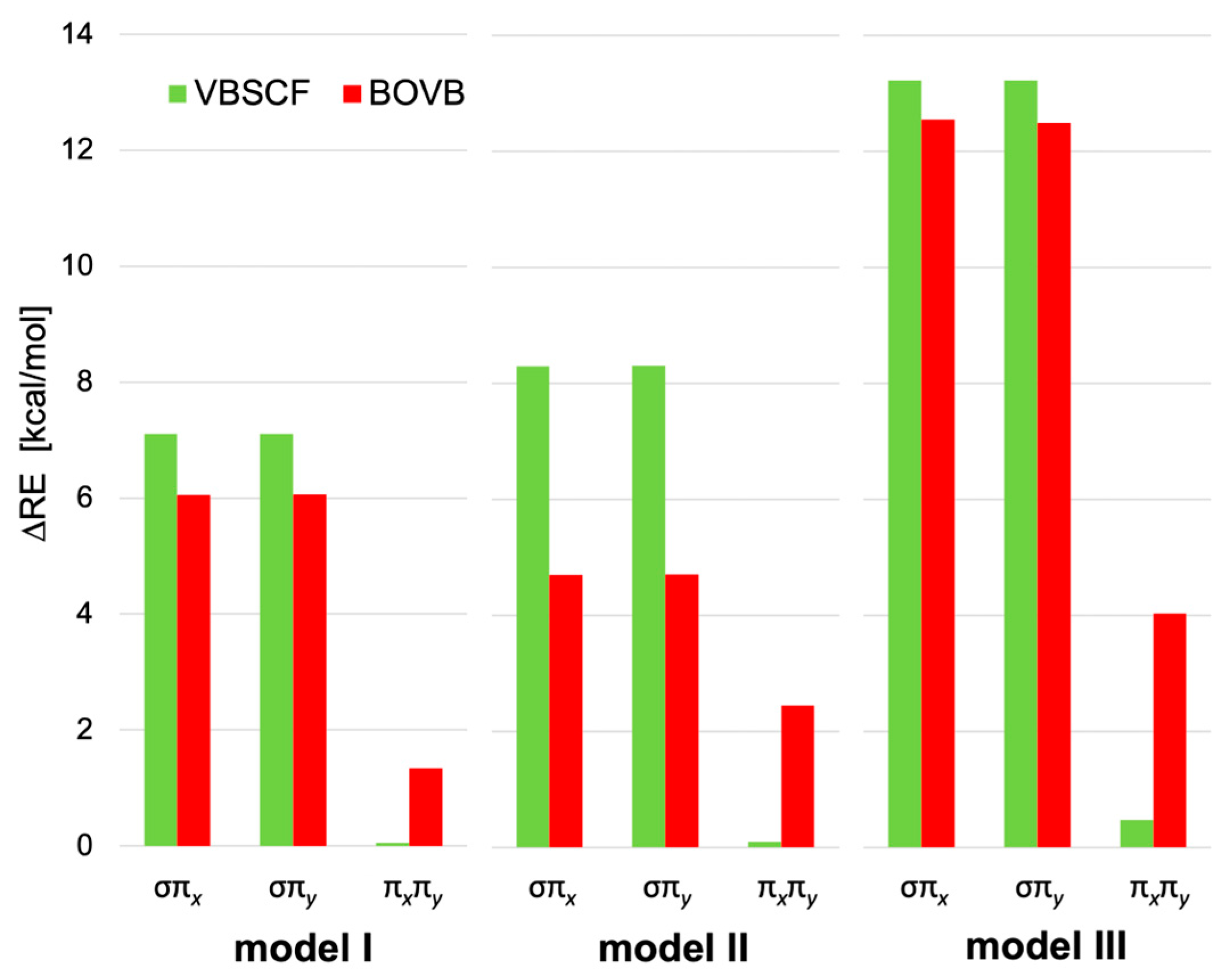
2.2. Energy Analysis: Resonance between VB Structures
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ortiz de Montellano, P.R. Cytochrome P450: Structure, Mechanism, and Biochemistry, 4th ed.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Klingenberg, M. Pigments of Rat Liver Microsomes. Arch. Biochem. Biophys. 1958, 75, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Omura, T.; Sato, R. A New Cytochrome in Liver Microsomes. J. Biol. Chem. 1962, 237, PC1375–PC1376. [Google Scholar] [CrossRef]
- Kitagawa, T.; Kyogoku, Y.; Iizuka, T.; Saito, M.I. Nature of the Iron-Ligand Bond in Ferrous Low Spin Hemoproteins Studied by Resonance Raman Scattering. J. Am. Chem. Soc. 1976, 98, 5169–5173. [Google Scholar] [CrossRef] [PubMed]
- Spiro, T.G.; Soldatova, A.V.; Balakrishnan, G. CO, NO and O2 as Vibrational Probes of Heme Protein Interactions. Coord. Chem. Rev. 2013, 257, 511–527. [Google Scholar] [CrossRef]
- Guengerich, F.P.; Martin, M.V.; Sohl, C.D.; Cheng, Q. Measurement of Cytochrome P450 and NADPH–Cytochrome P450 Reductase. Nat. Protoc. 2009, 4, 1245–1251. [Google Scholar] [CrossRef] [PubMed]
- Bloom, J.D.; Labthavikul, S.T.; Otey, C.R.; Arnold, F.H. Protein Stability Promotes Evolvability. Proc. Natl. Acad. Sci. USA 2006, 103, 5869–5874. [Google Scholar] [CrossRef]
- Kawahara, B.; Faull, K.F.; Janzen, C.; Mascharak, P.K. Carbon Monoxide Inhibits Cytochrome P450 Enzymes CYP3A4/2C8 in Human Breast Cancer Cells, Increasing Sensitivity to Paclitaxel. J. Med. Chem. 2021, 64, 8437–8446. [Google Scholar] [CrossRef]
- Liu, S.; Hirao, H. Energy Decomposition Analysis of the Nature of Coordination Bonding at the Heme Iron Center in Cytochrome P450 Inhibition. Chem.-Asian J. 2022, 17, e202200360. [Google Scholar] [CrossRef]
- Liu, S.; Xia, S.; Yue, D.; Sun, H.; Hirao, H. The Bonding Nature of Fe–CO Complexes in Heme Proteins. Inorg. Chem. 2022, 61, 17494–17504. [Google Scholar] [CrossRef]
- Hirao, H.; Zhang, E. Bidirectional Charge Transfer at the Heme Iron in Reversible and Quasi-Irreversible Cytochrome P450 Inhibition. Inorg. Chem. 2023, 62, 16599–16608. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Bell, A.T.; Head-Gordon, M. Analysis of Charge Transfer Effects in Molecular Complexes Based on Absolutely Localized Molecular Orbitals. J. Chem. Phys. 2008, 128, 184112. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Matta, C.F. Atomic Charges Are Measurable Quantum Expectation Values: A Rebuttal of Criticisms of QTAIM Charges. J. Phys. Chem. 2004, 108, 8385–8394. [Google Scholar] [CrossRef]
- Pauling, L. Valence Bond Theory in Coordination Chemistry. J. Chem. Educ. 1962, 39, 461–463. [Google Scholar] [CrossRef]
- Shaik, S.; Hiberty, P.C. A Chemist’s Guide to Valence Bond Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wu, W.; Su, P.; Shaik, S.; Hiberty, P.C. Classical Valence Bond Approach by Modern Methods. Chem. Rev. 2011, 111, 7557–7593. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Hiberty, P.C. On the Nature of the Chemical Bond in Valence Bond Theory. J. Chem. Phys. 2022, 157, 090901. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Song, L.; Wu, W.; Zhang, Q. Charge Transfer in the Electron Donor−Acceptor Complex BH3NH3. J. Am. Chem. Soc. 2004, 126, 3974–3982. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, A.A.; Galbraith, J.M. A Valence Bond Description of Coordinate Covalent Bonding. J. Phys. Chem. A 2004, 108, 5126–5130. [Google Scholar] [CrossRef]
- Huang, D.; Ying, F.; Chen, S.; Zhou, C.; Su, P.; Wu, W. Metal–Ligand Bonds in Rare Earth Metal–Biphenyl Complexes. Inorg. Chem. 2022, 61, 8135–8143. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Mo, Y. Partial Double Metal–Carbon Bonding Model in Transition Metal Methyl Compounds. Inorg. Chem. 2022, 61, 2892–2902. [Google Scholar] [CrossRef] [PubMed]
- Đorđević, S.; Radenković, S.; Shaik, S.; Braïda, B. On the Nature of the Bonding in Coinage Metal Halides. Molecules 2022, 27, 490. [Google Scholar] [CrossRef]
- Joy, J.; Danovich, D.; Kaupp, M.; Shaik, S. Covalent vs Charge-Shift Nature of the Metal–Metal Bond in Transition Metal Complexes: A Unified Understanding. J. Am. Chem. Soc. 2020, 142, 12277–12287. [Google Scholar] [CrossRef] [PubMed]
- Linares, M.; Braida, B.; Humbel, S. Valence Bond Approach of Metal−Ligand Bonding in the Dewar−Chatt−Duncanson Model. Inorg. Chem. 2007, 46, 11390–11396. [Google Scholar] [CrossRef]
- Shearer, J.; Vasiliauskas, D.; Lancaster, K.M. Bonding and the Role of Electrostatics in Driving C–C Bond Formation in High Valent Organocopper Compounds. Chem. Commun. 2022, 59, 98–101. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Galbraith, J.M.; Braïda, B.; Wu, W.; Hiberty, P.C. Charge-Shift Bonding: A New and Unique Form of Bonding. Angew. Chem. Int. Ed. 2020, 59, 984–1001. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Wu, W.; Hiberty, P.C. Charge-Shift Bonding and Its Manifestations in Chemistry. Nat. Chem. 2009, 1, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Chirgwin, B.H.; Coulson, C.A. The Electronic Structure of Conjugated Systems. VI. Proc. R. Soc. Lond. Ser. A 1950, 201, 196–209. [Google Scholar]
- Cotton, F.A. I—Ligand Field Theory. J. Chem. Educ. 1964, 41, 466–476. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. A Density-Functional Model of the Dispersion Interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- van Lenthe, J.H.; Balint-Kurti, G.G. The Valence-Bond SCF (VB SCF) Method. Synopsis of Theory and Test Calculation of OH Potential Energy Curve. Chem. Phys. Lett. 1980, 76, 138–142. [Google Scholar] [CrossRef]
- van Lenthe, J.H.; Balint-Kurti, G.G. The Valence-Bond Self-Consistent Field Method (VB–SCF): Theory and Test Calculations. J. Chem. Phys. 1983, 78, 5699–5713. [Google Scholar] [CrossRef]
- Song, L.; Mo, Y.; Zhang, Q.; Wu, W. XMVB: A Program for Ab Initio Nonorthogonal Valence Bond Computations. J. Comput. Chem. 2005, 26, 514–521. [Google Scholar] [CrossRef]
- Chen, Z.; Ying, F.; Chen, X.; Song, J.; Su, P.; Song, L.; Mo, Y.; Zhang, Q.; Wu, W. XMVB 2.0: A New Version of Xiamen Valence Bond Program. Int. J. Quantum Chem. 2015, 115, 731–737. [Google Scholar] [CrossRef]
- Xiamen Atomistic Computing Suite (XACS). 2023. Available online: https://xacs.xmu.edu.cn (accessed on 12 November 2023).
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Gilbert, A. IQmol 3.1.2. 2023. Available online: http://iqmol.org/ (accessed on 16 November 2023).
- Ploshnik, E.; Danovich, D.; Hiberty, P.C.; Shaik, S. The Nature of the Idealized Triple Bonds Between Principal Elements and the σ Origins of Trans-Bent Geometries—A Valence Bond Study. J. Chem. Theory Comput. 2011, 7, 955–968. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Shaik, S. Breathing-Orbital Valence Bond Method—A Modern Valence Bond Method That Includes Dynamic Correlation. Theor. Chem. Acc. 2002, 108, 255–272. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Flament, J.P.; Noizet, E. Compact and Accurate Valence Bond Functions with Different Orbitals for Different Configurations: Application to the Two-Configuration Description of F2. Chem. Phys. Lett. 1992, 189, 259–265. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Humbel, S.; Byrman, C.P.; van Lenthe, J.H. Compact Valence Bond Functions with Breathing Orbitals: Application to the Bond Dissociation Energies of F2 and FH. J. Chem. Phys. 1994, 101, 5969–5976. [Google Scholar] [CrossRef]
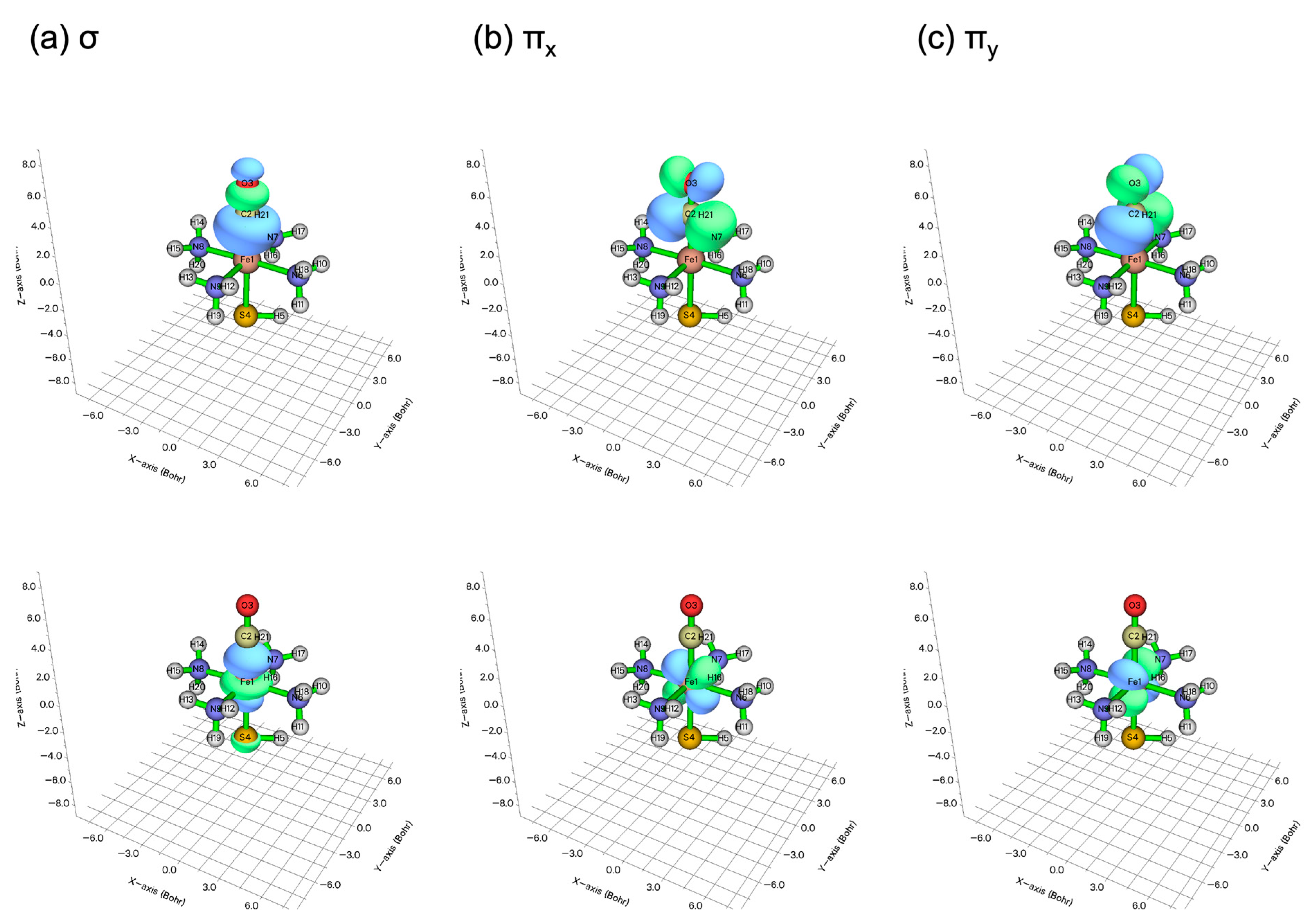
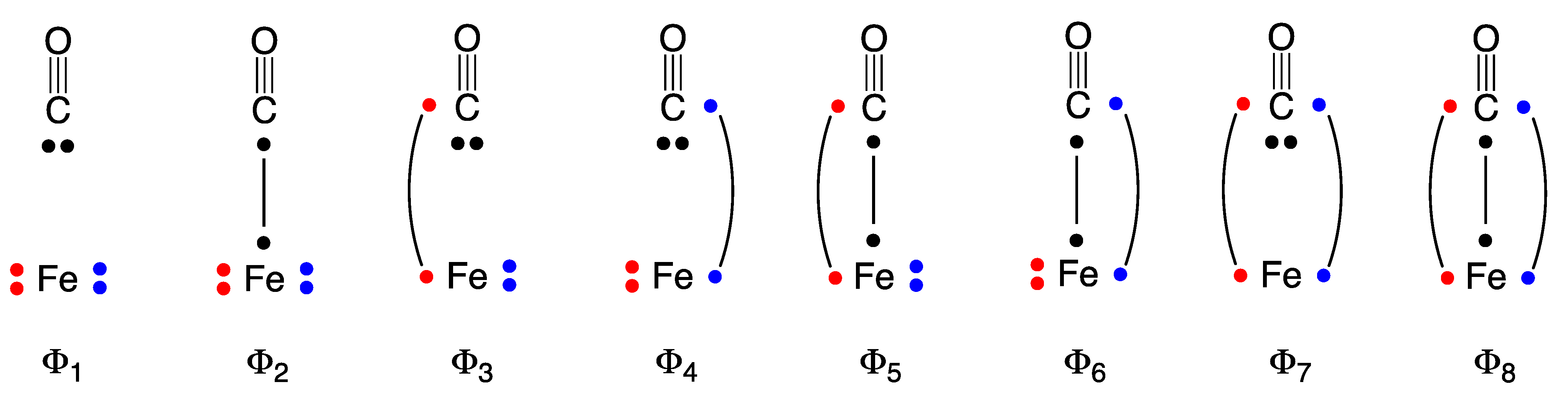
| (a) VBSCF | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 |
| I | 68.39 | 20.68 | 1.23 | 1.23 | 2.89 | 2.89 | −0.03 | 0.03 |
| II | 69.26 | 12.31 | 3.60 | 3.61 | 4.05 | 4.06 | −0.08 | 0.13 |
| III | 50.25 | 8.59 | 8.52 | 8.53 | 9.27 | 9.27 | −0.15 | 0.75 |
| (b) BOVB | ||||||||
| I | 60.22 | 25.81 | 2.40 | 2.40 | 3.81 | 3.81 | −0.03 | 0.16 |
| II | 58.12 | 18.52 | 5.83 | 5.84 | 5.03 | 5.05 | −0.08 | 0.43 |
| III | 37.22 | 14.24 | 12.74 | 12.76 | 9.50 | 9.52 | −0.20 | 1.84 |
| Model | W(σ) | W(π) |
|---|---|---|
| I | 23.6 (29.7) | 5.3 (8.7) |
| II | 16.4 (23.7) | 11.3 (16.9) |
| III | 18.1 (24.4) | 26.7 (36.0) |
| (a) | |||||||
|---|---|---|---|---|---|---|---|
| Model | σ | πx | πy | σπx | σπy | πxπy | σπxπy |
| I | 26.98 | 4.03 | 4.03 | 38.12 | 38.12 | 8.11 | 49.08 |
| II | 17.49 | 7.84 | 7.86 | 33.63 | 33.65 | 15.79 | 49.07 |
| III | 15.77 | 12.91 | 12.94 | 41.91 | 41.93 | 26.32 | 65.80 |
| (b) | |||||||
| I | 28.53 | 4.85 | 4.85 | 39.45 | 39.45 | 11.04 | 51.07 |
| II | 18.91 | 9.36 | 9.38 | 34.43 | 34.46 | 21.18 | 51.48 |
| III | 17.12 | 15.52 | 15.55 | 45.20 | 45.17 | 35.11 | 72.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Hirao, H. Synergistic Charge Transfer Effect in Ferrous Heme–CO Bonding within Cytochrome P450. Molecules 2024, 29, 873. https://doi.org/10.3390/molecules29040873
Zhang E, Hirao H. Synergistic Charge Transfer Effect in Ferrous Heme–CO Bonding within Cytochrome P450. Molecules. 2024; 29(4):873. https://doi.org/10.3390/molecules29040873
Chicago/Turabian StyleZhang, Enhua, and Hajime Hirao. 2024. "Synergistic Charge Transfer Effect in Ferrous Heme–CO Bonding within Cytochrome P450" Molecules 29, no. 4: 873. https://doi.org/10.3390/molecules29040873
APA StyleZhang, E., & Hirao, H. (2024). Synergistic Charge Transfer Effect in Ferrous Heme–CO Bonding within Cytochrome P450. Molecules, 29(4), 873. https://doi.org/10.3390/molecules29040873






