Percolation-Triggered Negative Permittivity in Nano Carbon Powder/Polyvinylidene Fluoride Composites
Abstract
1. Introduction
2. Results and Discussion
2.1. Phase Composition and Microstructure
2.2. AC Conductivity
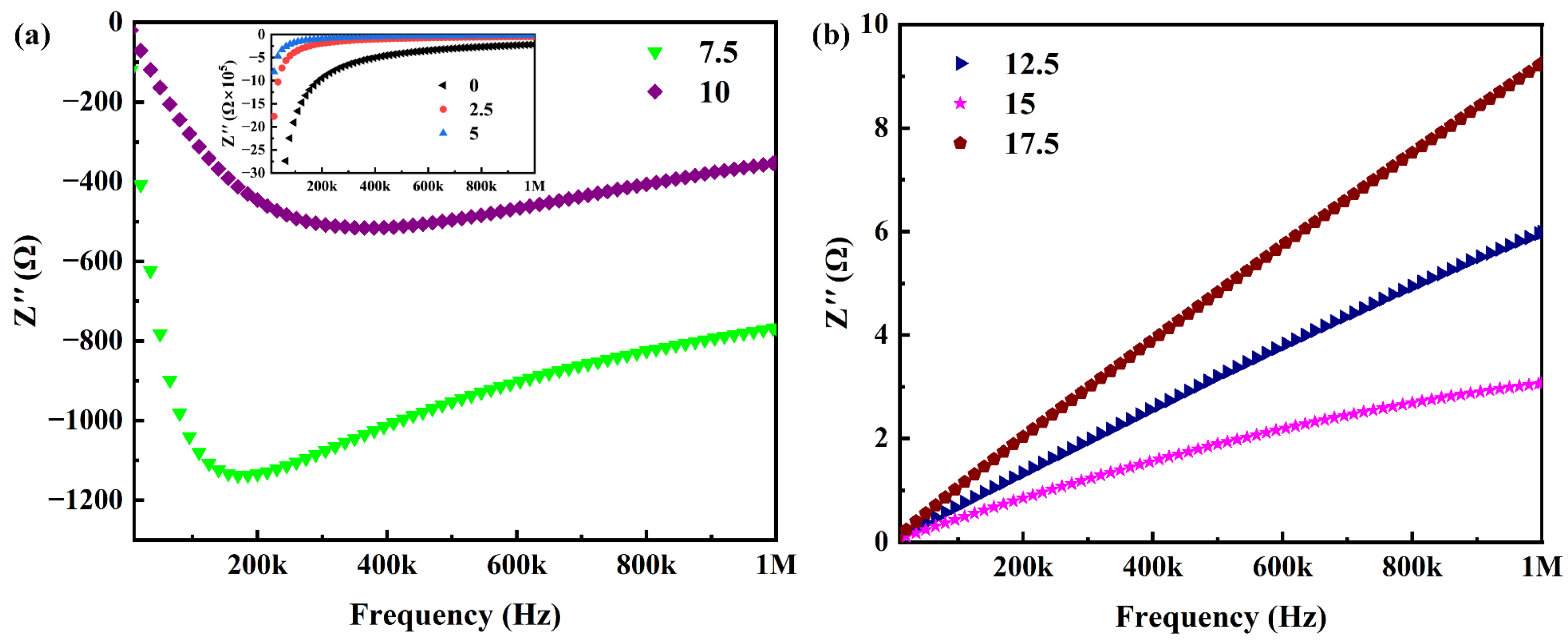
2.3. Reactance Analysis
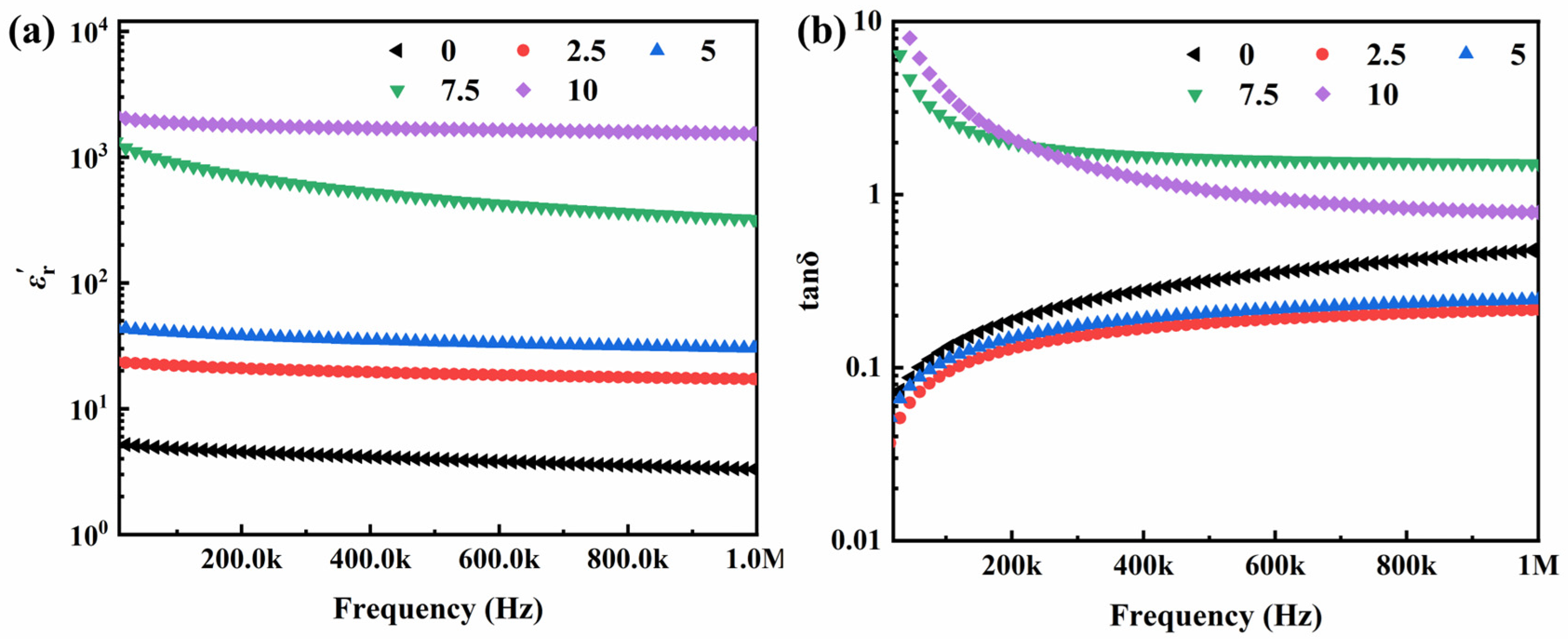
2.4. Negative-Permittivity Analysis
2.5. High Permittivity Analysis
3. Materials and Methods
3.1. Materials Preparation
3.2. Materials Characterization and Electrical Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, S.; Wang, T.; Liu, T.; Zhou, C.; Jiang, X.; Zhang, J. Active metamaterials and metadevices: A review. J. Phys. D Appl. Phys. 2020, 53, 503002. [Google Scholar] [CrossRef]
- Veselago, V.G. Electrodynamics of substances with simultaneously negative electrical and magnetic permeabilities. Sov. Phys. Usp. 1968, 10, 504–509. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef]
- Swetha, P.; Vidyadharan, D.M.; Sridharan, K.; Binesh, M.; Swaminathan, S. Investigation of negative permittivity in BaTiO3/TiN metacomposites at the radio frequency region. Mater. Chem. Phys. 2024, 317, 129156. [Google Scholar]
- Yuan, J.; Zhou, Y.; Manshaii, F.; Wang, S.; Yin, J.; Li, D.; Wang, S.; Qu, Y. Ultraweakly low-dispersion epsilon-negative response of GR-CNT/PVDF ternary metacomposites. Compos. Commun. 2024, 47, 101877. [Google Scholar] [CrossRef]
- Luo, H.; Qiu, J. Carbon nanotube/polyolefin elastomer metacomposites with adjustable radio-frequency negative permittivity and negative permeability. Adv. Electron. Mater. 2019, 5, 1900011. [Google Scholar] [CrossRef]
- Dou, R.; Shao, Y.; Li, S.; Yin, B.; Yang, M. Structuring tri-continuous structure multiphase composites with ultralow conductive percolation threshold and excellent electromagnetic shielding effectiveness using simple melt mixing. Polymer 2016, 83, 34–39. [Google Scholar] [CrossRef]
- Kasagi, T.; Yamamoto, S. Effect of particle shape on electrical conductivity and negative permittivity spectra of Cu granular composite materials. J. Mater. Sci. Mater. Electron. 2022, 33, 4974–4983. [Google Scholar] [CrossRef]
- Kono, K.; Tsutaoka, T.; Kasagi, T.; Yamamoto, S. Electromagnetic properties of Au/Fe53Ni47 hybrid granular composite materials. IEEE Trans. Magn. 2018, 55, 1–4. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, Y.; Wu, X.; Gao, Y.; Tang, B.; Yang, K.; Sun, K.; Zhao, Y.; Li, W.; Yu, J. A study of preparation and properties of epoxy resin/carbon fiber/phenolic residual carbon composites with adjustable negative permittivity behavior. Fuller. Nanotub. Carbon Nanostruct. 2022, 30, 675–682. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, Z.; Fan, G.; Xu, C.; Shi, G.; Zhang, G.; Liu, Y.; Fan, R. Low-frequency plasmonic state and negative permittivity in copper/titanium dioxide percolating composites. Ceram. Int. 2021, 47, 2208–2213. [Google Scholar] [CrossRef]
- Song, X.; Fan, G.; Liu, Y.; Fan, R. MOF-derived ZrO2/C-polyvinylidene fluoride composite towards negative permittivity regulation mechanism. J. Mater. Sci. Technol. 2024, 179, 50–56. [Google Scholar] [CrossRef]
- Qu, Y.; Lin, J.; Wu, J.; Wang, Z.; Sun, K.; Chen, M.; Dong, B.; Guo, Z.; Fan, R. Graphene–carbon black/CaCu3Ti4O12 ternary metacomposites toward a tunable and weakly ε-negative property at the radio-frequency region. J. Phys. Chem. C 2020, 124, 23361–23367. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Z.; Xie, P.; Hou, Q.; Liang, G.; Ni, Z.; Huang, Q.; Wu, H. Theoretically designed epsilon-negative materials: Ni nanoparticles encapsulated CNTs and their magnetic driven properties. Chem. Eng. J. 2024, 488, 150899. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Z.; Zheng, K.; Wu, Y.; Chen, Z.; Wang, C.; Shi, Z. Low dielectric loss in poly (vinyl alcohol)/graphene metacomposite films with negative permittivity prepared by spin coating. Polymer 2023, 281, 126092. [Google Scholar] [CrossRef]
- Leng, Z.; Wu, H.; Tang, X.; Li, Y.; Xin, Y.; Xie, P.; Li, G.; Yan, K.; Liu, C. Carbon nanotube/epoxy composites with low percolation threshold and negative dielectric constant. J. Mater. Sci. Mater. Electron. 2022, 33, 26015–26024. [Google Scholar] [CrossRef]
- Choudhary, H.K.; Kumar, R.; Pawar, S.P.; Sundararaj, U.; Sahoo, B. Enhancing absorption dominated microwave shielding in Co@C–PVDF nanocomposites through improved magnetization and graphitization of the Co@C-nanoparticles. Phys. Chem. Chem. Phys. 2019, 21, 15595–15608. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wu, H.; Wu, Y.; Xie, P.; Pashameah, R.A.; Abo-Dief, H.M.; El-Bahy, S.M.; Wei, Y.; Li, G.; Li, W. The weakly negative permittivity with low-frequency-dispersion behavior in percolative carbon nanotubes/epoxy nanocomposites at radio-frequency range. Adv. Compos. Hybrid Mater. 2022, 5, 2021–2030. [Google Scholar] [CrossRef]
- Lee, M.; Chen, C.Y.; Wang, S.; Cha, S.N.; Park, Y.J.; Kim, J.M.; Chou, L.J.; Wang, Z.L. A hybrid piezoelectric structure for wearable nanogenerators. Adv. Mater. 2012, 24, 1759–1764. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.; Lanceros-Mendez, S. Electroactive phases of poly (vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Salimi, A.; Yousefi, A. FTIR studies of β-phase crystal formation in stretched PVDF films. Polym. Test. 2003, 22, 699–704. [Google Scholar] [CrossRef]
- Indolia, A.P.; Gaur, M. Investigation of structural and thermal characteristics of PVDF/ZnO nanocomposites. J. Therm. Anal. Calorim. 2013, 113, 821–830. [Google Scholar] [CrossRef]
- Rajan, A.S.; Sampath, S.; Shukla, A.K. An in situ carbon-grafted alkaline iron electrode for iron-based accumulators. Energy Environ. Sci. 2014, 7, 1110–1116. [Google Scholar] [CrossRef]
- Choudhary, H.K.; Kumar, R.; Pawar, S.P.; Sundararaj, U.; Sahoo, B. Superiority of graphite coated metallic-nanoparticles over graphite coated insulating-nanoparticles for enhancing EMI shielding. New J. Chem. 2021, 45, 4592–4600. [Google Scholar] [CrossRef]
- Shen, J.; Liu, J.; Gao, Y.; Li, X.; Zhang, L. Elucidating and tuning the strain-induced non-linear behavior of polymer nanocomposites: A detailed molecular dynamics simulation study. Soft Matter 2014, 10, 5099–5113. [Google Scholar] [CrossRef] [PubMed]
- Maity, N.; Mandal, A.; Nandi, A.K. Interface engineering of ionic liquid integrated graphene in poly (vinylidene fluoride) matrix yielding magnificent improvement in mechanical, electrical and dielectric properties. Polymer 2015, 65, 154–167. [Google Scholar] [CrossRef]
- Kobayashi, M.; Tashiro, K.; Tadokoro, H. Molecular vibrations of three crystal forms of poly (vinylidene fluoride). Macromolecules 1975, 8, 158–171. [Google Scholar] [CrossRef]
- Guo, Y.; Ruan, K.; Yang, X.; Ma, T.; Kong, J.; Wu, N.; Zhang, J.; Gu, J.; Guo, Z. Constructing fully carbon-based fillers with a hierarchical structure to fabricate highly thermally conductive polyimide nanocomposites. J. Mater. Chem. C 2019, 7, 7035–7044. [Google Scholar] [CrossRef]
- Kumar, R.; Choudhary, H.K.; Pawar, S.P.; Bose, S.; Sahoo, B. Carbon encapsulated nanoscale iron/iron-carbide/graphite particles for EMI shielding and microwave absorption. Phys. Chem. Chem. Phys. 2017, 19, 23268–23279. [Google Scholar] [CrossRef]
- Shi, Z.; Fan, R.; Yan, K.; Sun, K.; Zhang, M.; Wang, C.; Liu, X.; Zhang, X. Preparation of iron networks hosted in porous alumina with tunable negative permittivity and permeability. Adv. Funct. Mater. 2013, 23, 4123–4132. [Google Scholar] [CrossRef]
- Dyre, J.C.; Schrøder, T.B. Universality of AC conduction in disordered solids. Rev. Mod. Phys. 2000, 72, 873. [Google Scholar] [CrossRef]
- Shi, G.; Qu, Y.; Fan, G.; Liu, Y. Tunable and weakly negative permittivity in CNTs-CBs/polystyrene metacomposites. ECS J. Solid State Sci. Technol. 2019, 8, N141. [Google Scholar] [CrossRef]
- Chen, M.; Sun, K.; Wang, X.; Wang, Y. Tunable negative permittivity of cobalt and epoxy composites at 3 kHz∼ 1 MHz frequency regions. ECS J. Solid State Sci. Technol. 2021, 10, 123007. [Google Scholar] [CrossRef]
- Qu, Y.; Peng, Q.; Zhou, Y.; Manshaii, F.; Wang, S.; Wang, K.; Xie, P.; Qi, X.; Sun, K. Fine-tunable ε′-negative response derived from low-frequency plasma oscillation in graphene/polyaniline metacomposites. Compos. Commun. 2023, 44, 101750. [Google Scholar] [CrossRef]
- Ma, R.; Cheng, C.; Liu, Y.; Wang, J.; Zhou, J.; Hu, Z.; Cui, H.; Li, J.; Fan, R. Temperature dependence of negative permittivity behavior in graphene/alumina ceramic metacomposites. J. Eur. Ceram. Soc. 2024, 44, 3012–3019. [Google Scholar] [CrossRef]
- Band, Y.; Kuzmenko, I.; Trippenbach, M. Negative refraction in isotropic achiral and chiral materials. Phys. Rev. A 2024, 109, 063514. [Google Scholar] [CrossRef]
- Tian, J.; Fan, R.; Zhang, Z.; Li, Y.; Wu, H.; Yang, P.; Xie, P.; Duan, W.; Lee, C.-S. Flexible and biocompatible poly (vinyl alcohol)/multi-walled carbon nanotubes hydrogels with epsilon-near-zero properties. J. Mater. Sci. Technol. 2022, 131, 91–99. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, P.; Wang, Z.; Liu, B.; Sun, K.; Pan, M.; Fan, R. Negative permittivity of polyimide-based percolative composites with zero/one dimensional functional fillers. Compos. Commun. 2024, 47, 101878. [Google Scholar] [CrossRef]
- Li, W.; Song, Z.; Zhong, J.; Qian, J.; Tan, Z.; Wu, X.; Chu, H.; Nie, W.; Ran, X. Multilayer-structured transparent MXene/PVDF film with excellent dielectric and energy storage performance. J. Mater. Chem. C 2019, 7, 10371–10378. [Google Scholar] [CrossRef]
- Nan, C.-W.; Shen, Y.; Ma, J. Physical properties of composites near percolation. Annu. Rev. Mater. Res. 2010, 40, 131–151. [Google Scholar] [CrossRef]
- Bie, X.; Yin, P.; Xu, W.; Shi, Z. Significantly enhanced permittivity and suppressed loss of P(VDF-HFP)-based composites by introducing PPy@BT-OH fillers. Mater. Lett. 2024, 364, 136368. [Google Scholar] [CrossRef]
- Li, H.; Jiang, M.; Dong, L.; Xie, H.; Xiong, C. Particle size dependence of the dielectric properties of polyvinyledene fluoride/silver composites. J. Macromol. Sci. Part B 2013, 52, 1073–1081. [Google Scholar] [CrossRef]





| Composites | Filler Content | Test Frequency | Negative Permittivity | Ref. |
|---|---|---|---|---|
| Carbon nanotubes/epoxy | 12 wt% | 1–1000 MHz | ~−100 | [18] |
| Graphene/poly (vinyl alcohol) | 10 wt% | 10–1000 kHz | ~−500 | [15] |
| Graphene/polyaniline | 2 wt% | 100–1000 MHz | ~−50 | [34] |
| Graphene–carbon nanotubes/ PVDF | 14 wt% | 100–1000 MHz | ~−25 | [5] |
| Acetylene black/polyimide | 24 wt% | 10–1000 kHz | ~−350 | [38] |
| Nano carbon powder/PVDF | 12.5 wt% | 10–1000 kHz | ~−4000 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Sun, X.; Liu, Y. Percolation-Triggered Negative Permittivity in Nano Carbon Powder/Polyvinylidene Fluoride Composites. Molecules 2024, 29, 3862. https://doi.org/10.3390/molecules29163862
Shi G, Sun X, Liu Y. Percolation-Triggered Negative Permittivity in Nano Carbon Powder/Polyvinylidene Fluoride Composites. Molecules. 2024; 29(16):3862. https://doi.org/10.3390/molecules29163862
Chicago/Turabian StyleShi, Guangyue, Xiaolei Sun, and Yao Liu. 2024. "Percolation-Triggered Negative Permittivity in Nano Carbon Powder/Polyvinylidene Fluoride Composites" Molecules 29, no. 16: 3862. https://doi.org/10.3390/molecules29163862
APA StyleShi, G., Sun, X., & Liu, Y. (2024). Percolation-Triggered Negative Permittivity in Nano Carbon Powder/Polyvinylidene Fluoride Composites. Molecules, 29(16), 3862. https://doi.org/10.3390/molecules29163862










