Phase Separation of Br-Doped CsPbI3: A Combined Cluster Expansion, Monte Carlo, and DFT Study
Abstract
:1. Introduction
2. Results
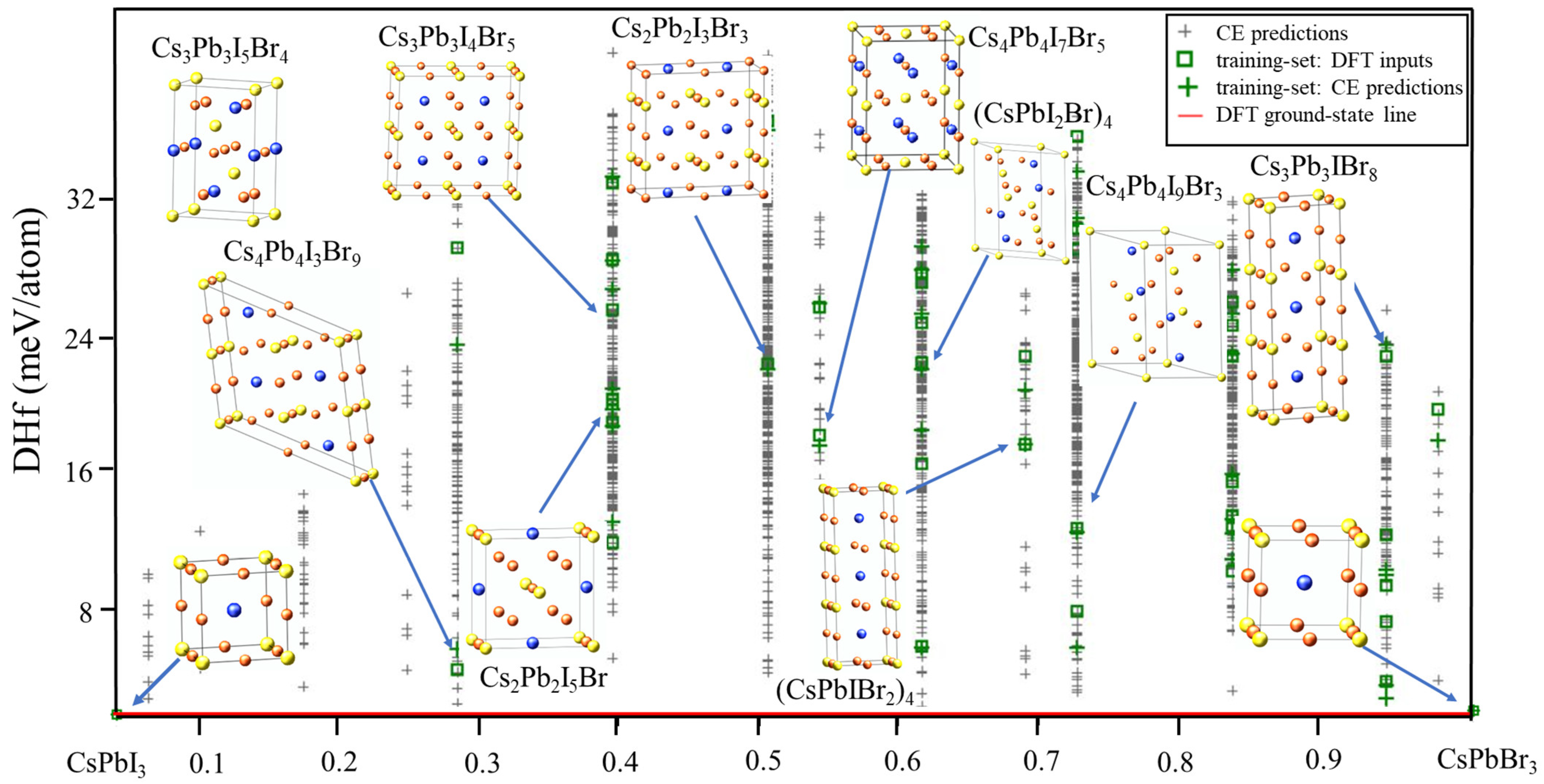
2.1. Ground State Search
2.2. Miscibility Gap
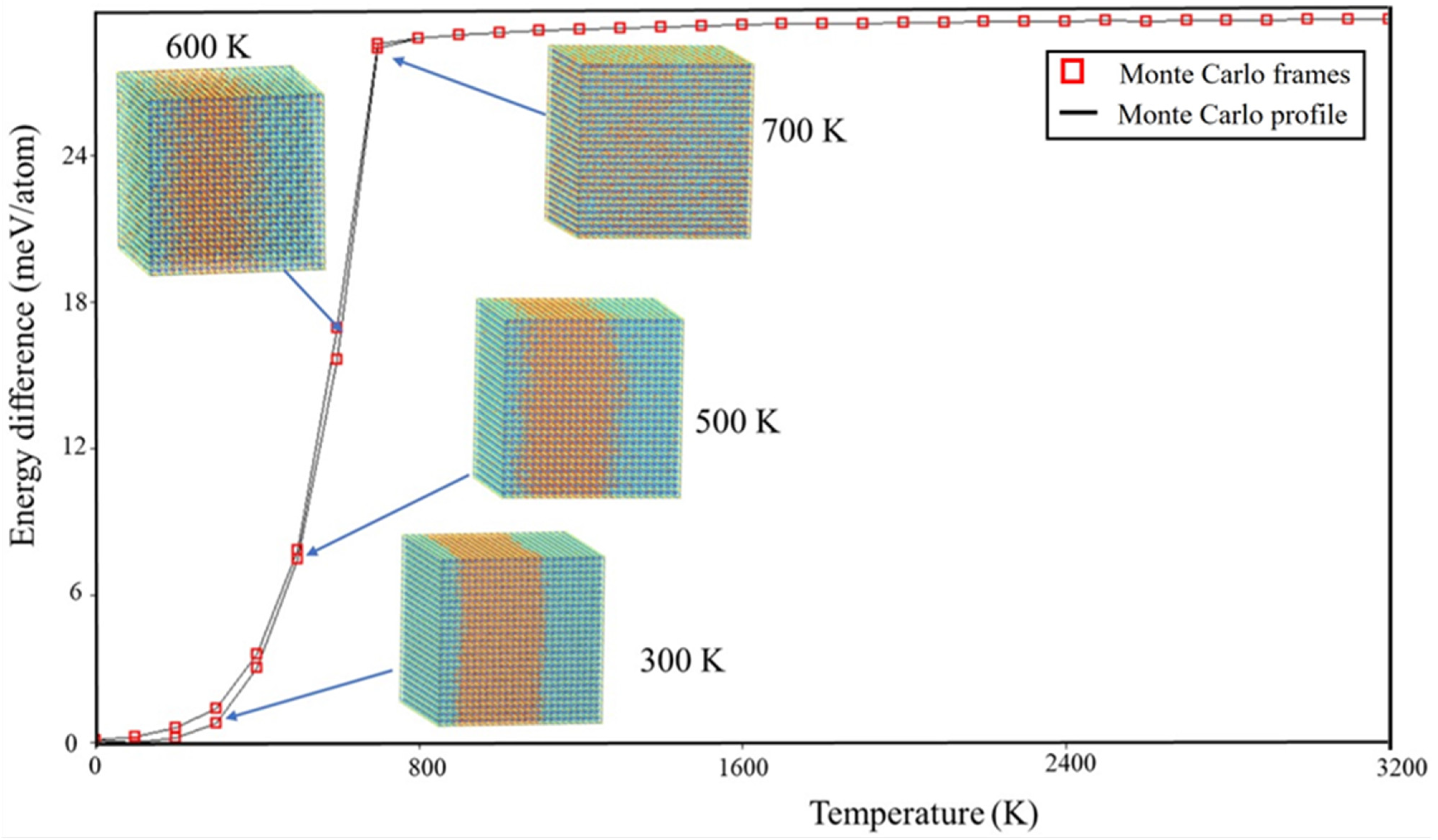
2.3. Monte Carlo
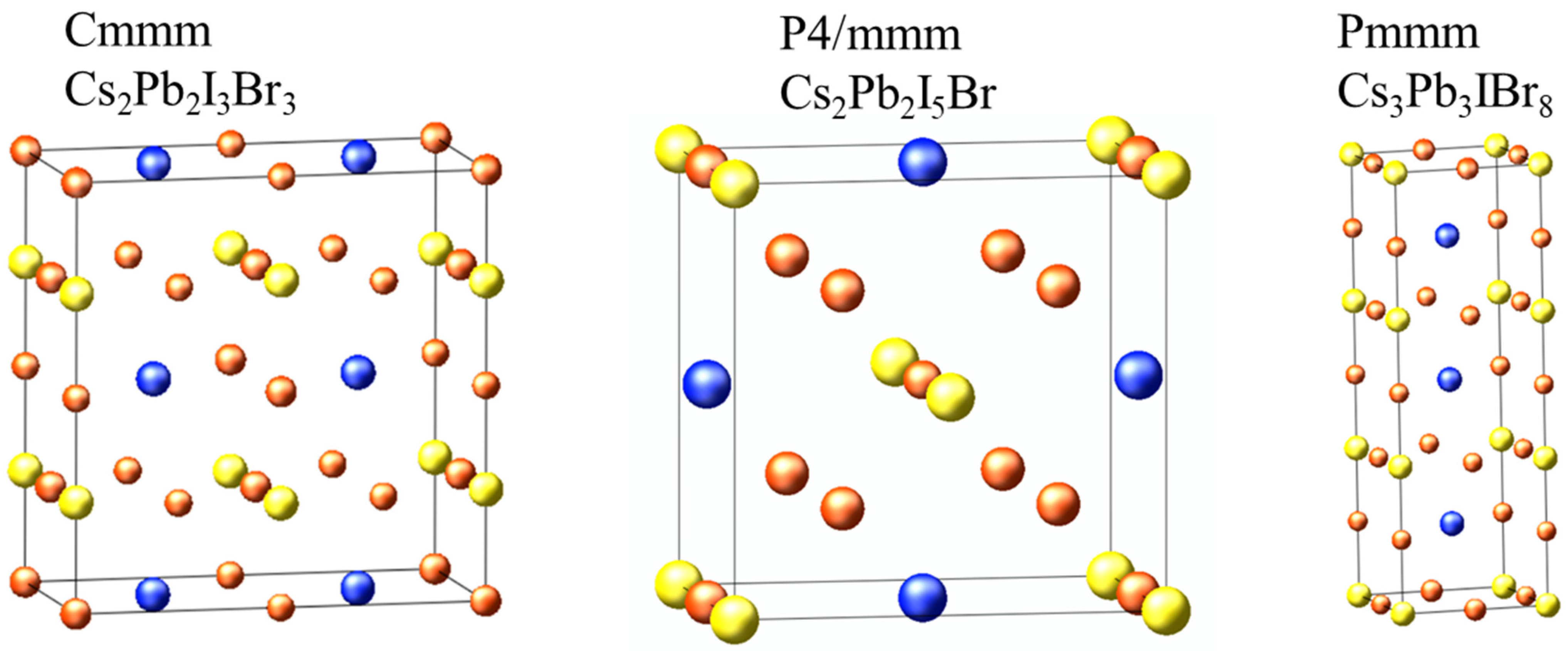
2.4. Structural Properties
2.5. Electronic Properties
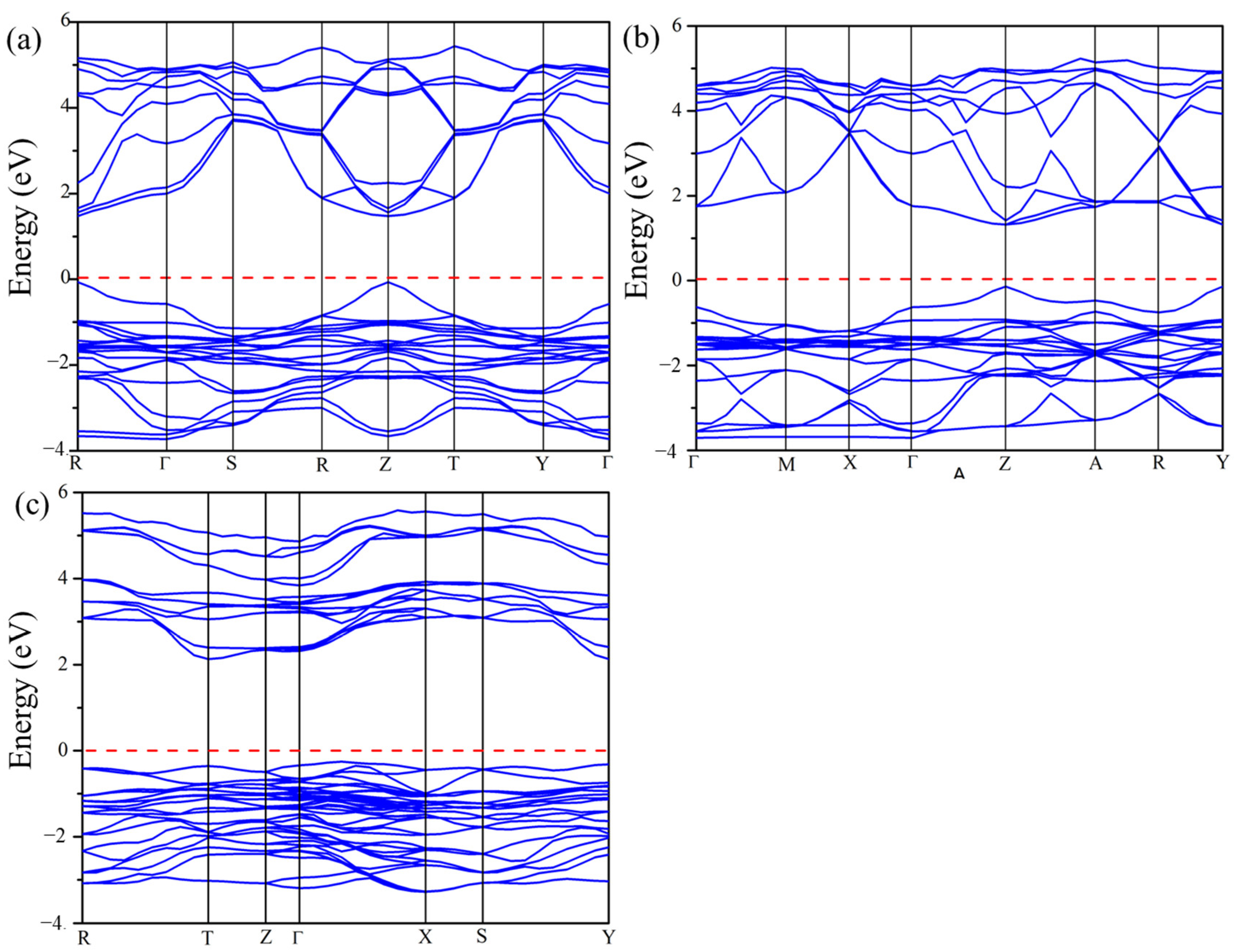
2.5.1. Band Structure
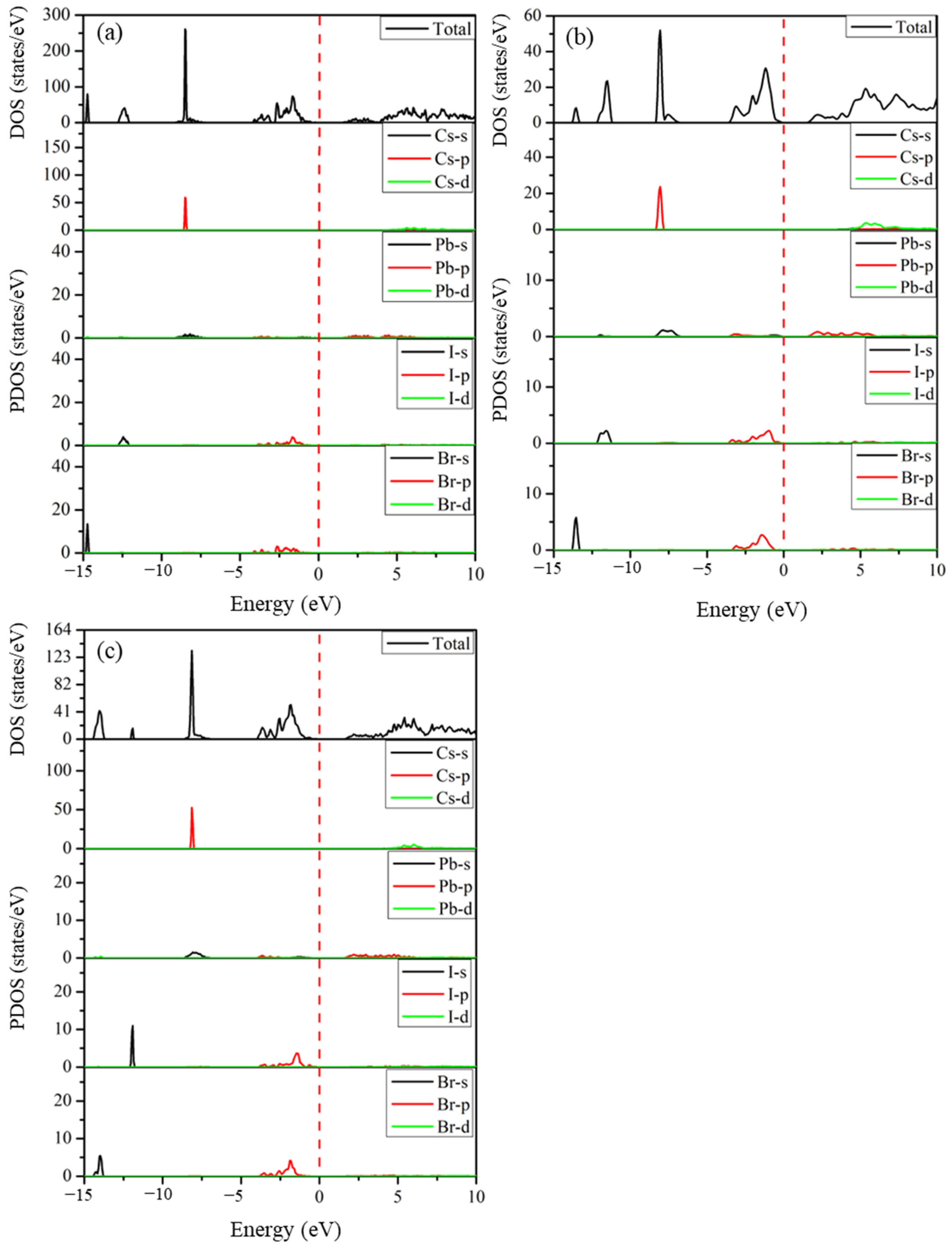
2.5.2. Density of States
2.6. Optical Properties
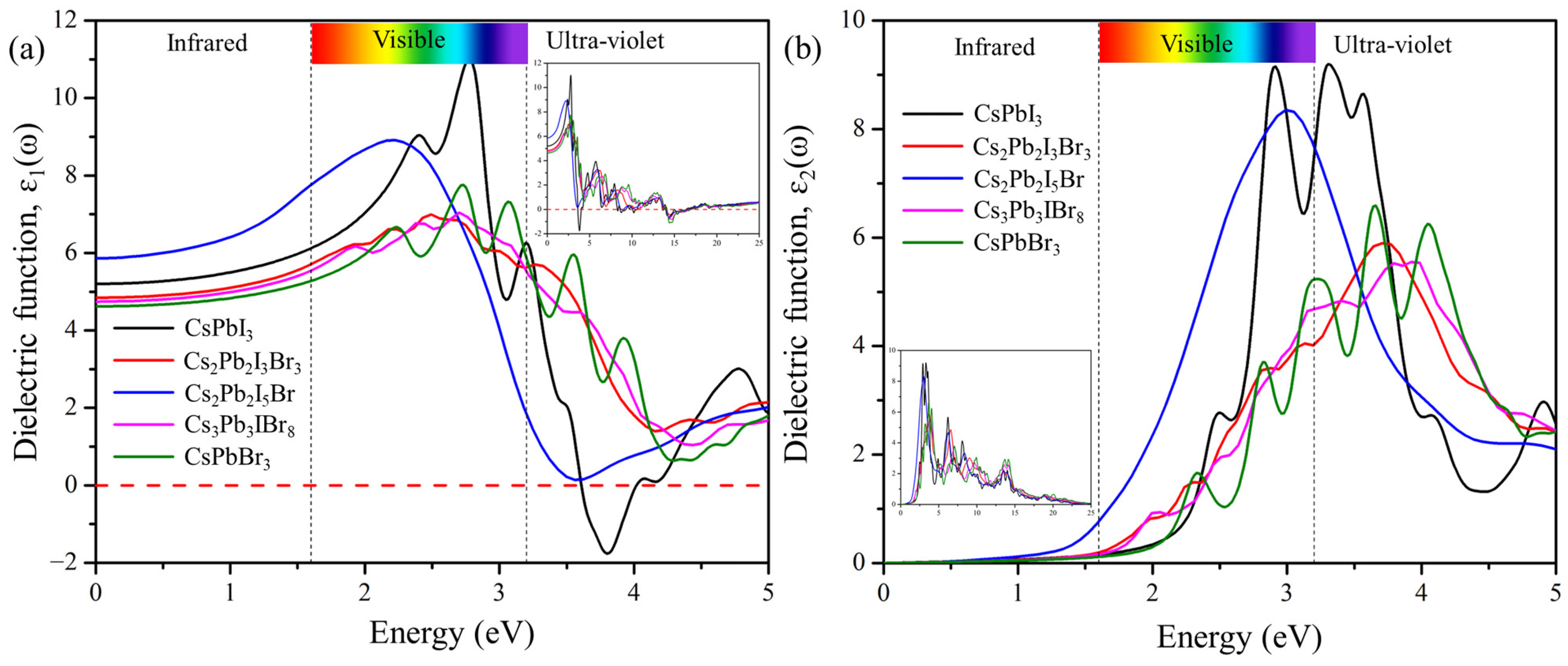
2.6.1. Dielectric Function
2.6.2. Refractive Index and Extinction Coefficient
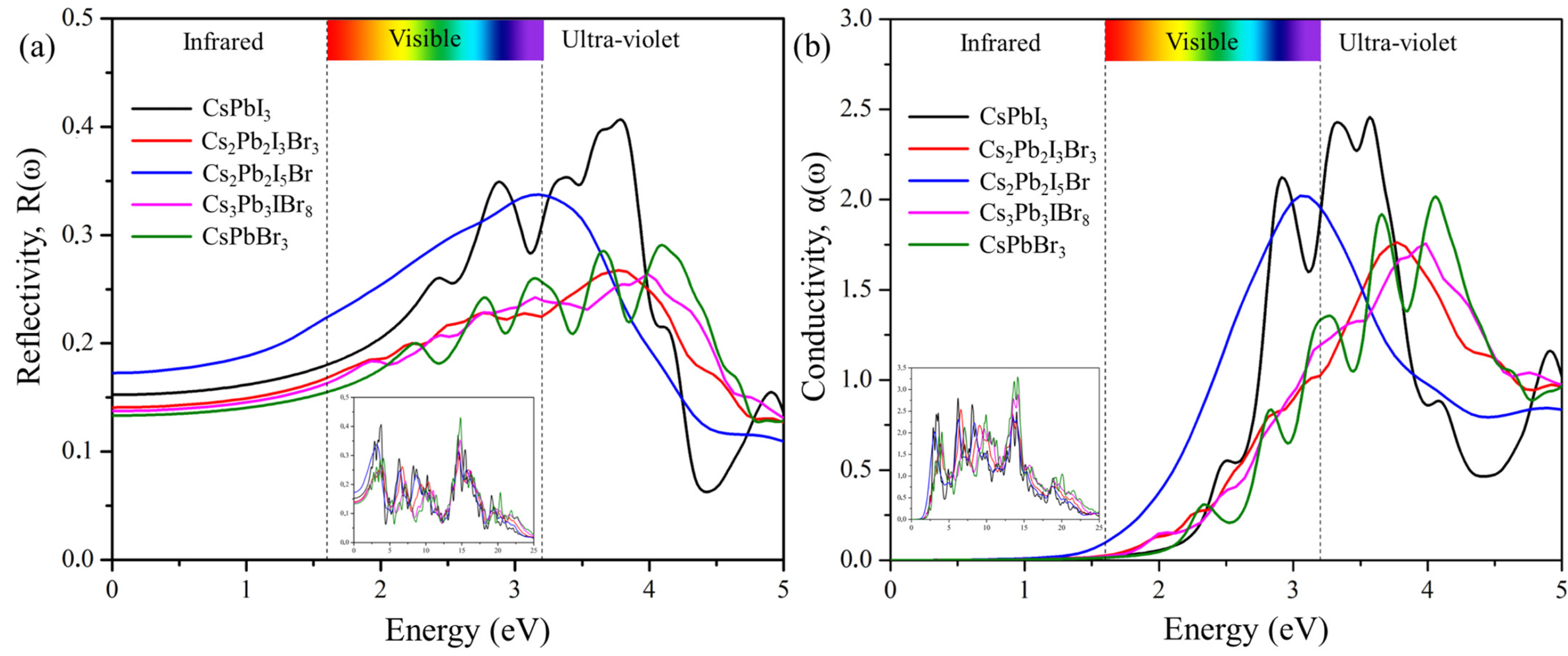
2.6.3. Reflectivity and Conductivity
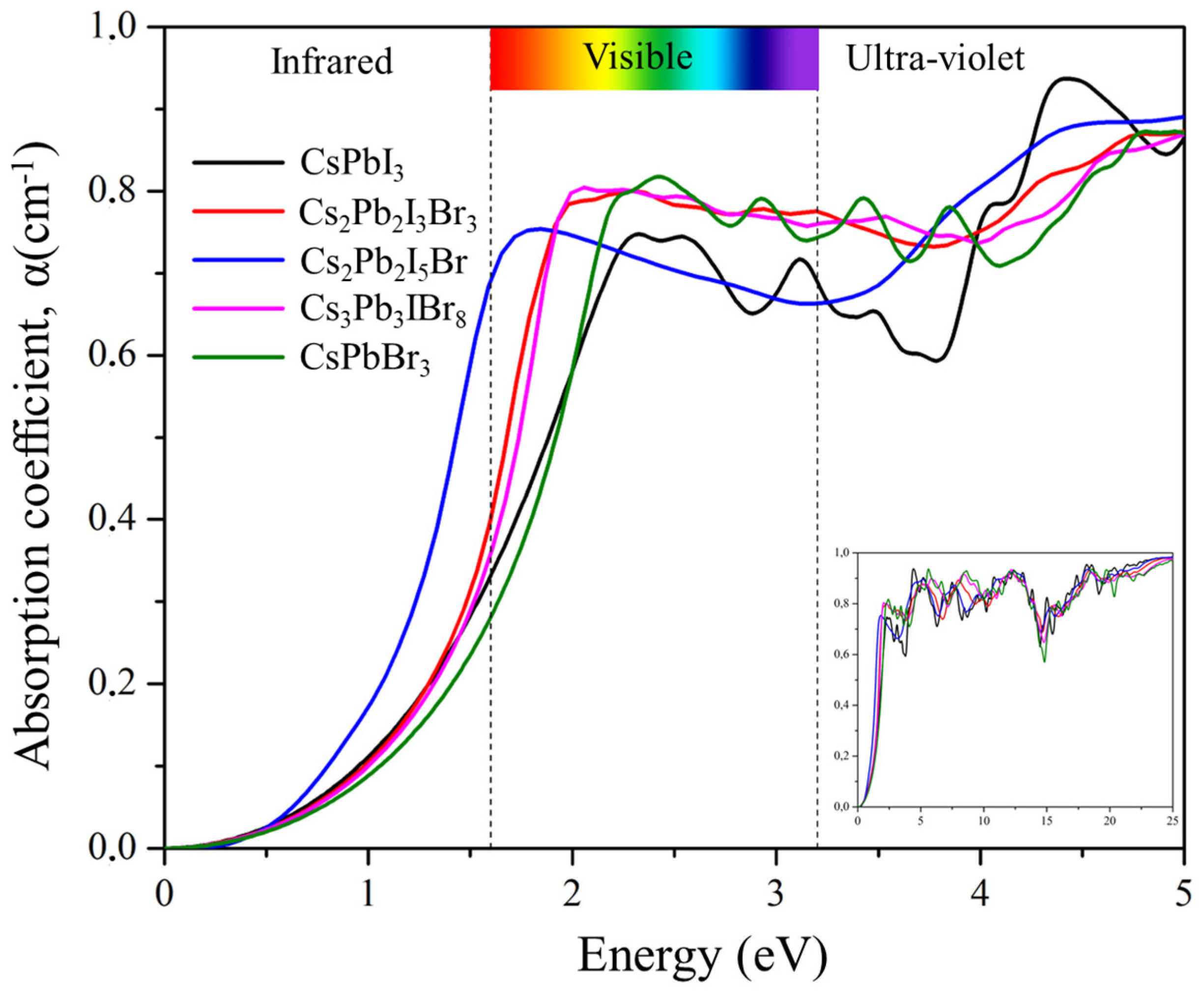
2.6.4. Absorption Coefficient
2.7. Elastic Properties
2.8. Thermodynamic Properties
3. Computational Methods
3.1. Cluster Expansion
3.2. Monte Carlo
3.3. Geometry Optimization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeong, J.; Kim, M.; Seo, J.; Lu, H.; Ahlawat, P.; Mishra, A.; Yang, Y.; Hope, M.A.; Eickemeyer, F.T.; Kim, M. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature 2021, 592, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Hoke, E.T.; Slotcavage, D.J.; Dohner, E.R.; Bowring, A.R.; Karunadasa, H.I.; McGehee, M.D. Reversible photo-induced trap formation in mixed-halide hybrid perovskites for photovoltaics. Chem. Sci. 2015, 6, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Kholil, M.I.; Bhuiyan, M.T.H.; Rahman, M.A.; Ali, M.S.; Aftabuzzaman, M. Effects of Fe doping on the visible light absorption and bandgap tuning of lead-free (CsSnCl3) and lead halide (CsPbCl3) perovskites for optoelectronic applications. AIP Adv. 2021, 11, 035229. [Google Scholar] [CrossRef]
- Kulbak, M.; Gupta, S.; Kedem, N.; Levine, I.; Bendikov, T.; Hodes, G.; Cahen, D. Cesium enhances long-term stability of lead bromide perovskite-based solar cells. J. Phys. Chem. Lett. 2016, 7, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Lang, L.; Yang, J.H.; Liu, H.R.; Xiang, H.; Gong, X. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. A 2014, 378, 290–293. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, L.; Xiang, S.; Wei, Y.; Xie, M.; Liu, H.; Li, W.; Chen, H. Growing high-quality CsPbBr3 by using porous CsPb2Br5 as an intermediate: A promising light absorber in carbon-based perovskite solar cells. Sustain. Energy Fuels 2019, 3, 184–194. [Google Scholar] [CrossRef]
- Maleka, P.M.; Dima, R.S.; Ntwaeaborwa, O.M.; Maphanga, R.R. Density functional theory study of Br doped CsPbI3 perovskite for photovoltaic and optoelectronic applications. Phys. Scr. 2023, 98, 045505. [Google Scholar] [CrossRef]
- Mao, X.; Sun, L.; Wu, T.; Chu, T.; Deng, W.; Han, K. First-principles screening of all-inorganic lead-free ABX3 perovskites. J. Phys. Chem. C 2018, 122, 7670–7675. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, S.; Chen, S.; Zhang, M.; Lau, C.F.J.; Lockrey, M.N.; Mulmudi, H.K.; Shan, Y.; Yao, J.; Zheng, J. The effect of stoichiometry on the stability of inorganic cesium lead mixed-halide perovskites solar cells. J. Phys. Chem. C 2017, 121, 19642–19649. [Google Scholar] [CrossRef]
- Eperon, G.E.; Paternò, G.M.; Sutton, R.J.; Zampetti, A.; Haghighirad, A.A.; Cacialli, F.; Snaith, H.J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A 2015, 3, 19688–19695. [Google Scholar] [CrossRef]
- Ezzeldien, M.; Al-Qaisi, S.; Alrowaili, Z.; Alzaid, M.; Maskar, E.; Es-Smairi, A.; Vu, T.V.; Rai, D. Electronic and optical properties of bulk and surface of CsPbBr3 inorganic halide perovskite a first principles DFT 1/2 approach. Sci. Rep. 2021, 11, 20622. [Google Scholar] [CrossRef] [PubMed]
- Lau, C.F.J.; Deng, X.; Ma, Q.; Zheng, J.; Yun, J.S.; Green, M.A.; Huang, S.; Ho-Baillie, A.W. CsPbIBr2 perovskite solar cell by spray-assisted deposition. ACS Energy Lett. 2016, 1, 573–577. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, S.; Wen, X.; Green, M.A.; Ho-Baillie, A.W. Hole transport layer free inorganic CsPbIBr2 perovskite solar cell by dual source thermal evaporation. Adv. Energy Mater. 2016, 6, 1502202. [Google Scholar] [CrossRef]
- Beal, R.E.; Slotcavage, D.J.; Leijtens, T.; Bowring, A.R.; Belisle, R.A.; Nguyen, W.H.; Burkhard, G.F.; Hoke, E.T.; McGehee, M.D. Cesium lead halide perovskites with improved stability for tandem solar cells. J. Phys. Chem. Lett. 2016, 7, 746–751. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Rothmann, M.U.; Liu, A.; Wang, Z.; Zhang, Y.; Pascoe, A.R.; Lu, J.; Jiang, L.; Chen, Y.; Huang, F. Phase segregation enhanced ion movement in efficient inorganic CsPbIBr2 solar cells. Adv. Energy Mater. 2017, 7, 1700946. [Google Scholar] [CrossRef]
- Brivio, F.; Caetano, C.; Walsh, A. Thermodynamic origin of photoinstability in the CH3NH3Pb(I1–xBrx)3 hybrid halide perovskite alloy. J. Phys. Chem. Lett. 2016, 7, 1083–1087. [Google Scholar] [CrossRef]
- Lin, Z.; Lei, J.; Wang, P.; Zhang, X.; Xu, L.; Chen, M.; Kang, Y.; Wei, G. Density functional study of structural, electronic and optical properties of bromine-doped CsPbI3 with the tetragonal symmetry. J. Alloy. Compd. 2022, 892, 162165. [Google Scholar] [CrossRef]
- Saliba, M.; Matsui, T.; Domanski, K.; Seo, J.Y.; Ummadisingu, A.; Zakeeruddin, S.M.; Correa-Baena, J.P.; Tress, W.R.; Abate, A.; Hagfeldt, A. Incorporation of rubidium cations into perovskite solar cells improves photovoltaic performance. Science 2016, 354, 206–209. [Google Scholar] [CrossRef]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 2012, 338, 643–647. [Google Scholar] [CrossRef]
- Sonia, Y.; Agrawalb, R.; Yadavc, V.; Singhd, P.; Singhe, S.; Ranif, U.; Vermaf, A. Electronic and optical properties of novel double perovskite compound Cs2RbInI6. J. Ovonic Res. 2023, 19, 579–585. [Google Scholar] [CrossRef]
- Seckman, B.L. Controlling Structure and Photophysical Properties of Bi Triple Perovskite through Substitutional Series Cs3Bi2Br(9−X)IX; University of Southern California: Los Angeles, CA, USA, 2018. [Google Scholar]
- Saparov, B.; Hong, F.; Sun, J.P.; Duan, H.S.; Meng, W.; Cameron, S.; Hill, I.G.; Yan, Y.; Mitzi, D.B. Thin-film preparation and characterization of Cs3Sb2I9: A lead-free layered perovskite semiconductor. Chem. Mater. 2015, 27, 5622–5632. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Hong, F.; Mao, X.; Zheng, K.; Yang, S.; Li, Y.; Pullerits, T.; Deng, W.; Han, K. Lead-free, air-stable all-inorganic cesium bismuth halide perovskite nanocrystals. Angew. Chem. Int. Ed. Engl. 2017, 56, 12471–12475. [Google Scholar] [CrossRef] [PubMed]
- Jun, T.; Sim, K.; Iimura, S.; Sasase, M.; Kamioka, H.; Kim, J.; Hosono, H. Lead-free highly efficient blue-emitting Cs3Cu2I5 with 0D electronic structure. Adv. Mater. 2018, 43, 1804547. [Google Scholar] [CrossRef] [PubMed]
- Yakunin, S.; Benin, B.M.; Shynkarenko, Y.; Nazarenko, O.; Bodnarchuk, M.I.; Dirin, D.N.; Hofer, C.; Cattaneo, S.; Kovalenko, M.V. High-resolution remote thermometry and thermography using luminescent low-dimensional tin-halide perovskites. Nat. Mater. 2019, 18, 846–852. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Guan, X.; Wang, W.; Zhao, H.; Kuai, Y.; Gao, S.; Chen, C.; Zou, W.; Lu, P. The effects of cation and halide anion on the stability, electronic and optical properties of double perovskite Cs2NaMX6 (M = In, Tl, Sb, bi; X = Cl, Br, I). Comput. Mater. Sci. 2023, 220, 112058. [Google Scholar] [CrossRef]
- Chen, W.; Liu, G.; Dong, C.; Guan, X.; Gao, S.; Hao, J.; Chen, C.; Lu, P. Investigation of vacancy-ordered double perovskite halides A2Sn1-xTixY6 (A = K, Rb, Cs; Y = Cl, Br, I): Promising materials for photovoltaic applications. Nanomaterials 2023, 13, 2744. [Google Scholar] [CrossRef] [PubMed]
- Urmi, S.S.; Khan, M.A.K.; Ferdous, T.T.; Adinehloo, D.; Perebeinos, V.; Alim, M.M. Cs2TiI6 (Cs2TiIxBr6-x) Halide perovskite solar cell and its point defect analysis. Nanomaterials 2023, 13, 2100. [Google Scholar] [CrossRef] [PubMed]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt, Rinehart and Winston: New York, NY, USA, 1976. [Google Scholar]
- Lerch, D.; Wieckhorst, O.; Hart, G.L.; Forcade, R.W.; Müller, S. UNCLE: A code for constructing cluster expansions for arbitrary lattices with minimal user-input. Model. Simul. Mater. Sci. Eng. 2009, 17, 055003. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]


| No. of Iterations | No. of Structures | No. of New Structures | CSV Score (meV/pos) |
|---|---|---|---|
| 0 | 0 | 2 | - |
| 0 | 0 | 12 | - |
| 1 | 12 | 22 | 0.026 |
| 2 | 22 | 10 | 0.461 |
| 3 | 32 | 10 | 0.603 |
| 4 | 42 | 10 | 0.652 |
| Cs2Pb2I3Br3 | Cs2Pb2I5Br | Cs3Pb3IBr8 | |
|---|---|---|---|
| Lattice constant () | a = 11.973 b = 12.412 c = 6.403 | a = b = 9.044 c = 6.206 | a = 5.987 b = 17.967 c = 5.152 |
| Volume () | V = 951.421 | V = 507.570 | V = 661.663 |
| Angle (°) | α= β = γ = 90.00 | α= β = γ = 90.00 | α= β = γ = 90.00 |
| Bond length () | Pb − I = 3.207 Pb − Br = 2.999 | Pb − I = 3.201 Pb − Br = 3.001 | Pb − I = 3.203 Pb − Br = 3.002 |
| Band gap (eV) | 1.692 | 1.520 | 1.901 |
| Elastic Constants | Cs2Pb2I3Br3 | Cs2Pb2I5Br | Cs3Pb3IBr8 |
|---|---|---|---|
| C11 | 41.921 | 23.290 | 39.602 |
| C12 | 6.393 | 16.494 | 6.111 |
| C13 | 5.960 | 5.163 | 5.242 |
| C22 | 41.782 | - | 37.723 |
| C23 | 5.961 | - | 4.843 |
| C33 | 40.373 | 35.890 | 36.921 |
| C44 | 3.972 | - | 3.451 |
| C55 | 4.020 | 4.221 | 3.794 |
| C66 | 4.431 | 3.751 | 4.673 |
| Elastic Constants | Cs2Pb2I3Br3 | Cs2Pb2I5Br | Cs3Pb3IBr8 |
|---|---|---|---|
| Bulk | 17.850 | 16.161 | 15.231 |
| Shear | 7.742 | 7.233 | 6.770 |
| Young | 20.171 | 18.771 | 17.590 |
| Poisson | 0.311 | 0.305 | 0.306 |
| Pugh | 2.306 | 2.235 | 2.248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleka, P.; Dima, R.; Tshwane, D.; Ntwaeaborwa, O.; Maphanga, R. Phase Separation of Br-Doped CsPbI3: A Combined Cluster Expansion, Monte Carlo, and DFT Study. Molecules 2024, 29, 92. https://doi.org/10.3390/molecules29010092
Maleka P, Dima R, Tshwane D, Ntwaeaborwa O, Maphanga R. Phase Separation of Br-Doped CsPbI3: A Combined Cluster Expansion, Monte Carlo, and DFT Study. Molecules. 2024; 29(1):92. https://doi.org/10.3390/molecules29010092
Chicago/Turabian StyleMaleka, Prettier, Ratshilumela Dima, David Tshwane, Odireleng Ntwaeaborwa, and Rapela Maphanga. 2024. "Phase Separation of Br-Doped CsPbI3: A Combined Cluster Expansion, Monte Carlo, and DFT Study" Molecules 29, no. 1: 92. https://doi.org/10.3390/molecules29010092
APA StyleMaleka, P., Dima, R., Tshwane, D., Ntwaeaborwa, O., & Maphanga, R. (2024). Phase Separation of Br-Doped CsPbI3: A Combined Cluster Expansion, Monte Carlo, and DFT Study. Molecules, 29(1), 92. https://doi.org/10.3390/molecules29010092








