Abstract
The structure and interactions of oxygenated aromatic molecules are of atmospheric interest due to their toxicity and as precursors of aerosols. Here, we present the analysis of 4-methyl-2-nitrophenol (4MNP) using chirped pulse and Fabry–Pérot Fourier transform microwave spectroscopy in combination with quantum chemical calculations. The rotational, centrifugal distortion, and 14N nuclear quadrupole coupling constants of the lowest-energy conformer of 4MNP were determined as well as the barrier to methyl internal rotation. The latter has a value of 106.4456(8) cm−1, significantly larger than those from related molecules with only one hydroxyl or nitro substituent in the same para or meta positions, respectively, as 4MNP. Our results serve as a basis to understand the interactions of 4MNP with atmospheric molecules and the influence of the electronic environment on methyl internal rotation barrier heights.
1. Introduction
A major class of pollutants and aerosol precursors are oxygenated aromatic compounds, including functional groups such as –OH, –CO, and –NO2 [1,2,3,4]. They are primary products of combustion and have higher toxicity than their parent, non-oxygenated compounds [5]. Among the oxygenated aromatic molecules, phenols and nitrophenols have attracted much attention due to their toxicity [6]. These constitute a large portion of the volatile organic compounds (VOCs) in urban areas, and their subsequent reactions are pivotal in determining atmospheric chemistry because they increase the proportion of oxidants, such as OH radicals, and the formation of secondary organic aerosol [7,8]. p-Cresol is one of the main atmospheric phenols, directly released to the atmosphere as a byproduct of diesel combustion and wood burning, as well as produced from photochemical reactions of other aromatic molecules. Its oxidation with NO3 radicals produces 4-methyl-2-nitrophenol (4MNP, see Figure 1), whose photolysis was recently discovered to be a potential source of the OH radical in polluted suburban environments [7]. 4MNP is also an important component of “brown carbon” from biomass burning [9,10] and is released into the atmosphere by combustion [11,12]. Despite their relevance to the Earth’s atmosphere, there are fundamental gaps in our knowledge of the competing reaction pathways for these pollutants, their evolution from the first aggregation stages and cluster growth to aerosol formation, and their interactions with water [13,14].
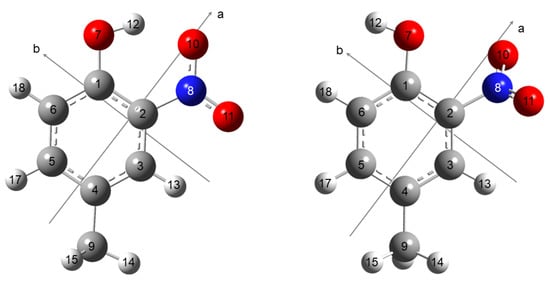
Figure 1.
Molecular structures of the two conformers of 4-methyl-2-nitrophenol, 4MNP-1 (left) and 4MNP-2 (right). The carbon atoms are gray, hydrogen atoms white, oxygen atoms red, and the nitrogen atom is blue. The principal inertial axes a, b are indicated. The c-axis is perpendicular to the ab plane.
To advance our understanding of the interactions of oxygenated aromatic compounds with other molecules in the atmosphere, it is necessary to characterize their structures and relative configurations. This can be achieved by applying high-resolution spectroscopic techniques in combination with high-level quantum chemistry calculations. Rotational spectroscopy [15,16] is a powerful technique for characterizing structures and large amplitude motions, such as methyl internal rotation, in the gas phase [17,18,19]. It can identify without ambiguity different conformers and isomers present in the sample because small differences in their structures will result in them showing different rotational spectra. Rotational spectroscopy has been successfully applied to investigate many atmospherically important molecules including amines, oxygenated organic compounds, terpenes, and their complexes [20,21,22,23,24,25,26]. Moreover, the results obtained from this experimental technique can be used to benchmark the performance of different theoretical methods.
In this study, we report the investigation of 4MNP, an aerosol precursor and pollutant [27,28,29,30,31,32], via a combination of rotational spectroscopy and quantum chemical calculations. 4MNP has a methyl group in para and meta with respect to the hydroxyl and nitro groups, respectively. The methyl torsion is expected to experience a V3 barrier, with each rotational transition split into two components, labeled A and E according to their symmetry. Only a few studies of methyl internal rotation barriers of doubly substituted toluene derivatives have been reported [17]. From the analysis of the rotational spectrum of 4MNP, we have determined its barrier to methyl internal rotation as well as its rotational and 14N nuclear quadrupole coupling constants.
2. Results
2.1. Computational
Geometry optimizations of 4MNP were initially performed with the Gaussian09 and Gaussian16 suites of programs [33,34] using density functional theory (DFT) [35,36] as well as ab initio second-order Møller–Plesset perturbation theory (MP2) [37] in combination with Pople’s 6-311G++(d,p) basis set [38,39]. The DFT calculations were carried out using the dispersion-corrected B3LYP-D3BJ functional, including Becke–Johnson damping [40,41] and the B3PW91 [36,42] functional, with tight optimization convergence criteria and an ultrafine grid. They yielded the computed rotational constants, dipole moment components, 14N nuclear quadrupole coupling constants (NQCCs), and energy differences between the conformers to guide the analysis of the experimental spectrum (see Table 1). Two conformers were obtained and are illustrated in Figure 1 with atomic numbering. Their atomic coordinates are available in Table S1 in the Supplementary Materials.

Table 1.
Theoretical spectroscopic parameters of the two conformers of 4MNP calculated using the B3LYP-D3BJ, B3PW91, and MP2 methods with the 6-311++G(d,p) basis set.
Because it has been reported that MP2 does not properly model the 14N nuclear quadrupole coupling of the –NO2 group [43,44], we also used two different DFT functionals to describe it. We chose B3LYP-D3BJ, as it usually provides a good description of structural parameters [21,45,46,47,48,49,50], and B3PW91, because it has been reported to be the best-performing method for describing nuclear quadrupole coupling [42]. Furthermore, we used Bailey’s method to compute the NQCCs by performing electric field gradient calculations at the B3PW91/6-311+G(d,p) level of theory on the molecular geometry optimized at the MP2/6-311++G(d,p) level [42]. The obtained values were corrected with the calibration factor eQ/h = −4.599 MHz a.u−1 recommended for molecules containing π-conjugation [51], yielding χaa = −0.7053 MHz, χbb = 0.0379 MHz, χcc = 0.6674 MHz, and χab = 0.7078 MHz.
The methyl internal rotation barriers were calculated by rotating the methyl group in steps of 10° by varying the dihedral angle α = ∠(C3C4C9H14) and allowing the rest of the molecule to relax at each point. The height of the barrier is consistently larger for 4MNP-1 at all levels of theory. The obtained energy points were parameterized using a Fourier expansion with the coefficients collected in Table S2. Using these coefficients, the potential energy curves are drawn as contour plots in Figure S1. Calculations using the B3LYP-D3BJ and B3PW91 methods resulted in a potential curve with perfect threefold symmetry, which is typical for methyl internal rotation. At the MP2 level, we obtained a strange shape of the potential curve, where the minima are not located at 0°, 120°, and 240°, but are shifted by 10°.
Furthermore, we carried out a two-dimensional contour plot using the B3PW91 method with the Q2DTor program [52] (see Figure 2). It shows the change in potential energy when the methyl and hydroxyl groups are rotated in steps of 10° while allowing the rest of the molecule to relax at each point. The resulting points were fitted to the Fourier series of Equation S1, which was employed to solve the 2D Schrödinger equation leading to the energy levels of Table S3 (see ref. [53] for details). There are three indistinguishable absolute minima corresponding to 4MNP-1 with Cs symmetry. The hydrogen atom of the –OH group points toward the –NO2, creating a strong hydrogen bond. This hydrogen bond in the 4MNP-1 structure avoids any internal rotation of the –OH group, and the molecule behaves as a system with a single methyl internal rotor. Notice that the comparison of the first 18th vibrational energy levels obtained from the diagonalization of the 1D and 2D potentials shows that these levels correspond exclusively to the vibrational excitation of the methyl group (see Table S3). 4MNP-2 lacks the hydrogen bond of 4MNP-1, and the repulsion between the oxygens of the –OH and –NO2 groups leads to a nonplanar structure with a very high energy above the global minimum. Therefore, the rotation of the hydroxyl group displaces the nitro group out of the phenylic plane, with angles of 31.1° (B3LYP-D3BJ), 31.0° (B3PW91), and 52.1° (MP2). Additionally, it affects the methyl group rotation, which presents a barrier of ca. 30 cm−1.
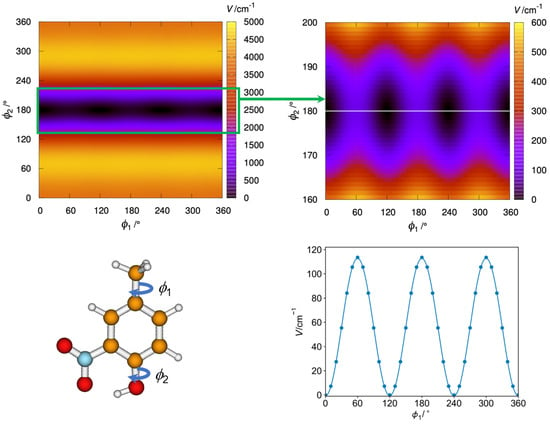
Figure 2.
(Top left): Contour plot showing the variation of potential energy (in cm−1) with the internal rotation of the methyl and hydroxyl groups of 4MNP (bottom left). A zoom of the contour plot enhancing the region of the absolute minima is depicted in the (top right) position. A one-dimensional cut (white line in the zoomed contour plot) that passes through the equilibrium structures shows the fit of the V3 potential to the B3PW91 points (bottom right).
The effect of the –NO2 group is thus substantial. Comparing 4MNP with the related 4-methylphenol (p-cresol) shows that whereas 4MNP-2 is very high-energy, the analogous structure of p-cresol is the absolute minimum, and the analogous structure of 4MNP-1 is a transition state that is 17 cm−1 above the minimum. Therefore, due to the symmetry in p-cresol, there is only one minimum, with the two eclipsed hydrogen atoms of the rotating tops in anti configuration but with the torsion about the methyl group close to a free rotation (see Figure 3).
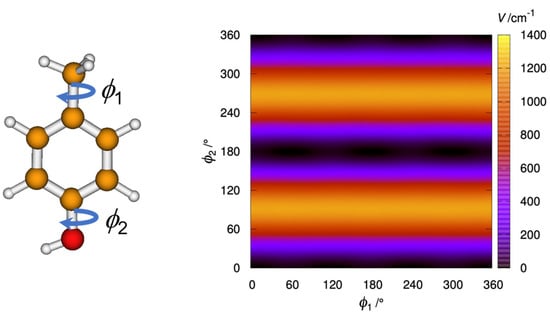
Figure 3.
Contour plot showing the variation of potential energy (in cm−1) with the internal rotation of the methyl and hydroxyl groups of p-cresol, generated at the B3PWB91/6-311++G(d,p) level.
2.2. Rotational Spectrum
There are two possible conformers of 4MNP, depending on the orientation of the hydroxyl group (see Figure 1 and Table 1). The global minimum 4MNP-1 exhibits an intramolecular O–H∙∙∙O hydrogen bond between the hydrogen of the hydroxyl group and one of the oxygens of the nitro group. This stabilizing interaction is missing in conformer 4MNP-2, leading to a much higher relative energy. 4MNP-2 is thus not expected to be populated in our supersonic expansion.
4MNP-1 is predicted to be a planar molecule with only µa and µb dipole moment components. Because µa is predicted to be much larger than µb, we initially looked for R-branch a-type transitions. A series of intense lines separated by approximately B + C and following the expected pattern for aR transitions was observed in the broadband rotational spectrum. They all showed nuclear quadrupole coupling splittings arising from the 14N nucleus. Each rotational transition was also split into A and E components (see Figure 4) arising from the interaction between the methyl internal rotation and the overall rotation of the molecule. The hydrogen bond between the hydroxyl and nitro groups in 4MNP-1 impedes the rotation of the –OH group, hence there is no splitting due to this motion. From initial fits of the A torsional components of a-type transitions using Pickett’s spfit program [54] and Watson’s S-reduced Hamiltonian [55], preliminary rotational constants were determined and further a-type and b-type transitions were assigned. Many of the most intense quadrupole hyperfine components were blended in the broadband rotational spectrum. Therefore, further measurements were performed, taking advantage of the higher resolution of the Fabry–Pérot Fourier transform microwave (FTMW) spectrometer (Figure 5). A total of 327 a- and b-type lines combining A and E transitions with fully resolved nuclear quadrupole coupling splittings were measured, with an estimated measurement accuracy of 4 kHz.
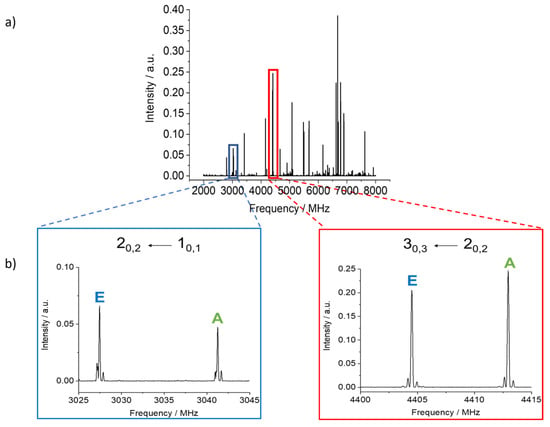
Figure 4.
(a) The chirped pulse FTMW spectrum of 4MNP-1 recorded from 2 to 8 GHz. (b) Sections of the spectrum showing assigned transitions and torsional species.
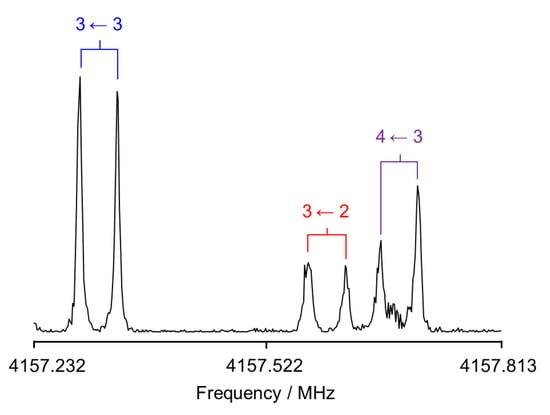
Figure 5.
A typical resonator-based FTMW spectrum of the a-type transition 31,3 ← 21,2 showing its 14N nuclear quadrupole hyperfine structure. Each transition is split into two components due to the Doppler effect. The line was polarized at 4157.313 MHz, and 241 free induction decays were co-added.
Internal rotation splittings can be treated only using appropriate theoretical models. We performed two fits using two different spectral fitting programs, the XIAM [56] and BELGI-Cs-hyperfine [57] codes, which allowed us to treat the rotational spectrum of internal rotation combined with a 14N quadrupole hyperfine structure. BELGI-Cs-hyperfine uses the rho axis method (RAM), which is discussed in detail in refs. [58,59]. The rotational constants and the NQCCs obtained from the fit in the RAM system were subsequently transformed into the principal axis system (PAM) with the rotation matrix of θRAM angle around the z-axis, using the equations described in ref. [58]. The XIAM code uses the combined axis method, wherein the rotor is first set up in the PAM system and then transformed into the RAM system to eliminate the Coriolis coupling terms. In the RAM system, XIAM calculates the eigenvalues in the product basis of the symmetric top functions for the overall rotation and the planar rotor functions for the methyl internal rotation, and then transforms the eigenvalue matrix back to the PAM system. One difference between the two methods is that the XIAM code fits mainly low-order terms of the Hamiltonian, while BELGI-Cs-hyperfine has more higher-order terms coupling the internal and global rotation. Furthermore, XIAM can fit each torsional state (vt = 0) by itself only and does not include interaction terms between different torsional states. BELGI-Cs-hyperfine considers a whole set of torsional states (truncated at vt = 8) in the Hamiltonian matrix, allowing it to obtain better root-mean-square (rms) deviation, especially for the E species of internal rotors with low torsional barriers. XIAM is faster and is convenient for spectral assignment, but the better rms deviation and predictive power has made BELGI-Cs-hyperfine a good complement to XIAM [19].
For 4MNP-1, using the XIAM code to determine a linear combination of the rotational constants A, B, and C, the quartic centrifugal distortion constants DJ and DJK, the 14N NQCCs χaa and χbb − χcc, the barrier to internal rotation V3, the angle ∠(i,a) between the a principal inertial axis and the internal rotor axis, and three higher-order terms , , and enabled us to reproduce the experimental spectra to an rms deviation of 7.8 kHz for 327 lines (Table 2). The internal rotation constant F0 is correlated to V3 and was fixed to the calculated value. The reduced constant F = ħ2/2rIα and the rotation-torsion coupling constant ρ were derived parameters.

Table 2.
Molecular parameters of 4MNP-1 in the PAM system obtained from fits with XIAM and BELGI-Cs-hyperfine.
For the BELGI-Cs-hyperfine fit, presented in Table 3 in the RAM system, the same dataset of 327 hyperfine components were fitted with an rms of 3.9 kHz, floating A, B, and C, ΔK, ΔJK, the 14N NQCCs χaa and χbb (χcc = −χaa −χbb, following Laplace condition), V3, and ρ. The use of the non-principal axis system in the BELGI-Cs-hyperfine fit requires an additional parameter to be fitted, Dab, which is directly related to the θRAM angle between the RAM and PAM systems. Two higher-order terms were used, c2 and Δab, which multiply the operators (1 − cos 3α) and {,}, respectively. The rms deviation is within the measurement accuracy of 4 kHz. For comparison with the XIAM results, some parameters were converted to the PAM system and are also presented in Table 2. The XIAM and BELGI-Cs-hyperfine parameters agree very well with each other. The frequency list and residuals of both fits are available in Table S5 of the Supplementary Materials.

Table 3.
Spectroscopic constants of 4MNP-1 in the RAM system obtained using the program BELGI-Cs-hyperfine.
3. Discussion and Conclusions
The most stable conformer of 4MNP was assigned, and global fits consisting of 168 A species and 159 E species transitions, including hyperfine components, were performed using two computer codes, XIAM and BELGI-Cs-hyperfine. The XIAM fit has a standard deviation of 7.8 kHz, which is reduced to 3.9 kHz, consistent with measurement accuracy, using BELGI-Cs-hyperfine. We can see from Table 2 that the XIAM and BELGI-Cs-hyperfine parameters are in good agreement with each other.
Ab initio and DFT calculations were carried out to guide the analysis of the rotational spectrum of 4MNP. All levels of theory predict equilibrium rotational constants close to the experimental ground state ones, probably because of the rigidity of the aromatic ring. This was confirmed by running additional calculations with a series of different methods and basis sets for benchmarking purposes, including MP2 [37], coupled cluster methods with a double excitation model (CCSD) [60], and the functionals M06-2X [61], ωB97X-D [62], MN15 [63], and PBE [64] (see Table S6). The NQCCs obtained from Bailey’s method or from B3LYP-D3BJ and B3PW91 calculations are in good agreement with the experimental ones, but those from MP2 have an average deviation of 44.6%, showing that this method is not reliable for predicting the electronic density around the 14N nucleus of an –NO2 group.
The NQCCs of 4MNP-1, and specifically χcc, can be compared with those from related molecules. The c principal inertial axis is perpendicular to the aromatic ring, as is the z quadrupole axis of the 14N atom. Therefore, χcc coincides with χzz and provides information on the electric field gradient along an axis perpendicular to the molecular plane. Our value of χcc = 0.885(17) MHz is effectively the same as those determined for nitrobenzene (χcc = 0.8394(36) MHz) [65] and ortho-nitrophenol (χcc = 0.886(3) MHz) [65]. The introduction of a hydroxyl group going from nitrobenzene to ortho-nitrophenol causes a very small change in the 14N electronic environment. No changes are observed going from ortho-nitrophenol to 4MNP-1, showing that the methyl group has no influence on the electronic environment of the 14N of the nitro group. Considering the definition of χzz and its relation to the unbalanced electrons in a pz orbital, its positive value indicates that there is an excess of electron density along the z axis of the 14N nucleus [66,67].
The inertial defect of 4MNP-1 is calculated to be −3.53815(48) uÅ2 from the XIAM fit. This value is consistent with a planar molecule in which only the hydrogen atoms of the methyl group are out of plane. The planar moment perpendicular to the ab plane, Pcc, has a value of 1.76908(24) uÅ2. This is similar to the expected value of 1.625 uÅ2 for two hydrogens out of plane with C–H distances of 1.1 Å and ∠HCH of 109.28° [66] and is comparable to the Pcc of other molecules wherein the only contribution to Pcc arises from out-of-plane methyl hydrogens [68].
The V3 torsional barriers obtained by XIAM and BELGI-Cs-hyperfine are 106.4456(8) cm−1 and 105.995(14) cm−1, respectively. The agreement between the values of V3 from XIAM and BELGI-Cs-hyperfine is extremely good, given the differences existing between the two methods. The barrier height for methyl internal rotation depends on steric interactions and electronic effects [17]. The methyl group in 4MNP is sufficiently far away from the –OH and –NO2 groups that steric interactions are unlikely, and this is reflected in the low barrier height. However, although the barrier is relatively low, it is higher than those of 18.39(3) cm−1 for the related 4-methylphenol (p-cresol) [69] and 6.7659(24) cm−1 for meta-nitrotoluene [44], which have their methyl groups in the same relative position, with respect to the –OH and –NO2 groups, as 4MNP-1. Other six-membered aromatic molecules where the methyl group is in para or meta with respect to a single substituent also have lower barriers than 4MNP-1 [17]. In 4MNP-1, the –NO2 group has negative inductive and mesomeric effects, removing electron density from the aromatic ring, while the –OH group has a positive mesomeric effect and donates electron density to the ring. Clearly the methyl group is “sensing” the presence of two other substituents in the ring, and changes in the electronic distribution induced by them (and the hydrogen bond connecting them) are very likely the cause of the higher barrier to methyl internal rotation. Further studies of toluene derivatives with two ring substituents will help get more insight into the chemical features that control the height of the barrier.
The results of this study can be used to compare the impact of the electronic environment on the methyl internal rotation barrier with other isomers of methylnitrophenol, such as 5-methyl-2-nitrophenol. The structural determination of 4MNP lays a basis to undertake future studies of the chemical reactions and atmospheric aggregation processes of 4MNP; for example, with multiple water molecules.
4. Materials and Methods
The rotational spectrum of 4MNP was recorded using broadband and Fabry–Pérot FTMW spectrometers. We employed first a chirped pulse FTMW spectrometer in the 2–8 GHz frequency range at King’s College London, UK [70,71]. 4MNP was purchased from Sigma-Aldrich (99% purity) and used without further purification. As 4MNP is a solid at room temperature (m.p. 305–308 K), it was heated to 369 K using a bespoke heating receptacle attached to the solenoid valve and then supersonically expanded into the vacuum chamber using neon as a carrier gas at a backing pressure of 5 bar. The vaporized molecules were excited by microwave chirped pulses of 4 µs, amplified by a travelling wave tube amplifier of 200 W, and broadcasted into the vacuum chamber using a broadband horn antenna. Once the microwave radiation stopped, the emission signal was collected in the form of a free induction decay (FID) in the time domain and converted to the frequency domain via a fast Fourier transform. The final rotational spectrum collected had 1.2 MFIDs and is shown in Figure 4.
A Fabry–Pérot FTMW spectrometer covering the 2–26.5 GHz frequency range [72] was used to determine the frequencies at higher resolutions and to expand the data set to measure transitions with higher J and K values. Solid 4MNP was put on a small piece of pipe cleaner placed in a metal tube upstream of the nozzle. The tube was also heated to about 369 K. Helium was used as the carrier gas at a backing pressure of 2 bar, flown over the 4MNP sample, and then the 4MNP–helium mixture was expanded into the cavity. A typical spectrum of the 31,3 ← 21,2 transition is illustrated in Figure 5.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28052153/s1, Figure S1: Potential energy curve of 4MNP-1 by varying the dihedral angle α = ∠(C3C4C9H14), corresponding to a rotation of the methyl group about the C4–C9 bond; Table S1: Nuclear coordinates of conformer 4MNP-1; Tables S2–S4: Fourier coefficients; Table S5: Frequency list and residuals obtained with the XIAM and BELGI-Cs-hyperfine programs; Table S6: Rotational constants of 4MNP-1 calculated at different levels of theory.
Author Contributions
Conceptualization, M.E.S.; methodology, I.K., M.E.S. and H.V.L.N.; software, I.K.; validation, I.K., H.V.L.N. and M.E.S.; formal analysis, S.B., E.A., S.H., A.F.-R., I.K., H.V.L.N. and M.E.S.; investigation, S.B., E.A., S.H., A.F.-R., I.K., H.V.L.N. and M.E.S.; resources, I.K., H.V.L.N. and M.E.S.; data curation, S.B., E.A., S.H., A.F.-R., H.V.L.N. and M.E.S.; writing—original draft preparation, S.B.; writing—review and editing, S.B., E.A., S.H., A.F.-R., I.K., H.V.L.N. and M.E.S.; visualization, S.B., E.A., A.F.-R., I.K., M.E.S. and H.V.L.N.; supervision, H.V.L.N. and M.E.S.; project administration, H.V.L.N. and M.E.S.; funding acquisition, I.K., H.V.L.N. and M.E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Université de Paris–King’s College London Joint Research Award and was co-funded by the Agence Nationale de la Recherche (ANR, grant number ANR-18-CE29-0011), by the European Union (ERC grant 101040480-LACRIDO, and PCIG12-GA-2012-334525), and Ministerio de Ciencia e Innovación (grant PID2019-107307RB-I00). S.B. thanks King’s College London for a PGR International Scholarship. We acknowledge use of the research computing facilities at King’s College London, Rosalind (https://rosalind.kcl.ac.uk) and CREATE (King’s Computational Research, Engineering and Technology Environment. https://doi.org/10.18742/rnvf-m076, accessed on 31 January 2023).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lammel, G.; Kitanovski, Z.; Kukučka, P.; Novák, J.; Arangio, A.M.; Codling, G.P.; Filippi, A.; Hovorka, J.; Kuta, J.; Leoni, C.; et al. Oxygenated and Nitrated Polycyclic Aromatic Hydrocarbons in Ambient Air—Levels, Phase Partitioning, Mass Size Distributions, and Inhalation Bioaccessibility. Environ. Sci. Technol. 2020, 54, 2615–2625. [Google Scholar] [CrossRef]
- Bandowe, B.A.M.; Meusel, H. Nitrated Polycyclic Aromatic Hydrocarbons (Nitro-PAHs) in the Environment—A Review. Sci. Total Environ. 2017, 581–582, 237–257. [Google Scholar] [CrossRef]
- Delgado-Saborit, J.M.; Alam, M.S.; Godri Pollitt, K.J.; Stark, C.; Harrison, R.M. Analysis of Atmospheric Concentrations of Quinones and Polycyclic Aromatic Hydrocarbons in Vapour and Particulate Phases. Atmos. Environ. 2013, 77, 974–982. [Google Scholar] [CrossRef]
- Mallah, M.A.; Changxing, L.; Mallah, M.A.; Noreen, S.; Liu, Y.; Saeed, M.; Xi, H.; Ahmed, B.; Feng, F.; Mirjat, A.A.; et al. Polycyclic Aromatic Hydrocarbon and Its Effects on Human Health: An Overview. Chemosphere 2022, 296, 133948. [Google Scholar] [CrossRef]
- Walgraeve, C.; Demeestere, K.; Dewulf, J.; Zimmermann, R.; Van Langenhove, H. Oxygenated Polycyclic Aromatic Hydrocarbons in Atmospheric Particulate Matter: Molecular Characterization and Occurrence. Atmos. Environ. 2010, 44, 1831–1846. [Google Scholar] [CrossRef]
- Minero, C.; Maurino, V.; Pelizzetti, E.; Vione, D. Assessing the Steady-State [•NO2] in Environmental Samples: Implication for Aromatic Photonitration Processes Induced by Nitrate and Nitrite. Environ. Sci. Pollut. Res. 2007, 14, 241–243. [Google Scholar] [CrossRef]
- Bejan, I.G.; Olariu, R.I.; Wiesen, P. Secondary Organic Aerosol Formation from Nitrophenols Photolysis under Atmospheric Conditions. Atmosphere 2020, 11, 1346. [Google Scholar] [CrossRef]
- Srivastava, D.; Vu, T.V.; Tong, S.; Shi, Z.; Harrison, R.M. Formation of Secondary Organic Aerosols from Anthropogenic Precursors in Laboratory Studies. NPJ Clim. Atmos. Sci. 2022, 5, 22. [Google Scholar] [CrossRef]
- Desyaterik, Y.; Sun, Y.; Shen, X.; Lee, T.; Wang, X.; Wang, T.; Collett, J.L. Speciation of “Brown” Carbon in Cloud Water Impacted by Agricultural Biomass Burning in Eastern China. J. Geophys. Res. Atmos. 2013, 118, 7389–7399. [Google Scholar] [CrossRef]
- Wang, H.; Gao, Y.; Wang, S.; Wu, X.; Liu, Y.; Li, X.; Huang, D.; Lou, S.; Wu, Z.; Guo, S.; et al. Atmospheric Processing of Nitrophenols and Nitrocresols From Biomass Burning Emissions. J. Geophys. Res. Atmos. 2020, 125, e2020JD033401. [Google Scholar] [CrossRef]
- Coeur-Tourneur, C.; Henry, F.; Janquin, M.A.; Brutier, L. Gas-Phase Reaction of Hydroxyl Radicals with m-, o- and p-Cresol. Int. J. Chem. Kinet. 2006, 38, 553–562. [Google Scholar] [CrossRef]
- Li, M.; Wang, X.; Lu, C.; Li, R.; Zhang, J.; Dong, S.; Yang, L.; Xue, L.; Chen, J.; Wang, W. Nitrated Phenols and the Phenolic Precursors in the Atmosphere in Urban Jinan, China. Sci. Total Environ. 2020, 714, 136760. [Google Scholar] [CrossRef] [PubMed]
- Kroll, J.H.; Seinfeld, J.H. Chemistry of Secondary Organic Aerosol: Formation and Evolution of Low-Volatility Organics in the Atmosphere. Atmos. Environ. 2008, 42, 3593–3624. [Google Scholar] [CrossRef]
- Hallquist, M.; Wenger, J.C.; Baltensperger, U.; Rudich, Y.; Simpson, D.; Claeys, M.; Dommen, J.; Donahue, N.M.; George, C.; Goldstein, A.H.; et al. The Formation, Properties and Impact of Secondary Organic Aerosol: Current and Emerging Issues. Atmos. Chem. Phys. 2009, 9, 5155–5236. [Google Scholar] [CrossRef]
- Park, G.B.; Field, R.W. Perspective: The First Ten Years of Broadband Chirped Pulse Fourier Transform Microwave Spectroscopy. J. Chem. Phys. 2016, 144, 200901. [Google Scholar] [CrossRef]
- Grabow, J.-U.; Caminati, W. Microwave Spectroscopy: Experimental Techniques. Front. Mol. Spectrosc. 2009, 383–454. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Caminati, W.; Grabow, J.U. The LAM of the Rings: Large Amplitude Motions in Aromatic Molecules Studied by Microwave Spectroscopy. Molecules 2022, 27, 3948. [Google Scholar] [CrossRef]
- Lin, C.C.; Swalen, J.D. Internal Rotation and Microwave Spectroscopy. Rev. Mod. Phys. 1959, 31, 841–891. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Kleiner, I. Understanding (Coupled) Large Amplitude Motions: The Interplay of Microwave Spectroscopy, Spectral Modeling, and Quantum Chemistry. In Theoretical and Computational Chemistry: Applications in Industry, Pharma, and Materials Science; De Gruyter: Berlin, Germany, 2021; pp. 41–92. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Mouhib, H.; Klahm, S.; Stahl, W.; Kleiner, I. A Touch of Lavender: Gas-Phase Structure and Dynamics of the Monoterpene Linalool Validated by Microwave Spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 10012–10018. [Google Scholar] [CrossRef]
- Uriarte, I.; Insausti, A.; Cocinero, E.J.; Jabri, A.; Kleiner, I.; Mouhib, H.; Alkorta, I. Competing Dispersive Interactions: From Small Energy Differences to Large Structural Effects in Methyl Jasmonate and Zingerone. J. Phys. Chem. Lett. 2018, 9, 5906–5914. [Google Scholar] [CrossRef]
- Murugachandran, S.I.; Tang, J.; Peña, I.; Loru, D.; Sanz, M.E. New Insights into Secondary Organic Aerosol Formation: Water Binding to Limonene. J. Phys. Chem. Lett. 2021, 12, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
- Baweja, S.; Panchagnula, S.; Sanz, M.E.; Evangelisti, L.; West, C.; Pate, B.H. Competition between In-Plane vs Above-Plane Configurations of Water with Aromatic Molecules: Non-Covalent Interactions in 1,4- Naphthoquinone-(H2O)1−3 Complexes. J. Phys. Chem. Lett. 2022, 13, 9510–9516. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.V.L.; Stahl, W. The Effects of Nitrogen Inversion Tunneling, Methyl Internal Rotation, and 14N Quadrupole Coupling Observed in the Rotational Spectrum of Diethyl Amine. J. Chem. Phys. 2011, 135, 024310. [Google Scholar] [CrossRef] [PubMed]
- Vigorito, A.; Calabrese, C.; Maris, A.; Loru, D.; Peña, I.; Sanz, M.E.; Melandri, S. The Shapes of Sulfonamides: A Rotational Spectroscopy Study. Molecules 2022, 27, 2820. [Google Scholar] [CrossRef] [PubMed]
- Burevschi, E.; Peña, I.; Sanz, M.E. Geminal Diol Formation from the Interaction of a Ketone with Water in the Gas Phase: Structure and Reactivity of Cyclooctanone-(H2O)1,2 Clusters. J. Phys. Chem. Lett. 2021, 12, 12419–12425. [Google Scholar] [CrossRef] [PubMed]
- Delhomme, O.; Morville, S.; Millet, M. Seasonal and Diurnal Variations of Atmospheric Concentrations of Phenols and Nitrophenols Measured in the Strasbourg Area, France. Atmos. Pollut. Res. 2010, 1, 16–22. [Google Scholar] [CrossRef]
- Lüttke, J.; Scheer, V.; Levsen, K.; Wünsch, G.; Cape, J.N.; Hargreaves, K.J.; Storeton-West, R.L.; Acker, K.; Wieprecht, W.; Jones, B. Occurrence and Formation of Nitrated Phenols in and out of Cloud. Atmos. Environ. 1997, 31, 2637–2648. [Google Scholar] [CrossRef]
- Belloli, R.; Barletta, B.; Bolzacchini, E.; Meinardi, S.; Orlandi, M.; Rindone, B. Determination of Toxic Nitrophenols in the Atmosphere by High-Performance Liquid Chromatography. J. Chromatogr. A 1999, 846, 277–281. [Google Scholar] [CrossRef]
- Cecinato, A.; Di Palo, V.; Pomata, D.; Tomasi Scianò, M.C.; Possanzini, M. Measurement of Phase-Distributed Nitrophenols in Rome Ambient Air. Chemosphere 2005, 59, 679–683. [Google Scholar] [CrossRef]
- Leuenberger, C.; Czuczwa, J.; Tremp, J.; Giger, W. Nitrated Phenols in Rain: Atmospheric Occurrence of Phytotoxic Pollutants. Chemosphere 1988, 17, 511–515. [Google Scholar] [CrossRef]
- Nishioka, M.G.; Lewtas, J. Quantification of Nitro- and Hydroxylated Nitro-Aromatic/Polycyclic Aromatic Hydrocarbons in Selected Ambient Air Daytime Winter Samples. Atmos. Environ. Part A Gen. Top. 1992, 26, 2077–2087. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09, Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 3785–3789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5656. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Bailey, W.C. DFT and HF-DFT Calculations of 14N Quadrupole Coupling Constants in Molecules. Chem. Phys. 2000, 252, 57–66. [Google Scholar] [CrossRef]
- Roucou, A.; Kleiner, I.; Goubet, M.; Bteich, S.; Mouret, G.; Bocquet, R.; Hindle, F.; Meerts, W.L.; Cuisset, A. Towards the Detection of Explosive Taggants: Microwave and Millimetre-Wave Gas-Phase Spectroscopies of 3-Nitrotoluene. ChemPhysChem 2018, 19, 1056–1067. [Google Scholar] [CrossRef]
- Roucou, A.; Goubet, M.; Kleiner, I.; Bteich, S.; Cuisset, A. Large Amplitude Torsions in Nitrotoluene Isomers Studied by Rotational Spectroscopy and Quantum Chemistry Calculations. ChemPhysChem 2020, 21, 2523–2538. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.; Panchagnula, S.; Sanz, M.E.; Pérez, C.; Evangelisti, L.; Pate, B.H. Structural Changes Induced by Quinones: High Resolution Microwave Study of 1,4-Naphthoquinone. ChemPhysChem 2020, 21, 2579–2584. [Google Scholar] [CrossRef]
- Tsoi, V.W.Y.; Burevschi, E.; Saxena, S.; Sanz, M.E. Conformational Panorama of Cycloundecanone: A Rotational Spectroscopy Study. J. Phys. Chem. A 2022, 126, 6185–6193. [Google Scholar] [CrossRef] [PubMed]
- Burevschi, E.; Eugenia Sanz, M. Seven Conformations of the Macrocycle Cyclododecanone Unveiled by Microwave Spectroscopy. Molecules 2021, 26, 5162. [Google Scholar] [CrossRef] [PubMed]
- Graneek, J.B.; Bailey, W.C.; Schnell, M. Electron-Withdrawing Effects on the Molecular Structure of 2- and 3-Nitrobenzonitrile Revealed by Broadband Rotational Spectroscopy and Their Comparison with 4-Nitrobenzonitrile. Phys. Chem. Chem. Phys. 2018, 20, 22210–22217. [Google Scholar] [CrossRef] [PubMed]
- Juanes, M.; Usabiaga, I.; León, I.; Evangelisti, L.; Fernández, J.A.; Lesarri, A. The Six Isomers of the Cyclohexanol Dimer: A Delicate Test for Dispersion Models. Angew. Chem.-Int. Ed. 2020, 59, 14081–14085. [Google Scholar] [CrossRef] [PubMed]
- Salvitti, G.; Blanco, S.; Lòpez, J.C.; Melandri, S.; Evangelisti, L.; Maris, A. Probing Intra- and Inter-Molecular Interactions through Rotational Spectroscopy: The Case of the Odorant 2′-Aminoacetophenone and Its 1:1 Water and Neon Complexes. J. Chem. Phys. 2022, 157, 144303. [Google Scholar] [CrossRef]
- Kannengießer, R.; Stahl, W.; Nguyen, H.V.L.; Bailey, W.C. 14N Quadrupole Coupling in the Microwave Spectra of N-Vinylformamide. J. Mol. Spectrosc. 2015, 317, 50–53. [Google Scholar] [CrossRef]
- Ferro-Costas, D.; Cordeiro, M.N.D.S.; Truhlar, D.G.; Fernández-Ramos, A. Q2DTor: A Program to Treat Torsional Anharmonicity through Coupled Pair Torsions in Flexible Molecules. Comput. Phys. Commun. 2018, 232, 190–205. [Google Scholar] [CrossRef]
- Fernández-Ramos, A. Accurate Treatment of Two-Dimensional Non-Separable Hindered Internal Rotors. J. Chem. Phys. 2013, 138, 134112. [Google Scholar] [CrossRef]
- Pickett, H.M. The Fitting and Prediction of Vibration-Rotation Spectra with Spin Interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
- Watson, J.K.G. Simplification of the Molecular Vibration-Rotation Hamiltonian. Mol. Phys. 1968, 15, 479–490. [Google Scholar] [CrossRef]
- Hartwig, H.; Dreizler, H. The Microwave Spectrum of Trans-2,3-Dimethyloxirane in Torsional Excited States. Zeitschrift fur Naturforsch.-Sect. A J. Phys. Sci. 1996, 51, 923–932. [Google Scholar] [CrossRef]
- Kannengießer, R.; Stahl, W.; Nguyen, H.V.L.; Kleiner, I. 14N Nuclear Quadrupole Coupling and Methyl Internal Rotation in N-Tert-Butylacetamide As Observed by Microwave Spectroscopy. J. Phys. Chem. A 2016, 120, 3992–3997. [Google Scholar] [CrossRef] [PubMed]
- Hougen, J.T.; Kleiner, I.; Godefroid, M. Selection Rules and Intensity Calculations for a Cs Asymmetric Top Molecule Containing a Methyl Group Internal Rotor. J. Mol. Spectrosc. 1994, 163, 559–586. [Google Scholar] [CrossRef]
- Kleiner, I. Asymmetric-Top Molecules Containing One Methyl-like Internal Rotor: Methods and Codes for Fitting and Predicting Spectra. J. Mol. Spectrosc. 2010, 260, 1–18. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Scheiner, A.C.; Lee, T.J.; Rice, J.E.; Schaefer, H.F. The Closed-Shell Coupled Cluster Single and Double Excitation (CCSD) Model for the Description of Electron Correlation. A Comparison with Configuration Interaction (CISD) Results. J. Chem. Phys. 1987, 86, 2881–2890. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Da Chai, J.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Heineking, N.; Dreizler, H. Nitrogen Quadrupole Coupling Constants of Nitrobenzene and o-Nitrophenol. Ber. Bunsenges. Phys. Chem. 1993, 97, 663–665. [Google Scholar] [CrossRef]
- Gordy, W.; Cook, R.L. Microwave Molecular Spectra; John Wiley & Sons: Hoboken, NJ, USA, 1984; Chapter 14. [Google Scholar]
- Pinacho, P.; Obenchain, D.A.; Schnell, M. New Findings from Old Data: A Semi-Experimental Value for the eQq of the Nitrogen Atom. J. Chem. Phys. 2020, 153, 234307. [Google Scholar] [CrossRef] [PubMed]
- Bohn, R.K.; Montgomery, J.A.; Michels, H.H.; Fournier, J.A. Second Moments and Rotational Spectroscopy. J. Mol. Spectrosc. 2016, 325, 42–49. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C. On the Internal Rotations in p-resol in its Ground and First Electronically Excited States. J. Chem. Phys. 2007, 127, 024307. [Google Scholar] [CrossRef]
- Loru, D.; Bermúdez, M.A.; Sanz, M.E. Structure of Fenchone by Broadband Rotational Spectroscopy. J. Chem. Phys. 2016, 145, 074311. [Google Scholar] [CrossRef]
- Loru, D.; Peña, I.; Sanz, M.E. Ethanol Dimer: Observation of Three New Conformers by Broadband Rotational Spectroscopy. J. Mol. Spectrosc. 2017, 335, 93–101. [Google Scholar] [CrossRef]
- Grabow, J.-U.; Stahl, W.; Dreizler, H. A Multioctave Coaxially Oriented Beam-Resonator Arrangement Fourier-Transform Microwave Spectrometer. Rev. Sci. Instrum. 1996, 67, 4072–4084. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).