Rovibrational Spectroscopy of Trans and Cis Conformers of 2-Furfural from High-Resolution Fourier Transform and QCL Infrared Measurements
Abstract
1. Introduction
2. Results
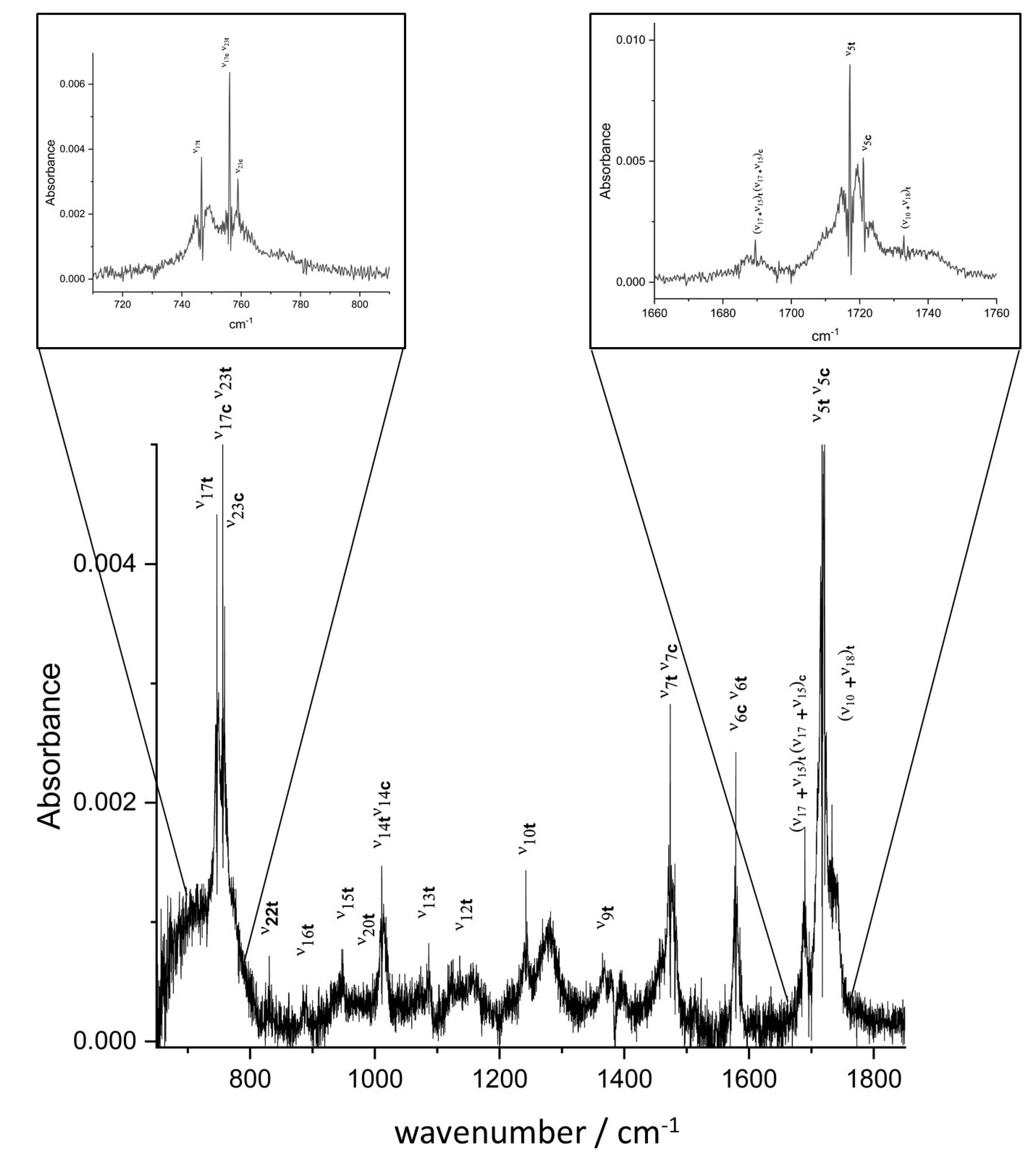
2.1. Vibrational Analysis
2.2. Supersonic Jet Measurements
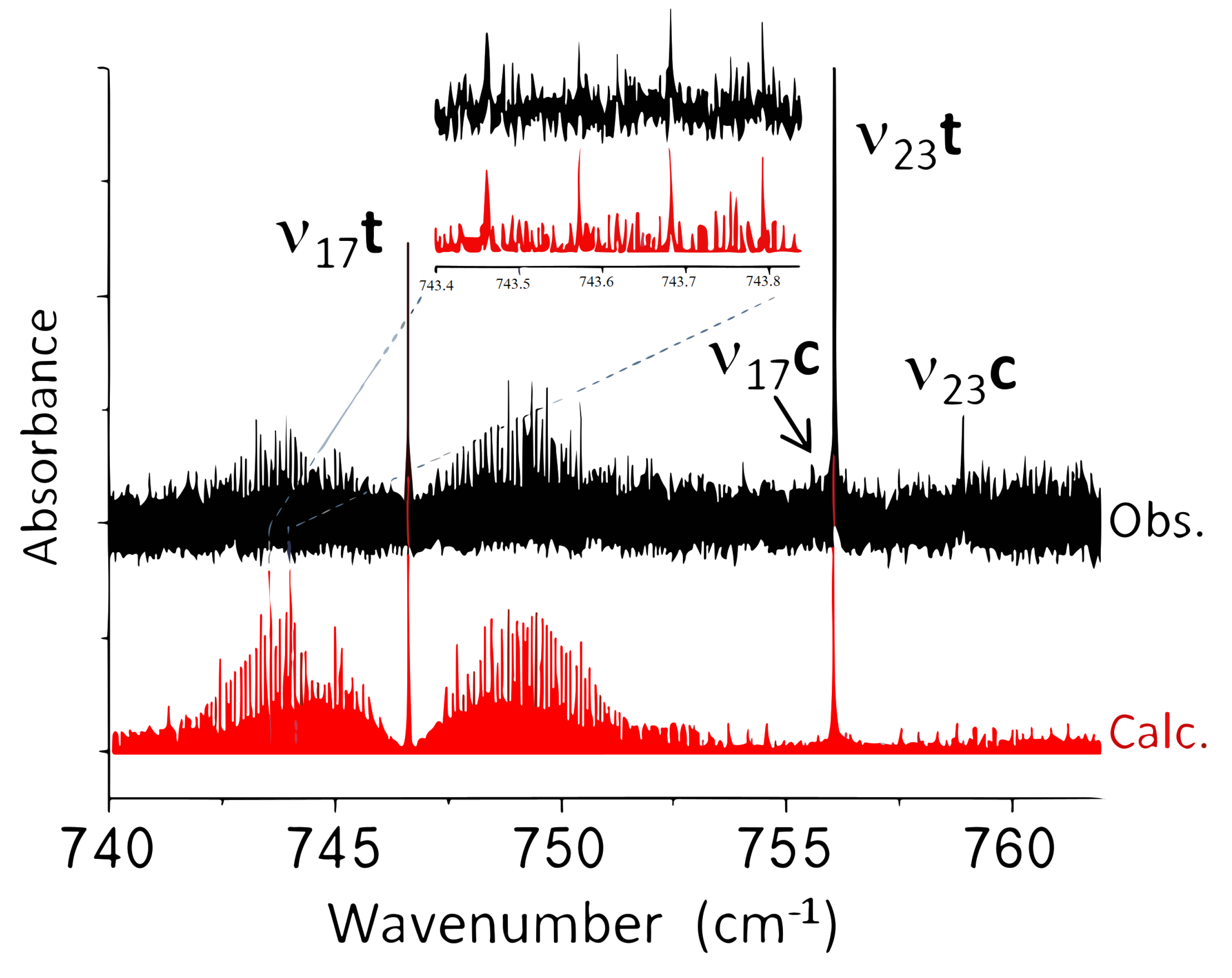
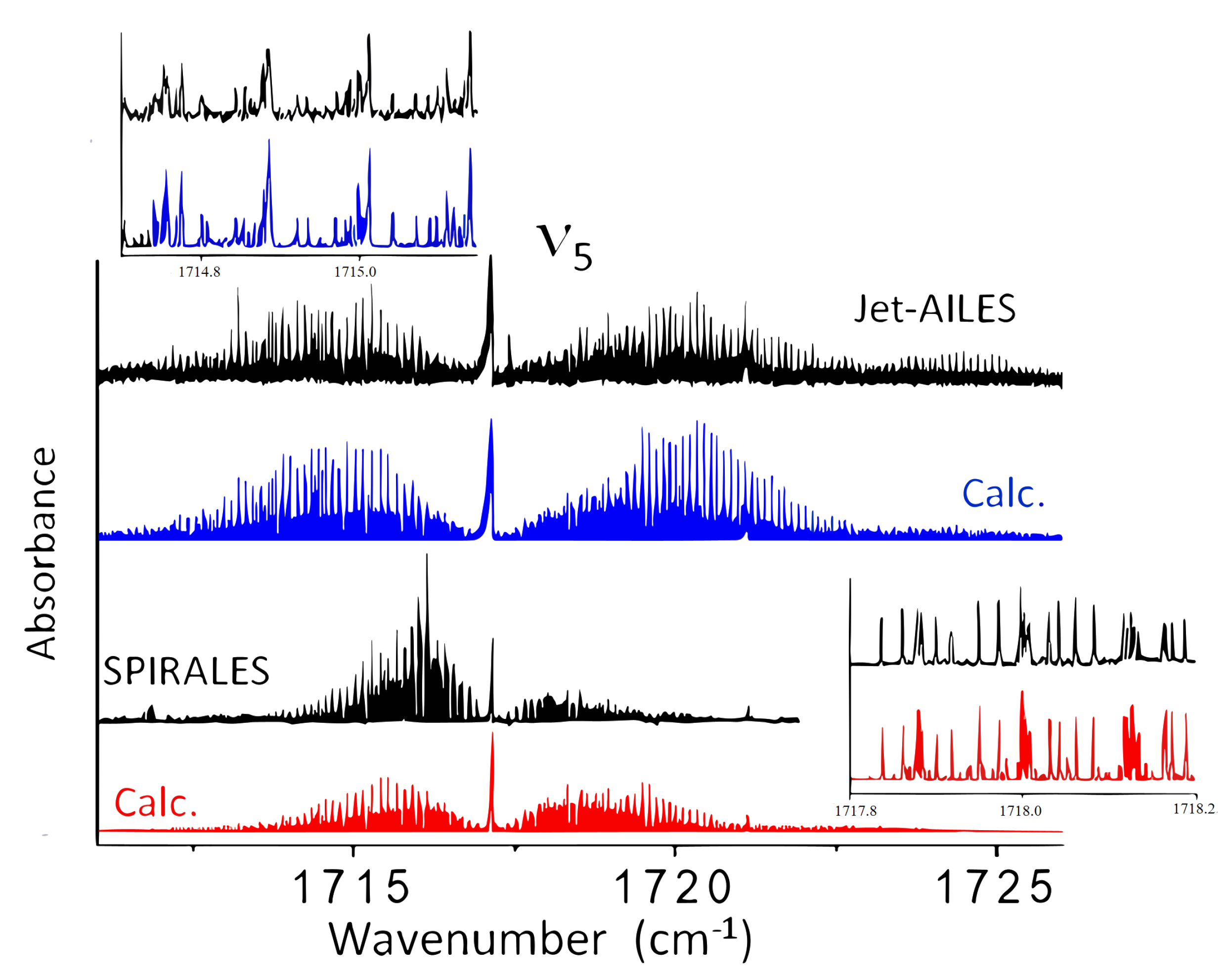
2.2.1. Jet-AILES Measurements: , and Rovibrational Bands
2.2.2. SPIRALES Measurements: Rovibrational Bands
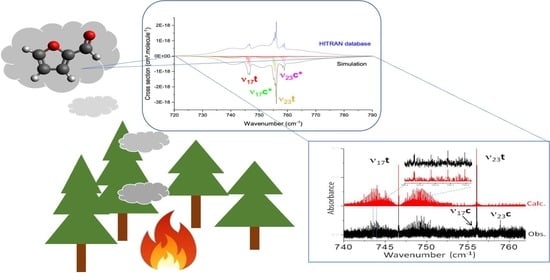
2.2.3. SPIRALES and Jet-AILES Measurements: Rovibrational Bands
2.3. Rovibrational Analysis
3. Discussion
3.1. Comparison between Theoretical and High-Resolution Experimental Results
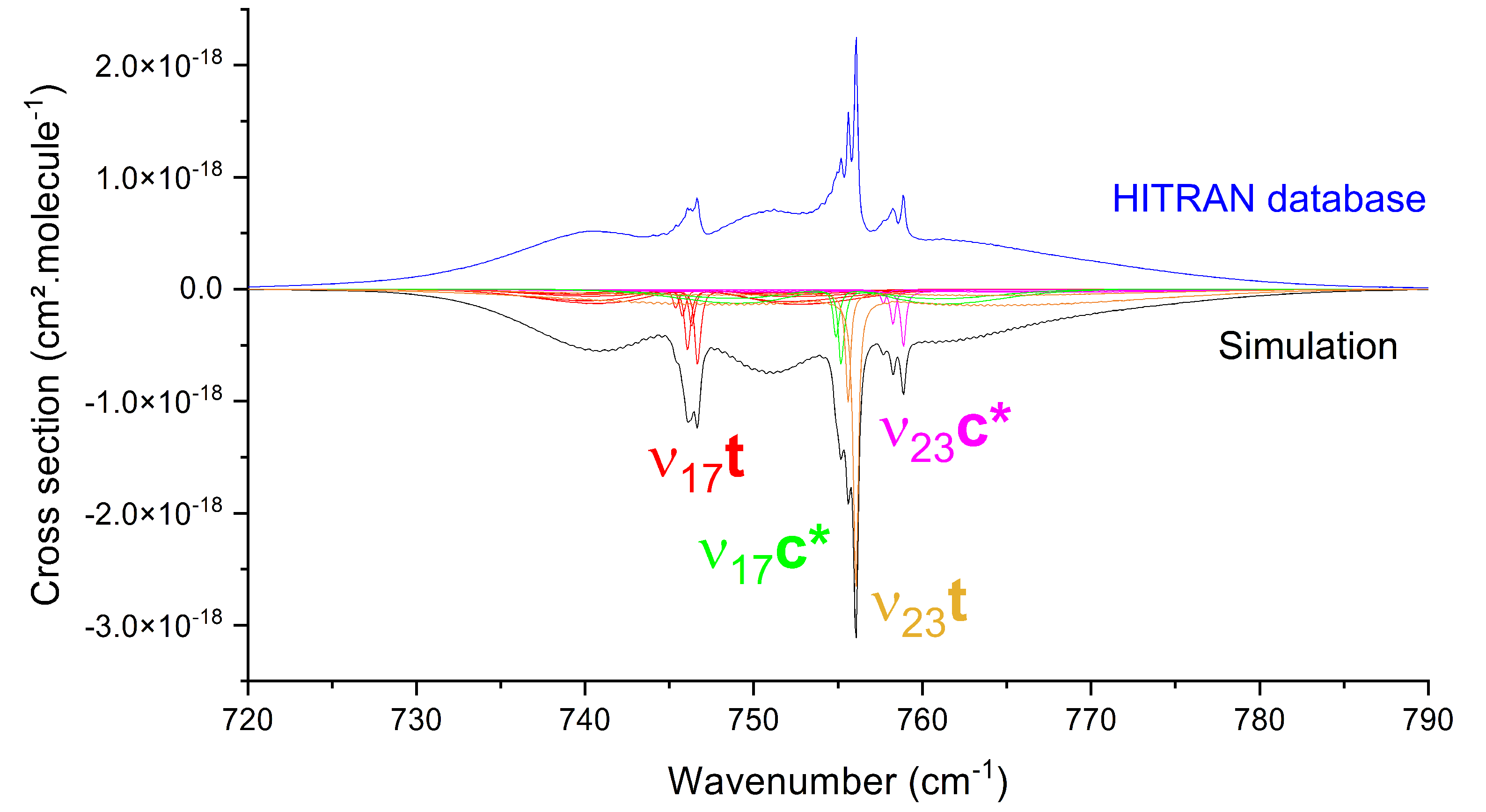
3.2. Mid-IR Cross Sections
4. Materials and Methods
4.1. Theoretical Methods
4.2. JET-AILES
4.3. SPIRALES
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| AILES | Advanced Infrared Line Exploited for Spectroscopy |
| CBS | Complete Basis Set |
| CD | Centrifugal Distortion |
| CEM | Controlled Evaporation Mixer |
| DFT | Density Functional Theory |
| EC-QCL | External-Cavity Quantum Cascade Laser |
| ES | Excited State |
| FF | Furfural |
| FT | Fourier Transform |
| FTIR | Fourier Transform InfraRed |
| FTMW | Fourier Transform MicroWave |
| FWHM | Full Width at Half Maximum |
| GS | Ground State |
| HITRAN | High-Resolution Transmission |
| IR | InfraRed |
| ip | In-Plane |
| MAE | Mean Absolute Error |
| MP2 | Møller-Plesset perturbation theory at 2nd order |
| MW | MicroWave |
| oop | out-of-plane |
| PNNL | Pacific Northwest National Laboratory |
| PT | Piezoelectric Transducer |
| QCL | Quantum Cascade Laser |
| RMS | Root Mean Square |
| slm | Standard liter per minute |
| SNR | Signal-to-Noise Ratio |
| SOA | Secondary Organic Aerosol |
| SOLEIL | Source Optimisée de Lumière d’Énergie Intermédiaire du LURE |
| SPIRALES | SPectroscopie InfraRouge Accordable par Laser dans une Expansion Supersonique |
| VOC | Volatile Organic Compound |
| VUV | Visible-UltraViolet |
References
- Edye, L.A.; Richards, G.N. Analysis of Condensates from Wood Smoke: Components Derived from Polysaccharides and Lignins. Environ. Sci. Technol. 1991, 25, 1133–1137. [Google Scholar] [CrossRef]
- Andreae, M.O.; Merlet, P. Emission of trace gases and aerosols from biomass burning. Glob. Biogeochem. Cycles 2001, 15, 955–966. [Google Scholar] [CrossRef]
- Paczkowski, S.; Paczkowska, M.; Dippel, S.; Schulze, N.; Schütz, S.; Sauerwald, T.; Weiß, A.; Bauer, M.; Gottschald, J.; Kohl, C.D. The olfaction of a fire beetle leads to new concepts for early fire warning systems. Sens. Actuators B Chem. 2013, 183, 273–282. [Google Scholar] [CrossRef]
- Colmenar, I.; Martín, P.; Cabañas, B.; Salgado, S.; Villanueva, F.; Ballesteros, B. Evaluation of the SOA Formation in the Reaction of Furfural with Atmospheric Oxidants. Atmosphere 2020, 11, 927. [Google Scholar] [CrossRef]
- Al Ali, F.; Coeur, C.; Houzel, N.; Bouya, H.; Tomas, A.; Romanias, M.N. Rate Coefficients for the Gas-Phase Reactions of Nitrate Radicals with a Series of Furan Compounds. J. Phys. Chem. A 2022, 126, 8674–8681. [Google Scholar] [CrossRef]
- Doiseau, A.C. Déshydratation Catalytique du Xylose en Furfural. Ph.D Thesis, 2014. Available online: https://theses.hal.science/tel-01127442 (accessed on 1 April 2023).
- Little, T.S.; Qiu, J.; Durig, J.R. Asymmetric torsional potential function and conformational analysis of furfural by far infrared and Raman spectroscopy. Spectrochim. Acta Part A Mol. Spectrosc. 1989, 45, 789–794. [Google Scholar] [CrossRef]
- Ferreira da Silva, F.; Lange, E.; Limão-Vieira, P.; Jones, N.C.; Hoffmann, S.V.; Hubin-Franskin, M.J.; Delwiche, J.; Brunger, M.J.; Neves, R.F.C.; Lopes, M.C.A.; et al. Electronic excitation of furfural as probed by high-resolution vacuum ultraviolet spectroscopy, electron energy loss spectroscopy, and ab initio calculations. J. Chem. Phys. 2015, 143, 144308. [Google Scholar] [CrossRef]
- Johnson, T.J.; Profeta, L.T.M.; Sams, R.L.; Griffith, D.W.T.; Yokelson, R.L. An infrared spectral database for detection of gases emitted by biomass burning. Vib. Spectrosc. 2010, 53, 97–102. [Google Scholar] [CrossRef]
- Motiyenko, R.A.; Alekseev, E.A.; Dyubko, S.F.; Lovas, F.J. Microwave spectrum and structure of furfural. J. Mol. Spectrosc. 2006, 240, 93–101. [Google Scholar] [CrossRef]
- Gregory, C.; van Wijngaarden, J. Investigation of the rotamers of 3-furfural by microwave spectroscopy. J. Mol. Spectrosc. 2020, 373, 111374. [Google Scholar] [CrossRef]
- Asselin, P.; Bruckhuisen, J.; Roucou, A.; Goubet, M.; Martin-Drumel, M.A.; Jabri, A.; Belkhodja, Y.; Soulard, P.; Georges, R.; Cuisset, A. Jet-cooled rovibrational spectroscopy of methoxyphenols using two complementary FTIR and QCL based spectrometers. J. Chem. Phys. 2019, 151, 194302. [Google Scholar] [CrossRef] [PubMed]
- Herzberg, G.; Spinks, J. Molecular Spectra and Molecular Structure: Infrared and Raman Spectra of Polyatomic Molecules; Molecular Spectra and Molecular Structure, D. Van Nostrand Company: New York, NY, USA, 1939. [Google Scholar]
- Adámek, P.; Volka, K.; Ksandr, Z.; Stibor, I. Vibrational spectra of 2-furaldehyde. J. Mol. Spectrosc. 1973, 47, 252–267. [Google Scholar] [CrossRef]
- Motiyenko, R.; Alekseev, E.; Dyubko, S. Microwave spectroscopy of furfural in vibrationally excited states. J. Mol. Spectrosc. 2007, 244, 9–12. [Google Scholar] [CrossRef]
- Western, C.M. PGOPHER: A program for simulating rotational, vibrational and electronic spectra. J. Quant. Spectrosc. Radiat. Transfer 2017, 186, 221–242. [Google Scholar] [CrossRef]
- Gruet, S.; Pirali, O.; Goubet, M.; Tokaryk, D.W.; Brechignac, P. High-Resolution Far-Infrared Spectroscopy of N-Substituted Two-Ring Polycyclic Aromatic Hydrocarbons: An Extended Study. J. Phys. Chem. A 2016, 120, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Bteich, S.; Goubet, M.; Motiyenko, R.; Margulès, L.; Huet, T. Vibrational dynamic and spectroscopic molecular parameters of trans-Methylglyoxal, a gaseous precursor of secondary organic aerosols. J. Mol. Spectrosc. 2018, 348, 124–129. [Google Scholar] [CrossRef]
- Roucou, A.; Goubet, M.; Kleiner, I.; Bteich, S.; Cuisset, A. Large Amplitude Torsions in Nitrotoluene Isomers Studied by Rotational Spectroscopy and Quantum Chemistry Calculations. ChemPhysChem 2020, 21, 2523–2538. [Google Scholar] [CrossRef]
- Montgomery, J.; Michels, H.; Fournier, J. Second Moments and Rotational Spectroscopy. J. Mol. Spectrosc. 2016, 325, 42–49. [Google Scholar] [CrossRef]
- Kochanov, R.; Gordon, I.; Rothman, L.; Shine, K.; Sharpe, S.; Johnson, T.; Wallington, T.; Harrison, J.; Bernath, P.; Birk, M.; et al. Infrared absorption cross-sections in HITRAN2016 and beyond: Expansion for climate, environment, and atmospheric applications. J. Quant. Spectrosc. Radiat. Transf. 2019, 230, 172–221. [Google Scholar] [CrossRef]
- Senent, M.L.; Dalbouha, S.; Cuisset, A.; Sadovskii, D. Theoretical Spectroscopic Characterization at Low Temperatures of Dimethyl Sulfoxide: The Role of Anharmonicity. J. Phys. Chem. A 2015, 119, 9644–9652. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Benchmark calculations with correlated molecular wave functions. VI. Second row A2 and first row/second row AB diatomic molecules. J. Chem. Phys. 1994, 101, 8877–8893. [Google Scholar] [CrossRef]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Biczysko, M.; Panek, P.; Scalmani, G.; Bloino, J.; Barone, V. Harmonic and Anharmonic Vibrational Frequency Calculations with the Double-Hybrid B2PLYP Method: Analytic Second Derivatives and Benchmark Studies. J. Chem. Theory Comput. 2010, 6, 2115–2125. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Steinmetz, M. Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase. Phys. Chem. Chem. Phys. 2013, 15, 16031–16042. [Google Scholar] [CrossRef]
- Pirali, O.; Goubet, M.; Boudon, V.; DAccolti, L.; Fusco, C.; Annese, C. Characterization of isolated 1-aza-adamantan-4-one (C9H13NO) from microwave, millimeter-wave and infrared spectroscopy supported by electronic structure calculations. J. Mol. Spectrosc. 2017, 338, 6–14. [Google Scholar] [CrossRef]
- Cirtog, M.; Asselin, P.; Soulard, P.; Tremblay, B.; Madebène, B.; Alikhani, M.E.; Georges, R.; Moudens, A.; Goubet, M.; Huet, T.R.; et al. The (CH2)2O–H2O Hydrogen Bonded Complex. Ab Initio Calculations and Fourier Transform Infrared Spectroscopy from Neon Matrix and a New Supersonic Jet Experiment Coupled to the Infrared AILES Beamline of Synchrotron SOLEIL. J. Phys. Chem. A 2011, 115, 2523–2532. [Google Scholar] [CrossRef]
- Asselin, P.; Potapov, A.; Turner, A.C.; Boudon, V.; Bruel, L.; Gaveau, M.A.; Mons, M. Conformational landscape of the SF6 dimer as revealed by high resolution infrared spectroscopy and complexation with rare gas atoms. Phys. Chem. Chem. Phys. 2017, 19, 17224–17232. [Google Scholar] [CrossRef]
- Jabri, A.; Belkhodja, Y.; Berger, Y.; Kleiner, I.; Asselin, P. High resolution rovibrational analysis of dimethyl sulfide spectrum in the 10 μm atmospheric window combining supersonic jet-quantum cascade laser and FTIR spectroscopies. J. Mol. Spectrosc. 2018, 349, 32–36. [Google Scholar] [CrossRef]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Belkhodja, Y.; Loreau, J.; Van der Avoird, A.; Berger, Y.; Asselin, P. Intermolecular dynamics of NH3-rare gas complexes in the ν2 umbrella region of NH3 investigated by rovibrational laser jet-cooled spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2021, 23, 10864–10874. [Google Scholar] [CrossRef] [PubMed]
- Brookes, M.D.; Xia, C.; Anstey, J.A.; Fulsom, B.G.; Au Yong, K.X.; King, J.M.; McKellar, A.R.W. Tunable diode laser spectrometer for pulsed supersonic jets: Application to weakly-bound complexes and clusters. Spectrochim. Acta Part A 2004, 60, 3235–3242. [Google Scholar] [CrossRef] [PubMed]
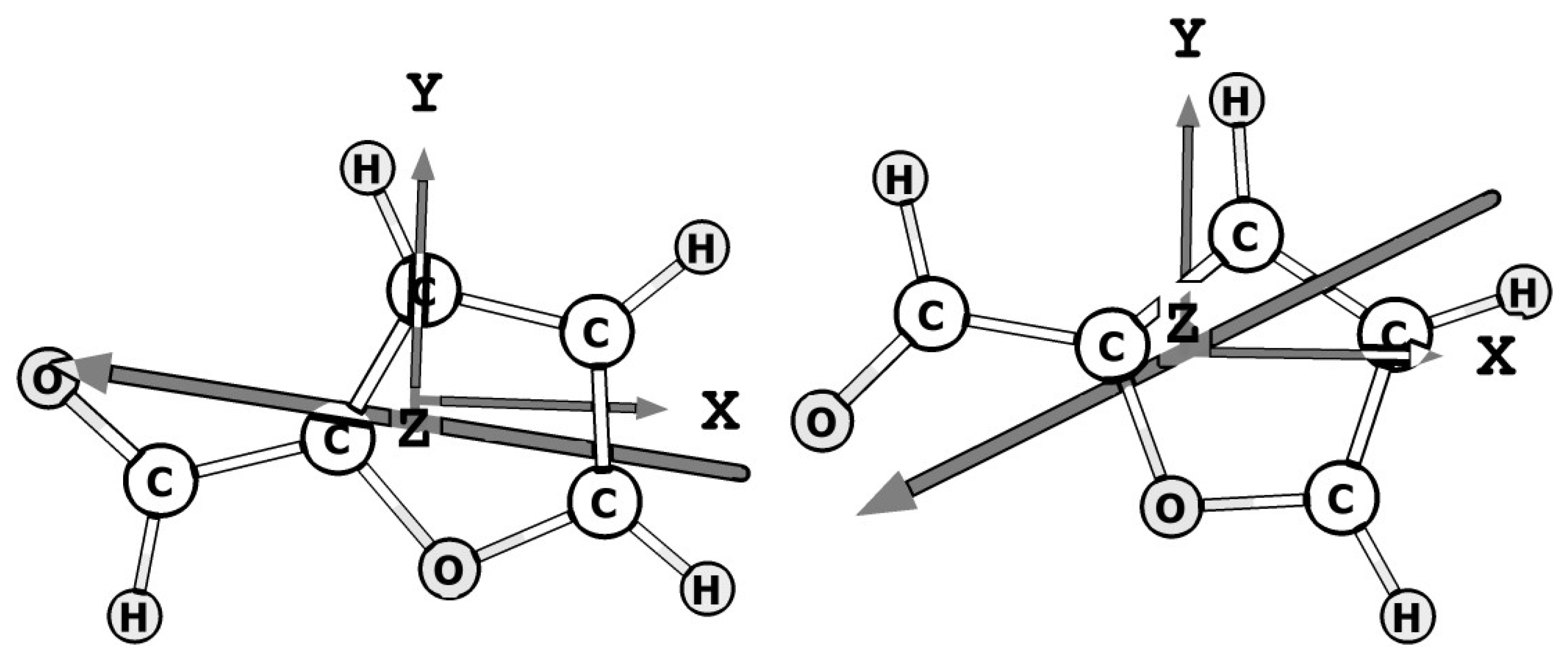



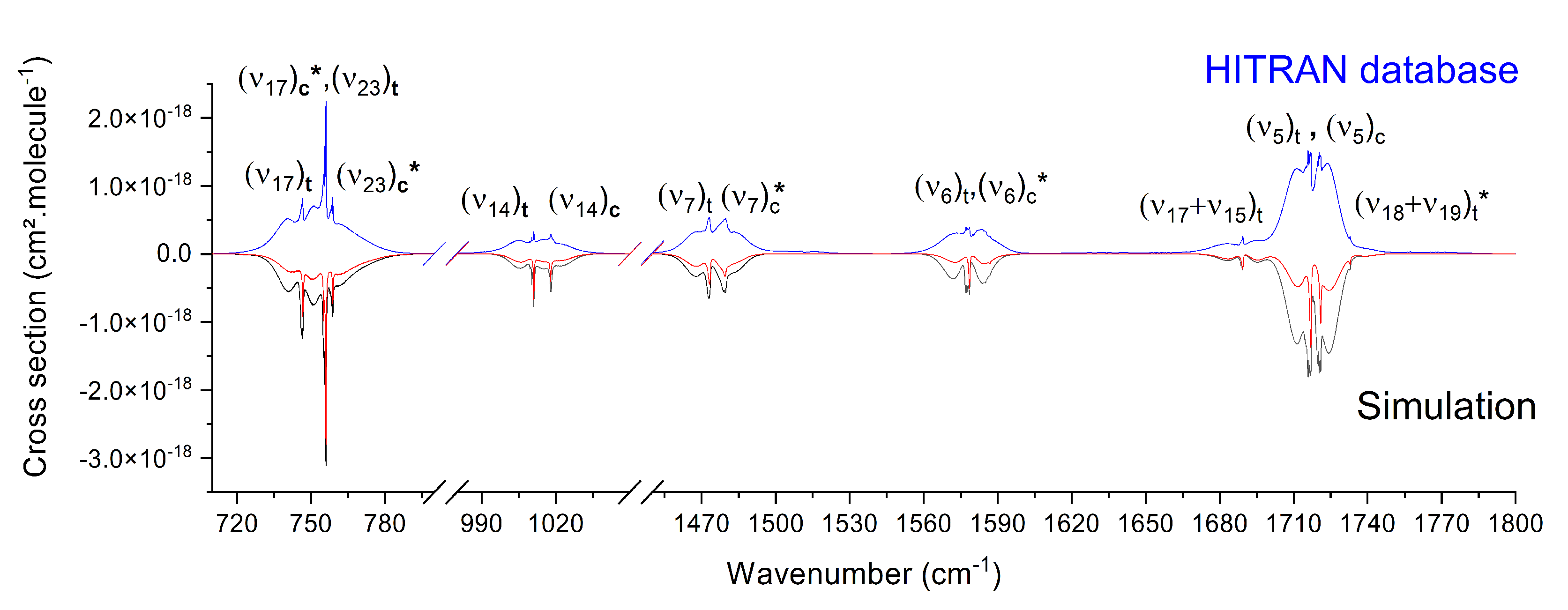
| Mode | Symmetry | Conformer | Description | |||
|---|---|---|---|---|---|---|
| 1732.9 | A’ | trans | 1779.6 | 1755.4 | ||
| 1721.1 | A’ | cis | 1732.5 | 1705.3 | C=O stretching | |
| 1717.1 | A’ | trans | 1726.4 | 1704.8 | C=O stretching | |
| 1689.5 | A’ | trans | 1719.4 | 1700.5 | ||
| 1687.2 | A’ | cis | 1722.2 | 1692.1 | ||
| 1578.8 | A’ | trans | 1595.0 | 1566.1 * | ring C=C asym stretching | |
| 1577.1 | A’ | cis | 1584.4 | 1554.2 * | ring C=C asym stretching | |
| 1481.1 | A’ | cis | 1506.8 | 1479.2 * | ring C=C sym stretching | |
| 1473.6 | A’ | trans | 1500.1 | 1475.8 * | ring C=C sym stretching | |
| 1365.0 | A’ | trans | 1402.1 | 1368.8 | C-H ip bending | |
| 1242.1 | A’ | trans | 1281.7 | 1259.0 | ring C-H ip bending | |
| 1136.0 | A’ | trans | 1193.6 | 1173.3 | ring C-H ip bending | |
| 1086.4 | A’ | trans | 1116.2 | 1101.8 | ring C-H ip bending | |
| 1017.7 | A’ | cis | 1044.3 | 1022.7 * | ring C-H ip bending | |
| 1011.0 | A’ | trans | 1038.6 | 1016.9 * | ring C-H ip bending | |
| 948.6 | A’ | trans | 963.7 | 952.4 | ring ip bending | |
| 886.9 | A’ | trans | 896.1 | 888.2 | ring ip bending | |
| 755.6 | A’ | cis | 769.7 | 759.2 | C-C-H scissoring | |
| 746.6 | A’ | trans | 755.7 | 750.6 | C-C-H scissoring | |
| 996.4 | A” | trans | 1010.5 | 996.7 * | C-H oop bending | |
| 830.6 | A” | trans | 840.9 | 814.6 * | ring C-H oop bending | |
| 758.9 | A” | cis | 775.5 | 757.9 * | ring C-H oop bending | |
| 756.1 | A” | trans | 769.2 | 755.2 * | ring C-H oop bending |
| Frequency | GS | |||||||
|---|---|---|---|---|---|---|---|---|
| (cm) | 746.59621(2) | 756.05273(2) | 1011.05284(2) | 1473.58372(3) | 1578.77264(3) | 1689.52004(2) | 1717.14825(2) | |
| A | 8191.77383(13) | 8196.9940(13) | 8178.0125(220) | 8196.3949(148) | 8168.443(32) | 8184.040(38) | 8181.784(119) | 8179.2141(305) |
| B | 2045.929569(13) | 2045.2823(58) | 2045.3409(170) | 2046.3469(48) | 2041.9928(86) | 2044.0863(87) | 2043.6672(124) | 2043.8979(101) |
| C | 1637.183877(12) | 1636.2156(47) | 1637.5243(238) | 1637.2606(37) | 1636.8828(54) | 1635.6319(25) | 1635.0497(96) | 1635.5041(61) |
| 0.1361873(39) | 0.1342(20) | 0.155(8) | 0.1379(18) | 0.1361873 | 0.1361873 | 0.110(8) | 0.1269(41) | |
| 1.7829(24) | 1.7316(21) | 2.114(111) | 2.694(45) | 1.7829 | 1.7829 | .0456(26) | 2.771(135) | |
| 0.706618(18) | 0.9057(13) | 0.808(57) | 0.875(16) | 0.706618 | 0.706618 | 3.59(32) | 0.642(44) | |
| 0.0314688(12) | 0.0306(14) | 0.0418(122) | 0.0283(12) | 0.0314688 | 0.0314688 | 0.0314688 | 0.0469(32) | |
| 0.82192(118) | 0.544(82) | 0.82192 | 0.877(75) | 0.82192 | 0.82192 | 0.82192 | 0.82192 | |
| 0.01758(44) | ||||||||
| 0.6571(32) | ||||||||
| 5.097(13) | ||||||||
| IR RMS | 0.0099 | 10.8 | 9.9 | 17.4 | 18.9 | 24.6 | 15.9 | 13.8 |
| N lines | 1844 | 2401 | 1224 | 3446 | 513 | 508 | 662 | 999 |
| 1–99 | 1–56 | 1–39 | 1–56 | 2–33 | 4–52 | 4–52 | 1–52 | |
| 0–53 | 0–35 | 0-21 | 0–22 | 0–14 | 0–14 | 0–10 | 0–20 |
| Frequency | GS | ||
|---|---|---|---|
| (cm | 1017.76832(2) | 1721.12234(3) | |
| A | 8143.738729(71) | 8149.490(40) | 8135.273(67) |
| B | 2098.724250(14) | 2099.3461(62) | 2096.7713(99) |
| C | 1668.872904(14) | 1668.9979(58) | 1667.4017(61) |
| 0.1726591(62) | 0.1625(37) | 0.1779(38) | |
| 1.81403(24) | 1.894(173) | 1.81403 | |
| 0.49995(32) | 0.106(50) | 0.49995 | |
| 0.0403044(13) | 0.0403044 | 0.0403044 | |
| 0.80893(11) | 0.80893 | 0.80893 | |
| 0.02717(76) | |||
| .3231(55) | |||
| .2598(265) | |||
| IR RMS | 0.0125 | 12.6 | 12.9 |
| N lines | 2488 | 624 | 244 |
| 1–89 | 1–42 | 5–46 | |
| 0–38 | 0–18 | 0–12 |
| Trans-Furfural | |||||
|---|---|---|---|---|---|
| Calculated | Experimental | = exp-calc | corrected | ||
| from GS deviation | |||||
| GS | A | 8175.217 | 8191.774 | 016.557 | |
| B | 2049.726 | 2045.930 | −3.796 | ||
| C | 1638.853 | 1637.184 | −1.669 | ||
| 0.002 | 0.011 | 00.009 | |||
| A | 8186.172 | 8196.994 | 010.822 | −5.758 | |
| B | 2049.251 | 2045.282 | −3.968 | −0.173 | |
| C | 1637.714 | 1636.216 | −1.499 | 00.169 | |
| −0.118 | −0.061 | 00.057 | 00.052 | ||
| A | 8161.189 | 8178.013 | 016.824 | 00.295 | |
| B | 2049.062 | 2045.341 | −3.722 | 00.074 | |
| C | 1639.227 | 1637.524 | −1.703 | −0.034 | |
| 0.130 | 0.131 | 00.001 | −0.008 | ||
| A | 8185.472 | 8196.395 | 010.923 | −5.655 | |
| B | 2050.262 | 2045.341 | −4.921 | −1.123 | |
| C | 1638.627 | 1637.524 | −1.103 | 00.565 | |
| −0.090 | 0.061 | 00.151 | 00.142 | ||
| A | 8162.687 | 8168.443 | 05.756 | −10.776 | |
| B | 2048.163 | 2041.993 | −6.170 | −2.377 | |
| C | 1637.428 | 1636.883 | −0.545 | 01.122 | |
| 0.009 | 0.309 | 00.300 | 00.290 | ||
| A | 8158.790 | 8184.040 | 025.250 | 08.726 | |
| B | 2047.264 | 2044.086 | −3.177 | 00.614 | |
| C | 1637.128 | 1635.632 | −1.496 | 00.170 | |
| 0.050 | 0.005 | −0.045 | −0.060 | ||
| A | 8191.921 | 8181.784 | −10.137 | −26.729 | |
| B | 2048.112 | 2043.667 | −4.445 | ||
| C | 1635.617 | 1635.504 | −0.113 | 01.553 | |
| −0.269 | 0.027 | 00.296 | 00.264 | ||
| A | 8165.685 | 8179.214 | 013.529 | −3.009 | |
| B | 2047.563 | 2043.898 | −3.666 | 00.127 | |
| C | 1637.128 | 1635.504 | −1.624 | 00.043 | |
| 0.006 | 0.023 | 00.017 | 00.008 | ||
| Cis-Furfural | |||||
| GS | A | 8139.736 | 8143.739 | 04.002 | |
| B | 2101.222 | 2098.724 | −2.497 | ||
| C | 1670.151 | 1668.873 | −1.278 | ||
| 0.005 | 0.017 | 00.012 | |||
| A | 8149.311 | 8149.490 | 00.179 | −3.829 | |
| B | 2101.883 | 2099.346 | −2.537 | −0.039 | |
| C | 1670.162 | 1668.998 | −1.164 | 00.113 | |
| −0.068 | −0.029 | 00.039 | 00.027 | ||
| A | 8131.539 | 8135.273 | 03.734 | −0.265 | |
| B | 2099.061 | 2096.771 | −2.290 | 00.205 | |
| C | 1668.441 | 1667.402 | −1.039 | 00.237 | |
| 0.005 | 0.028 | 00.023 | 00.010 | ||
| Wavenumber | Calculated from Our Simulations | Calculated from HITRAN | |
|---|---|---|---|
| Without Hot Bands | With Hot Bands | ||
| cm | cm.molecule | cm.molecule | cm.molecule |
| 700–795 | |||
| 980–1050 | |||
| 1450–1550 | |||
| 1550–1610 | |||
| 1660–1800 | |||
| Resolution | Optical Filter | Number of | Ar Flow | FF Flow | P | P | Slit Width | |
|---|---|---|---|---|---|---|---|---|
| Bandwidth | Averaged Scans | |||||||
| cm | cm | slm | slm | hPa | hPa | m | ||
| 0.55 | None | 30/30/30 | 5 | 0.5 | 95/123/252 | 0.23 | 100/80/50 | |
| 0.00102 | 650–950 | 84 | 10 | 1.0 | 97 | 0.37 | 130 | |
| 0.00102 | 1200–1800 | 160 | 10 | 1.0 | 320 | 0.37 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chawananon, S.; Asselin, P.; Claus, J.A.; Goubet, M.; Roucou, A.; Georges, R.; Sobczuk, J.; Bracquart, C.; Pirali, O.; Cuisset, A. Rovibrational Spectroscopy of Trans and Cis Conformers of 2-Furfural from High-Resolution Fourier Transform and QCL Infrared Measurements. Molecules 2023, 28, 4165. https://doi.org/10.3390/molecules28104165
Chawananon S, Asselin P, Claus JA, Goubet M, Roucou A, Georges R, Sobczuk J, Bracquart C, Pirali O, Cuisset A. Rovibrational Spectroscopy of Trans and Cis Conformers of 2-Furfural from High-Resolution Fourier Transform and QCL Infrared Measurements. Molecules. 2023; 28(10):4165. https://doi.org/10.3390/molecules28104165
Chicago/Turabian StyleChawananon, Sathapana, Pierre Asselin, Jordan A. Claus, Manuel Goubet, Anthony Roucou, Robert Georges, Joanna Sobczuk, Colwyn Bracquart, Olivier Pirali, and Arnaud Cuisset. 2023. "Rovibrational Spectroscopy of Trans and Cis Conformers of 2-Furfural from High-Resolution Fourier Transform and QCL Infrared Measurements" Molecules 28, no. 10: 4165. https://doi.org/10.3390/molecules28104165
APA StyleChawananon, S., Asselin, P., Claus, J. A., Goubet, M., Roucou, A., Georges, R., Sobczuk, J., Bracquart, C., Pirali, O., & Cuisset, A. (2023). Rovibrational Spectroscopy of Trans and Cis Conformers of 2-Furfural from High-Resolution Fourier Transform and QCL Infrared Measurements. Molecules, 28(10), 4165. https://doi.org/10.3390/molecules28104165