Real-Time Extension of TAO-DFT
Abstract
:1. Introduction
2. Ground-State Theory: TAO-DFT
2.1. Overview of TAO-DFT
2.2. Density Representation in TAO-DFT
2.3. Approximate Energy Functionals and Fictitious Temperatures in TAO-DFT
2.4. Comparison of KS-DFT, TAO-DFT, and FT-DFT
2.5. TAO-DFT-Related Methods
2.5.1. TAO-DFT with
2.5.2. KS-DFA with the rTAO Energy Correction
3. Real-Time Theory: RT-TAO-DFT
3.1. RT-TAO Equation
3.2. Matrix Representation
- Construct the initial one-electron density matrix (see Equation (56)) and the initial RT-TAO matrix (see Equation (57)) for the GS of the unperturbed physical system at time using TAO-DFT (i.e., the respective GS theory).
- Apply the TD field to the physical system for , and propagate the one-electron density matrix and the RT-TAO matrix in the time domain, according to the RT-TAO equation (given by the matrix representation, e.g., see Equation (55)).
- Post-process the resulting TD observables (electron density, dipole moment, etc.).
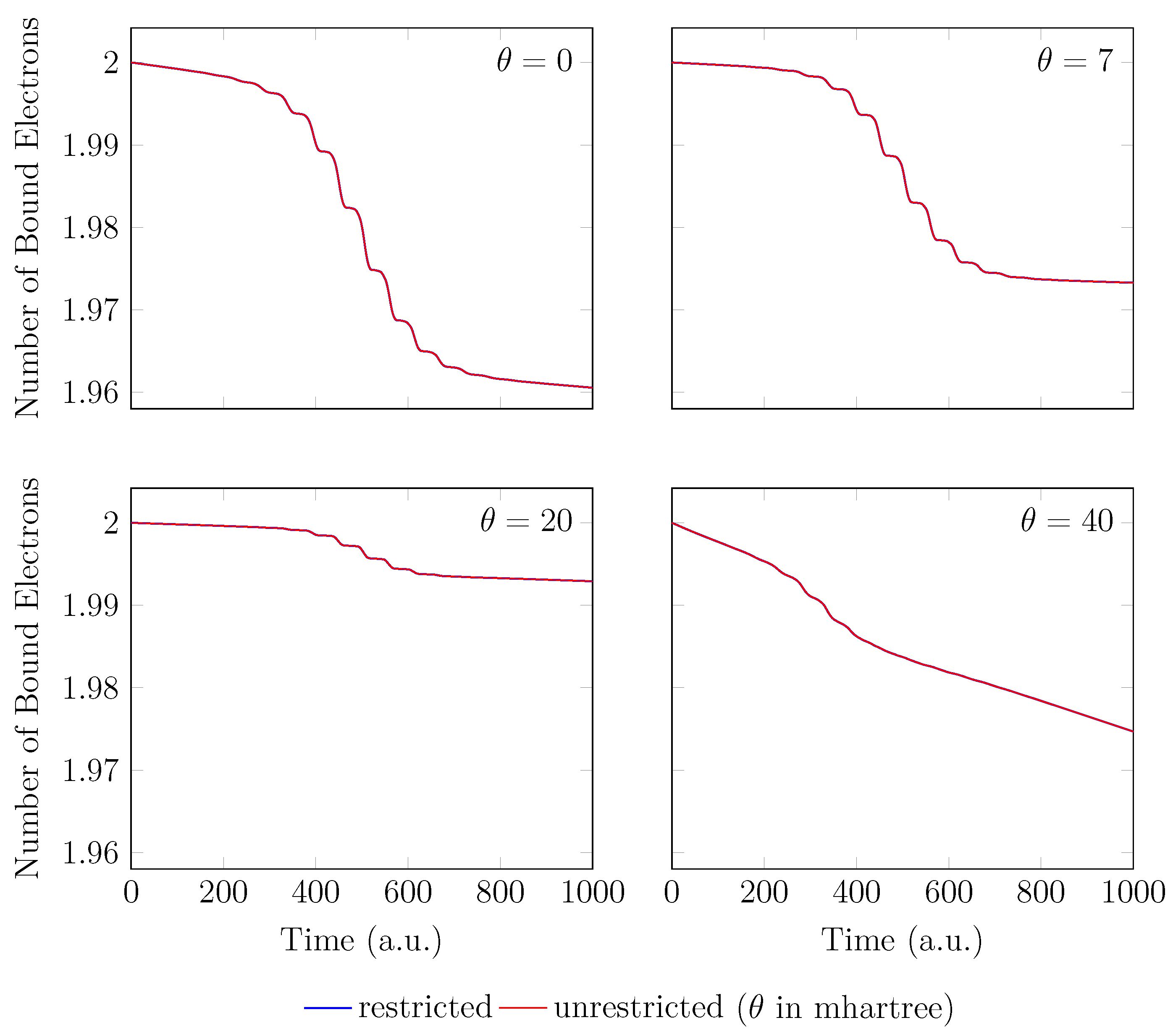
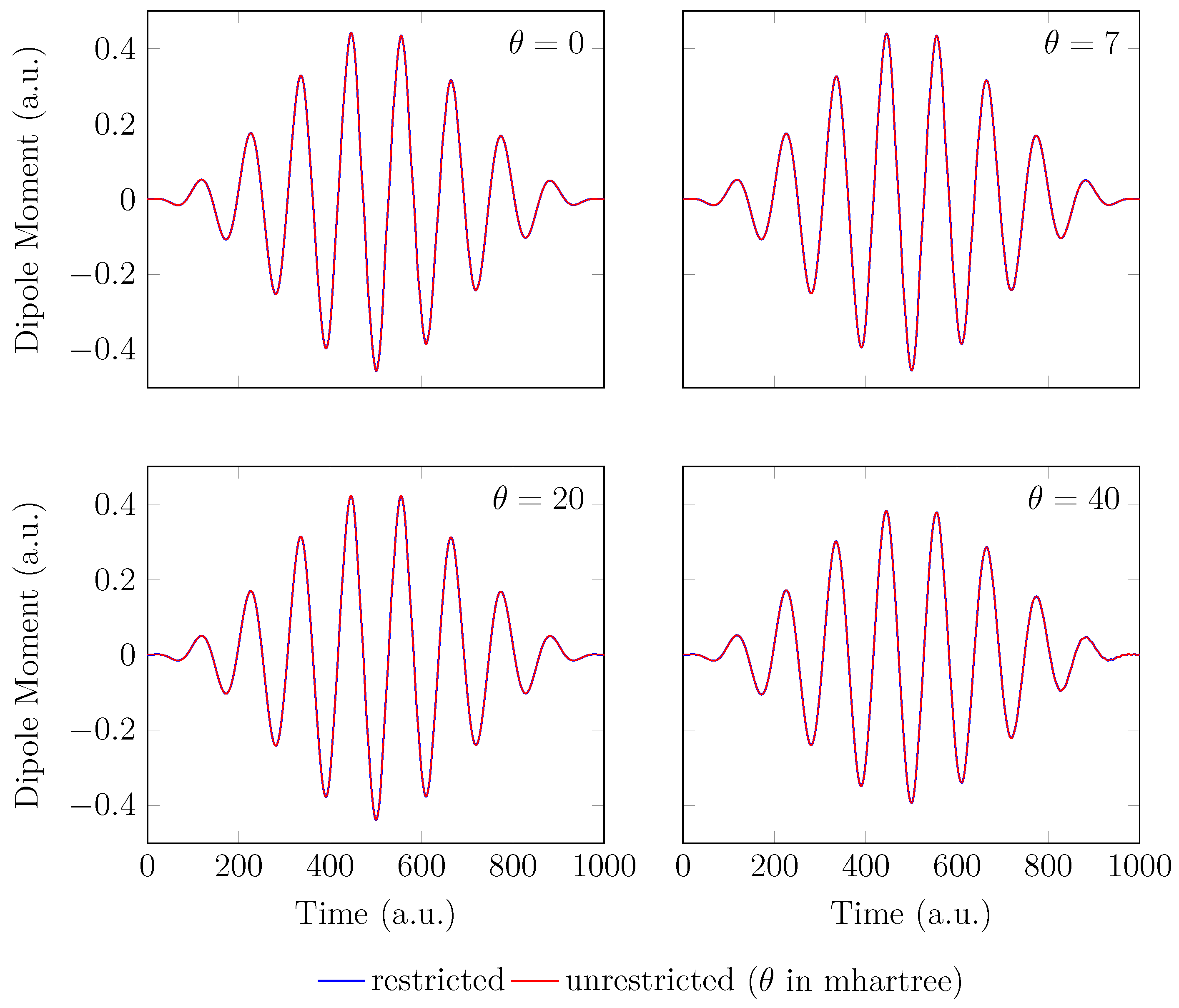
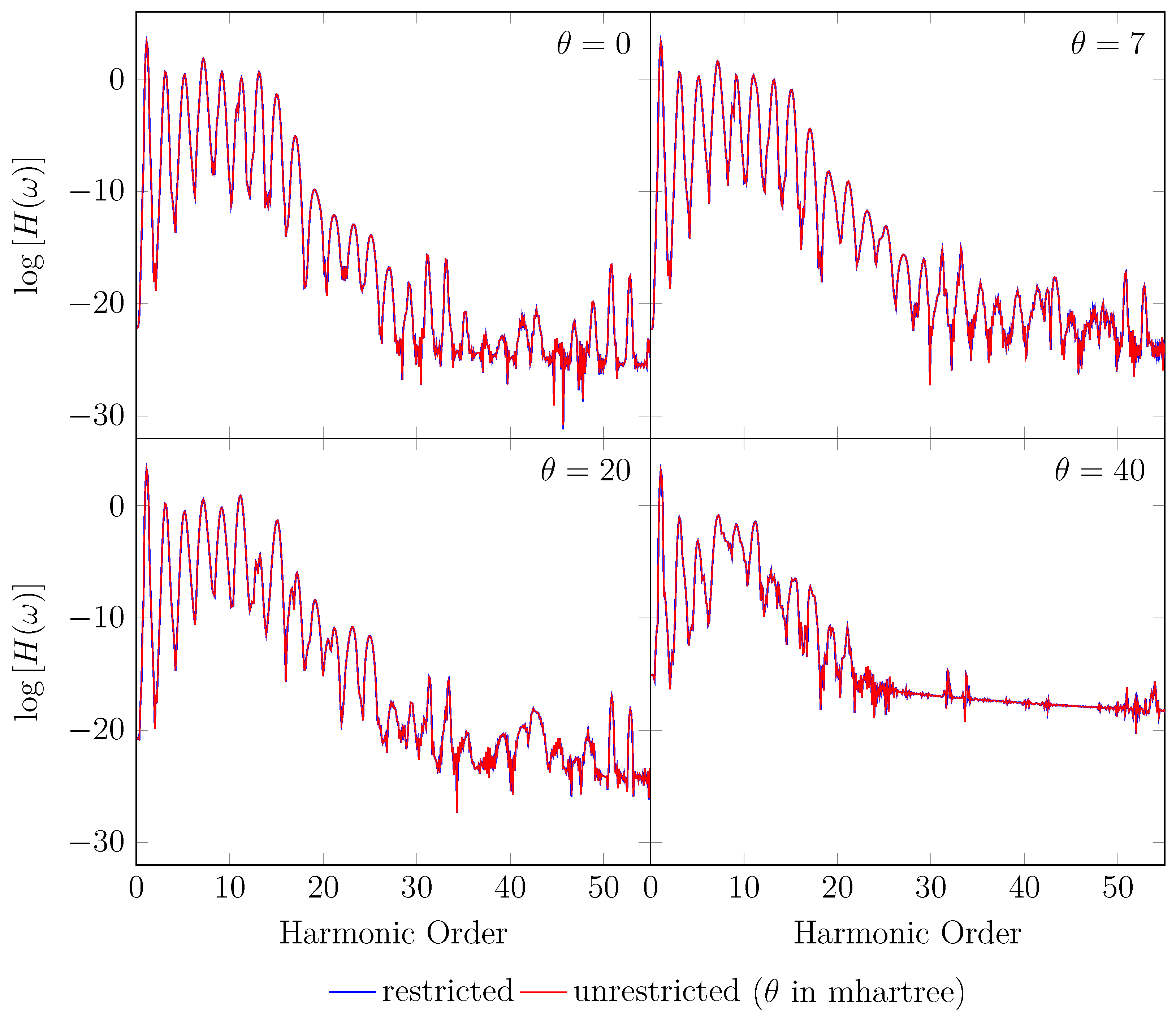
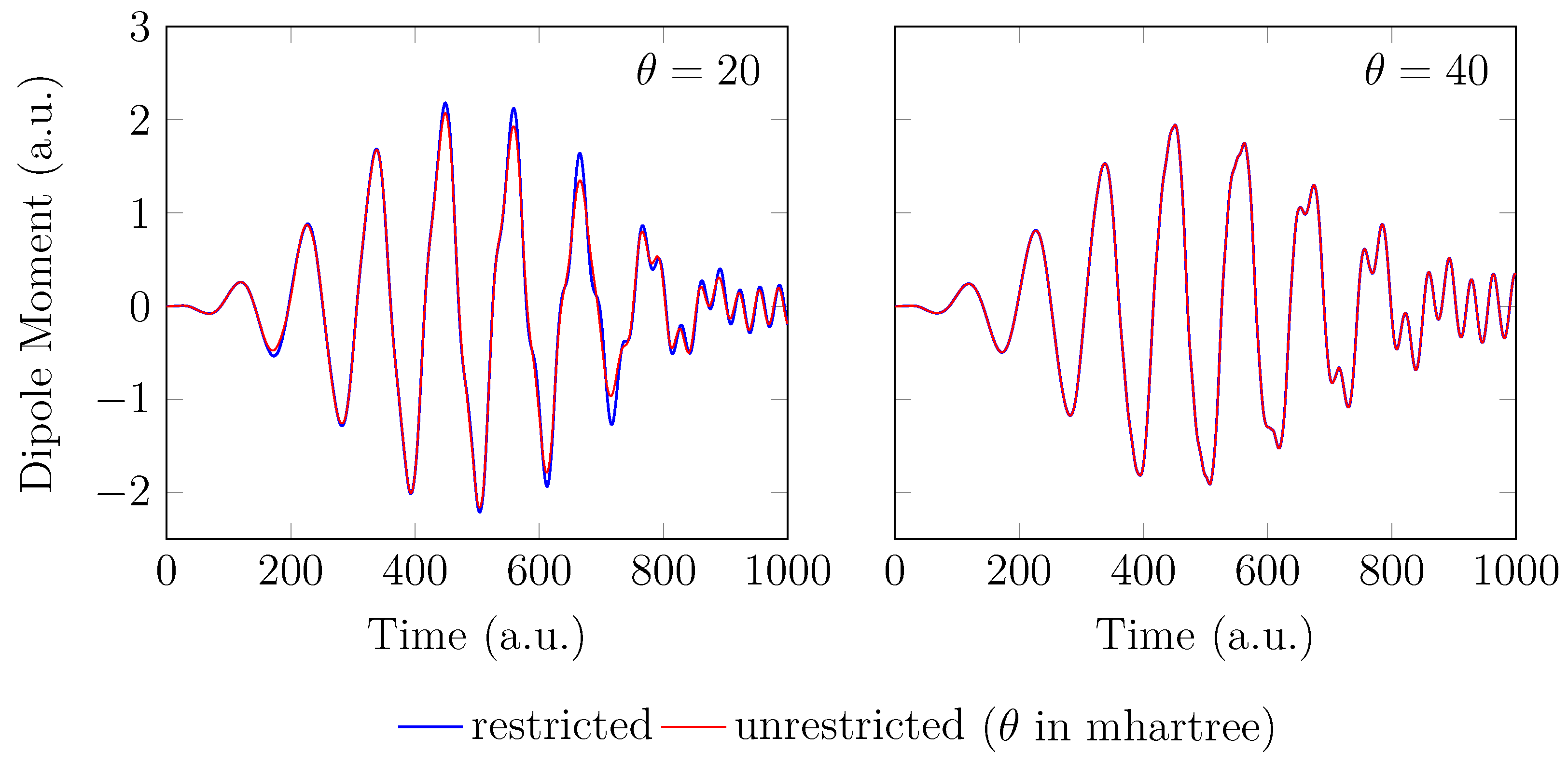
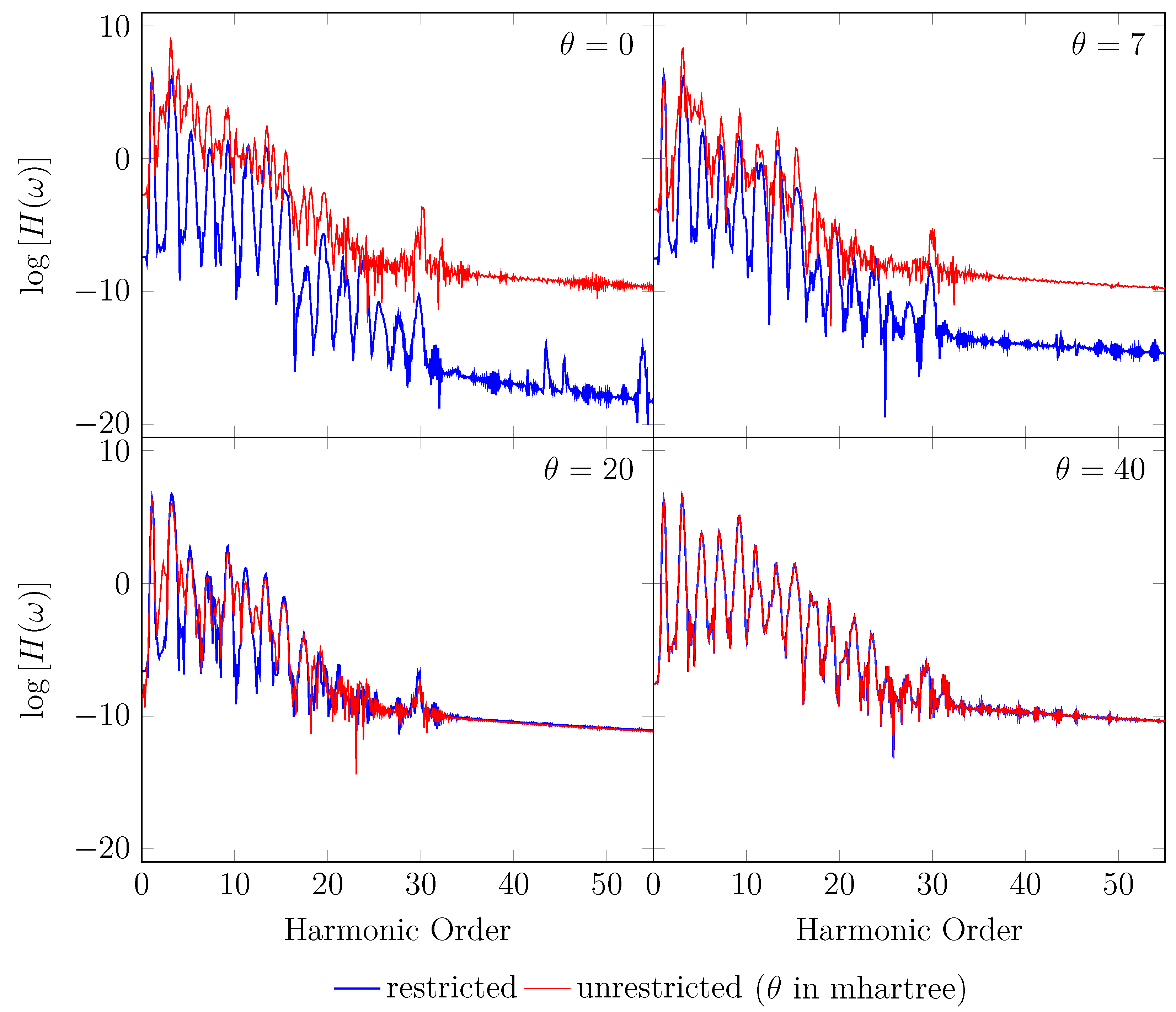
4. HHG Spectra from RT-TAO-DFT
- with an equilibrium bond length of 1.45 bohr (≈0.767 Å).
- with a stretched bond length of 3.78 bohr (≈2.00 Å).
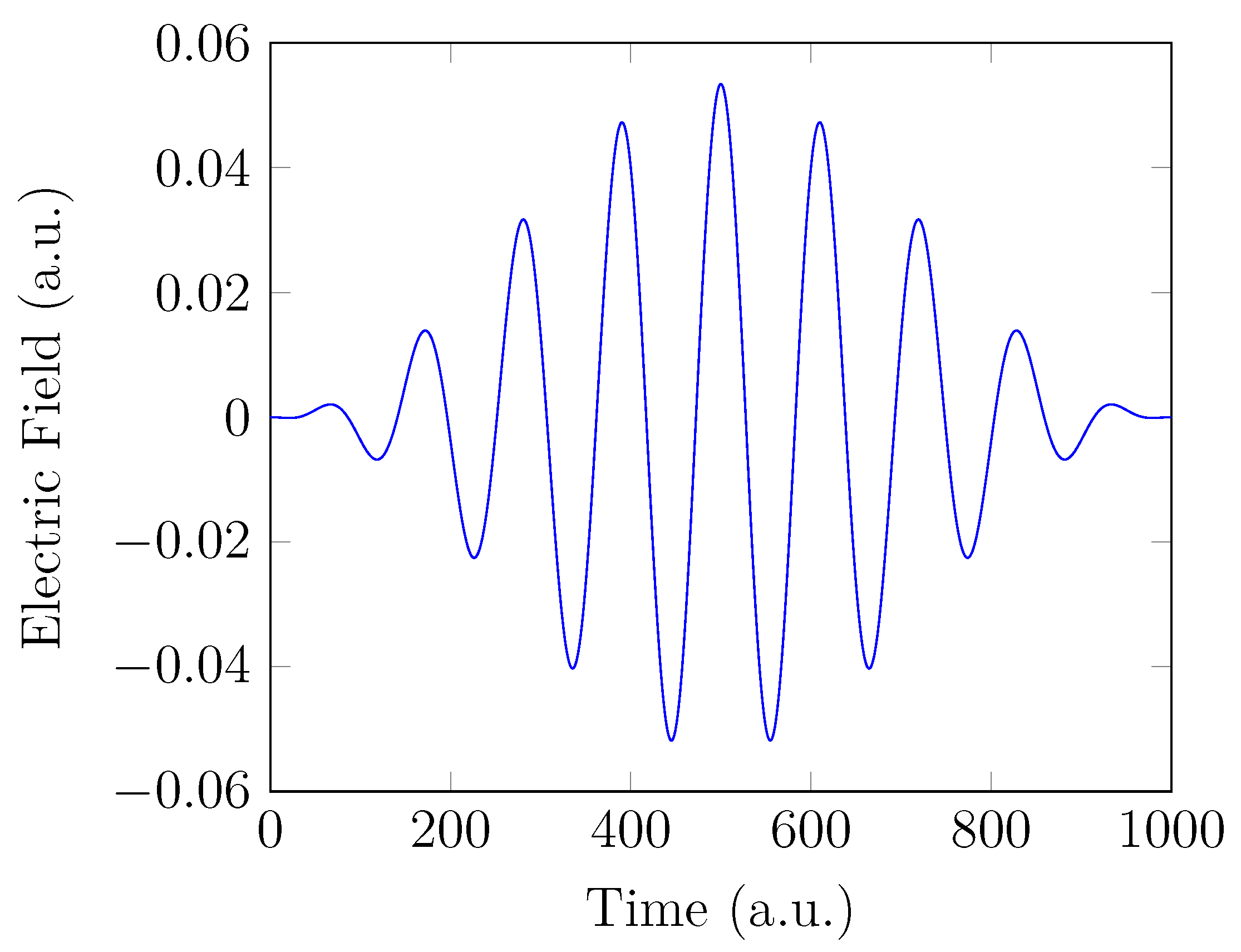
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Engel, E.; Dreizler, R.M. Density Functional Theory: An Advanced Course; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- Dreuw, A.; Head-Gordon, M. Single-reference ab initio methods for the calculation of excited states of large molecules. Chem. Rev. 2005, 105, 4009–4037. [Google Scholar] [CrossRef]
- Ullrich, C.A. Time-Dependent Density-Functional Theory: Concepts and Applications; Oxford University: New York, NY, USA, 2012. [Google Scholar]
- Casida, M.E. Recent Advances in Density Functional Methods, Part I; World Scientific: Singapore, 1995. [Google Scholar]
- Dirac, P.A.M. Note on exchange phenomena in the Thomas atom. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Casida, M.E.; Jamorski, C.; Casida, K.C.; Salahub, D.R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 1998, 108, 4439–4449. [Google Scholar] [CrossRef]
- Casida, M.E.; Salahub, D.R. Asymptotic correction approach to improving approximate exchange-correlation potentials: Time-dependent density-functional theory calculations of molecular excitation spectra. J. Chem. Phys. 2000, 113, 8918–8935. [Google Scholar] [CrossRef]
- Dreuw, A.; Weisman, J.L.; Head-Gordon, M. Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange. J. Chem. Phys. 2003, 119, 2943–2946. [Google Scholar] [CrossRef]
- Dreuw, A.; Head-Gordon, M. Failure of time-dependent density functional theory for long-range charge-transfer excited states: The zincbacteriochlorin-bacteriochlorin and bacteriochlorophyll-spheroidene complexes. J. Am. Chem. Soc. 2004, 126, 4007–4016. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Peng, D.; Steinmann, S.N.; van Aggelen, H.; Yang, W. Equivalence of particle-particle random phase approximation correlation energy and ladder-coupled-cluster doubles. J. Chem. Phys. 2013, 139, 104112. [Google Scholar] [CrossRef] [PubMed]
- van Aggelen, H.; Yang, Y.; Yang, W. Exchange-correlation energy from pairing matrix fluctuation and the particle-particle random-phase approximation. Phys. Rev. A 2013, 88, 030501(R). [Google Scholar] [CrossRef]
- Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014, 140, 18A521. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D. Role of exact exchange in thermally-assisted-occupation density functional theory: A proposal of new hybrid schemes. J. Chem. Phys. 2017, 146, 044102. [Google Scholar] [CrossRef] [PubMed]
- Xuan, F.; Chai, J.-D.; Su, H. Local density approximation for the short-range exchange free energy functional. ACS Omega 2019, 4, 7675–7683. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-S.; Chai, J.-D. Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT. J. Chem. Theory Comput. 2015, 11, 2003–2011. [Google Scholar] [CrossRef] [PubMed]
- Yeh, C.-N.; Chai, J.-D. Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: A TAO-DFT study. Sci. Rep. 2016, 6, 30562. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: A dispersion-corrected TAO-DFT study. Sci. Rep. 2016, 6, 33081. [Google Scholar] [CrossRef]
- Wu, C.-S.; Lee, P.-Y.; Chai, J.-D. Electronic properties of cyclacenes from TAO-DFT. Sci. Rep. 2016, 6, 37249. [Google Scholar] [CrossRef]
- Tönshoff, C.; Bettinger, H.F. Pushing the limits of acene chemistry: The recent surge of large acenes. Chem. Eur. J. 2021, 27, 3193–3212. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Omont, A.; Bettinger, H.F. Energetics of formation of cyclacenes from 2,3-didehydroacenes and implications for astrochemistry. Chem. Eur. J. 2021, 27, 4605–4616. [Google Scholar] [CrossRef] [PubMed]
- Hanson-Heine, M.W.D. Static correlation in vibrational frequencies studied using thermally-assisted-occupation density functional theory. Chem. Phys. Lett. 2020, 739, 137012. [Google Scholar] [CrossRef]
- Hanson-Heine, M.W.D. Static electron correlation in anharmonic molecular vibrations: A hybrid TAO-DFT study. J. Phys. Chem. A 2022, 126, 7273–7282. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.-J.; Chai, J.-D. TAO-DFT fictitious temperature made simple. RSC Adv. 2022, 12, 12193–12210. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-Y.; Hui, K.; Chung, J.-H.; Chai, J.-D. Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory. RSC Adv. 2017, 7, 50496–50507. [Google Scholar] [CrossRef]
- Li, S.; Chai, J.-D. TAO-DFT-based ab initio molecular dynamics. Front. Chem. 2020, 8, 589432. [Google Scholar] [CrossRef]
- Seenithurai, S.; Chai, J.-D. TAO-DFT with the polarizable continuum model. Nanomaterials 2023, 13, 1593. [Google Scholar] [CrossRef]
- Yeh, S.-H.; Manjanath, A.; Cheng, Y.-C.; Chai, J.-D.; Hsu, C.-P. Excitation energies from thermally assisted-occupation density functional theory: Theory and computational implementation. J. Chem. Phys. 2020, 153, 084120. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817–821. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Chu, S.-I. Self-interaction-free time-dependent density-functional theory for molecular processes in strong fields: High-order harmonic generation of H2 in intense laser fields. Phys. Rev. A 2001, 63, 023411. [Google Scholar] [CrossRef]
- Litvinyuk, I.V.; Lee, K.F.; Dooley, P.W.; Rayner, D.M.; Villeneuve, D.M.; Corkum, P.B. Alignment-dependent strong field ionization of molecules. Phys. Rev. Lett. 2003, 90, 233003. [Google Scholar] [CrossRef]
- Kanai, T.; Minemoto, S.; Sakai, H. Quantum interference during high-order harmonic generation from aligned molecules. Nature 2005, 435, 470–474. [Google Scholar] [CrossRef]
- Guan, X.X.; Tong, X.M.; Chu, S.-I. Effect of electron correlation on high-order-harmonic generation of helium atoms in intense laser fields: Time-dependent generalized pseudospectral approach in hyperspherical coordinates. Phys. Rev. A 2006, 73, 023403. [Google Scholar] [CrossRef]
- Baker, S.; Robinson, J.S.; Haworth, C.A.; Teng, H.; Smith, R.A.; Chirilaa, C.C.; Lein, M.; Tisch, J.W.G.; Marangos, J.P. Probing proton dynamics in molecules on an attosecond time scale. Science 2006, 312, 424–427. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Baker, S.; Robinson, J.S.; Lein, M.; Chirilă, C.C.; Torres, R.; Bandulet, H.C.; Comtois, D.; Kieffer, J.C.; Villeneuve, D.M.; Tisch, J.W.G.; et al. Dynamic two-center interference in high-order harmonic generation from molecules with attosecond nuclear motion. Phys. Rev. Lett. 2008, 101, 053901. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Mack, M.R.; Whitenack, D.; Wasserman, A. Exchange-correlation asymptotics and high harmonic spectra. Chem. Phys. Lett. 2013, 558, 15–19. [Google Scholar] [CrossRef]
- Li, P.-C.; Sheu, Y.-L.; Laughlin, C.; Chu, S.-I. Dynamical origin of near- and below-threshold harmonic generation of Cs in an intense mid-infrared laser field. Nat. Comm. 2015, 6, 7178. [Google Scholar] [CrossRef] [PubMed]
- Heslar, J.; Telnov, D.A.; Chu, S.-I. Subcycle dynamics of high-harmonic generation in valence-shell and virtual states of Ar atoms: A self-interaction-free time-dependent density-functional-theory approach. Phys. Rev. A 2015, 91, 023420. [Google Scholar] [CrossRef]
- Chou, Y.; Li, P.-C.; Ho, T.-S.; Chu, S.-I. Optimal control of high-order harmonics for the generation of an isolated ultrashort attosecond pulse with two-color midinfrared laser fields. Phys. Rev. A 2015, 91, 063408. [Google Scholar] [CrossRef]
- Sun, H.-L.; Peng, W.-T.; Chai, J.-D. Assessment of the LFAs-PBE exchange-correlation potential for high-order harmonic generation of aligned molecules. RSC Adv. 2016, 6, 33318–33325. [Google Scholar] [CrossRef]
- Zhu, Y.; Herbert, J.M. High harmonic spectra computed using time-dependent Kohn-Sham theory with Gaussian orbitals and a complex absorbing potential. J. Chem. Phys. 2022, 156, 204123. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Mermin, N.D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
- Helgaker, T.; Jørgensen, P.; Olsen, J. Molecular Electronic-Structure Theory; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Löwdin, P.-O.; Shull, H. Natural orbitals in the quantum theory of two-electron systems. Phys. Rev. 1956, 101, 1730–1739. [Google Scholar] [CrossRef]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Levy, M. Electron densities in search of Hamiltonians. Phys. Rev. A 1982, 26, 1200–1208. [Google Scholar] [CrossRef]
- Lieb, E.H. Density functionals for coulomb systems. Int. J. Quantum Chem. 1983, 24, 243–277. [Google Scholar] [CrossRef]
- Schipper, P.R.T.; Gritsenko, O.V.; Baerends, E.J. One-determinantal pure state versus ensemble Kohn-Sham solutions in the case of strong electron correlation: CH2 and C2. Theor. Chem. Acc. 1998, 99, 329–343. [Google Scholar] [CrossRef]
- Morrison, R.C. Electron correlation and noninteracting v-representability in density functional theory: The Be isoelectronic series. J. Chem. Phys. 2002, 117, 10506–10511. [Google Scholar] [CrossRef]
- Katriel, J.; Roy, S.; Springborg, M. A study of the adiabatic connection for two-electron systems. J. Chem. Phys. 2004, 121, 12179–12190. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.W.; Yang, W. Legendre-transform functionals for spin-density-functional theory. J. Chem. Phys. 2006, 124, 224108. [Google Scholar] [CrossRef] [PubMed]
- Kanhere, D.G.; Panat, P.V.; Rajagopal, A.K.; Callaway, J. Exchange-correlation potentials for spin-polarized systems at finite temperatures. Phys. Rev. A 1986, 33, 490–497. [Google Scholar] [CrossRef]
- Desjarlais, M.P.; Kress, J.D.; Collins, L.A. Electrical conductivity for warm, dense aluminum plasmas and liquids. Phys. Rev. E 2002, 66, 025401(R). [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A. A practicable real-space measure and visualization of static electron-correlation effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
- Bauer, C.A.; Hansen, A.; Grimme, S. The fractional occupation number weighted density as a versatile analysis tool for molecules with a complicated electronic structure. Chem. Eur. J. 2017, 23, 6150–6164. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Guardiola, A.; Sandoval-Salinas, M.E.; Casanova, D.; San-Fabián, E.; Pérez-Jiménez, A.J.; Sancho-Garcia, J.C. The role of topology in organic molecules: Origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Phys. Chem. Chem. Phys. 2018, 20, 7112–7124. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, T.; Doi, T.; Nakai, H. Finite-temperature-based linear-scaling divide-and-conquer self-consistent field method for static electron correlation systems. Chem. Phys. Lett. 2019, 725, 18–23. [Google Scholar] [CrossRef]
- Liu, F.; Duan, C.; Kulik, H.J. Rapid detection of strong correlation with machine learning for transition-metal complex high-throughput screening. J. Phys. Chem. Lett. 2020, 11, 8067–8076. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Nandy, A.; Duan, C.; Kulik, H.J. DFT-based multireference diagnostics in the solid state: Application to metal-organic frameworks. J. Chem. Theory Comput. 2023, 19, 190–197. [Google Scholar] [CrossRef] [PubMed]
- Sandoval-Salinas, M.E.; Bernabeu-Cabanero, R.; Pérez-Jiménez, A.J.; San-Fabián, E.; Sancho-Garcia, J.C. Electronic structure of rhombus-shaped nanographenes: System size evolution from closed- to open-shell ground states. Phys. Chem. Chem. Phys. 2023, 25, 11697–11706. [Google Scholar] [CrossRef] [PubMed]
- Nieman, R.; Carvalho, J.R.; Jayee, B.; Hansen, A.; Aquino, A.; Kertesz, M.; Lischka, H. Polyradical character assessment using multireference calculations and comparison with density-functional derived fractional occupation number weighted density analysis. Phys. Chem. Chem. Phys. 2023, 25, 27380–27393. [Google Scholar] [CrossRef]
- Yeh, S.-H.; Yang, W.; Hsu, C.-P. Reformulation of thermally assisted-occupation density functional theory in the Kohn-Sham framework. J. Chem. Phys. 2022, 156, 174108. [Google Scholar] [CrossRef]
- Teale, A.M.; Helgaker, T.; Savin, A.; Adamo, C.; Aradi, B.; Arbuznikov, A.V.; Ayers, P.W.; Baerends, E.J.; Barone, V.; Calaminici, P.; et al. DFT exchange: Sharing perspectives on the workhorse of quantum chemistry and materials science. Phys. Chem. Chem. Phys. 2022, 24, 28700–28781. [Google Scholar] [CrossRef]
- Greiner, M.; Carrier, P.; Görling, A. Extension of exact-exchange density functional theory of solids to finite temperatures. Phys. Rev. B 2010, 81, 155119. [Google Scholar] [CrossRef]
- Li, T.-C.; Tong, P.-Q. Hohenberg-Kohn theorem for time-dependent ensembles. Phys. Rev. A 1985, 31, 1950–1951. [Google Scholar] [CrossRef] [PubMed]
- van Leeuwen, R. Mapping from densities to potentials in time-dependent density-functional theory. Phys. Rev. Lett. 1999, 82, 3863–3866. [Google Scholar] [CrossRef]
- Dufty, J.; Luo, K.; Trickey, S.B. Density response from kinetic theory and time-dependent density-functional theory for matter under extreme conditions. Phys. Rev. E 2018, 98, 033203. [Google Scholar] [CrossRef]
- Li, X.; Smith, S.M.; Markevitch, A.N.; Romanov, D.A.; Levis, R.J.; Schlegel, H.B. A time-dependent Hartree-Fock approach for studying the electronic optical response of molecules in intense fields. Phys. Chem. Chem. Phys. 2005, 7, 233–239. [Google Scholar] [CrossRef]
- Zhu, Y.; Herbert, J.M. Self-consistent predictor/corrector algorithms for stable and efficient integration of the time-dependent Kohn-Sham equation. J. Chem. Phys. 2018, 148, 044117. [Google Scholar] [CrossRef] [PubMed]
- Bedurke, F.; Klamroth, T.; Saalfrank, P. Many-electron dynamics in laser-driven molecules: Wavefunction theory vs. density functional theory. Phys. Chem. Chem. Phys. 2021, 23, 13544–13560. [Google Scholar] [CrossRef] [PubMed]
- Cormier, E.; Lambropoulos, P. Optimal gauge and gauge invariance in non-perturbative time-dependent calculation of above-threshold ionization. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 1667–1680. [Google Scholar] [CrossRef]
- Bedurke, F.; Klamroth, T.; Krause, P.; Saalfrank, P. Discriminating organic isomers by high harmonic generation: A time-dependent configuration interaction singles study. J. Chem. Phys. 2019, 150, 234114. [Google Scholar] [CrossRef]
- Isborn, C.M.; Li, X. Singlet-triplet transitions in real-time time-dependent Hartree-Fock/density functional theory. J. Chem. Theory Comput. 2009, 5, 2415–2419. [Google Scholar] [CrossRef]
- White, A.F.; Heide, C.J.; Saalfrank, P.; Head-Gordon, M.; Luppi, E. Computation of high-harmonic generation spectra of the hydrogen molecule using time-dependent configuration-interaction. Mol. Phys. 2016, 114, 947–956. [Google Scholar] [CrossRef]
- Epifanovsky, E.; Gilbert, A.T.; Feng, X.; Lee, J.; Mao, Y.; Mardirossian, N.; Pokhilko, P.; White, A.F.; Coons, M.P.; Dempwolff, A.L.; et al. Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package. J. Chem. Phys. 2021, 155, 084801. [Google Scholar] [CrossRef]


| KS-DFT | TAO-DFT | FT-DFT | |
|---|---|---|---|
| Electronic Temperature | 0 | 0 | ≥0 |
| Fictitious Temperature | 0 | ≥0 | ≥0 |
| Is assumed? | Yes | No | Yes |
| Electronic Property | GS | GS | Thermal Equilibrium |
| Electron Density | GS | GS | Thermal Equilibrium |
| Density Representation | NI-PS-VR | NI-TE-VR | NI-TE-VR |
| Universal Functional | Hohenberg–Kohn | Hohenberg–Kohn | Mermin |
| Approximate Functional |
| TAO-DFT (with ) | FT-DFT (with ) | |
|---|---|---|
| Electronic Temperature | 0 | ≥0 |
| Fictitious Temperature | ≥0 | ≥0 |
| Is assumed? | No | Yes |
| Electronic Property | GS | Thermal Equilibrium |
| Electron Density | GS | Thermal Equilibrium |
| Density Representation | NI-TE-VR | NI-TE-VR |
| Approximate Functional |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, H.-Y.; Chai, J.-D. Real-Time Extension of TAO-DFT. Molecules 2023, 28, 7247. https://doi.org/10.3390/molecules28217247
Tsai H-Y, Chai J-D. Real-Time Extension of TAO-DFT. Molecules. 2023; 28(21):7247. https://doi.org/10.3390/molecules28217247
Chicago/Turabian StyleTsai, Hung-Yi, and Jeng-Da Chai. 2023. "Real-Time Extension of TAO-DFT" Molecules 28, no. 21: 7247. https://doi.org/10.3390/molecules28217247
APA StyleTsai, H.-Y., & Chai, J.-D. (2023). Real-Time Extension of TAO-DFT. Molecules, 28(21), 7247. https://doi.org/10.3390/molecules28217247






