(Ro)vibrational Spectroscopic Constants, Lifetime and QTAIM Evaluation of Fullerene Dimers Stability
Abstract
1. Introduction
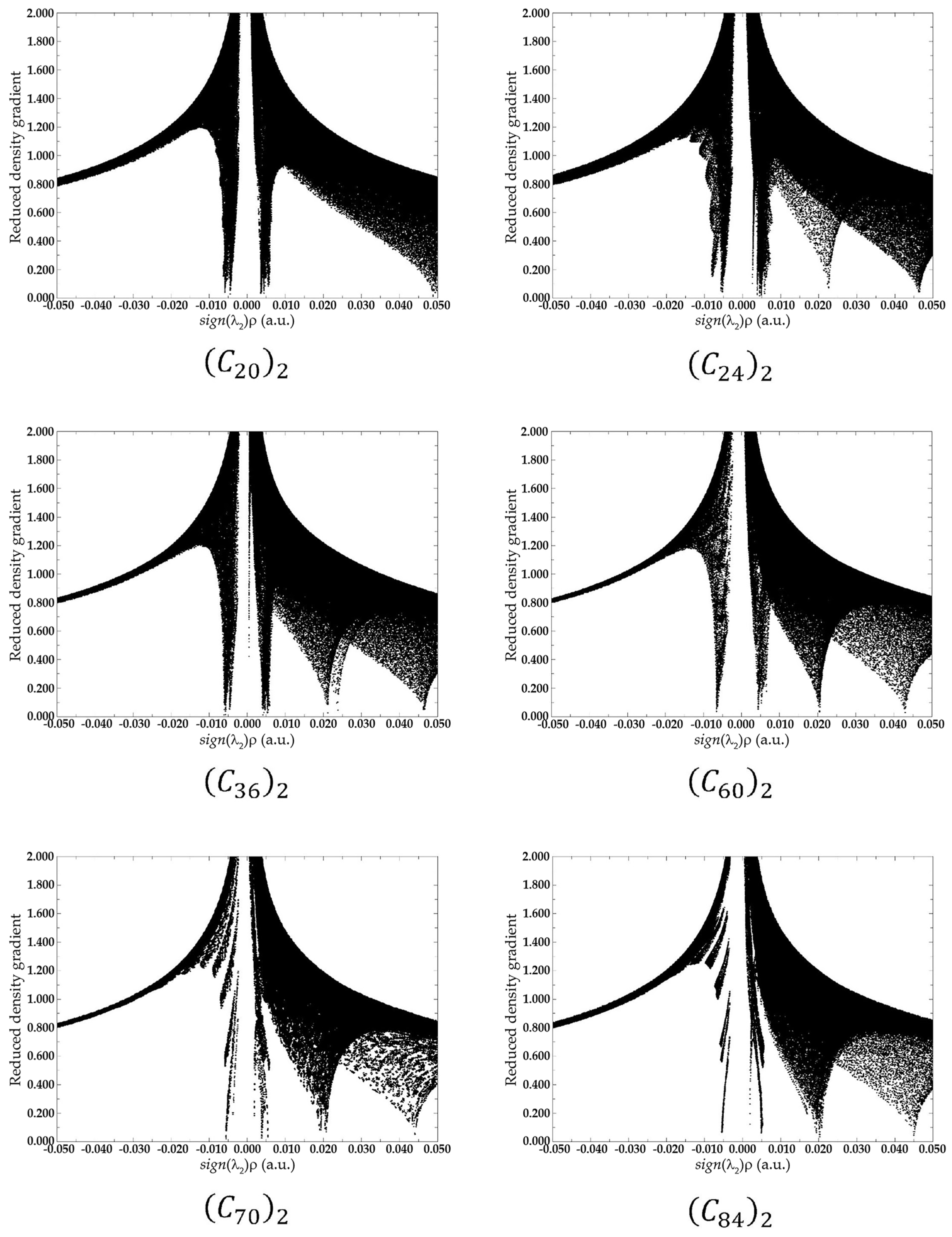
2. Results and Discussion
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osawa, E.; Kroto, H.W.; Fowler, P.W.; Wasserman, E. The evolution of the football structure for the C60 molecule: A retrospective. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1993, 343, 1–8. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Kroto, H.W. The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70. Nature 1987, 329, 529–531. [Google Scholar] [CrossRef]
- Saunders, M.; Jimenezvazquez, H.A.; Cross, R.J.; Poreda, R.J. Stable Compounds of Helium and Neon: He@C60 and Ne@C60. Science 1993, 259, 1428–1430. [Google Scholar] [CrossRef]
- Cooper, H.J.; Hendrickson, C.L.; Marshall, A.G.; Cross, R.J.; Saunders, M. Direct detection and quantitation of He@C60 by ultrahigh-resolution fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 2002, 13, 1349–1355. [Google Scholar] [CrossRef]
- Zhao, Y.; Kim, Y.H.; Dillon, A.C.; Heben, M.J.; Zhang, S.B. Hydrogen storage in novel organometallic buckyballs. Phys. Rev. Lett. 2005, 94, 155504. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host–guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Zhao, G.J.; He, Y.J.; Li, Y. 6.5% efficiency of polymer solar cells based on poly(3-hexylthiophene) and indene-C60 bisadduct by device optimization. Adv. Mater. 2010, 22, 4355–4358. [Google Scholar] [CrossRef]
- He, Y.; You, J.; Dou, L.; Chen, C.-C.; Richard, E.; Cha, K.C.; Wu, Y.; Li, G.; Yang, Y. High performance low band gap polymer solar cells with a non-conventional acceptor. Chem. Commun. 2012, 48, 7616–7618. [Google Scholar] [CrossRef]
- Silva, L.; Machado, S.; Lemos Silva, R.A.; Scalabrini Machado, D.F.; Maria, N.; Rodrigues, N.; De Oliveira, H.C.B.; Ribeiro, L.; Da, D.A.; Filho, S. Harnessing Greenhouse Gases Absorption by Doped Fullerenes with Externally Oriented Electric Field. Molecules 2022, 27, 2968. [Google Scholar] [CrossRef]
- Lemos Silva, R.A.; Scalabrini Machado, D.F.; de Oliveira, H.C.B.; Ribeiro, L.; da Silva Filho, D.A. Theoretical study of the interaction of fullerenes with the emerging contaminant carbamazepine for detection in aqueous environments. Sci. Rep. 2022, 12, 15848. [Google Scholar] [CrossRef]
- Leitherer, S.; Jäger, C.M.; Halik, M.; Clark, T.; Thoss, M. Modeling charge transport in C 60-based self-assembled monolayers for applications in field-effect transistors. J. Chem. Phys. 2014, 140, 204702. [Google Scholar] [CrossRef]
- Jäger, C.M.; Schmaltz, T.; Novak, M.; Khassanov, A.; Vorobiev, A.; Hennemann, M.; Krause, A.; Dietrich, H.; Zahn, D.; Hirsch, A.; et al. Improving the charge transport in self-assembled monolayer field-effect transistors: From theory to devices. J. Am. Chem. Soc. 2013, 135, 4893–4900. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, C.; García-Frutos, E.M.; Da Silva Filho, D.A.; López Navarrete, J.T.; Ruiz Delgado, M.C.; Gómez-Lor, B. Symmetry lowering in triindoles: Impact on the electronic and photophysical properties. J. Phys. Chem. C 2014, 118, 5470–5477. [Google Scholar] [CrossRef]
- Sweetman, A.; Rashid, M.A.; Jarvis, S.P.; Dunn, J.L.; Rahe, P.; Moriarty, P. Visualizing the orientational dependence of an intermolecular potential. Nat. Commun. 2016, 7, 10621. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.A.L.; de Brito, S.F.; Machado, D.F.S.; Carvalho-Silva, V.H.; de Oliveira, H.C.B.; Ribeiro, L. The influence of the configuration of the (C70)2 dimer on its rovibrational spectroscopic properties: A theoretical survey. J. Mol. Model. 2018, 24, 235. [Google Scholar] [CrossRef]
- Baggio, A.R.; Machado, D.F.S.; Carvalho-Silva, V.H.; Paterno, L.G.; de Oliveira, H.C.B.; Kummel, A.C.; Trogler, W.C.; Sanyal, B.; Eriksson, O.; Puglia, C.; et al. Rovibrational spectroscopic constants of the interaction between ammonia and metallo-phthalocyanines: A theoretical protocol for ammonia sensor design. Phys. Chem. Chem. Phys. 2017, 19, 10843–10853. [Google Scholar] [CrossRef]
- David, W.I.F.; Ibberson, R.M.; Dennis, T.J.S.; Hare, J.P.; Prassides, K. Structural phase transitions in the fullerene c60. Europhys. Lett. 1992, 18, 735–736. [Google Scholar] [CrossRef]
- Esteves, C.S.; de Oliveira, H.C.B.; Ribeiro, L.; Gargano, R.; Mundim, K.C. Modeling diatomic potential energy curves through the generalized exponential function. Chem. Phys. Lett. 2006, 427, 10–13. [Google Scholar] [CrossRef]
- Machado, D.F.S.; Silva, V.H.C.; Esteves, C.S.; Gargano, R.; Macedo, L.G.M.; Mundim, K.C.; de Oliveira, H.C.B. Fully relativistic rovibrational energies and spectroscopic constants of the lowest x:10g+,A’:12u, B’:10u, and B:(1)0u+states of molecular chlorine. J. Mol. Model. 2012, 18, 4343–4348. [Google Scholar] [CrossRef]
- Machado, D.F.S.; Silva, R.A.L.; de Oliveira, A.P.; Carvalho-Silva, V.H.; Gargano, R.; Ribeiro, L.; de Oliveira, H.C.B. A novel analytical potential function for dicationic diatomic molecular systems based on deformed exponential function. J. Mol. Model. 2017, 23, 182. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990; ISBN 9780198558651. [Google Scholar]
- Sharapa, D.I.; Margraf, J.T.; Hesselmann, A.; Clark, T. Accurate intermolecular potential for the C60 dimer: The performance of different levels of quantum theory. J. Chem. Theory Comput. 2017, 13, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Sabirov, D.S. Polarizability of C60 fullerene dimer and oligomers: The unexpected enhancement and its use for rational design of fullerene-based nanostructures with adjustable properties. RSC Adv. 2013, 3, 19430–19439. [Google Scholar] [CrossRef]
- Branz, W.; Malinowski, N.; Enders, A.; Martin, T.P. Structural transition in [C60]n clusters. Phys. Rev. B 2002, 66, 094107. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Bulgakov, R.G. Polarizability of fullerene [2+2]-dimers: A DFT study. Phys. Chem. Chem. Phys. 2014, 16, 14594–14600. [Google Scholar] [CrossRef] [PubMed]
- Zettergren, H.; Schmidt, H.T.; Reinhed, P.; Cederquist, H.; Jensen, J.; Hvelplund, P.; Tomita, S.; Manil, B.; Rangama, J.; Huber, B.A. Even-odd effects in the ionization cross sections of [C60]2 and [C60C70] dimers. Phys. Rev. A 2007, 75, 051201. [Google Scholar] [CrossRef]
- Zettergren, H.; Wang, Y.; Lamsabhi, A.M.; Alcamí, M.; Martín, F.; Zettergren, H.; Wang, Y.; Lamsabhi, A.M.; Alcamí, M.; Martín, F. Density functional theory study of multiply ionized weakly bound fullerene dimers. J. Chem. Phys. 2009, 130, 224302. [Google Scholar] [CrossRef]
- Wolfgang, R. Energy and chemical reaction. II. Intermediate complexes vs. direct mechanisms. Acc. Chem. Res. 1970, 3, 48–54. [Google Scholar] [CrossRef]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Gao, H.; Feng, W.; Li, X.; Li, N.; Du, Y.; Wu, Y.; Bai, H.; Qiao, W. Insights into the non-covalent interaction between modified nucleobases and graphene nanoflake from first-principles. Phys. E Low-Dimens. Syst. Nanostructures 2019, 107, 73–79. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Astakhov, A.V.; Chernyshev, V.M. Molecular structure of 3-amino[1,2,4]triazolo-[4,3-a]pyrimidin-5-one in various tautomeric forms: Investigation by DFT and Qtaim methods. Chem. Heterocycl. Compd. 2014, 50, 319–326. [Google Scholar] [CrossRef]
- Baryshnikov, G.V.; Minaev, B.F.; Minaeva, V.A.; Baryshnikova, A.T. Structure and intramolecular stabilization of geometric isomers of Bi- and trithiazolidine-4-ones and their methyl derivatives: A DFT and QTAIM study. J. Struct. Chem. 2012, 53, 428–435. [Google Scholar] [CrossRef]
- Baryshnikov, G.V.; Minaev, B.F.; Korop, A.A.; Minaeva, V.A.; Gusev, A.N. Structure of zinc complexes with 3-(pyridin-2-yl)-5-(arylideneiminophenyl)- 1H-1,2,4-triazoles in different tautomeric forms: DFT and QTAIM study. Russ. J. Inorg. Chem. 2013, 58, 928–934. [Google Scholar] [CrossRef]
- Ayarde-Henríquez, L.; Guerra, C.; Duque-Noreña, M.; Rincón, E.; Pérez, P.; Chamorro, E. Are There Only Fold Catastrophes in the Diels-Alder Reaction between Ethylene and 1,3-Butadiene? J. Phys. Chem. A 2021, 125, 5152–5165. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Wavefunction methods for noncovalent interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 2, 304–326. [Google Scholar] [CrossRef]
- Tomanek, D.; Frederick, N. C n Fullerenes. Available online:http://www.nanotube.msu.edu/fullerene/fullerene-isomers.html (accessed on 15 November 2022).
- Zhang, B.L.; Wang, C.Z.; Ho, K.M. Search for the ground-state structure of C84. J. Chem. Phys. 1992, 96, 7183–7185. [Google Scholar] [CrossRef]
- Grossman, J.C.; Côté, M.; Louie, S.G.; Cohen, M.L. Electronic and structural properties of molecular C 36. Chem. Phys. Lett. 1998, 284, 344–349. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, revision C. 01; Gaussian. Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- William, F. Sheehan Rydberg Potential Energy Function for Diatomic Molecules as Extended to Polyatomic Species and Activated Complex. J. Chem. Inf. Model. 1965, 53, 1689–1699. [Google Scholar] [CrossRef]
- Mundim, K.C.; Tsallis, C. Geometry optimization and conformational analysis through generalized simulated annealing. Int. J. Quant. Chem. 1996, 58, 373–381. [Google Scholar] [CrossRef]
- de Andrade, M.D.; Mundim, K.C.; Malbouisson, L.A.C. Convergence of the generalized simulated annealing method with independent parameters for the acceptance probability, visitation distribution, and temperature functions. Int. J. Quantum Chem. 2008, 108, 2392–2397. [Google Scholar] [CrossRef]
- Neto, J.J.S.; Costa, L.S. Numerical Generation of Optimized Discrete Variable Representations. Braz. J. Phys. 1998, 28, 1–11. [Google Scholar] [CrossRef]
- Dunham, J.L. The Energy Levels of a Rotating Vibrator. Phys. Rev. 1932, 41, 721–731. [Google Scholar] [CrossRef]
- Slater, N.B. The rates of unimolecular reactions in gases. Math. Proc. Camb. Philos. Soc. 1939, 35, 56–69. [Google Scholar] [CrossRef]
- de Aquino, A.B.M.; Leal, L.A.; Carvalho-Silva, V.H.; Gargano, R.; Ribeiro Junior, L.A.; da Cunha, W.F. Krypton-methanol spectroscopic study: Assessment of the complexation dynamics and the role of the van der Waals interaction. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 205, 179–185. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Esseén, H. The characterization of atomic interactions. J. Chem. Phys. 1984, 80, 1943–1960. [Google Scholar] [CrossRef]
- Kumar, P.S.V.; Raghavendra, V.; Subramanian, V. Bader’s Theory of Atoms in Molecules (AIM) and its Applications to Chemical Bonding. J. Chem. Sci. 2016, 128, 1527–1536. [Google Scholar] [CrossRef]
- Silva, R.A.L.; da Silva Filho, D.A.; Moberg, M.E.; Pappenfus, T.M.; Janzen, D.E. Halogen Interactions in Halogenated Oxindoles: Crystallographic and Computational Investigations of Intermolecular Interactions. Molecules 2021, 26, 5487. [Google Scholar] [CrossRef] [PubMed]
- Saadat, K.; Tavakol, H. An exceptional functionalization of doped fullerene observed via theoretical studies on the interactions of sulfur-doped fullerenes with halogens and halides. RSC Adv. 2015, 5, 55227–55237. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Girifalco, L.A. Molecular properties of fullerene in the gas and solid phases. J. Phys. Chem. 1992, 96, 858–861. [Google Scholar] [CrossRef]
- Liu, F.-L.; Wang, J. The intermolecular potential function of Smith–Thakkar type for C60. J. Mol. Struct. THEOCHEM 2006, 778, 105–109. [Google Scholar] [CrossRef]
- Lim, T.-C. Preliminary assessment of a multifunctional potential energy function. Mol. Phys. 2010, 108, 1589–1597. [Google Scholar] [CrossRef]


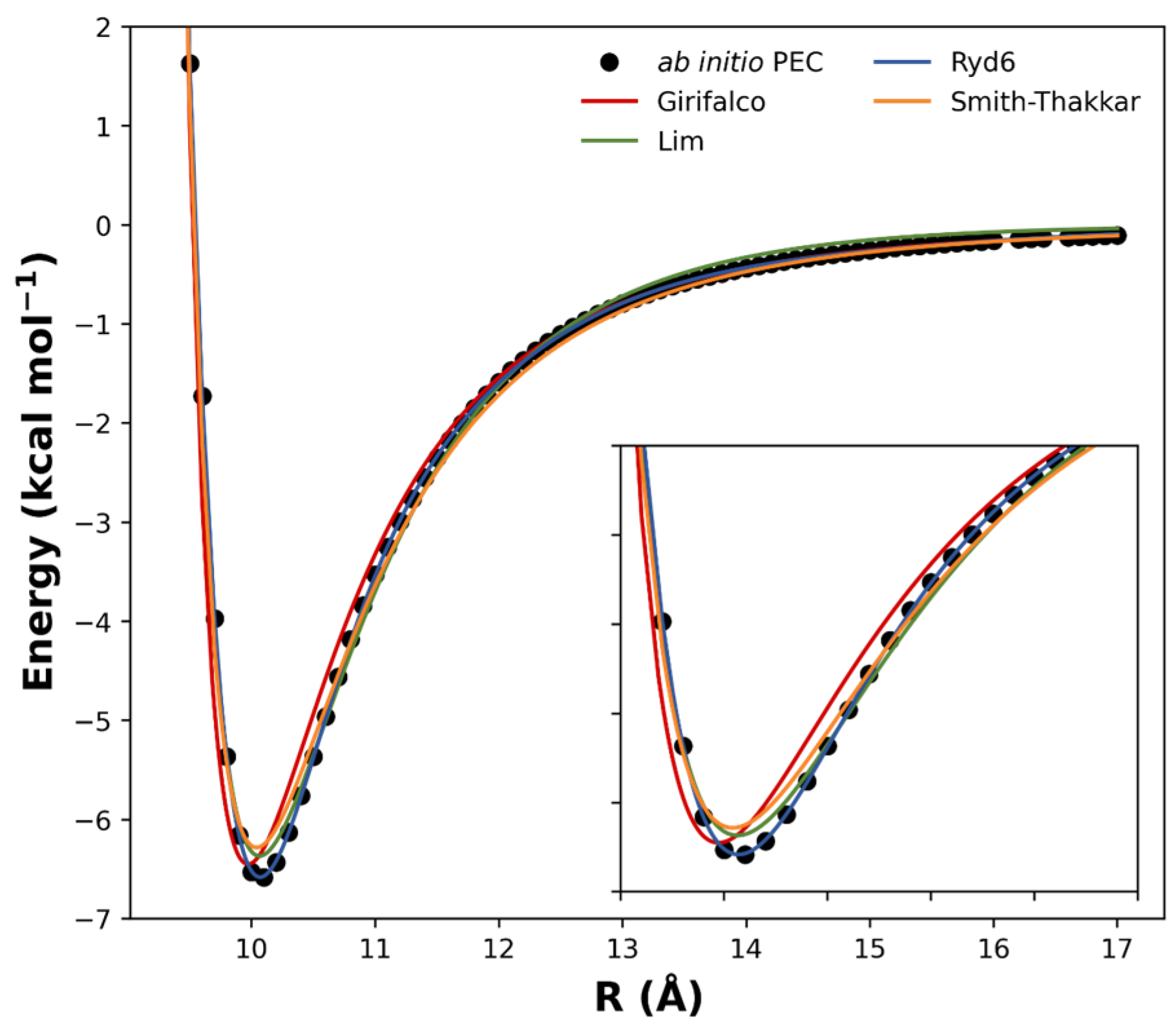
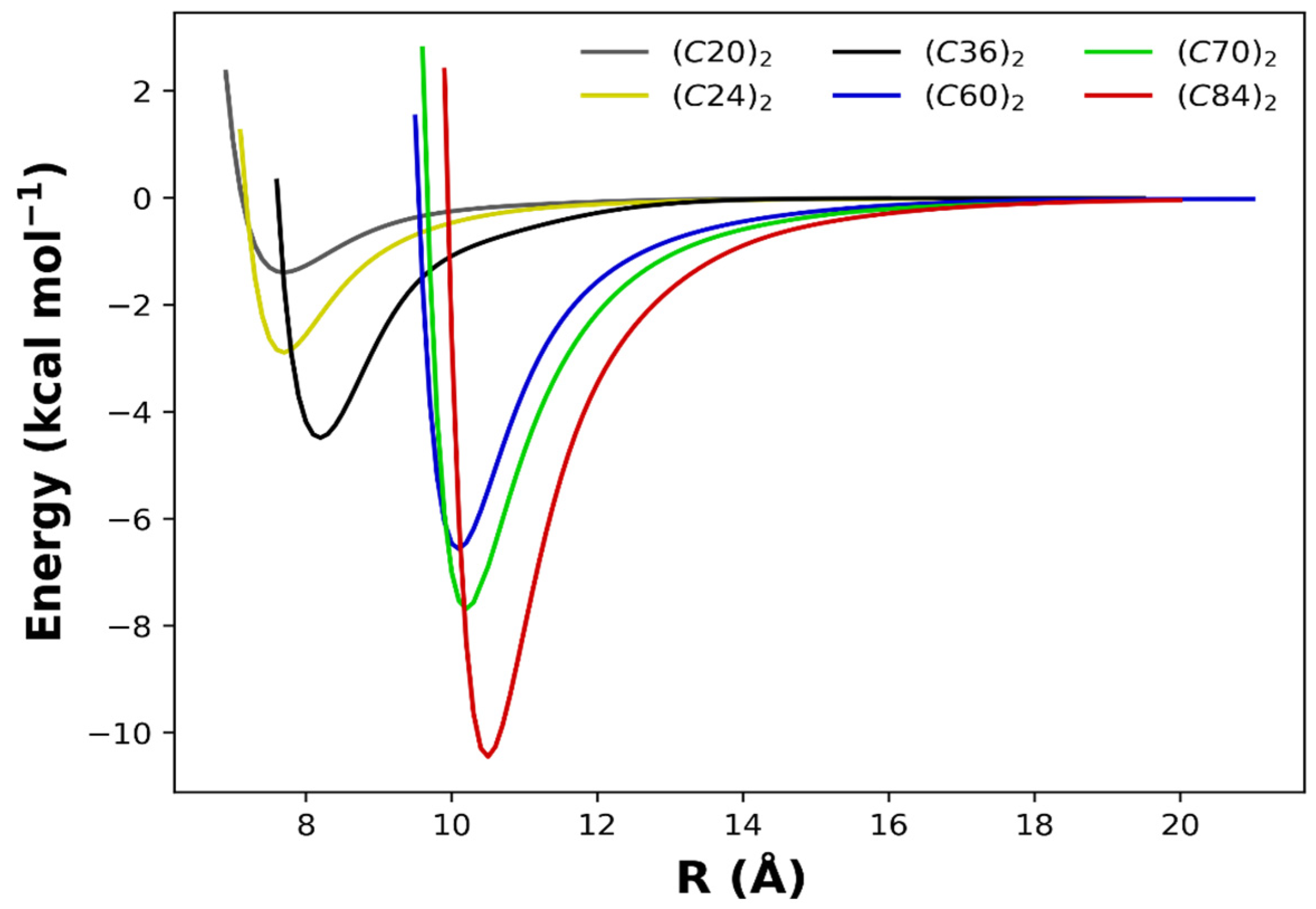
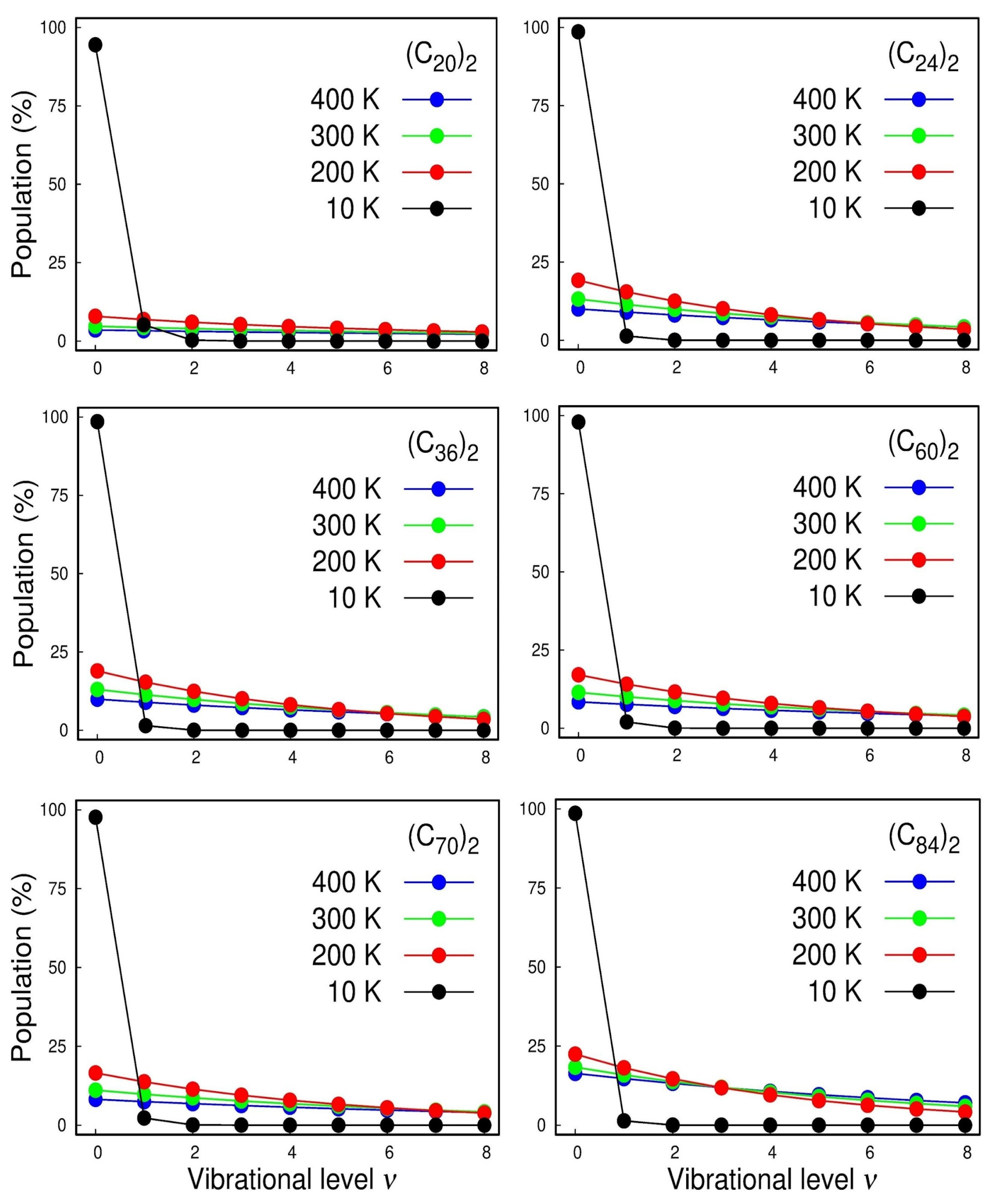


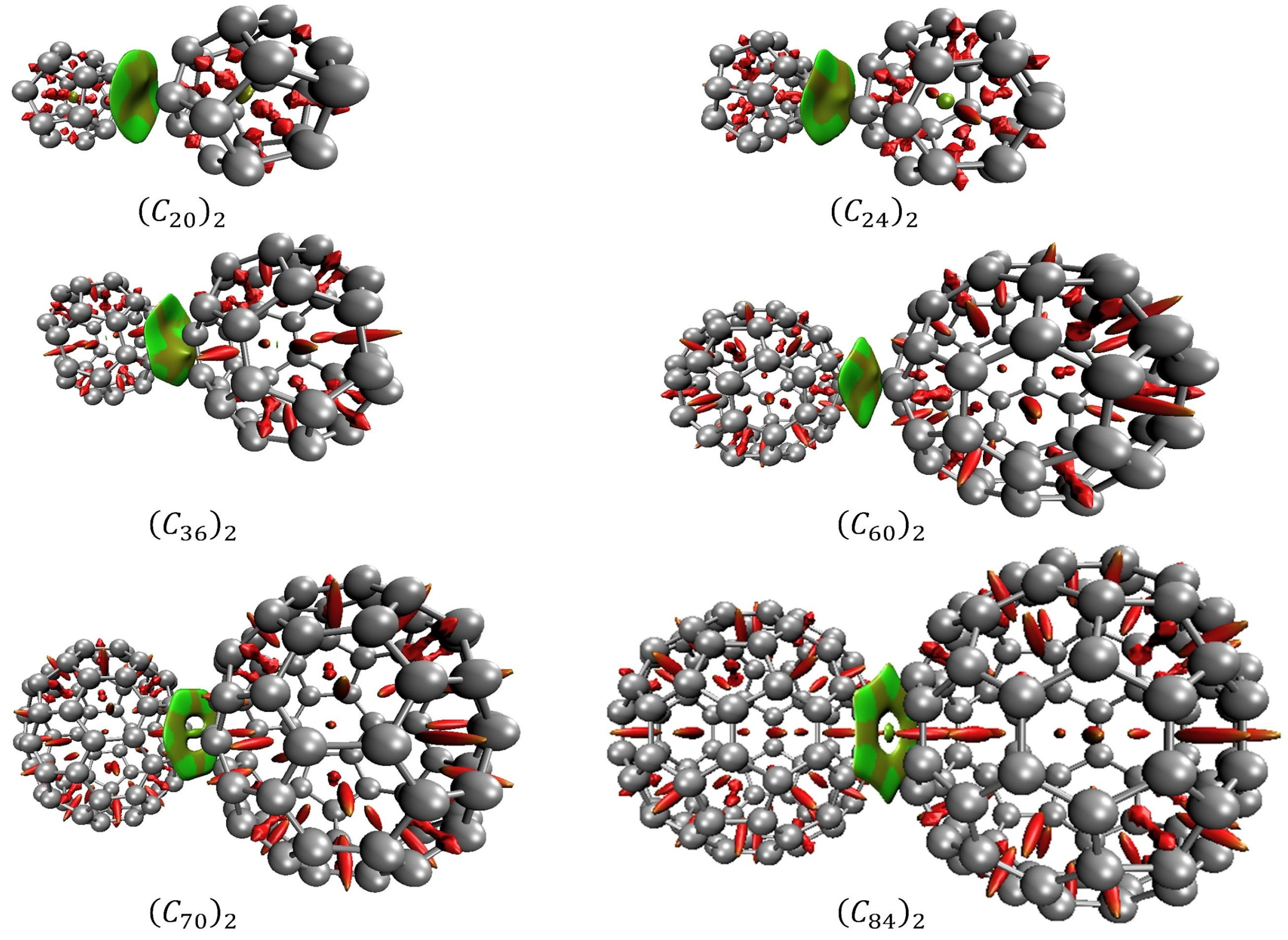
| Fullerene Dimers | ||
|---|---|---|
| 7.657 | 1.399 | |
| 7.690 | 2.905 | |
| 8.143 | 4.523 | |
| 10.069 | 6.580 | |
| 9.1 [24] * | (6.342 ± 1.845) [25] * | |
| 10.05 [25,26,27] * | 6.389 [27] * | |
| 10.0 [28] * | 7.748 [28] * | |
| 10.201 | 7.667 | |
| 10.110 [25] * | (7.218 ± 1.845) [26] * | |
| 10.467 | 10.414 |
| System | Method | ||||
|---|---|---|---|---|---|
| Dunham | 23.94 | 20.77 | 26.60 | 157.59 | |
| DVR | - | 20.76 | 26.82 | 157.45 | |
| Dunham | 19.78 | 29.91 | 24.49 | 74.52 | |
| DVR | - | 29.19 | 22.37 | 76.05 | |
| Dunham | 11.76 | 29.39 | 15.45 | 28.30 | |
| DVR | - | 29.38 | 15.46 | 29.82 | |
| Dunham | 4.61 | 27.33 | 9.29 | 6.00 | |
| DVR | - | 27.28 | 9.18 | 3.00 | |
| Dunham | 3.85 | 26.33 | 7.54 | 4.25 | |
| DVR | - | 26.32 | 7.55 | 6.25 | |
| Dunham | 3.05 | 29.04 | 6.90 | 3.05 | |
| DVR | - | 29.89 | 7.64 | 2.26 |
| Υ | ||||||
|---|---|---|---|---|---|---|
| 0 | 10.3 | 14.8 | 14.5 | 13.6 | 13.1 | 19.1 |
| 1 | 30.0 | 43.5 | 43.6 | 40.7 | 39.3 | 44.7 |
| 2 | 50.0 | 71.8 | 72.4 | 67.6 | 65.3 | 74.3 |
| 3 | 69.0 | 99.7 | 100.8 | 94.3 | 91.2 | 103.7 |
| 4 | 87.98 | 127.0 | 128.9 | 120.8 | 116.9 | 133.0 |
| 5 | 106.1 | 154.0 | 156.8 | 147.2 | 142.5 | 162.1 |
| 6 | 123.6 | 180.4 | 184.3 | 173.4 | 167.9 | 191.1 |
| 7 | 140.7 | 206.4 | 211.5 | 199.4 | 193.2 | 219.9 |
| 8 | 157.2 | 231.9 | 238.4 | 225.2 | 218.3 | 248.6 |
| 9 | 173.2 | 256.9 | 254.5 | 250.7 | 243.2 | 277.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemos Silva, R.A.; Barbosa, M.R.; Martins, C.R.; Scalabrini Machado, D.F.; Ribeiro, L.; de Oliveira, H.C.B.; da Silva Filho, D.A. (Ro)vibrational Spectroscopic Constants, Lifetime and QTAIM Evaluation of Fullerene Dimers Stability. Molecules 2023, 28, 5023. https://doi.org/10.3390/molecules28135023
Lemos Silva RA, Barbosa MR, Martins CR, Scalabrini Machado DF, Ribeiro L, de Oliveira HCB, da Silva Filho DA. (Ro)vibrational Spectroscopic Constants, Lifetime and QTAIM Evaluation of Fullerene Dimers Stability. Molecules. 2023; 28(13):5023. https://doi.org/10.3390/molecules28135023
Chicago/Turabian StyleLemos Silva, Rodrigo A., Mateus R. Barbosa, Caio R. Martins, Daniel F. Scalabrini Machado, Luciano Ribeiro, Heibbe C. B. de Oliveira, and Demétrio A. da Silva Filho. 2023. "(Ro)vibrational Spectroscopic Constants, Lifetime and QTAIM Evaluation of Fullerene Dimers Stability" Molecules 28, no. 13: 5023. https://doi.org/10.3390/molecules28135023
APA StyleLemos Silva, R. A., Barbosa, M. R., Martins, C. R., Scalabrini Machado, D. F., Ribeiro, L., de Oliveira, H. C. B., & da Silva Filho, D. A. (2023). (Ro)vibrational Spectroscopic Constants, Lifetime and QTAIM Evaluation of Fullerene Dimers Stability. Molecules, 28(13), 5023. https://doi.org/10.3390/molecules28135023






