Phase Correction for Absorption Mode Two-Dimensional Mass Spectrometry
Abstract
1. Introduction
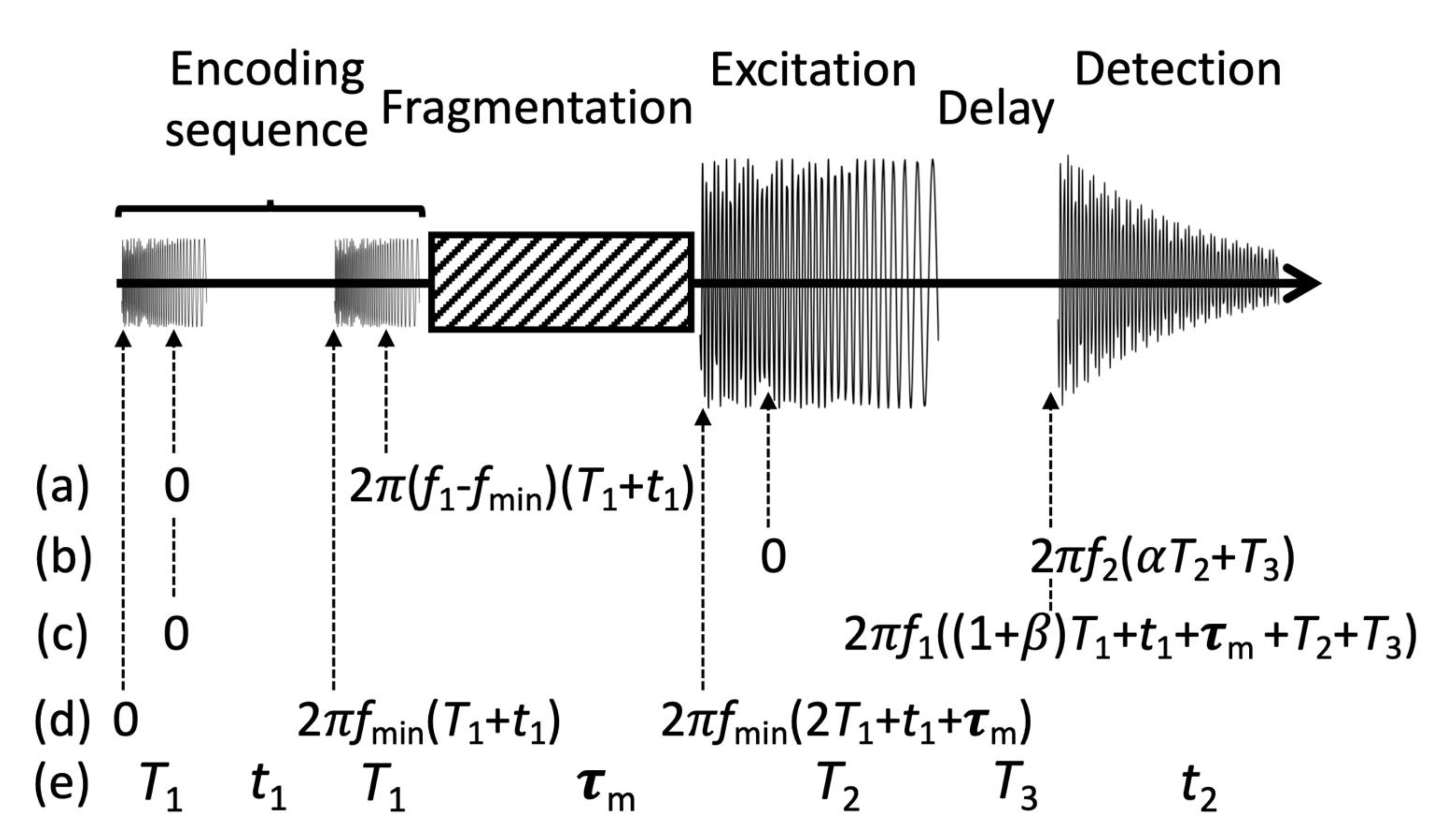
2. Theory
3. Experimental Methods
3.1. Sample Preparation
3.2. Instrument Parameters
3.3. Data Processing
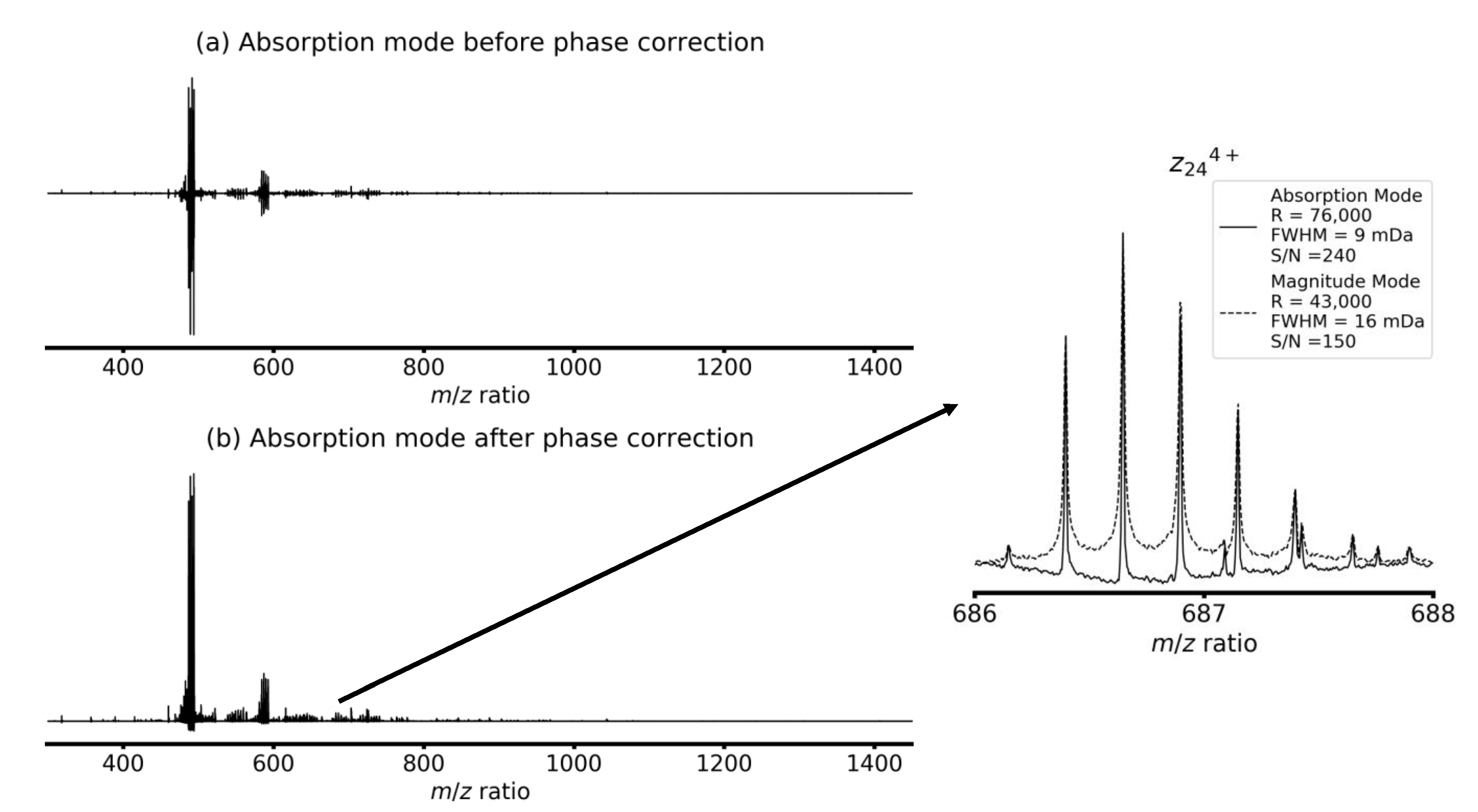
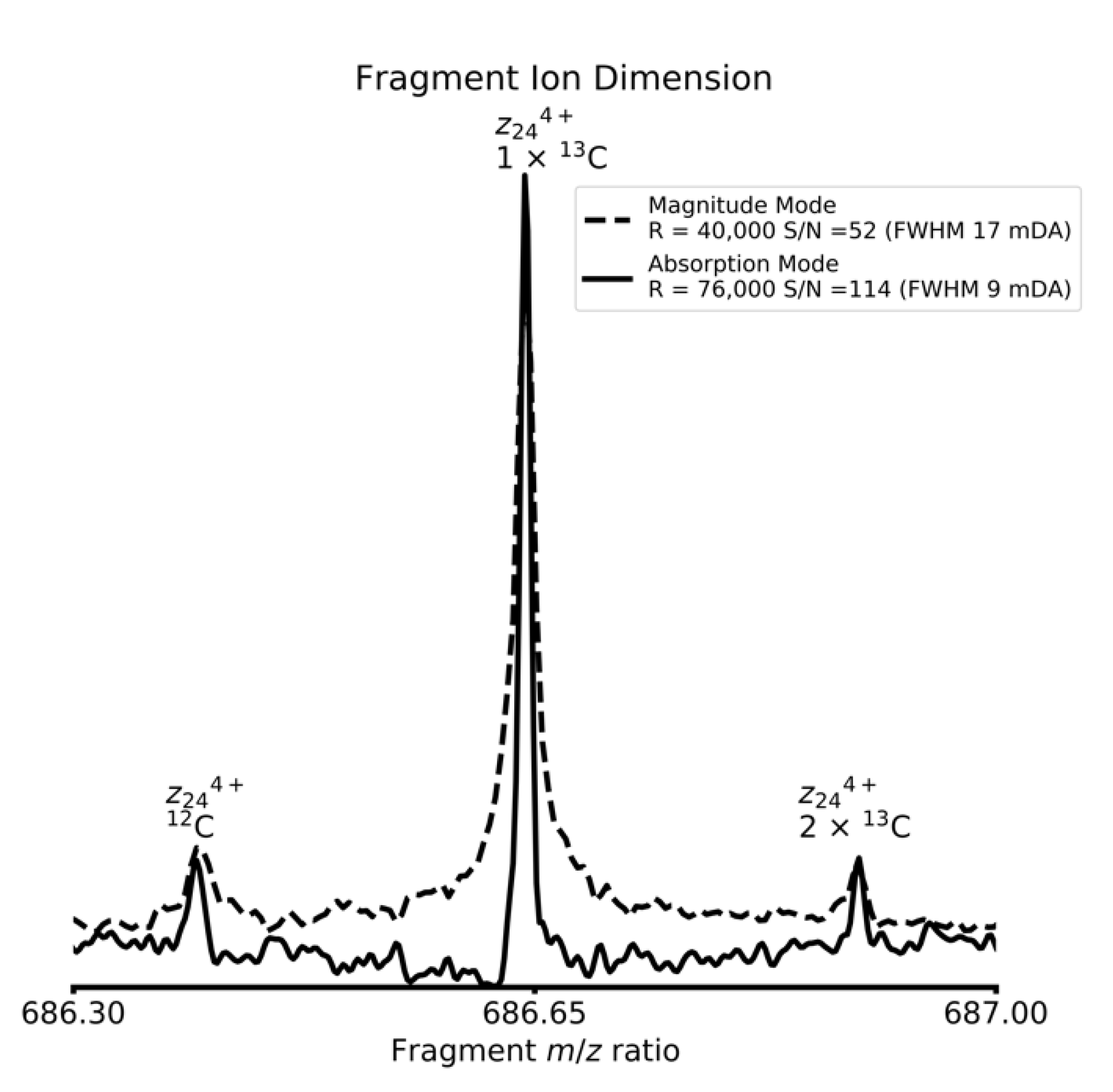
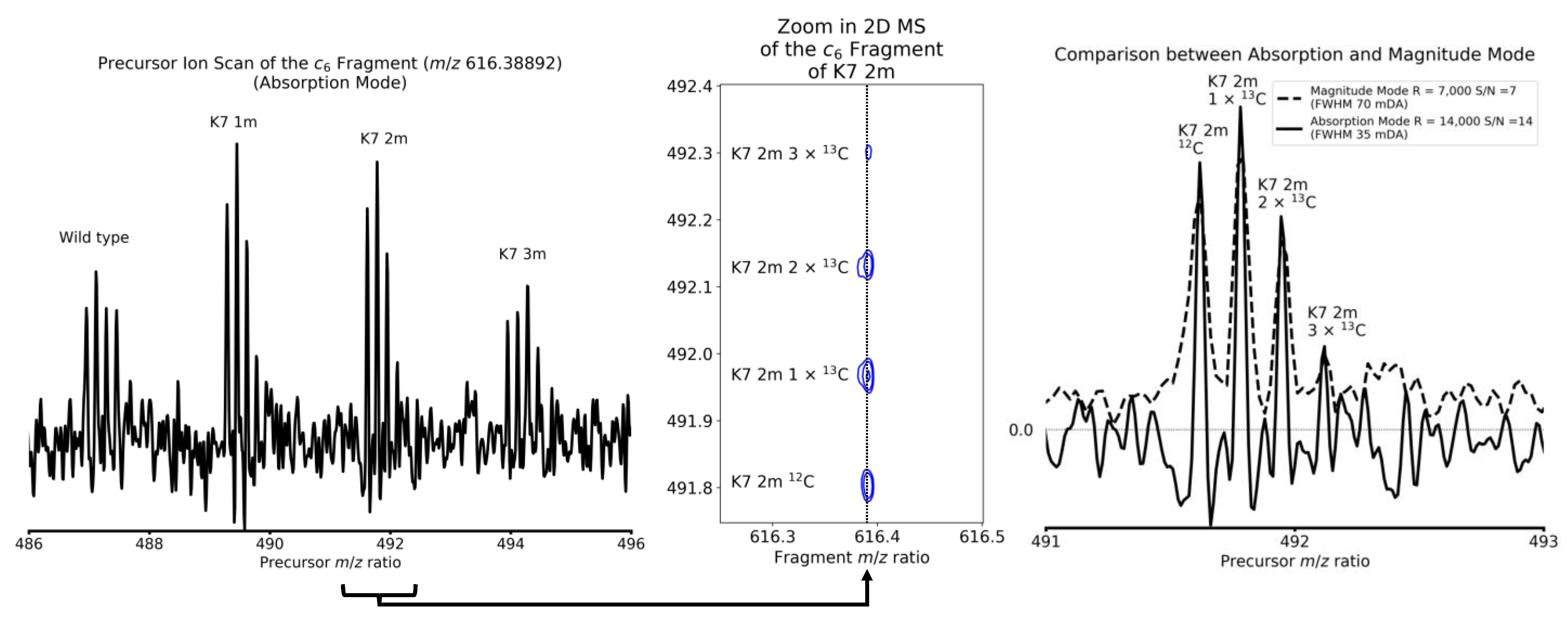
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Appendix A
- # Import necessary modules
- import spike
- from spike.File import Apex
- # Load 2D data set:
- d = Apex.Import_2D(“histonepeptide_2D_000002.d”)
- # Apodisation with a sine bell with a maximum at 15% of the transient, double zero-filling in #the horizontal dimension, Fourier transform in the horizontal dimension
- d.apod_sin(axis = 2, maxi = 0.15).chsize(d.size1,4*d.size2).rfft(axis = 2)
- # Digital demodulation by multiplying every row by:
- d.flipphase(0.0, 180*d.axis1.htoi(74,659.79), axis = 1)
- # Quadratic phase correction in the horizontal dimension with -9/360+564(f2/fN)+4595.7(f2/fN)2:*
- d.phase(-9, 564.0, 4595.7, 0.0, axis = 2)
- # Discard of the imaginary part of the data in the horizontal dimension
- d.real(axis = 2)
- # Apodisation with a sine bell with a maximum at 15% of the transient, double zero-filling in the vertical dimension, Fourier transform in the vertical dimension
- d.apod_sin(axis = 1, maxi = 0.15).chsize(4*d.size1,d.size2).rfft(axis = 1)
- # Linear phase correction in the vertical dimension with 59.9/360+7.8(f1/fN):*
- d.phase(59.9, 7.8, 0.0, 0.00, axis = 1)
- # Discard of the imaginary part of the data in the vertical dimension
- d.real(axis = 1)
- # Offset of the frequencies for narrowband 2D mass spectrometry
- offset = 74659.79
- d.axis1.offsetfreq = 14*d.axis1.specwidth + offset
- d.axis1.leftpoint = 0
References
- Pfändler, P.; Bodenhausen, G.; Rapin, J.; Houriet, R.; Gäumann, T. Two-dimensional Fourier transform ion cyclotron resonance mass spectrometry. Chem. Phys. Lett. 1987, 138, 195–200. [Google Scholar] [CrossRef]
- Pfändler, P.; Bodenhausen, G.; Rapin, J.; Walser, M.E.; Gäumann, T. Broad-band two-dimensional Fourier transform ion cyclotron resonance. J. Am. Chem. Soc. 1988, 110, 5625–5628. [Google Scholar] [CrossRef]
- Bensimon, M.; Zhao, G.; Gäumann, T. A method to generate phase continuity in two-dimensional Fourier transform ion cyclotron resonance mass spectrometry. Chem. Phys. Lett. 1989, 157, 97–100. [Google Scholar] [CrossRef]
- Snyder, D.T.; Szalwinski, L.J.; Wells, J.M.; Cooks, R.G. Logical MS/MS scans: A new set of operations for tandem mass spectrometry. Analyst 2018, 143, 5438–5452. [Google Scholar] [CrossRef]
- Snyder, D.T.; Szalwinski, L.J.; St. John, Z.; Cooks, R.G. Two-Dimensional Tandem Mass Spectrometry in a Single Scan on a Linear Quadrupole Ion Trap. Anal. Chem. 2019, 91, 13752–13762. [Google Scholar] [CrossRef]
- Szalwinski, L.J.; Holden, D.T.; Morato, N.M.; Cooks, R.G. 2D MS/MS Spectra Recorded in the Time Domain Using Repetitive Frequency Sweeps in Linear Quadrupole Ion Traps. Anal. Chem. 2020, 92, 10016–10023. [Google Scholar] [CrossRef]
- Szalwinski, L.J.; Cooks, R.G. Complex mixture analysis by two-dimensional mass spectrometry using a miniature ion trap. Talanta Open 2021, 3, 100028. [Google Scholar] [CrossRef]
- van Agthoven, M.A.; O’Connor, P.B. Two-dimensional mass spectrometry in a linear ion trap, an in silico model. Rapid Comm. Mass Spectrom. 2017, 31, 674–684. [Google Scholar] [CrossRef]
- Driver, T.; Cooper, B.; Ayers, R.; Pipkorn, R.; Patchkovskii, S.; Averbukh, V.; Klug, D.R.; Marangos, J.P.; Frasinski, L.J.; Edelson-Averbukh, M. Two-Dimensional Partial-Covariance Mass Spectrometry of Large Molecules Based on Fragment Correlations. Phys. Rev. X 2020, 10, 041004. [Google Scholar] [CrossRef]
- van Agthoven, M.A.; Delsuc, M.-A.; Bodenhausen, G.; Rolando, C. Towards analytically useful two-dimensional Fourier transform ion cyclotron resonance mass spectrometry. Anal. Bioanal. Chem. 2013, 405, 51–61. [Google Scholar] [CrossRef]
- van Agthoven, M.A.; Lam, Y.P.Y.; O’Connor, P.B.; Rolando, C.; Delsuc, M.-A. Two-dimensional mass spectrometry: N ew perspectives for tandem mass spectrometry. Eur. Biophys. J. 2019, 48, 213–229. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Coutouly, M.-A.; Rolando, C.; Delsuc, M.-A. Two-dimensional Fourier transform ion cyclotron resonance mass spectrometry: Reduction of scintillation noise using Cadzow data processing. Rapid. Commun. Mass Spectrom. 2011, 25, 1609–1616. [Google Scholar] [CrossRef]
- Chiron, L.; van Agthoven, M.A.; Kieffer, B.; Rolando, C.; Delsuc, M.-A. Efficient denoising algorithms for large experimental datasets and their applications in Fourier transform ion cyclotron resonance mass spectrometry. Proc. Natl. Acad. Sci. USA 2014, 111, 1385–1390. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Chiron, L.; Coutouly, M.-A.; Sehgal, A.A.; Pelupessy, P.; Delsuc, M.-A.; Rolando, C. Optimization of the discrete pulse sequence for two-dimensional FT-ICR mass spectrometry using infrared multiphoton dissociation. Int. J. Mass Spectrom. 2014, 370, 114–124. [Google Scholar] [CrossRef]
- Bray, F.; Bouclon, J.; Chiron, L.; Witt, M.; Delsuc, M.-A.; Rolando, C. Nonuniform Sampling Acquisition of Two-Dimensional Fourier Transform Ion Cyclotron Resonance Mass Spectrometry for Increased Mass Resolution of Tandem Mass Spectrometry Precursor Ions. Anal. Chem. 2017, 89, 8589–8593. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Delsuc, M.-A.; Rolando, C. Two-dimensional FT-ICR/MS with IRMPD as fragmentation mode. Int. J. Mass Spectrom. 2011, 306, 196–203. [Google Scholar] [CrossRef]
- van Agthoven, M.A.; Chiron, L.; Coutouly, M.-A.; Delsuc, M.-A.; Rolando, C. Two-Dimensional ECD FT-ICR Mass Spectrometry of Peptides and Glycopeptides. Anal. Chem. 2012, 84, 5589–5595. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Barrow, M.P.; Chiron, L.; Coutouly, M.-A.; Kilgour, D.; Wootton, C.A.; Wei, J.; Soulby, A.; Delsuc, M.-A.; Rolando, C.; et al. Differentiating Fragmentation Pathways of Cholesterol by Two-Dimensional Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2015, 26, 2105–2114. [Google Scholar] [CrossRef]
- Floris, F.; van Agthoven, M.; Chiron, L.; Soulby, A.J.; Wootton, C.A.; Lam, Y.P.Y.; Barrow, M.P.; Delsuc, M.-A.; O’Connor, P.B. 2D FT-ICR MS of Calmodulin: A Top-Down and Bottom-Up Approach. J. Am. Soc. Mass Spectrom. 2016, 27, 1531–1538. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Wootton, C.A.; Chiron, L.; Coutouly, M.-A.; Soulby, A.; Wei, J.; Barrow, M.P.; Delsuc, M.-A.; Rolando, C.; O’Connor, P.B. Two-Dimensional Mass Spectrometry for Proteomics, a Comparative Study with Cytochrome c. Anal. Chem. 2016, 88, 4409–4417. [Google Scholar] [CrossRef]
- Floris, F.; van Agthoven, M.A.; Chiron, L.; Wootton, C.A.; Lam, P.Y.Y.; Barrow, M.P.; Delsuc, M.-A.; O’Connor, P.B. Bottom-Up Two-Dimensional Electron-Capture Dissociation Mass Spectrometry of Calmodulin. J. Am. Soc. Mass Spectrom. 2018, 29, 207–210. [Google Scholar] [CrossRef] [PubMed]
- van Agthoven, M.A.; Lynch, A.M.; Morgan, T.E.; Wootton, C.A.; Lam, Y.P.Y.; Chiron, L.; Barrow, M.P.; Delsuc, M.-A.; O’Connor, P.B. Can Two-Dimensional IR-ECD Mass Spectrometry Improve Peptide de Novo Sequencing? Anal. Chem. 2018, 90, 3496–3504. [Google Scholar] [CrossRef] [PubMed]
- Paris, J.; Morgan, T.E.; Wootton, C.A.; Barrow, M.P.; O’Hara, J.; O’Connor, P.B. Facile Determination of Phosphorylation Sites in Peptides Using Two-Dimensional Mass Spectrometry. Anal. Chem. 2020, 92, 6817–6821. [Google Scholar] [CrossRef]
- Marzullo, B.P.; Morgan, T.E.; Wootton, C.A.; Perry, S.J.; Saeed, M.; Barrow, M.P.; O’Connor, P.B. Advantages of Two-Dimensional Electron-Induced Dissociation and Infrared Multiphoton Dissociation Mass Spectrometry for the Analysis of Agrochemicals. Anal. Chem. 2020, 92, 11687–11695. [Google Scholar] [CrossRef]
- Halper, M.; Delsuc, M.-A.; Breuker, K.; van Agthoven, M.A. Narrowband Modulation Two-Dimensional Mass Spectrometry and Label-Free Relative Quantification of Histone Peptides. Anal. Chem. 2020, 92, 13945–13952. [Google Scholar] [CrossRef]
- Xian, F.; Hendrickson, C.L.; Blakney, G.T.; Beu, S.C.; Marshall, A.G. Automated Broadband Phase Correction of Fourier Transform Ion Cyclotron Resonance Mass Spectra. Anal. Chem. 2010, 82, 8807–8812. [Google Scholar] [CrossRef]
- Qi, Y.; Thompson, C.J.; Van Orden, S.L.; O’Connor, P.B. Phase correction of Fourier transform ion cyclotron resonance mass spectra using MatLab. J. Am. Soc. Mass Spectrom. 2011, 22, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Kilgour, D.P.A.; Wills, R.; Qi, Y.; O’Connor, P.B. Autophaser: An Algorithm for Automated Generation of Absorption Mode Spectra for FT-ICR MS. Anal. Chem. 2013, 85, 3903–3911. [Google Scholar] [CrossRef] [PubMed]
- Kilgour, D.P.A.; Nagornov, K.O.; Kozhinov, A.N.; Zhurov, K.O.; Tsybin, Y.O. Producing absorption mode Fourier transform ion cyclotron resonance mass spectra with non-quadratic phase correction functions. Rapid Commun. Mass Spectrom. 2015, 29, 1087–1093. [Google Scholar] [CrossRef]
- Kilgour, D.P.A.; Van Orden, S.L.; Tran, B.Q.; Goo, Y.A.; Goodlett, D.R. Producing Isotopic Distribution Models for Fully Apodized Absorption Mode FT-MS. Anal. Chem. 2015, 87, 5797–5801. [Google Scholar] [CrossRef]
- Qi, Y.; Li, H.; Wills, R.H.; Perez-Hurtado, P.; Yu, X.; Kilgour, D.P.A.; Barrow, M.P.; Lin, C.; O’Connor, P.B. Absorption-Mode Fourier Transform Mass Spectrometry: The Effects of Apodization and Phasing on Modified Protein Spectra. J. Am. Soc. Mass Spectrom. 2013, 24, 828–834. [Google Scholar] [CrossRef]
- Smith, D.F.; Kilgour, D.P.A.; Konijnenburg, M.; O’Connor, P.B.; Heeren, R.M.A. Absorption mode FTICR mass spectrometry imaging. Anal. Chem. 2013, 85, 11180–11184. [Google Scholar] [CrossRef]
- Kilgour, D.P.A.; Neal, M.J.; Soulby, A.J.; O’Connor, P.B. Improved optimization of the Fourier transform ion cyclotron resonance mass spectrometry phase correction function using a genetic algorithm. Rapid Commun. Mass Spectrom. 2013, 27, 1977–1982. [Google Scholar] [CrossRef]
- Qi, Y.; Witt, M.; Jertz, R.; Baykut, G.; Barrow, M.P.; Nikolaev, E.N.; O’Connor, P.B. Absorption-mode spectra on the dynamically harmonized Fourier transform ion cyclotron resonance cell. Rapid Commun. Mass Spectrom. 2012, 26, 2021–2026. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Barrow, M.P.; Li, H.; Meier, J.E.; Van Orden, S.L.; Thompson, C.J.; O’Connor, P.B. Absorption-Mode: The Next Generation of Fourier Transform Mass Spectra. Anal. Chem. 2012, 84, 2923–2929. [Google Scholar] [CrossRef]
- Cho, Y.; Qi, Y.; O’Connor, P.B.; Barrow, M.P.; Kim, S. Application of Phase Correction to Improve the Interpretation of Crude Oil Spectra Obtained Using 7 T Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2014, 25, 154–157. [Google Scholar] [CrossRef]
- Qi, Y.; Luo, R.; Schrader, W.; Volmer, D.A. Application of phase correction to improve the characterization of photooxidation products of lignin using 7 Tesla Fourier-transform ion cyclotron resonance mass spectrometry. FACETS 2017, 2, 461–475. [Google Scholar] [CrossRef]
- van Agthoven, M.A.; Kilgour, D.P.A.; Lynch, A.M.; Barrow, M.P.; Morgan, T.E.; Wootton, C.A.; Chiron, L.; Delsuc, M.-A.; O’Connor, P.B. Phase relationships in two-dimensional mass spectrometry. J. Am. Soc. Mass Spectrom. 2019, 30, 2594–2607. [Google Scholar] [CrossRef] [PubMed]
- Delsuc, M.-A. Spectral Representation of 2D NMR Spectra by Hypercomplex Numbers. J. Mag. Res. 1988, 77, 119–124. [Google Scholar] [CrossRef]
- Schuyler, A.D.; Maciejewski, M.W.; Stern, A.S.; Hoch, J.C. Formalism for hypercomplex multidimensional NMR employing partial-component subsampling. J. Mag. Res. 2013, 227, 20–24. [Google Scholar] [CrossRef] [PubMed]
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions, 1st ed.; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Le Bihan, N.; Sangwine, S.J.; Ell, T.A. Instantaneous frequency and amplitude of orthocomplex modulated signals based on quaternion Fourier transform. Signal Process. 2014, 94, 308–318. [Google Scholar] [CrossRef]
- Sehgal, A.A.; Pelupessy, P.; Rolando, C.; Bodenhausen, G. Theory for spiralling ions for 2D FT-ICR and comparison with precessing magnetization vectors in 2D NMR. Phys. Chem. Chem. Phys. 2016, 18, 9167–9175. [Google Scholar] [CrossRef]
- Caravatti, P.; Allemann, M. The infinity cell: A new trapped-ion cell with radiofrequency covered trapping electrodes for Fourier transform ion cyclotron resonance mass spectrometry. Org. Mass Spectrom. 1991, 26, 514–518. [Google Scholar] [CrossRef]
- Tsybin, Y.O.; Witt, M.; Baykut, G.; Kjeldsen, F.; Hakansson, P. Combined infrared multiphoton dissociation and electron capture dissociation with a hollow electron beam in Fourier transform ion cyclotron resonance mass spectrometry. Rapid Commun. Mass Spectrom. 2003, 17, 1759–1768. [Google Scholar] [CrossRef]
- Chiron, L.; Coutouly, M.-A.; Starck, J.-P.; Rolando, C.; Delsuc, M.-A. SPIKE a processing software dedicated to Fourier spectroscopies. arXiv 2016, arXiv:1608.06777. [Google Scholar]
- Kilgour, D.P.A.; Van Orden, S.L. Absorption mode Fourier transform mass spectrometry with no baseline correction using a novel asymmetric apodization function. Rapid Commun. Mass Spectrom. 2015, 29, 1009–1018. [Google Scholar] [CrossRef]
- Qi, Y.; Barrow, M.P.; Van Orden, S.L.; Thompson, C.J.; Li, H.; Perez-Hurtado, P.; O’Connor, P.B. Variation of the Fourier Transform Mass Spectra Phase Function with Experimental Parameters. Anal. Chem. 2011, 83, 8477–8483. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, P.B.; McLafferty, F.W. High-resolution ion isolation with the ion cyclotron resonance capacitively coupled open cell. J. Am. Soc. Mass Spectrom. 1995, 6, 533–535. [Google Scholar] [CrossRef][Green Version]
- O’Connor, P.B.; Little, D.P.; McLafferty, F.W. Isotopic Assignment in Large-Molecule Mass Spectra by Fragmentation of a Selected Isotopic Peak. Anal. Chem. 1996, 68, 542–545. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.F.; Blakney, G.T.; Beu, S.C.; Anderson, L.C.; Weisbrod, C.R.; Hendrickson, C.L. Ultrahigh Resolution Ion Isolation by Stored Waveform Inverse Fourier Transform 21 T Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. Anal. Chem. 2020, 92, 3213–3219. [Google Scholar] [CrossRef] [PubMed]
- Thomas, M.J.; Collinge, E.; Witt, M.; Palacio Lozano, D.C.; Vane, C.H.; Moss-Hayes, V.; Barrow, M.P. Petroleomic depth profiling of Staten Island salt marsh soil: 2ω detection FTICR MS offers a new solution for the analysis of environmental contaminants. Sci. Total Environ. 2019, 662, 852–862. [Google Scholar] [CrossRef]
- Grosshans, P.B.; Marshall, A.G. Can Fourier transform mass spectral resolution be improved by detection at harmonic multiples of the fundamental ion cyclotron orbital frequency? Int. J. Mass Spectrom. Ion Process. 1991, 107, 49–81. [Google Scholar] [CrossRef]
- Vorobyev, A.; Gorshkov, M.V.; Tsybin, Y.O. Towards data acquisition throughput increase in Fourier transform mass spectrometry of proteins using double frequency measurements. Int. J. Mass Spectrom. 2011, 306, 227–231. [Google Scholar] [CrossRef]
- Park, S.-G.; Anderson, G.A.; Bruce, J.E. Parallel Detection of Fundamental and Sixth Harmonic Signals Using an ICR Cell with Dipole and Sixth Harmonic Detectors. J. Am. Soc. Mass Spectrom. 2020, 31, 719–726. [Google Scholar] [CrossRef] [PubMed]
- Lam, Y.P.Y.; Wootton, C.A.; Hands-Portman, I.; Wei, J.; Chiu, C.K.C.; Romero-Canelon, I.; Lermyte, F.; Barrow, M.P.; O’Connor, P.B. Does deamidation of islet amyloid polypeptide accelerate amyloid fibril formation? Chem. Comm. 2018, 54, 13853–13856. [Google Scholar] [CrossRef] [PubMed]
- Stensland, M.; Holm, A.; Kiehne, A.; Fleckenstein, B. Targeted analysis of protein citrullination using chemical modification and tandem mass spectrometry. Rapid Comm. Mass Spectrom. 2009, 23, 2754–2762. [Google Scholar] [CrossRef] [PubMed]
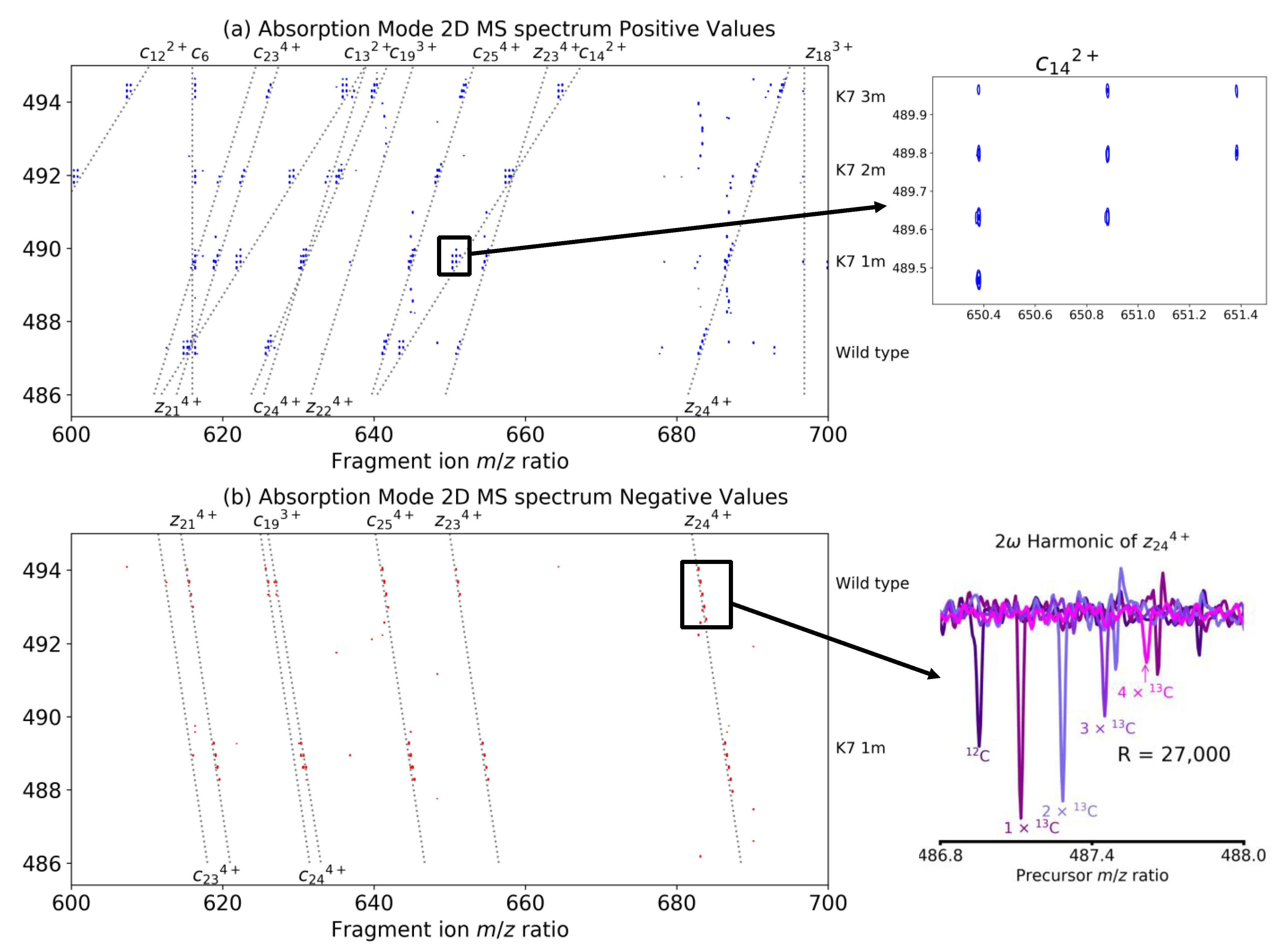
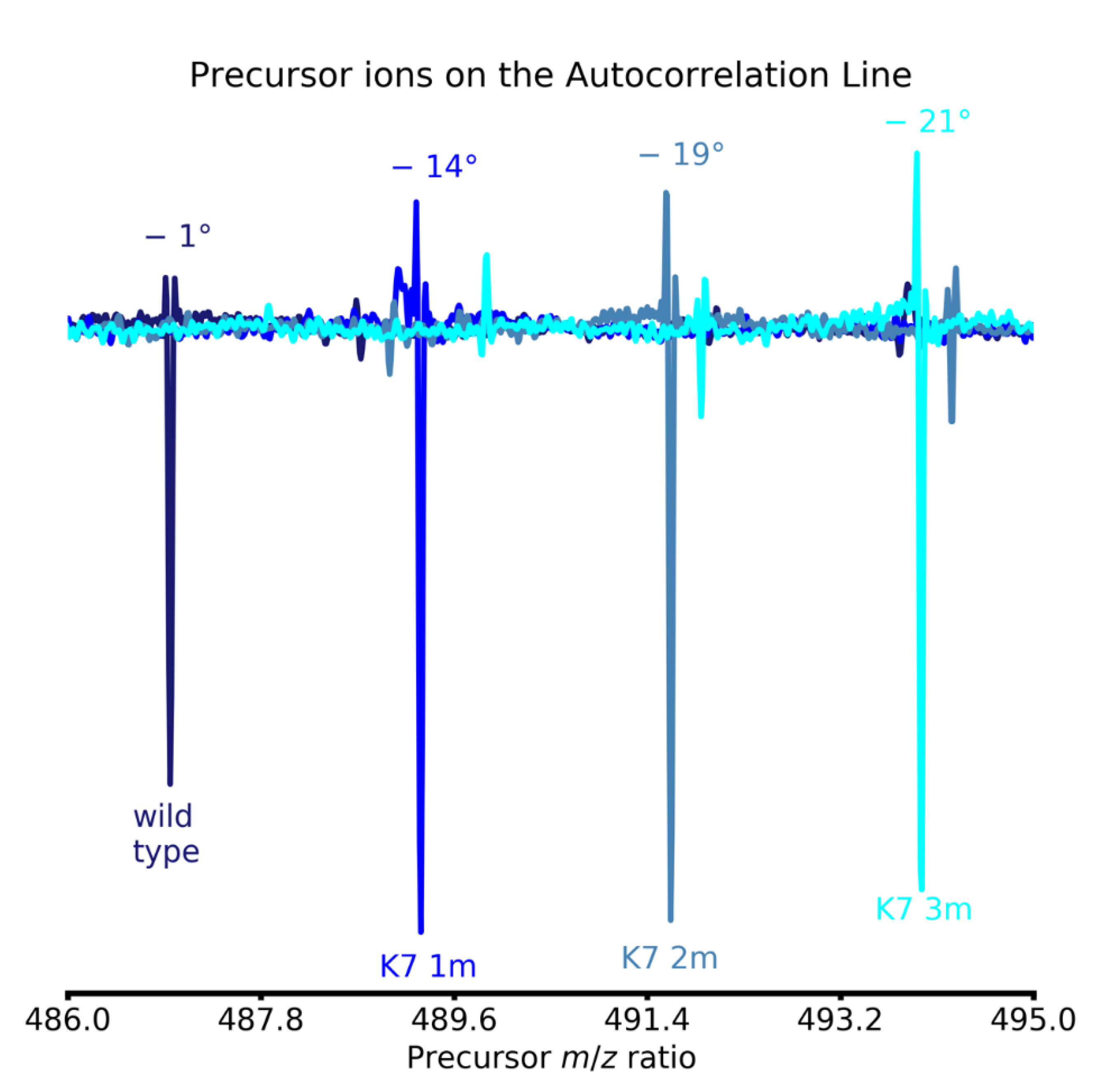
| Coefficient | Theory | Theoretical Value | Empirical Value |
|---|---|---|---|
| 0 order (vertical) | 88.2 | 59.9 | |
| 1st order (vertical) | 7.44 | 7.8 | |
| 0 order (horizontal) | N/A | N/A | −9 |
| 1st order (horizontal) | 632 | 564 | |
| 2nd order (horizontal) | 4607 | 4595 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delsuc, M.-A.; Breuker, K.; van Agthoven, M.A. Phase Correction for Absorption Mode Two-Dimensional Mass Spectrometry. Molecules 2021, 26, 3388. https://doi.org/10.3390/molecules26113388
Delsuc M-A, Breuker K, van Agthoven MA. Phase Correction for Absorption Mode Two-Dimensional Mass Spectrometry. Molecules. 2021; 26(11):3388. https://doi.org/10.3390/molecules26113388
Chicago/Turabian StyleDelsuc, Marc-André, Kathrin Breuker, and Maria A. van Agthoven. 2021. "Phase Correction for Absorption Mode Two-Dimensional Mass Spectrometry" Molecules 26, no. 11: 3388. https://doi.org/10.3390/molecules26113388
APA StyleDelsuc, M.-A., Breuker, K., & van Agthoven, M. A. (2021). Phase Correction for Absorption Mode Two-Dimensional Mass Spectrometry. Molecules, 26(11), 3388. https://doi.org/10.3390/molecules26113388







