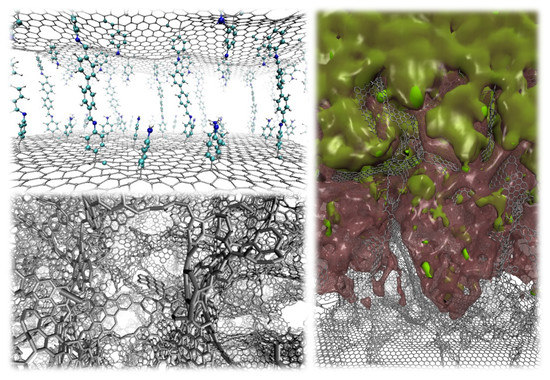
Engineering 3D Graphene-Based Materials: State of the Art and Perspectives
Abstract
1. Introduction
2. Graphene-Based Nano-Porous Materials: Production and Computer Modeling
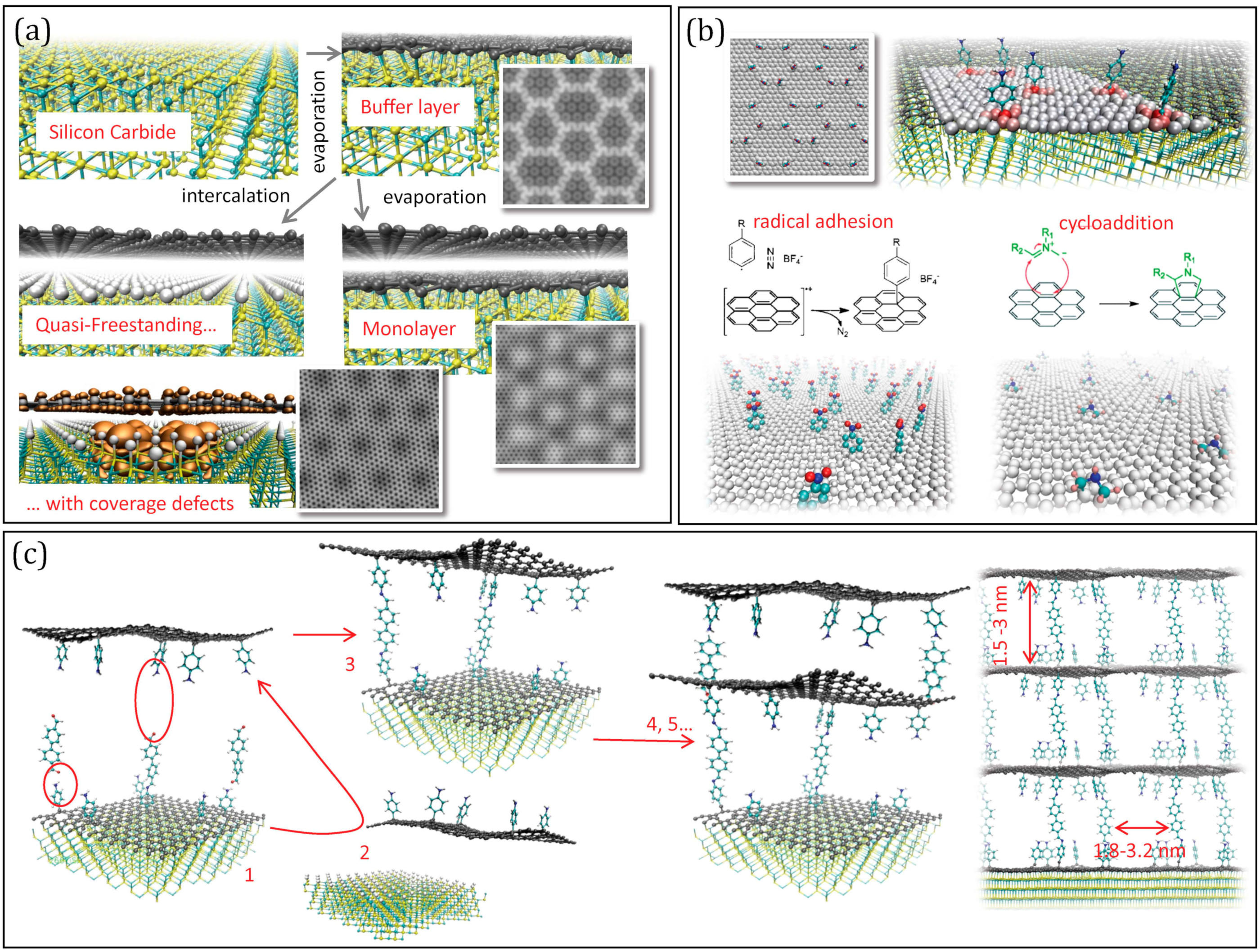
3. Pillared Materials: State of the Art and Open Problems
4. Multilayers from Epitaxy: A Perspective
5. Summary, Conclusions and Possible Developments
Funding
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; NMRPeres Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385. [Google Scholar] [CrossRef] [PubMed]
- Camiola, V.D.; Farchioni, R.; Pellegrini, V.; Tozzini, V. Hydrogen transport within graphene multilayers by means of flexural phonons. 2D Mater. 2015, 2, 014009. [Google Scholar] [CrossRef]
- Fasolino, A.; Los, J.H.; Katsnelson, M.I. Intrinsic ripples in graphene. Nat. Mater. 2007, 6, 858–861. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Colombo, L.; Yu, G.; Stoller, M.; Tozzini, V.; Ferrari, A.C.; Ruoff, R.S.; Pellegrini, V. Graphene, related two-dimensional crystals, and hybrid systems for energy conversion and storage. Science 2015, 347, 1246501. [Google Scholar] [CrossRef]
- Sun, P.; Wang, K.; Zhu, H. Recent Developments in Graphene-Based Membranes: Structure, Mass-Transport Mechanism and Potential Applications. Adv. Mater. 2016, 28, 2287–2310. [Google Scholar] [CrossRef]
- Büch, H.; Rossi, A.; Forti, S.; Convertino, D.; Tozzini, V.; Coletti, C. Superlubricity of epitaxial monolayer WS2 on graphene. Nano Res. 2018, 11, 5946–5956. [Google Scholar] [CrossRef]
- Chee, W.K.; Lim, H.N.; Zainal, Z.; Huang, N.M.; Harrison, I.; Andou, Y. Flexible Graphene-Based Supercapacitors: A Review. J. Phys. Chem. C 2016, 120, 4153–4172. [Google Scholar] [CrossRef]
- Mahmoudi, T.; Wang, Y.; Hahn, Y.-B. Graphene and its derivatives for solar cells application. Nano Energy 2018, 47, 51–65. [Google Scholar] [CrossRef]
- Denis, P.A.; Huelmo, C.P. Martins AS Band Gap Opening in Dual-Doped Monolayer Graphene. J. Phys. Chem. C 2016, 120, 13. [Google Scholar] [CrossRef]
- Iyakutti, K.; Kumar, E.M.; Lakshmi, I.; Thapa, R.; Rajeswarapalanichamy, R.; Surya, V.J.; Kawazoe, Y. Effect of surface doping on the band structure of graphene: A DFT study. J. Mater. Sci. 2016, 27, 2728–2740. [Google Scholar] [CrossRef]
- Deng, S.; Berry, V. Wrinkled, rippled and crumpled graphene: An overview of formation mechanism, electronic properties, and applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Zaminpayma, E.; Emami Razavi, M.; Nayebi, P. Electronic properties of graphene with single vacancy and Stone-Wales defects. Appl. Surf. Sci. 2017, 31, 101–106. [Google Scholar] [CrossRef]
- Nair, M.N.; Palacio, I.; Celis, A.; Zobelli, A.; Gloter, A.; Kubsky, S.; Turmaud, J.-P.; Conrad, M.; Berger, C.; de Heer, W.; et al. Band Gap Opening Induced by the Structural Periodicity in Epitaxial Graphene Buffer Layer. Nano Lett. 2017, 174, 2681–2689. [Google Scholar] [CrossRef]
- Cavallucci, T.; Tozzini, V. Intrinsic structural and electronic properties of the Buffer Layer on Silicon Carbide unraveled by Density Functional Theory. Sci. Rep. 2018, 8, 13097. [Google Scholar] [CrossRef]
- Loh, K.P.; Tong, S.W.; Wu, J. Graphene and Graphene-like Molecules: Prospects in Solar Cells. J. Am. Chem. Soc. 2016, 138, 1095–1102. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Lin, D.-C.; Grossman, J.C. Multilayer Nanoporous Graphene Membranes for Water Desalination. Nano Lett. 2016, 16, 1027–1033. [Google Scholar] [CrossRef]
- Guinea, F.; Katsnelson, M.I.; Geim, A.K. Energy gaps and a zero-field quantum Hall effect in graphene by strain engineering. Nat. Phys. 2010, 6, 30. [Google Scholar] [CrossRef]
- Hicks, J.; Tejeda, A.; Taleb-Ibrahimi, A.; Nevius, M.S.; Wang, F.; Shepperd, K.; Palmer, J.; Bertran, F.; Le Fèvre, P.; Kunc, J.; et al. A wide-bandgap metal–semiconductor–metal nanostructure made entirely from graphene. Nat. Phys. 2012, 9, 49. [Google Scholar] [CrossRef]
- Rossi, A.; Piccinin, S.; Pellegrini, V.; de Gironcoli, S.; Tozzini, V. Nano-Scale Corrugations in Graphene: A Density Functional Theory study of Structure, Electronic Properties and Hydrogenation. J. Phys. Chem. C 2015, 119, 7900. [Google Scholar] [CrossRef]
- McKay, H.; Wales, D.J.; Jenkins, S.J.; Verges, J.A.; de Andres, P.L. Hydrogen on graphene under stress: Molecular dissociation and gap opening. Phys. Rev. B 2010, 81, 075425. [Google Scholar] [CrossRef]
- Goler, S.; Coletti, C.; Tozzini, V.; Piazza, V.; Mashoff, T.; Beltram, F.; Pellegrini, V.; Heun, S. Influence of Graphene Curvature on Hydrogen Adsorption: Towards Hydrogen Storage Devices. J. Phys. Chem. C 2013, 117, 11506. [Google Scholar] [CrossRef]
- Boukhvalov, D.W.; Son, Y.-W. Covalent Functionalization of Strained Graphene. Chem. Phys. Chem. 2012, 13, 1463. [Google Scholar] [CrossRef]
- Wang, Z.F.; Zhang, Y.; Liu, F. Formation of hydrogenated graphene nanoripples by strain engineering and directed surface self-assembly. Phys. Rev. B 2011, 83, 041403(R). [Google Scholar] [CrossRef]
- Cavallucci, T.; Kakhiani, K.; Farchioni, R.; Tozzini, V. Morphing Graphene-Based Systems for Applications: Perspectives from Simulations. In GraphITA Carbon Nanostructures; Springer: Cham, Switzerland, 2017; pp. 87–111. [Google Scholar]
- Camiola, V.D.; Farchioni, R.; Cavallucci, T.; Rossi, A.; Pellegrini, V.; Tozzini, V. Hydrogen storage in rippled graphene: Perspectives from multi-scale simulations. Front. Mater. 2015, 2, 3. [Google Scholar] [CrossRef]
- Quesnel, E.; Roux, F.; Emieux, F.; Faucherand, P.; Kymakis, E.; Volonakis, G.; Giustino, F.; Martín-García, B.; Moreels, I.; Gürsel, S.A.; et al. Graphene-based technologies for energy applications, challenges and perspectives. 2D Mater. 2015, 2, 030204. [Google Scholar] [CrossRef]
- Klechikov, A.G.; Mercier, G.; Merino, P.; Blanco, S.; Merino, C.; Talyzin, A.V. Hydrogen storage in bulk graphene-related materials. Micropor. Mesopor. Mater. 2015, 210, 46–51. [Google Scholar] [CrossRef]
- Qiu, B.; Xing, M.; Zhang, J. Recent advances in three-dimensional graphene based materials for catalysis applications. Chem. Soc. Rev. 2018, 47, 2165. [Google Scholar] [CrossRef]
- Bustillos, J.; Zhang, C.; Boesl, B.; Agarwal, A. Three-Dimensional Graphene Foam−Polymer Composite with Superior Deicing Efficiency and Strength. ACS Appl. Mater. Interfaces 2018, 10, 5022–5029. [Google Scholar] [CrossRef]
- Neves, A.I.S.; Rodrigues, D.P.; De Sanctis, A.; Alonso, E.T.; Pereira, M.S.; Amaral, V.S.; Melo, L.V.; Russo, S.; de Schrijver, I.; HAlves, M.F. Craciun Towards conductive textiles: Coating polymeric fibres with graphene. Sci. Rep. 2017, 7, 4250. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Liu, Y.; Bai, Y.; Zhang, J.; Han, Z.; Ren, L. Fabrication of biomimetic hydrophobic patterned graphene surface with ecofriendly anti-corrosion properties for Al alloy. Coll. Surf. A Physicochem. Eng. Asp. 2016, 500, 64–71. [Google Scholar] [CrossRef]
- Xu, Y.; Sheng, K.; Li, C.; Shi, G. Self-assembled graphene hydrogel via a one-step hydrothermal process. ACS Nano 2010, 4, 4324. [Google Scholar] [CrossRef]
- Mercier, G.; Klechikov, A.; Hedenstroöm, M.; Johnels, D.; Baburin, I.A.; Seifert, G.; Mysyk, R.; Talyzin, A.V. Porous Graphene Oxide/Diboronic Acid Materials: Structure and Hydrogen Sorption. J. Phys. Chem. C 2015, 119, 27179–27191. [Google Scholar] [CrossRef]
- Sun, J.; Morales-Lara, F.; Klechikov, A.; Talyzin, A.V.; Baburin, A.; Seifert, G.; Cardano, F.; Baldrighi, M.; Frasconi, M.; Giordani, S. Porous graphite oxide pillared with tetrapod-shaped molecules. Carbon 2017, 120, 145–156. [Google Scholar] [CrossRef]
- Liang, C.; Li, Z.; Dai, S. Mesoporous carbon materials: Synthesis and modification. Angew. Chem. Int. Ed. 2008, 47, 3696–3717. [Google Scholar] [CrossRef] [PubMed]
- Talyzin, A.V.; Mercier, G.; Klechikov, A.; Hedenström, M.; Johnels, D.; Wei, D.; Cotton, D.; Moons, A.E. Brodie vs Hummers graphite oxides for preparation of multi-layered materials. Carbon 2017, 115, 430–440. [Google Scholar] [CrossRef]
- Talyzin, A.V.; Szabó, T.; Dékány, I.; Langenhorst, F.; Sokolov, P.S.; Solozhenko, V.L. Nanocarbons by High-Temperature Decomposition of Graphite Oxide at Various Pressures. J. Phys. Chem. C 2009, 113, 11279–11284. [Google Scholar] [CrossRef]
- Zhu, Y.; Murali, S.; Stoller, M.D.; Ganesh, K.J.; Cai, W.; Ferreira, P.J.; Pirkle, A.; Wallace, R.M.; Cychosz, K.A.; Thommes, M.; et al. Carbon-based supercapacitors produced by activation of graphene. Science 2011, 332, 1537–1541. [Google Scholar] [CrossRef]
- Zhu, Y.; Murali, S.; Stoller, M.D.; Velamakanni, A.; Piner, R.D.; Ruoff, R.S. Microwave assisted exfoliation and reduction of graphite oxide for ultracapacitors. Carbon 2010, 48, 2118–2122. [Google Scholar] [CrossRef]
- Zhang, C.; Lv, W.; Xie, X.; Tang, D.; Liu, C.; Yang, Q.-H. Towards low temperature thermal exfoliation of graphite oxide for graphene production. Carbon 2013, 62, 11–24. [Google Scholar] [CrossRef]
- Kovtun, A.; Treossi, E.; Mirotta, N.; Scidà, A.; Liscio, A.; Christian, M.; Valorosi, F.; Boschi, A.; Young, R.J.; Galiotis, C.; et al. Benchmarking of graphene-based materials: Real commercial products versus ideal graphene. 2D Mater. 2019, 6, 025006. [Google Scholar] [CrossRef]
- Klechikov, A.; Mercier, G.; Sharifi, T.; Baburin, I.A.; Seifert, G.; Talyzin, A.V. Hydrogen storage in high surface area graphene scaffolds. Chem. Comm. 2015, 51, 15280–15283. [Google Scholar] [CrossRef] [PubMed]
- Raccichini, R.; Varzi, A.; Passerini, S.; Scrosati, B. The role of graphene for electrochemical energy storage. Nature Mater. 2015, 14, 271–279. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Song, S.; Li, F.; Xue, D. Structural design of graphene for use in electrochemical energy storage devices. Chem. Soc. Rev. 2015, 44, 6230–6257. [Google Scholar] [CrossRef] [PubMed]
- Minuto, F.D.; Policicchio, A.; Aloise, A.; Agostino, R.G. Liquid-like hydrogen in the micropores of commercial activated carbons. Int. J. Hydrog. Energy 2015, 40, 14562–14572. [Google Scholar] [CrossRef]
- Nomura, K.; Nishihara, H.; Kobayashi, N.; Asada, T.; Kyotani, T. 4.4 V supercapacitors based on super-stable mesoporous carbon sheet made of edge-free graphene walls. Energy Environ. Sci. 2019, 12, 1542–1549. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Lin, R.; Murali, S.; Zhang, L.; McDonough, J.K.; Ruoff, R.S.; Taberna, P.-L.; Gogotsi Yu Simon, P. Outstanding performance of activated graphene based supercapacitors in ionic liquid electrolyte from −50 to 80 °C. Nano Energy 2013, 2, 403–411. [Google Scholar] [CrossRef]
- Méndez-Morales, T.; Ganfoud, N.; Li, Z.; Haefele, M.; Rotenberg, B.; Salanne, M. Performance of microporous carbon electrodes for supercapacitors: Comparing graphene with disordered materials. Energy Storage Mater. 2019, 17, 88–92. [Google Scholar] [CrossRef]
- Kondrat, S.; Kornyshev, A.A. Pressing a spring: What does it take to maximize the energy storage in nanoporous supercapacitors? Nanoscale Horiz. 2016, 1, 45–52. [Google Scholar] [CrossRef]
- Salanne, M.; Rotenberg, B.; Naoi, K.; Kaneko, K.; Taberna, P.-L.; Grey, C.P.; Dunn, B.; Simon, P. Efficient storage mechanisms for building better supercapacitors. Nat. Energy 2016, 1, 16070. [Google Scholar] [CrossRef]
- Huang, J.-Q.; Zhuang, T.-Z.; Zhang, Q.; Peng, H.-J.; Chen, C.-M.; Wei, F. Permselective Graphene Oxide Membrane for Highly Stable and Anti-Self-Discharge Lithium–Sulfur Batteries. ACS Nano 2015, 9, 3002–3011. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Tang, J.; Zhang, K.; Yuan, J.; Li, J.; Zhu, D.-M.; Ozawa, K.; Qin, L.-C. Comparison of reduction products from graphite oxide and graphene oxide for anode applications in lithium-ion batteries and sodium-ion batteries. Nanoscale 2017, 9, 2585–2595. [Google Scholar] [CrossRef] [PubMed]
- Bellucci, L.; Tozzini, V. In Silico Design of Nano-Porous Graphene Scaffolds, in preparation.
- Yang, T.; Lin, H.; Zheng, X.; Loh, K.P.; Jia, B. Tailoring pores in graphene-based materials: From generation to applications. J. Mater. Chem. A 2017, 5, 16537–16558. [Google Scholar] [CrossRef]
- Fang, T.-H.; Lee, Z.-W.; Chang, W.-J.; Huang, C.-C. Determining porosity effect on the thermal conductivity of single-layer graphene using a molecular dynamics simulation. Phys. E Low Dimens. Syst. Nanostruct. 2019, 106, 90–94. [Google Scholar] [CrossRef]
- Wu, C.D.; Fang, T.H.; Lo, J.Y.; Feng, Y.L. Molecular dynamics simulations of hydrogen storage capacity of few-layer graphene. J. Mol. Model. 2013, 19, 3813–3819. [Google Scholar] [CrossRef]
- Gotzias, A.; Tylianakis, E.; Froudakis, G.; Steriotis, T.H. Theoretical study of hydrogen adsorption in oxygen functionalized carbon slit pores. Micropor. Mesopor. Mater. 2012, 154, 38–44. [Google Scholar] [CrossRef]
- Cabria, I.; López, M.J.; Alonso, J.A. The optimum average nanopore size for hydrogen storage in carbon nanoporous materials. Carbon 2007, 45, 2649–2658. [Google Scholar] [CrossRef]
- Georgakis, M.; Stavropoulos, G.; Sakellaropoulos, G.P. Alteration of graphene based slit pores and the effect on hydrogen molecular adsorption: A simulation study. Micropor. Mesopor. Mater. 2014, 191, 67–73. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Gauden, P.A.; Furmaniak, S.; Terzyk, A.P.; Wisniewski, M.; Ilnicka, A.; Łukaszewicz, J.; Burian, A.; Włoch, J.; Neimark, A.V. Morphologically disordered pore model for characterization of micro-mesoporous carbons. Carbon 2017, 111, 358–370. [Google Scholar] [CrossRef]
- Patchkovskii, S.; John, S.T.; Yurchenko, S.N.; Zhechkov, L.; Heine, T.; Seifert, G. Graphene nanostructures as tunable storage media for molecular hydrogen. Proc. Natl. Acad. Sci. USA 2005, 102, 10439–10444. [Google Scholar] [CrossRef] [PubMed]
- Kuchta, B.; Firlej, L.; Mohammadhosseini, A.; Boulet, P.; Beckner, M.; Romanos, J.; Pfeifer, P. Hypothetical high-surface-area carbons with exceptional hydrogen storage capacities: Open carbon frameworks. J. Am. Chem. Soc. 2012, 134, 15130–15137. [Google Scholar] [CrossRef] [PubMed]
- Krainyukova, N.V.; Zubarev, E.N. Carbon honeycomb high capacity storage for gaseous and liquid species. Phys. Rev. Lett. 2016, 116, 055501. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Xu, M.; Song, W.; Ovcharenko, A.; Zhang, G.; Jia, D. The effect of empirical potential functions on modeling of amorphous carbon using molecular dynamics method. Appl. Surf. Sci. 2013, 286, 287–297. [Google Scholar] [CrossRef]
- Tersoff, J. Modelling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6648. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Valeriani, C.; Los, J.H.; Meijer, E.J.; Fasolino, A.; Frenkel, D. State-of-the-art models for the phase diagram of carbon and diamond nucleation. Mol. Phys. 2010, 106, 2011–2038. [Google Scholar] [CrossRef]
- Chenoweth, K.; Van Duin, A.C.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef]
- Ganfoud, N.; Sene, A.; Haefele, M.; Marin-Laflèche, A.; Daffos, B.; Taberna, P.L.; Salanne, M.; Simon, P.; Rotenberg, B. Effect of the carbon microporous structure on the capacitance of aqueous supercapacitors Energy Storage Mater. Energy Storage Mater 2019, 21, 190–195. [Google Scholar] [CrossRef]
- Mejía-Mendoza, L.M.; Valdez-Gonzalez, M.; Muniz, J.; Santiago, U.; Cuentas-Gallegos, A.K.; Robles, M. A theoretical approach to the nanoporous phase diagram of carbon. Carbon 2017, 120, 233–0243. [Google Scholar] [CrossRef]
- Thompson, M.W.; Dyatkin, B.; Wang, H.-W.; Turner, C.H.; Sang, X.; Unocic, R.R.; Iacovella, C.R.; Gogotsi, Y.; van Duin Cummings, P.T. An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics. J. Carbon Res. C 2017, 3, 32. [Google Scholar] [CrossRef]
- Ranganathan, R.; Rokkam, S.; Desa, T.; Keblinski, P. Generation of amorphous carbon models using liquid quench method: A reactive molecular dynamics study. Carbon 2017, 113, 87–99. [Google Scholar] [CrossRef]
- Surendra, K.J.; Roland, J.-M.P.; Pikunic, J.P.; Gubbins, K.E. Molecular Modeling of Porous Carbons Using the Hybrid Reverse Monte Carlo Method. Langmuir 2006, 22, 9942–9948. [Google Scholar]
- Farmahini, A.H.; Bhatia, S.K. Hybrid Reverse Monte Carlo simulationof amorphous carbon: Distinguishing betweencompeting structures obtained using differentmodeling protocols. Carbon 2015, 83, 53–70. [Google Scholar] [CrossRef]
- Sarkisov, L. Accessible Surface Area of Porous Materials: Understanding Theoretical Limits. Adv. Mater. 2012, 24, 3130–3133. [Google Scholar] [CrossRef]
- Baburin, I.A.; Klechikov, A.; Mercier, G.; Talyzin, A.; Seifert, G. Hydrogen adsorption by perforated graphene. Int. J. Hydrog. Energy 2015, 40, 6594–6599. [Google Scholar] [CrossRef]
- Kostoglou, N.; Tarat, A.; Walters, I.; Ryzhkov, V.; Tampaxis, C.; Charalambopoulou, G.; Steriotis, T.; Mitterer, C.; Rebholz, C. Few-layer graphene-like flakes derived by plasma treatment: A potential material for hydrogen adsorption and storage. Microporous Mesoporous Mater. 2016, 225, 482–487. [Google Scholar] [CrossRef]
- Klontzas, E.; Tylianakis, E.; Varshney, V.; Roy, A.K.; Froudakis, G.E. Organically interconnected graphene flakes: A flexible 3-D material with tunable electronic bandgap. Sci. Rep. 2019, 9, 13676. [Google Scholar] [CrossRef]
- Burress, J.W.; Gadipelli, S.; Ford, J.; Simmons, J.M.; Zhou, W.; Yildirim, T. Graphene Oxide Framework Materials: Theoretical Predictions and Experimental Results. Angew. Chem. Int. Ed. 2010, 49, 8902–8904. [Google Scholar] [CrossRef]
- Hung, W.-S.; Tsou, C.-H.; De Guzman, M.; An, Q.-F.; Liu, Y.-L.; Zhang, Y.a.-M.; Hu, C.-C.; Lee, K.-R.; Lai, J.-Y. Cross-Linking with Diamine Monomers To Prepare Composite Graphene Oxide-Framework Membranes with Varying d-Spacing. Chem. Mater. 2014, 26, 2983–2990. [Google Scholar] [CrossRef]
- Banda, H.; Périé, S.; Daffos, B.; Taberna, P.-L.; Dubois, L.; Crosnier, O.; Simon, P.; Lee, D.; De Paëpe, G.; Duclairoir, F. Sparsely Pillared Graphene Materials for High- Performance Supercapacitors: Improving Ion Transport and Storage Capacity. ACS Nano 2019, 13, 1443–1453. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Yoon, Y.; Cho, Y.; Lee, S.M.; Shin, Y.; Lee, H.; Lee, H. Tunable Sub-nanopores of Graphene Flake Interlayers with Conductive Molecular Linkers for Supercapacitors. ACS Nano 2016, 10, 6799–6807. [Google Scholar] [CrossRef] [PubMed]
- Sekar, P.; Anothumakkool, B.; Kurungot, S. 3D Polyaniline Porous Layer Anchored Pillared Graphene Sheets: Enhanced Interface Joined with High Conductivity for Better Charge Storage Applications. ACS Appl. Mater. Interfaces 2015, 7, 7661–7669. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.; Xu, Y.; Uihlein, J.; Brunklaus, G.; Shi, L.; Heiderhoff, R.; Que, M.; Forster, M.; Chassé, T.; Pichler, T.; et al. Straightforward Generation of Pillared, Microporous Graphene Frameworks for Use in Supercapacitors. Adv. Mater. 2015, 27, 6714–6721. [Google Scholar] [CrossRef]
- Lee, J.H.; Kang, S.; Jaworski, J.; Kwon, K.-Y.; Seo, M.L.; Lee, J.Y.; Jung, J.H. Fluorescent Composite Hydrogels of Metal–Organic Frameworks and Functionalized Graphene Oxide. Chem. Eur. J. 2012, 18, 765–769. [Google Scholar] [CrossRef]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared Graphene: A New 3-D Network Nanostructure for Enhanced Hydrogen Storage. Nano Lett. 2008, 8, 3166. [Google Scholar] [CrossRef]
- Hassani, A.; Taghi, M.; Mosavian, H.; Ahmadpour, A.; Farhadian, N. Hybrid molecular simulation of methane storage inside pillared graphene. J. Chem. Phys. 2015, 142, 234704. [Google Scholar] [CrossRef]
- Pedrielli, A.; Taioli, S.; Garberoglio, G.; Pugno, N.M. Gas adsorption and dynamics in Pillared Graphene Frameworks. Microporous Mesoporous Mater. 2018, 257, 222–231. [Google Scholar] [CrossRef]
- Garberoglio, G.; Pugno, N.M.; Taioli, S. Gas adsorption and separation in realistic and idealized frameworks of organic pillared graphene: A comparative study. J. Phys. Chem. C 2015, 119, 1980–1987. [Google Scholar] [CrossRef]
- Mahdizadeh, S.J.; Goharshadi, E.K.; Akhlamadia, G. Seawater desalination using pillared graphene as a novel nano-membrane in reverse osmosis process: Nonequilibrium MD simulation study. Phys. Chem. Chem. Phys. 2018, 20, 22241. [Google Scholar] [CrossRef]
- Wang, Y.C.; Zhu, Y.; FCWang Liu, X.Y.; Wu, H.A. Super-elasticity and deformation mechanism of three-dimensional pillared graphene network structures. Carbon 2017, 118, 588–596. [Google Scholar] [CrossRef]
- Ciammaruchi, L.; Bellucci, L.; Comeron Castillo, G.; Martínez-DenegriSanchez, G.; Liu, Q.; Tozzini Martorell, J. Water splitting for hydrogen chemisorption in graphene oxide dynamically evolving to a graphane character lattice. Carbon 2019, 153, 234–241. [Google Scholar] [CrossRef]
- Morimoto, N.; Kubo, T.; Nishina, Y. Tailoring the Oxygen Content of Graphite and Reduced Graphene Oxide for Specific Applications. Sci. Rep. 2016, 6, 21715. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, L.; Zhou, C. Review of Chemical Vapor Deposition of Graphene and Related Applications. Acc. Chem. Res. 2013, 46, 2329–2339. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Starke, U. Structural and Electronic Properties of Epitaxial Graphene on SiC(0001): A Review of Growth, Characterization, Transfer Doping and Hydrogen Intercalation. J. Phys. D Appl. Phys. 2010, 43, 374009. [Google Scholar] [CrossRef]
- Mashoff, T.; Convertino, D.; Miseikis, V.; Coletti, C.; Piazza, V.; Tozzini, V.; Beltram, F.; Heun, S. Increasing the active surface of titanium islands on graphene by nitrogen sputtering. Appl. Phys. Lett. 2015, 106, 083901. [Google Scholar] [CrossRef]
- Takahashi, K.; Isobe, S.; Omori, K.; Mashoff, T.; Convertino, D.; Miseikis, V.; Coletti, C.; Tozzini, V.; Heun, S. Revealing the Multi-Bonding State Between Hydrogen and Graphene-Supported Ti Clusters. J. Phys. Chem. C 2016, 120, 12974. [Google Scholar] [CrossRef]
- Wang, Q.H.; Jin, Z.; Kim, K.K.; Hilmer, A.J.; Paulus, G.L.C.; Shih, C.-J.; Ham, M.-H.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; et al. Understanding and controlling the substrate effect on graphene electron-transfer chemistry via reactivity imprint lithography. Nat. Chem. 2012, 4, 724. [Google Scholar] [CrossRef]
- Navarro, J.J.; Leret, S.; Calleja, F.; Stradi, D.; Black, A.; Bernardo-Gavito, R.; Garnica, M. Organic Covalent Patterning of Nanostructured Graphene with Selectivity at the Atomic Level. Nano Lett. 2016, 16, 355–361. [Google Scholar] [CrossRef]
- Romero-Muñiz, C.; Martín-Recio, A.; Pou, P.; Gómez-Rodríguez, J.M.; Pérez, R. Substrate-induced enhancement of the chemical reactivity in metal-supported graphene. Phys. Chem. Chem. Phys. 2018, 20, 19492–19499. [Google Scholar] [CrossRef]
- Criado, A.; Melchionna, M.; Marchesan, S.; Prato, M. The Covalent Functionalization of Graphene on Substrates. Angew. Chem. 2015, 54, 10734. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Wu, Y.; Hao, Y.; Geng, J.; Charlton, M.; Chen, S.; Ren, Y.; Ji, H.; Li, H.; Boukhvalov, D.W.; et al. Selective surface functionalization at regions of high local curvature in graphene. Chem. Commun. 2013, 49, 677–679. [Google Scholar] [CrossRef] [PubMed]
- Bissett, M.A.; Konabe, S.; Okada, S.; Tsuji, M.; Ago, H. Enhanced chemical reactivity of graphene induced by mechanical strain. ACS Nano 2013, 7, 10335–10343. [Google Scholar] [CrossRef] [PubMed]
- Bellucci, L.; Cavallucci, T.; Tozzini, V. From the Buffer Layer to Graphene on Silicon Carbide: Exploring Morphologies by Computer Modeling. Front. Mater. 2019, 6, 198. [Google Scholar] [CrossRef]
- Goler, S.; Coletti, C.; Piazza, V.; Pingue, P.; Colangelo, F.; Pellegrini, V.; Emtsev, K.V.; Forti, S.; Starke, U.; Heun, S.; et al. Revealing the Atomic Structure of the Buffer Layer between SiC (0001) and Epitaxial Graphene. Carbon 2013, 51, 249. [Google Scholar] [CrossRef]
- Cavallucci, T.; Tozzini, V. Multistable Rippling of Graphene on SiC: A Density Functional Theory Study. J. Phys. Chem C 2016, 120, 7670. [Google Scholar] [CrossRef]
- Fiori, S.; Murata, Y.; Veronesi, S.; Rossi, A.; Coletti, C.; Heun, S. Li-intercalated graphene on SiC (0001): An STM study. Phys. Rev. B 2017, 96, 125429. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Iwasaki, T.; Zakharov, A.A.; Starke, U. Quasi-Free-Standing Epitaxial Graphene on SiC Obtained by Hydrogen Intercalation. Phys. Rev. Lett. 2009, 103, 246804. [Google Scholar] [CrossRef]
- Murata, Y.; Mashoff, T.; Takamura, M.; Tanabe, S.; Hibino, H.; Beltram, F.; Heun, S. Correlation between morphology and transport properties of quasi free standing monolayer graphene. Appl. Phys. Lett. 2014, 105, 221604. [Google Scholar] [CrossRef]
- Murata, Y.; Cavallucci, T.; Tozzini, V.; Pavliček, N.; Gross, L.; Meyer, G.; Takamura, M.; Hibino, H.; Beltram, F.; Heun, S. Atomic and electronic structure of Si dangling bonds in quasi-free-standing monolayer graphene. Nano Res. 2018, 11, 864. [Google Scholar] [CrossRef]
- Cavallucci, T.; Murata, Y.; Heun, S.; Tozzini, V. Unraveling localized states in quasi free standing monolayer graphene by means of Density Functional Theory. Carbon 2018, 130, 466–474. [Google Scholar] [CrossRef]
- Hess, L.H.; Lyuleeva, A.; Blaschke, B.M.; Sachsenhauser, M.; Seifert, M.; Garrido, J.A.; Coulombwall, A. Graphene Transistors with Multifunctional Polymer Brushes for Biosensing Applications. ACS Appl. Mater. Interfaces 2014, 6, 9705. [Google Scholar] [CrossRef] [PubMed]
| Precursor | Method/Treatment | SSA m2/g | PSV cm3/g or Avg Pore Size | Density cm3/g | H2 Uptake (% at 77K) or Capacitance (F/g) | Ref. |
|---|---|---|---|---|---|---|
| Graphite oxide | TEGO, TEGO + KOH | 2300 | 5% | 2015 [29] | ||
| Graphite oxide | TEGO + KOH | 3300 | 2.2 (PSV) | 7% | 2015 [44] | |
| Graphite oxide | TEGO + KOH | 2900 | 1.4 (PSV) | ~1 | 5.5% | 2015 [78] |
| Slit pores | Modelling | 5100 | 0.95 (PSV) | ~1 | 6.5% | 2015 [78] |
| Graphite | plasma-induced exfoliation | ~800 | ~0.8 nm | 2% | 2016 [79] | |
| Graphite-/diamond-like | Heating/Quenching MD simulations | 600–3000 | 0–1.6 (PSV) | 0.5–3.5 | 2017 [72] | |
| activated carbon | Thermal treatment | 2220 | 0.67 nm | 1.95 | 5.5% | 2015 [47] |
| Carbon atoms | Quench MD simulations | ~1900 | 3–15 nm | ~0.9 | 123 F/g | 2019 [71] |
| Precursor | Pillars | Reaction/Method | SSA m2/g | Structural Features | H2 Uptake (% at 77K) | Ref. |
|---|---|---|---|---|---|---|
| GO | Diboronic acid | Solvothermal Acid+OH dehydration | ~200 | ~11 Å interlayer spacing; pillars distance: 7–8 Å | 1% experiment 5% simulation | 2010 [80] |
| GO | Diboronic acid | Solvothermal | 500–600 | Interlayer: 8–15 (swelling) Pore size > 2 nm | ~1.5% | 2015 [34] |
| GO | “tetrapod” amine | Solvothermal | >660 | Interlayer: 10–13 to ~16 Å (swelling) | ~1.5% | 2017 [35] |
| GO | Different types of diamine | Cross-linking, thermally promoted | Interlayer 8.5–11 Å Pillar dist ~10 Å | 2019 [84] | ||
| GO reduced | 1–6 diaminohexane | Cross-linking | 150–200 | Inter layer: 7.8 Å Pore size: 1 nm, 15 nm | 2018 [85] | |
| rGO | Aryl bis-diazionium salts (and variants) | Radical reaction | 200–400 | Interlayer: 5–10 Å inter-pillar ext: ~5 Å | 2016 [86] | |
| rGO | Benzoic acid, polyaniline | Polyaniline is grown on benzoic acid on flakes | 330 | Inter layer 1.5–2.5 nm Density 0.68 g/cm3 Pore size 0.8 nm | 2015 [87] | |
| rGO | 4-iodophenyl diazionium salts | Aryl-aryl coupling reaction for cross-linking | Pore size 1–10 nm | 2015 [88] | ||
| rGO | Azobenzoic acid-based ligands | Zn2+ coordination for cross-linking | inter-layer distance ~3 nm in the hydrogel | 2012 [89] | ||
| graph | Diboronic acid variants | Density Functional Theory, Tight binding | Interlayer 1.1–2.2 nm inter pillar 3–5 Å | 1.5% | 2019 [84] | |
| graph | nanotubes | Density Functional Theory, Grand Canonical MC | 1.2 nm interlayer, 1.5 nm inter-pillar | 6% | 2017 [71,72] | |
| GO, gr | Organic aromatic pillars | Reax FF Grand Canonical MC | Pore size 0.8,1,1.1 nm Inter-layer ~3 nm | ~4% | 2017 [73,74] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellucci, L.; Tozzini, V. Engineering 3D Graphene-Based Materials: State of the Art and Perspectives. Molecules 2020, 25, 339. https://doi.org/10.3390/molecules25020339
Bellucci L, Tozzini V. Engineering 3D Graphene-Based Materials: State of the Art and Perspectives. Molecules. 2020; 25(2):339. https://doi.org/10.3390/molecules25020339
Chicago/Turabian StyleBellucci, Luca, and Valentina Tozzini. 2020. "Engineering 3D Graphene-Based Materials: State of the Art and Perspectives" Molecules 25, no. 2: 339. https://doi.org/10.3390/molecules25020339
APA StyleBellucci, L., & Tozzini, V. (2020). Engineering 3D Graphene-Based Materials: State of the Art and Perspectives. Molecules, 25(2), 339. https://doi.org/10.3390/molecules25020339