Influence of Partial Acid Hydrolysis on Size, Dispersity, Monosaccharide Composition, and Conformation of Linearly-Branched Water-Soluble Polysaccharides
Abstract
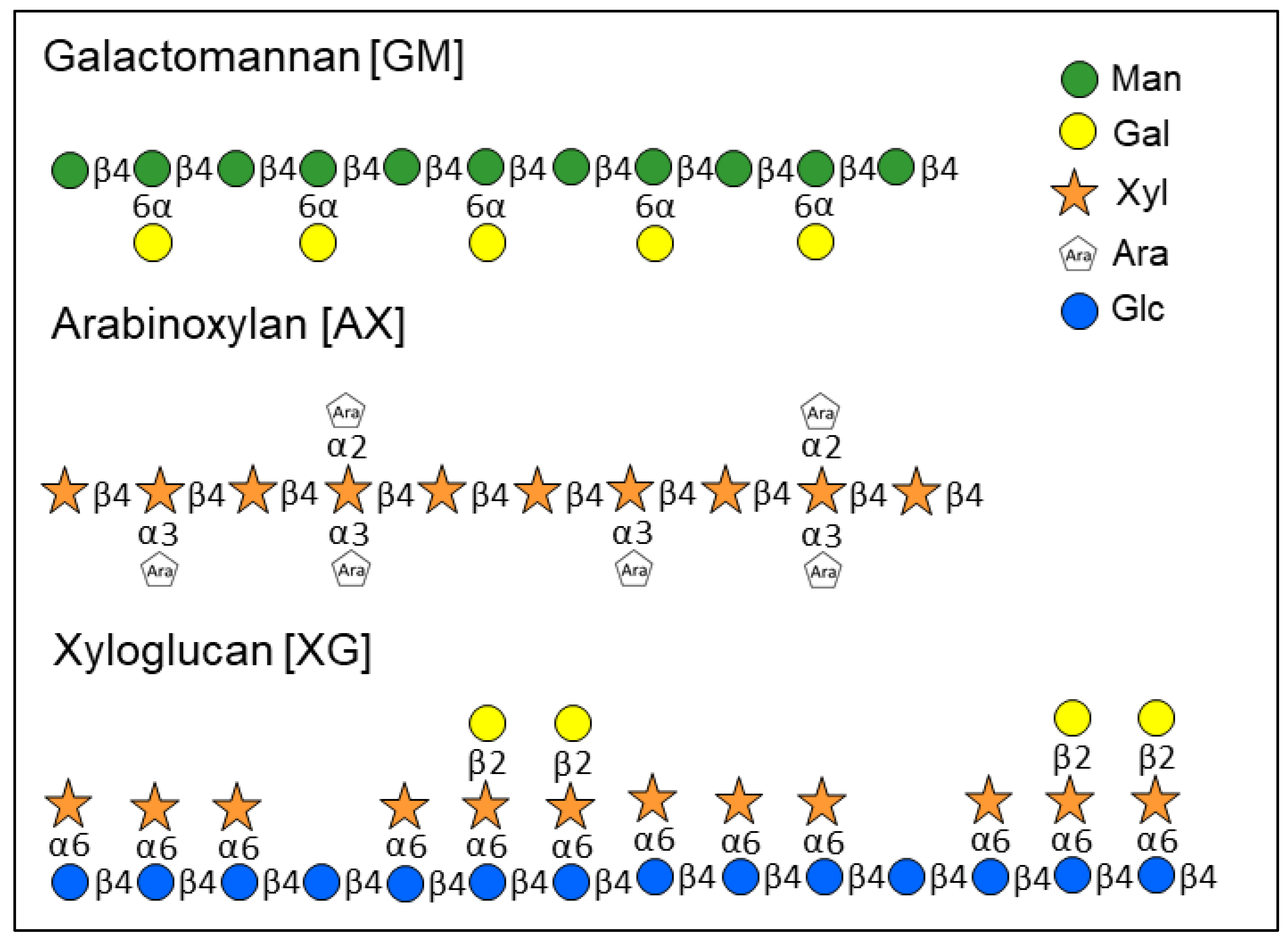
1. Introduction
2. Results and Discussion
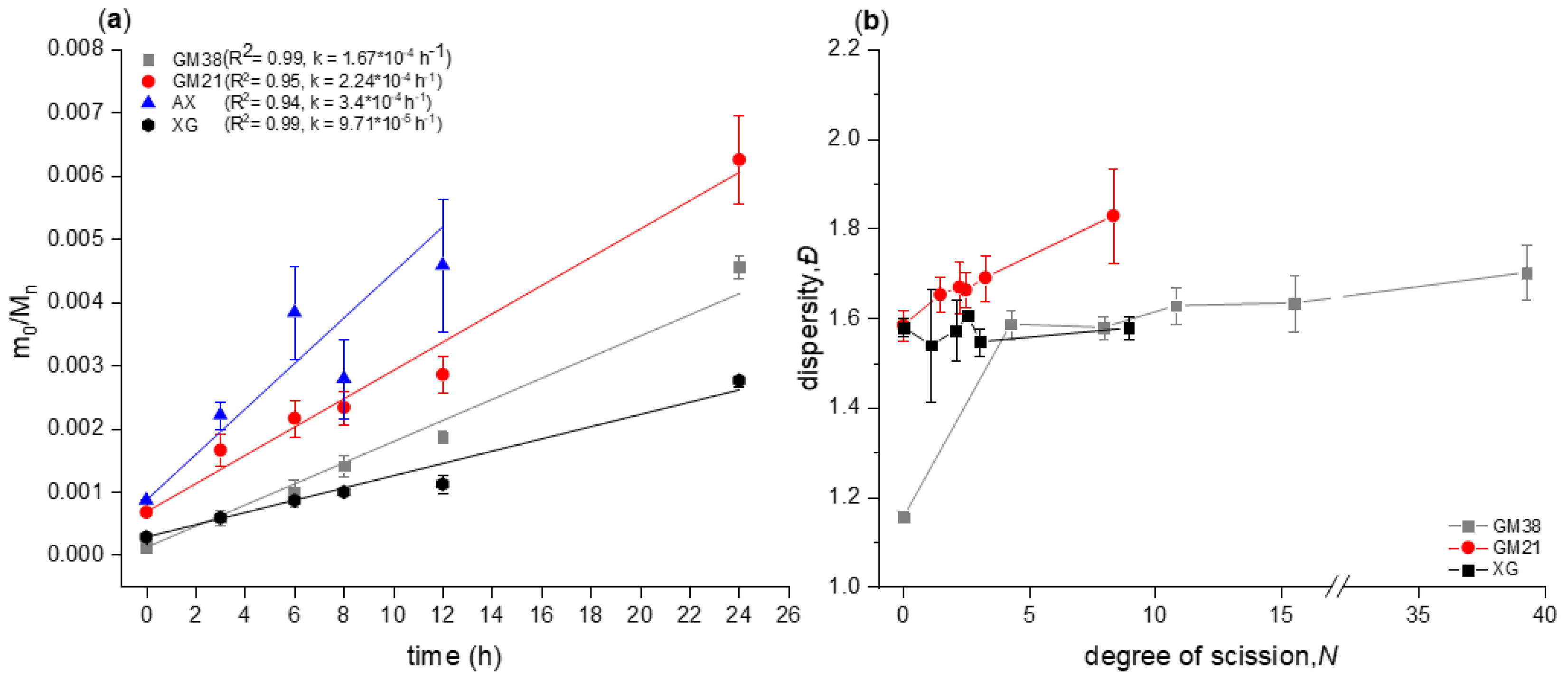
2.1. Chain Scission Kinetics of Acid Hydrolysis and Dispersity Analysis
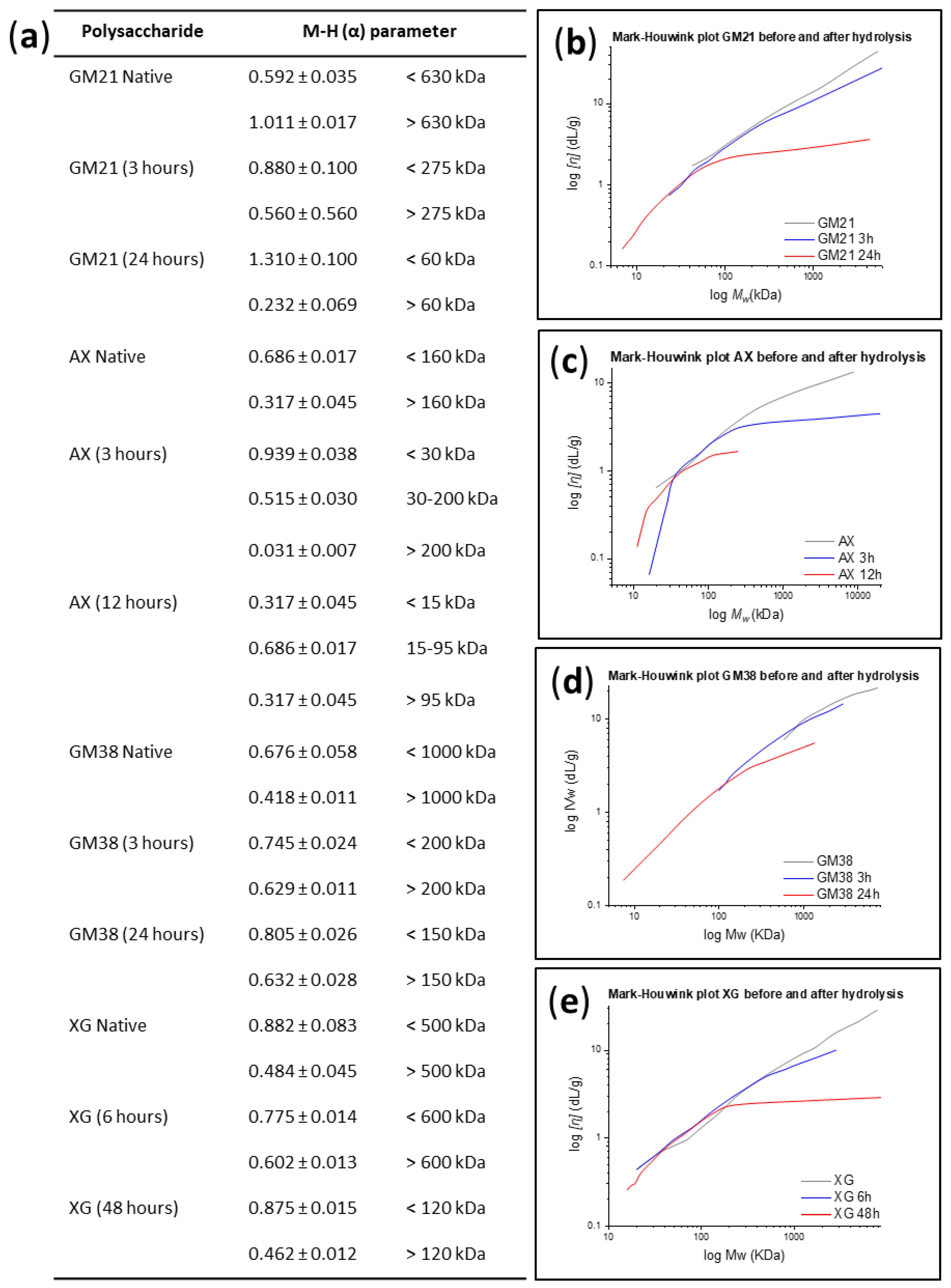
2.1.1. Conformational Analysis
2.1.2. Relationship Between Hydrodynamic Radius and Intrinsic Viscosity
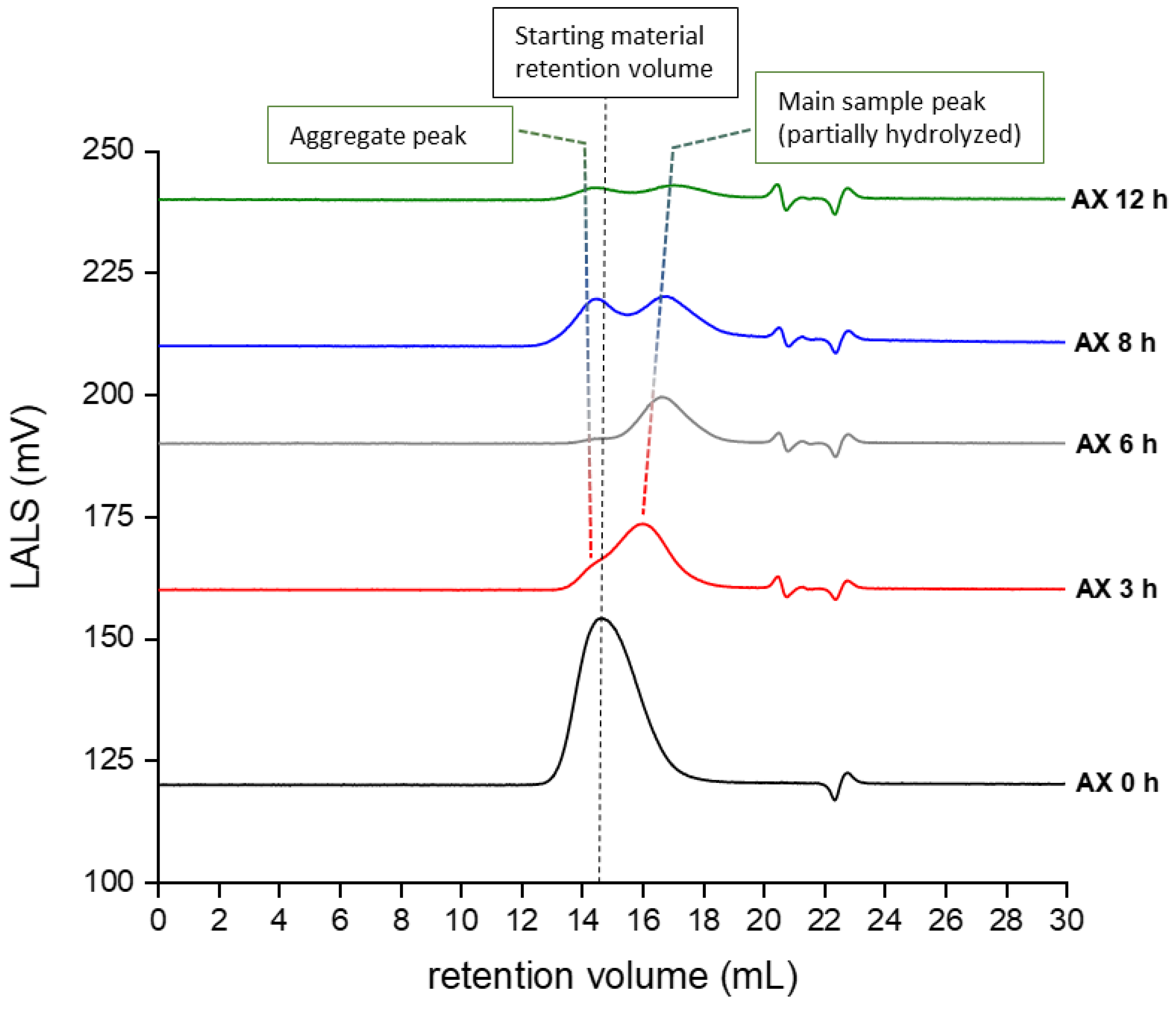
2.1.3. Molecular Weight and Dispersity Analysis of Hydrolyzed and Fractionated Polysaccharides
2.2. Monosaccharide Ratios
3. Materials and Methods
3.1. Materials
3.2. Acid Hydrolysis in Dilute Solution
3.3. Collection of Low Dispersity Polysaccharide Fractions by Isopropanol Precipitation
3.4. Chain scission Kinetics
3.5. Molecular Weight and Dispersity Analysis
3.5.1. Mark-Houwink-Sakurada Relationship
3.5.2. Relationship Between Intrinsic Viscosity and Hydrodynamic Radius
3.6. Monosaccharide Composition by HPAEC-PAD
3.7. Statistical Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Freire, J.J. Conformational Properties of Branched Polymers: Theory and Simulations. In Branched Polymers II; Springer Science and Business Media LLC: Volberg, Germany, 2007; Volume 143, pp. 35–112. [Google Scholar]
- Hokputsa, S.; Jumel, K.; Alexander, C.; Harding, S.E. Hydrodynamic characterisation of chemically degraded hyaluronic acid. Carbohydr. Polym. 2003, 52, 111–117. [Google Scholar] [CrossRef]
- Kuei, B.; Gomez, E.D. Chain conformations and phase behavior of conjugated polymers. Soft Matter 2017, 13, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q. Understanding the Physical Properties of Food Polysaccharides. Food Carbohydrates 2005. [Google Scholar] [CrossRef]
- Jones, O.G.; McClements, D.J. Functional Biopolymer Particles: Design, Fabrication, and Applications. Compr. Rev. Food Sci. Food Saf. 2010, 9, 374–397. [Google Scholar] [CrossRef]
- Mikkonen, K.S.; Rita, H.; Helén, H.; Talja, R.A.; Hyvönen, L.; Tenkanen, M. Effect of Polysaccharide Structure on Mechanical and Thermal Properties of Galactomannan-Based Films. Biomacromolecules 2007, 8, 3198–3205. [Google Scholar] [CrossRef] [PubMed]
- Kochumalayil, J.J.; Berglund, L.A. Water-soluble hemicelluloses for high humidity applications—Enzymatic modification of xyloglucan for mechanical and oxygen barrier properties. Green Chem. 2014, 16, 1904–1910. [Google Scholar] [CrossRef]
- Kasaai, M.R. A comparative study of molecular structures, solution properties and food applications for three branched polysaccharides: Amylopectin, glycogen, and dextran. Polymer 2012, 16, 49–63. [Google Scholar]
- Thombare, N.; Jha, U.; Mishra, S.; Siddiqui, M. Guar gum as a promising starting material for diverse applications: A review. Int. J. Boil. Macromol. 2016, 88, 361–372. [Google Scholar] [CrossRef]
- Fessas, D.; Schiraldi, A. State diagrams of arabinoxylan-water binaries. Thermochim. Acta 2001, 370, 83–89. [Google Scholar] [CrossRef]
- Zhang, Y.; Pitkänen, L.; Douglade, J.; Tenkanen, M.; Rémond, C.; Joly, C. Wheat bran arabinoxylans: Chemical structure and film properties of three isolated fractions. Carbohydr. Polym. 2011, 86, 852–859. [Google Scholar] [CrossRef]
- Nishinari, K.; Takemasa, M.; Yamatoya, K.; Shirakawa, M. Xyloglucan. In Handbook of Hydrocolloids; Elsevier: Cambridge, England, 2009; pp. 535–566. [Google Scholar]
- McCutchen, C.M.; Duffaud, G.D.; LeDuc, P.; Petersen, A.R.H.; Tayal, A.; Khan, S.A.; Kelly, R.M. Characterization of extremely thermostable enzymatic breakers (α-1,6-galactosidase and β-1,4-mannanase) from the hyperthermophilic bacterium Thermotoga neapolitana 5068 for hydrolysis of guar gum. Biotechnol. Bioeng. 2000, 52, 332–339. [Google Scholar] [CrossRef]
- Maeda, T.; Yamashita, H.; Morita, N. Application of xyloglucan to improve the gluten membrane on breadmaking. Carbohydr. Polym. 2007, 68, 658–664. [Google Scholar] [CrossRef]
- Ogawa, K.; Takeuchi, M.; Nakamura, N. Immunological Effects of Partially Hydrolyzed Arabinoxylan from Corn Husk in Mice. Biosci. Biotechnol. Biochem. 2005, 69, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Bezakova, Z.; Hermannová, M.; Dřímalová, E.; Malovíková, A.; Ebringerova, A.; Velebny, V. Effect of microwave irradiation on the molecular and structural properties of hyaluronan. Carbohydr. Polym. 2008, 73, 640–646. [Google Scholar] [CrossRef]
- Cieśla, K.A. Radiation modification of polysaccharides and their composites/nanocomposites. In Applications of Ionizing Radiation in Materials Processing; Institute of Nuclear Chemistry and Technology: Warszawa, Poland, 2017; pp. 327–354. [Google Scholar]
- Ulanski, P.; Rosiak, J. Preliminary studies on radiation-induced changes in chitosan. Int. J. Radiat. Appl. Instrum. Part C Radiat. Phys. Chem. 1992, 39, 53–57. [Google Scholar] [CrossRef]
- Suslick, K.S.; Didenko, Y.; Fang, M.M.; Hyeon, T.; Kolbeck, K.J.; McNamara, W.B.; Mdleleni, M.M.; Wong, M. Acoustic cavitation and its chemical consequences. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1999, 357, 335–353. [Google Scholar] [CrossRef]
- Gogate, P.; Prajapat, A.L. Depolymerization using sonochemical reactors: A critical review. Ultrason. Sonochem. 2015, 27, 480–494. [Google Scholar] [CrossRef]
- De Moura, F.A.; Macagnan, F.T.; Da Silva, L.P. Oligosaccharide production by hydrolysis of polysaccharides: A review. Int. J. Food Sci. Technol. 2014, 50, 275–281. [Google Scholar] [CrossRef]
- Cheng, Y.; Brown, K.M.; Prud’Homme, R.K. Preparation and characterization of molecular weight fractions of guar galactomannans using acid and enzymatic hydrolysis. Int. J. Boil. Macromol. 2002, 31, 29–35. [Google Scholar] [CrossRef]
- Jian, H.-L.; Lin, X.-J.; Zhang, W.-A.; Sun, D.; Jiang, J.; Zhang, W.-M. Characterization of fractional precipitation behavior of galactomannan gums with ethanol and isopropanol. Food Hydrocoll. 2014, 40, 115–121. [Google Scholar] [CrossRef]
- Pituch-Zdanowska, A.; Banaszkiewicz, A.; Albrecht, P. The role of dietary fibre in inflammatory bowel disease. Gastroenterol. Rev. 2015, 10, 135–141. [Google Scholar] [CrossRef]
- Theuwissen, E.; Mensink, R.P. Water-soluble dietary fibers and cardiovascular disease. Physiol. Behav. 2008, 94, 285–292. [Google Scholar] [CrossRef]
- Moiseev, Y.V.; Khalturinskii, N.A.; Zaikov, G.E. The mechanism of the acid-catalysed hydrolysis of glucosides. Carbohydr. Res. 1976, 51, 23–37. [Google Scholar] [CrossRef]
- Timell, T.E. The acid hydrolysis of glycosides: I. General conditions and the effect of the nature of the aglycone. Can. J. Chem. 1964, 42, 1456–1472. [Google Scholar] [CrossRef]
- BeMiller, J. Acid-catalyzed hydrolysis of glycosides. In Advances in Carbohydrate Chemistry; Elsevier: San Diego, CA, USA, 1967; Volume 22, pp. 25–108. [Google Scholar]
- Yoon, J.-S.; Chin, I.-J.; Kim, M.-N.; Kim, C. Degradation of Microbial Polyesters: A Theoretical Prediction of Molecular Weight and Polydispersity. Macromolecules 1996, 29, 3303–3307. [Google Scholar] [CrossRef]
- Halabalová, V.; Šimek, L.; Dostál, J.; Bohdanecký, M. Note on the Relation between the Parameters of the Mark-Houwink-Kuhn-Sakurada Equation. Int. J. Polym. Anal. Charact. 2004, 9, 65–75. [Google Scholar] [CrossRef]
- Guo, M.Q.; Hu, X.; Wang, C.; Ai, L. Polysaccharides: Structure and Solubility. Solubility Polysacch. 2017, 7–21. [Google Scholar] [CrossRef]
- Dervilly-Pinel, G.; Saulnier, L.; Roger, P.; Thibault, J.-F. Isolation of homogeneous fractions from wheat water-soluble arabinoxylans. Influence of the structure on their macromolecular characteristics. J. Agric. Food Chem. 2000, 48, 270–278. [Google Scholar] [CrossRef]
- Gentekos, D.T.; Sifri, R.; Fors, B.P. Controlling polymer properties through the shape of the molecular-weight distribution. Nat. Rev. Mater. 2019, 4, 761–774. [Google Scholar] [CrossRef]
- Robinson, G.; Ross-Murphy, S.B.; Morris, E.R. Viscosity-molecular weight relationships, intrinsic chain flexibility, and dynamic solution properties of guar galactomannan. Carbohydr. Res. 1982, 107, 17–32. [Google Scholar] [CrossRef]
- Tayal, A.; Kelly, R.M.; Khan, S.A. Rheology and Molecular Weight Changes during Enzymatic Degradation of a Water-Soluble Polymer. Macromolecules 1999, 32, 294–300. [Google Scholar] [CrossRef]
- Whistler, R.L.; Durso, D.F. The Isolation and Characterization of Two Crystalline Disaccharides from Partial Acid Hydrolysis of Guaran1,2. J. Am. Chem. Soc. 1951, 73, 4189–4190. [Google Scholar] [CrossRef]
- Calvini, P. The role of the Ekenstam equation on the kinetics of cellulose hydrolytic degradation. Cellulose 2012, 19, 313–318. [Google Scholar] [CrossRef]
- Wang, Q.; Ellis, P.; Ross-Murphy, S. The stability of guar gum in an aqueous system under acidic conditions. Food Hydrocoll. 2000, 14, 129–134. [Google Scholar] [CrossRef]
- Fazeli, N.; Mohammadi, N.; Taromi, F. A relationship between hydrodynamic and static properties of star-shaped polymers. Polym. Test. 2004, 23, 431–435. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |
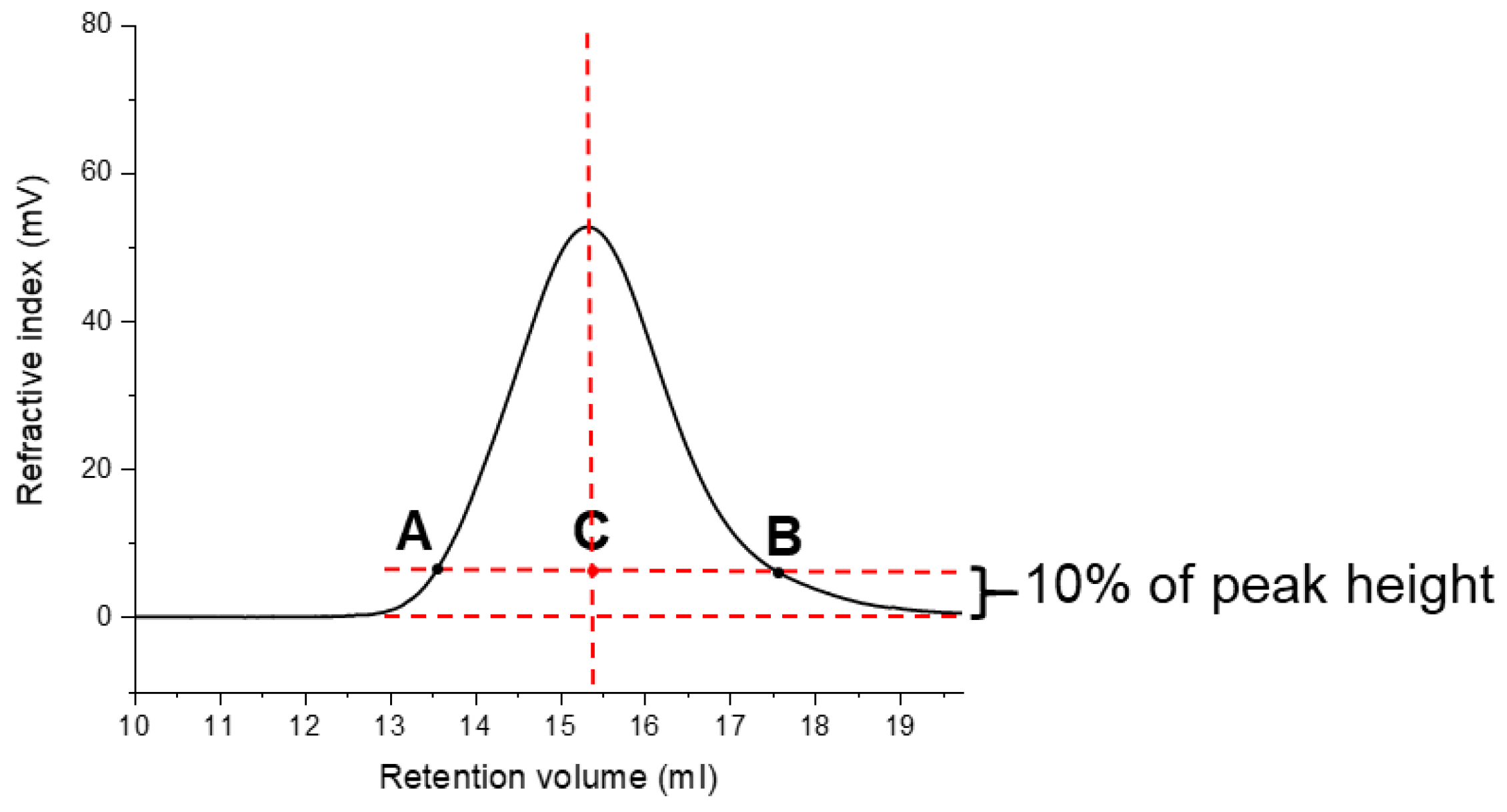
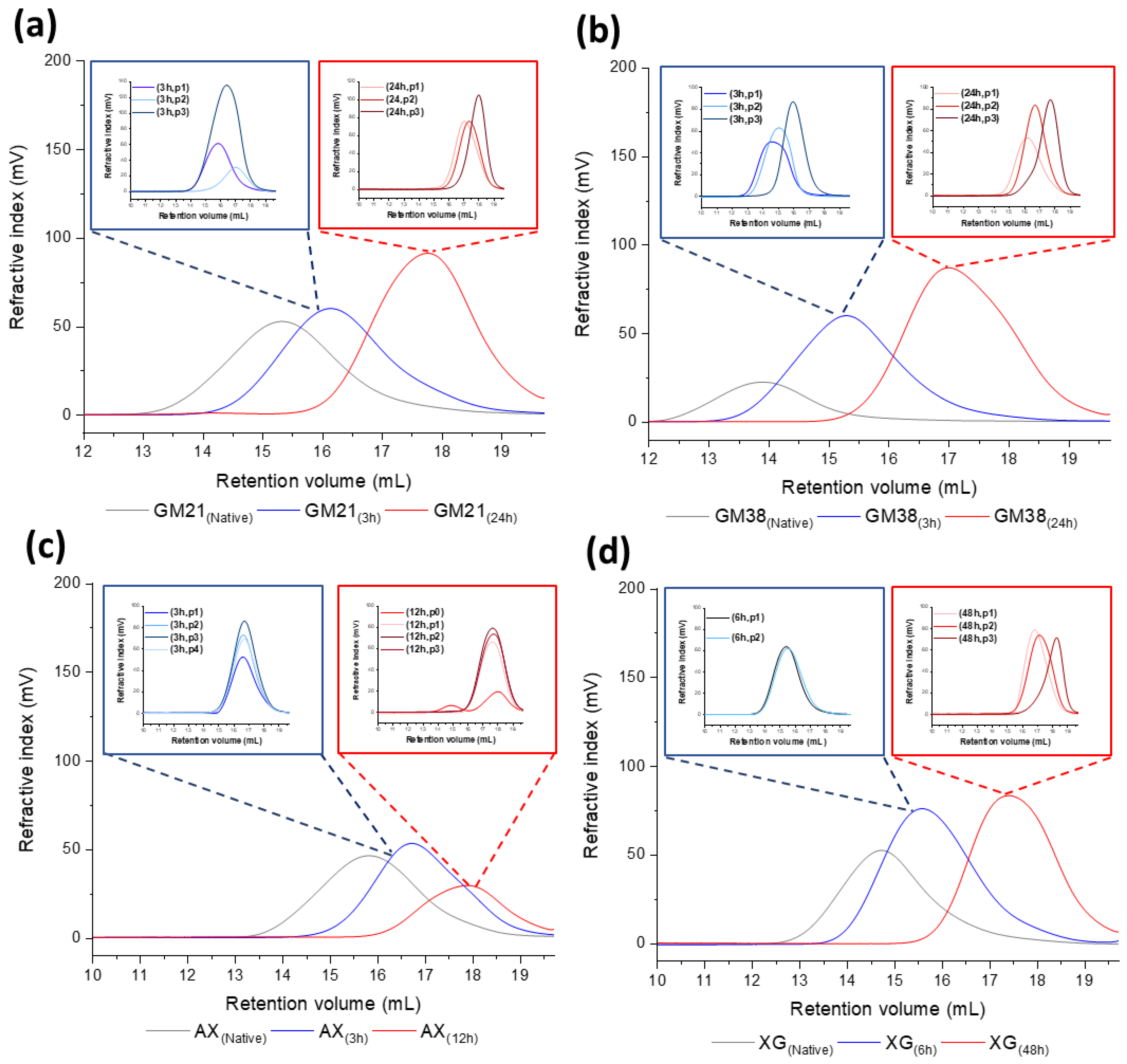
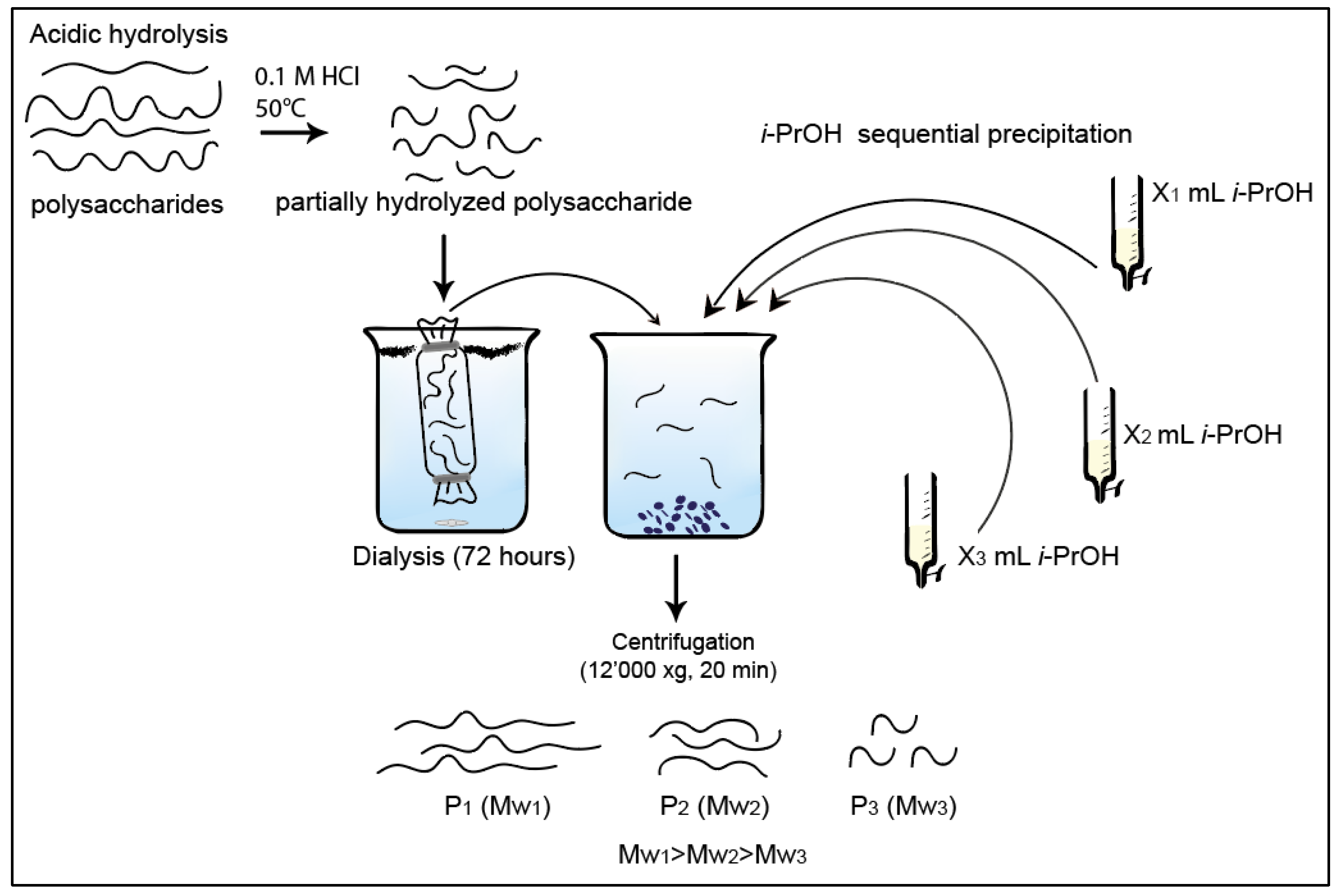
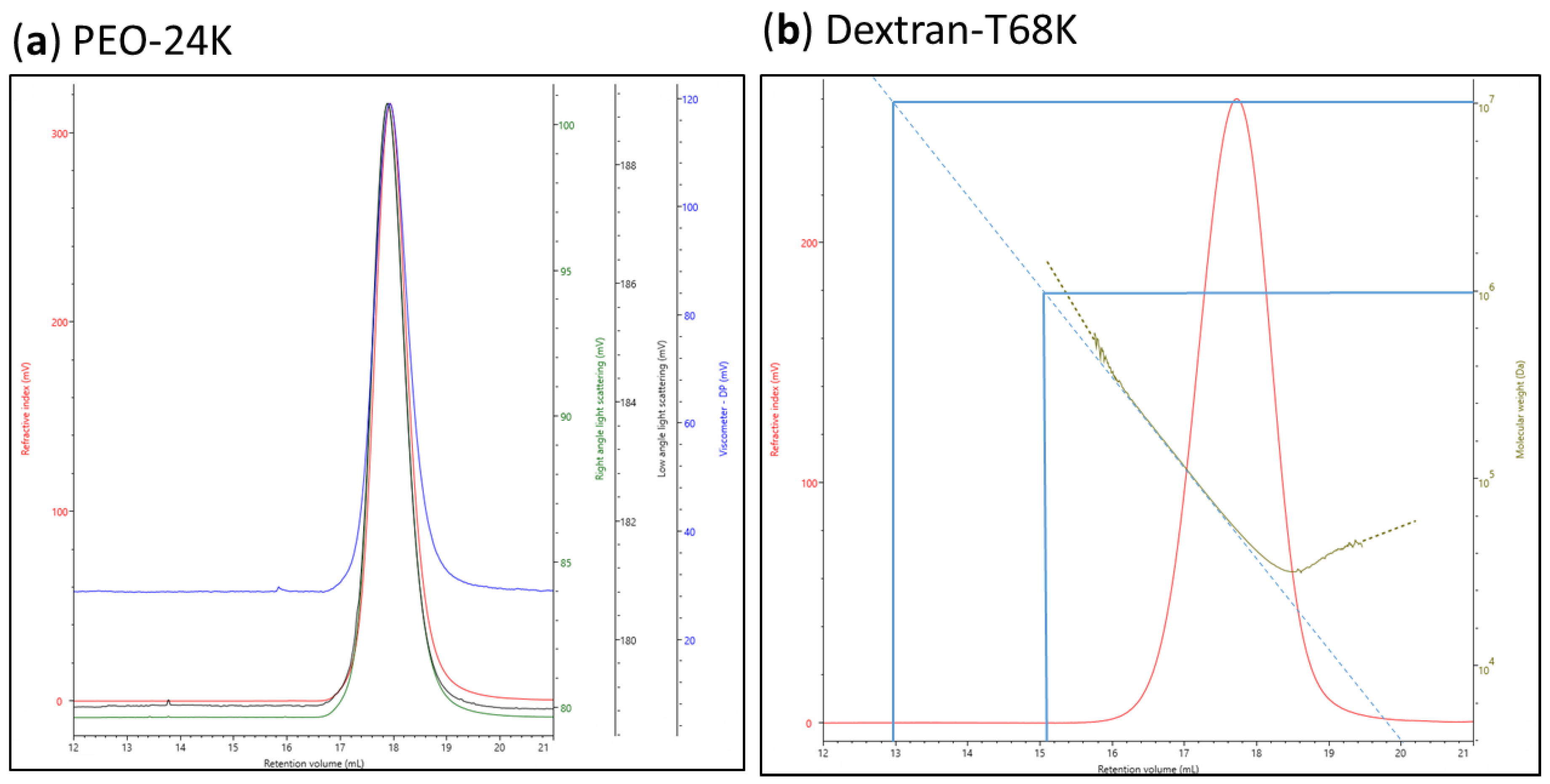
| Polysaccharides | Hydrolysis Time (h) | Rh (nm) | [η] (dL/g) |
|---|---|---|---|
| GM21 | 0 (native) | 32.69 ± 0.15 | 6.61 ± 0.04 |
| 3 | 19.80 ± 1.13 | 3.62 ± 0.31 | |
| 24 | 8.20 ± 0.57 | 0.98 ± 0.08 | |
| GM38 | 0 (native) | 67.80 ± 1.10 | 12.31 ± 0.25 |
| 3 | 31.90 ± 3.70 | 5.18 ± 0.75 | |
| 24 | 10.34 ± 0.98 | 1.25 ± 0.19 | |
| AX | 0 (native) | 24.57 ± 0.23 | 3.57 ± 0.04 |
| 3 | 14.62 ± 0.82 | 1.95 ± 0.15 | |
| 12 | 7.94 ± 0.48 | 0.84 ± 0.05 | |
| XG | 0 (native) | 41.91 ± 0.35 | 5.69 ± 0.05 |
| 6 | 24.83 ± 0.46 | 3.47 ± 0.09 | |
| 48 | 8.20 ± 0.25 | 0.85 ± 0.03 |
| Guar Galactomannan [GM21] HCl Hydrolysis | ||||||
|---|---|---|---|---|---|---|
| (%) i-PrOH | (%) Purity | (%) Yield | Gal:Man | Mw (kDa) | Đ (Mw/Mn) | |
| Native | - | - | 19:81 a | 380.00 ± 9.90 a | 1.58 ± 0.03 | |
| 3 h | 151.00 ± 17.00 b | 1.65 ± 0.02 | ||||
| p1 | 14 | 62 | 23 | 21:79 b | 30.49 ± 0.52 c | 1.03 ± 0.003 |
| p2 | 18 | 69 | 31 | 18:82 a | 13.26 ± 0.54 c | 1.12 ± 0.03 |
| p3 | 23 | 62 | 1 | 18:82 a | 24.51 ± 0.36 c | 1.02 ± 0.001 |
| 24 h | 32.30 ± 1.40 B | 1.86 ± 0.04 | ||||
| p1 | 15 | 73 | 15 | 16:84 c | 12.44 ± 0.22 C | 1.31 ± 0.02 |
| p2 | 21 | 73 | 29 | 19:81 a | 7.39 ± 0.02 C | 1.00 ± 0.002 |
| p3 | 26 | 65 | 2 | 19:81 a | 4.47 ± 0.03 C | 1.05 ± 0.005 |
| Guar Galactomannan [GM38] HCl Hydrolysis | ||||||
|---|---|---|---|---|---|---|
| (%) i-PrOH | (%) Purity | (%) Yield | Gal:Man | Mw (kDa) | Đ (Mw/Mn) | |
| Native | - | 74 | - | 41:59 a | 1657.00 ± 43.00 a | 1.55 ± 0.01 |
| 3 h | 552.00 ± 5.00 b | 1.53 ± 0.01 | ||||
| p1 | 16 | 92 | 11 | 37:63 b | 673.00 ± 8.00 c | 1.36 ± 0.02 |
| p2 | 19 | 95 | 54 | 37:63 b | 587.00 ± 4.00 b | 1.19 ± 0.003 |
| p3 | 23 | 96 | 5 | 37:63 b | 178.00 ± 1.00 d | 1.26 ± 0.01 |
| 24 h | 76.08 ± 2.25 B | 1.65 ± 0.03 | ||||
| p1 | 19 | 89 | 9 | 37:63 b | 158.61 ± 0.33 C | 1.56 ± 0.06 |
| p2 | 24 | 91 | 42 | 37:63 b | 89.98 ± 0.52 B | 1.33 ± 0.005 |
| p3 | 29 | 85 | 14 | 38:62 b | 43.60 ± 0.65 B | 1.44 ± 0.02 |
| Tamarind Xyloglucan [XG] HCl hydrolysis | ||||||
|---|---|---|---|---|---|---|
| (%) i-PrOH | (%) Purity | (%) Yield | Ara:Gal:Xyl:Glc | Mw (kDa) | Đ (Mw/Mn) | |
| Native | - | 95 | - | 2:15:23:60 a | 916.00 ± 10.00 a | 1.57 ± 0.03 |
| 6 h | 279.00 ± 17.00 b | 1.66 ± 0.14 | ||||
| p1 | 15 | 86 | 30 | <LOD:15:24:60 a | 380.00 ± 25.00 c | 1.28 ± 0.06 |
| p2 | 19 | 64 | 33 | <LOD:15:24:60 a | 337.00 ± 2.00 d | 1.40 ± 0.006 |
| 48 h | 73.41 ± 0.83 A | 1.66 ± 0.11 | ||||
| p1 | 17 | 94 | 17 | <LOD:11:29:59 a | 90.00 ± 7.10 A,B | 1.38 ± 0.11 |
| p2 | 25 | 95 | 48 | <LOD:12:27:61 a | 60.44 ± 0.46 A,C | 1.28 ± 0.002 |
| p3 | 27 | 92 | 2 | <LOD:13:31:55 b | 28.75 ± 0.42 C,D | 1.33 ± 0.001 |
| Wheat Arabinoxylan [AX] HCl Hydrolysis | ||||||
|---|---|---|---|---|---|---|
| (%) i-PrOH | (%)Purity | (%) Yield | Ara:Xyl | Mw (kDa) | Đ (Mw/Mn) | |
| Native | - | 83 | - | 40:60 a | 320.00 ± 3.00 a | 2.08 ± 0.04 |
| 3 h | 109.00 ± 7.00 b | 1.91 ± 0.18 | ||||
| p1 | 18 | 58 | 6 | 27:73 b | 84.00 ± 7.20 c | 1.35 ± 0.04 |
| p2 | 22 | 69 | 6 | 30:70 b | 102.00 ± 8.00 b,c | 1.40 ± 0.03 |
| p3 | 27 | 68 | 5 | 30:70 c | 114.00 ± 13.00 b,d | 1.48 ± 0.05 |
| p4 | 30 | 64 | 3 | 30:70 c | 114.00 ± 8.00 b,d | 1.53 ± 0.05 |
| 12 h | 53.89 ± 11.30 B | 1.47 ± 0.05 | ||||
| p0 Ϯ | 0 | 84 | 16 | 13:87 d | 2360.00 ± 200.00 Ϯ D | 10.56 ± 0.62 Ϯ |
| p1 | 15 | 80 | 1 | 20:80 d | 136.00 ± 22.00 C | 1.49 ± 0.08 |
| p2 | 21 | 76 | 20 | 24:76 e | 53.10 ± 8.90 B | 1.34 ± 0.04 |
| p3 | 26 | 70 | 2 | 30:70 c | 39.10 ± 1.70 B | 1.32 ± 0.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lupo, C.; Boulos, S.; Nyström, L. Influence of Partial Acid Hydrolysis on Size, Dispersity, Monosaccharide Composition, and Conformation of Linearly-Branched Water-Soluble Polysaccharides. Molecules 2020, 25, 2982. https://doi.org/10.3390/molecules25132982
Lupo C, Boulos S, Nyström L. Influence of Partial Acid Hydrolysis on Size, Dispersity, Monosaccharide Composition, and Conformation of Linearly-Branched Water-Soluble Polysaccharides. Molecules. 2020; 25(13):2982. https://doi.org/10.3390/molecules25132982
Chicago/Turabian StyleLupo, Cristina, Samy Boulos, and Laura Nyström. 2020. "Influence of Partial Acid Hydrolysis on Size, Dispersity, Monosaccharide Composition, and Conformation of Linearly-Branched Water-Soluble Polysaccharides" Molecules 25, no. 13: 2982. https://doi.org/10.3390/molecules25132982
APA StyleLupo, C., Boulos, S., & Nyström, L. (2020). Influence of Partial Acid Hydrolysis on Size, Dispersity, Monosaccharide Composition, and Conformation of Linearly-Branched Water-Soluble Polysaccharides. Molecules, 25(13), 2982. https://doi.org/10.3390/molecules25132982






