Efficient Computation of Free Energy Surfaces of Diels–Alder Reactions in Explicit Solvent at Ab Initio QM/MM Level
Abstract
1. Introduction
2. Methods
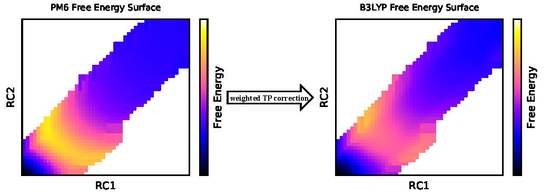
2.1. Multistate Bennett Acceptance Ratio and Weighted Thermodynamic Perturbation (MBAR+wTP) Method
2.2. Gaussian Process Regression for FE Surfaces Smoothing
2.3. Locating the Transition State on the Free Energy Surface
2.4. Solvent-Assisted Charge Transfer on the Transition State
2.5. Gibbs Free Energies in Implicit Water Solvent
2.6. Molecular Dynamics Simulations
3. Results and Discussion
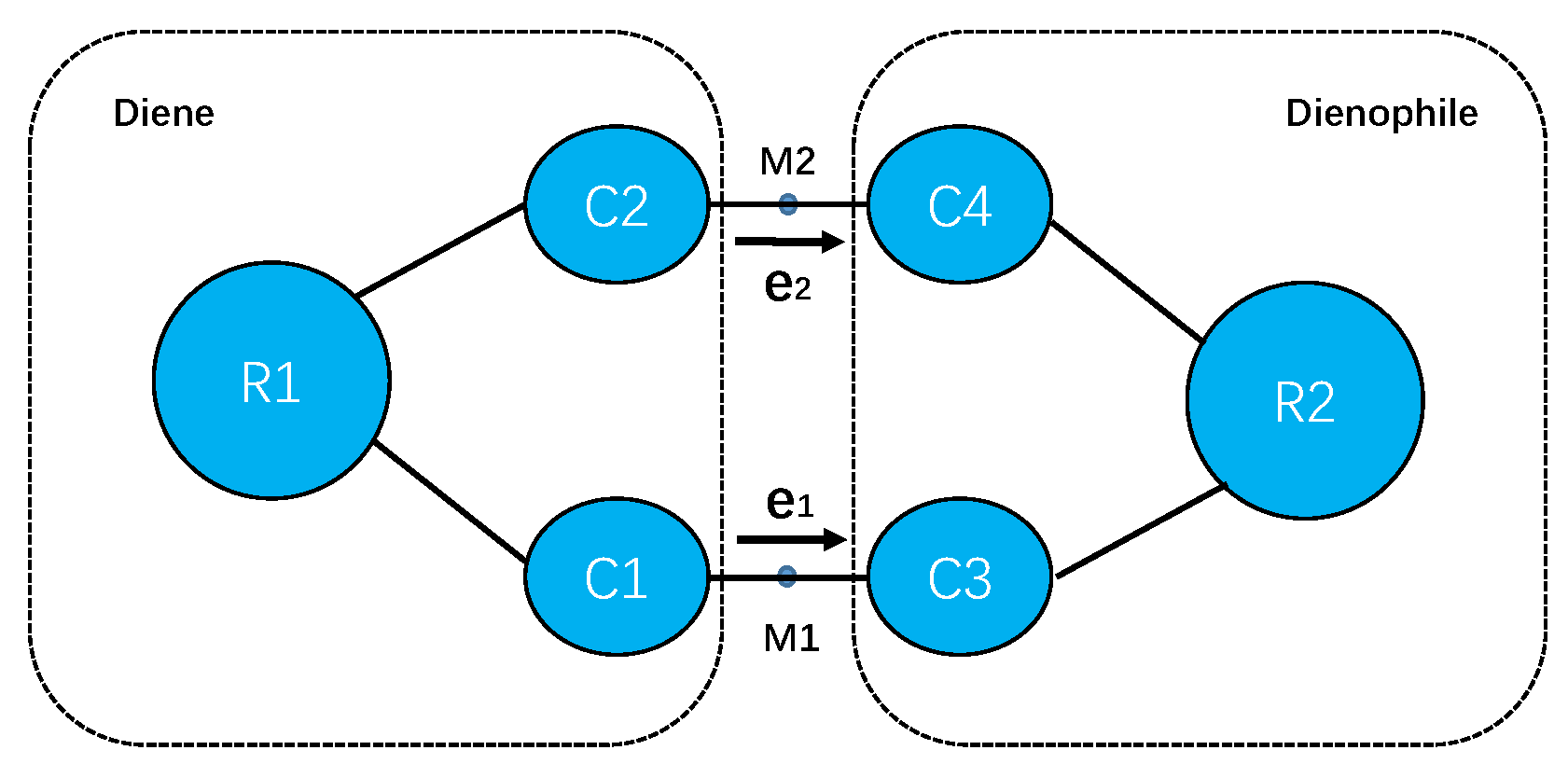
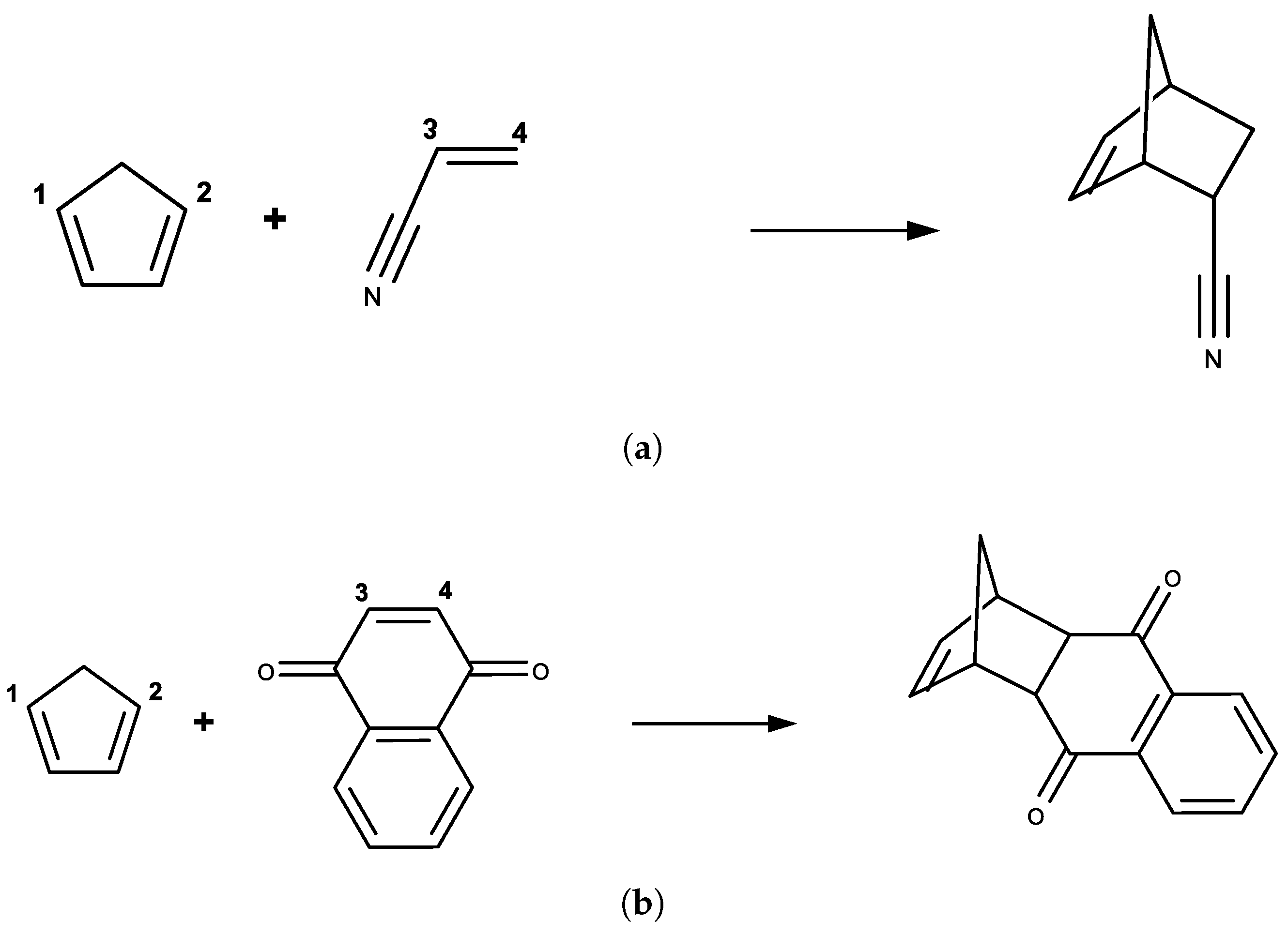
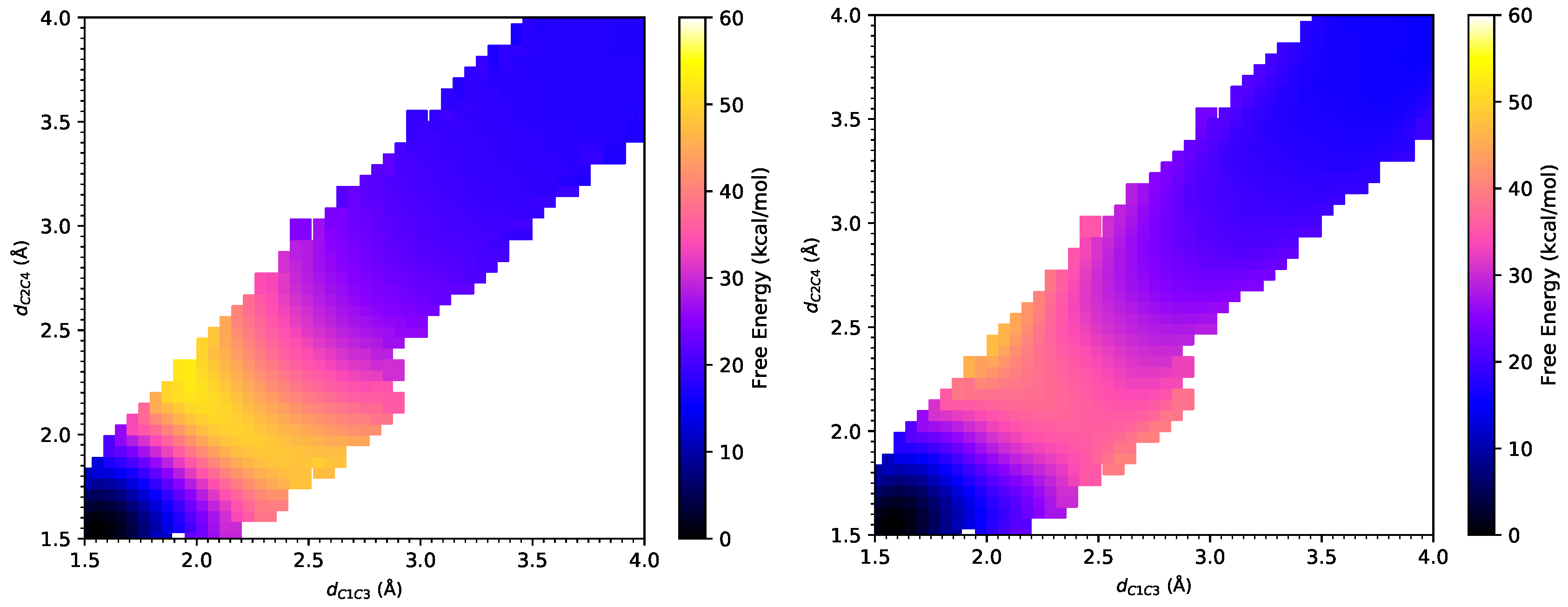
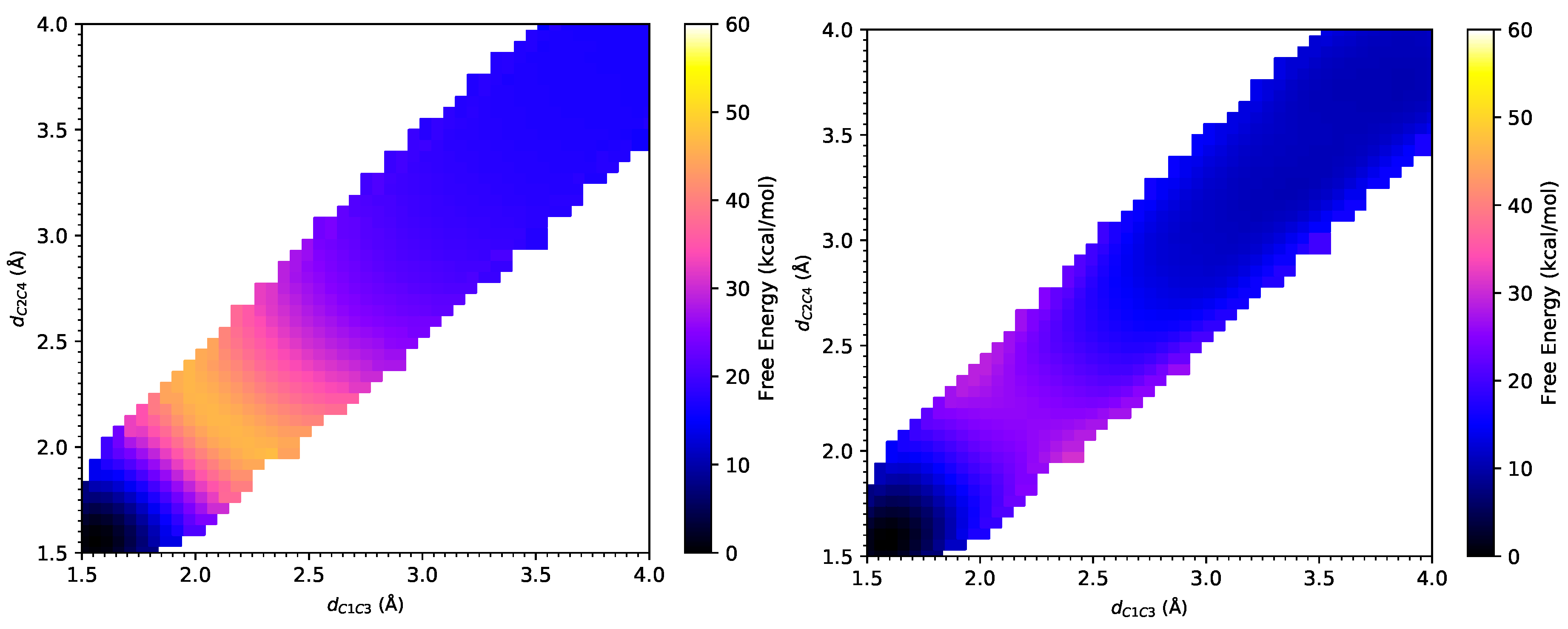
3.1. DA Reaction between CP and ACR
3.2. DA Reaction between CP and NAP
3.3. Computational Expense
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DA | Diels–Alder |
| FE | Free Energy |
| ai | ab initio |
| QM | Quantum Mechanical |
| MM | Molecular Mechanical |
| US | Umbrella Sampling |
| MD | Molecular Dynamics |
| SE | Semi-Empirical |
| MBAR | Multistate Bennett Acceptance Ratio |
| wTP | weighted Thermodynamic Perturbation |
| CP | Cyclopentadiene |
| ACR | Acrylonitrile |
| NAP | 1-4-Naphthoquinone |
| FEP | Free Energy Perturbation |
| TS | Transition State |
| EVB | Empirical Valence Bond |
| SAMPL | Statistical Assessment of the Modeling of Proteins and Ligands |
| RC | Reaction Coordinate |
| GPR | Gaussian Processes Regression |
| RRHO | Rigid-Rotor/Harmonic-Oscillator |
| IRC | Intrinsic Reaction Coordinate |
| IEF-PCM | Integral Equation Formalism of the Polarizable Continuous Solvent Model |
| MP2 | 2nd-Order Møller–Plesset Perturbation Theory |
| AM1 | Austin Model 1 |
| PM3 | Parameterization Method 3 |
| PM6 | Parameterization Method 6 |
References
- Breslow, R.; Maitra, U. On the Origin of Product Selectivity in Aqueous Diels-Alder Reactions. Tetrahedron Lett. 1984, 25, 1239–1240. [Google Scholar] [CrossRef]
- Engberts, J.B. Diels-Alder Reactions in Water: Enforced Hydrophobic Interaction and Hydrogen Bonding. Pure Appl. Chem. 1995, 67, 823–828. [Google Scholar] [CrossRef]
- Rideout, D.C.; Breslow, R. Hydrophobic Acceleration of Diels-Alder Reactions. J. Am. Chem. Soc. 1980, 102, 7816–7817. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Lim, D.; Blake, J.F. Ab initio Study of Diels-Alder Reactions of Cyclopentadiene with Ethylene, Isoprene, Cyclopentadiene, Acrylonitrile, and Methyl Vinyl Ketone. J. Am. Chem. Soc. 1993, 115, 2936–2942. [Google Scholar] [CrossRef]
- Cativiela, C.; Garcia, J.; Gil, J.; Martinez, R.; Mayoral, J.; Salvatella, L.; Urieta, J.; Mainar, A.; Abraham, M. Solvent Effects on Diels-Alder Reactions. The Use of Aqueous Mixtures of Fluorinated Alcohols and the Study of Reactions of Acrylonitrile. J. Chem. Soc. Perkin Trans. 2 1997, 4, 653–660. [Google Scholar] [CrossRef]
- Chandrasekhar, J.; Shariffskul, S.; Jorgensen, W.L. QM/MM Simulations for Diels-Alder Reactions in Water: Contribution of Enhanced Hydrogen Bonding at the Transition State to the Solvent Effect. J. Phys. Chem. B 2002, 106, 8078–8085. [Google Scholar] [CrossRef]
- Acevedo, O.; Jorgensen, W.L. Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology. J. Chem. Theory Comput. 2007, 3, 1412–1419. [Google Scholar] [CrossRef] [PubMed]
- Thomas, L.L.; Tirado-Rives, J.; Jorgensen, W.L. Quantum Mechanical/Molecular Mechanical Modeling Finds Diels-Alder Reactions Are Accelerated Less on the Surface of Water Than in Water. J. Am. Chem. Soc. 2010, 132, 3097–3104. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Levitt, M. Theoretical Studies of Enzymic Reactions: Dielectric, Electrostatic and Steric Stabilization of the Carbonium Ion in the Reaction of Lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Lin, H.; Truhlar, D.G. QM/MM: What Have We Learned, Where Are We, and Where Do We Go from Here? Theor. Chem. Acc. 2006, 117, 185. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- van der Kamp, M.W.; Mulholland, A.J. Combined Quantum Mechanics/Molecular Mechanics (QM/MM) Methods in Computational Enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, S.; Uchida, Y.; Hasegawa, T.; Higashi, M.; Kosugi, T.; Kamiya, M. QM/MM Geometry Optimization on Extensive Free-Energy Surfaces for Examination of Enzymatic Reactions and Design of Novel Functional Properties of Proteins. Annu. Rev. Phys. Chem. 2017, 68, 135–154. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, J.; Smith, S.F.; Jorgensen, W.L. Theoretical Examination of the SN2 Reaction Involving Chloride Ion and Methyl Chloride in the Gas Phase and Aqueous Solution. J. Am. Chem. Soc. 1985, 107, 154–163. [Google Scholar] [CrossRef]
- Chandrasekhar, J.; Jorgensen, W.L. Energy Profile for a Nonconcerted SN2 Reaction in Solution. J. Am. Chem. Soc. 1985, 107, 2974–2975. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Free Energy Calculations: A Breakthrough for Modeling Organic Chemistry in Solution. Acc. Chem. Res. 1989, 22, 184–189. [Google Scholar] [CrossRef]
- Stanton, R.V.; Peräkylä, M.; Bakowies, D.; Kollman, P.A. Combined ab initio and Free Energy Calculations To Study Reactions in Enzymes and Solution: Amide Hydrolysis in Trypsin and Aqueous Solution. J. Am. Chem. Soc. 1998, 120, 3448–3457. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Yang, W. Free Energy Calculation on Enzyme Reactions with An Efficient Iterative Procedure to Determine Minimum Energy Paths on A Combined ab initio QM/MM Potential Energy Surface. J. Chem. Phys. 2000, 112, 3483–3492. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Zhang, Y.; Lee, T.S.; Yang, W. A Pseudobond Approach to Combining Quantum Mechanical and Molecular Mechanical Methods. J. Chem. Phys. 1999, 110, 46–54. [Google Scholar] [CrossRef]
- Kästner, J.; Senn, H.M.; Thiel, S.; Otte, N.; Thiel, W. QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction. J. Chem. Theory Comput. 2006, 2, 452–461. [Google Scholar] [CrossRef] [PubMed]
- Blake, J.F.; Jorgensen, W.L. Solvent Effects on a Diels-Alder Reaction from Computer Simulations. J. Am. Chem. Soc. 1991, 113, 7430–7432. [Google Scholar] [CrossRef]
- Blake, J.F.; Lim, D.; Jorgensen, W.L. Enhanced Hydrogen Bonding of Water to Diels-Alder Transition States. ab initio Evidence. J. Org. Chem. 1994, 59, 803–805. [Google Scholar] [CrossRef]
- Cunningham, M.A.; Ho, L.L.; Nguyen, D.T.; Gillilan, R.E.; Bash, P.A. Simulation of the Enzyme Reaction Mechanism of Malate Dehydrogenase. Biochemistry 1997, 36, 4800–4816. [Google Scholar] [CrossRef] [PubMed]
- Alhambra, C.; Wu, L.; Zhang, Z.Y.; Gao, J. Walden-Inversion-Enforced Transition-State Stabilization in a Protein Tyrosine Phosphatase. J. Am. Chem. Soc. 1998, 120, 3858–3866. [Google Scholar] [CrossRef]
- Bentzien, J.; Muller, R.P.; Florián, J.; Warshel, A. Hybrid ab initio Quantum Mechanics/Molecular Mechanics Calculations of Free Energy Surfaces for Enzymatic Reactions: The Nucleophilic Attack in Subtilisin. J. Phys. Chem. B 1998, 102, 2293–2301. [Google Scholar] [CrossRef]
- Qian, P.; Guo, H.B.; Yue, Y.; Wang, L.; Yang, X.; Guo, H. Understanding the Catalytic Mechanism of Xanthosine Methyltransferase in Caffeine Biosynthesis from QM/MM Molecular Dynamics and Free Energy Simulations. J. Chem. Inf. Model. 2016, 56, 1755–1761. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Yang, Z.; Mei, Y.; Houk, K.N. QM/QM’ Direct Molecular Dynamics of Water-Accelerated Diels-Alder Reaction. J. Phys. Chem. B 2016, 120, 6250–6254. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Thiel, W. Computational Insights into an Enzyme-Catalyzed [4+2] Cycloaddition. J. Org. Chem. 2017, 82, 13563–13571. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Absolute Free Energy of Solvation from Monte Carlo Simulations Using Combined Quantum and Molecular Mechanical Potentials. J. Phys. Chem. 1992, 96, 537–540. [Google Scholar] [CrossRef]
- Gao, J.; Xia, X. A Priori Evaluation of Aqueous Polarization Effects through Monte Carlo QM-MM Simulations. Science 1992, 258, 631–635. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Weiss, R.M. An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes. J. Am. Chem. Soc. 1980, 102, 6218–6226. [Google Scholar] [CrossRef]
- Warshel, A. Computer Modeling of Chemical Reactions in Enzymes and Solutions; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Plotnikov, N.V.; Kamerlin, S.C.L.; Warshel, A. Paradynamics: An Effective and Reliable Model for ab initio QM/MM Free-Energy Calculations and Related Tasks. J. Phys. Chem. B 2011, 115, 7950–7962. [Google Scholar] [CrossRef] [PubMed]
- Plotnikov, N.V.; Warshel, A. Exploring, Refining, and Validating the Paradynamics QM/MM Sampling. J. Phys. Chem. B 2012, 116, 10342–10356. [Google Scholar] [CrossRef] [PubMed]
- Lameira, J.; Kupchencko, I.; Warshel, A. Enhancing Paradynamics for QM/MM Sampling of Enzymatic Reactions. J. Phys. Chem. B 2016, 120, 2155–2164. [Google Scholar] [CrossRef] [PubMed]
- Rod, T.H.; Ryde, U. Quantum Mechanical Free Energy Barrier for an Enzymatic Reaction. Phys. Rev. Lett. 2005, 94, 138302. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Wang, M.; Shao, Y.; König, G.; Brooks, B.R.; Zhang, J.Z.H.; Mei, Y. Calculations of Solvation Free Energy through Energy Reweighting from Molecular Mechanics to Quantum Mechanics. J. Chem. Theory Comput. 2016, 12, 499–511. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Jia, X.; Wang, M.; Li, P.; Wang, X.; Hu, W.; Zheng, J.; Mei, Y. Calculations of the Absolute Binding Free Energies for Ralstonia solanacearum Lectins Bound with Methyl-α-l-fucoside at Molecular Mechanical and Quantum Mechanical/Molecular Mechanical Levels. RSC Adv. 2017, 7, 38570–38580. [Google Scholar] [CrossRef]
- Li, P.; Jia, X.; Shao, Y.; Mei, Y. Computation of Free Energy Profile at ab initio QM/MM Level Made Orders of Magnitude Faster via the Reference-Potential Approach Using Weighted Thermodynamics Perturbation. arXiv, 2018; arXiv:1801.03674. [Google Scholar]
- Shirts, M.R.; Chodera, J.D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R. Reweighting from the Mixture Distribution as a Better Way to Describe the Multistate Bennett Acceptance Ratio. arXiv, 2017; arXiv:1704.00891. [Google Scholar]
- Torrie, G.; Valleau, J. Nonphysical Sampling Distributions in Monte Carlo Free-energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Rasmussen, C.; Williams, C. Regression. In Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; pp. 7–32. [Google Scholar]
- Wang, M.; Li, P.; Jia, X.; Liu, W.; Shao, Y.; Hu, W.; Zheng, J.; Brooks, B.R.; Mei, Y. Efficient Strategy for the Calculation of Solvation Free Energies in Water and Chloroform at the Quantum Mechanical/Molecular Mechanical Level. J. Chem. Inf. Model. 2017, 57, 2476–2489. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Vasilevskaya, T.; Thiel, W. Periodic Boundary Conditions in QM/MM Calculations: Implementation and Tests. J. Chem. Theory Comput. 2016, 12, 3561–3570. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Andersen, H.C. Molecular Dynamics Simulations at Constant Pressure and/or Temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar] [CrossRef]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Greene, D.; Homeyer, N.; et al. AMBER 2017; University of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Klimovich, P.V.; Shirts, M.R.; Mobley, D.L. Guidelines for the Analysis of Free Energy Calculations. J. Comput. Aided Mol. Des. 2015, 29, 397–411. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |
| Dienophile | Method | |||
|---|---|---|---|---|
| ACR | PM3/MM | 34.0 ± 0.5 | −16.7 ± 0.6 | (2.28, 2.00) |
| AM1/MM | 24.7 | −26.2 | ||
| PM6/MM | 30.9 ± 0.1 | −17.5 ± 0.1 | (2.41, 1.92) | |
| B3LYP/MM | 20.5 ± 0.6 | −15.7 ± 0.6 | (2.49, 2.05) | |
| B3LYP/IEFPCM | 30.3 | −2.69 | (2.54, 2.04) | |
| MP2/IEFPCM | 17.6 | −15.8 | (2.40, 2.18) | |
| Exp. | 22.2 | |||
| NAP | PM3/MM | 26.0 ± 0.5 | −20.1 ± 0.6 | (2.25, 2.22) |
| AM1/MM | 27.6 | −4.4 | ||
| PM6/MM | 29.6 ± 0.1 | −16.7 ± 0.1 | (2.14, 2.18) | |
| B3LYP-D3/MM | 14.3 ± 0.7 | −11.5 ± 0.7 | (2.23, 2.19) | |
| B3LYP-D3/IEFPCM | 20.7 | −2.62 | (2.18, 2.18) | |
| MP2/IEFPCM | 6.6 | −13.9 | (2.26, 2.26) | |
| Exp. e | 16.6 |
| Dienophile | Method | Locations | Projection of E-Field |
|---|---|---|---|
| ACR | B3LYP/MM | M1 | −14.6 ± 0.3 |
| M2 | −19.7 ± 0.4 | ||
| NAP | B3LYP−D3/MM | M1 | −28.0 ± 0.5 |
| M2 | −36.2 ± 0.7 |
| Dienophile | Method | Atoms | Reactant State | Transition State | Product State |
|---|---|---|---|---|---|
| ACR | B3LYP/MM | C1 | −0.13 | −0.01 | −0.05 |
| C2 | −0.15 | −0.17 | −0.05 | ||
| C3 | −0.18 | −0.36 | −0.13 | ||
| C4 | −0.20 | −0.11 | −0.28 | ||
| R1 | 0.29 | 0.35 | 0.22 | ||
| R2 | 0.38 | 0.29 | 0.28 | ||
| NAP | B3LYP−D3/MM | C1 | −0.15 | −0.06 | −0.04 |
| C2 | −0.14 | −0.04 | −0.03 | ||
| C3 | −0.21 | −0.26 | −0.25 | ||
| C4 | −0.23 | −0.26 | −0.26 | ||
| R1 | 0.30 | 0.34 | 0.26 | ||
| R2 | 0.44 | 0.29 | 0.32 |
| Dienophile | PM6/MM to B3LYP/MM Indirect | Direct B3LYP/MM | ||
|---|---|---|---|---|
| Sampling | Energy Evaluation | Total | ||
| ACR | 5762 | 1459 | 7221 | 1,006,041 |
| NAP | 5945 | 3907 | 9852 | 3,704,062 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Liu, F.; Jia, X.; Shao, Y.; Hu, W.; Zheng, J.; Mei, Y. Efficient Computation of Free Energy Surfaces of Diels–Alder Reactions in Explicit Solvent at Ab Initio QM/MM Level. Molecules 2018, 23, 2487. https://doi.org/10.3390/molecules23102487
Li P, Liu F, Jia X, Shao Y, Hu W, Zheng J, Mei Y. Efficient Computation of Free Energy Surfaces of Diels–Alder Reactions in Explicit Solvent at Ab Initio QM/MM Level. Molecules. 2018; 23(10):2487. https://doi.org/10.3390/molecules23102487
Chicago/Turabian StyleLi, Pengfei, Fengjiao Liu, Xiangyu Jia, Yihan Shao, Wenxin Hu, Jun Zheng, and Ye Mei. 2018. "Efficient Computation of Free Energy Surfaces of Diels–Alder Reactions in Explicit Solvent at Ab Initio QM/MM Level" Molecules 23, no. 10: 2487. https://doi.org/10.3390/molecules23102487
APA StyleLi, P., Liu, F., Jia, X., Shao, Y., Hu, W., Zheng, J., & Mei, Y. (2018). Efficient Computation of Free Energy Surfaces of Diels–Alder Reactions in Explicit Solvent at Ab Initio QM/MM Level. Molecules, 23(10), 2487. https://doi.org/10.3390/molecules23102487