Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters
Abstract
1. Introduction
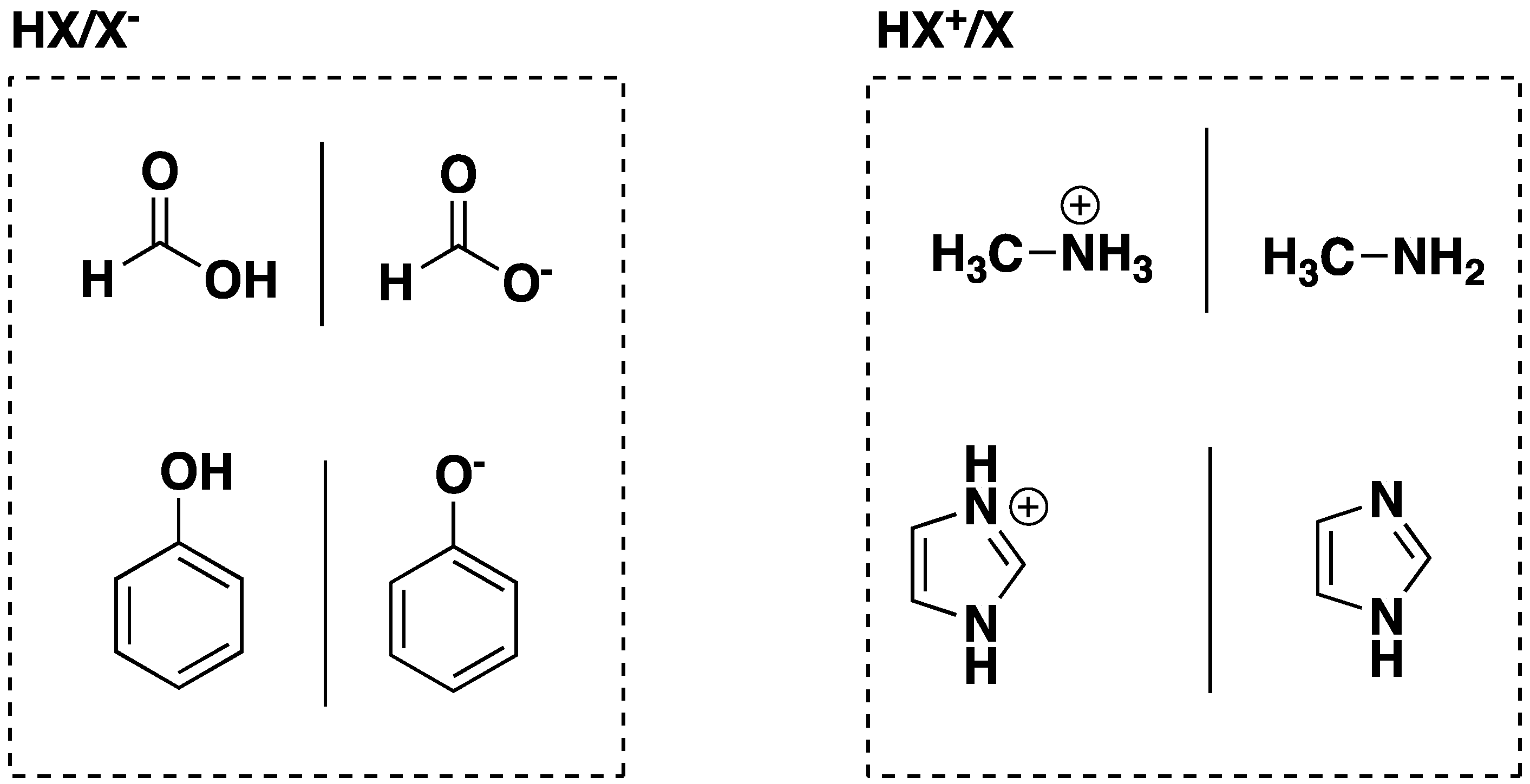
2. Experimental Design and Methods
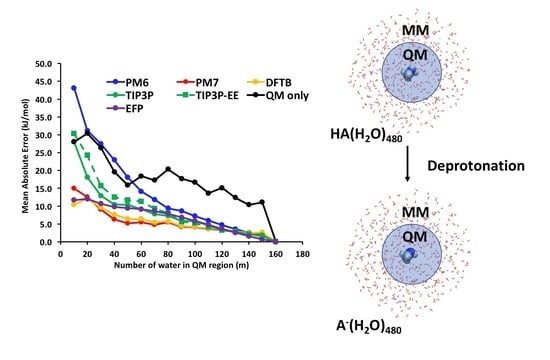
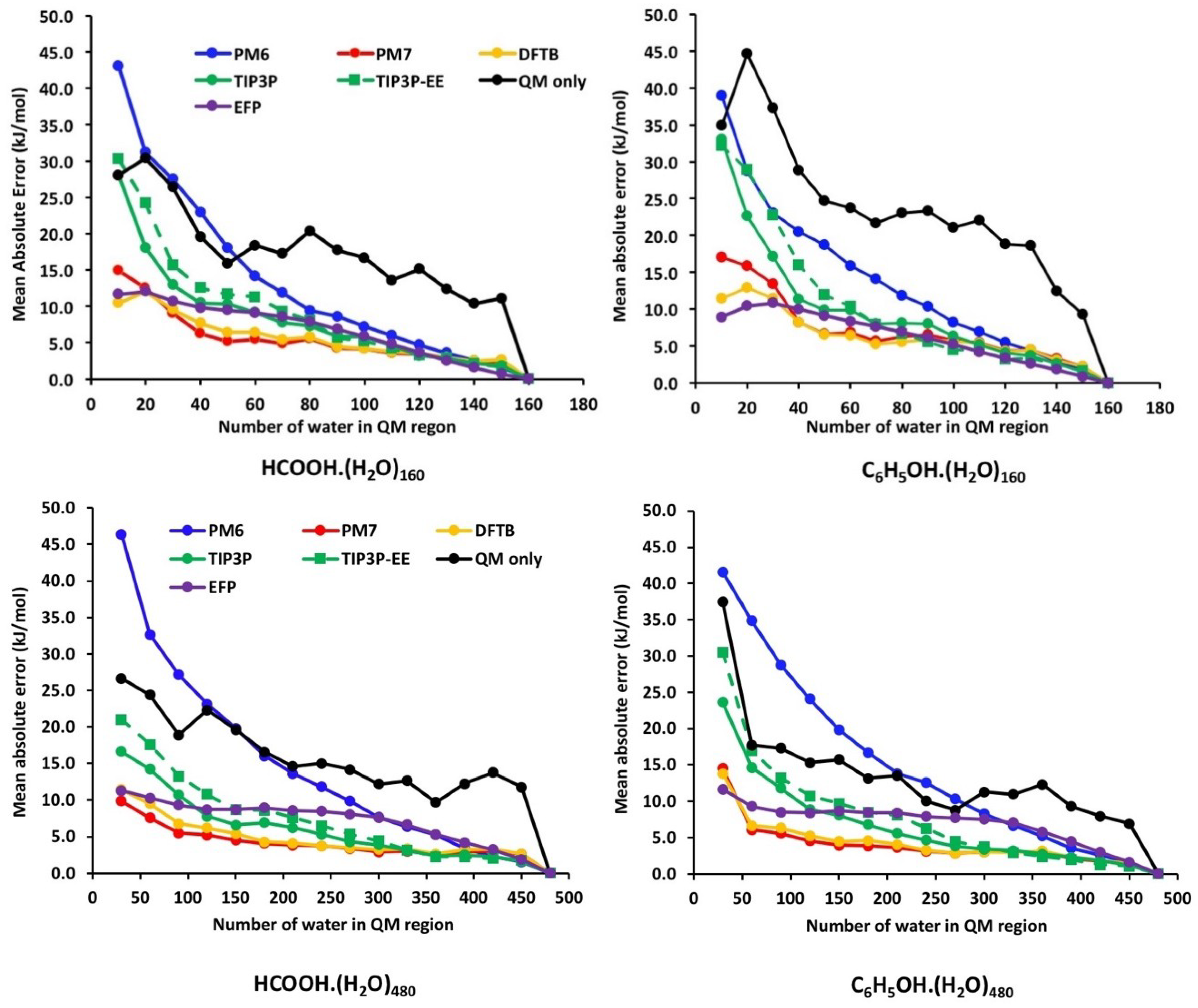
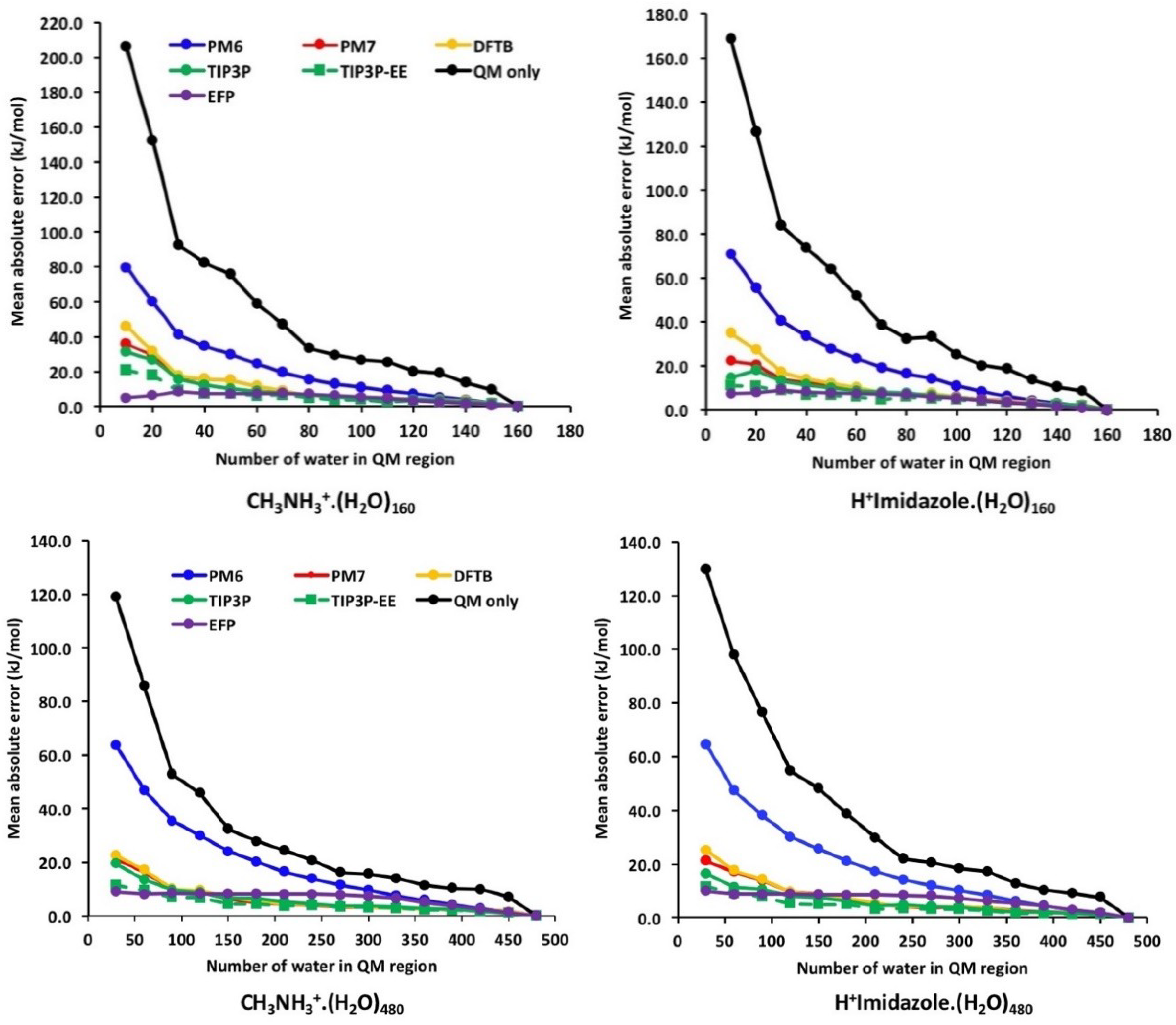
3. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2006, 117, 185. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Acevedo, O.; Jorgensen, W.L. Advances in Quantum and Molecular Mechanical (QM/MM) simulations for organic and enzymatic reactions. Acc. Chem. Res. 2010, 43, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Van der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Rothlisberger, U. Mixed Quantum Mechanical/Molecular Mechanical Molecular Dynamics simulations of biological systems in ground and electronically excited states. Chem. Rev. 2015, 115, 6217–6263. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, Y.; Chen, Y.; Field, M.J.; Gao, J. QM/MM through the 1990s: The first twenty years of method development and applications. Isr. J. Chem. 2014, 54, 1250–1263. [Google Scholar] [CrossRef] [PubMed]
- Flaig, D.; Beer, M.; Ochsenfeld, C. Convergence of electronic structure with the size of the QM Region: example of QM/MM NMR shieldings. J. Chem. Theory Comput. 2012, 8, 2260–2271. [Google Scholar] [CrossRef] [PubMed]
- Hartman, J.D.; Neubauer, T.J.; Caulkins, B.G.; Mueller, L.J.; Beran, G.J. Converging nuclear magnetic shielding calculations with respect to basis and system size in protein systems. J. Biomol. NMR 2015, 62, 327–340. [Google Scholar] [CrossRef] [PubMed]
- Nåbo, L.J.; Olsen, J.M.H.; Martínez, T.J.; Kongsted, J. The Quality of the embedding potential is decisive for minimal quantum region size in embedding calculations: The case of the green fluorescent protein. J. Chem. Theory Comput. 2017, 13, 6230–6236. [Google Scholar] [CrossRef] [PubMed]
- Provorse, M.R.; Peev, T.; Xiong, C.; Isborn, C.M. Convergence of excitation energies in mixed quantum and classical solvent: comparison of continuum and point charge models. J. Phys. Chem. B 2016, 120, 12148–12159. [Google Scholar] [CrossRef] [PubMed]
- Milanese, J.M.; Provorse, M.R.; Alameda, E.; Isborn, C.M. Convergence of computed aqueous absorption spectra with explicit quantum mechanical solvent. J. Chem. Theory Comput. 2017, 13, 2159–2171. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.-Z.; Thiel, W. Convergence in the QM-only and QM/MM modeling of enzymatic reactions: A case study for acetylene hydratase. J. Comput. Chem. 2013, 34, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Kulik, H.J.; Zhang, J.; Klinman, J.P.; Martínez, T.J. How large should the QM region be in QM/MM calculations? The case of catechol O-methyltransferase. J. Phys. Chem. B 2016, 120, 11381–11394. [Google Scholar] [CrossRef] [PubMed]
- Jindal, G.; Warshel, A. Exploring the dependence of QM/MM calculations of enzyme catalysis on the size of the QM region. J. Phys. Chem. B 2016, 120, 9913–9921. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.-Z.; Thiel, W. Comparison of QM-Only and QM/MM models for the mechanism of tungsten-dependent acetylene hydratase. J. Chem. Theory Comput. 2012, 8, 3793–3803. [Google Scholar] [CrossRef] [PubMed]
- Benediktsson, B.; Bjornsson, R. QM/MM study of the nitrogenase mofe protein resting state: Broken-symmetry states, protonation states, and QM region convergence in the FeMoco active site. Inorg. Chem. 2017, 56, 13417–13429. [Google Scholar] [CrossRef] [PubMed]
- Roßbach, S.; Ochsenfeld, C. Influence of Coupling and embedding schemes on QM size convergence in QM/MM approaches for the example of a proton transfer in DNA. J. Chem. Theory Comput. 2017, 13, 1102–1107. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Nam, K.; Major, D.T. Rapid convergence of energy and free energy profiles with quantum mechanical size in quantum mechanical-molecular mechanical simulations of proton transfer in DNA. J. Chem. Theory Comput. 2018, 14, 1695–1805. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Söderhjelm, P.; Ryde, U. On the convergence of QM/MM energies. J. Chem. Theory Comput. 2011, 7, 761–777. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, M.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Pruitt, S.R.; Bertoni, C.; Brorsen, K.R.; Gordon, M.S. Efficient and Accurate fragmentation methods. Acc. Chem. Res. 2014, 47, 2786–2794. [Google Scholar] [CrossRef] [PubMed]
- Gordon, M.S.; Fedorov, D.G.; Pruitt, S.R.; Slipchenko, L.V. Fragmentation methods: A route to accurate calculations on large systems. Chem. Rev. 2012, 112, 632–672. [Google Scholar] [CrossRef] [PubMed]
- Gordon, M.S.; Mullin, J.M.; Pruitt, S.R.; Roskop, L.B.; Slipchenko, L.V.; Boatz, J.A. Accurate methods for large molecular systems. J. Phys. Chem. B 2009, 113, 9646–9663. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Witek, H.A.; Bobadova-Parvanova, P.; Irle, S.; Musaev, D.G.; Prabhakar, R.; Morokuma, K.; Lundberg, M.; Elstner, M.; Köhler, C.; Frauenheim, T. Parameter calibration of transition-metal elements for the spin-polarized self-consistent-charge density-functional tight-binding (DFTB) method: Sc, Ti, Fe, Co, and Ni. J. Chem. Theory Comput. 2007, 3, 1349–1367. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM method and Its applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Hirao, H.; Li, X.; Morokuma, K. The ONIOM method: Its foundation and applications to metalloenzymes and photobiology. WIRES Comput. Mol. Sci. 2011, 2, 327–350. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K. Hybrid methods: ONIOM(QM:MM) and QM/MM. Annu. Rep. Comput. Chem. 2006, 2, 35–51. [Google Scholar]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. JACS 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry: The First Forty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ghosh, D.; Kosenkov, D.; Vanovschi, V.; Flick, J.; Kaliman, I.; Shao, Y.; Gilbert, A.T.B.; Krylov, A.I.; Slipchenko, L.V. Effective fragment potential method in Q-CHEM: A guide for users and developers. J. Comput. Chem. 2013, 34, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.B.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D.J.; Bashford, D.; Bellott, M.; Dunbrack, R.L.J.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Cao, L.; Ryde, U. On the difference between additive and subtractive QM/MM calculations. Front. Chem. 2018, 6, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tissandier, M.D.; Cowen, K.A.; Feng, W.Y.; Gundlach, E.; Cohen, M.H.; Earhart, A.D.; Coe, J.V.; Tuttle, T.R., Jr. The proton’s absolute aqueous enthalpy and gibbs free energy of solvation from cluster-ion solvation data. J. Phys. Chem. A 1998, 102, 7787–7794. [Google Scholar] [CrossRef]
- Karelina, M.; Kulik, H.J. Systematic quantum mechanical region determination in QM/MM simulation. J. Chem. Theory Comput. 2017, 13, 563–576. [Google Scholar] [CrossRef] [PubMed]

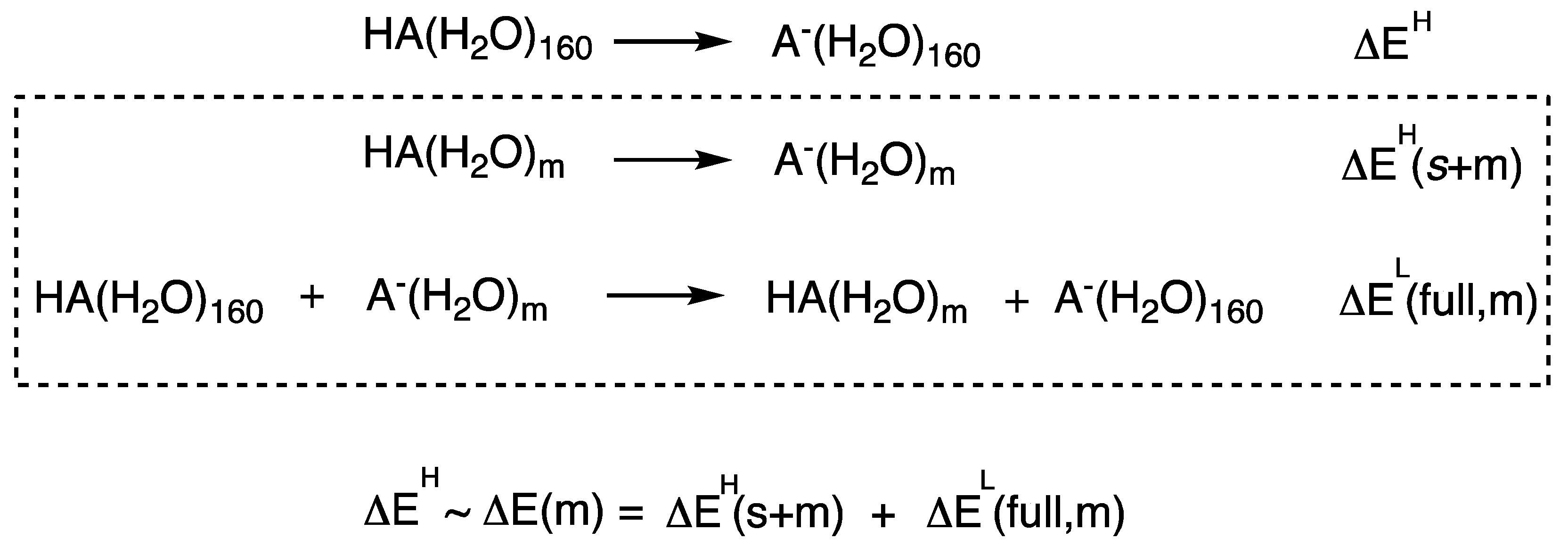
| Theory | CH3NH3+ | Phenol | ||
|---|---|---|---|---|
| Frame 0 | Frame 10 | Frame 0 | Frame 10 | |
| ωB97X-D/6-31G(d) | 296.0 (0.0) | 206.7 (0.0) | −31.2 (0.0) | −46.9 (0.0) |
| AMBER/TIP3P | 258.2 (−37.9) | 173.3 (−33.4) | −5.1 (26.2) | −1.3 (45.7) |
| PM7 | 240.9 (−55.2) | 172.9 (−33.7) | −18.1 (13.2) | −24.8 (22.1) |
| DFTB | 226.5 (−69.5) | 156.5 (−50.1) | −18.9 (12.4) | −32.6 (14.3) |
| HF/6-31G(d) | 296.9 (0.9) | 204.8 (−1.9) | −28.7 (2.5) | −51.4 (-4.4) |
| Method | HCOOH | C6H5OH | CH3NH3+ | H-Imidazole+ |
|---|---|---|---|---|
| QM-only | >150 (28.0) | 150 (35.0) | 150 (204.9) | 150 (168.8) |
| TIP3P | 60 (28.0) | 50 (32.9) | 60 (32.5) | 50 (14.6) |
| TIP3P-EE | 70 (30.3) | 70 (32.5) | 30 (21.0) | 30 (11.0) |
| EFP | 40 (11.7) | 10 (8.9) | 10 (5.1) | 10 (7.5) |
| PM6 | 80 (43.1) | 100 (39.1) | 110 (79.9) | 110 (71.0) |
| PM7 | 30 (14.9) | 40 (17.0) | 70 (36.1) | 60 (22.3) |
| DFTB | 30 (10.4) | 40 (11.4) | 70 (45.2) | 70 (35.0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, J.; Shao, Y.; Kato, J. Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules 2018, 23, 2466. https://doi.org/10.3390/molecules23102466
Ho J, Shao Y, Kato J. Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules. 2018; 23(10):2466. https://doi.org/10.3390/molecules23102466
Chicago/Turabian StyleHo, Junming, Yihan Shao, and Jin Kato. 2018. "Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters" Molecules 23, no. 10: 2466. https://doi.org/10.3390/molecules23102466
APA StyleHo, J., Shao, Y., & Kato, J. (2018). Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules, 23(10), 2466. https://doi.org/10.3390/molecules23102466