Density Functional Studies on Secondary Amides: Role of Steric Factors in Cis/Trans Isomerization
Abstract
1. Introduction
2. Results and Discussion
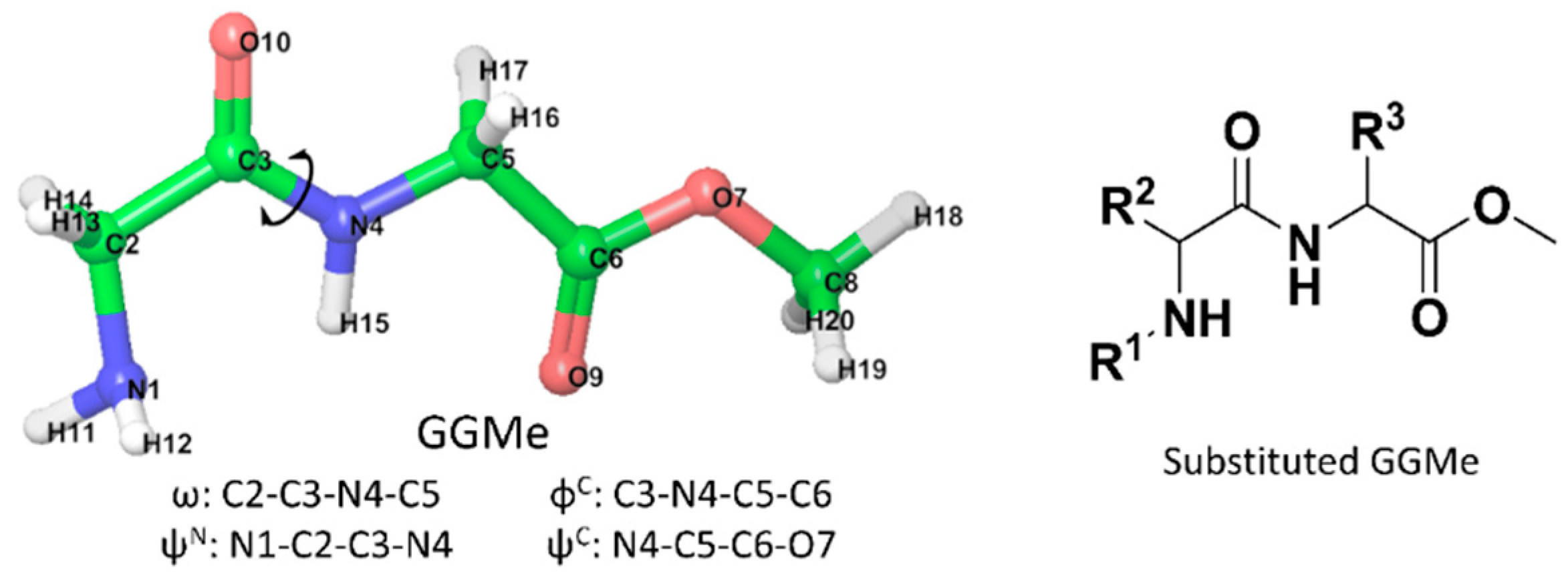
2.1. Model Structures
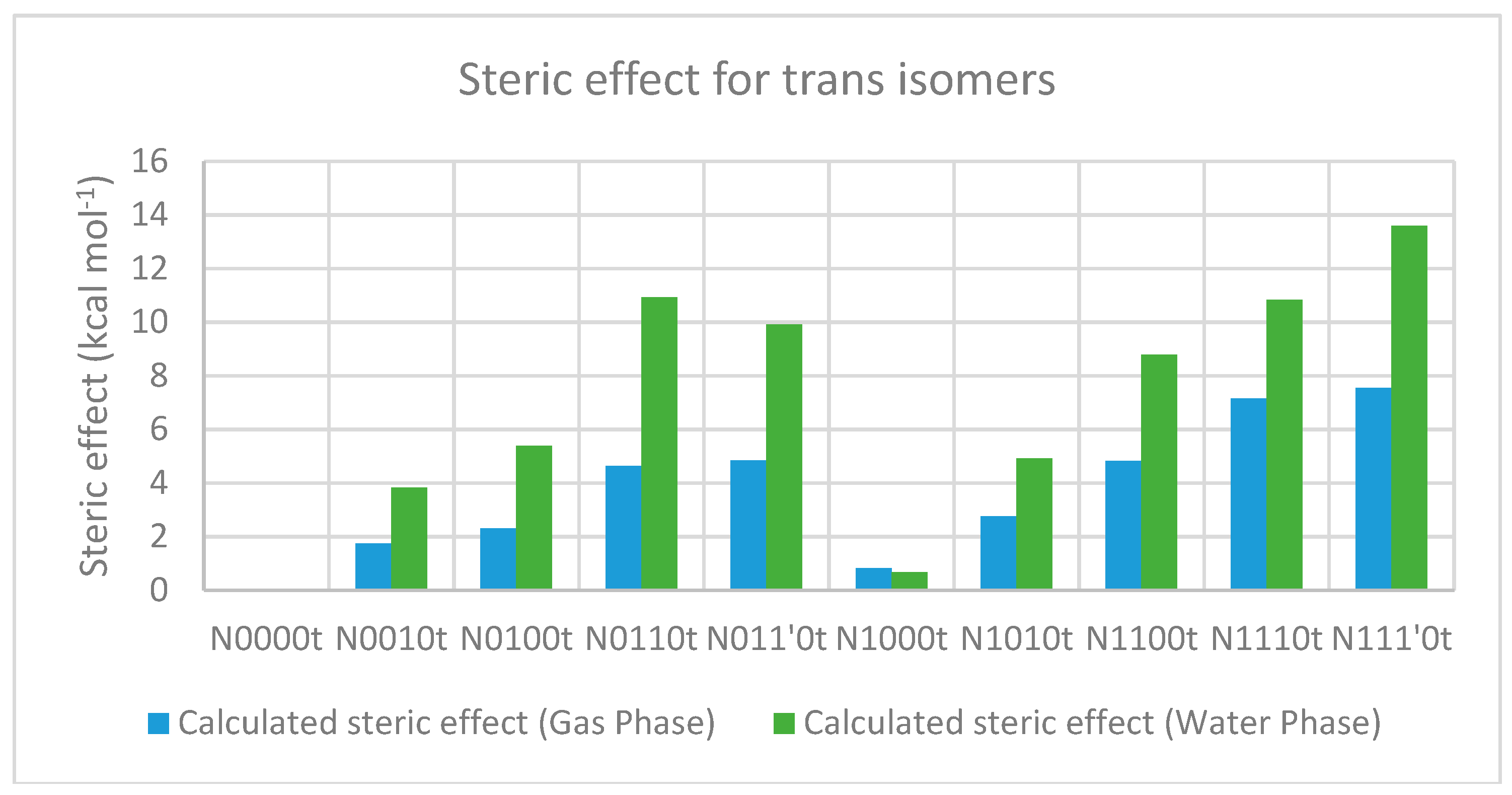
2.2. Trans Geometries
2.3. Cis Geometries
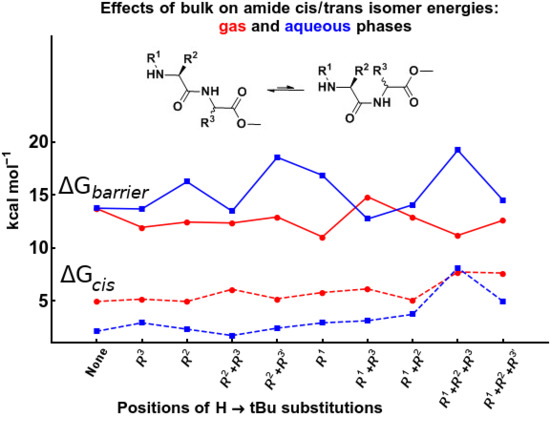
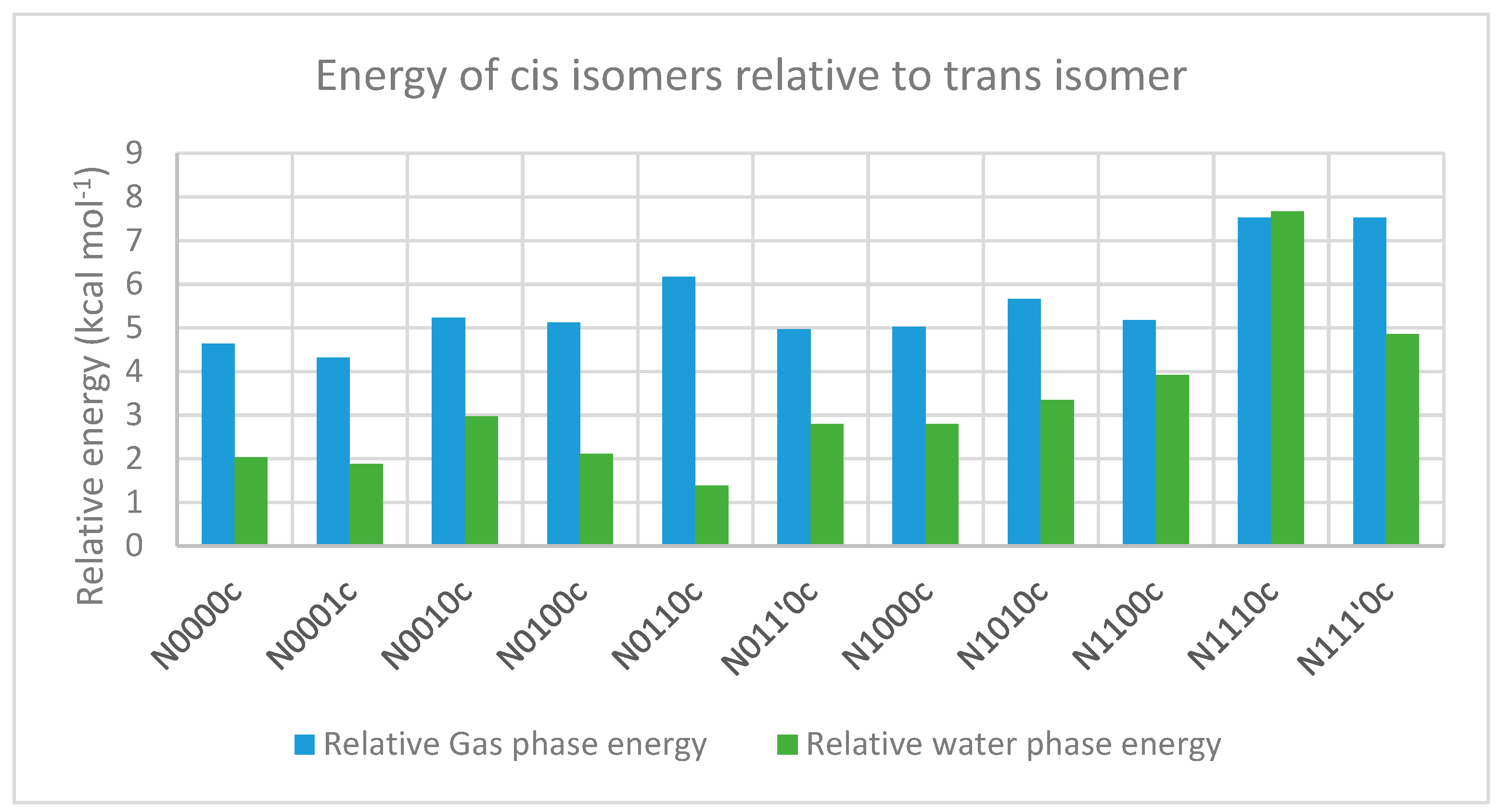
2.3.1. The Relative Stabilities of Cis vs. Trans Isomers
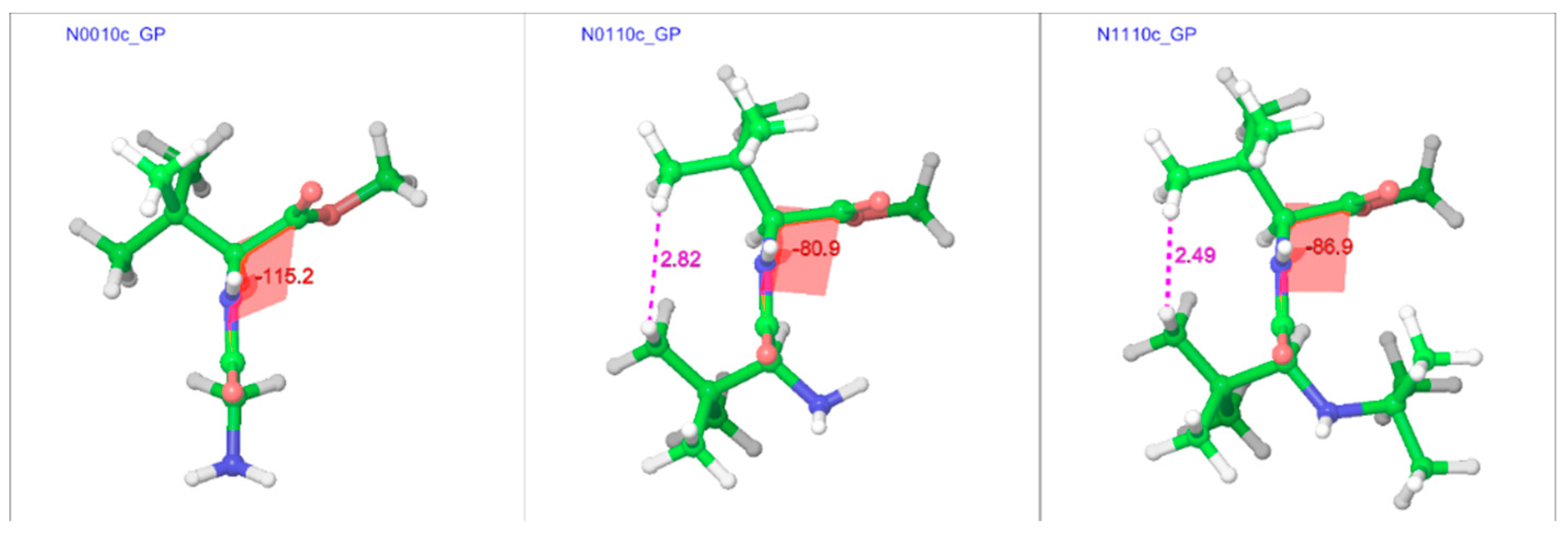
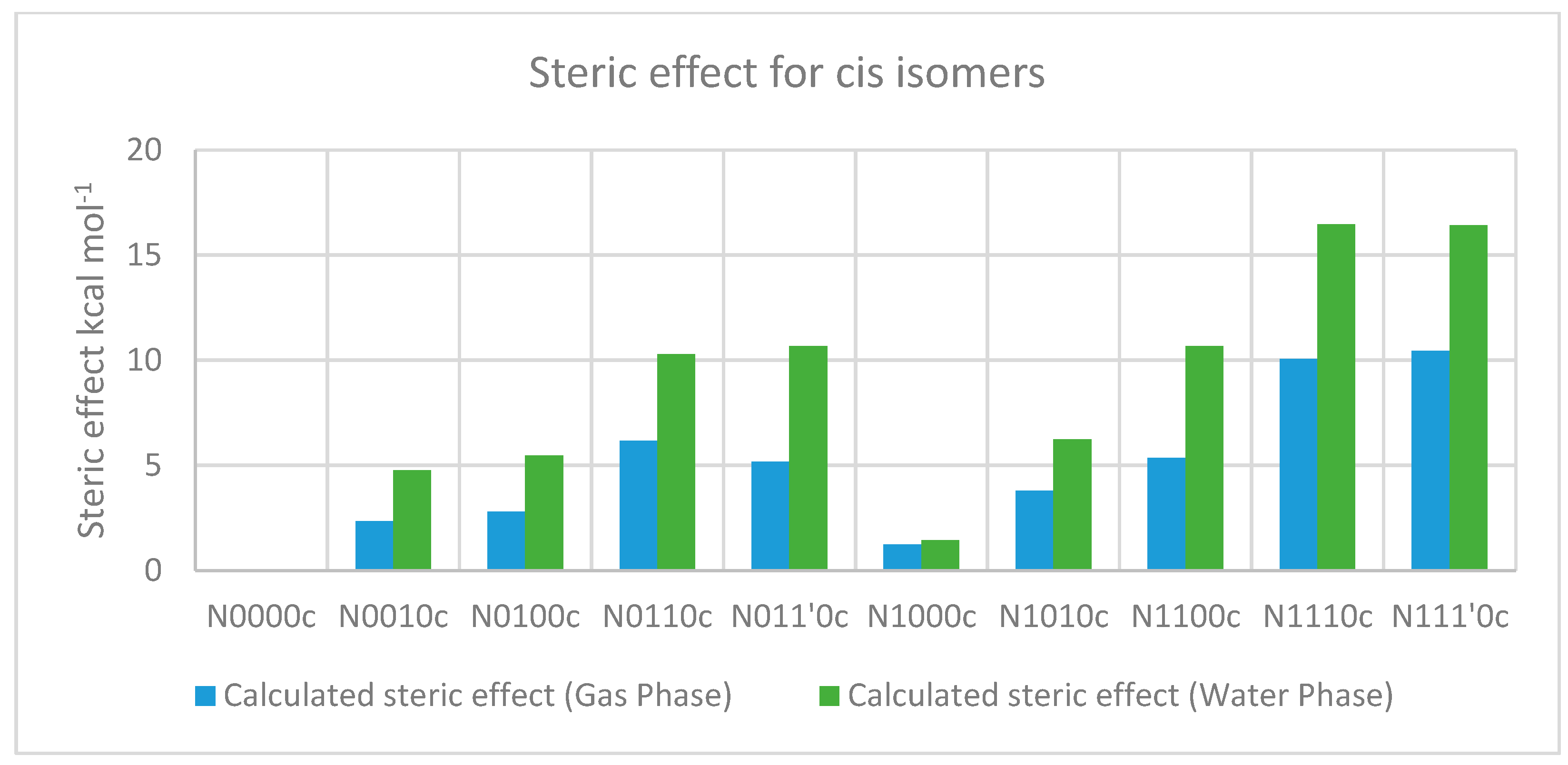
2.3.2. The Effect of Bulk on Cis Isomers
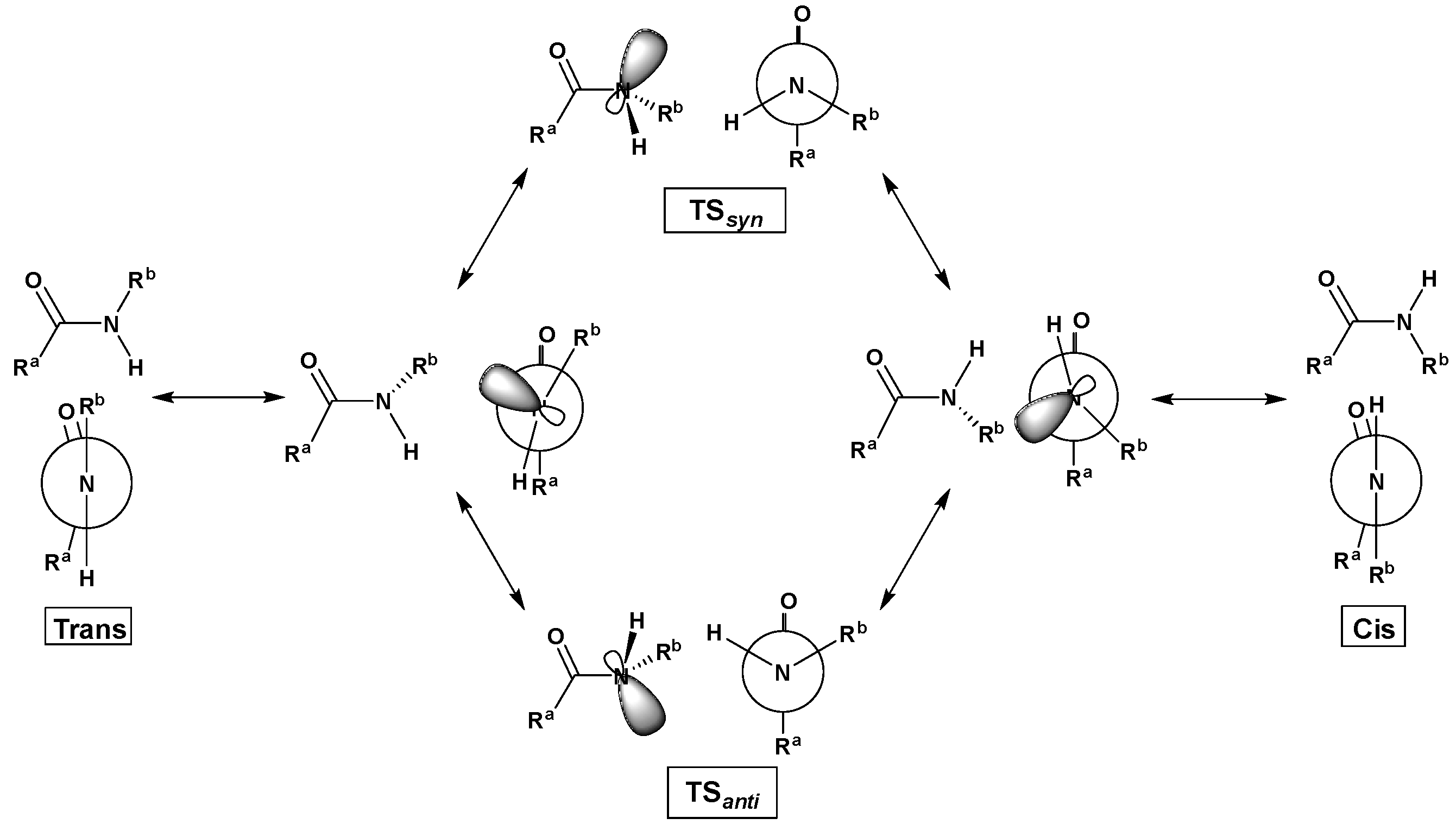
2.4. Cis/Trans Isomerization Barrier
3. Methods
3.1. Generation of Structures
3.2. Conformational Search
3.3. Geometric Optimization
3.4. Relaxed Coordinate Scan (RCS)
3.5. Single-Point Energy Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- LaPlanche, L.A.; Rogers, M.T. Cis and trans Configurations of the Peptide Bond in N-Monosubstituted Amides by Nuclear Magnetic Resonance. J. Am. Chem. Soc. 1964, 86, 337–341. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Mitra, A.K. An explanation for the rare occurrence of cis peptide units in proteins and polypeptides. J. Mol. Biol. 1976, 107, 85–92. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Sasisekharan, V. Conformation of polypeptides and proteins. Adv. Protein Chem. 1968, 23, 283–438. [Google Scholar] [PubMed]
- Liu, C.; Szostak, M. Twisted Amides: From Obscurity to Broadly Useful Transition-Metal-Catalyzed Reactions by N−C Amide Bond Activation. Chem. Eur. J. 2017, 23, 7157–7173. [Google Scholar] [CrossRef] [PubMed]
- Mock, W.L. Torsional strain considerations in the mechanism of the proteolytic enzymes, with particular application to carboxypeptidase A. Bioorg. Chem. 1975, 4, 270–278. [Google Scholar] [CrossRef]
- Mock, W.L. Torsional-strain considerations in enzymology: Some applications to proteases and ensuing mechanistic consequences. Bioorg. Chem. 1976, 5, 403–414. [Google Scholar] [CrossRef]
- Thakkar, B.S.; Svendsen, J.-S.M.; Engh, R.A. Cis/Trans Isomerization in Secondary Amides: Reaction Paths, Nitrogen Inversion, and Relevance to Peptidic Systems. J. Phys. Chem. A 2017, 121, 6830–6837. [Google Scholar] [CrossRef] [PubMed]
- Stewart, D.E.; Sarkar, A.; Wampler, J.E. Occurrence and role of cis peptide bonds in protein structures. J. Mol. Biol. 1990, 214, 253–260. [Google Scholar] [CrossRef]
- Weiss, M.S.; Jabs, A.; Hilgenfeld, R. Peptide bonds revisited. Nat. Struct. Mol. Biol. 1998, 5, 676. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Chakrabarti, P. Cis peptide bonds in proteins: Residues involved, their conformations, interactions and locations. J. Mol. Biol. 1999, 294, 271–288. [Google Scholar] [CrossRef] [PubMed]
- Tchaicheeyan, O. Is peptide bond cis/trans isomerization a key stage in the chemo-mechanical cycle of motor proteins? FASEB J. 2004, 18, 783–789. [Google Scholar] [CrossRef] [PubMed]
- Odefey, C.; Mayr, L.M.; Schmid, F.X. Non-prolyl cis-trans peptide bond isomerization as a rate-determining step in protein unfolding and refolding. J. Mol. Biol. 1995, 245, 69–78. [Google Scholar] [CrossRef]
- Vanhove, M.; Raquet, X.; Palzkill, T.; Pain, R.H.; Frère, J.-M. The rate-limiting step in the folding of the cis-Pro167Thr mutant of TEM-1 β-lactamase is the trans to cis isomerization of a non-proline peptide bond. Proteins Struct. Funct. Bioinform. 1996, 25, 104–111. [Google Scholar] [CrossRef]
- Wheeler, K.A.; Hawkins, A.R.; Pain, R.; Virden, R. The slow step of folding of Staphylococcus aureus PC1 β-lactamase involves the collapse of a surface loop rate limited by the Trans to Cis isomerization of a non-proline peptide bond. Proteins Struct. Funct. Bioinform. 1998, 33, 550–557. [Google Scholar] [CrossRef]
- Agarwal, P.K. Cis/trans isomerization in HIV-1 capsid protein catalyzed by cyclophilin A: Insights from computational and theoretical studies. Proteins Struct. Funct. Bioinform. 2004, 56, 449–463. [Google Scholar] [CrossRef] [PubMed]
- Ledvina, A.R.; Chung, T.W.; Hui, R.; Coon, J.J.; Tureček, F. Cascade dissociations of peptide cation-radicals. Part 2. Infrared multiphoton dissociation and mechanistic studies of z-ions from pentapeptides. J. Am. Soc. Mass Spectrom. 2012, 23, 1351–1363. [Google Scholar] [CrossRef] [PubMed]
- Baldoni, H.A.; Zamarbide, G.N.; Enriz, R.D.; Jauregui, E.A.; Farkas, Ö.; Perczel, A.; Salpietro, S.J.; Csizmadia, I.G. Peptide models XXIX. cis–trans Isomerism of peptide bonds: Ab initio study on small peptide model compound; the 3D-Ramachandran map of formylglycinamide. J. Mol. Struct. THEOCHEM 2000, 500, 97–111. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Rablen, P.R.; Rush, D.J.; Keith, T.A. Amides. 3. Experimental and Theoretical Studies of the Effect of the Medium on the Rotational Barriers for N,N-Dimethylformamide and N,N-Dimethylacetamide. J. Am. Chem. Soc. 1995, 117, 4261–4270. [Google Scholar] [CrossRef]
- Lauvergnat, D.; Hiberty, P.C. Role of Conjugation in the Stabilities and Rotational Barriers of Formamide and Thioformamide. An ab Initio Valence-Bond Study. J. Am. Chem. Soc. 1997, 119, 9478–9482. [Google Scholar] [CrossRef]
- Mantz, Y.A.; Gerard, H.; Iftimie, R.; Martyna, G.J. Ab Initio and Empirical Model MD Simulation Studies of Solvent Effects on the Properties of N-Methylacetamide along a cis−trans Isomerization Pathway. J. Phys. Chem. B 2006, 110, 13523–13538. [Google Scholar] [CrossRef] [PubMed]
- Taha, A.N.; True, N.S. Experimental 1H NMR and Computational Studies of Internal Rotation of Solvated Formamide. J. Phys. Chem. A 2000, 104, 2985–2993. [Google Scholar] [CrossRef]
- Kang, Y.K.; Park, H.S. Internal rotation about the C.–N. bond of amides. J. Mol. Struct. THEOCHEM 2004, 676, 171–176. [Google Scholar] [CrossRef]
- Mantz, Y.A.; Branduardi, D.; Bussi, G.; Parrinello, M. Ensemble of Transition State Structures for the Cis−Trans Isomerization of N-Methylacetamide. J. Phys. Chem. B 2009, 113, 12521–12529. [Google Scholar] [CrossRef] [PubMed]
- Thakkar, B.S.; Engh, R.A. Comparative conformational analyses and molecular dynamics studies of glycylglycine methyl ester and glycylglycine N-methylamide. RSC Adv. 2018, 8, 4445–4453. [Google Scholar] [CrossRef]
- Yoder, C.H.; Gardner, R.D. Multiple-substituent parameter analysis of the effects of substituents at nitrogen on the barriers to rotation in amides. J. Org. Chem. 1981, 46, 64–66. [Google Scholar] [CrossRef]
- Fischer, G. Chemical aspects of peptide bond isomerisation. Chem. Soc. Rev. 2000, 29, 119–127. [Google Scholar] [CrossRef]
- Moure, A.; Sanclimens, G.; Bujons, J.; Masip, I.; Alvarez-Larena, A.; Pérez-Payá, E.; Alfonso, I.; Messeguer, A. Chemical modulation of peptoids: Synthesis and conformational studies on partially constrained derivatives. Chem.-Eur. J. 2011, 17, 7927–7939. [Google Scholar] [CrossRef] [PubMed]
- Laursen, J.S.; Engel-Andreasen, J.; Fristrup, P.; Harris, P.; Olsen, C.A. Cis-trans amide bond rotamers in β-peptoids and peptoids: Evaluation of stereoelectronic effects in backbone and side chains. J. Am. Chem. Soc. 2013, 135, 2835–2844. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, D.; Simerska, P.; Toth, I. Peptides as therapeutics with enhanced bioactivity. Curr. Med. Chem. 2012, 19, 4451–4461. [Google Scholar] [CrossRef] [PubMed]
- Avan, I.; Hall, C.D.; Katritzky, A.R. Peptidomimetics via modifications of amino acids and peptide bonds. Chem. Soc. Rev. 2014, 43, 3575–3594. [Google Scholar] [CrossRef] [PubMed]
- Muller, P. Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994). Pure Appl. Chem. 2009, 66, 1077–1184. [Google Scholar] [CrossRef]
- Hirsch, J.A. Table of Conformational Energies—1967. In Topics in Stereochemistry; Allinger, N.L., Eliel, E.L., Eds.; John Wiley & Sons, Inc.: Manhattan, NY, USA, 1967; pp. 199–222. ISBN 978-0-470-14710-8. [Google Scholar]
- Charton, M. Steric effects. I. Esterification and acid-catalyzed hydrolysis of esters. J. Am. Chem. Soc. 1975, 97, 1552–1556. [Google Scholar] [CrossRef]
- Charton, M. The upsilon steric parameter—Definition and determination. In Steric Effects in Drug Design; Topics in Current Chemistry; Springer: Berlin/Heidelberg, Germany, 1983; pp. 57–91. ISBN 978-3-540-12398-9. [Google Scholar]
- Icli, S.; Kandil, K.A.; Thankachan, C.; Tidwell, T.T. Steric Crowding and the Reactivity of Substituted tert-Butyl Perbenzoates. Can. J. Chem. 1975, 53, 979–985. [Google Scholar] [CrossRef]
- Marcelin, G.; Brooks, P.R. Steric hindrance in potassium atom-oriented molecule reactions. Methyl iodide and tert-butyl iodide. J. Am. Chem. Soc. 1975, 97, 1710–1715. [Google Scholar] [CrossRef]
- Bartell, L.S.; Bradford, W.F. Molecular structures of neopentane and di-tert-butylmethane by vapor-phase electron diffraction. J. Mol. Struct. 1977, 37, 113–126. [Google Scholar] [CrossRef]
- Toniolo, C. Intramolecularly hydrogen-bonded peptide conformations. CRC Crit. Rev. Biochem. 1980, 9, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger Release 2016-1: Maestro; Schrödinger, LLC: New York, NY, USA, 2016.
- Schrödinger Release 2016-1: MacroModel; Schrödinger, LLC: New York, NY, USA, 2016.
- Bochevarov, A.D.; Harder, E.; Hughes, T.F.; Greenwood, J.R.; Braden, D.A.; Philipp, D.M.; Rinaldo, D.; Halls, M.D.; Zhang, J.; Friesner, R.A. Jaguar: A high-performance quantum chemistry software program with strengths in life and materials sciences. Int. J. Quantum Chem. 2013, 113, 2110–2142. [Google Scholar] [CrossRef]
- Schrödinger Release 2016-1: Jaguar; Schrödinger, LLC: New York, NY, USA, 2016.
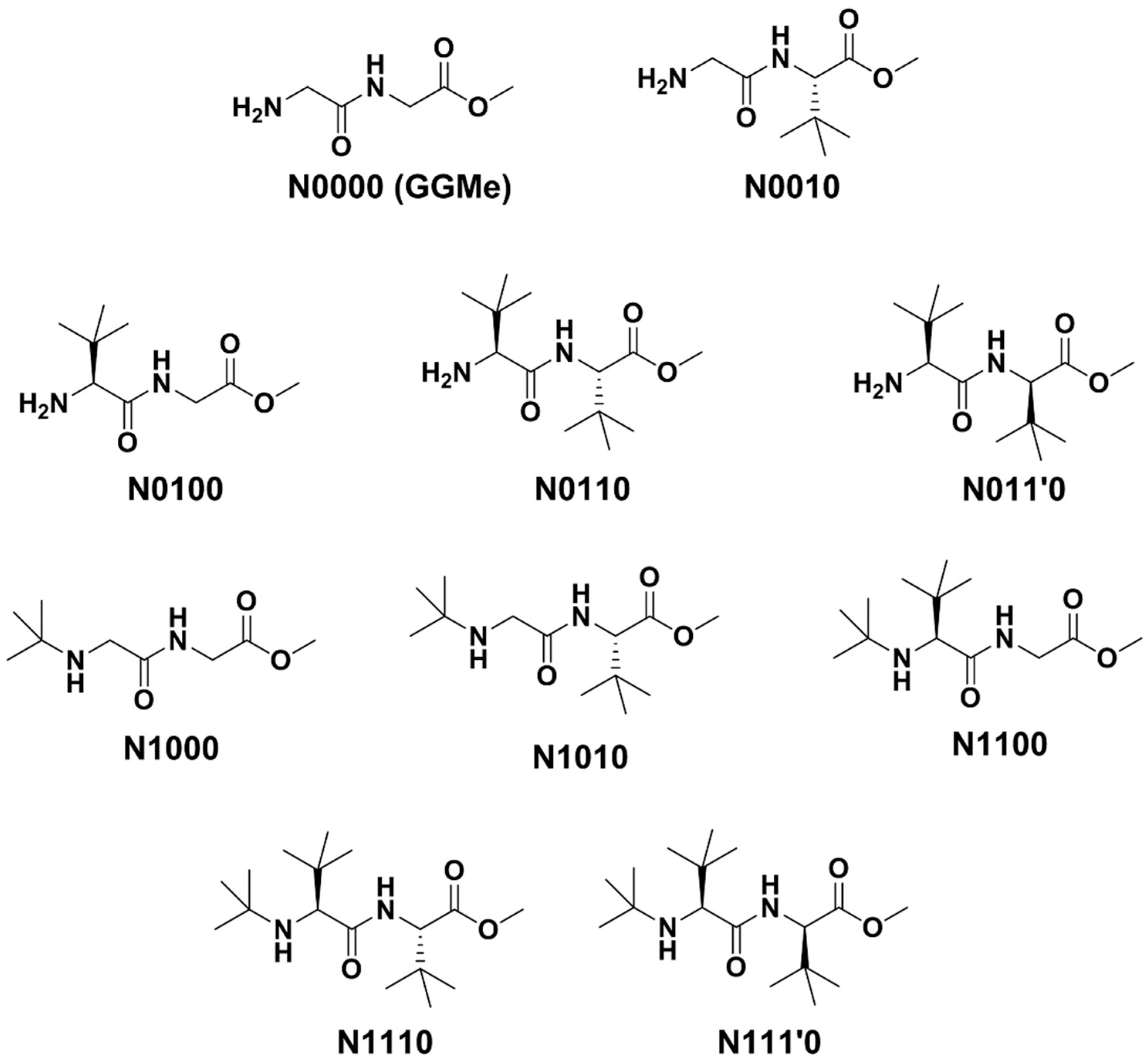
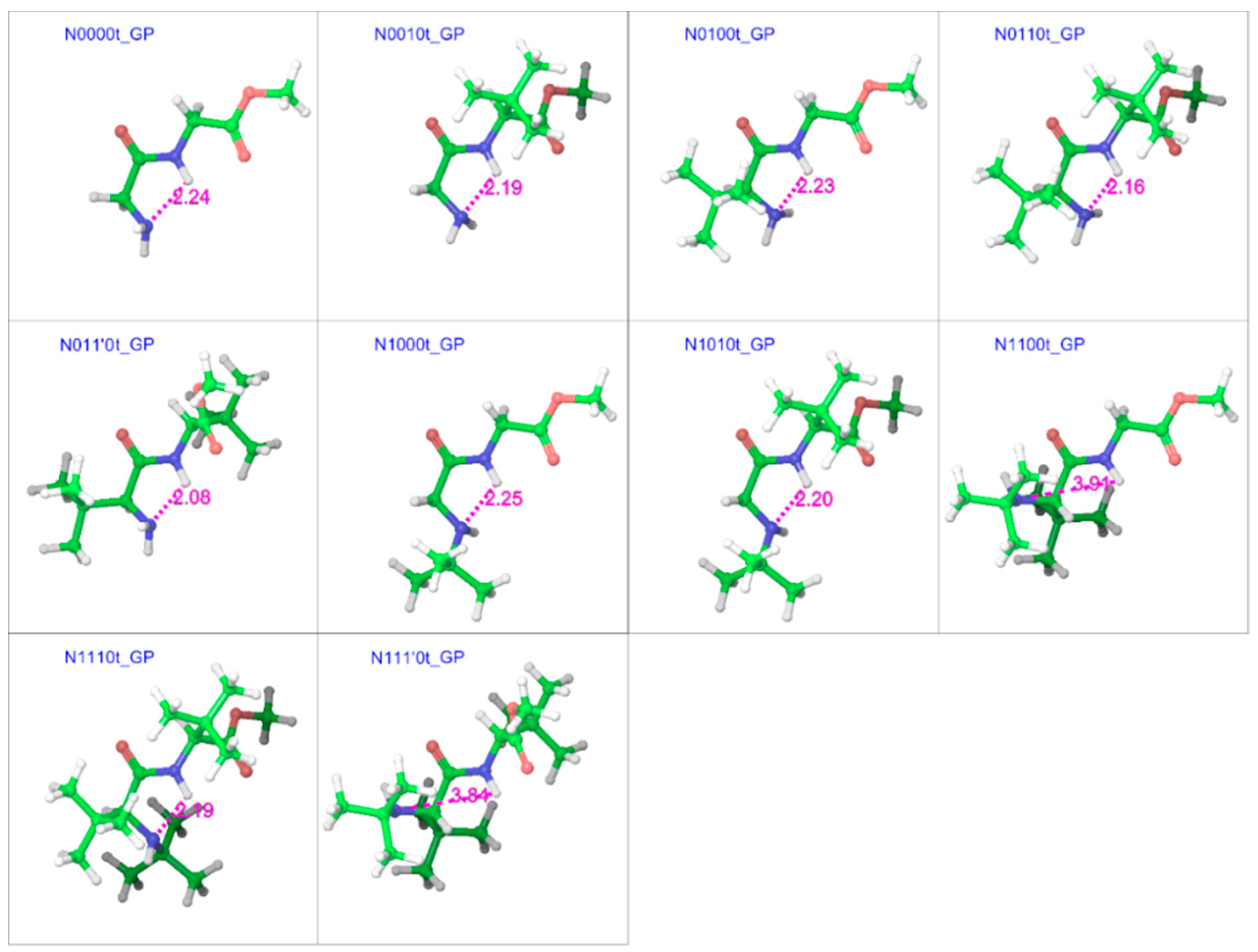
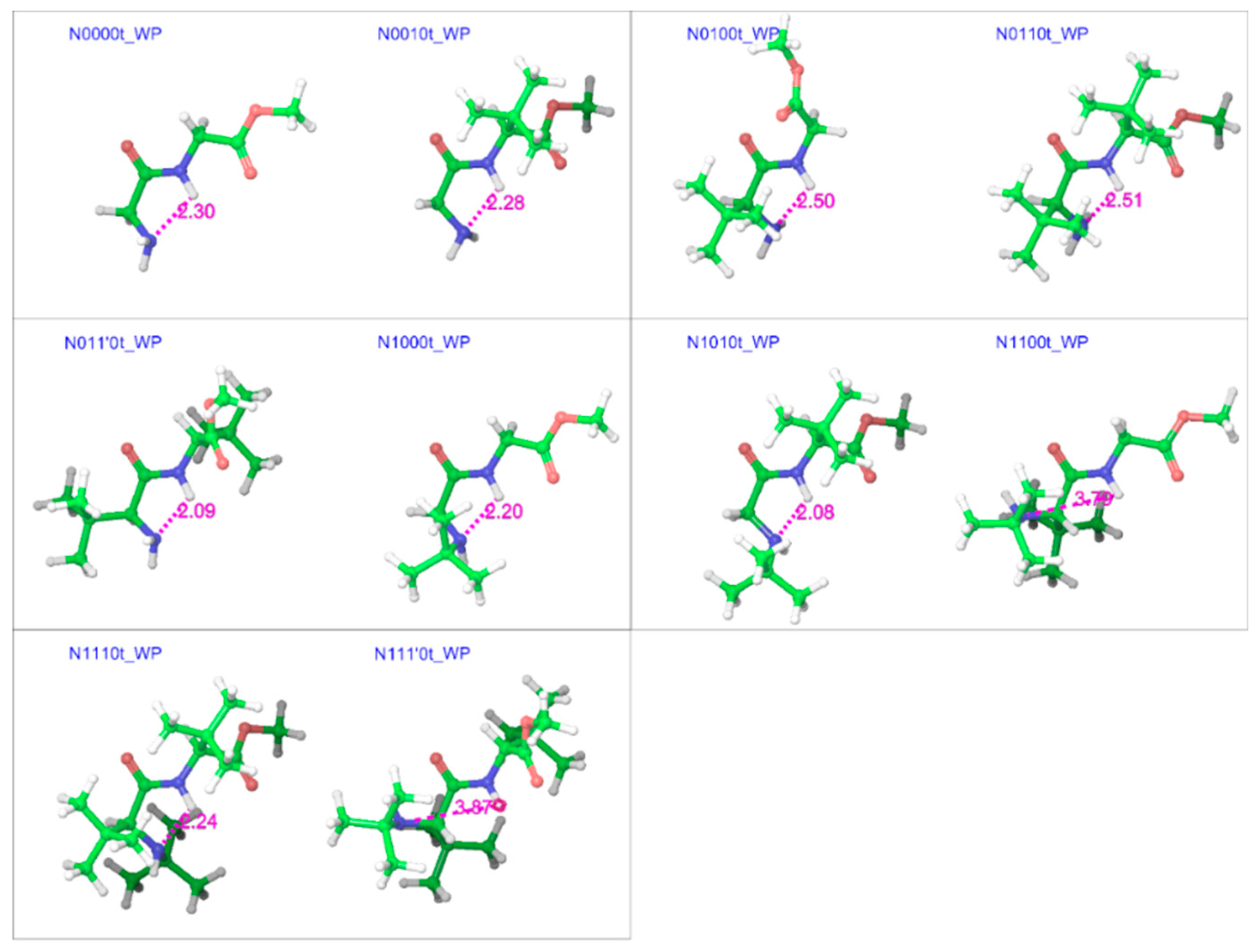
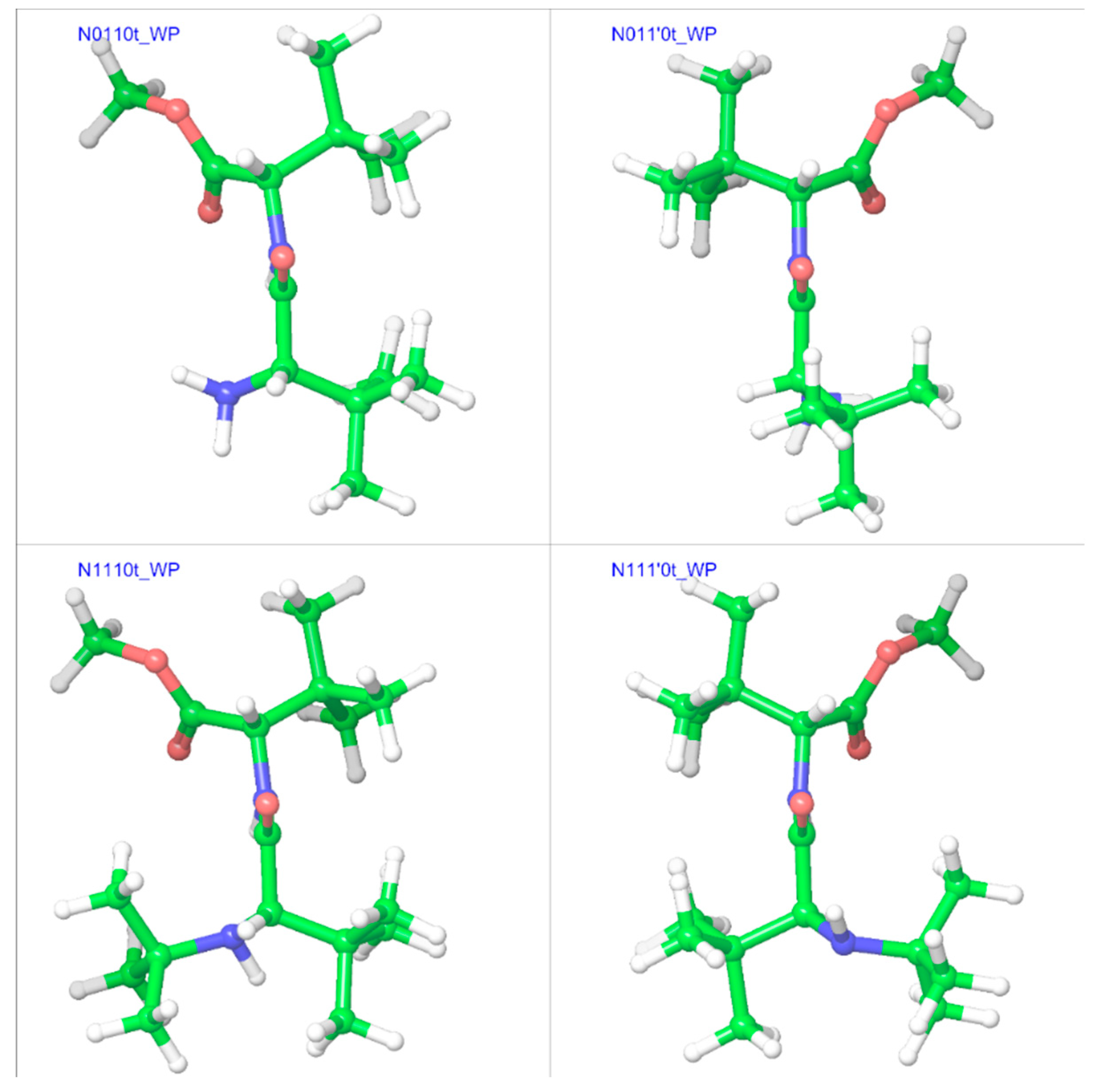
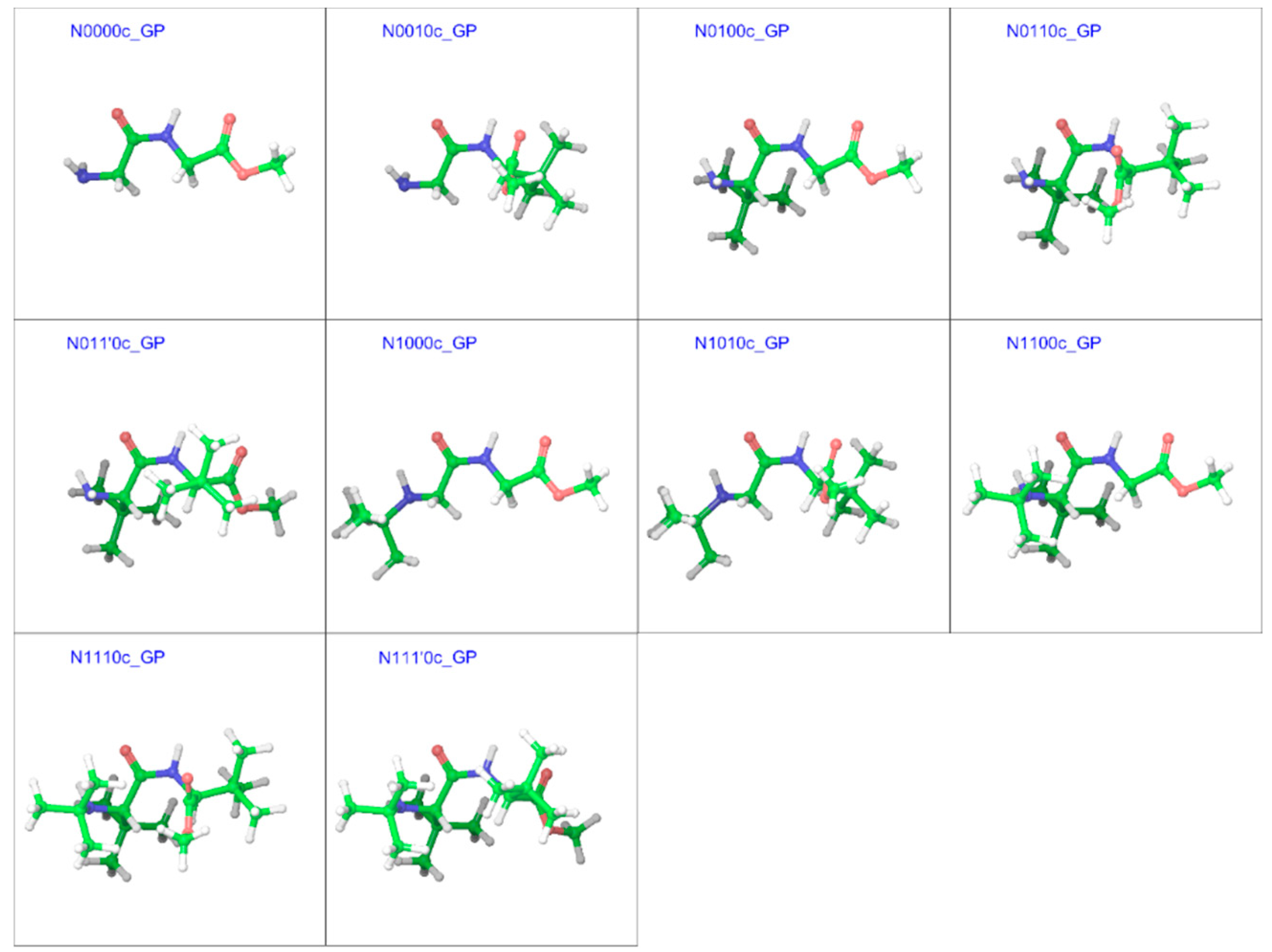
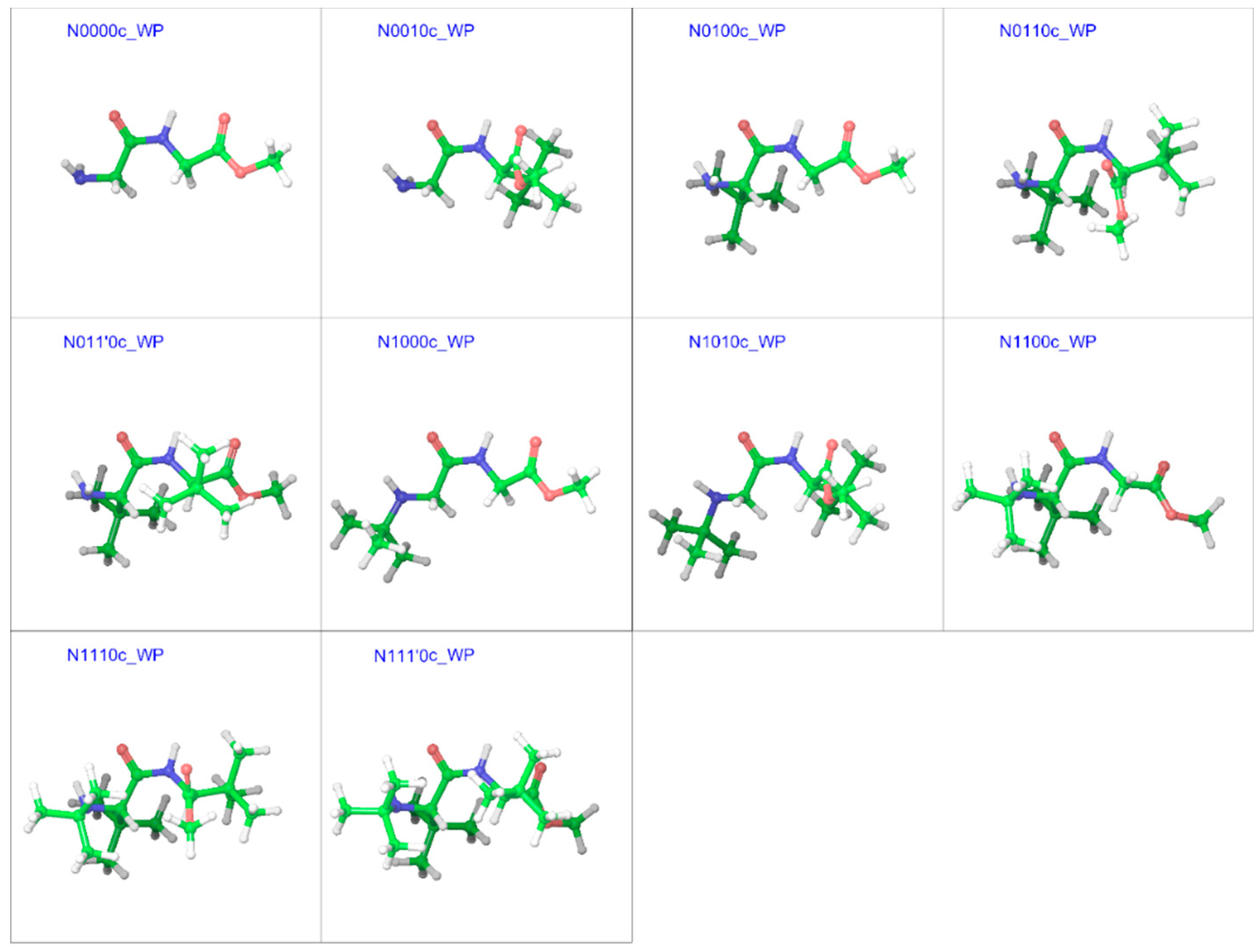
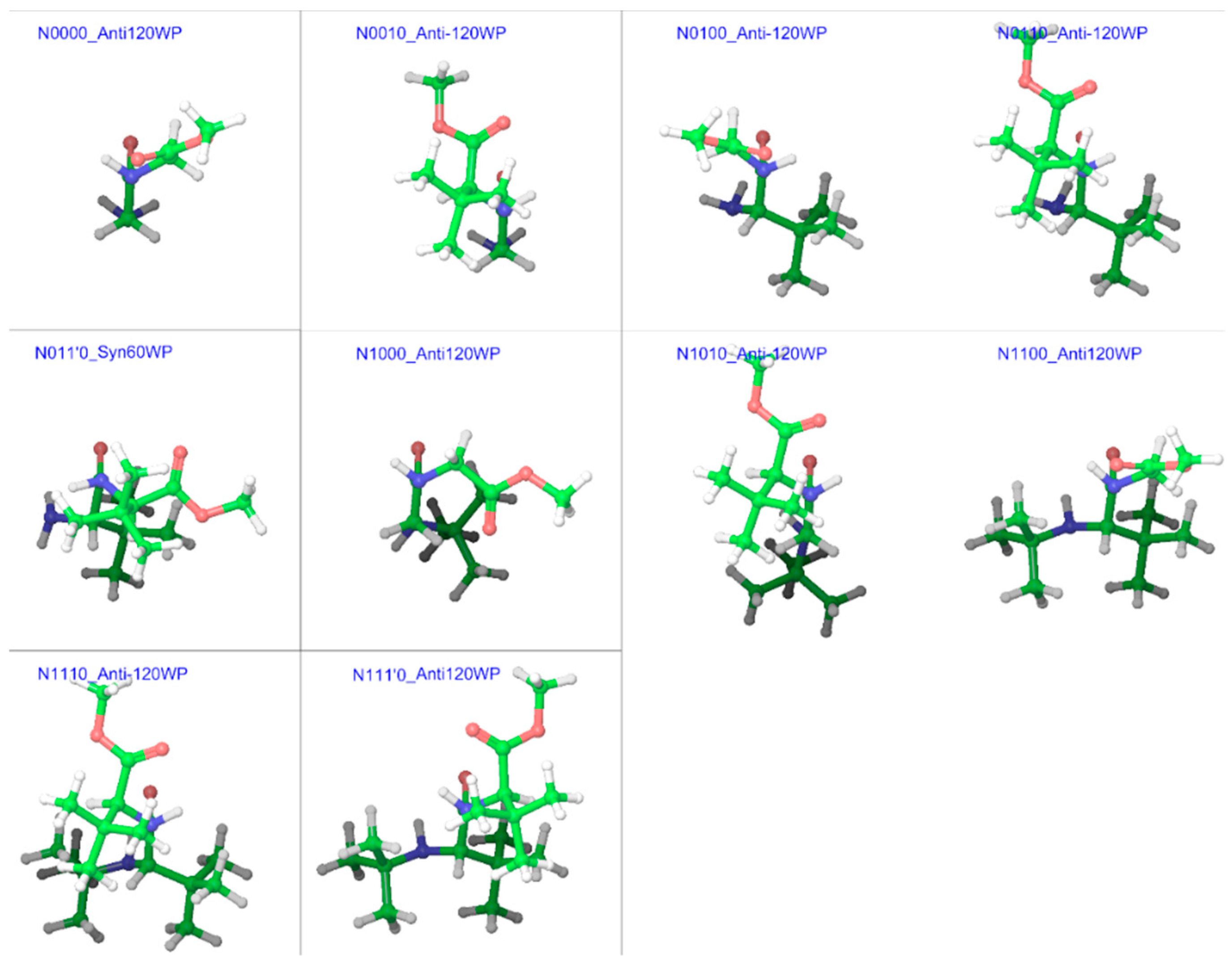
| Compound a | R1 | R2 | R3 |
|---|---|---|---|
| N0000 (GGMe) | H | H | H |
| N0010 | H | H | S-t-Bu |
| N0100 | H | S-t-Bu | H |
| N0110 | H | S-t-Bu | S-t-Bu |
| N011’0 | H | S-t-Bu | R-t-Bu |
| N1000 | t-Bu | H | H |
| N1010 | t-Bu | H | S-t-Bu |
| N1100 | t-Bu | S-t-Bu | H |
| N1110 | t-Bu | S-t-Bu | S-t-Bu |
| N111’0 | t-Bu | S-t-Bu | R-t-Bu |
| Compound | Gas Phase | Water Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| ψN | ω | φC | ψC | ψN | ω | φC | ψC | |
| N0000t | 12.8 | 178.3 | 175.6 | −179.3 | 15.2 | 179.2 | 178.5 | −177.4 |
| N0010t | −14.3 | 177.0 | −122.7 | 141.7 | −19.3 | 178.8 | −124.4 | 142.6 |
| N0100t | −22.8 | −179.7 | −173.1 | 178.8 | −40.5 | −177.9 | 66.3 | −146.4 |
| N0110t | −23.8 | 169.5 | −114.3 | 141.2 | −50.8 | 171.3 | −135.3 | 152.0 |
| N011’0t | 14.3 | −178.8 | 123.0 | −140.9 | 13.4 | 178.5 | 127.3 | −143.2 |
| N1000t | −15.6 | −178.0 | −179.1 | 179.6 | 12.7 | 179.5 | 175.3 | −177.3 |
| N1010t | −17.9 | 176.6 | −123.7 | 141.8 | −12.2 | 178.7 | −127.5 | 141.4 |
| N1100t | 140.7 | 177.5 | −175.0 | −179.9 | 134.6 | 174.6 | −163.7 | 171.2 |
| N1110t | −27.1 | 172.5 | −117.0 | 140.5 | −32.7 | 174.2 | −123.1 | 141.1 |
| N111’0t | 143.0 | −169.7 | 127.2 | −145.3 | 148.2 | −173.4 | 136.1 | −147.7 |
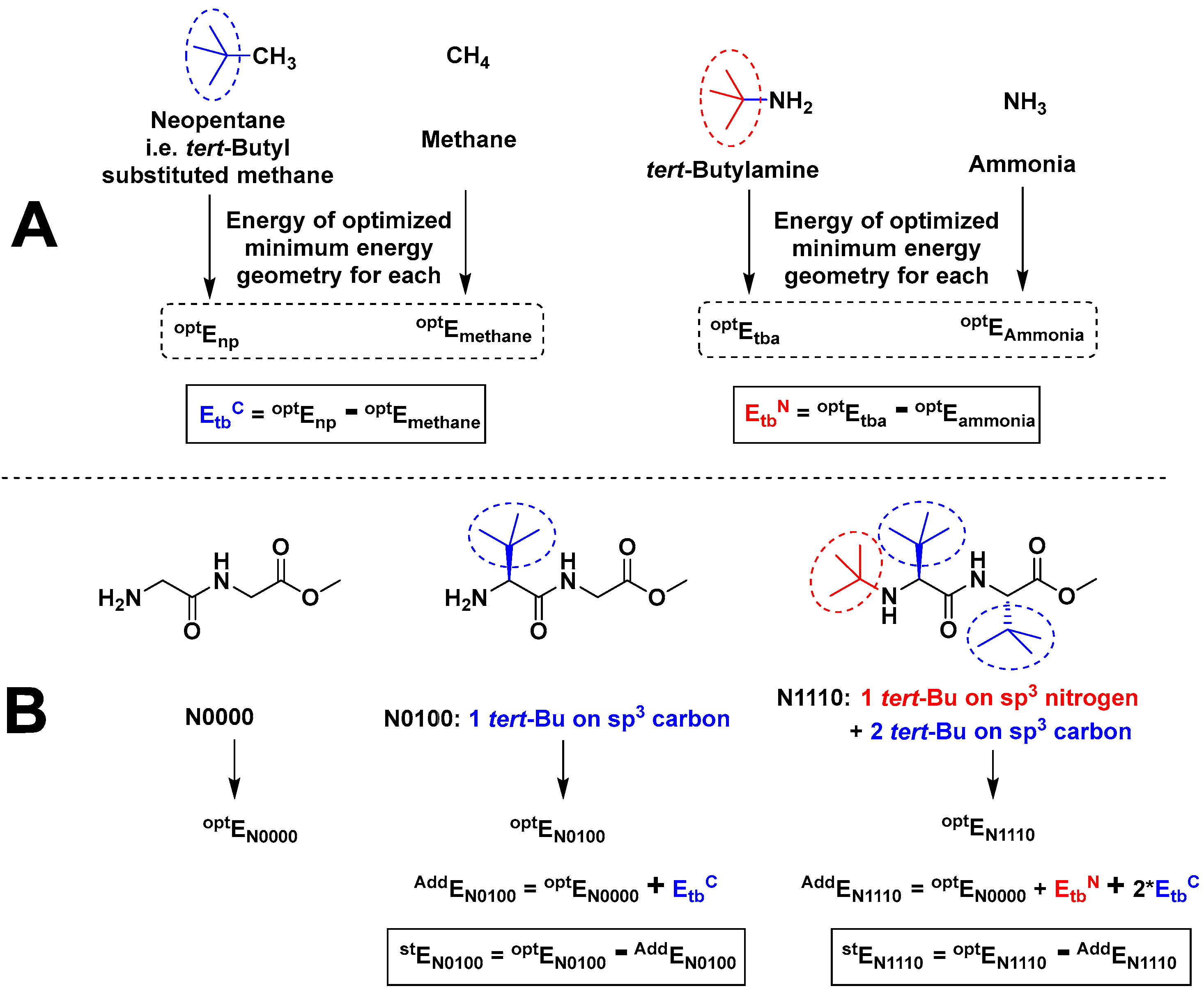
| Compound | optE | Attachment Point | tert-Bu Additive Energy kcal mol−1 (Etb) |
|---|---|---|---|
| NH3 | −35,508.975 | sp3 nitrogen | EtbN = −98,709.131 |
| tert-Bu-NH2 | −134,218.106 | ||
| CH4 | −25,437.531 | sp3 carbon | EtbC = −98,712.134 |
| tert-Bu-CH3 | −124,149.665 |
| Compound | optE | Attachment Point | tert-Bu Additive Energy Kcal mol−1 (Etb) |
|---|---|---|---|
| NH3 | −35,514.577 | sp3 nitrogen | EtbN = −98,707.646 |
| tert-Bu-NH2 | −134,222.223 | ||
| CH4 | −25,436.175 | sp3 carbon | EtbC = −98,711.962 |
| tert-Bu-CH3 | −124,148.137 |
| Compound a | optE kcal mol−1 | No. of t-Bu on sp3 Nitrogen | No. of t-Bu on sp3 Carbon | AddE kcal mol−1 | stE kcal mol−1 |
|---|---|---|---|---|---|
| N0000t | −333,806.071 | −333,806.071 | 0 | ||
| N0010t | −432,516.46 | 1 | −432,518.205 | 1.745 | |
| N0100t | −432,515.901 | 1 | −432,518.205 | 2.304 | |
| N0110t | −531,225.709 | 2 | −531,230.339 | 4.63 | |
| N011’0t | −531,225.494 | 2 | −531,230.339 | 4.845 | |
| N1000t | −432,514.375 | 1 | −432,515.202 | 0.827 | |
| N1010t | −531,224.575 | 1 | 1 | −531,227.336 | 2.761 |
| N1100t | −531,222.518 | 1 | 1 | −531,227.336 | 4.818 |
| N1110t | −629,932.315 | 1 | 2 | −629,939.47 | 7.155 |
| N111’0t | −629,931.92 | 1 | 2 | −629,939.47 | 7.55 |
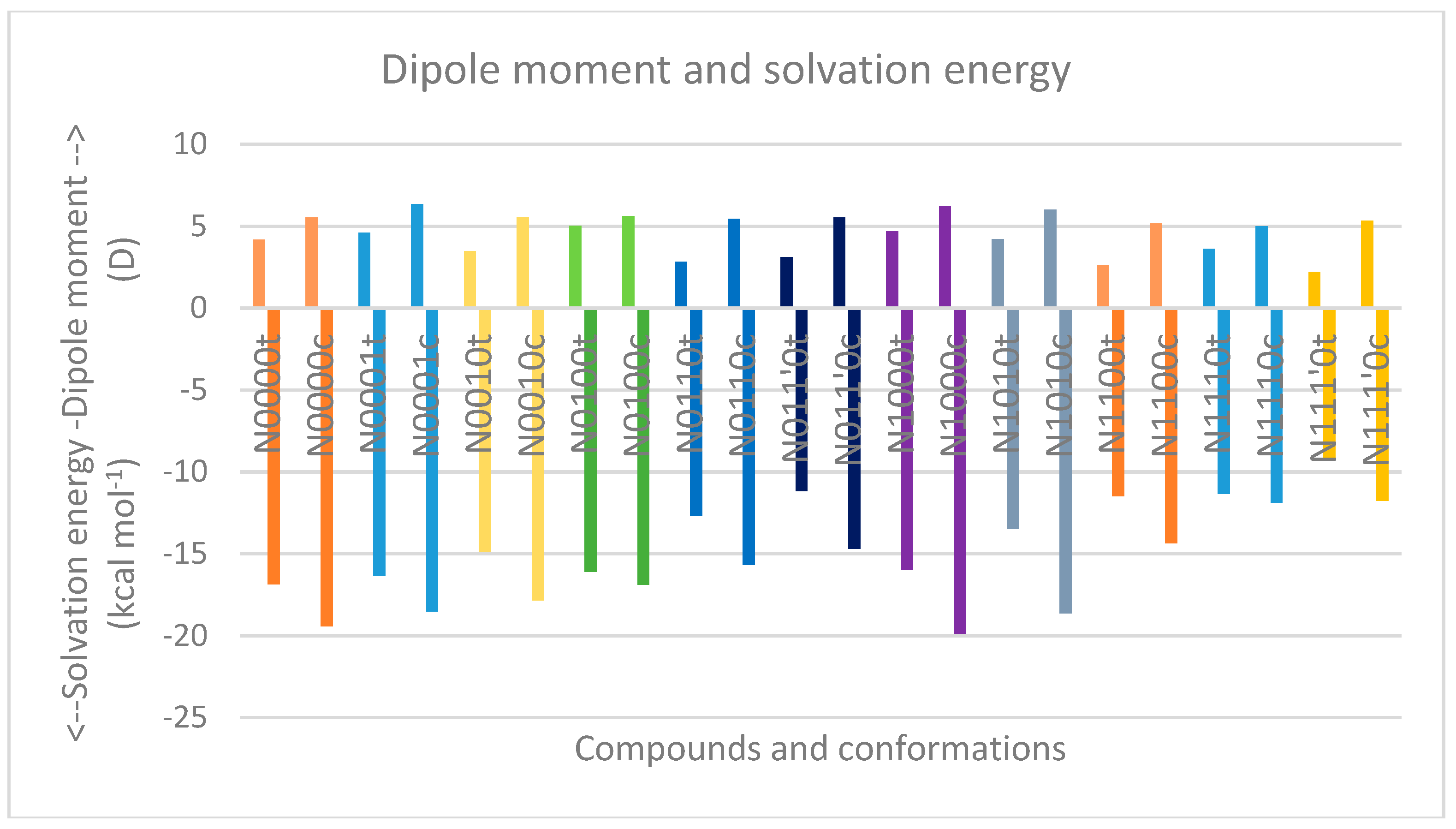
| Compound a | Solvation Energy (kcal mol−1) | optE kcal mol−1 | No. of t-Bu on sp3 nitrogen | No. of t-Bu on sp3 carbon | AddE kcal mol-1 | stE kcal mol−1 |
|---|---|---|---|---|---|---|
| N0000t | −16.33 | −381,811.506 | −381,811.506 | 0 | ||
| N0010t | −16.85 | −480,519.643 | 1 | −480,523.468 | 3.825 | |
| N0100t | −14.86 | −480,518.077 | 1 | −480,523.468 | 5.391 | |
| N0110t | −16.1 | −579,224.507 | 2 | −579,235.43 | 10.923 | |
| N011’0t | −12.66 | −579,225.518 | 2 | −579,235.43 | 9.912 | |
| N1000t | −11.16 | −480,518.478 | 1 | −480,519.152 | 0.674 | |
| N1010t | −15.97 | −579,226.192 | 1 | 1 | −579,231.114 | 4.922 |
| N1100t | −13.47 | −579,222.324 | 1 | 1 | −579,231.114 | 8.79 |
| N1110t | −11.49 | −677,932.254 | 1 | 2 | −677,943.076 | 10.822 |
| N111’0t | −11.34 | −677,929.486 | 1 | 2 | −677,943.076 | 13.59 |
| Compound a | ψN | ω | φC | ψC | ΔE b | ΔG c |
|---|---|---|---|---|---|---|
| N0000c | 179.9 | 0.1 | −179.9 | 179.8 | 4.63 | 4.92 |
| N0010c | −176.7 | −6.1 | −115.2 | 132.8 | 5.23 | 5.14 |
| N0100c | 130.7 | −2.4 | −178.5 | −179.3 | 5.12 | 4.92 |
| N0110c | 130.0 | −8.5 | −80.9 | 131.9 | 6.17 | 6.07 |
| N011’0c | 131.2 | 0.0 | 127.3 | −136.5 | 4.96 | 5.18 |
| N1000c | −162.2 | 2.1 | −177.6 | 178.5 | 5.02 | 5.77 |
| N1010c | −158.2 | −5.1 | −121.5 | 135.7 | 5.67 | 6.11 |
| N1100c | 137.5 | −6.4 | −175.1 | −178.3 | 5.17 | 5.05 |
| N1110c | 138.9 | −3.5 | −86.9 | 132.0 | 7.52 | 7.71 |
| N111’0c | 140.4 | 6.9 | 104.4 | −143.9 | 7.52 | 7.61 |
| Compound a | Solvation Energy (kcal mol−1) | φN | ω | φC | ψC | ΔE b | ΔG c |
|---|---|---|---|---|---|---|---|
| N0000c | −19.43 | 179.5 | 0.1 | −179.6 | 179.7 | 2.03 | 2.1 |
| N0010c | −17.85 | −163.8 | −0.6 | −129.8 | 144.4 | 2.97 | 2.9 |
| N0100c | −16.88 | 127.5 | −2.1 | −176.4 | −177.4 | 2.11 | 2.3 |
| N0110c | −15.67 | 128.2 | 4.3 | −80.8 | 143.6 | 1.38 | 1.7 |
| N011’0c | −14.7 | 130.7 | 8.3 | 133.4 | −141.9 | 2.80 | 2.4 |
| N1000c | −19.86 | −174.0 | 0.7 | −167.2 | 178.3 | 2.79 | 2.9 |
| N1010c | −18.63 | −159.0 | 0.0 | −128.3 | 143.1 | 3.34 | 3.1 |
| N1100c | −14.35 | 140.1 | 0.7 | 113.8 | −163.8 | 3.92 | 3.7 |
| N1110c | −11.87 | 134.6 | −5.4 | −94.3 | 138.8 | 7.66 | 8.1 |
| N111’0c | −11.76 | 141.2 | 9.5 | 109.1 | −147.5 | 4.86 | 4.94 |
| Compound a | optE kcal mol−1 | No. of t-Bu on sp3 Nitrogen | No. of t-Bu on sp3 Carbon | AddE kcal mol−1 | stE kcal mol−1 |
|---|---|---|---|---|---|
| N0000c | −333,801.441 | −333,801.441 | 0 | ||
| N0010c | −432,511.233 | 1 | −432,513.575 | 2.342 | |
| N0100c | −432,510.785 | 1 | −432,513.575 | 2.79 | |
| N0110c | −531,219.543 | 2 | −531,225.709 | 6.166 | |
| N011’0c | −531,220.53 | 2 | −531,225.709 | 5.179 | |
| N1000c | −432,509.352 | 1 | −432,510.572 | 1.22 | |
| N1010c | −531,218.91 | 1 | 1 | −531,222.706 | 3.796 |
| N1100c | −531,217.348 | 1 | 1 | −531,222.706 | 5.358 |
| N1110c | −629,924.792 | 1 | 2 | −629,934.84 | 10.048 |
| N111’0c | −629,924.4 | 1 | 2 | −629,934.84 | 10.44 |
| Compound a | optE kcal mol−1 | No. of t-Bu on sp3 Nitrogen | No. of t-Bu on sp3 Carbon | AddE kcal mol−1 | stE kcal mol−1 |
|---|---|---|---|---|---|
| N0000c | −333,819.556 | −333,819.556 | 0 | ||
| N0010c | −432,526.761 | 1 | −432,531.518 | 4.757 | |
| N0100c | −432,526.055 | 1 | −432,531.518 | 5.463 | |
| N0110c | −531,233.207 | 2 | −531,243.48 | 10.273 | |
| N011’0c | −531,232.806 | 2 | −531,243.48 | 10.674 | |
| N1000c | −432,525.775 | 1 | −432,527.202 | 1.427 | |
| N1010c | −531,232.932 | 1 | 1 | −531,239.164 | 6.232 |
| N1100c | −531,228.49 | 1 | 1 | −531,239.164 | 10.674 |
| N1110c | −629,934.673 | 1 | 2 | −629,951.126 | 16.453 |
| N111’0c | −629,934.711 | 1 | 2 | −629,951.126 | 16.415 |
| Compound | Anti120GP | Anti-120GP | Syn60GP | Syn-60GP | ΔGeff | ||||
|---|---|---|---|---|---|---|---|---|---|
| ΔE a | ΔG b | ΔE a | ΔG b | ΔE a | ΔG b | ΔE a | ΔG b | ||
| N0000 | 19.53 | 13.70 | 19.53 | 13.72 | 25.46 | 19.91 | 25.26 | 19.84 | 13.70 |
| N0010 | 24.22 | 18.34 | 19.34 | 11.93 | 25.22 | 17.86 | 27.99 | 20.23 | 11.93 |
| N0100 | 20.96 | 13.40 | 20.51 | 12.43 | 26.30 | 18.63 | 25.26 | 20.38 | 12.43 |
| N0110 | 25.64 | 18.72 | 19.76 | 12.34 | 23.98 | 17.63 | 28.18 | 22.10 | 12.34 |
| N011’0 | 19.99 | 12.91 | 24.92 | 17.54 | 27.33 | 19.06 | 29.92 | 22.79 | 12.91 |
| N1000 | 19.55 | 11.03 | 19.82 | 11.09 | ND c | ND | 25.09 | 19.31 | 11.03 |
| N1010 | 24.33 | 17.92 | 20.10 | 14.82 | 24.95 | 17.65 | 27.80 | 22.20 | 14.82 |
| N1100 | 21.54 | 12.90 | 20.59 | 13.14 | 26.61 | 19.13 | 25.40 | 17.49 | 12.90 |
| N1110 | 26.08 | 17.27 | 20.15 | 11.17 | 28.29 | 20.62 | 34.39 | 28.17 | 11.17 |
| N111’0 | 21.43 | 12.59 | 26.18 | 17.45 | 30.79 | 22.72 | 23.68 | 14.51 | 12.59 |
| Compound | Anti120WP | Anti-120WP | Syn60WP | Syn-60WP | ΔGeff | ||||
|---|---|---|---|---|---|---|---|---|---|
| ΔE a | ΔG b | ΔE a | ΔG b | ΔE a | ΔG b | ΔE a | ΔG b | ||
| N0000 | 19.18 | 13.82 | 19.18 | 13.74 | 24.29 | 20.07 | ND c | ND | 13.74 |
| N0010 | 25.40 | 20.48 | 19.03 | 13.67 | 29.42 | 23.23 | 24.23 | 20.47 | 13.67 |
| N0100 | 22.45 | 18.28 | 20.66 | 16.24 | 23.31 | 18.6 | 26.09 | 19.91 | 16.24 |
| N0110 | 25.13 | 21.06 | 19.32 | 13.46 | 22.23 | 19.06 | 20.47 | 16.61 | 13.46 |
| N011’0 | 26.44 | 20.83 | 26.55 | 20.67 | 23.39 | 18.55 | 26.51 | 21.71 | 18.55 |
| N1000 | 22.30 | 16.89 | 22.35 | 16.85 | ND | ND | 23.86 | 19.40 | 16.85 |
| N1010 | 26.60 | 20.05 | 19.00 | 12.72 | 29.60 | 23.96 | 24.29 | 19.71 | 12.72 |
| N1100 | 22.54 | 14.06 | 23.71 | 16.92 | 26.50 | 19.28 | 23.04 | 16.86 | 14.06 |
| N1110 | 29.46 | 21.96 | 24.53 | 19.22 | 29.24 | 24.21 | 30.37 | 23.98 | 19.22 |
| N111’0 | 23.15 | 14.50 | 27.71 | 21.34 | 26.65 | 19.74 | 23.78 | 17.50 | 14.50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakkar, B.S.; Svendsen, J.S.M.; Engh, R.A. Density Functional Studies on Secondary Amides: Role of Steric Factors in Cis/Trans Isomerization. Molecules 2018, 23, 2455. https://doi.org/10.3390/molecules23102455
Thakkar BS, Svendsen JSM, Engh RA. Density Functional Studies on Secondary Amides: Role of Steric Factors in Cis/Trans Isomerization. Molecules. 2018; 23(10):2455. https://doi.org/10.3390/molecules23102455
Chicago/Turabian StyleThakkar, Balmukund S., John Sigurd M. Svendsen, and Richard A. Engh. 2018. "Density Functional Studies on Secondary Amides: Role of Steric Factors in Cis/Trans Isomerization" Molecules 23, no. 10: 2455. https://doi.org/10.3390/molecules23102455
APA StyleThakkar, B. S., Svendsen, J. S. M., & Engh, R. A. (2018). Density Functional Studies on Secondary Amides: Role of Steric Factors in Cis/Trans Isomerization. Molecules, 23(10), 2455. https://doi.org/10.3390/molecules23102455