Free and Forced Convective Flow in Pleural Fluid with Effect of Injection between Different Permeable Regions
Abstract
1. Introduction
2. Formulation of the Problem
- An unsteady case concurrent laminar flow of pleural fluid, viscoelastic mucous gel and epithelial tissue are considered to be the porous medium.
- Boussinesq approximation is applied.
- Two porous regions have been taken to analyze the model of the flow.
- Free and forced convective effects of injection on pleural fluid with thermal radiation.
3. Calculation of the Problem
4. Results and Discussion
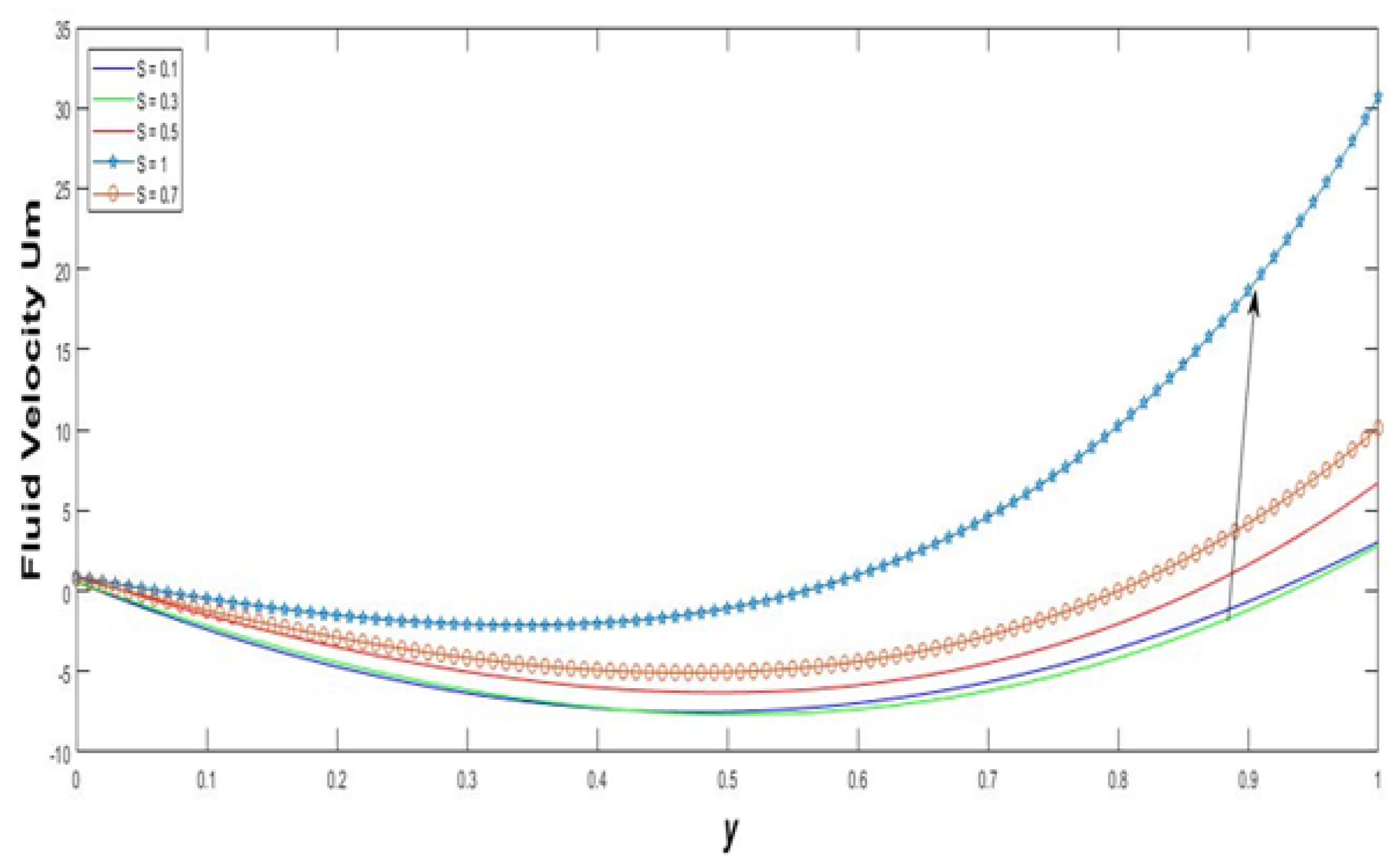
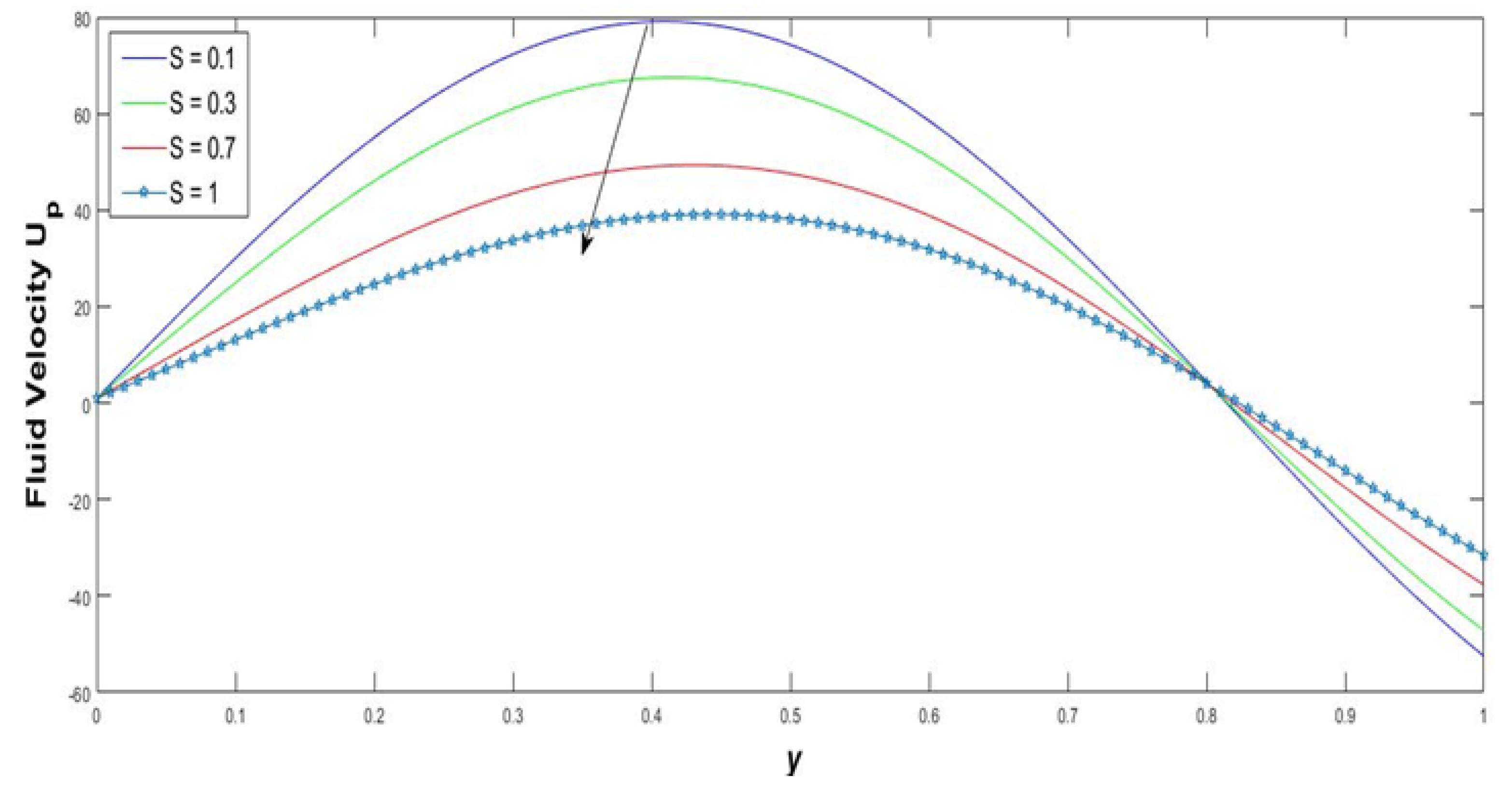
- Figure 2 shows that the velocity fields are increased with effect of increasing the injection parameter. An injected fluid particle does not spread completely, but to part of a human respiratory tract. The mucus layer has many tissues in the epithelial wall. Few of the coronavirus inflamed patients that deal with oxaliplatin intrathoracic injection were enrolled in the regular and observation group by Xiaoju Chen et al. [15]. This injection was successful in treating dangerous pleural radiation of cellular breakdown in the lungs.
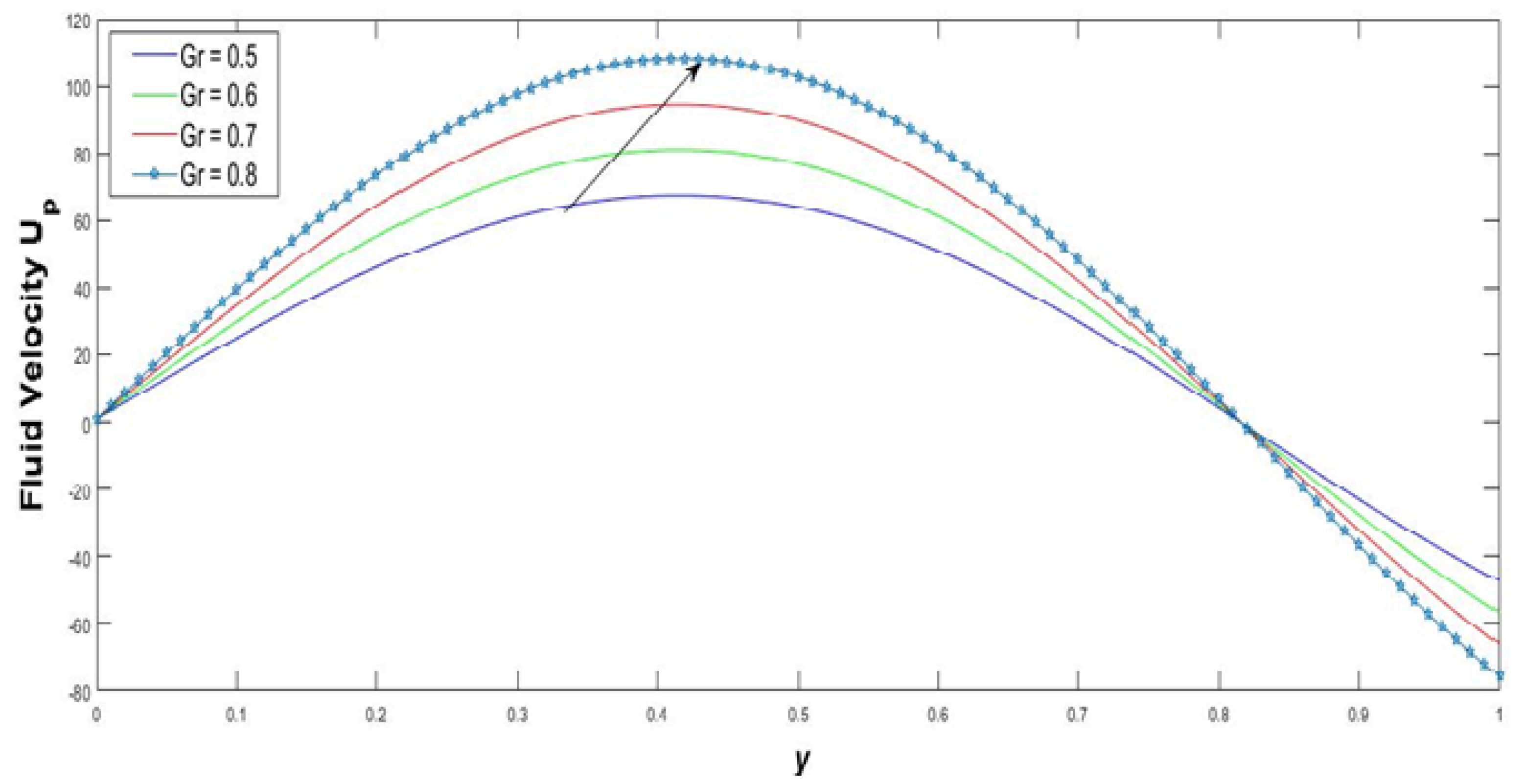
- Figure 3 represents the velocity of the fluid flow progressively that enhances the effect of increased Grashof numbers. Free convection leads to variation in the density continuously because of the temperature gradient. Normally, density will be reduced with increasing temperature. This type of dynamics occurred in the human respiratory tract due to buoyancy force. The velocity profiles are enhanced with increasing buoyancy force. This implies that increasing the buoyancy force enhances the heat in the human body.
- Viscoelasticity of mucus recuperates quickly and reversibly reinforces a lot of elastic and viscous properties in seconds. This fast recuperation is basic to mucociliary transport and lung fluid sheared by coughing from streaming lower to the alveoli by gravity. We observed from Figure 4 that the effect of Young’s modulus parameter ultimately increases the rate of velocity distribution is enhanced. The present model establishes elasticity of the fluid kept permeability parameter as . Elasticity of the mucous gel will be increased in the respiratory tract with increased COVID-19 transmission. It is also used to establish continuous material deformation under prominent enforced load. Pleural liquid assortment between the pleural leaves because of neighborhood/foundational illness of the pleura, lung or extra pulmonary organs. Regularly, 0.1 to 0.2 ml/kg of liquid is available in the pleural leaves to work with pleural development. The stage when the harmony between the creation and reabsorption of this liquid weakens is called pleural effusion.
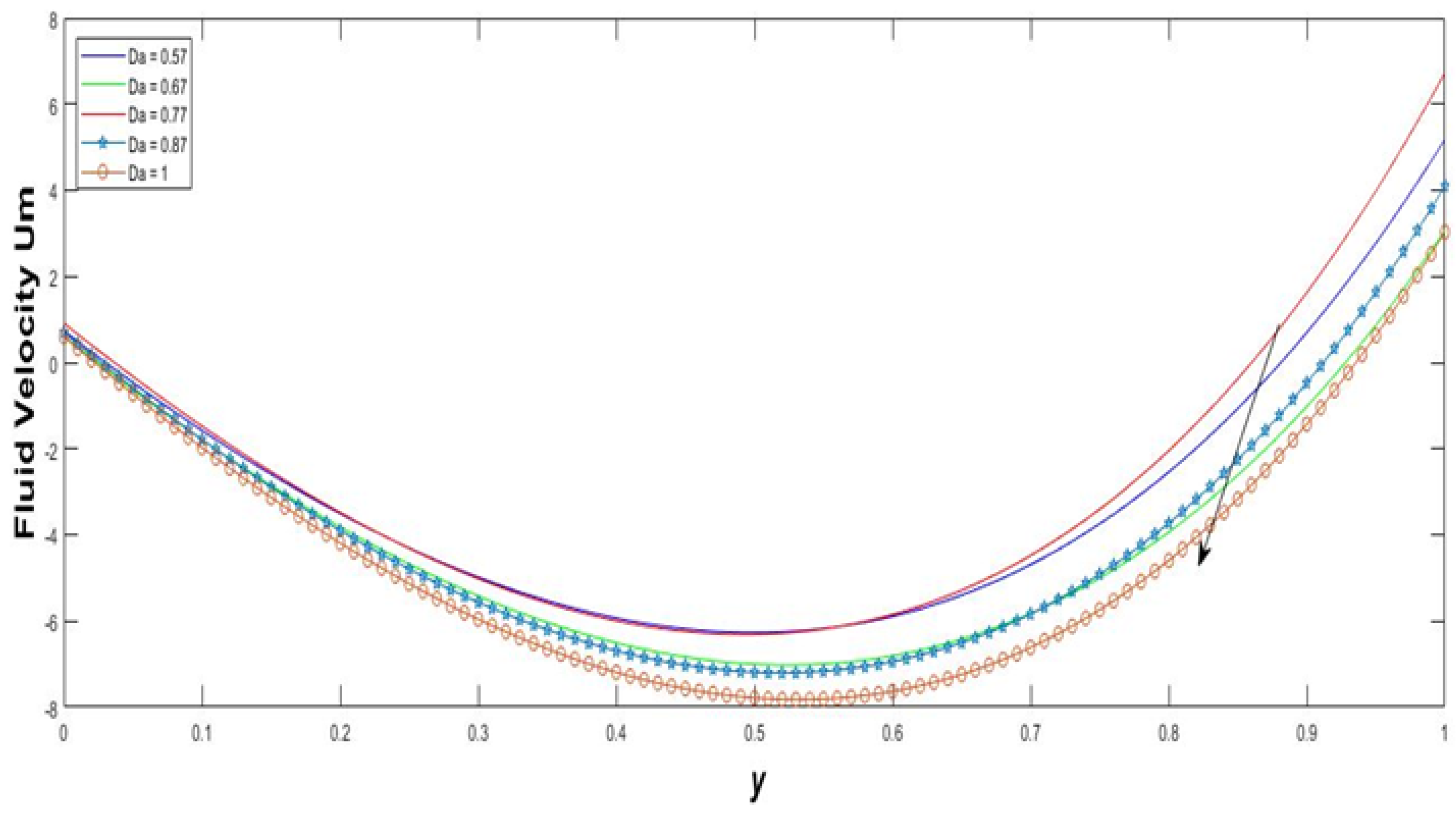
- Quantitatively, pore volume to the bulk volume proportion is called porosity. Inadequate porosity is correlated to pore space that contains the rectifiable pleural fluid in the lungs. Heat transportation of pleural fluid is controlled primarily by linked pores. Figure 5 demonstrates that the rate of velocity profile in the form of a graph is decreased with increasing porosity parameter.The range of lung pores lies between (0 to 1). It may fluctuate by time, and it can be evaluated through averaged time. Porosity of mucus gel phase is lower than in the pleural phase because of compaction by gravity. Porosity of 0.1 is viewed as typical for chaotic tissue material at the extent beneath the biomantle. Porosity in better material underneath the accumulating impact of pedogenesis can be anticipated to be near this amount.
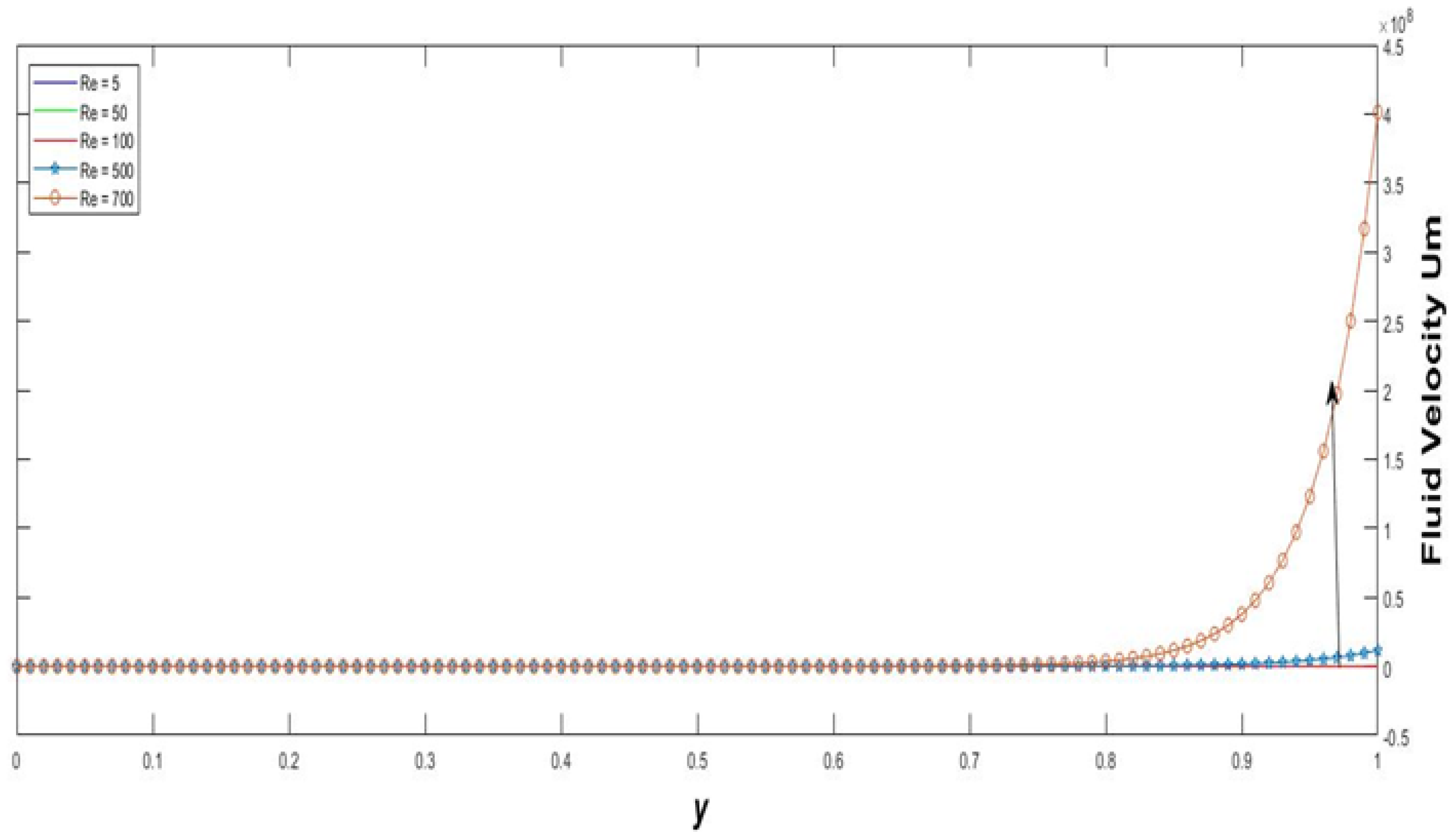
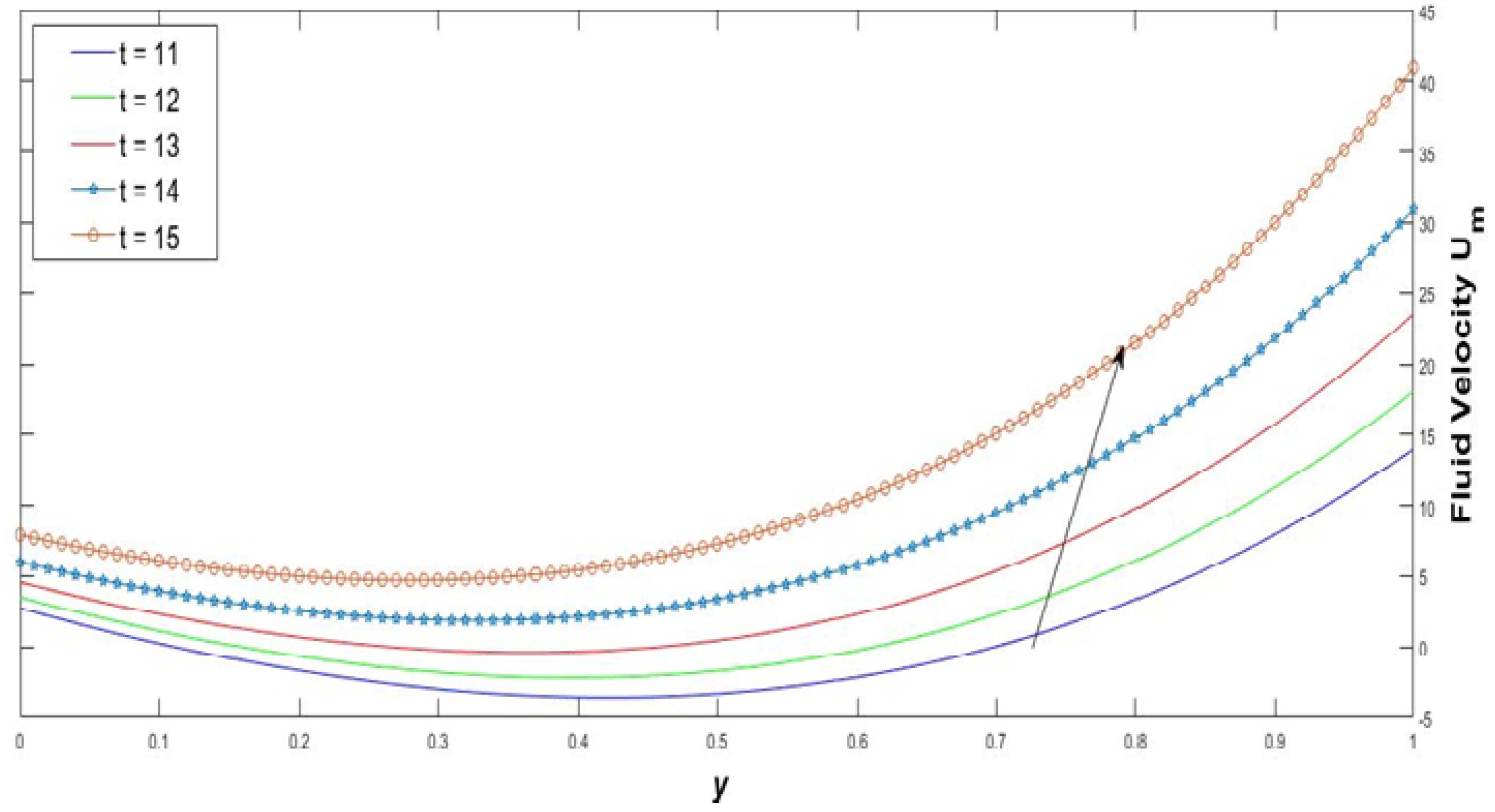
- The Reynolds number can be identified for various factors with relative motion of the fluid to a surface. The difference between the direction and the momentum of the viscous pleural fluid may be the reason for the turbulence and laminar flow. It is clear from Figure 6 that the mucous gel layer flow increased faster with increasing Reynolds number. goes towards the upward direction at a quick speed. Concurrently, goes towards the downward direction with a perfect unstable speed. The rate of fluid flow also varies with an increased range of time immediately. Laminar flow can happen only at a diminished Reynolds number parameter. While , which infers that turbulence devours more energy that empathizes with the laminar stream. This outcome is addressed schematically in Figure 7. The turbulent stream loses occasions more energy compared with the laminar stream. Pleural layer, being bi-inward, could change the neighborhood communications between the cells and the blood plasma with the goal that the stream will in general remain laminar. The frame of the lung upgrades the productivity of blood stream, as well as expanding the surface region for oxygen conveyance in the respiratory tract. According to Fitridge et al. [25], the liquid stream can arrive at its own consistent state in situations where the Reynolds number takes on values are lower than 1000. Moreover, with the basic Reynolds number, the stream field keeps on being undermined by the expanding arrangement at a wavy aspect. After diminishing the Reynolds number to 1200, the pleural layer vortices fluctuated.
- Due to some external force, pressure may be retained and lead to variation, and it can be used to alter two indeterminant energies, namely kinetic and potential. Furthermore, this is called the “first law of thermodynamics”. When the pressure difference is less than 1 velocity, the fluid is increased. When the pressure difference is , decreasing velocity profiles are initiated. The pressure gradient during pleural effusion varies from 7 mm Hg to 14 mm Hg and the variation in air passage interstitial pressure between the two lungs in any given creature shifted from −8 mm Hg to −5 mm Hg.
- Figure 17 represents the variation of different values of the radiation parameter on the non-dimensional velocity distributions. It is noted that increasing leads to a decrease in the flow velocity when it is more than 1. We also observed from the same Figure moving towards increased the velocity of the fluid at the epithelial tissue surface enhance due to diffusivity of the momentum over the radiation effect of the fluid.
- The Prandtl number increases as well as thickness of thermal boundary layer decreases.
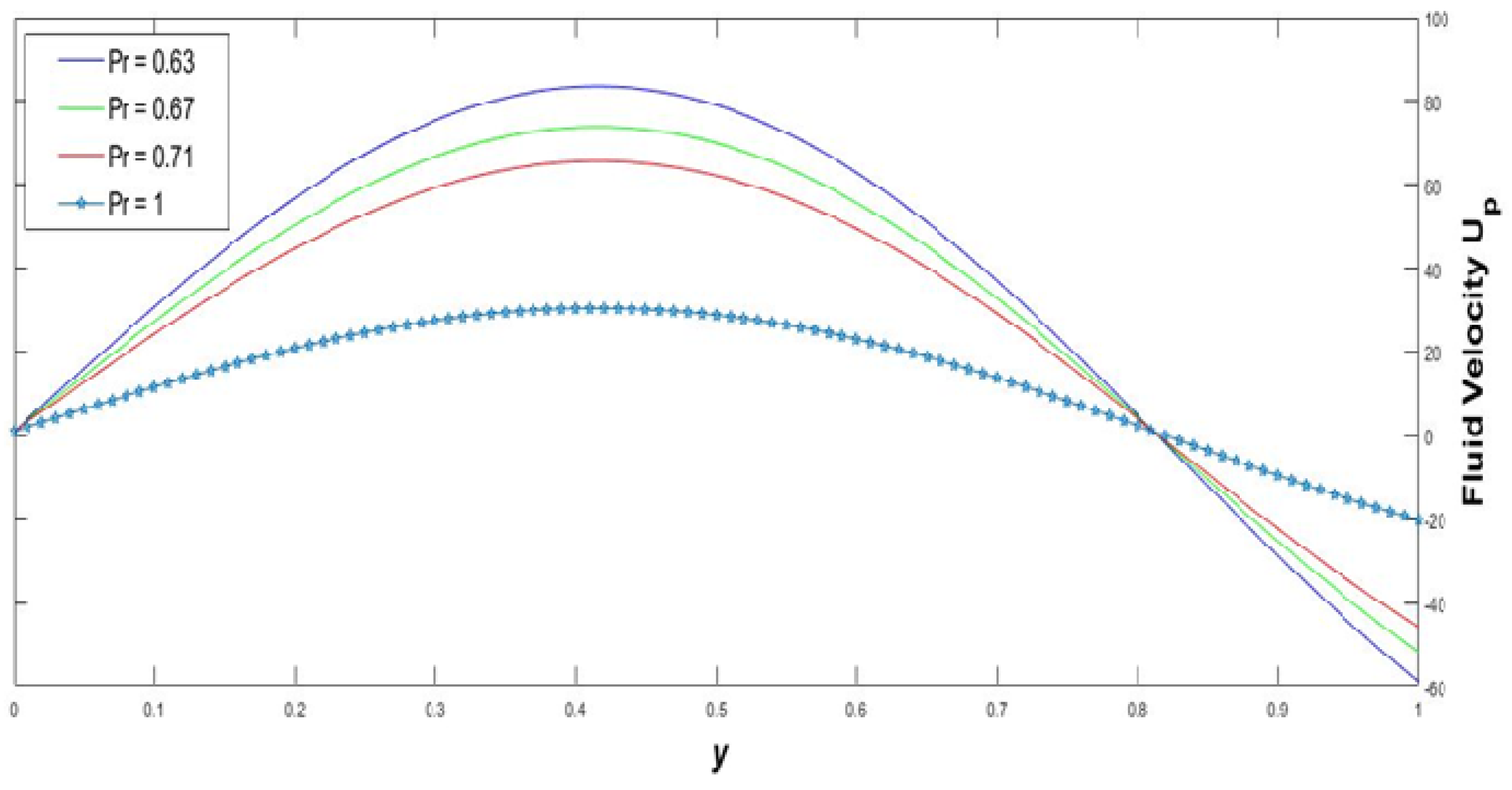
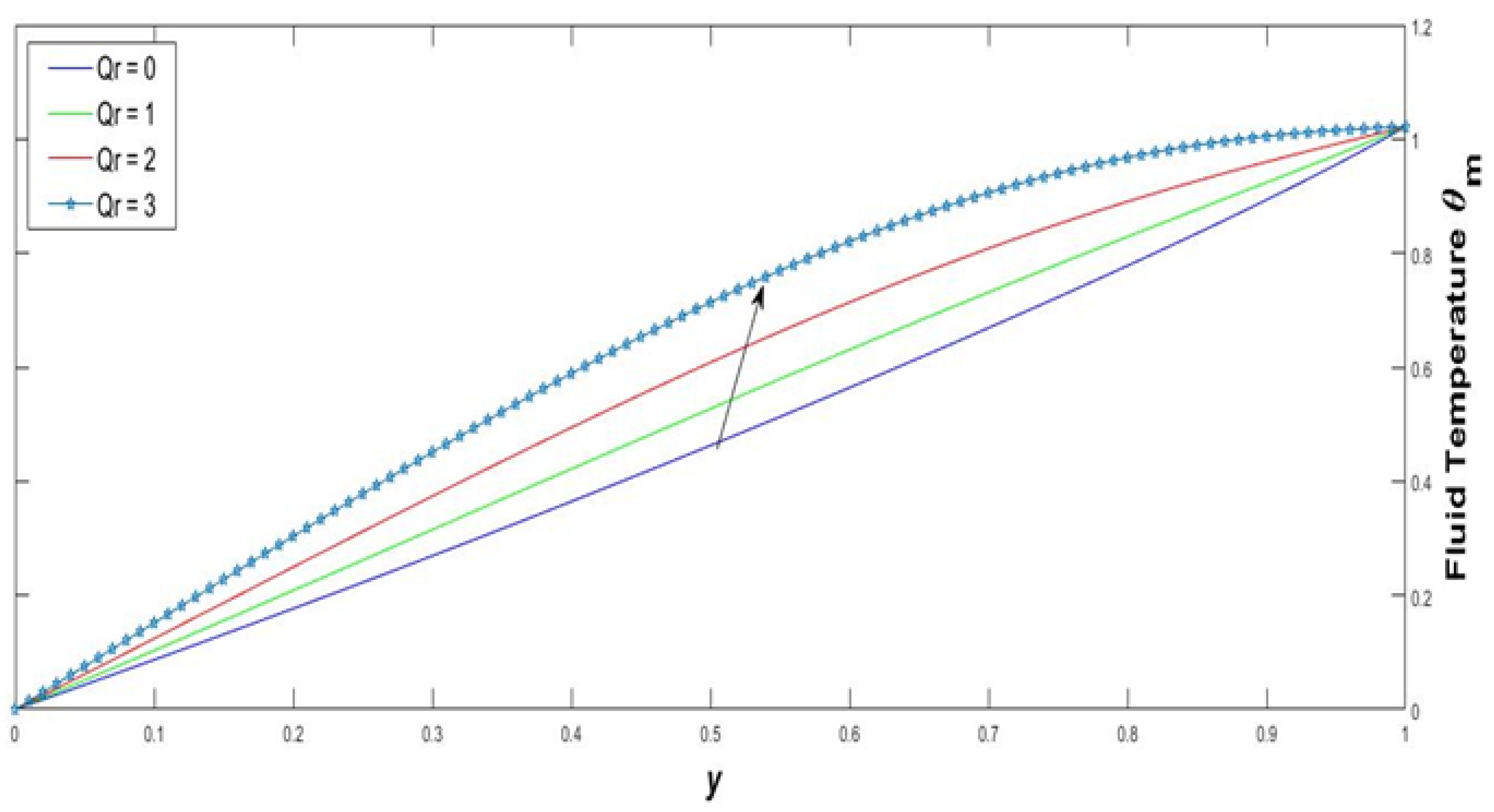
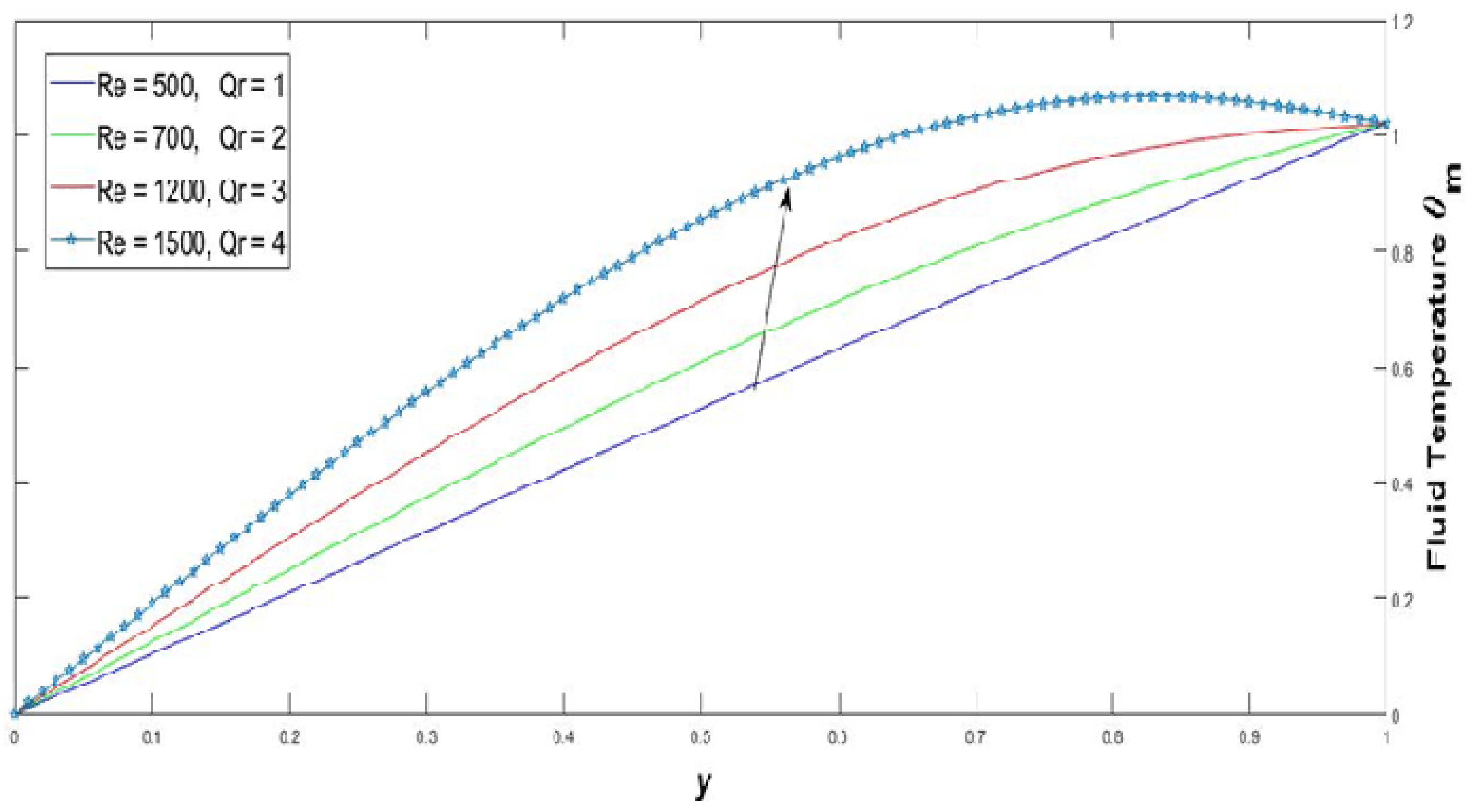
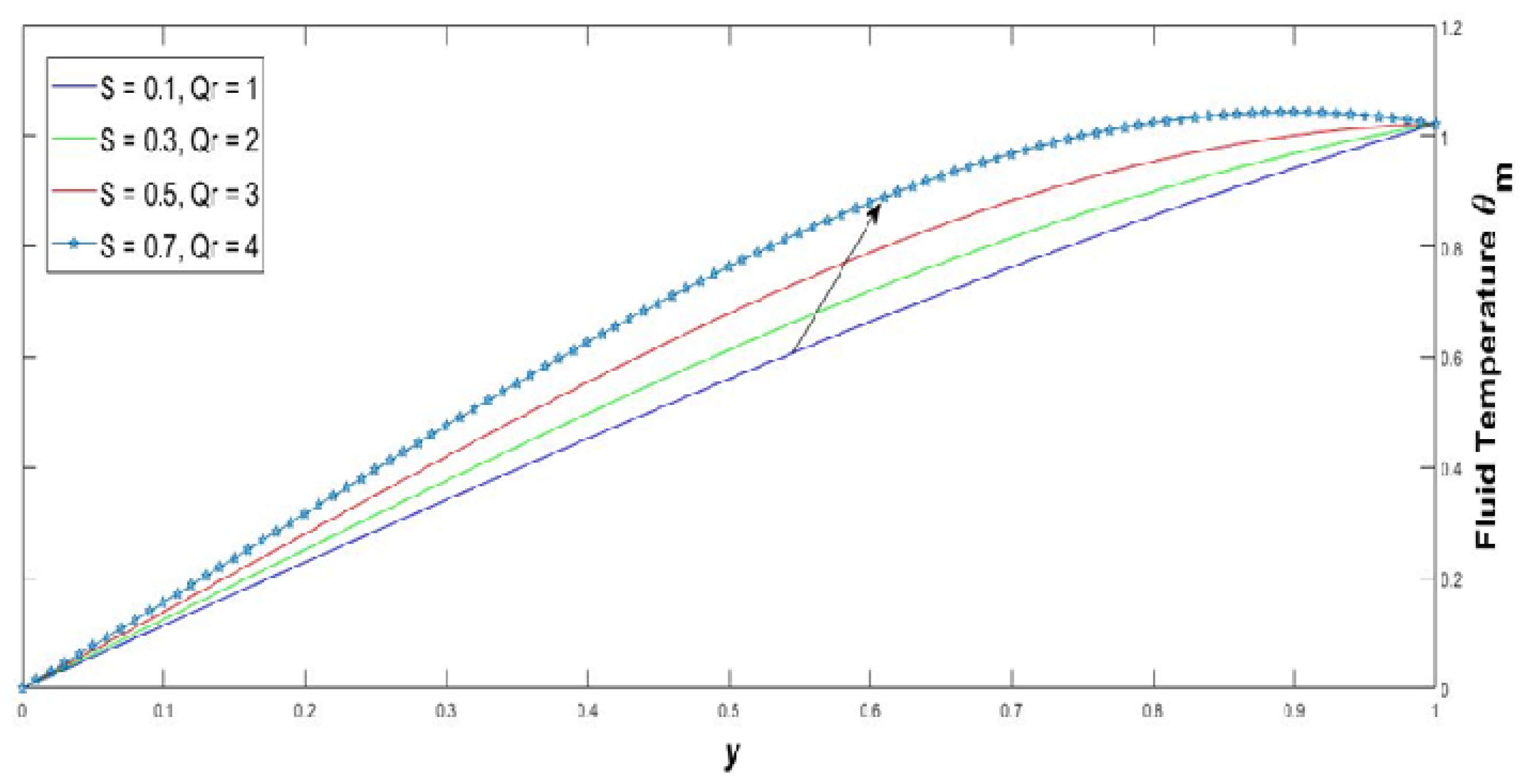
- The heat transfer process was enriched when both convection and conduction modes only appeared in the fluid. The ratio between the kinematic viscosity and thermal diffusivity express the dimensionless Prandtl number. A high Prandtl number shows a lack in the convection process. Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 show that the temperature profile of the Pleural fluid is elevated with rising Radiation parameter, Prandtl number, Re, and injection parameter. Furthermore, it is diminished with low Prandtl number. Address the stream structure for the instance of a Prandtl number equivalent to Pr = 0.7(air). In the two layers, similar Prandtl numbers act correspondingly. The temperature of the fluid increased because of the presence of coronavirus airborne transmission in human lungs.
- Figure 23 initially represents the effect of temperature profile enhancement with an increasing Reynolds number parameter dynamic divergence out from a significant point.
- Figure 24 shows that various increasing dimensionless injection parameters remain vigorously increased in the temperature profiles. In the case of fluid being injected through the lung wall, the velocity gradient increases gradually at the lung wall. The temperature gradient is also evaluated by increased injection/suction parameter strictly restricted to 1.
- Figure 25 shows that the influence of heat energy is transferred through the respiratory tract. It may be because temperature fields are boosted with an increasing heat absorption parameter. Convective heat transfer coefficient performs a vital role in the free convection and forced convection inside the human lungs regarding the impact of COVID-19. Tragically, the laboratory discoveries of pleural effusion were not accessible. In spite of, this review concentrated on the clinical elements of COVID-19 convoluted with pleural effusion, and we trust that our outcomes could assist clinicians to better assess and oversee COVID-19 patients with PE.
5. Conclusions
- The momentum of the fluid flow progressively enhances the reaction of increased Grashof numbers.
- The velocity fields are increased with the effect of increasing the injection parameter.
- The effect of increasing Young’s modulus parameter ultimately increased the rate of velocity distributions.
- The rate of the velocity field in the form of a graph is decreased with increasing porosity parameter and Prandtl number.
- The effect of velocity distribution is increased quickly with increasing Reynolds number.
- Velocity of the fluid is increased while the pressure differences were less than 1. Velocity fields are decreased at pressure differences much greater than 1.
- Temperature field of the mucous gel is enhanced with growing Prandtl numbers. Thickness of the thermal boundary layer decreased when the Prandtl number increased.
- Temperature fields are increased with increases in parameters.
- The temperature fields fixed state while increasing dimensionless radiation parameter.
- The velocity distributions are decreased passionately as various dimensionless numbers are increasing.
- The momentum of the pleural fluid layer increases with corresponding non-dimensional parameters , and the time radiant increases.
- Thermal heat transfer is boosted when the fluid particle of the Prandtl number is enlarged.
- Increased injection parameter increases in the temperature fields.
- Increasing Reynolds number parameter with a dynamic divergence out from a significant point.
- Temperature gradient increases gradually at the lung wall with an increasing heat absorption parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| x | Cartesian co-ordinate along the surface |
| y | Cartesian co-ordinate perpendicular the surface |
| u | velocity component u along x ditections |
| v | velocity component v along y ditections |
| g | acceleration due to gravity |
| p | pressure of the mucous gel and pleural fliud |
| density of the fluid | |
| kinematic viscosity of the fluid | |
| permeability of the porous medium | |
| Young’s modulus of the fluid (elasticity) | |
| coefficient of thermal expansion | |
| T | Temperature of the fluid |
| constant temperature | |
| increased temperature | |
| J | Heat source |
| Specific heat of constant pressure | |
| Thermal conductivity | |
| Porosity of the fluid | |
| Q | coefficient of dimensional heat absorbtion |
| C | species concentration of the fliud |
| constant concentration | |
| Raised concentration | |
| S | Injection parameter |
| Reynold’s number | |
| Grashof number | |
| Prandtl number | |
| Radiative heat flux | |
| Stefan-Boltzmann constant | |
| Mean absorption coefficient | |
| Radiation parameter |
Appendix A
References
- Incekara, F.O.; Tikici, D.K.; Nomenoglu, H. Pleural Effusions. Insights Chest. Dis. 2018, 3, 1. [Google Scholar] [CrossRef]
- Shaheen, S.; Maqbool, K.; Gul, F.; Sohail, A. Effect of Chemical Reaction Furthermore, Thermal Radiation on Axisymmetric MHD Flow of Jeffrey Nanofluid Through A Ciliated Channel Filled With Porous Medium. Biomed. Eng. Appl. Basis Commun. 2021, 33, 2150025. [Google Scholar] [CrossRef]
- Jha, B.K.; Isah, B.Y.; Uwanta, I.J. Combined effect of suction/injection on MHD free-convection flow in a vertical channel with thermal radiation. Ain Shams Eng. J. 2018, 9, 1069–1088. [Google Scholar] [CrossRef]
- Satpathi, D.K.; Ramu, A. A Laminar Flow Model for Mucous Gel Transport in a Cough Machine Simulating Trachea: Effect of Surfactant as a Sol Phase Layer. Open J. Appl. Sci. 2013, 3, 312–317. [Google Scholar] [CrossRef][Green Version]
- Uwanta, I.J.; Hamza, M.M. Effect of Suction/Injection on Unsteady Hydromagnetic Convective Flow of Reactive Viscous Fluid between Vertical Porous Plates with Thermal Diffusion. Int. Sch. Res. Not. 2014, 2014, 980270. [Google Scholar] [CrossRef]
- Ratchagar, N.P.; Hemalatha, S.V. Study of Oil Spill on the Sea Surface in the Presence of Thermal and Concentration Buoyancy Effects. Int. J. Math. Model. Comput. 2013, 3, 157–168. [Google Scholar]
- Govindarajan, A.; Vijayalakshmi, R.; Ramamurthy, V. Combined effects of heat and mass transfer to magnetohydrodynamics oscillatory dusty fluid flow in a porous channel. J. Phys. Conf. Ser. 2018, 1000, 012003. [Google Scholar] [CrossRef]
- Miserocchi, G. Mechanisms controlling the volume of pleural fluid and extravascular lung water. Eur. Respir. Rev. 2009, 18, 244–252. [Google Scholar] [CrossRef]
- Ishak, A.; Merkin, J.H.; Nazar, R.; Pop, I. Mixed convection boundary layer flow over a permeable vertical surface with prescribed wall heat flux. ZAMP: Z. Fur Angew. Math. Und Phys. 2008, 59, 100–123. [Google Scholar] [CrossRef]
- Jena, S.K.; Mathur, M.N. Free convection in the laminar boundary layer flow of a thermo micropolar fluid past a vertical flat plate with suction/injection. Acta Mech. 1982, 42, 227–238. [Google Scholar] [CrossRef]
- Mansour, M.A.; El-Shaer, N.A. Radiation effect on magnetohydrodynamic natural convection flows saturated in porous media. J. Magn. Magn. Mater. 2001, 237, 325–341. [Google Scholar] [CrossRef]
- Pal, D.; Talukdar, B. Perturbation technique for unsteady MHD mixed convection periodic flow, heat and mass transfer in micropolar fluid with chemical reaction in the presence of thermal radiation. Cent. Eur. J. Phys. 2012, 10, 1150–1167. [Google Scholar] [CrossRef]
- Jakhmola Mani, R.; Sehgal, N.; Dogra, N.; Saxena, S.; Pande Katare, D. Deciphering underlying mechanism of Sars-CoV-2 infection in humans and revealing the therapeutic potential of bioactive constituents from Nigella sativa to combat COVID19: In-silico study. J. Biomol. Struct. Dyn. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Zhang, X. The effect of pleural fluid layers on lung surface wave speed measurement:Experimental and numerical studies on a sponge lung phantom. J. Mech. Behav. Biomed. Mater. 2019, 89, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lu, J.; Yao, Y.; Huang, Z.; Liu, K.; Jiang, W.; Li, C. Effects of bevacizumab combined with oxaliplatin intrathoracic injection on tumor markers and survival rate in patients with malignant pleural effusion of lung cancer. Am. J. Transl. Res. 2021, 13, 2899–2906. [Google Scholar] [PubMed]
- Li, J.; Yao, H.; Lei, Y.; Ye, Y. Establishment of a human intrapleural hyperthermic perfusion model and analysis of pleural malignancy treatment depth. Respir. Med. 2018, 138, 144–149. [Google Scholar] [CrossRef]
- Lazzari, G.; Silvano, G. ARDS in radiation induced lung injury and COVID-19 pneumonia: Two different sides of the same coin. A case series comparison. J. Cancer Prev. Curr. Res. 2020, 11, 121–124. [Google Scholar] [CrossRef]
- DeGroot, C.T.; Straatman, A.G. Towards a Porous Media Model of the Human Lung. AIP Conf. Proc. 2012, 1453, 69–74. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Mixed convection boundary layer flow over a permeable vertical flat plate embedded in an anisotropic porous medium. Hindawi Publ. Corp. Math. Probl. Eng. 2010, 2010, 659023. [Google Scholar] [CrossRef]
- Islam, M.S.; Larpruenrudee, P.; Saha, S.C.; Pourmehran, O.; Paul, A.R.; Gemci, T.; Collins, R.; Paul, G.; Gu, Y. How severe acute respiratory syndrome coronavirus-2 aerosol propagates through the age-specific upper airways. Phys. Fluids 2021, 33, 081911. [Google Scholar] [CrossRef] [PubMed]
- Cahill, R.A.; Dalli, J.; Khan, M.; Flood, M.; Nolan, K. Solving the problems of gas leakage at laparoscopy. Br. J. Surg. 2020, 107, 1401–1405. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Liu, M.; Zhang, C.; Yan, H.; Zhang, M.; Wu, Q.; Liu, M.; Jiang, L. Bio-inspired drag reduction: From nature organisms to artificial functional surfaces. Giant 2020, 2, 100017. [Google Scholar] [CrossRef]
- Rose, J.B.R.; Natarajan, S.G.; Gopinathan, V.T. Biomimetic flow control techniques for aerospace applications: A comprehensive review. Rev. Environ. Sci. Biotechnol. 2021, 20, 645–677. [Google Scholar] [CrossRef]
- Padmavathi, T.; Senthamilselvi, S. Effect of Hartmann number on Natural Convection of Pleural Effusion. Turk. J. Comput. Math. Educ. 2021, 12, 5672–5681. [Google Scholar]
- Fitridge, R.; Thompson, M. Mechanisms of Vascular Disease: A Reference Book for Vascular Specialists; University of Adelaide Press: Adelaide, Australia, 2011. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiyagarajan, P.; Sathiamoorthy, S.; Santra, S.S.; Ali, R.; Govindan, V.; Noeiaghdam, S.; Nieto, J.J. Free and Forced Convective Flow in Pleural Fluid with Effect of Injection between Different Permeable Regions. Coatings 2021, 11, 1313. https://doi.org/10.3390/coatings11111313
Thiyagarajan P, Sathiamoorthy S, Santra SS, Ali R, Govindan V, Noeiaghdam S, Nieto JJ. Free and Forced Convective Flow in Pleural Fluid with Effect of Injection between Different Permeable Regions. Coatings. 2021; 11(11):1313. https://doi.org/10.3390/coatings11111313
Chicago/Turabian StyleThiyagarajan, Padmavathi, Senthamilselvi Sathiamoorthy, Shyam Sundar Santra, Rifaqat Ali, Vediyappan Govindan, Samad Noeiaghdam, and Juan J. Nieto. 2021. "Free and Forced Convective Flow in Pleural Fluid with Effect of Injection between Different Permeable Regions" Coatings 11, no. 11: 1313. https://doi.org/10.3390/coatings11111313
APA StyleThiyagarajan, P., Sathiamoorthy, S., Santra, S. S., Ali, R., Govindan, V., Noeiaghdam, S., & Nieto, J. J. (2021). Free and Forced Convective Flow in Pleural Fluid with Effect of Injection between Different Permeable Regions. Coatings, 11(11), 1313. https://doi.org/10.3390/coatings11111313









