On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations
Abstract
:1. Introduction
2. The Extended Hyperbolic Function Method
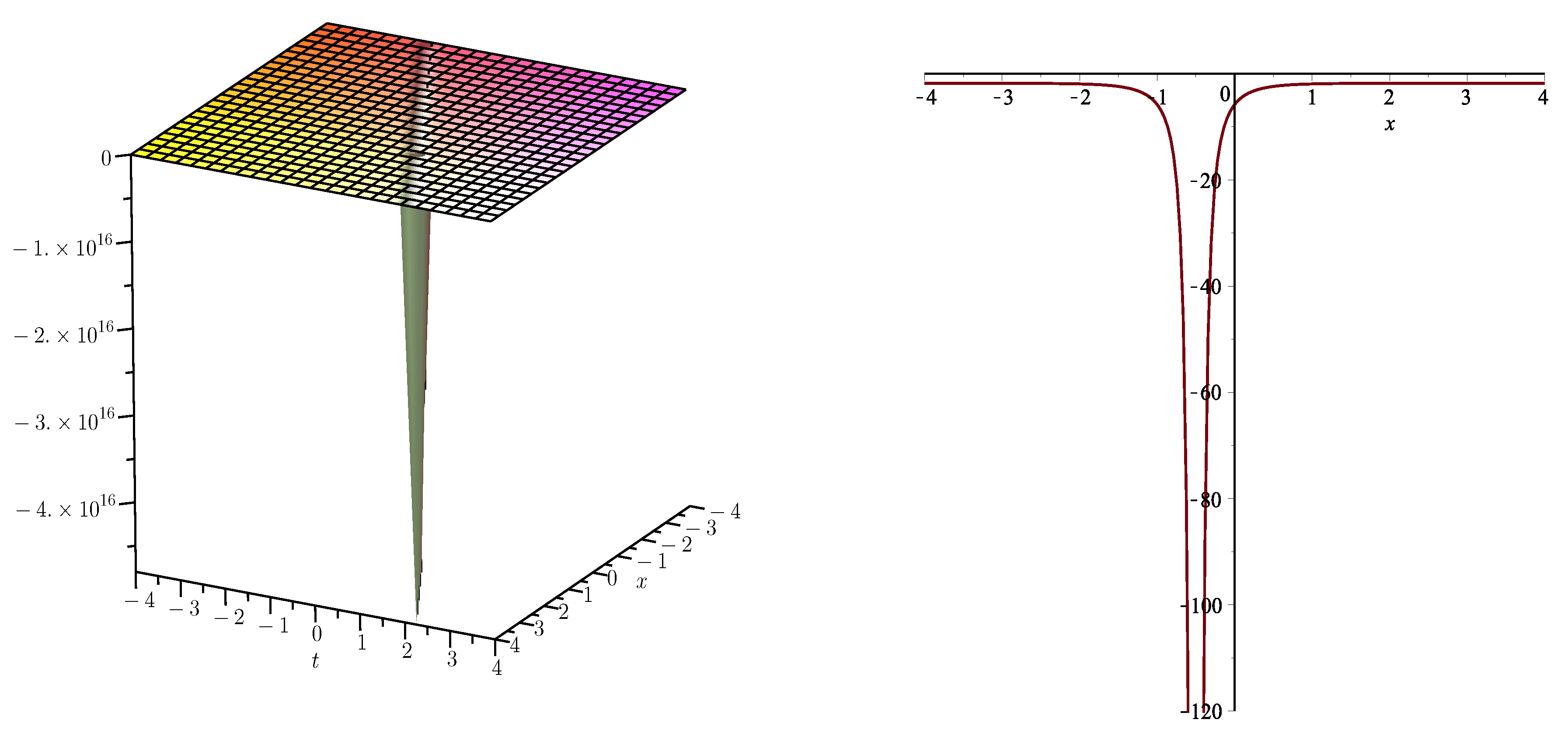
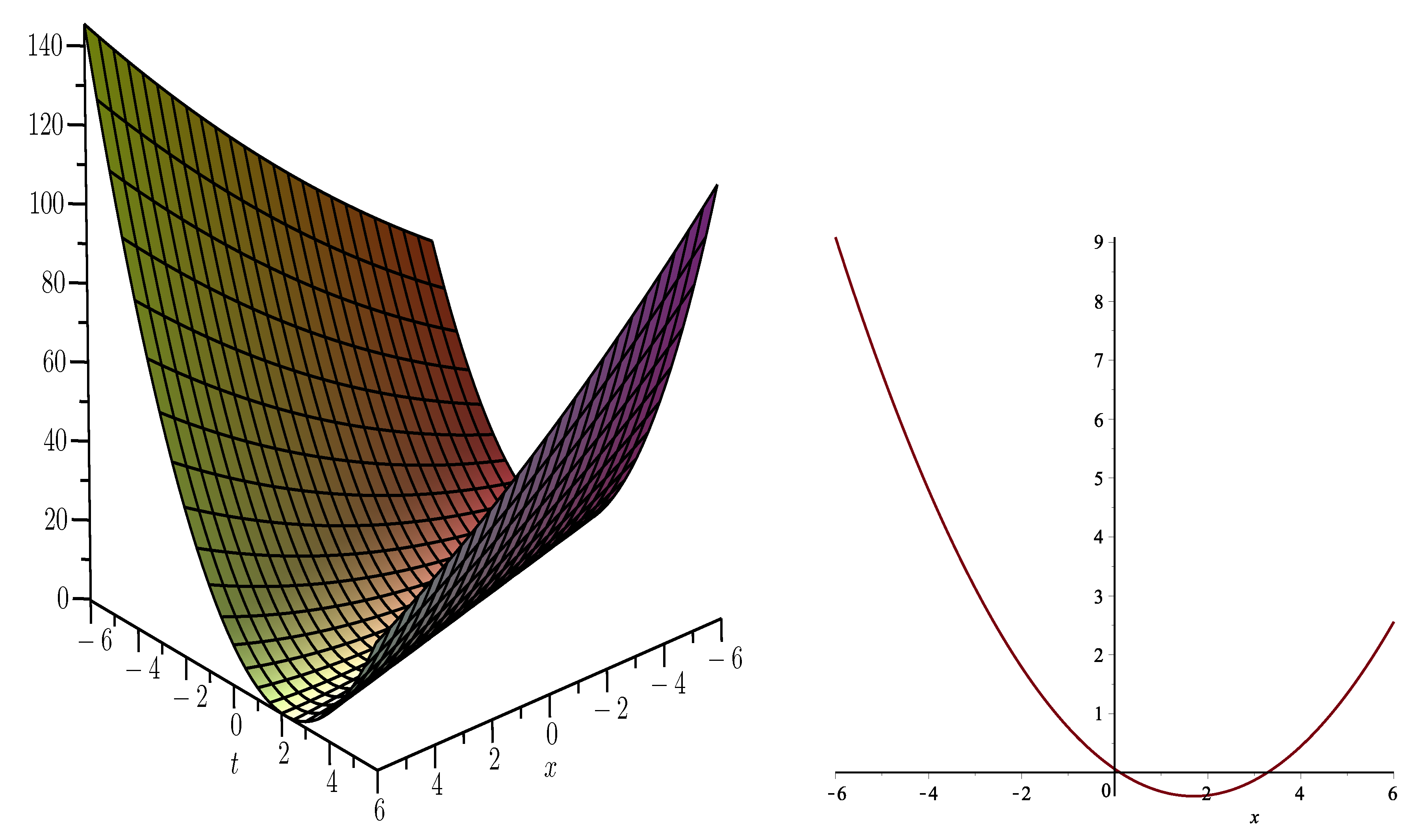
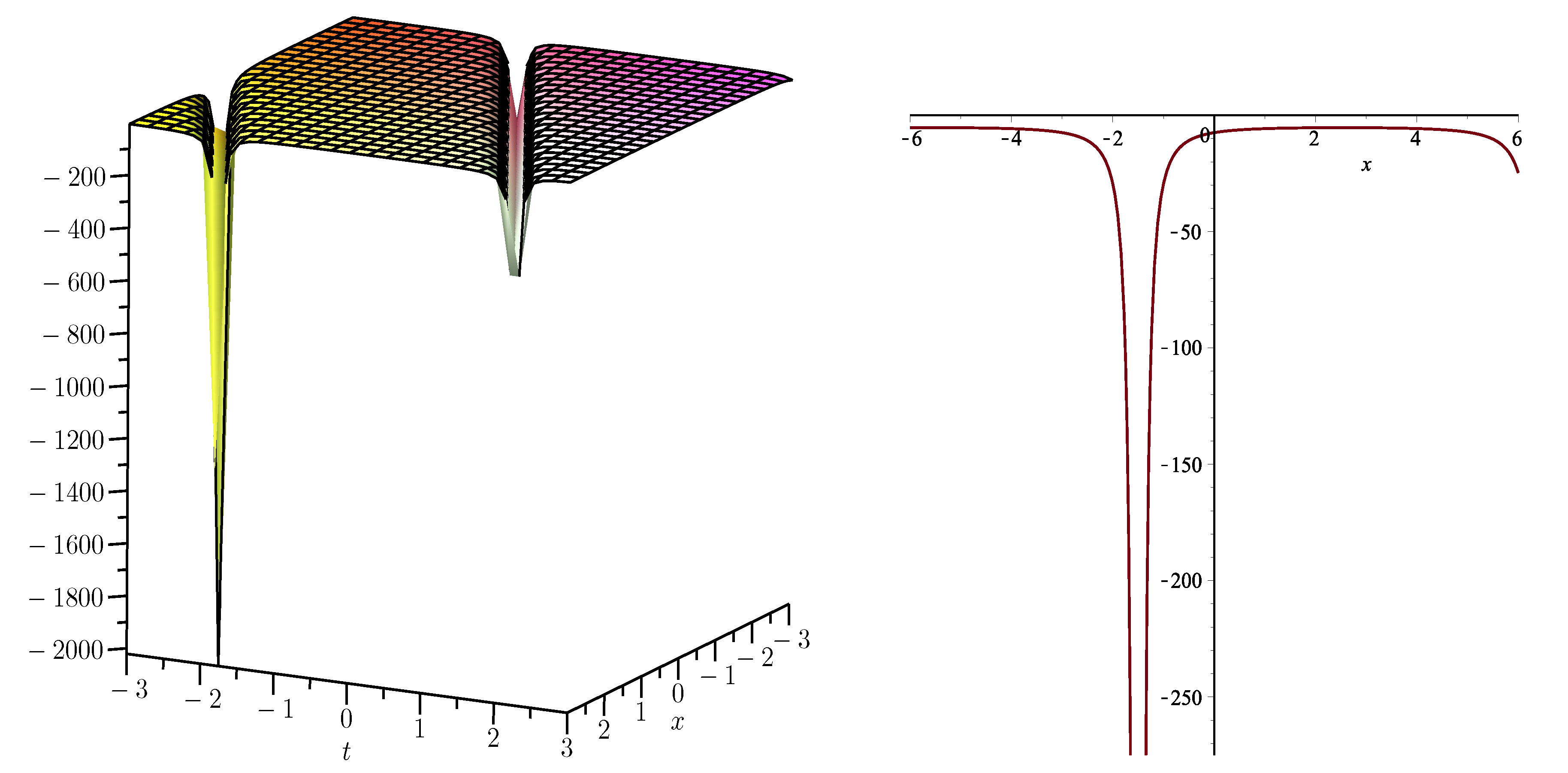
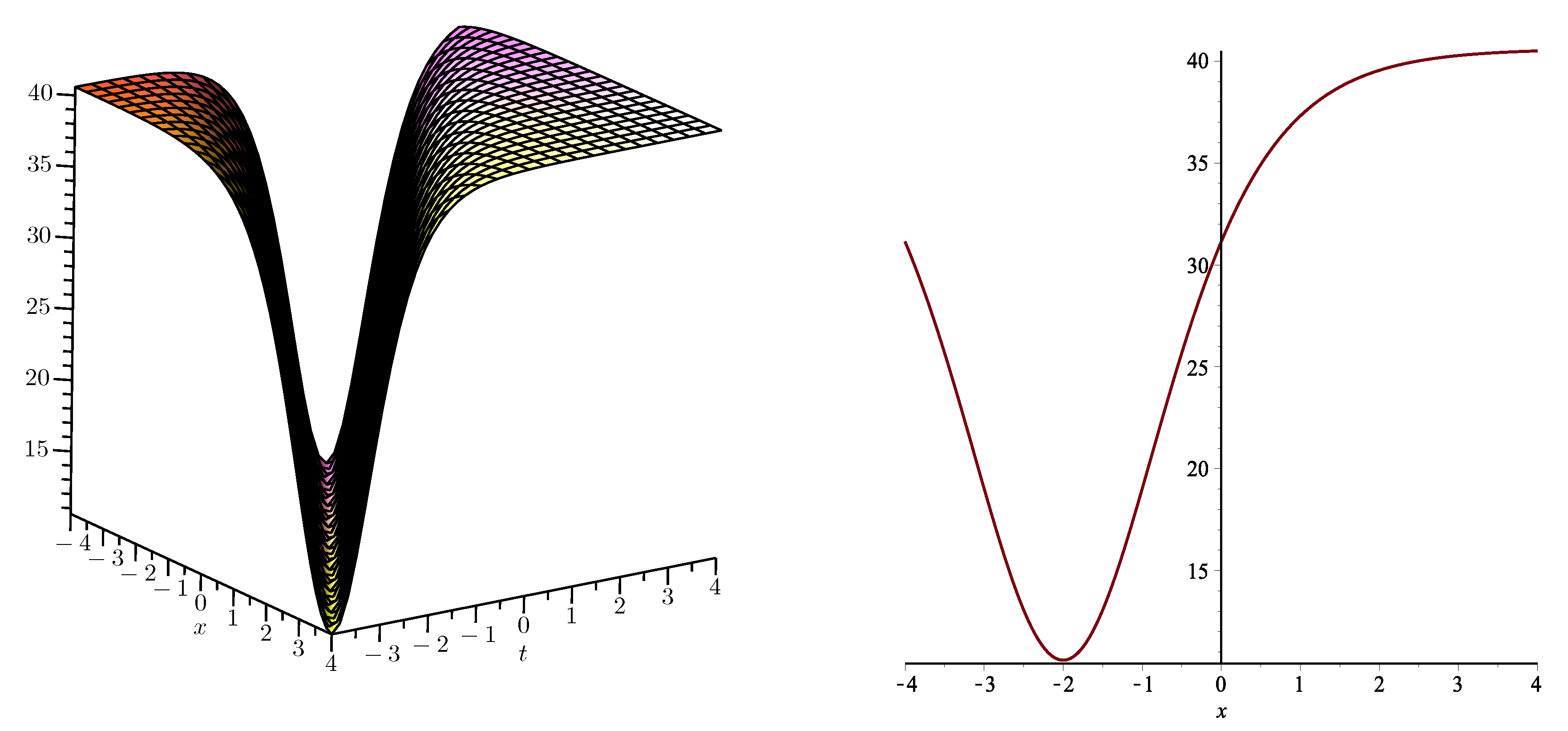
3. Solutions to the Perturbed Boussinesq Equation
4. Solutions to the KdV–CDG Equation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A. An investigation of abundant traveling wave solution of complex nonlinear evolution equation. Cogent Math. 2016, 3, 1277506. [Google Scholar] [CrossRef]
- Yong, H.; Yadong, S.; Wenjum, Y. Symbolic Computation and the Extended Hyperbolic Function Method for Constructing Exact Traveling Solution of Nonlinear PDEs. J. Appl. Math. 2012, 1, 716719. [Google Scholar] [CrossRef]
- Islam, W.; Rehman, H.U.; Younis, M. Weakly Nonlocal Single and Combined Solitons in Nonlinear Optics with Cubic quintic Nonlinearities. Nanoelectron. Optoelectron. 2017, 12, 1008–1012. [Google Scholar] [CrossRef]
- Rehman, H.U.; Saleem, M.S.; Zubair, M.; Jafar, S.; Latif, I. Optical solitons with Biswas-Arshed model using mapping method. Optik 2019, 194, 163091. [Google Scholar] [CrossRef]
- Rehman, H.U.; Jafar, S.; Javed, A.; Hussain, S.; Tahir, M. New optical solitons of Biswas-Arshed equation using different techniques. Optik 2020, 206, 163670. [Google Scholar] [CrossRef]
- Younis, M.; Rehman, H.U.; Rizvi, S.T.; Mahmood, S.A. Dark and singular optical solitons perturbation with fractional temporal evolution. Superlattices Microstruct. 2017, 104, 525–531. [Google Scholar] [CrossRef]
- Younis, M.; Rehman, H.U.; Iftikhar, M. Traveling wave solutions to some time-space nonlinear evolution equations. Appl. Math. Comput. 2014, 249, 81–88. [Google Scholar]
- Ullah, N.; Rehman, H.U.; Imran, M.A.; Jawad, T.A. Highly dispersive optical solitons with cubic law and cubic-quintic-septic law nonlinerity. Results Phys. 2020, 17, 103021. [Google Scholar] [CrossRef]
- Fu, T.Z.; Liu, S.K.; Shi-Da, L. A new approach to solve nonlinear wave equations. Commun. Theor. Phys. 2003, 39, 27–30. [Google Scholar]
- Liu, S.K.; Fu, Z.T.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Yan, Y.Z. Abundant families of Jacobi elliptic function solution of the (2+1)-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Fan, E.G. Extended tanh-function method and its application to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Parkes, E.J.; Duffy, B.R. An automated tanh-function method for finding solitory wave solutions to nonlinear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Yan, Y.Z. New explicit traveling wave solutions for two new integrable coupled nonlinear evolution equation. Phys. Lett. A 2001, 292, 100–106. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M. Exp-function method for Duffing equation and new solutions of (2+1)-dimensional dispersive long wave equations. Program Appl. Math. 2011, 1, 30–42. [Google Scholar]
- He, H.J.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z. Extended F-expansion method and periodic wave solutions for generalized Zakharov equations. Phys. Lett. A 2005, 343, 48–54. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z. Applications at F-expansion to periodic wave solutions for a new Hamiltonian amplitude equation. Chaos Solitons Fractals 2005, 24, 1257–1268. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. Various exact solutions of nonlinear Schrodinger equation with two nonlinear terms. Chaos Solitons Fractals 2007, 31, 594–601. [Google Scholar] [CrossRef]
- Wang, M.L.; Zhou, Y.B. The periodic wave solutions for the Klein-Gordon-Schrodinger equations. Phys. Lett. A 2003, 318, 84–92. [Google Scholar] [CrossRef]
- Zhou, B.Y.; Wang, M.L.; Mian, T.D. The periodic wave solutions for a class of nonlinear partial differential equations. Phys. Lett. A 2004, 323, 77–88. [Google Scholar] [CrossRef]
- Seadawy, A.R. Modulation instability analysis for the generalized derivative higher order nonlinear Schrodinger equation and its the bright and dark soliton solutions. J. Electromagn. Waves Appl. 2017, 31, 1353–1362. [Google Scholar] [CrossRef]
- Guo, Y.; Lai, S. New exact solutions for an (N+1)-dimensional generalized Boussinesq equation. Nonlinear Anal. Theory Method Appl. 2010, 72, 2863–2873. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y. On Weierstrass elliptic function solutions for a (N+1)-dimensional potential KdV equation. Appl. Math. Comput. 2011, 217, 8080–8092. [Google Scholar] [CrossRef]
- Wang, M.L. Solitary wave solutions for variant Boussinesq equations. Phys. Lett. A 1995, 199, 169–172. [Google Scholar] [CrossRef]
- Wang, M.L. Exact solutions for a compound KdV-Burgers equation. Phys. Lett. A 1996, 213, 279–287. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Zayed, E.M.E. Abundant exact traveling wave solutions of generalized bretherton equation via improved (G′/G)-expansion method. Commun. Theor. Phys. 2012, 57, 173–178. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion and traveling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Petkovir, A.J.J.M.D.; Biswas, A. Modified simple equation for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 869–877. [Google Scholar]
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys. Lett. A 1990, 147, 287–291. [Google Scholar] [CrossRef]
- Zhang, Z. New exact solution to be generalized nonlinear Schrodinger equation. Fizika A 2008, 17, 125–134. [Google Scholar]
- Khater, A.H.; Callebaut, D.K.; Helal, M.A.; Seadawy, A.R. Variational method for the nonlinear dynamic of an elliptic magnetic stagnation line. Eur. Phys. J. D 2006, 39, 237–245. [Google Scholar] [CrossRef]
- Heal, M.A.; Seadawy, A.R. Variational method for the derivative nonlinear Schrodinger equation with computational applications. Phys. Scr. 2009, 80, 035004. [Google Scholar] [CrossRef]
- Seadawy, A.R. Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus 2015, 130, 182. [Google Scholar] [CrossRef]
- Li, X.Z.; Wang, M.L. A sub-ODE method for finding exact solutions of a generalized KdV-mKdV equation with high order nonlinear terms. Phys. Lett. A 2007, 361, 115–118. [Google Scholar] [CrossRef]
- Khater, A.H.; Callebaut, D.K.; Seadawy, A.R. General soliton solutions of an n-dimentional complex Ginzburg-Landau equation, Physica Scripta. Int. J. Exp. Theor. Phys. 2000, 62, 353–357. [Google Scholar]
- Khater, A.H.; Callebaut, D.K.; Seadawy, A.R. Nonlinear dispersive instabilities in Kelvin-Helmholtz magnetohydrodynamic flows. Phys. Scrita 2003, 67, 340–349. [Google Scholar] [CrossRef]
- Helal, M.A.; Seadawy, A.R. Exact soliton solutions of a D-dimensional nonlinear Schrodinger terms. Zeitschrift fur Angewandte Mathematik und Physik 2011, 62, 839–847. [Google Scholar] [CrossRef]
- Huang, Y.; Shang, Y. Thr Extended Hyperbolic Function Method for Generalized Forms of Nonlinear Heat Conducted and Huxley Equations. J. Appl. Math. 2012, 2012, 769843. [Google Scholar] [CrossRef] [Green Version]
- Yadong, S. The Extended Hyperbolic Function Method and exact solutions of the long-short wave resonance equations. Chaos Solitons Fractals 2008, 36, 762–771. [Google Scholar]
- Rehman, H.U.; Ullah, M.A.I.N.; Akgul, A. Exact solutions of (2+1)-dimensional Schrödinger’s hyperbolic equation using different techniques. In Numerical Methods for Partial Differential Equations; Wiley Periodicals, LLC.: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Yadong, S. Explicit and exact solutions for a generalized long-short wave equations with strong nonlinear term. Chaos Solitons Fractals 2005, 26, 527–539. [Google Scholar]
- Yadong, S. Explicit and exact solutions for a class of nonlinear wave equations. Acta Math Appl. Sin. 2000, 23, 21–30. [Google Scholar]
- Ebadi, G.; Johnson, S.; Zerrad, E.; Biswas, A. Solitons and the other non-linear waves for the perturberd Boussinesq equation with power law nonlinearity. J. King Saud Univ.-Sci. 2012, 24, 237–241. [Google Scholar] [CrossRef] [Green Version]
- Akbar, M.A.; Ali, N.H.M.; Tanjim, T. Adequate soliton solutions to the perturbed Boussinesq equation and the KdV-Caudrey-Dodd-Gibbon equation. J. King Saud Univ.-Sci. 2020, 32, 2777–2785. [Google Scholar] [CrossRef]
- Biswas, A.; Ebadi, G.; Triki, H.; Yildirim, A.; Yousefzadeh, N. Tolopogical soliton and other exact solutions to KdV-Caudrey-Dodd-Gibbon equation. Results Math. 2013, 63, 687–703. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asjad, M.I.; Ur Rehman, H.; Ishfaq, Z.; Awrejcewicz, J.; Akgül, A.; Riaz, M.B. On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations. Coatings 2021, 11, 1429. https://doi.org/10.3390/coatings11111429
Asjad MI, Ur Rehman H, Ishfaq Z, Awrejcewicz J, Akgül A, Riaz MB. On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations. Coatings. 2021; 11(11):1429. https://doi.org/10.3390/coatings11111429
Chicago/Turabian StyleAsjad, Muhammad Imran, Hamood Ur Rehman, Zunaira Ishfaq, Jan Awrejcewicz, Ali Akgül, and Muhammad Bilal Riaz. 2021. "On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations" Coatings 11, no. 11: 1429. https://doi.org/10.3390/coatings11111429
APA StyleAsjad, M. I., Ur Rehman, H., Ishfaq, Z., Awrejcewicz, J., Akgül, A., & Riaz, M. B. (2021). On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations. Coatings, 11(11), 1429. https://doi.org/10.3390/coatings11111429








