Rate-Distortion Analysis of Distributed Indirect Source Coding
Abstract
1. Introduction
- M independent encoders, where encoder assigns an index to each sequence ;
- A decoder that produces the estimate to each index tuple and side information .
2. An Achievable Rate Region
3. A General Outer Bound
4. Conclusive Rate-Distortion Results
5. Iterative Optimization Framework Based on BA Algorithm
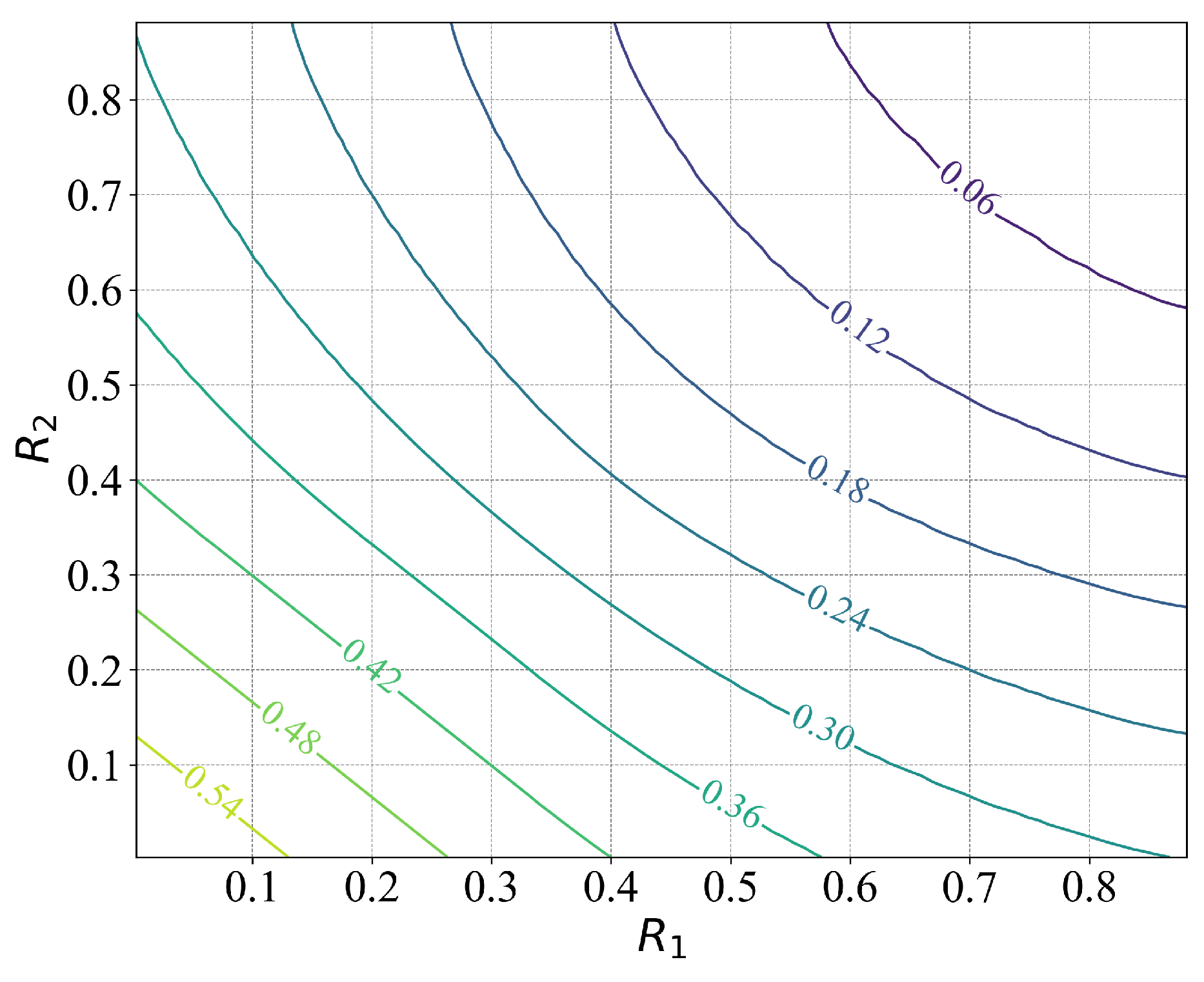
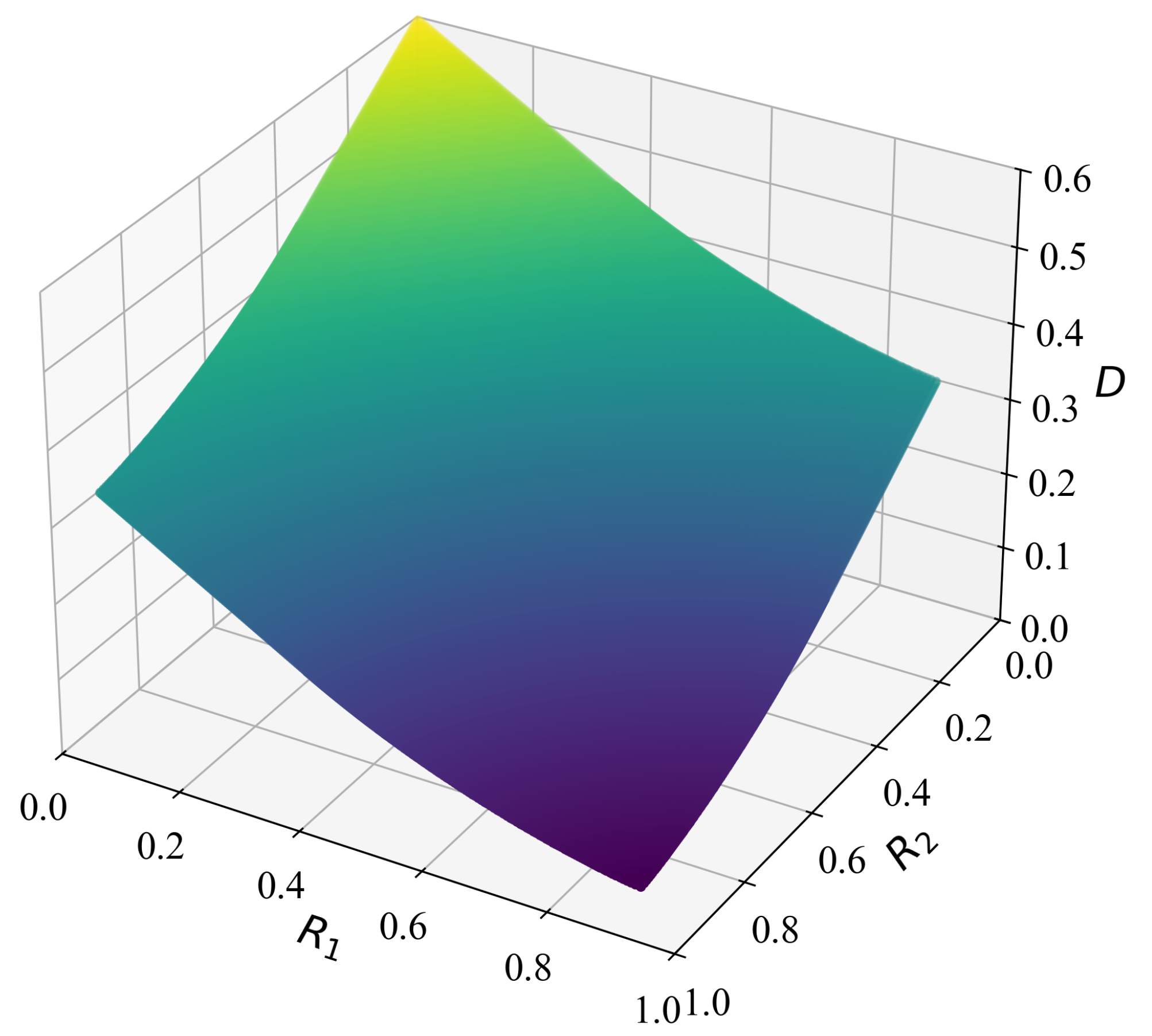
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Han, T.; Yang, Q.; Shi, Z.; He, S.; Zhang, Z. Semantic-preserved communication system for highly efficient speech transmission. IEEE J. Sel. Areas Commun. 2022, 41, 245–259. [Google Scholar] [CrossRef]
- Adikari, T.; Draper, S. Two-terminal source coding with common sum reconstruction. In Proceedings of the 2022 IEEE International Symposium on Information Theory (ISIT), Espoo, Finland, 26 June–1 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1420–1424. [Google Scholar]
- Korner, J.; Marton, K. How to encode the modulo-two sum of binary sources (corresp.). IEEE Trans. Inf. Theory 1979, 25, 219–221. [Google Scholar] [CrossRef]
- Pastore, A.; Lim, S.H.; Feng, C.; Nazer, B.; Gastpar, M. Distributed Lossy Computation with Structured Codes: From Discrete to Continuous Sources. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1681–1686. [Google Scholar]
- Amiri, M.M.; Gunduz, D.; Kulkarni, S.R.; Poor, H.V. Federated Learning with Quantized Global Model Updates. arXiv 2020, arXiv:2006.10672. [Google Scholar] [CrossRef]
- Gruntkowska, K.; Tyurin, A.; Richtárik, P. Improving the Worst-Case Bidirectional Communication Complexity for Nonconvex Distributed Optimization under Function Similarity. arXiv 2024, arXiv:2402.06412. [Google Scholar] [CrossRef]
- Amiri, M.M.; Gündüz, D.; Kulkarni, S.R.; Poor, H.V. Convergence of Federated Learning Over a Noisy Downlink. IEEE Trans. Wirel. Commun. 2022, 21, 1422–1437. [Google Scholar] [CrossRef]
- Stavrou, P.A.; Kountouris, M. The Role of Fidelity in Goal-Oriented Semantic Communication: A Rate Distortion Approach. IEEE Trans. Commun. 2023, 71, 3918–3931. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Poor, H.V. A rate-distortion framework for characterizing semantic information. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Virtual, 12–20 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2894–2899. [Google Scholar]
- Dobrushin, R.; Tsybakov, B. Information transmission with additional noise. IRE Trans. Inf. Theory 1962, 8, 293–304. [Google Scholar] [CrossRef]
- Wolf, J.; Ziv, J. Transmission of noisy information to a noisy receiver with minimum distortion. IEEE Trans. Inf. Theory 1970, 16, 406–411. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Y.; Han, J.; Wu, H.; Bai, B.; Han, W. Semantic compression with side information: A rate-distortion perspective. arXiv 2022, arXiv:2208.06094. [Google Scholar] [CrossRef]
- Wyner, A.; Ziv, J. The rate-distortion function for source coding with side information at the decoder. IEEE Trans. Inf. Theory 1976, 22, 1–10. [Google Scholar] [CrossRef]
- Slepian, D.; Wolf, J. Noiseless coding of correlated information sources. IEEE Trans. Inf. Theory 1973, 19, 471–480. [Google Scholar] [CrossRef]
- Wagner, A.B.; Anantharam, V. An improved outer bound for multiterminal source coding. IEEE Trans. Inf. Theory 2008, 54, 1919–1937. [Google Scholar] [CrossRef]
- Lim, S.H.; Feng, C.; Pastore, A.; Nazer, B.; Gastpar, M. Towards an algebraic network information theory: Distributed lossy computation of linear functions. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1827–1831. [Google Scholar]
- Cheng, S.; Stankovic, V.; Xiong, Z. Computing the channel capacity and rate-distortion function with two-sided state information. IEEE Trans. Inf. Theory 2005, 51, 4418–4425. [Google Scholar] [CrossRef]
- Gastpar, M. The Wyner-Ziv problem with multiple sources. IEEE Trans. Inf. Theory 2004, 50, 2762–2768. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Ku, G.; Ren, J.; Walsh, J.M. Computing the rate distortion region for the CEO problem with independent sources. IEEE Trans. Signal Process. 2014, 63, 567–575. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Yang, Q. Rate-Distortion Analysis of Distributed Indirect Source Coding. Entropy 2025, 27, 844. https://doi.org/10.3390/e27080844
Tang J, Yang Q. Rate-Distortion Analysis of Distributed Indirect Source Coding. Entropy. 2025; 27(8):844. https://doi.org/10.3390/e27080844
Chicago/Turabian StyleTang, Jiancheng, and Qianqian Yang. 2025. "Rate-Distortion Analysis of Distributed Indirect Source Coding" Entropy 27, no. 8: 844. https://doi.org/10.3390/e27080844
APA StyleTang, J., & Yang, Q. (2025). Rate-Distortion Analysis of Distributed Indirect Source Coding. Entropy, 27(8), 844. https://doi.org/10.3390/e27080844






