Multifractal Nonlinearity in Behavior During a Computer Task with Increasing Difficulty: What Does It Teach Us?
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedure
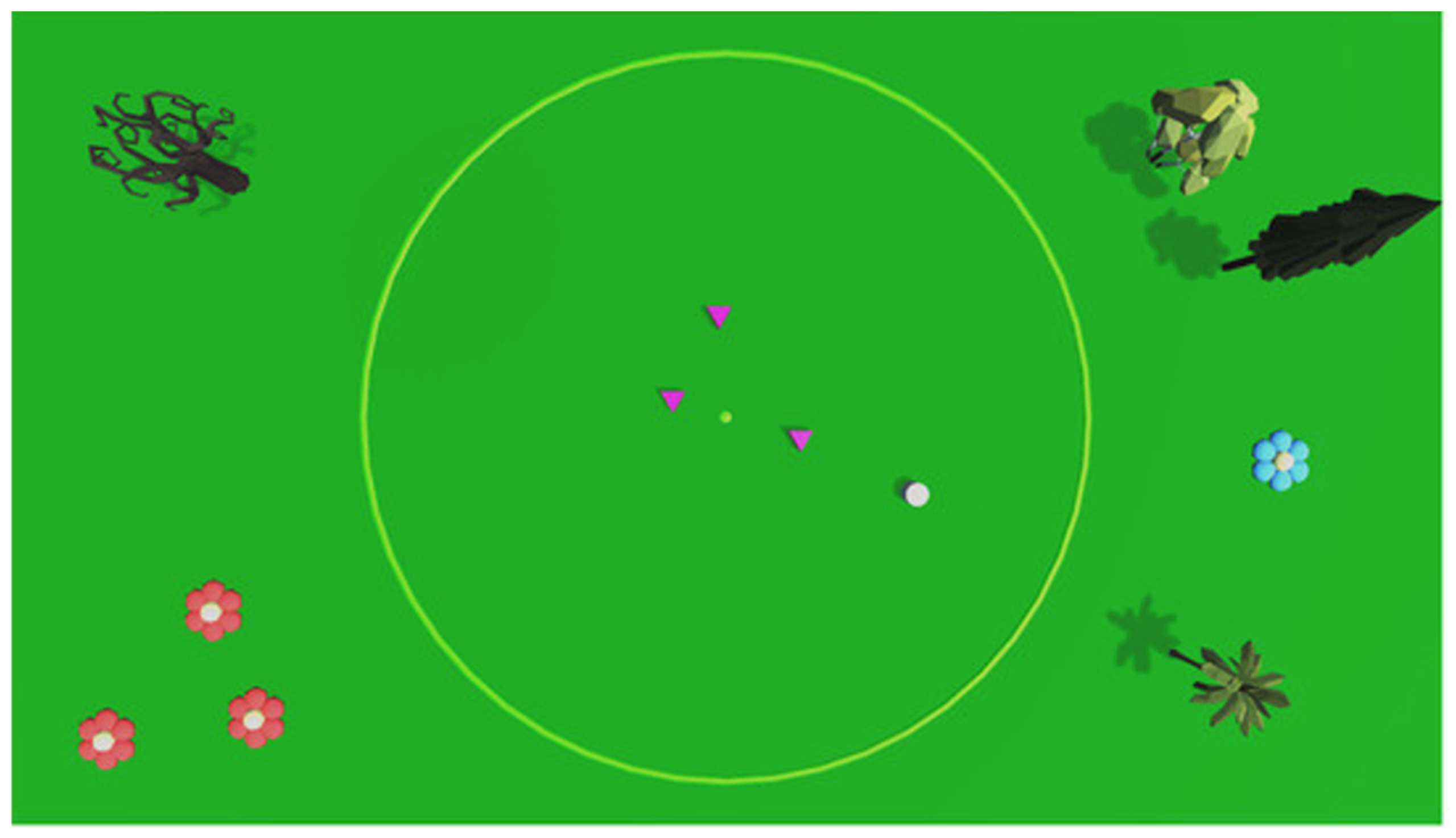
2.3. Experimental Setup
2.3.1. Scoring System and Task Difficulty
2.3.2. Cursor Displacements
2.4. The Multifractal Spectrum Width
2.4.1. Linearized Surrogates Obtained with IAAFT
2.4.2. Nonlinear Multifractality: Surrogate Data Testing
2.5. Statistics
2.5.1. Between-Phase Comparisons
2.5.2. Factor Analysis of Data
3. Results
3.1. Score Dynamics During Each Phase
3.2. Multifractal Nonlinear Metrics of Behavior: MF and tMF
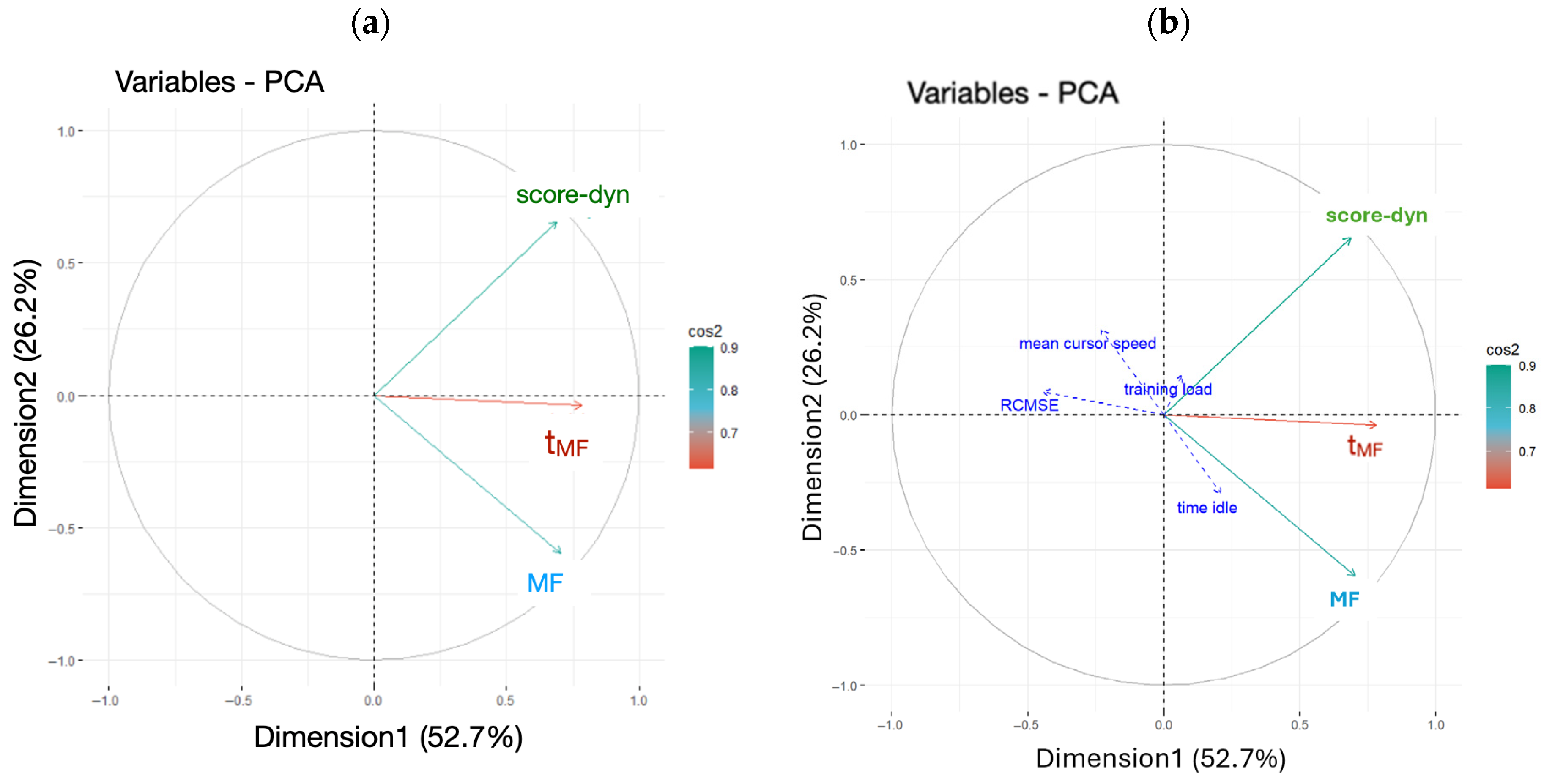
3.3. Hierarchical Clustering on Principal Component
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MF | Multifractality; MF designates the width of the multifractal spectrum |
| tMF | A t-statistic value that indicates the degree of multifractal nonlinearity |
| score-dyn | This indicates the score dynamics, the rate of change in the score (evolution over time of the number of points gained and lost by the subject during the task) as a function of time |
References
- Goldberger, A.L. Non-Linear Dynamics for Clinicians: Chaos Theory, Fractals, and Complexity at the Bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef]
- Wijnants, M.L. A review of theoretical perspectives in cognitive science on the presence of scaling in coordinated physiological and cognitive processes. J. Nonlinear Dyn. 2014, 2014, 962043. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.; Dixon, J.A. When Physics Is Not “Just Physics”: Complexity Science Invites New Measurement Frames for Exploring the Physics of Cognitive and Biological Development. Crit. Rev. Biomed. Eng. 2012, 40, 471–483. [Google Scholar] [CrossRef]
- Anastas, J.R.; Kelty-Stephen, D.G.; Dixon, J.A. Executive Function as an Interaction-Dominant Process. Ecol. Psychol. 2014, 26, 262–282. [Google Scholar] [CrossRef]
- Stephen, D.G.; Anastas, J.R.; Dixon, J.A. Scaling in Executive Control Reflects Multiplicative Multifractal Cascade Dynamics. Front. Physiol. 2012, 3, 102. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ihlen, E.A.F.; Vereijken, B. Interaction-Dominant Dynamics in Human Cognition: Beyond 1/Ƒα Fluctuation. J. Exp. Psychol. Gen. 2010, 139, 436–463. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.A.F.; Vereijken, B. Multifractal Formalisms of Human Behavior. Hum. Mov. Sci. 2013, 32, 633–651. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, A.; Jensen, R. Direct Determination of the f(Alpha) Singularity Spectrum. Phys. Rev. Lett. 1989, 62, 1327–1330. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.G.; Lane, E.; Bloomfield, L.; Mangalam, M. Multifractal Test for Nonlinearity of Interactions across Scales in Time Series. Behav. Res. 2023, 55, 2249–2282. [Google Scholar] [CrossRef]
- Arsac, L.M. Entropy-Based Multifractal Testing of Heart Rate Variability during Cognitive-Autonomic Interplay. Entropy 2023, 25, 1364. [Google Scholar] [CrossRef]
- Bennett, D.; Roudaut, A.; Metatla, O. Multifractal Mice: Operationalising Dimensions of Readiness-to-Hand via a Feature of Hand Movement. In Proceedings of the 2022 CHI Conference on Human Factors in Computing Systems, New Orleans, LA, USA, 30 April–5 May 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1–18. [Google Scholar]
- Arsac, L.M. Multifractal Dynamics in Executive Control When Adapting to Concurrent Motor Tasks. Front. Physiol. 2021, 12, 662076. [Google Scholar] [CrossRef] [PubMed]
- Mangalam, M.; Lee, I.-C.; Newell, K.M.; Kelty-Stephen, D.G. Visual Effort Moderates Postural Cascade Dynamics. Neurosci. Lett. 2021, 742, 135511. [Google Scholar] [CrossRef] [PubMed]
- Bell, C.A.; Carver, N.S.; Zbaracki, J.A.; Kelty-Stephen, D.G. Non-Linear Amplification of Variability Through Interaction Across Scales Supports Greater Accuracy in Manual Aiming: Evidence from a Multifractal Analysis with Comparisons to Linear Surrogates in the Fitts Task. Front. Physiol. 2019, 10, 998. [Google Scholar] [CrossRef] [PubMed]
- Dixon, J.A.; Holden, J.G.; Mirman, D.; Stephen, D.G. Multifractal Dynamics in the Emergence of Cognitive Structure. Top. Cogn. Sci. 2012, 4, 51–62. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.G.; Lee, J.; Cole, K.R.; Shields, R.K.; Mangalam, M. Multifractal Nonlinearity Moderates Feedforward and Feedback Responses to Suprapostural Perturbations. Percept. Mot. Ski. 2023, 130, 622–657. [Google Scholar] [CrossRef]
- Dotov, D.G.; Nie, L.; Chemero, A. A Demonstration of the Transition from Ready-to-Hand to Unready-to-Hand. PLoS ONE 2010, 5, e9433. [Google Scholar] [CrossRef]
- Pratviel, Y.; Deschodt-Arsac, V.; Larrue, F.; Arsac, L.M. Tool Embodiment Is Reflected in Movement Multifractal Nonlinearity. Fractal Fract. 2022, 6, 240. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Lee, K.-Y.; Peng, C.-K. Analysis of Complex Time Series Using Refined Composite Multiscale Entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Torre, K.; Vergotte, G.; Viel, É.; Perrey, S.; Dupeyron, A. Fractal Properties in Sensorimotor Variability Unveil Internal Adaptations of the Organism before Symptomatic Functional Decline. Sci. Rep. 2019, 9, 15736. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Peng, C.K.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Is Walking a Random Walk? Evidence for Long-Range Correlations in Stride Interval of Human Gait. J. Appl. Physiol. 1995, 78, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Slifkin, A.B.; Eder, J.R. Fitts’ Index of Difficulty Predicts the 1/f Structure of Movement Amplitude Time Series. Exp. Brain Res. 2014, 232, 1653–1662. [Google Scholar] [CrossRef] [PubMed]
- Wallot, S.; Coey, C.A.; Richardson, M.J. Cue Predictability Changes Scaling in Eye-Movement Fluctuations. Atten. Percept. Psychophys. 2015, 77, 2169–2180. [Google Scholar] [CrossRef] [PubMed]
- Mangalam, M.; Likens, A.D.; Kelty-Stephen, D.G. Multifractal Nonlinearity as a Robust Estimator of Multiplicative Cascade Dynamics. Phys. Rev. E 2025, 111, 034126. [Google Scholar] [CrossRef]
- Furmanek, M.P.; Mangalam, M.; Kelty-Stephen, D.G.; Juras, G. Postural Constraints Recruit Shorter-Timescale Processes into the Non-Gaussian Cascade Processes. Neurosci. Lett. 2021, 741, 135508. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.G.; Furmanek, M.P.; Mangalam, M. Multifractality Distinguishes Reactive from Proactive Cascades in Postural Control. Chaos Solitons Fractals 2021, 142, 110471. [Google Scholar] [CrossRef]
- Mangalam, M.; Kelty-Stephen, D. Hypothetical Control of Postural Sway. J. R. Soc. Interface 2021, 18, 20200951. [Google Scholar] [CrossRef]
- Carver, N.S.; Bojovic, D.; Kelty-Stephen, D.G. Multifractal Foundations of Visually-Guided Aiming and Adaptation to Prismatic Perturbation. Hum. Mov. Sci. 2017, 55, 61–72. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.G.; Dixon, J.A. Interwoven Fluctuations during Intermodal Perception: Fractality in Head Sway Supports the Use of Visual Feedback in Haptic Perceptual Judgments by Manual Wielding. J. Exp. Psychol. Hum. Percept. Perform. 2014, 40, 2289–2309. [Google Scholar] [CrossRef]
- Mangalam, M.; Carver, N.S.; Kelty-Stephen, D.G. Global Broadcasting of Local Fractal Fluctuations in a Bodywide Distributed System Supports Perception via Effortful Touch. Chaos Solitons Fractals 2020, 135, 109740. [Google Scholar] [CrossRef]
- Mangalam, M.; Carver, N.S.; Kelty-Stephen, D.G. Multifractal Signatures of Perceptual Processing on Anatomical Sleeves of the Human Body. J. R. Soc. Interface 2020, 17, 20200328. [Google Scholar] [CrossRef] [PubMed]
- Mangalam, M.; Kelty-Stephen, D.G. Multiplicative-Cascade Dynamics Supports Whole-Body Coordination for Perception via Effortful Touch. Hum. Mov. Sci. 2020, 70, 102595. [Google Scholar] [CrossRef] [PubMed]
- Palatinus, Z.; Kelty-Stephen, D.G.; Kinsella-Shaw, J.; Carello, C.; Turvey, M.T. Haptic Perceptual Intent in Quiet Standing Affects Multifractal Scaling of Postural Fluctuations. J. Exp. Psychol. Hum. Percept. Perform. 2014, 40, 1808–1818. [Google Scholar] [CrossRef] [PubMed]
- Kelty-Stephen, D.; Similton, O.D.; Rabinowitz, E.; Allen, M. Multifractal Auditory Stimulation Promotes the Effect of Multifractal Torso Sway on Spatial Perception: Evidence from Distance Perception by Blindwalking. Ecol. Psychol. 2023, 35, 136–182. [Google Scholar] [CrossRef]
- Mangalam, M.; Kelty-Stephen, D.G.; Seleznov, I.; Popov, A.; Likens, A.D.; Kiyono, K.; Stergiou, N. Older Adults and Individuals with Parkinson’s Disease Control Posture along Suborthogonal Directions That Deviate from the Traditional Anteroposterior and Mediolateral Directions. Sci. Rep. 2024, 14, 4117. [Google Scholar] [CrossRef]
- Kelty-Stephen, D.G.; Kiyono, K.; Stergiou, N.; Mangalam, M. Spatial Variability and Directional Shifts in Postural Control in Parkinson’s Disease. Clin. Park. Relat. Disord. 2024, 10, 100249. [Google Scholar] [CrossRef]
- Cavanaugh, J.T.; Kelty-Stephen, D.G.; Stergiou, N. Multifractality, Interactivity, and the Adaptive Capacity of the Human Movement System: A Perspective for Advancing the Conceptual Basis of Neurologic Physical Therapy. J. Neurol. Phys. Ther. 2017, 41, 245–251. [Google Scholar] [CrossRef]

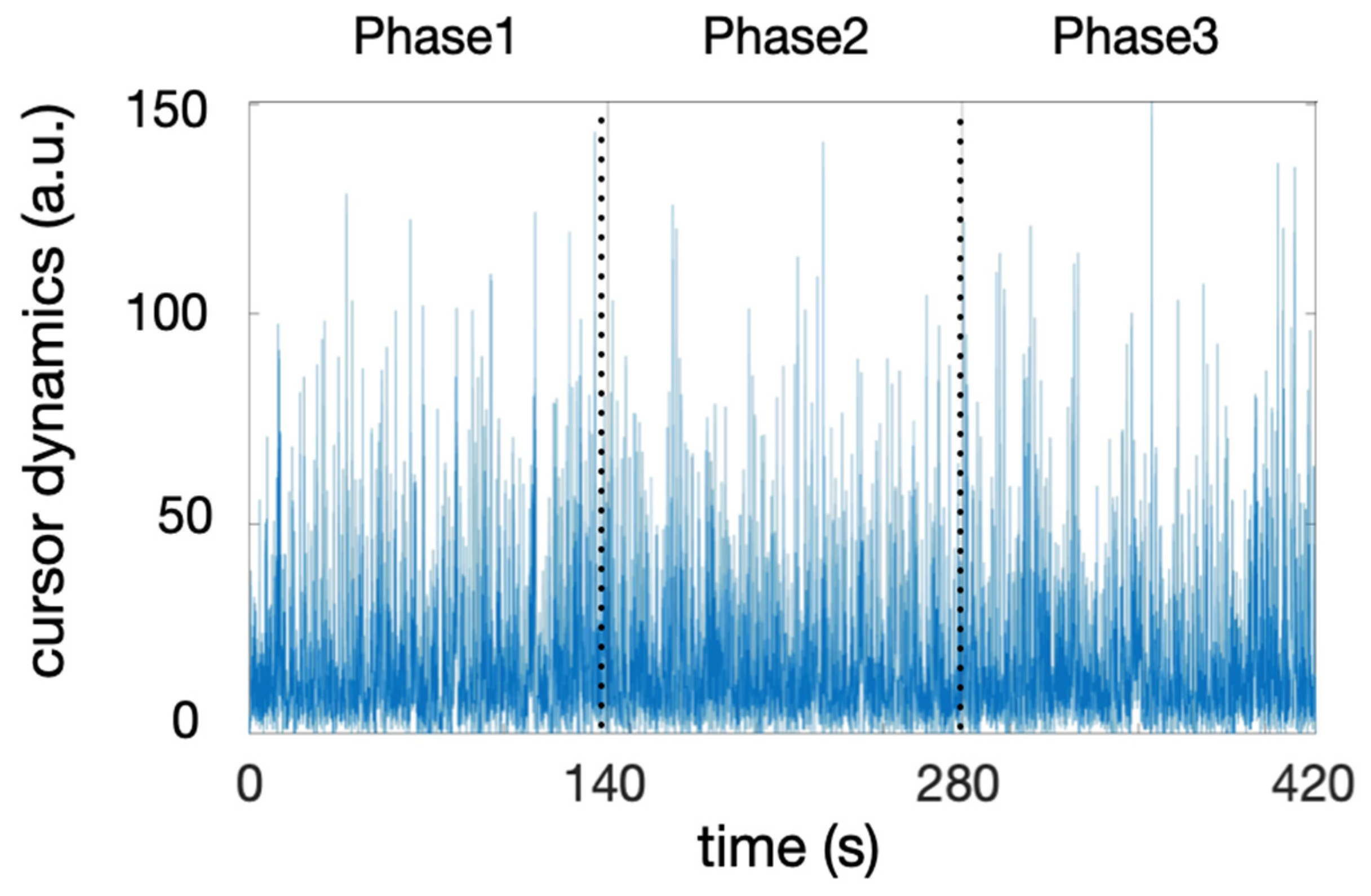



| Variable | Phase 1 | Phase 2 | Phase 3 |
|---|---|---|---|
| score-dyn | 38.1 ± 5.6 * [22.3:45.2] | 27.3 ± 6.2 * [14.8:37.8] | 16.0 ± 7.2 * [2.7:31.8] |
| MF | 0.58 ± 0.07 [0.41:0.74] | 0.60 ± 0.08 [0.45:0.77] | 0.60 ± 0.06 [0.51:0.70] |
| tMF | 8.8 ± 10.8 [−8.0:31.0] | 10.8 ± 11.3 [−8.1:36.3] | 6.5 ± 7. 6 [−5.0:16.6] |
| scoreMax | 5082 ± 609 * [3542:5922] | 9146 ± 1214 * [6184:10,837] | 11,451 ± 1650 * [8427:15,108] |
| Cluster Id. | Score-dyn | MF | tMF |
|---|---|---|---|
| Cluster 1 | 12.5 ± 5.6 | 0.56 ± 0.04 | 0.88 ± 5.10 |
| Cluster 2 | 16.4 ± 5.4 | 0.67 ± 0.03 | 10.34 ± 6.00 |
| Cluster 3 | 26.4 ± 5.8 | 0.57 ± 0.04 | 14.97 ± 1.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouni, A.; Arsac, L.M.; Chevalerias, O.; Deschodt-Arsac, V. Multifractal Nonlinearity in Behavior During a Computer Task with Increasing Difficulty: What Does It Teach Us? Entropy 2025, 27, 843. https://doi.org/10.3390/e27080843
Bouni A, Arsac LM, Chevalerias O, Deschodt-Arsac V. Multifractal Nonlinearity in Behavior During a Computer Task with Increasing Difficulty: What Does It Teach Us? Entropy. 2025; 27(8):843. https://doi.org/10.3390/e27080843
Chicago/Turabian StyleBouni, Alix, Laurent M. Arsac, Olivier Chevalerias, and Veronique Deschodt-Arsac. 2025. "Multifractal Nonlinearity in Behavior During a Computer Task with Increasing Difficulty: What Does It Teach Us?" Entropy 27, no. 8: 843. https://doi.org/10.3390/e27080843
APA StyleBouni, A., Arsac, L. M., Chevalerias, O., & Deschodt-Arsac, V. (2025). Multifractal Nonlinearity in Behavior During a Computer Task with Increasing Difficulty: What Does It Teach Us? Entropy, 27(8), 843. https://doi.org/10.3390/e27080843







