Linking Optimization Success and Stability of Finite-Time Thermodynamics Heat Engines
Abstract
1. Introduction
1.1. An Optimization Quest
1.2. Local Equilibrium and Realizations of the Endoreversible Model
1.3. Optimization Due to Stability
2. Irreversible Carnot-like Heat Engine
Maximizing Power, Efficiency, Ecological and Omega Figures of Merit
3. Losses and Success of Energy Converters
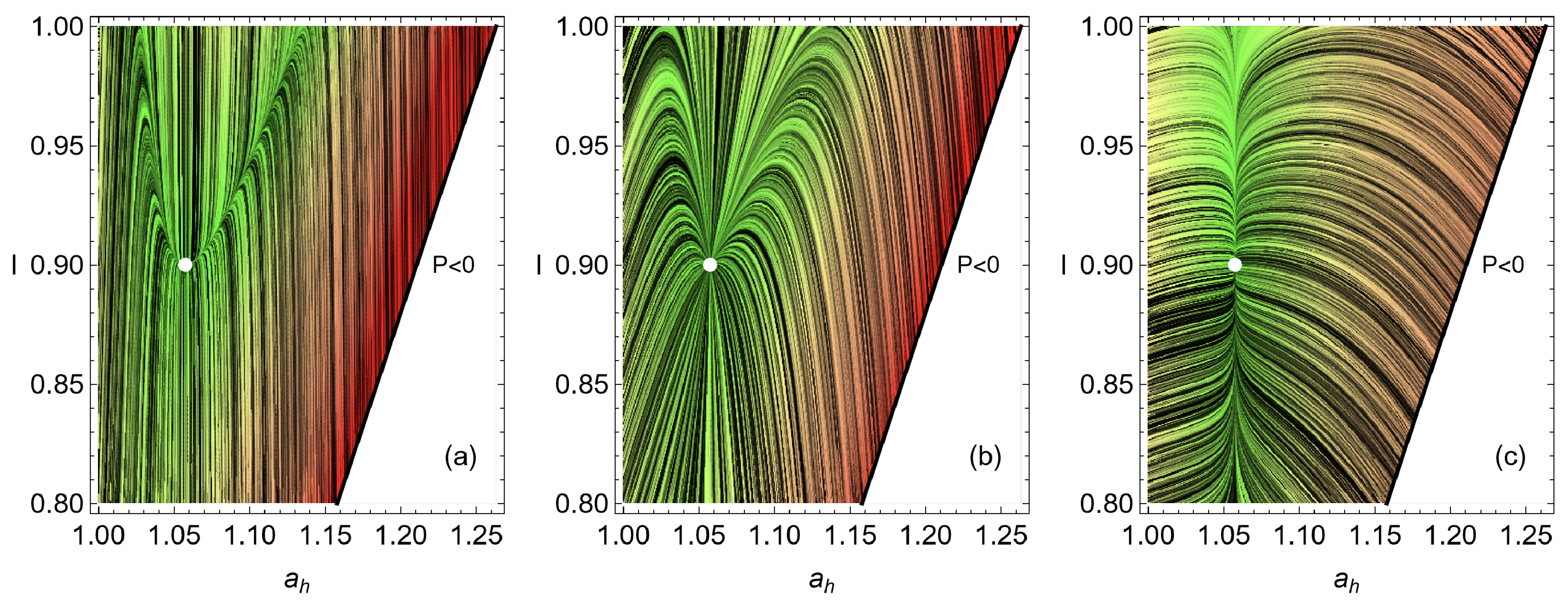
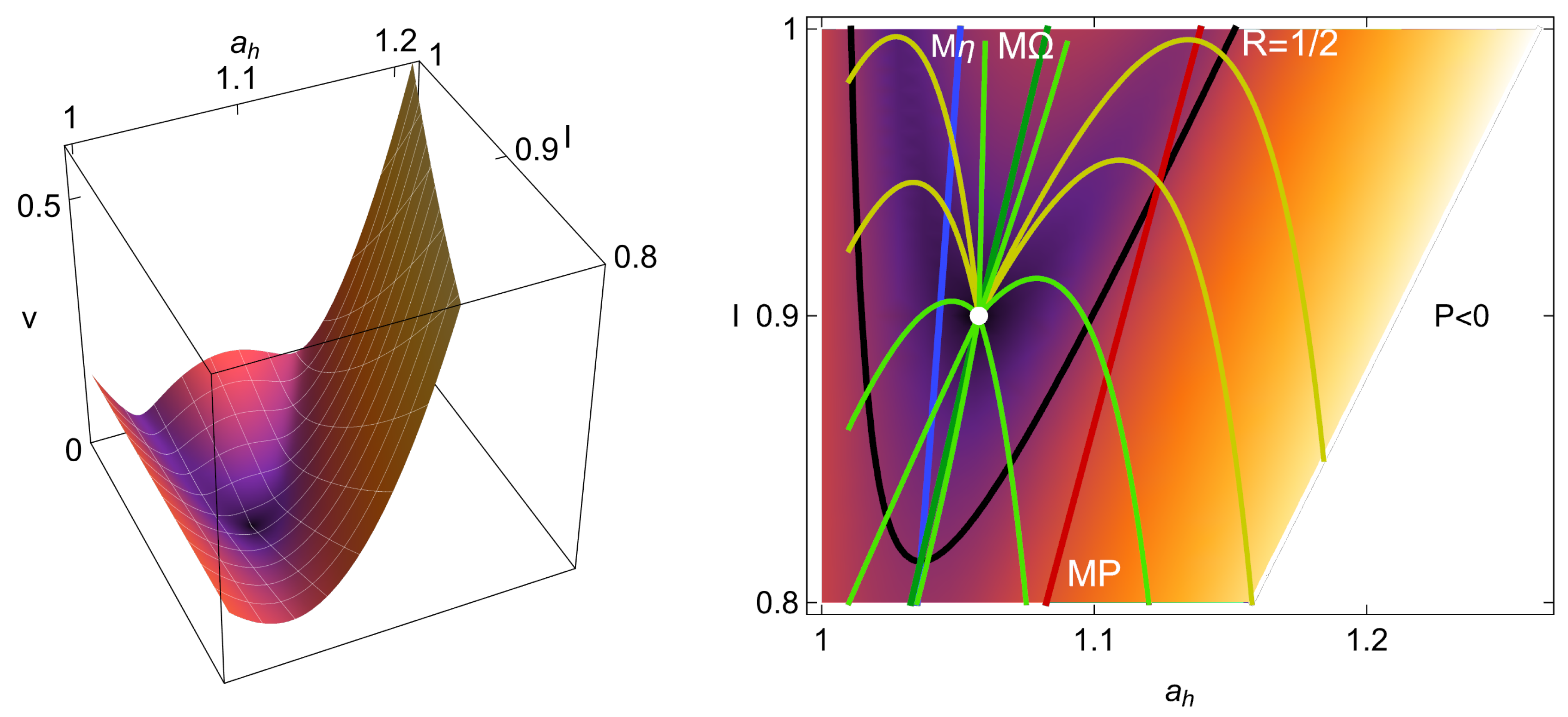
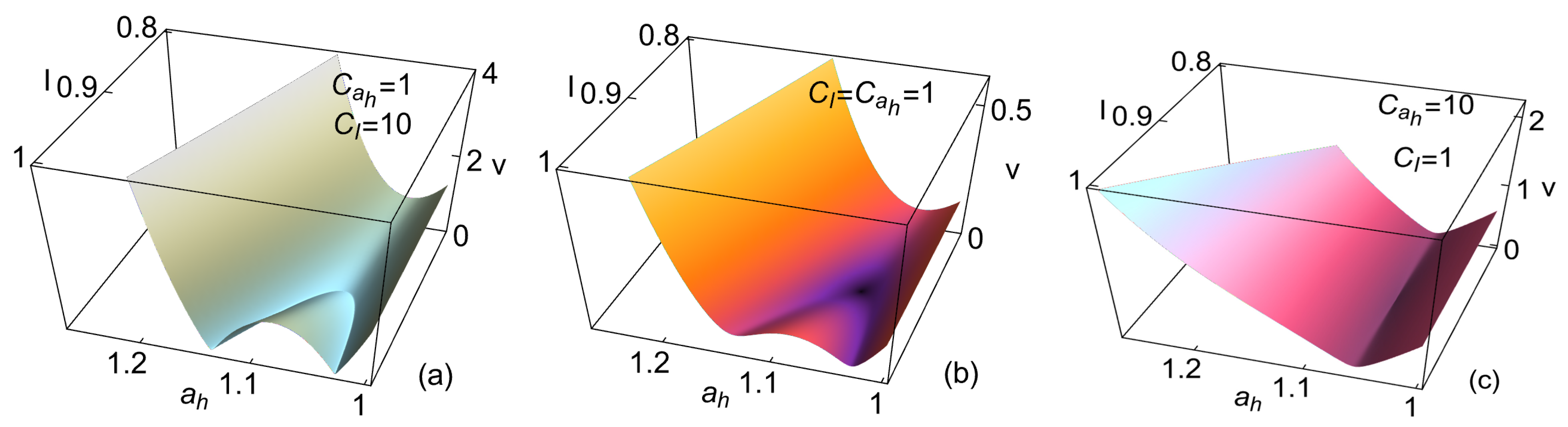
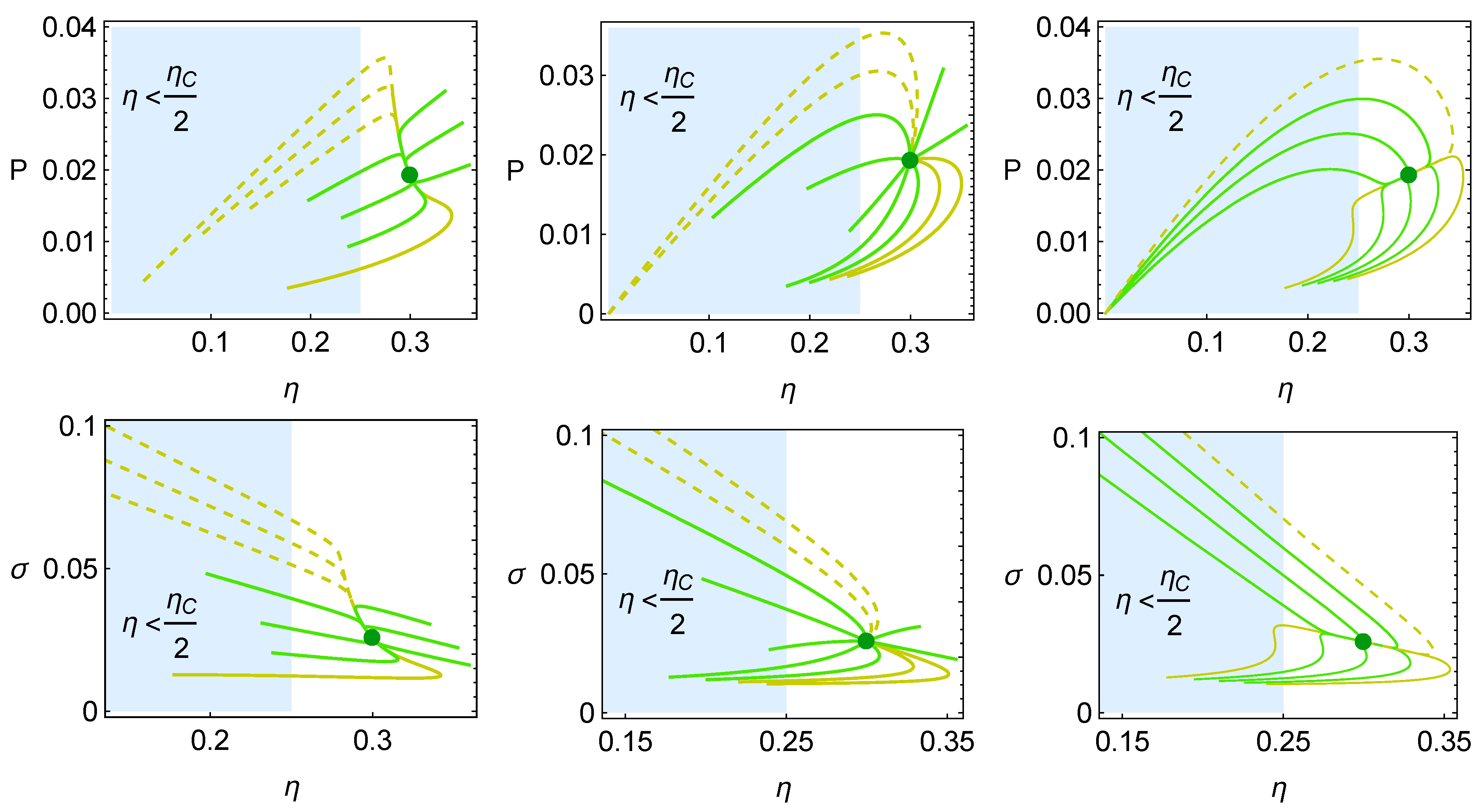
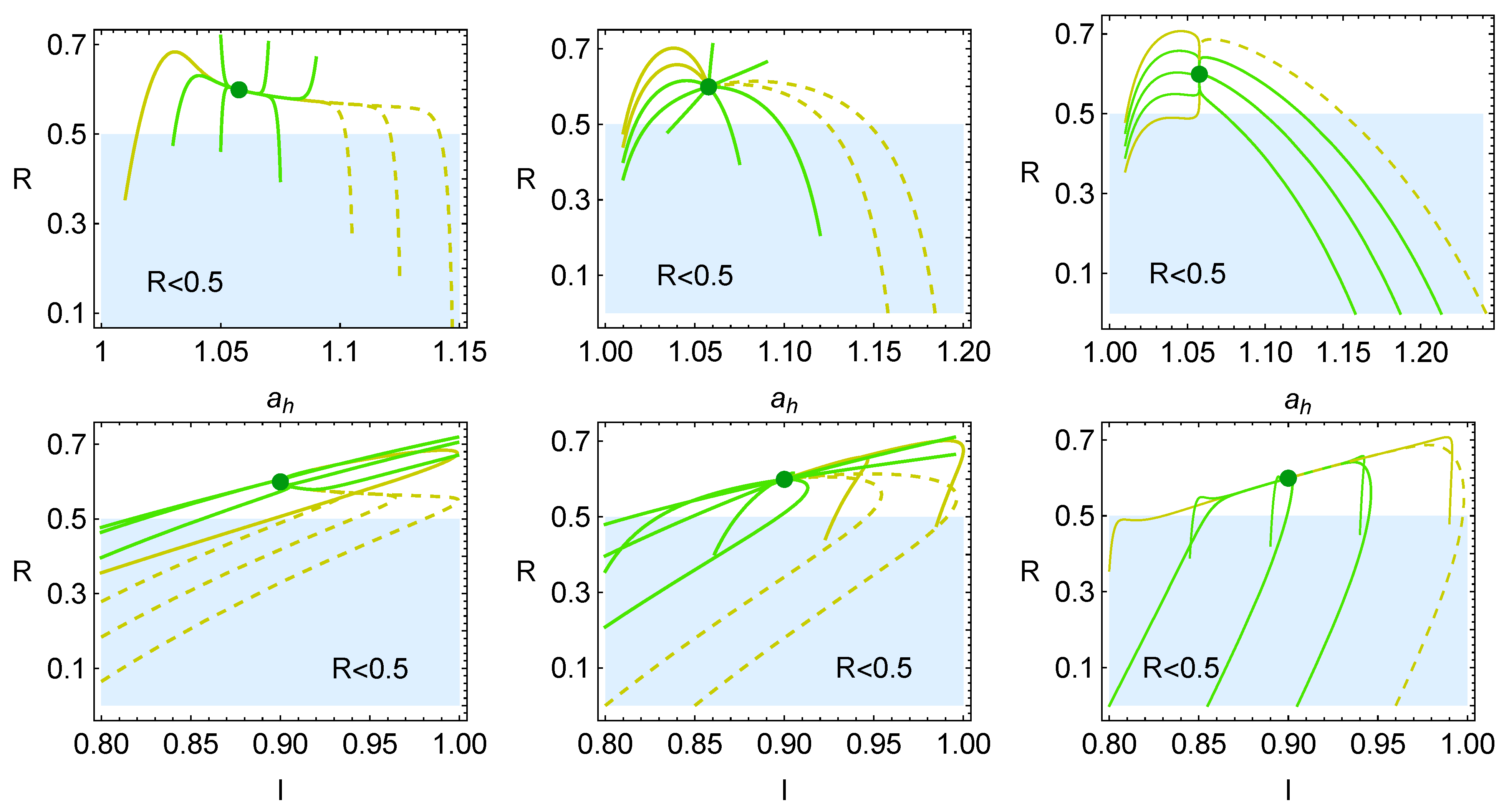
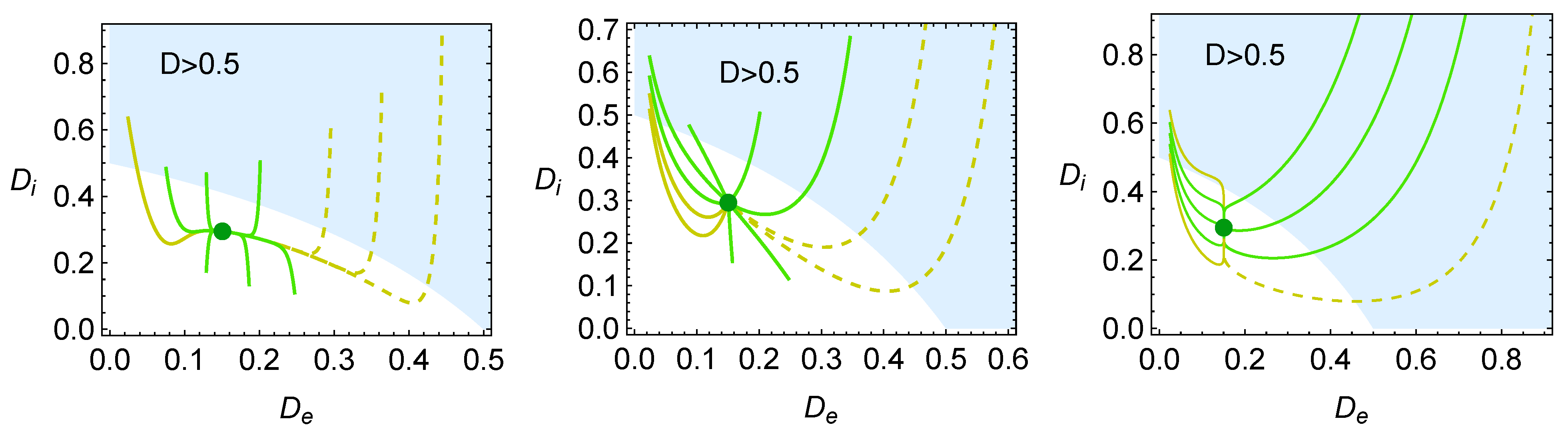
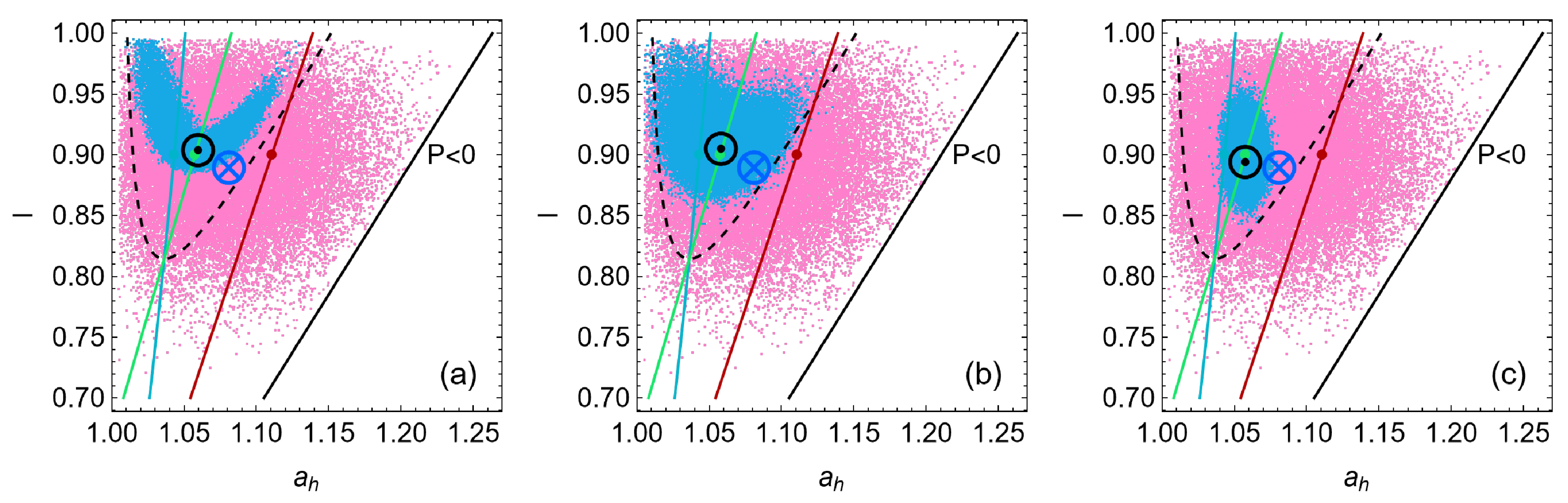
4. Heat Reservoirs Stability
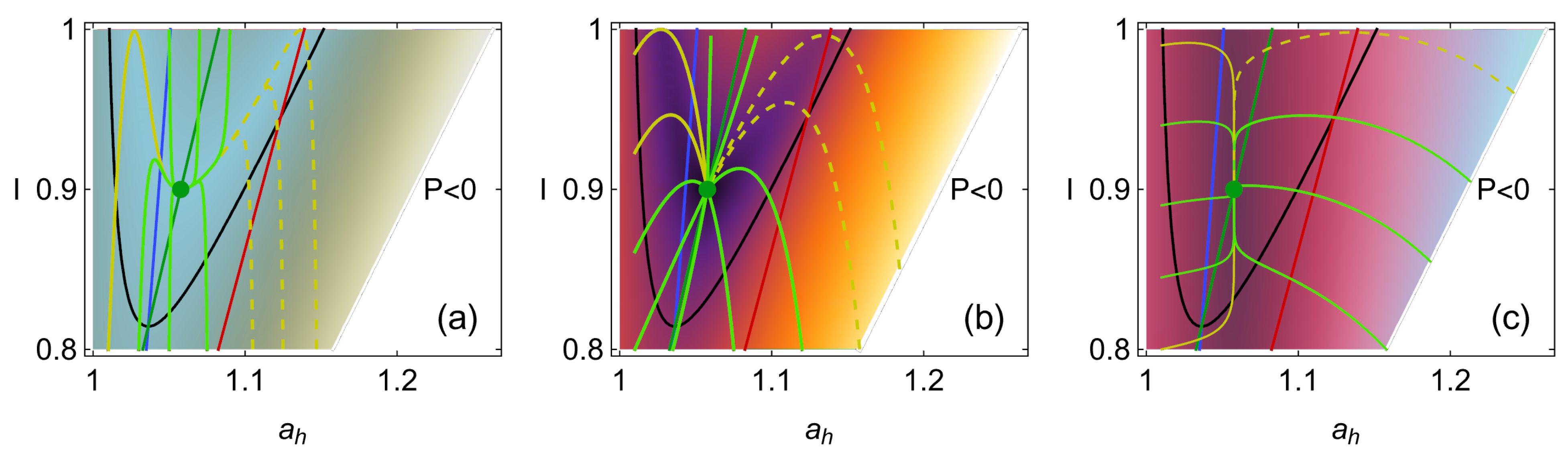
5. Stability Dynamics
6. Energetic Evolution in the Relaxation Towards the Steady State
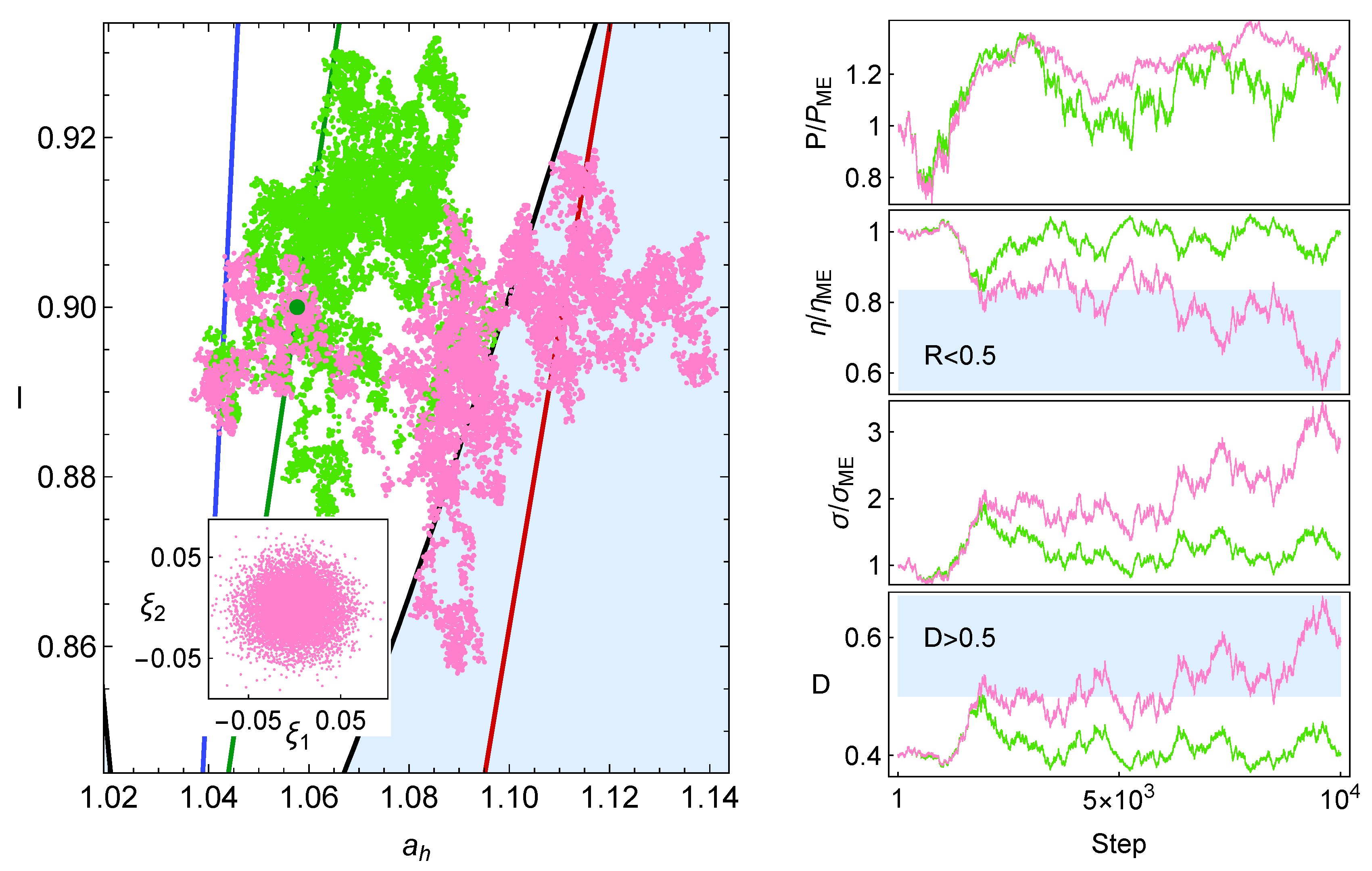
7. Consecutive Perturbations
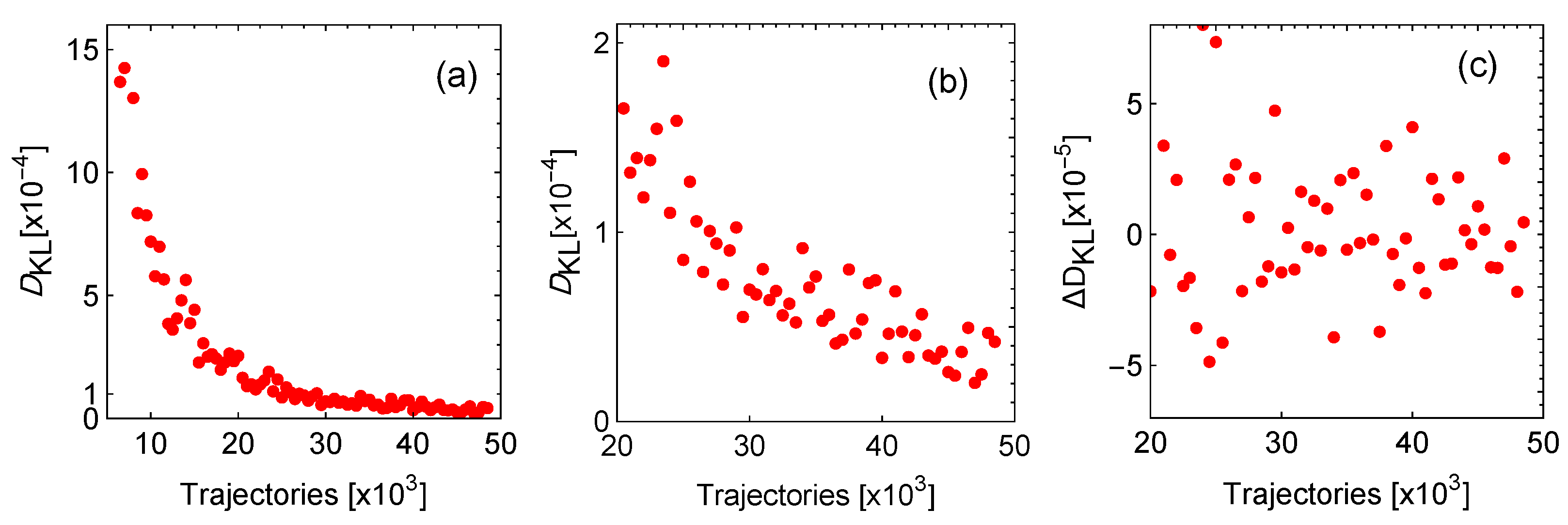
7.1. Stochastic Trajectories
7.2. Statistical Convergence
7.3. Effect of Stability on Many Trajectories
8. Summary and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Carnot, S. Reflexions sur la Puissance Motrice du Feu et sur les Machines Propres a Developper cette Puissance; Bachelier: Paris, France, 1824. [Google Scholar]
- Ferreira da Silva, M.F. Some considerations about thermodynamic cycles. Eur. J. Phys. 2012, 33, 13–42. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Angulo-Brown, F. The universality of the Carnot theorem. Eur. J. Phys. 2013, 34, 273–289. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Arias-Hernandez, L.A.; Angulo-Brown, F. Connection between maximum-work and maximum-power thermal cycles. Phys. Rev. E 2013, 88, 052142. [Google Scholar] [CrossRef]
- Wu, J. Three factors causing the thermal efficiency of a heat engine to be less than unity and their relevance to daily life. Eur. J. Phys. 2015, 36, 015008. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22. [Google Scholar] [CrossRef]
- Sekulic, D.P. A fallacious argument in the finite time thermodynamics concept of endoreversibility. J. Appl. Phys. 1998, 83, 4561. [Google Scholar] [CrossRef]
- Andresen, B. Comment on “A fallacious argument in the finite time thermodynamic concept of endoreversibility” [J. Appl. Phys. 1998, 83, 4561]. J. Appl. Phys. 2001, 90, 6557. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z.; Lin, G.; Andresen, B. On the Curzon–Ahlborn efficiency and its connection with the efficiencies of real heat engines. Energy Convers. Manag. 2001, 42, 173. [Google Scholar] [CrossRef]
- Gyftopoulos, E.P. On the Curzon–Ahlborn efficiency and its lack of connection to power producing processes. Energy Convers. Manag. 2002, 43, 609–615. [Google Scholar] [CrossRef]
- Berry, R.S.; Salamon, P.; Andresen, B. How It All Began. Entropy 2020, 22, 908. [Google Scholar] [CrossRef]
- Rojas-Gamboa, D.A.; Rodríguez, J.I.; Gonzalez-Ayala, J.; Angulo-Brown, F. Ecological efficiency of finite-time thermodynamics: A molecular dynamics study. Phys. Rev. E 2018, 98, 022130. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Onsager coefficients of a finite-time Carnot cycle. Phys. Rev. E 2009, 80, 021121. [Google Scholar] [CrossRef] [PubMed]
- Leff, H.S. Thermal efficiency at maximum work output: New results for old heat engines. Am. J. Phys. 1987, 55, 602–610. [Google Scholar] [CrossRef]
- Gordon, J.M. Generalized power versus efficiency characteristics of heat engines: The thermoelectric generator as an instructive illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Gordon, J.M.; Huleihil, M. General performance characteristics of real heat engines. J. Appl. Phys. 1992, 72, 829–837. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D Appl. Phys. 1994, 27, 1144–1149. [Google Scholar] [CrossRef]
- Qin, X.; Chen, L.; Sun, F.; Wu, C. The universal power and efficiency characteristics for irreversible reciprocating heat engines cycles. Eur. J. Phys. 2003, 24, 359–366. [Google Scholar] [CrossRef]
- Agrawal, D.C. A simplified version of the Curzon-Ahlborn engine. Eur. J. Phys. 2009, 30, 1173–1179. [Google Scholar] [CrossRef]
- Pescetti, D. On the optimization of endoreversible processes. Eur. J. Phys. 2014, 35, 025014. [Google Scholar] [CrossRef]
- Vaudrey, A.; Lanzetta, F.; Feidt, M.H.B. Reitlinger and the origins of the Efficiency at Maximum Power formula for Heat Engines. J. Non-Equilib Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Van den Broeck, C.; Kumar, N.; Lindenberg, K. Efficiency of Isothermal Molecular Machines at Maximum Power. Phys. Rev. Lett. 2012, 108, 210602. [Google Scholar] [CrossRef]
- Golubeva, N.; Imparato, A. Efficiency at Maximum Power of Interacting Molecular Machines. Phys. Rev. Lett. 2012, 109, 190602. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. Efficiency at maximum power of thermally coupled heat engines. Phys. Rev. E 2012, 85, 041144. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; He, J.; Ma, Y. Efficiency at maximum power of a heat engine working with a two-level atomic system. Phys. Rev. E 2013, 87, 042119. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; He, J.; Ma, Y.; Wang, J. Efficiency at maximum power of a quantum Otto engine: Both within finite-time and irreversible thermodynamics. Phys. Rev. E 1990, 90, 062134. [Google Scholar] [CrossRef]
- Sheng, S.Q.; Tu, Z.C. Hidden symmetries and nonlinear constitutive relations for tight-coupling heat engines. New J. Phys. 2015, 17, 045013. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Linear irreversible heat engines based on the local equilibrium assumptions. New J. Phys. 2015, 17, 085011. [Google Scholar] [CrossRef]
- Ouerdane, H.; Apertet, Y. Goupil and Ph. Lecoeur, Continuity and boundary conditions in thermodynamics: From Carnot’s efficiency to efficiencies at maximum power. Eur. Phys. J. Spec. Top. 2015, 224, 839–862. [Google Scholar] [CrossRef][Green Version]
- Landsberg, P.; Leff, H. Thermodynamic cycles with nearly universal maximum-work efficiencies. J. Phys. A Math. Gen. 1989, 22, 4019. [Google Scholar] [CrossRef]
- Esposito, M.; Lindenberg, K.; Van den Broeck, C. Universality of efficiency at maximum power. Phys. Rev. Lett. 2009, 102, 130602. [Google Scholar] [CrossRef]
- Wang, Y.; Tu, Z.C. Efficiency at maximum power output of linear irreversible Carnot-like heat engines. Phys. Rev. E 2012, 85, 011127. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Wang, Y.; Chen, J. Universal efficiency bounds of weak-dissipative thermodynamic cycles at the maximum power output. Phys. Rev. E 2013, 87, 012133. [Google Scholar] [CrossRef]
- Sheng, S.; Tu, Z.C. Universality of energy conversion efficiency for optimal tight-coupling heat engines and refrigerators. J. Phys. A Math. Theor. 2013, 46, 402001. [Google Scholar] [CrossRef]
- Uzdin, R.; Kosloff, R. Universal features in the efficiency at maximum work of hot quantum Otto engines. Europhys. Lett. 2014, 108, 40001. [Google Scholar] [CrossRef]
- Sheng, S.Q.; Tu, Z.C. Constitutive relation for nonlinear response and universality of efficiency at maximum power for tight-coupling heat engines. Phys. Rev. E 2015, 91, 022136. [Google Scholar] [CrossRef] [PubMed]
- Cleuren, B.; Rutten, B.; Van den Broeck, C. Universality of efficiency at maximum power: Macroscopic manifestation of microscopic constraints. Eur. Phys. J. Spec. Top. 2015, 224, 879. [Google Scholar] [CrossRef]
- Ye, Z.; Hu, Y.; He, J.; Wang, J. Universality of maximum-work efficiency of a cyclic heat engine based on a finite system of ultracold atoms. Sci. Rep. 2017, 7, 6289. [Google Scholar] [CrossRef] [PubMed]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Arias-Hernández, L.A.; Angulo-Brown, F. A general property of endoreversible thermal engines. J. Appl. Phys. 1997, 81, 2973. [Google Scholar] [CrossRef]
- Hern, A.C.; Medina, A.; Roco, J.M.M.; White, J.A.; Velasco, S. Unified optimization criterion for energy converters. Phys. Rev. E 2001, 63, 037102. [Google Scholar] [CrossRef]
- Stucki, J.W. The Optimal Efficiency and the Economic Degrees of Coupling of Oxidative Phosphorylation. Eur. J. Biochem. 1980, 109, 269–283. [Google Scholar] [CrossRef] [PubMed]
- Arias-Hernandez, L.A.; Angulo-Brown, F.; Paez-Hernandez, R.T. First-order irreversible thermodynamic approach to a simple energy converter. Phys. Rev. E 2008, 77, 011123. [Google Scholar] [CrossRef]
- Long, R.; Liu, W. Unified trade-off optimization for general heat devices with nonisothermal processes. Phys. Rev. E 2015, 91, 042127. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Liu, W. Ecological optimization for general heat engines. Phys. A Stat. Mech. Appl. 2015, 434, 232–239. [Google Scholar] [CrossRef]
- Singh, V.; Johal, R.S. Feynman’s Ratchet and Pawl with Ecological Criterion: Optimal Performance versus Estimation with Prior Information. Entropy 2017, 19, 576. [Google Scholar] [CrossRef]
- Iyyappan, I.; Ponmurugan, M. Thermoelectric energy converters under a trade-off figure of merit with broken time-reversal symmetry. J. Stat. Mech. 2017, 2017, 093207. [Google Scholar] [CrossRef]
- Lu, C.; Bai, L. Nonlinear Dissipation Heat Devices in Finite-Time Thermodynamics: An Analysis of the Trade-Off Optimization. J. Non-Equilib. Thermodyn. 2017, 42, 277–286. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Calvo Hernández, A.; Roco, J.M.M. From maximum power to a trade-off optimization of low-dissipation heat engines: Influence of control parameters and the role of entropy generation. Phys. Rev. E 2017, 95, 022131. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, C.; Lin, G.; Chen, J. Universality of efficiency at unified trade-off optimization. Phys. Rev. E 2016, 93, 032152. [Google Scholar] [CrossRef]
- Holubec, V.; Ryabov, A. Maximum efficiency of low-dissipation heat engines at arbitrary power. J. Stat. Mech. 2016, 2016, 073204. [Google Scholar] [CrossRef]
- Shiraishi, N.; Saito, K.; Tasaki, H. Universal Trade-Off Relation between Power and Efficiency for Heat Engines. Phys. Rev. Lett. 2016, 117, 190601. [Google Scholar] [CrossRef]
- Iyyappan, I.; Ponmurugan, M. General relations between the power, efficiency, and dissipation for the irreversible heat engines in the nonlinear response regime. Phys. Rev. E 2018, 97, 012141. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Optimal Finite-Time Processes In Stochastic Thermodynamics. Phys. Rev. Lett. 2007, 98, 108301. [Google Scholar] [CrossRef]
- Bauer, M.; Brandner, K.; Seifert, U. Optimal performance of periodically driven, stochastic heat engines under limited control. Phys. Rev. E 2016, 93, 042112. [Google Scholar] [CrossRef] [PubMed]
- Funo, K.; Ueda, M. Work Fluctuation-Dissipation Trade-Off in Heat Engines. Phys. Rev. Lett. 2015, 115, 260601. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Liu, W. Efficiency and its bounds of minimally nonlinear irreversible heat engines at arbitrary power. Phys. Rev. E 2016, 94, 052114. [Google Scholar] [CrossRef] [PubMed]
- Pietzonka, P.; Seifert, U. Universal Trade-Off between Power, Efficiency, and Constancy in Steady-State Heat Engines. Phys. Rev. Lett. 2018, 120, 190602. [Google Scholar] [CrossRef] [PubMed]
- Holubec, V.; Ryabov, A. Cycling tames power fluctuations near optimum efficiency. Phys. Rev. Lett. 2018, 121, 120601. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef]
- Dillenschneider, R.; Lutz, E. Energetics of quantum correlations. Europhys. Lett. 2009, 88, 50003. [Google Scholar] [CrossRef]
- Abah, O.; Lutz, E. Efficiency of heat engines coupled to nonequilibrium reservoirs. Europhys. Lett. 2014, 106, 20001. [Google Scholar] [CrossRef]
- Polettini, M.; Verley, G.; Esposito, M. Efficiency Statistics at All Times: Carnot Limit at Finite Power. Phys. Rev. Lett. 2015, 114, 050601. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Park, H. Carnot efficiency is reachable in an irreversible process. Sci. Rep. 2017, 7, 10725. [Google Scholar] [CrossRef]
- Niedenzu, W.; Mukherjee, V.; Ghosh, A.; Kofman, A.G.; Kurizki, G. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018, 9, 165. [Google Scholar] [CrossRef]
- Proesmans, K.; Dreher, Y.; Gavrilov, M.; Bechhoefer, J.; Van den Broeck, C. Brownian Duet: A Novel Tale of Thermodynamic Efficiency. Phys. Rev. X 2016, 6, 041010. [Google Scholar] [CrossRef]
- Uzdin, R.; Levy, A.; Kosloff, R. Equivalence of quantum heat machines, and quantum-thermodynamic signatures. Phys. Rev. X 2015, 5, 031044. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The quantum harmonic Otto cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Hernández, A.C. Carnot-Like Heat Engines Versus Low-Dissipation Models. Entropy 2017, 19, 182. [Google Scholar] [CrossRef]
- Ye, Z.; Holubec, V. Optimizing low-dissipation Carnot-like thermal devices with heat leak. arXiv 2025, arXiv:2504.12655. [Google Scholar] [CrossRef]
- Anacleto, J.; Ferreira, J.M. Minimizing the generation of entropy: Which sequence of reservoirs to choose? Eur. J. Phys. 2010, 31, L1. [Google Scholar] [CrossRef]
- Aneja, P.; Katyayan, H.; Johal, R.S. Optimal engine performance using inference for non-identical finite source and sink. Mod. Phys. Lett. B 2015, 29, 1550217. [Google Scholar] [CrossRef]
- Wang, Y. Optimizing work output for finite-sized heat reservoirs: Beyond linear response. Phys. Rev. E 2016, 93, 012120. [Google Scholar] [CrossRef]
- Esposito, M.; Lindenberg, K.; Van den Broeck, C. Entropy production as correlation between system and reservoir. New J. Phys. 2010, 12, 013013. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Calvo Hernández, A.; White, J.A.; Medina, A.; Roco, J.M.M.; Velasco, S. Success versus failure: Efficient heat devices in thermodynamics. Phys. Rev. E 2022, 105, 014115. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Ayala, J.; Angulo-Brown, F.; Calvo Hernández, A.; Velasco, S. On reversible, endoreversible, and irreversible heat device cycles versus the Carnot cycle: A pedagogical approach to account for losses. Eur. J. Phys. 2016, 37, 045103. [Google Scholar] [CrossRef]
- Andresen, B.; Rubin, M.H.; Berry, R.S. Availability for finite-time processes. General theory and a model. J. Phys. Chem. 1983, 87, 2704–2713. [Google Scholar] [CrossRef]
- Berry, R.S.; Kazakov, V.A.; Sieniutycz, S.; Szwast, Z.; Tsirlin, A.M. Thermodynamic Optimization of Finite Time Processes; Wiley: Chichester, UK, 1999; ISBN 0-471-967521. [Google Scholar]
- Feidt, M. The History and Perspectives of Efficiency at Maximum Power of the Carnot Engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Costea, M.; Petrescu, S.; Feidt, M.; Dobre, C.; Borcila, B. Optimization Modeling of Irreversible Carnot Engine from the Perspective of Combining Finite Speed and Finite Time Analysis. Entropy 2021, 23, 504. [Google Scholar] [CrossRef] [PubMed]
- Tsirlin, A.M.; Balunov, A.I.; Sukin, I.A.; Vasilyev, A.M. Methods of Optimization Thermodynamics in Distillation Processes. Theor. Found Chem. Eng. 2023, 57, 537–548. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Santillán, M.; Reyes-Ramírez, I.; Calvo Hernández, A. Link between optimization and local stability of a low dissipation heat engine: Dynamic and energetic behaviors. Phys. Rev. E 2018, 98, 032142. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Guo, J.; Medina, A.; Roco, J.M.M.; Calvo Hernández, A. Optimization induced by stability and the role of limited control near a steady state. Phys. Rev. E 2019, 100, 062128. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Guo, J.; Medina, A.; Roco, J.M.M.; Hernández, A.C. Energetic Self-Optimization Induced by Stability in Low-Dissipation Heat Engines. Phys. Rev. Lett. 2020, 124, 050603. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Calvo-Hernández, A. Optimization, Stability, and Entropy in Endoreversible Heat Engines. Entropy 2020, 22, 1323. [Google Scholar] [CrossRef]
- England, J.L. Dissipative adaptation in driven self-assembly. Nat. Nanotechnol. 2015, 10, 919–923. [Google Scholar] [CrossRef] [PubMed]
- Belete, M.K.; Bal, G. Optimality and adaptation of phenotypically switching cells in fluctuating environments. Phys. Rev. E 2015, 92, 062716. [Google Scholar] [CrossRef]
- Perunov, N.; Marsland, R.A.; England, J.L. Statistical Physics of Adaptation. Phys. Rev. X 2016, 6, 021036. [Google Scholar] [CrossRef]
- Rao, R.; Esposito, M. Nonequilibrium Thermodynamics of Chemical Reaction Networks: Wisdom from Stochastic Thermodynamics. Phys. Rev. X 2016, 6, 041064. [Google Scholar] [CrossRef]
- Kobayashi, T.J.; Sughiyama, Y. Stochastic and information-thermodynamic structures of population dynamics in a fluctuating environment. Phys. Rev. E 2017, 96, 012402. [Google Scholar] [CrossRef] [PubMed]
- Ouldridge, T.E.; Govern, C.C.; Wolde, P.R.T. Thermodynamics of Computational Copying in Biochemical Systems. Phys. Rev. X 2017, 7, 021004. [Google Scholar] [CrossRef]
- Helbing, D.; Vicsek, T. Optimal self-organization. New J. Phys. 1999, 1, 13.1–13.17. [Google Scholar] [CrossRef]
- Wächtler, C.W.; Strasberg, P.; Klapp, S.H.L.; Schaller, G.; Jarzynski, C. Stochastic thermodynamics of self-oscillations: The electron shuttle. New J. Phys. 2019, 21, 073009. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 3-540-54062-8. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Ayala, J.; Pérez-Gallego, D.; Medina, A.; Roco, J.M.M.; Calvo Hernández, A.; Velasco, S.; Angulo-Brown, F. Linking Optimization Success and Stability of Finite-Time Thermodynamics Heat Engines. Entropy 2025, 27, 822. https://doi.org/10.3390/e27080822
Gonzalez-Ayala J, Pérez-Gallego D, Medina A, Roco JMM, Calvo Hernández A, Velasco S, Angulo-Brown F. Linking Optimization Success and Stability of Finite-Time Thermodynamics Heat Engines. Entropy. 2025; 27(8):822. https://doi.org/10.3390/e27080822
Chicago/Turabian StyleGonzalez-Ayala, Julian, David Pérez-Gallego, Alejandro Medina, José M. Mateos Roco, Antonio Calvo Hernández, Santiago Velasco, and Fernando Angulo-Brown. 2025. "Linking Optimization Success and Stability of Finite-Time Thermodynamics Heat Engines" Entropy 27, no. 8: 822. https://doi.org/10.3390/e27080822
APA StyleGonzalez-Ayala, J., Pérez-Gallego, D., Medina, A., Roco, J. M. M., Calvo Hernández, A., Velasco, S., & Angulo-Brown, F. (2025). Linking Optimization Success and Stability of Finite-Time Thermodynamics Heat Engines. Entropy, 27(8), 822. https://doi.org/10.3390/e27080822









