Compressor Power and Efficiency Optimization: A Finite-Time Thermodynamics Approach
Abstract
1. Introduction
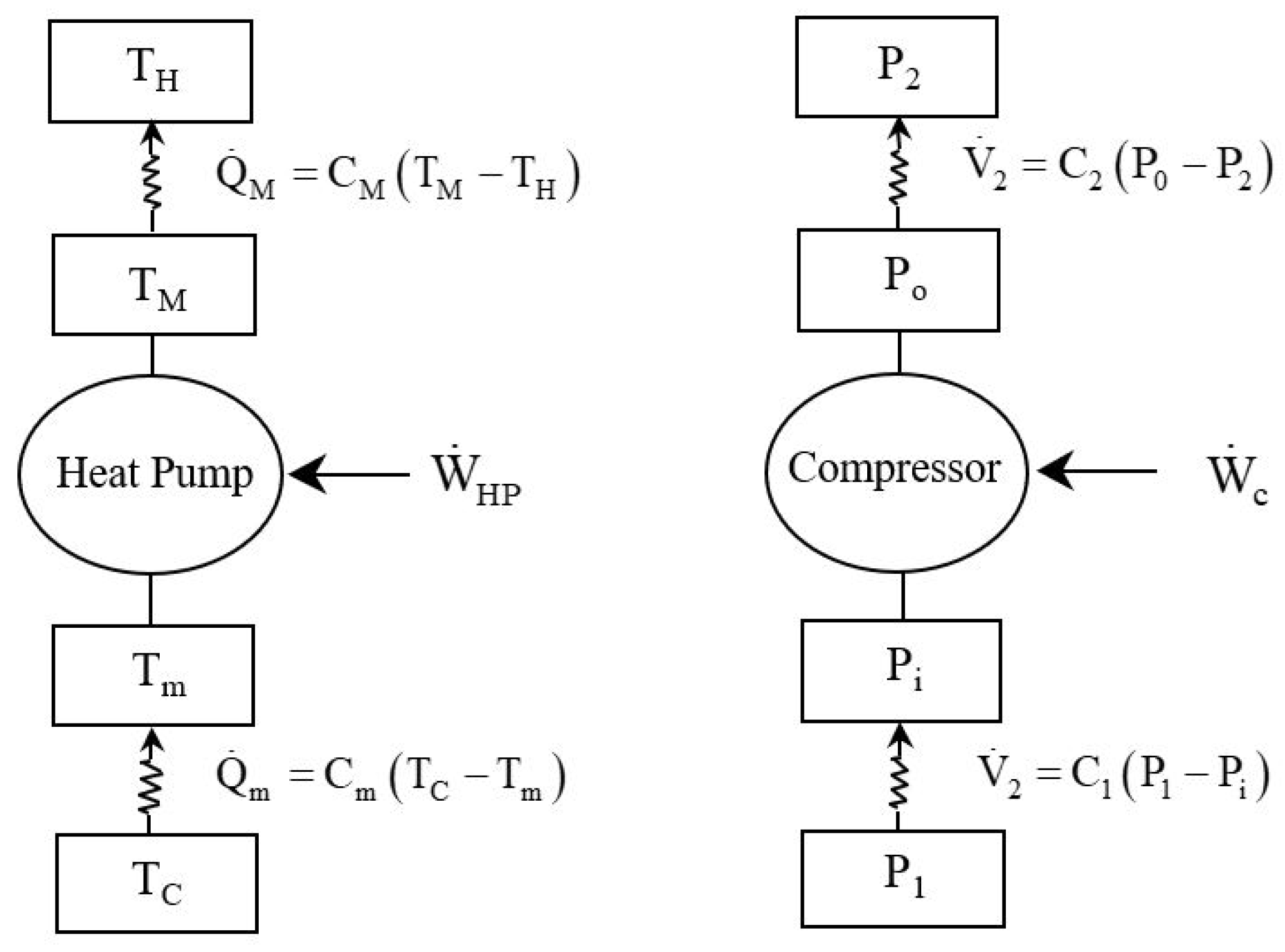
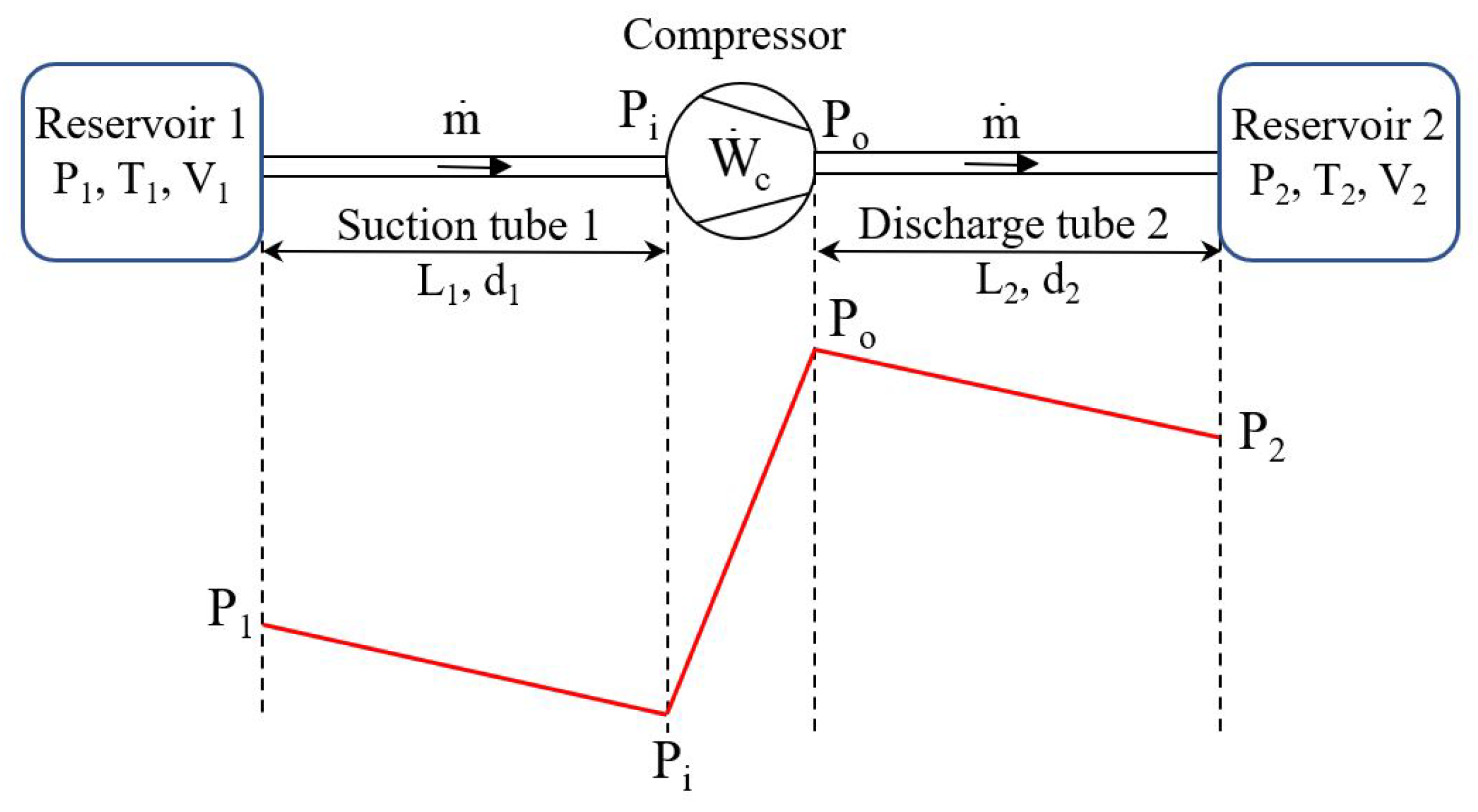
2. Mathematical Model
2.1. Optimal Mechanical Power of the Compressor
2.2. Energy Conversion Efficiency of the Compressor
3. Results and Discussion
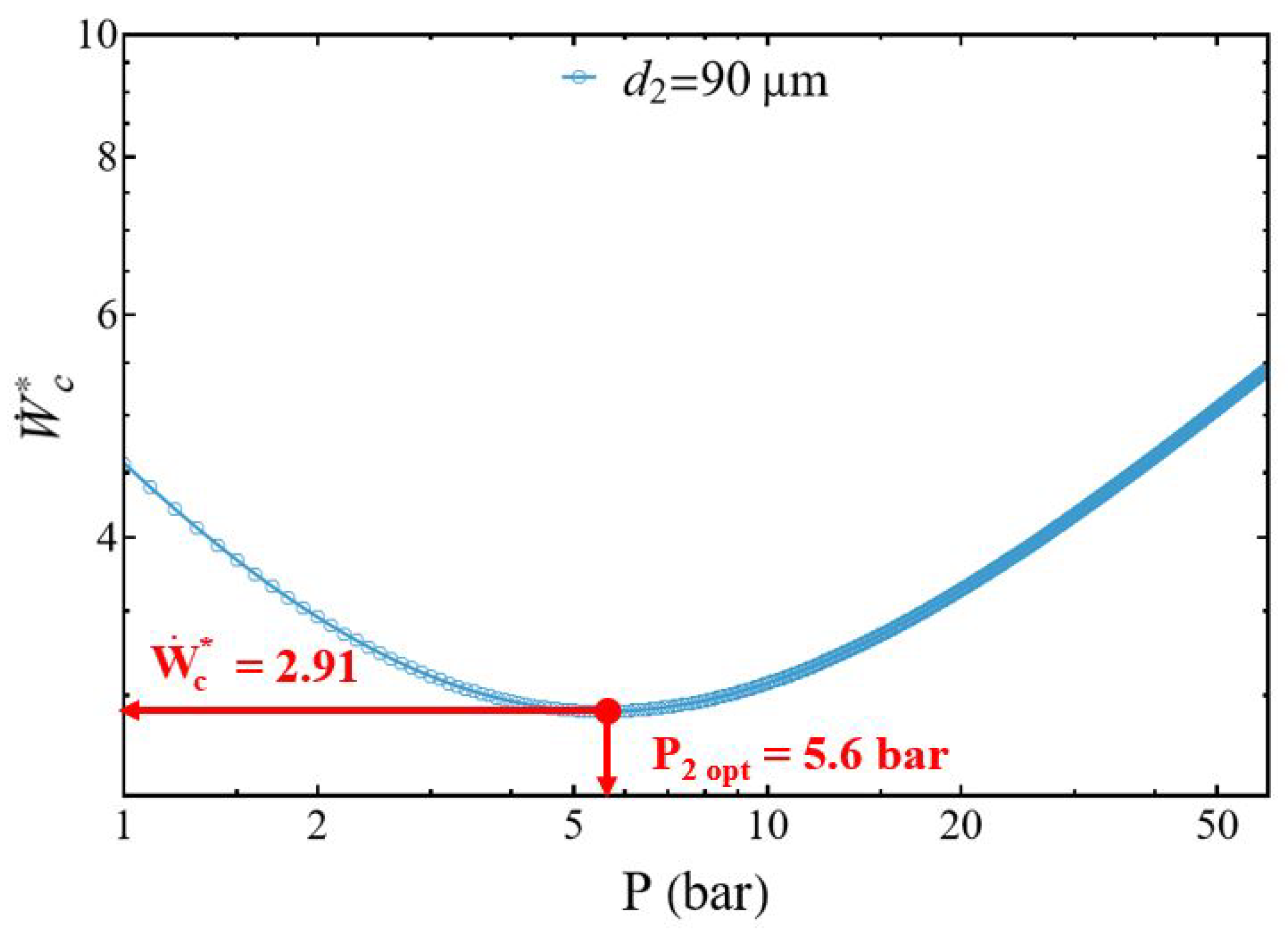
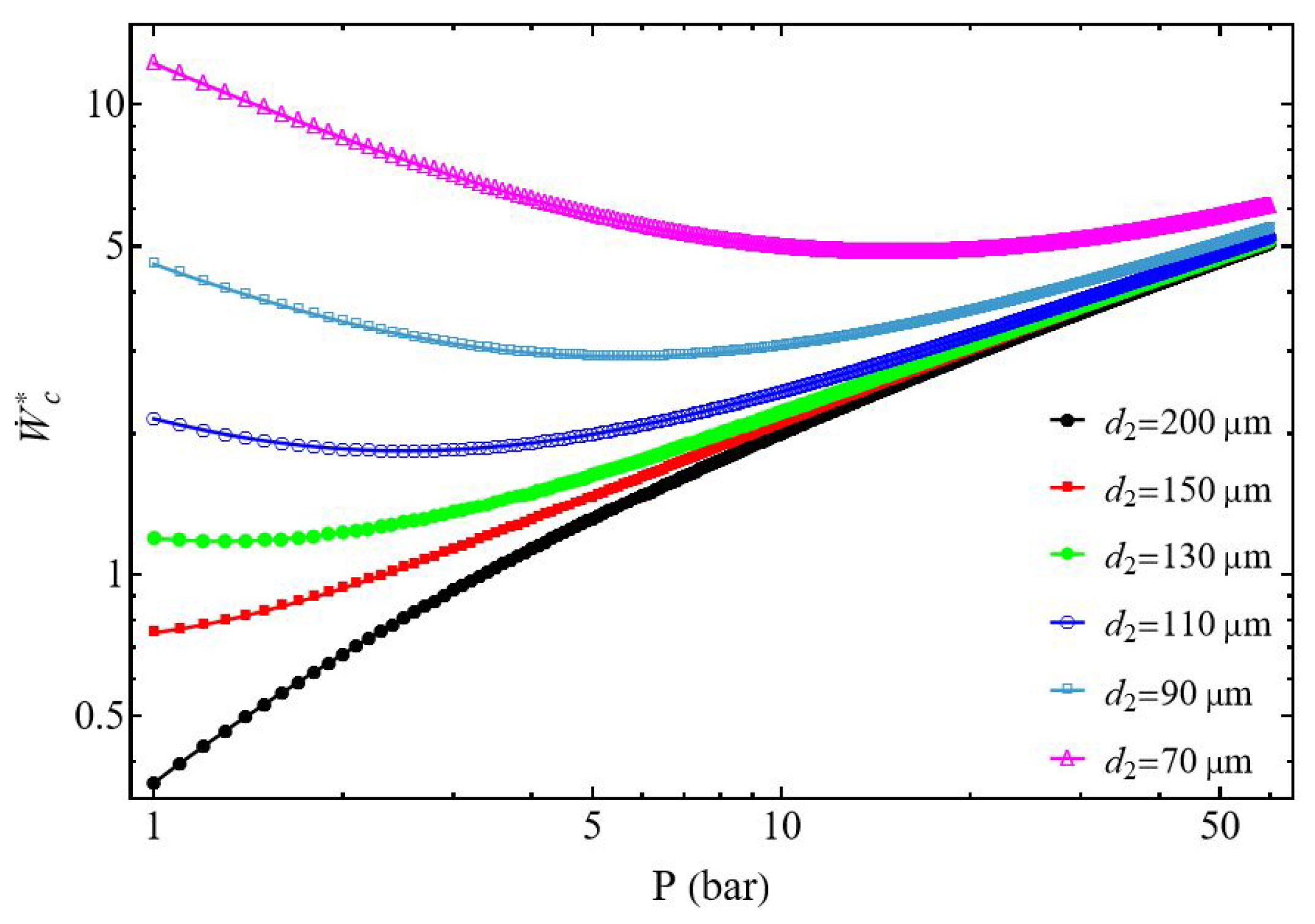
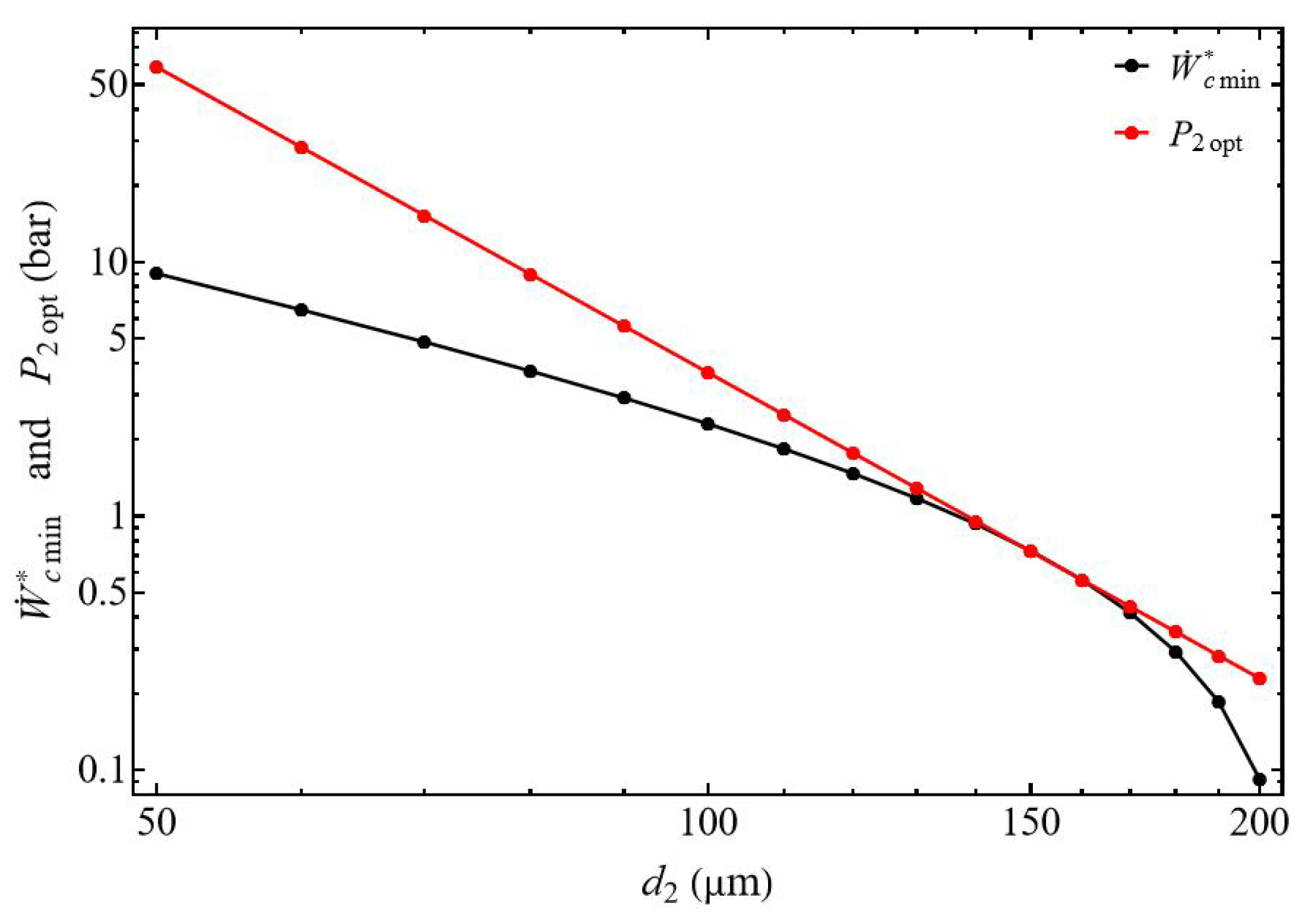
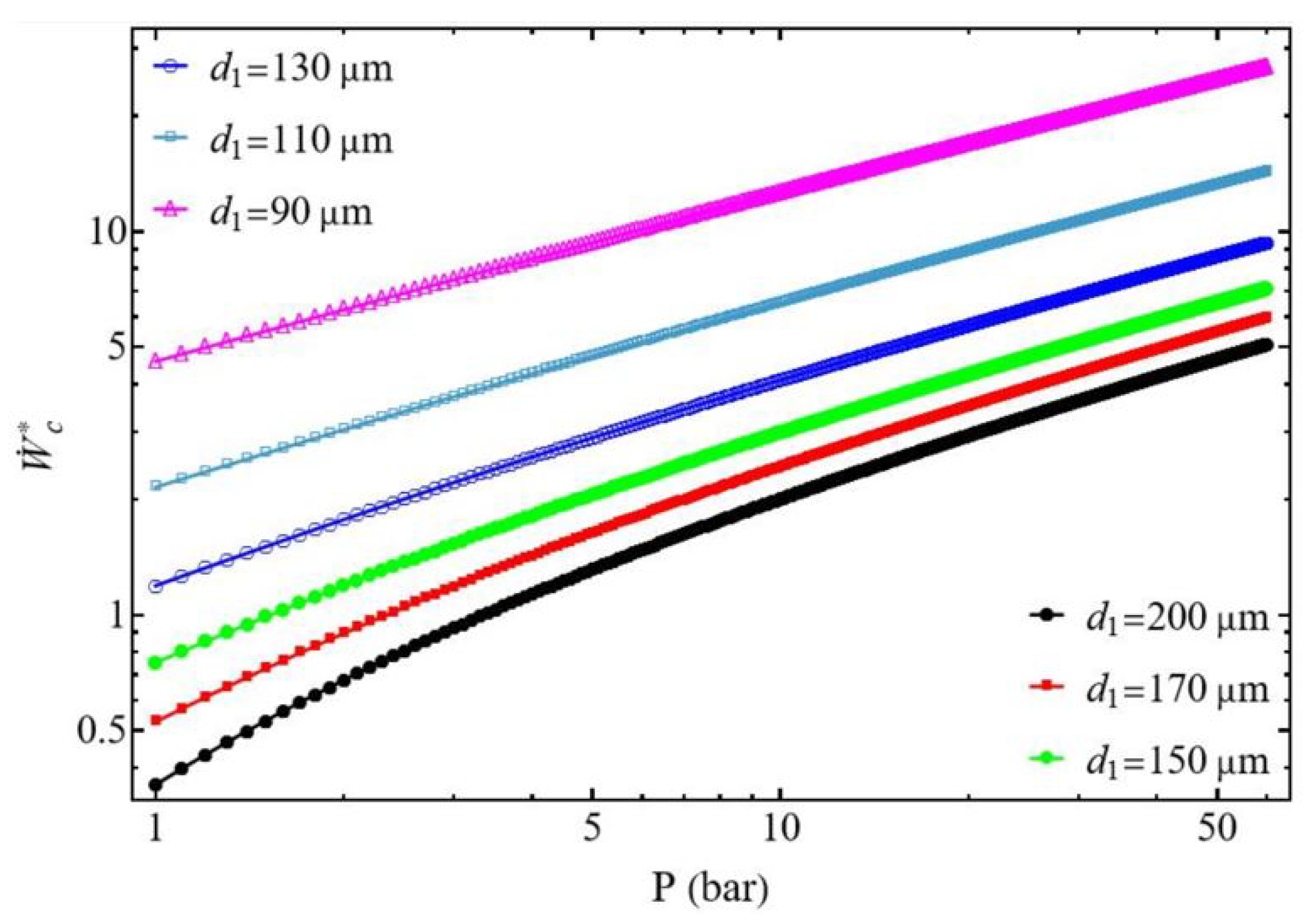
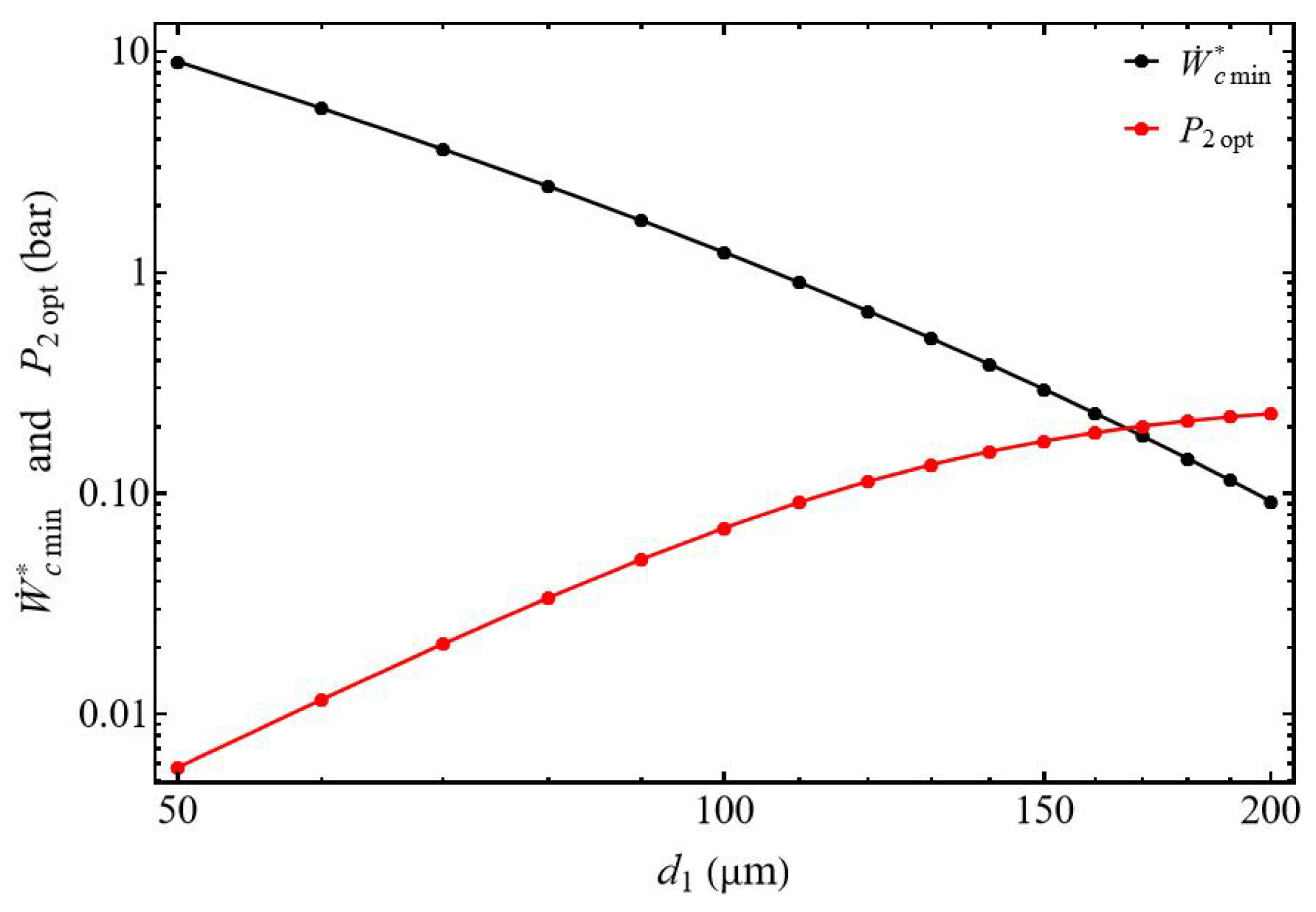
3.1. Compressor Power
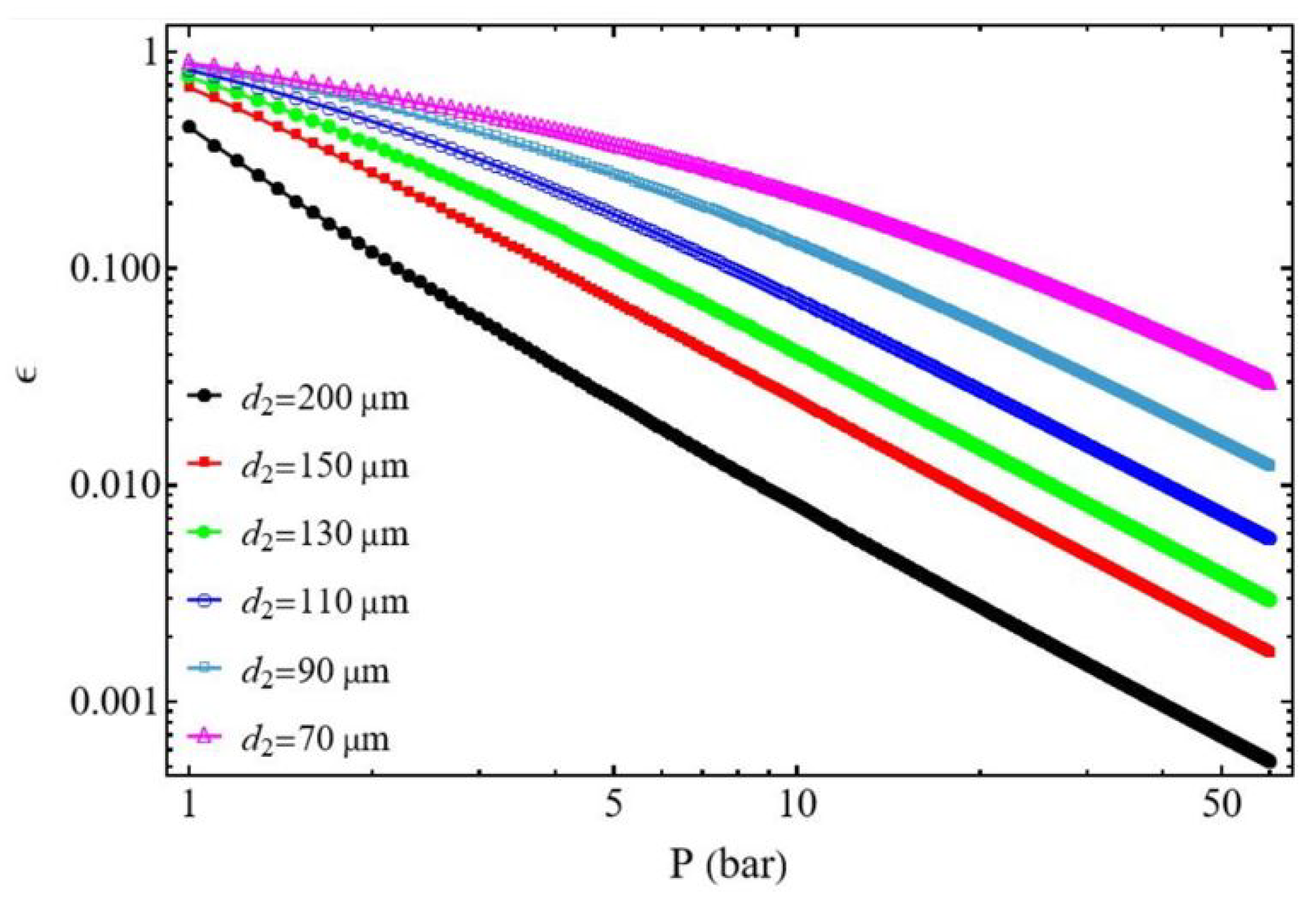
3.2. Compressor Efficiency
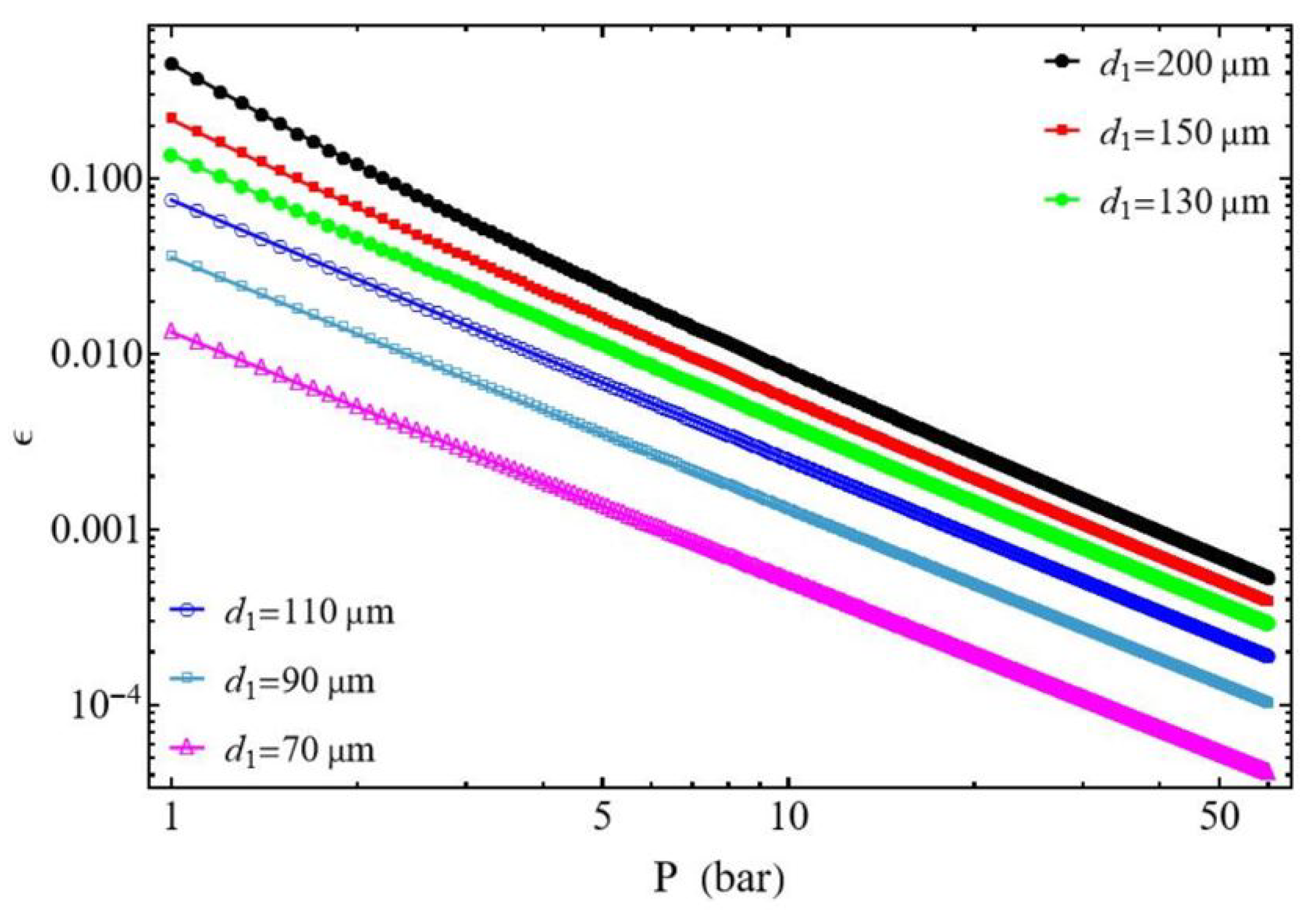
3.2.1. Effect of the Discharged Pressure
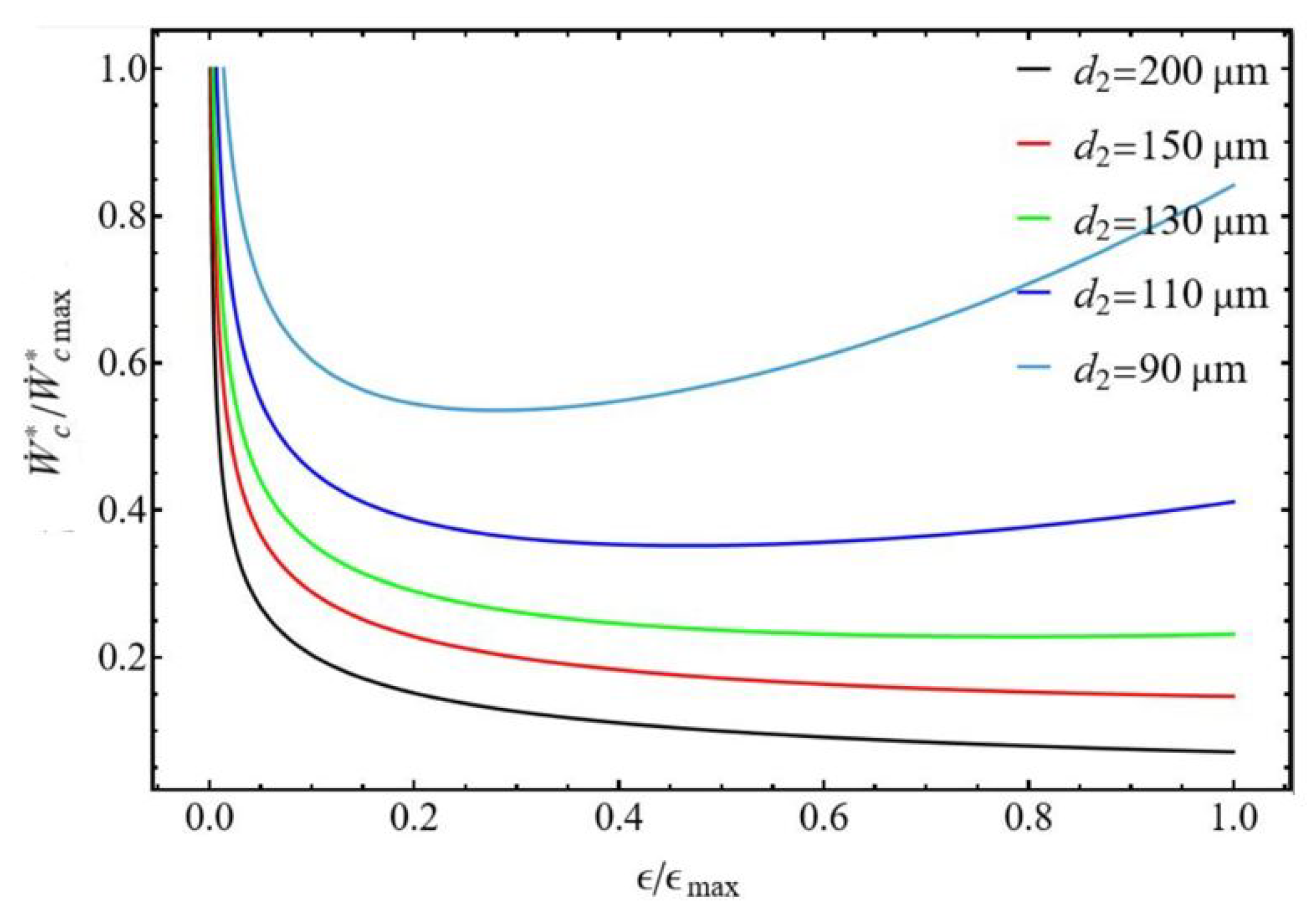
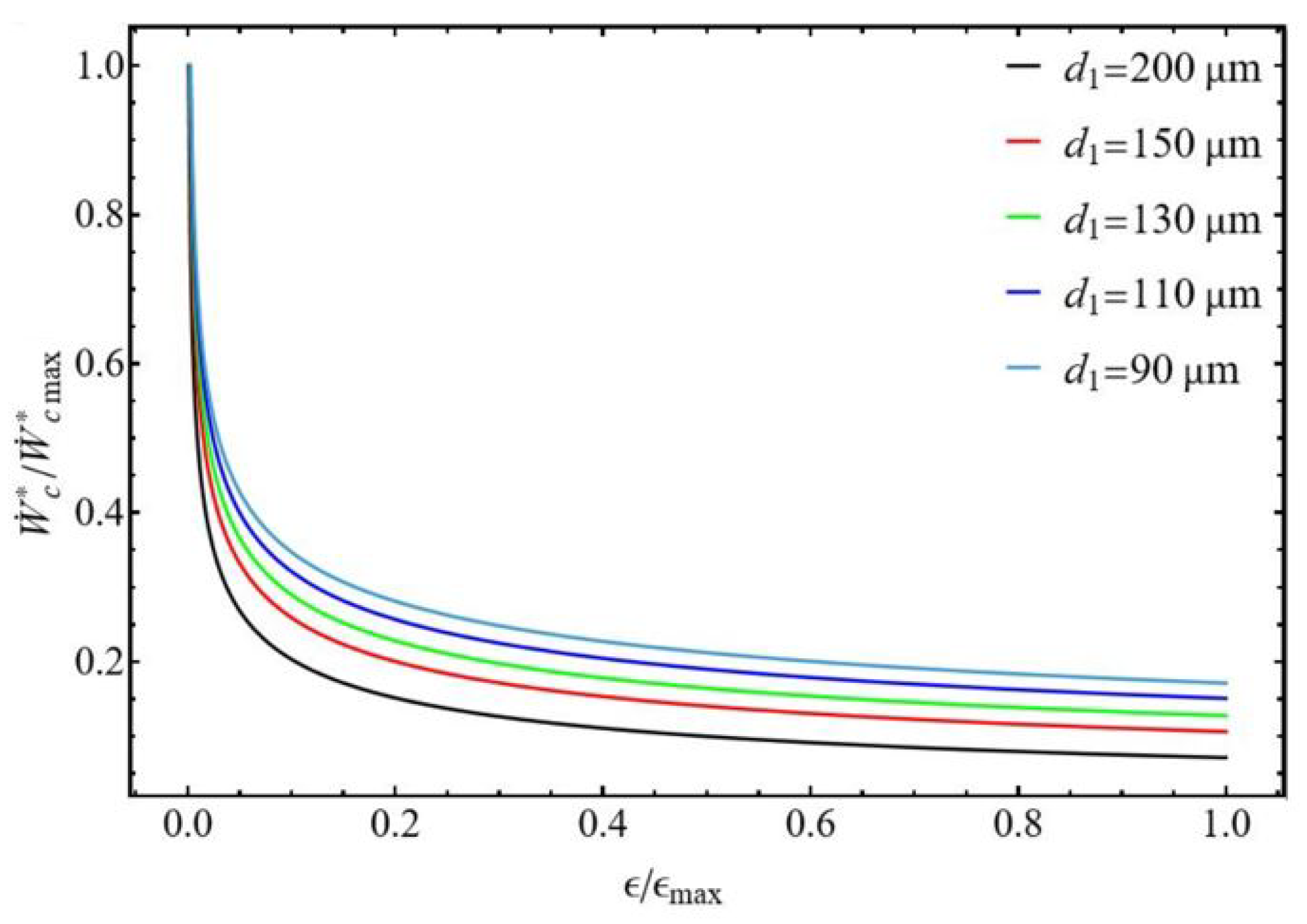
3.2.2. Bounds of Efficiency and Compression Power
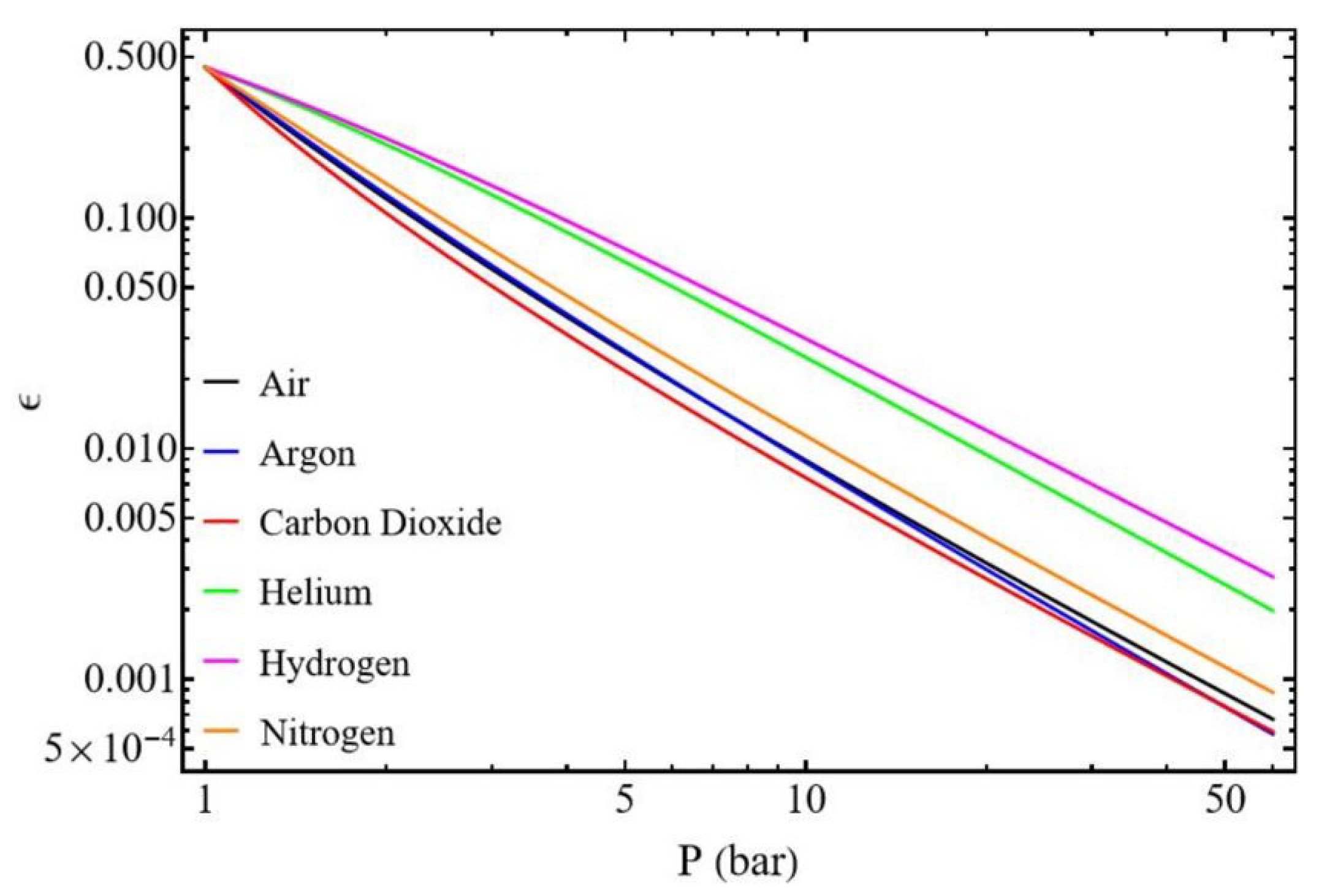
3.2.3. Influence of Gas Type
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chambadal, P. Les Centrales Nucléaires; Cambridge University Press: Cambridge, UK, 1957. [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations (a review). J. Nucl. Energy (1954) 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Rubin, M.H. Optimal configuration of a class of irreversible heat engines. I. Phys. Rev. A 1979, 19, 1272. [Google Scholar] [CrossRef]
- Rubin, M.H. Optimal configuration of a class of irreversible heat engines. II. Phys. Rev. A 1979, 19, 1277. [Google Scholar] [CrossRef]
- Andresen, B.; Rubin, M.H.; Berry, R.S. Availability for finite-time processes. General theory and a model. J. Phys. Chem. 1983, 87, 2704–2713. [Google Scholar] [CrossRef]
- Berry, R.S.; Salamon, P.; Andresen, B. How it all began. Entropy 2020, 22, 908. [Google Scholar] [CrossRef] [PubMed]
- Andresen, B. Finite-time thermodynamics and thermodynamic length. Rev. Générale Therm. 1996, 35, 647–650. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P. Future perspectives of finite-time thermodynamics. Entropy 2022, 24, 690. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Blank, D.A.; Davis, G.W.; Wu, C. Power optimization of an endoreversible Stirling cycle with regeneration. Energy 1994, 19, 125–133. [Google Scholar] [CrossRef]
- Blank, D.A.; Bhattacharyya, S. Chapter Heating rate limit and cooling rate limit of a reversed reciprocating Stirling cycle. In Recent Advances in Finite Time Thermodynamics; Nova Science Publishers: New York, NY, USA, 1999; pp. 87–103. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time: Extremals for imperfect heat engines. J. Chem. Phys. 1977, 66, 1571–1577. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D Appl. Phys. 1994, 27, 1144. [Google Scholar] [CrossRef]
- Chen, J. A universal model of an irreversible combined Carnot cycle system and its general performance characteristics. J. Phys. A Math. Gen. 1998, 31, 3383. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Yilmaz, T. A comparative performance analysis of irreversible Carnot heat engines under maximum power density and maximum power conditions. Energy Convers. Manag. 2000, 41, 235–248. [Google Scholar] [CrossRef]
- Ozkaynak, S.; Gokun, S.; Yavuz, H. Finite-time thermodynamic analysis of a radiative heat engine with internal irreversibility. J. Phys. D Appl. Phys. 1994, 27, 1139. [Google Scholar] [CrossRef]
- Wu, C.; Kiang, R.L. Finite-time thermodynamic analysis of a Carnot engine with internal irreversibility. Energy 1992, 17, 1173–1178. [Google Scholar] [CrossRef]
- Vaudrey, A.; Lanzetta, F.; Feidt, M. HB Reitlinger and the origins of the efficiency at maximum power formula for heat engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Muschik, W.; Hoffmann, K.H. Modeling, simulation, and reconstruction of 2-reservoir heat-to-power processes in finite-time thermodynamics. Entropy 2020, 22, 997. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Chen, L.; Sun, F. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Popescu, G.; Radcenco, V.; Costea, M.; Feidt, M. Optimisation thermodynamique en temps fini du moteur de Stirling endo-et exo-irréversible. Rev. Générale Therm. 1996, 35, 656–661. [Google Scholar] [CrossRef]
- Wu, F.; Chen, L.; Wu, C.; Sun, F. Optimum performance of irreversible Stirling engine with imperfect regeneration. Energy Convers. Manag. 1998, 39, 727–732. [Google Scholar] [CrossRef]
- Lanzetta, F.; Vaudrey, A.; Baucour, P. A new method to optimise finite dimensions thermodynamic models: Application to an irreversible Stirling engine. Int. J. Ambient Energy 2018, 39, 392–405. [Google Scholar] [CrossRef]
- Lai, H.Y.; Li, Y.T.; Chan, Y.H. Efficiency enhancement on hybrid power system composed of irreversible solid oxide fuel cell and Stirling engine by finite time thermodynamics. Energies 2021, 14, 1037. [Google Scholar] [CrossRef]
- Wu, B.; Chen, L.; Ge, Y.; Feng, H.; Liu, X. Finite-time thermodynamic multi-objective optimizations for an irreversible simple Brayton refrigeration cycle based on four objectives, NASG-II algorithm and three decision-making strategies. J. Therm. Anal. Calorim. 2025, 150, 4653–4668. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Lin, X.; Chen, H. Performance of pumped thermal electricity storage system based on reverse/forward Brayton cycle. Energy Storage Sci. Technol. 2021, 10, 1796. [Google Scholar]
- Qu, J.; Feng, Y.; Wu, B.; Zhu, Y.; Wang, J. Understanding the thermodynamic behaviors of integrated system including solid oxide fuel cell and Carnot battery based on finite time thermodynamics. Appl. Energy 2024, 372, 123762. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Tyagi, S.K.; Kumar, P. Finite Time Thermodynamics of Power and Refrigeration Cycles; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Dumitrascu, G.; Feidt, M.; Grigorean, S. Closed Irreversible Cycles Analysis Based on Finite Physical Dimensions Thermodynamics. Proceedings 2020, 58, 37. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamics applied to reverse cycle machines, a review. Int. J. Refrig. 2010, 33, 1327–1342. [Google Scholar] [CrossRef]
- Feidt, M. Finite Physical Dimensions Optimal Thermodynamics 1: Fundamentals; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Ahmadi, M.H.; Ahmadi, M.A.; Mehrpooya, M.; Hosseinzade, H.; Feidt, M. Thermodynamic and thermo-economic analysis and optimization of performance of irreversible four-temperature-level absorption refrigeration. Energy Convers. Manag. 2014, 88, 1051–1059. [Google Scholar] [CrossRef]
- Sahraie, H.; Mirani, M.R.; Ahmadi, M.H.; Ashouri, M. Thermo-economic and thermodynamic analysis and optimization of a two-stage irreversible heat pump. Energy Convers. Manag. 2015, 99, 81–91. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Wu, C.; Chen, L.; Chen, J. Recent Advances in Finite-Time Thermodynamics; Nova Publishers: Hauppauge, NY, USA, 1999. [Google Scholar]
- Chen, L.; Feng, H.; Sun, F. Optimal piston speed ratio analyses for irreversible Carnot refrigerator and heat pump using finite time thermodynamics, finite speed thermodynamics and direct method. J. Energy Inst. 2011, 84, 105–112. [Google Scholar] [CrossRef]
- Ge, Y.; Wu, H.; Chen, L.; Feng, H.; Xie, Z. Finite time and finite speed thermodynamic optimization for an irreversible Atkinson cycle. Energy 2023, 270, 126856. [Google Scholar] [CrossRef]
- Grosu, L.; Dobre, C.; Petrescu, S. Study of a Stirling engine used for domestic micro-cogeneration. Thermodynamic analysis and experiment. Int. J. Energy Res. 2015, 39, 1280–1294. [Google Scholar] [CrossRef]
- Petrescu, S.; Feidt, M.; Enache, V.; Costea, M.; Stanciu, C.; Boriaru, N. Unification perspective of finite physical dimensions thermodynamics and finite speed thermodynamics. Int. J. Energy Environ. Eng. 2015, 6, 245–254. [Google Scholar] [CrossRef]
- Agrawal, D.; Menon, V. The thermoelectric generator as an endoreversible Carnot engine. J. Phys. D Appl. Phys. 1997, 30, 357. [Google Scholar] [CrossRef]
- Bejan, A.; Dan, N. Maximum work from an electric battery model. Energy 1997, 22, 93–102. [Google Scholar] [CrossRef]
- Chen, L.; Bi, Y.; Wu, C. The influence of nonlinear flow resistance relations on the power and efficiency from fluid flow. J. Phys. D Appl. Phys. 1999, 32, 1346. [Google Scholar] [CrossRef]
- Lanzetta, F.; Désévaux, P.; Bailly, Y. Optimization performance of a microfluid flow power converter. Int. J. Fluid Power 2002, 3, 5–12. [Google Scholar] [CrossRef]
- Noack, B.R.; Schlegel, M.; Ahlborn, B.; Mutschke, G.; Morzyński, M.; Comte, P.; Tadmor, G. A finite-time thermodynamics of unsteady fluid flows. J. Non-Equilib. Thermodyn. 2008, 33, 103–148. [Google Scholar] [CrossRef]
- Bejan, A. Thermodynamic optimization of geometry in engineering flow systems. Exergy Int. J. 2001, 1, 269–277. [Google Scholar] [CrossRef]
- Madou, M. From MEMS to Bio-MEMS and Bio-NEMS Manufacturing Techniques and Applications; Routledge Taylor & Francis Group: London, UK, 2011. [Google Scholar]
- Nguyen, N.T.; Huang, X.; Chuan, T.K. MEMS-micropumps: A review. J. Fluids Eng. 2002, 124, 384–392. [Google Scholar] [CrossRef]
- Dang, H.; Tan, J.; Zha, R.; Li, J.; Zhang, T.; Zhao, Y.; Zhao, B.; Tan, H.; Xue, R. Review of recent advances in Stirling-type pulse tube cryocoolers. IOP Conf. Ser. Mater. Sci. Eng. 2019, 502, 012034. [Google Scholar] [CrossRef]
- Pfotenhauer, J.M.; Zhi, X. Pulse Tube Cryocoolers. In Handbook of Superconductivity; CRC Press: Boca Raton, FL, USA, 2022; pp. 519–534. [Google Scholar]
- Knudsen, M. Eine revision der gleichgewichtsbedingung der gase. Thermische molekularströmung. Ann. Phys. 1909, 336, 205–229. [Google Scholar] [CrossRef]
- Dushman, S. Flow of gases through tubes and orifices. In Scientific Foundations of Vacuum Technique; Wiley: Hoboken, NJ, USA, 1949; pp. 84–110. [Google Scholar]
- Ivchenko, I.N.; Loyalka, S.K.; Tompson, R., Jr. Analytical Methods for Problems of Molecular Transport; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamentals and Applications, 2nd ed.; Mcgraw and Hill: New York, NY, USA, 2010. [Google Scholar]
- Van Wylen, G.J.; Sonntag, R.E.; Borgnakke, C. Fundamentals of Classical Thermodynamics; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Kestin, J.; Knierim, K.; Mason, E.; Najafi, B.; Ro, S.; Waldman, M. Equilibrium and transport properties of the noble gases and their mixtures at low density. J. Phys. Chem. Ref. Data 1984, 13, 229–303. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T. The Mathematical Theory of Non-Uniform Gases; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 4th ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
| Gas | Dynamic Viscosity ( Pa s) | Density () | Specific Heat (J ) | Thermal Conductivity (W ) | Adiabatic Index | Molar Mass (kg ) |
|---|---|---|---|---|---|---|
| Air | 1.817 | 1.203 | 1015 | 0.02565 | 1.400 | 28.97 |
| Argon (Ar) | 2.240 | 1.661 | 520 | 0.01737 | 1.670 | 39.948 |
| Carbon dioxide () | 1.493 | 1.871 | 851 | 0.01626 | 1.294 | 44.009 |
| Helium (He) | 1.973 | 0.166 | 5196 | 0.14929 | 1.666 | 4.003 |
| Hydrogen () | 0.867 | 0.084 | 14285 | 0.17690 | 1.410 | 2.016 |
| Nitrogen () | 1.757 | 1.164 | 1040 | 0.02543 | 1.400 | 28.013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lanzetta, F. Compressor Power and Efficiency Optimization: A Finite-Time Thermodynamics Approach. Entropy 2025, 27, 842. https://doi.org/10.3390/e27080842
Lanzetta F. Compressor Power and Efficiency Optimization: A Finite-Time Thermodynamics Approach. Entropy. 2025; 27(8):842. https://doi.org/10.3390/e27080842
Chicago/Turabian StyleLanzetta, François. 2025. "Compressor Power and Efficiency Optimization: A Finite-Time Thermodynamics Approach" Entropy 27, no. 8: 842. https://doi.org/10.3390/e27080842
APA StyleLanzetta, F. (2025). Compressor Power and Efficiency Optimization: A Finite-Time Thermodynamics Approach. Entropy, 27(8), 842. https://doi.org/10.3390/e27080842







