Periodic Intermittent Adaptive Control with Saturation for Pinning Quasi-Consensus of Heterogeneous Multi-Agent Systems with External Disturbances
Abstract
:1. Introduction
2. Preliminary Preparation and Model Description
2.1. Graph Theory
2.2. Model Description
3. Main Result
3.1. Adaptive Control Protocol
3.2. Adaptive Pinning Control
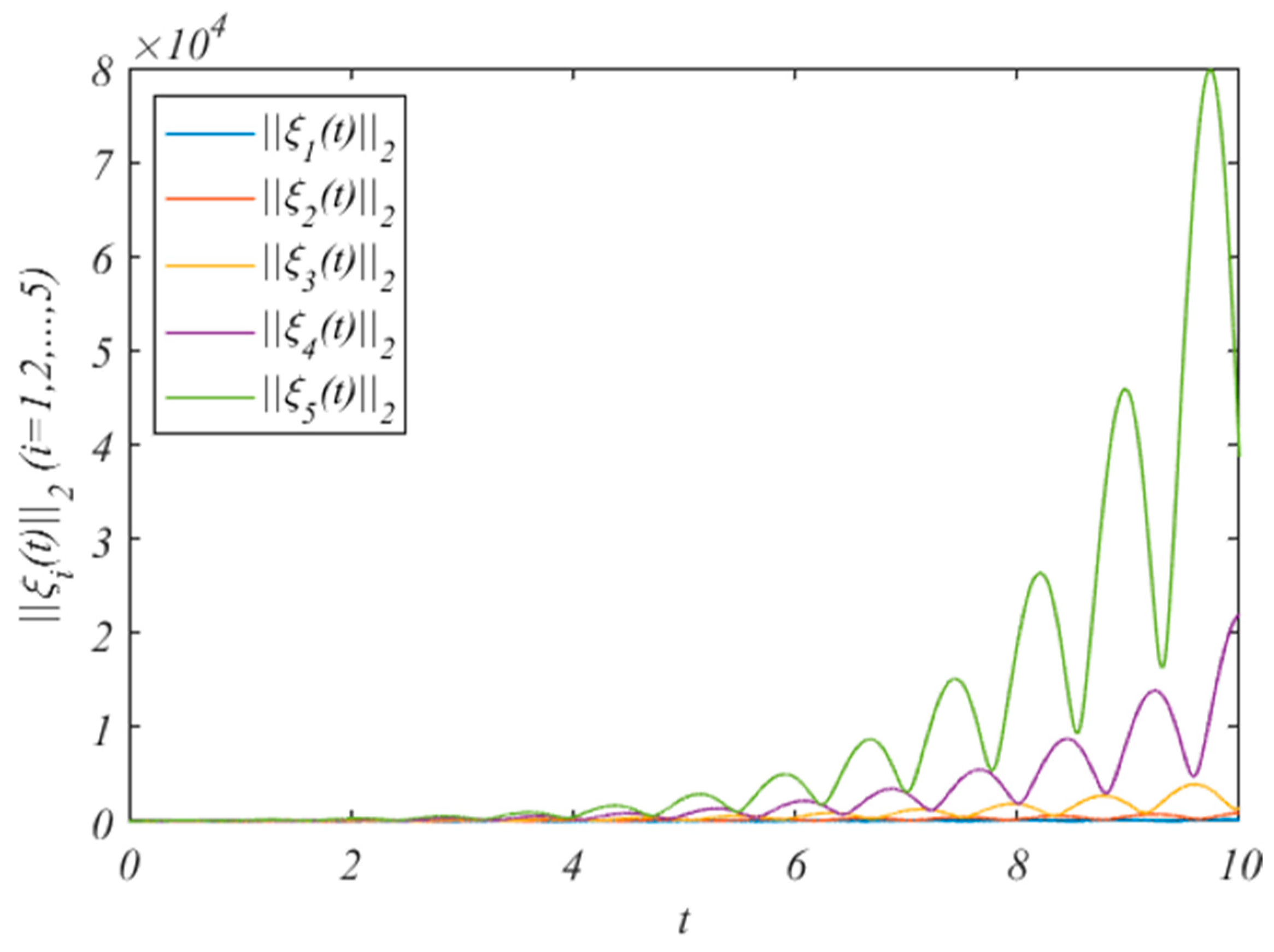
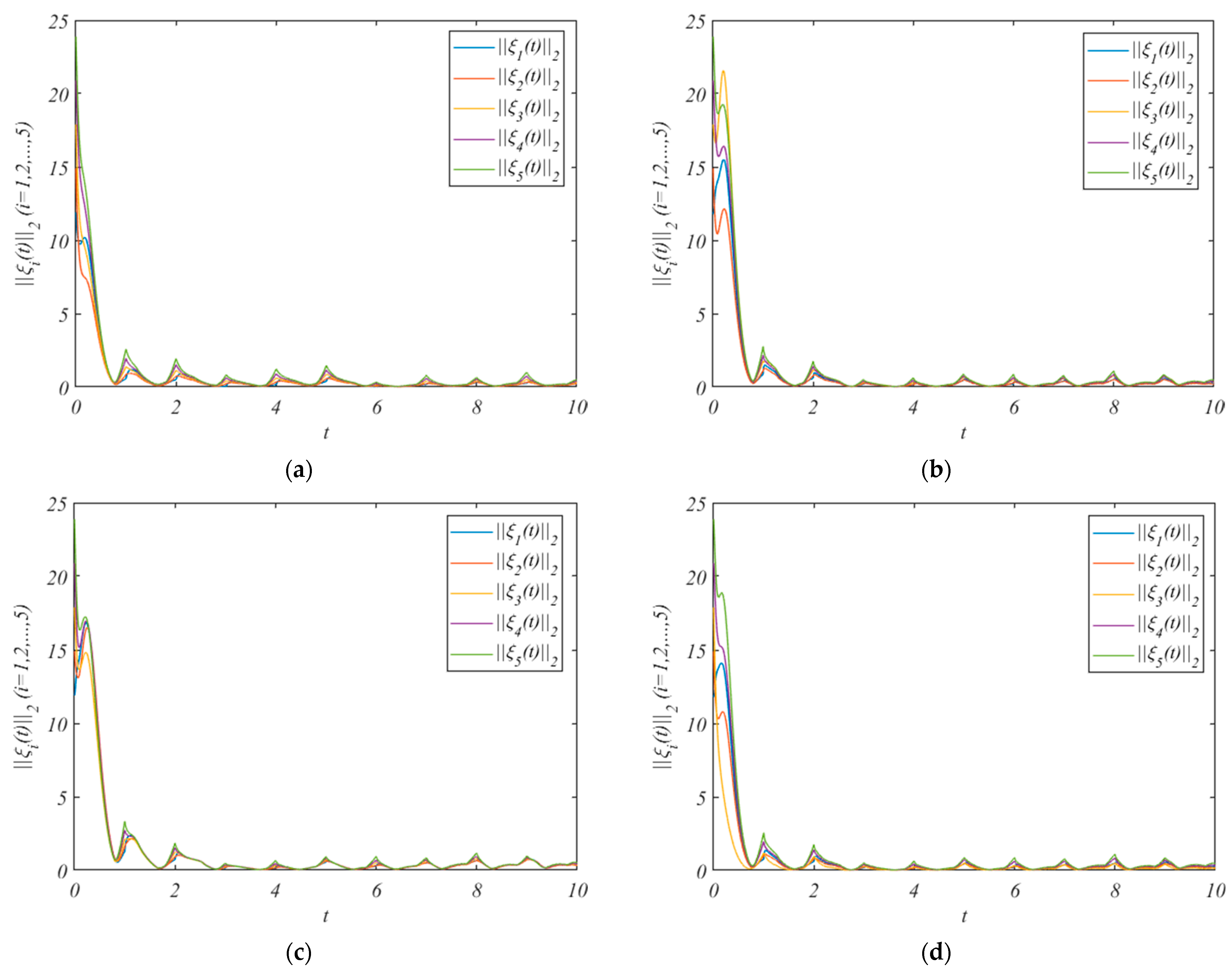
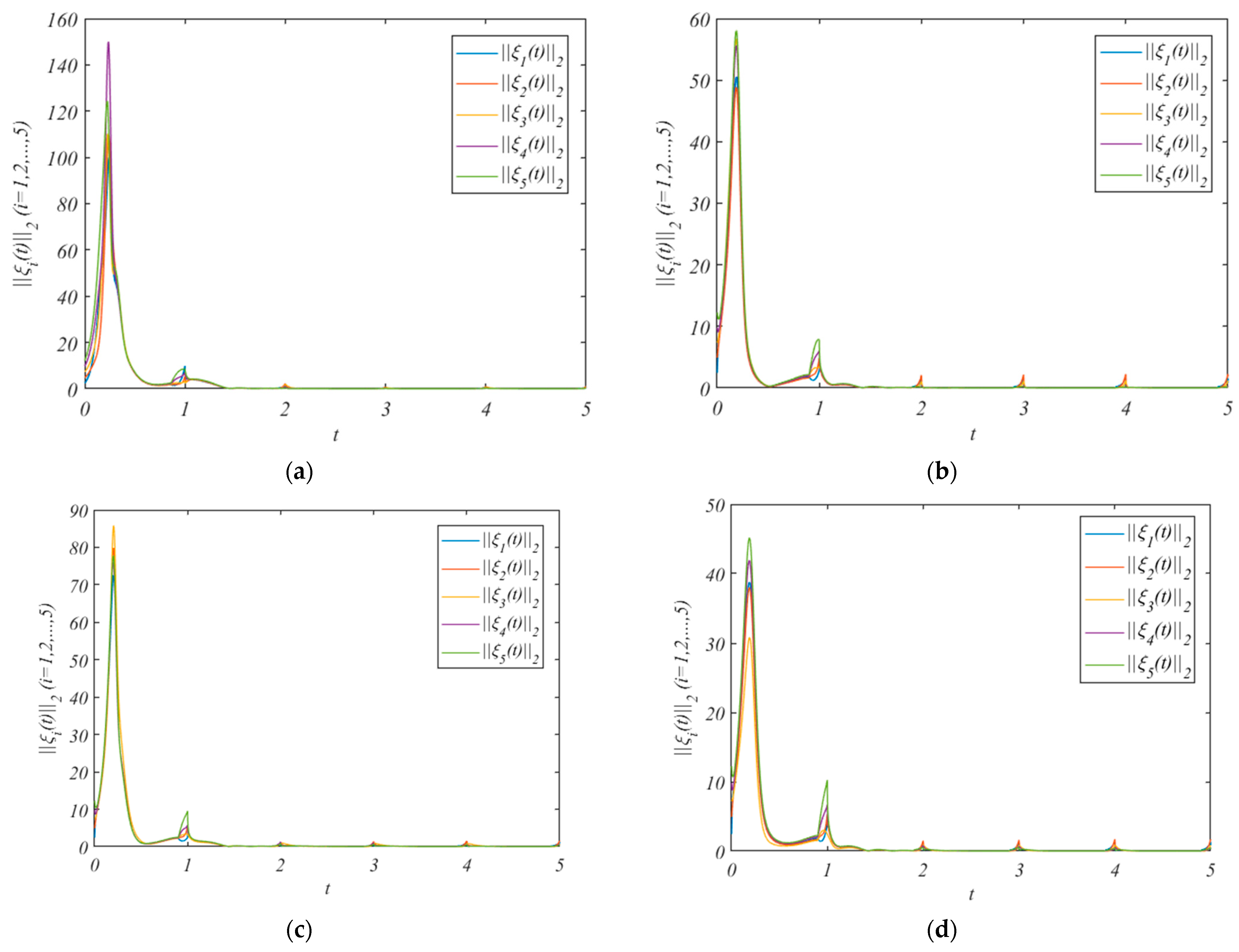
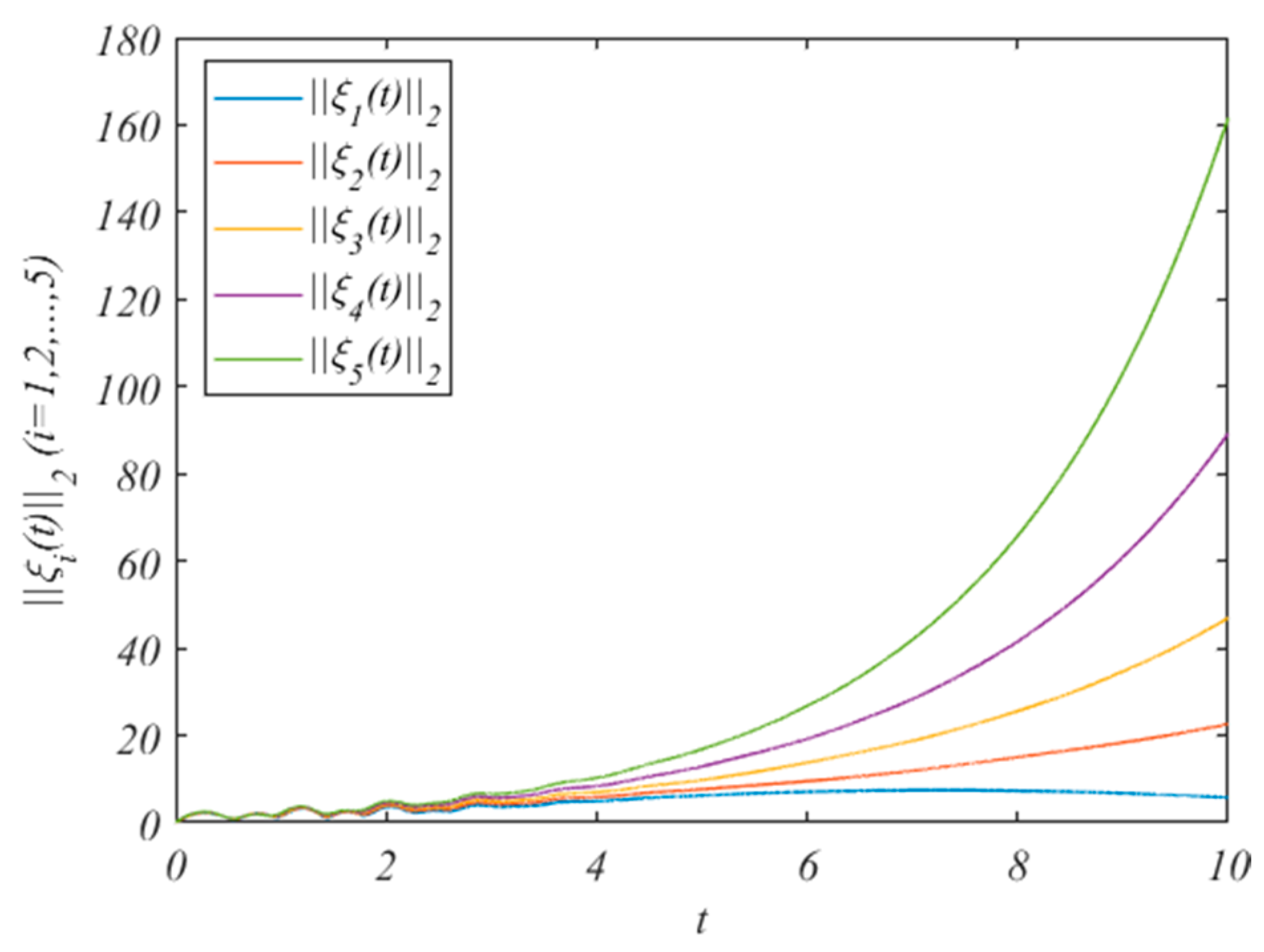
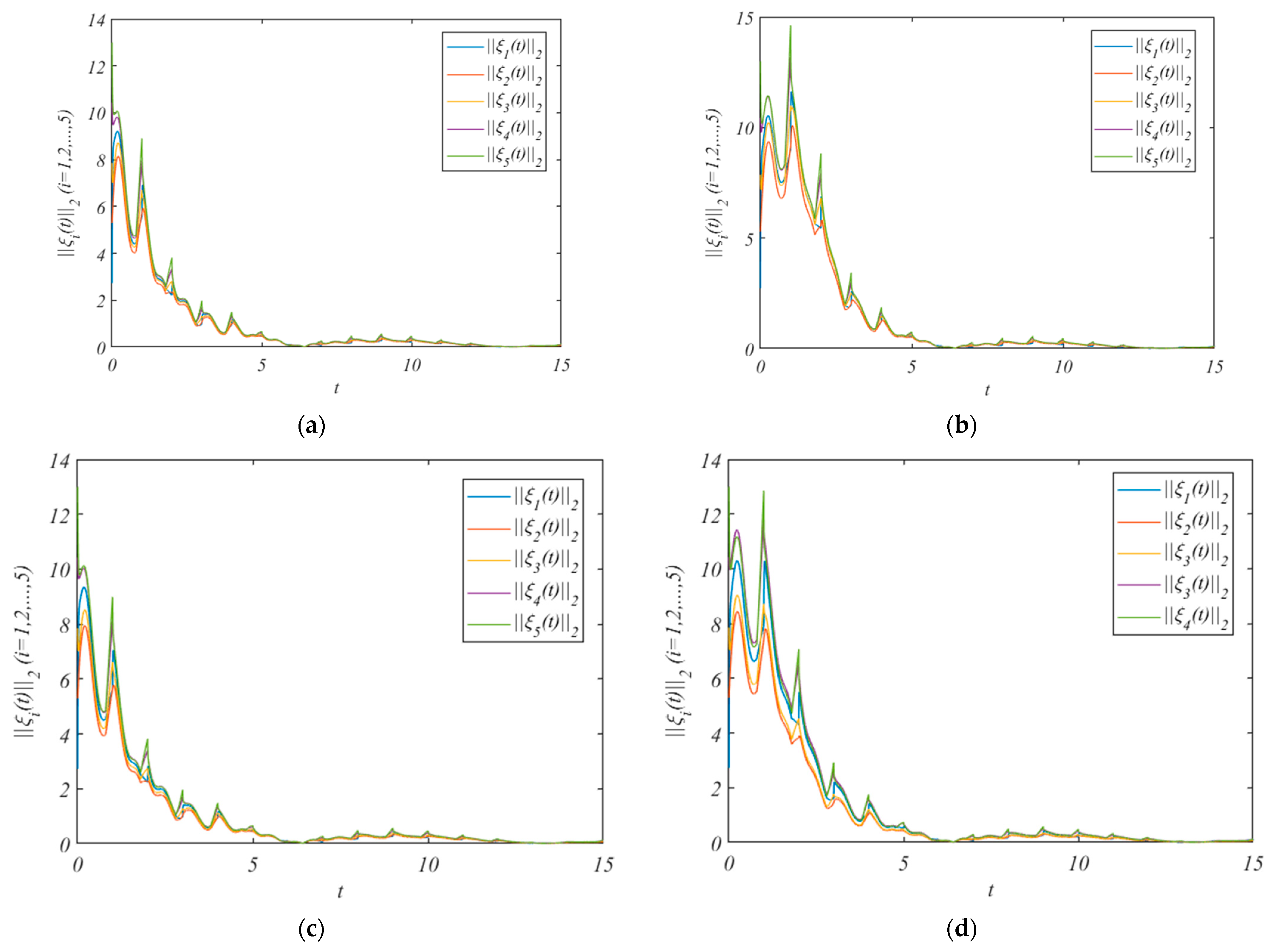
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Jadhav, A.M.; Patne, N.R. Priority-Based Energy Scheduling in a Smart Distributed Network With Multiple Microgrids. IEEE Trans. Ind. Inform. 2017, 13, 3134–3143. [Google Scholar] [CrossRef]
- Hector, R.; Vaidyanathan, R.; Sharma, G.; Trahan, J.L. Optimal Convex Hull Formation on a Grid by Asynchronous Robots With Lights. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 3532–3545. [Google Scholar] [CrossRef]
- Xue, D.; Yao, J.; Wang, J. H-infinity Formation Control and Obstacle Avoidance for Hybrid Multi-Agent Systems. J. Appl. Math. 2013, 2013, 123072. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y. Formation control for multi-agent systems through an iterative learning design approach. Int. J. Robust Nonlinear Control 2014, 24, 340–361. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Liu, Z. Formation control for nonlinear multi-agent systems by robust output regulation. Neurocomputing 2014, 140, 114–120. [Google Scholar] [CrossRef]
- Han, D.; Panagou, D. Robust Multitask Formation Control via Parametric Lyapunov-Like Barrier Functions. IEEE Trans. Autom. Control 2019, 64, 4439–4453. [Google Scholar] [CrossRef]
- Chai, X.; Liu, J.; Yu, Y.; Xi, J.; Sun, C. Practical Fixed-Time Event-Triggered Time-Varying Formation Tracking Control for Disturbed Multi-Agent Systems with Continuous Communication Free. Unmanned Syst. 2021, 9, 23–34. [Google Scholar] [CrossRef]
- Fan, W.; Chen, P.; Shi, D.; Guo, X.; Kou, L. Multi-Agent Modeling and Simulation in the AI Age. Tsinghua Sci. Technol. 2021, 26, 608–624. [Google Scholar] [CrossRef]
- Jiang, X.; Xia, G.; Feng, Z.; Jiang, Z. H-infinity delayed tracking protocol design of nonlinear singular multi-agent systems under Markovian switching topology. Inf. Sci. 2021, 545, 280–297. [Google Scholar] [CrossRef]
- Jiang, X.; Xia, G.; Feng, Z.; Jiang, Z. Consensus Tracking of Data-Sampled Nonlinear Multi-Agent Systems With Packet Loss and Communication Delay. IEEE Trans. Netw. Sci. Eng. 2021, 8, 126–137. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Guo, L.; Xu, B.; Gu, J.-Z. Collaboration Control of Fractional-Order Multiagent Systems with Sampling Delay. Math. Probl. Eng. 2013, 2013, 854960. [Google Scholar] [CrossRef]
- Liu, K.; Mu, X. Consensusability of multi-agent systems via observer with limited communication data rate. Int. J. Syst. Sci. 2016, 47, 3591–3597. [Google Scholar] [CrossRef]
- Hu, G. Robust consensus tracking of a class of second-order multi-agent dynamic systems. Syst. Control Lett. 2012, 61, 134–142. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of Multiagent Systems and Synchronization of Complex Networks: A Unified Viewpoint. IEEE Trans. Circuits Syst. I-Regul. Pap. 2010, 57, 213–224. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L.; Das, A. Optimal Design for Synchronization of Cooperative Systems: State Feedback, Observer and Output Feedback. IEEE Trans. Autom. Control 2011, 56, 1948–1952. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Ren, W.; Xie, L. Distributed Tracking Control for Linear Multiagent Systems With a Leader of Bounded Unknown Input. IEEE Trans. Autom. Control 2013, 58, 518–523. [Google Scholar] [CrossRef]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Sun, J.; Geng, Z. Adaptive consensus tracking for linear multi-agent systems with heterogeneous unknown nonlinear dynamics. Int. J. Robust Nonlinear Control 2016, 26, 154–173. [Google Scholar] [CrossRef]
- Fu, J.; Wen, G.; Huang, T.; Duan, Z. Consensus of Multi-Agent Systems With Heterogeneous Input Saturation Levels. IEEE Trans. Circuits Syst. II-Express Briefs 2019, 66, 1053–1057. [Google Scholar] [CrossRef]
- Li, C.-J.; Liu, G.-P. Consensus for heterogeneous networked multi-agent systems with switching topology and time-varying delays. J. Frankl. Inst.-Eng. Appl. Math. 2018, 355, 4198–4217. [Google Scholar] [CrossRef]
- Cruz-Ancona, C.D.; Martinez-Guerra, R.; Perez-Pinacho, C.A. A leader-following consensus problem of multi-agent systems in heterogeneous networks. Automatica 2020, 115, 108899. [Google Scholar] [CrossRef]
- Luo, S.; Xu, X.; Liu, L.; Feng, G. Output consensus of heterogeneous linear multi-agent systems with communication, input and output time-delays. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 12825–12839. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Jiang, H.; Sun, X. H-infinity consensus for linear heterogeneous multi-agent systems with state and output feedback control. Neurocomputing 2018, 275, 2635–2644. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W. Adaptive robust tracking control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2018, 92, 92–99. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Gao, Z.; Sun, S. The distributed output consensus control of linear heterogeneous multi-agent systems based on event-triggered transmission mechanism under directed topology. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 3267–3298. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Ren, W. Delay-Induced Consensus and Quasi-Consensus in Multi-Agent Dynamical Systems. IEEE Trans. Circuits Syst. I-Regul. Pap. 2013, 60, 2679–2687. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, J. Quasi-consensus of second-order leader-following multi-agent systems. IET Control Theory Appl. 2012, 6, 545–551. [Google Scholar] [CrossRef]
- Yu, W.; Ren, W.; Zheng, W.X.; Chen, G.; Lu, J. Distributed control gains design for consensus in multi-agent systems with second-order nonlinear dynamics. Automatica 2013, 49, 2107–2115. [Google Scholar] [CrossRef]
- Ye, D.; Shao, Y. Quasi-synchronization of heterogeneous nonlinear multi-agent systems subject to DOS attacks with impulsive effects. Neurocomputing 2019, 366, 131–139. [Google Scholar] [CrossRef]
- An, J.; Yang, W.; Xu, X.; Chen, T.; Du, B.; Tang, Y.; Xu, Q. Decentralized Adaptive Control for Quasi-Consensus in Heterogeneous Nonlinear Multiagent Systems. Discret. Dyn. Nat. Soc. 2021, 2021, 2230805. [Google Scholar] [CrossRef]
- Cheng, L.; Qiu, J.; Chen, X.; Zhang, A.; Yang, C.; Chen, X. Adaptive aperiodically intermittent control for pinning synchronization of directed dynamical networks. Int. J. Robust Nonlinear Control 2019, 29, 1909–1925. [Google Scholar] [CrossRef]
- Wang, J.-L.; Wu, H.-N.; Huang, T.; Ren, S.-Y.; Wu, J. Passivity Analysis of Coupled Reaction-Diffusion Neural Networks With Dirichlet Boundary Conditions. IEEE Trans. Syst. Man Cybern.-Syst. 2017, 47, 2148–2159. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, X.; Zhuang, S.; Xiao, J.; Song, C.; Che, C. New complex projective synchronization strategies for drive-response networks with fractional complex-variable dynamics. Appl. Math. Comput. 2018, 338, 552–566. [Google Scholar] [CrossRef]
- Xu, Q.; Zhuang, S.; Liu, S.; Xiao, J. Decentralized adaptive coupling synchronization of fractional-order complex-variable dynamical networks. Neurocomputing 2016, 186, 119–126. [Google Scholar] [CrossRef]
- Yu, W.; DeLellis, P.; Chen, G.; di Bernardo, M.; Kurths, J. Distributed Adaptive Control of Synchronization in Complex Networks. IEEE Trans. Autom. Control 2012, 57, 2153–2158. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, J.; Wei, P. Weak synchronization of chaotic neural networks with parameter mismatch via periodically intermittent control. Appl. Math. Model. 2011, 35, 612–620. [Google Scholar] [CrossRef]
- D’Angeli, D.; Donno, A. Shuffling matrices, Kronecker product and Discrete Fourier Transform. Discret. Appl. Math. 2017, 233, 1–18. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Xu, Q.; Zhang, J.; Tang, Y.; Wang, L.; Yuan, R.; Yuan, Y.; An, J. Periodic Intermittent Adaptive Control with Saturation for Pinning Quasi-Consensus of Heterogeneous Multi-Agent Systems with External Disturbances. Entropy 2023, 25, 1266. https://doi.org/10.3390/e25091266
Du B, Xu Q, Zhang J, Tang Y, Wang L, Yuan R, Yuan Y, An J. Periodic Intermittent Adaptive Control with Saturation for Pinning Quasi-Consensus of Heterogeneous Multi-Agent Systems with External Disturbances. Entropy. 2023; 25(9):1266. https://doi.org/10.3390/e25091266
Chicago/Turabian StyleDu, Bin, Quan Xu, Junfu Zhang, Yi Tang, Lei Wang, Ruihao Yuan, Yu Yuan, and Jiaju An. 2023. "Periodic Intermittent Adaptive Control with Saturation for Pinning Quasi-Consensus of Heterogeneous Multi-Agent Systems with External Disturbances" Entropy 25, no. 9: 1266. https://doi.org/10.3390/e25091266
APA StyleDu, B., Xu, Q., Zhang, J., Tang, Y., Wang, L., Yuan, R., Yuan, Y., & An, J. (2023). Periodic Intermittent Adaptive Control with Saturation for Pinning Quasi-Consensus of Heterogeneous Multi-Agent Systems with External Disturbances. Entropy, 25(9), 1266. https://doi.org/10.3390/e25091266






