Neural Adaptive H∞ Sliding-Mode Control for Uncertain Nonlinear Systems with Disturbances Using Adaptive Dynamic Programming
Abstract
:1. Introduction
2. Problem Formulation
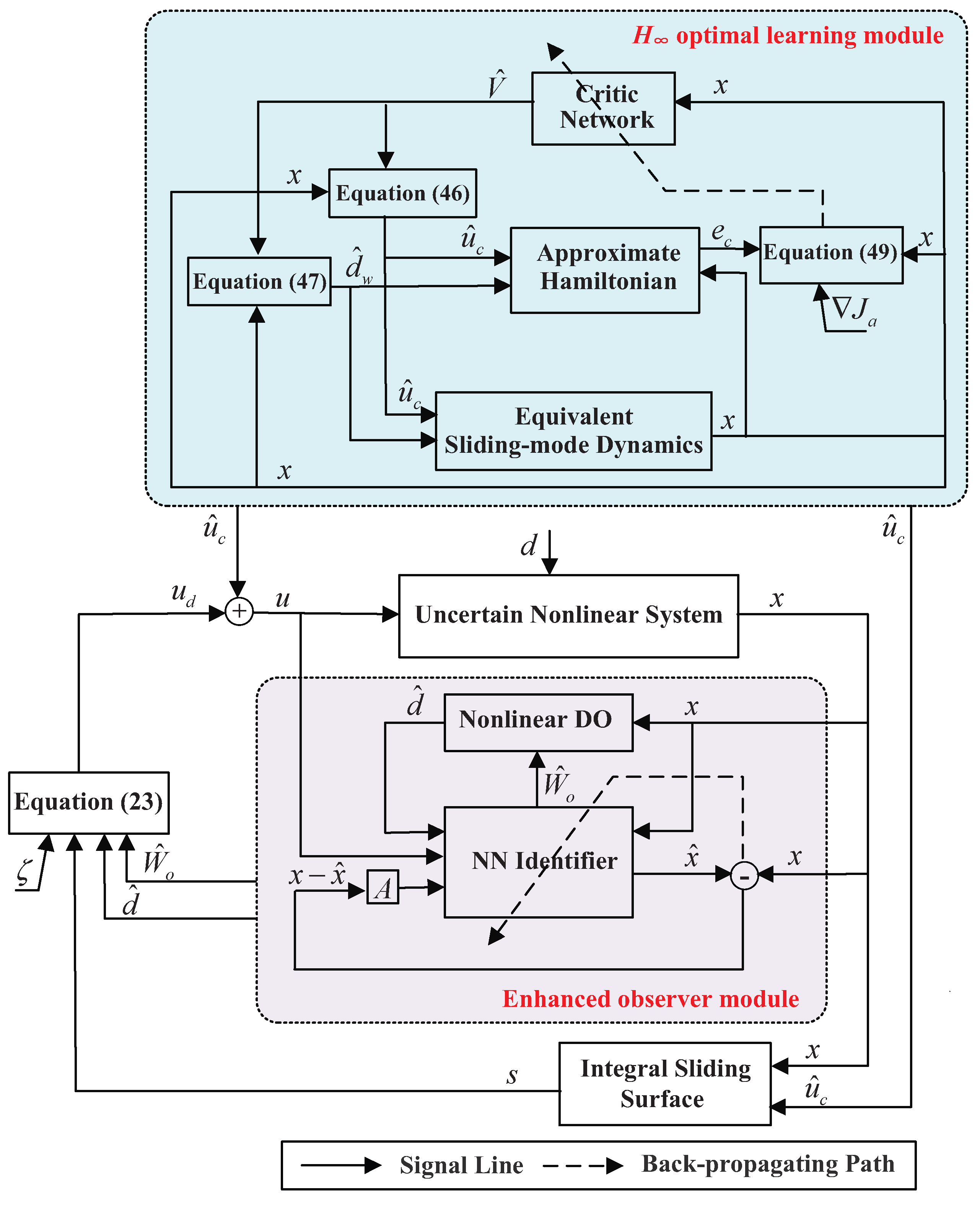
3. Integral SMC Design Based on the Enhanced Observer System
4. H∞ Control Design for Sliding-Mode Dynamics
5. Simulation Results
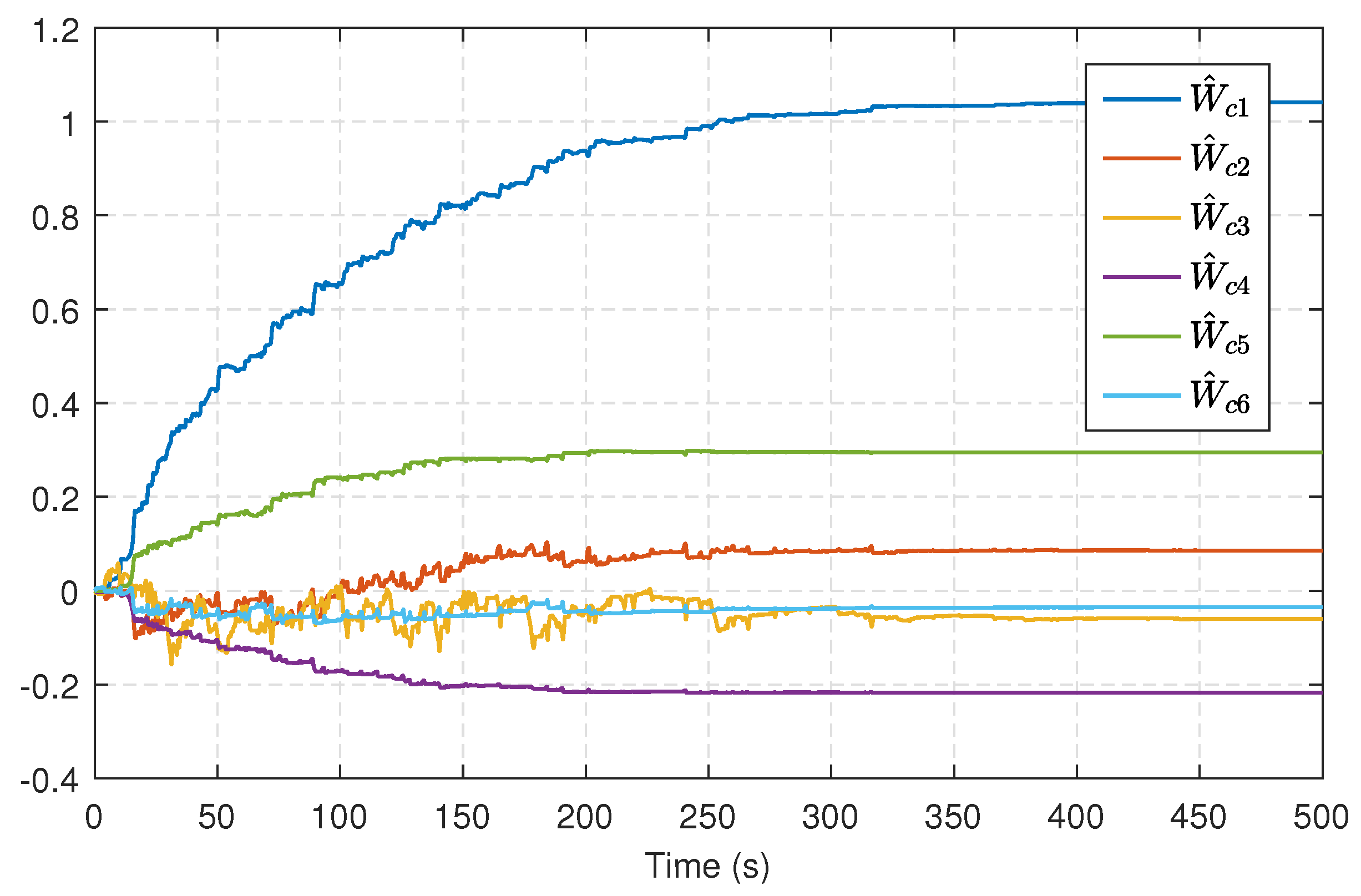
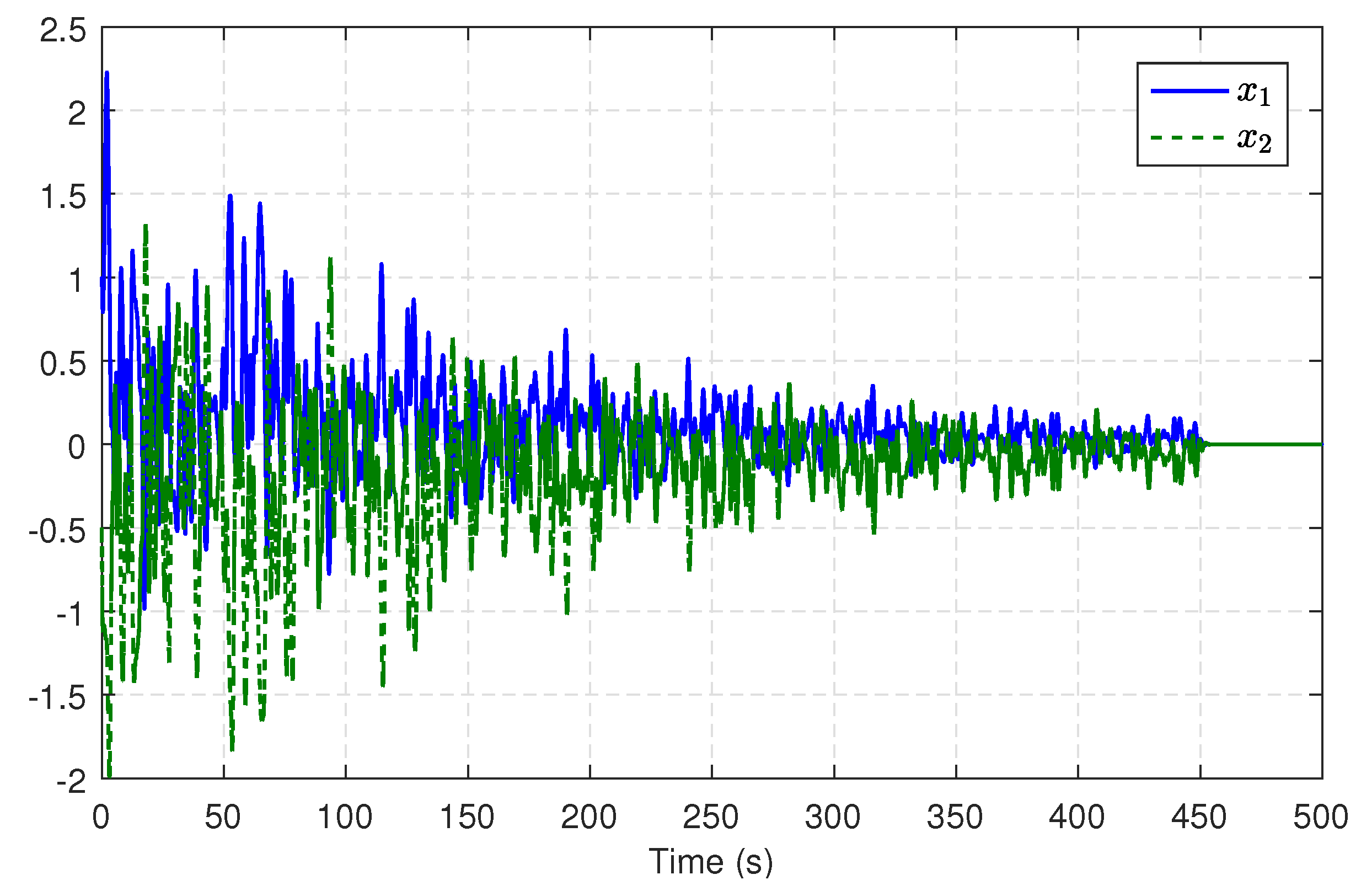
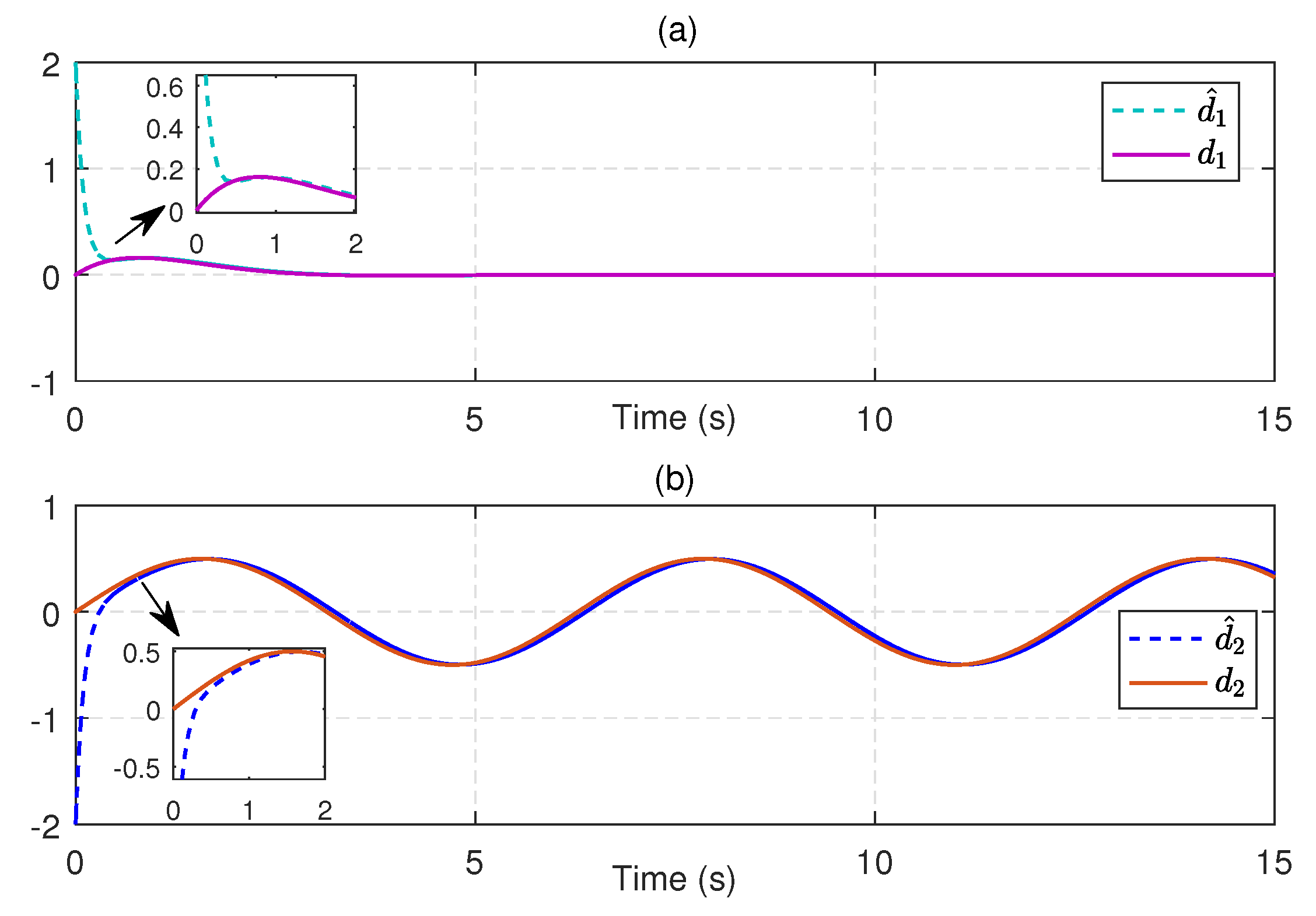
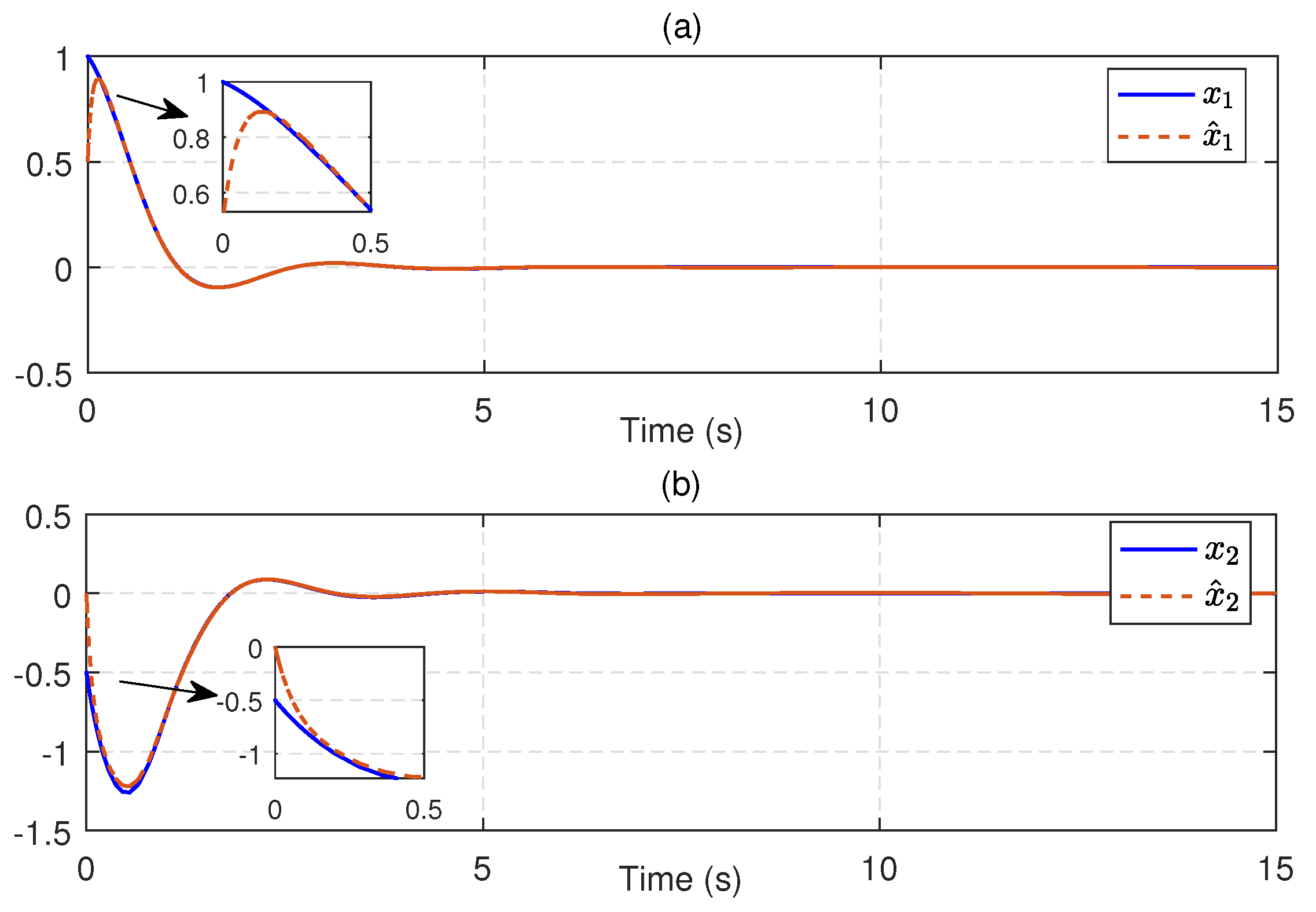
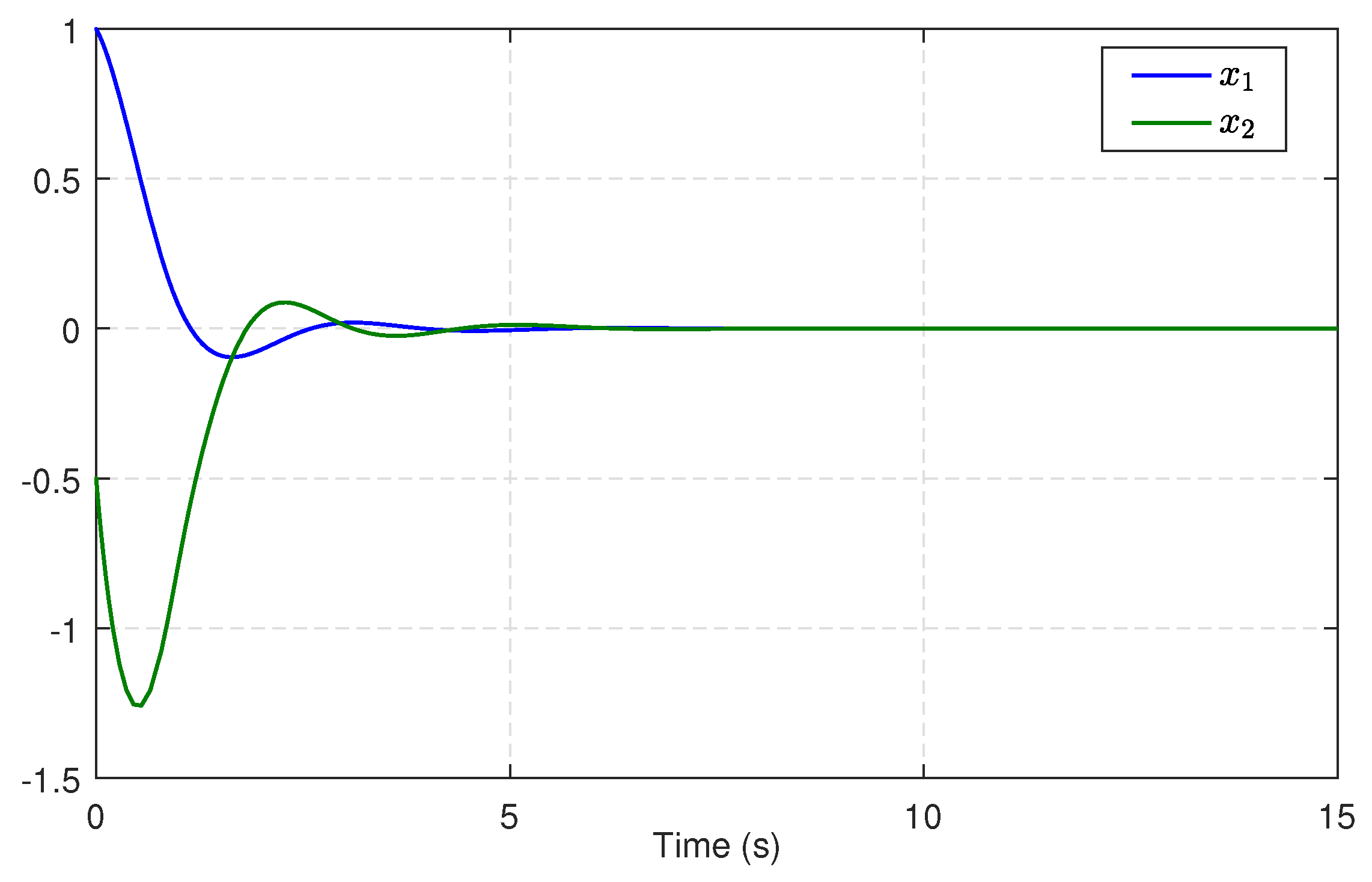
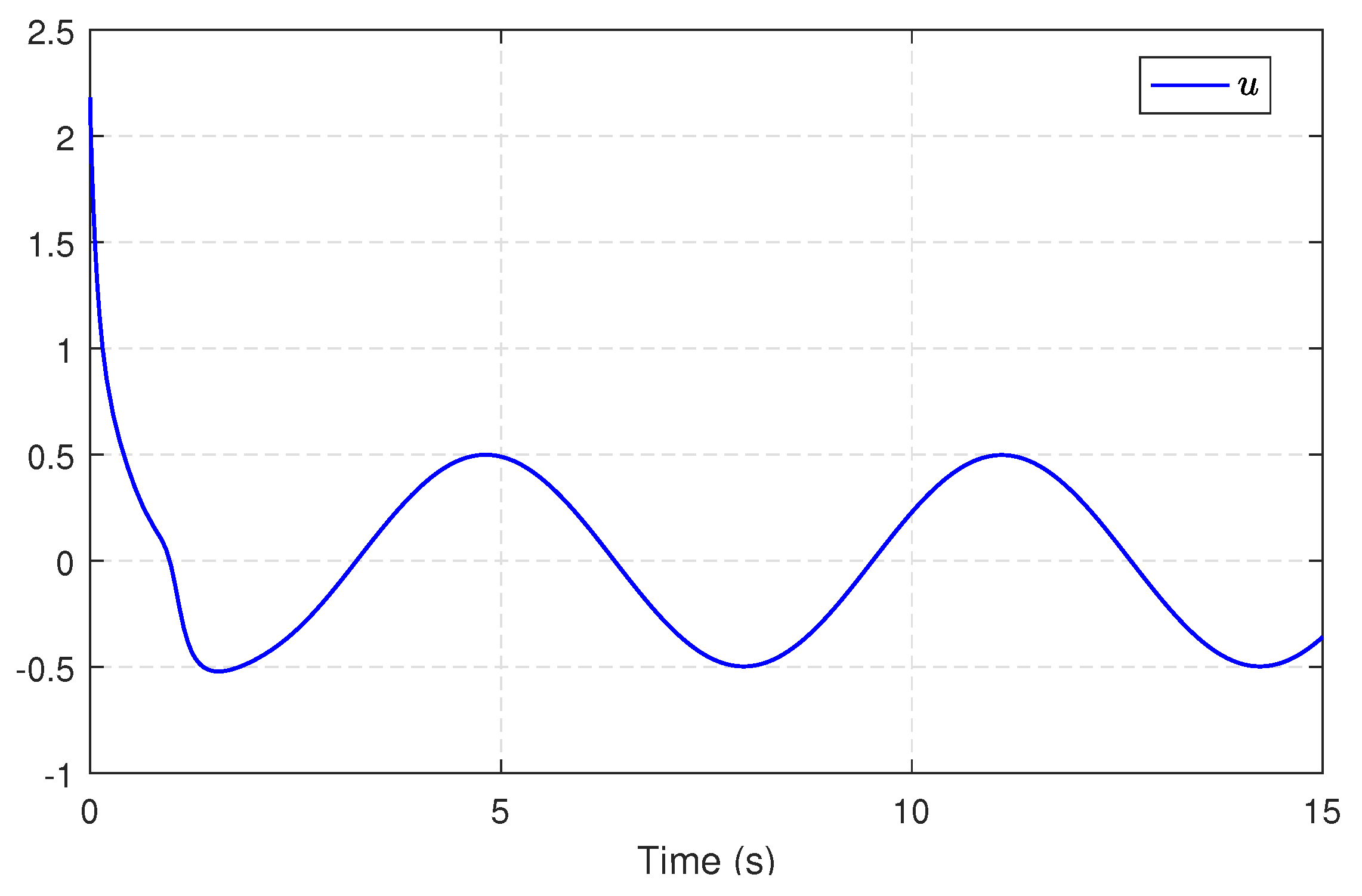
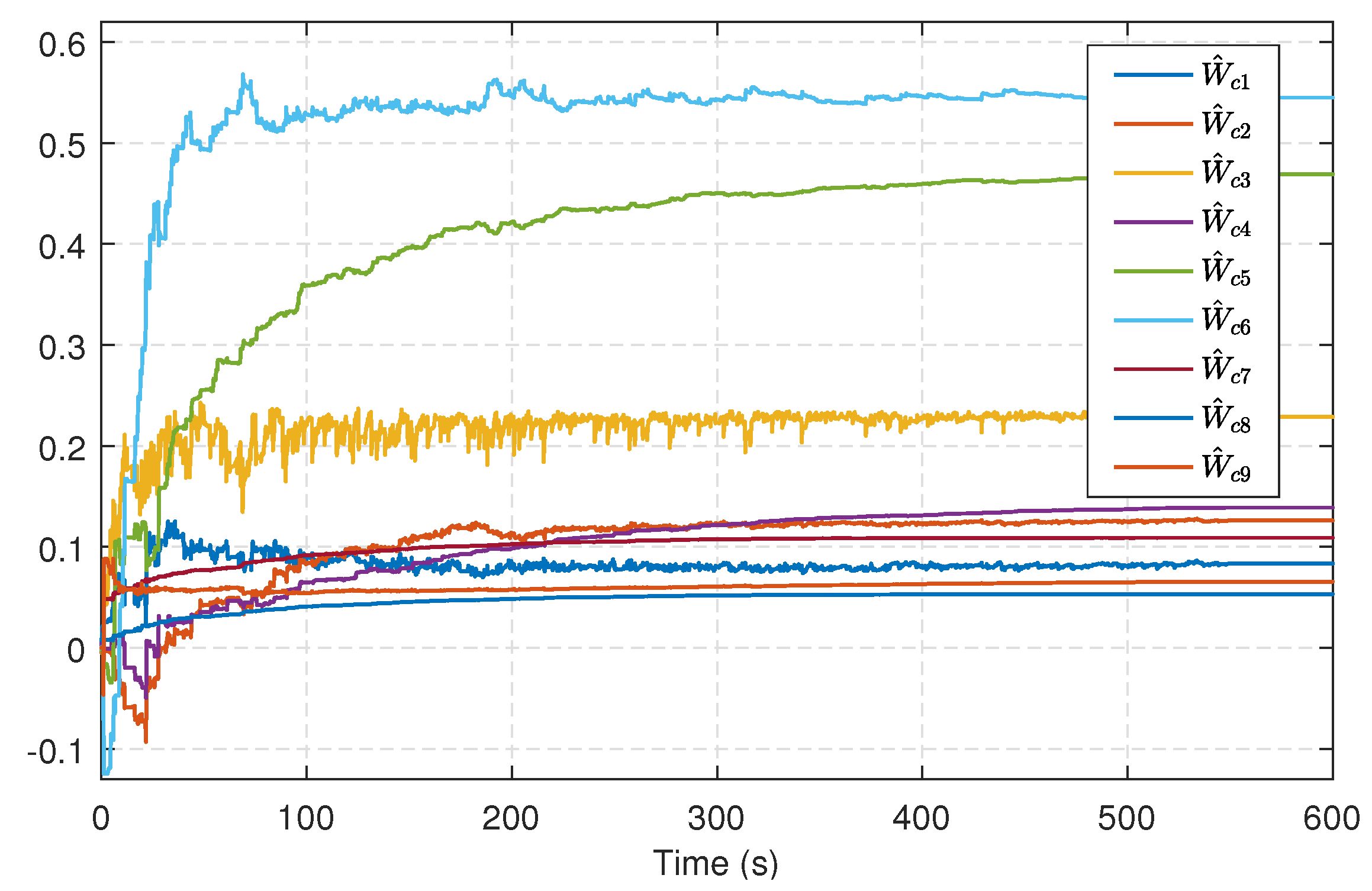
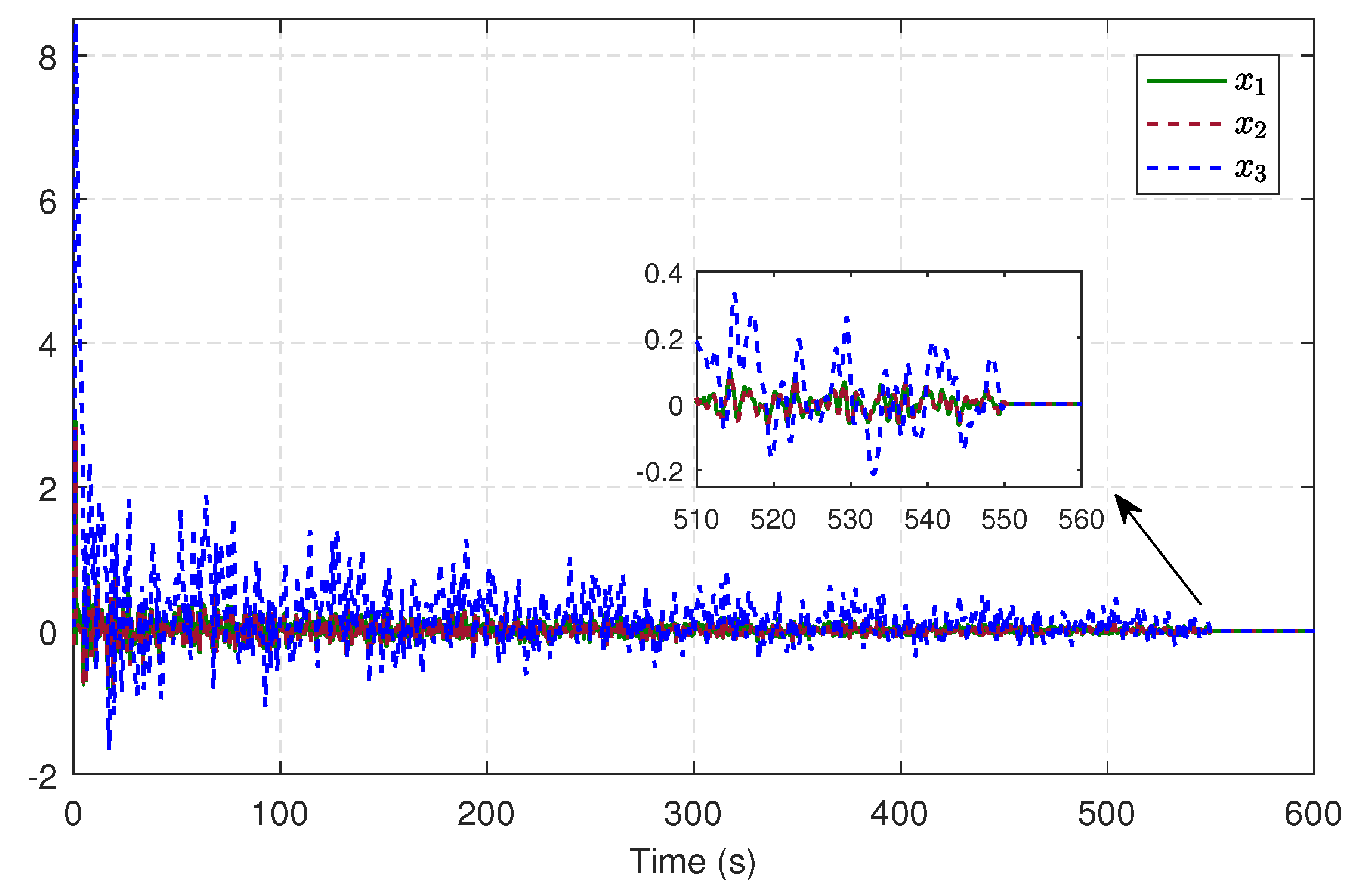
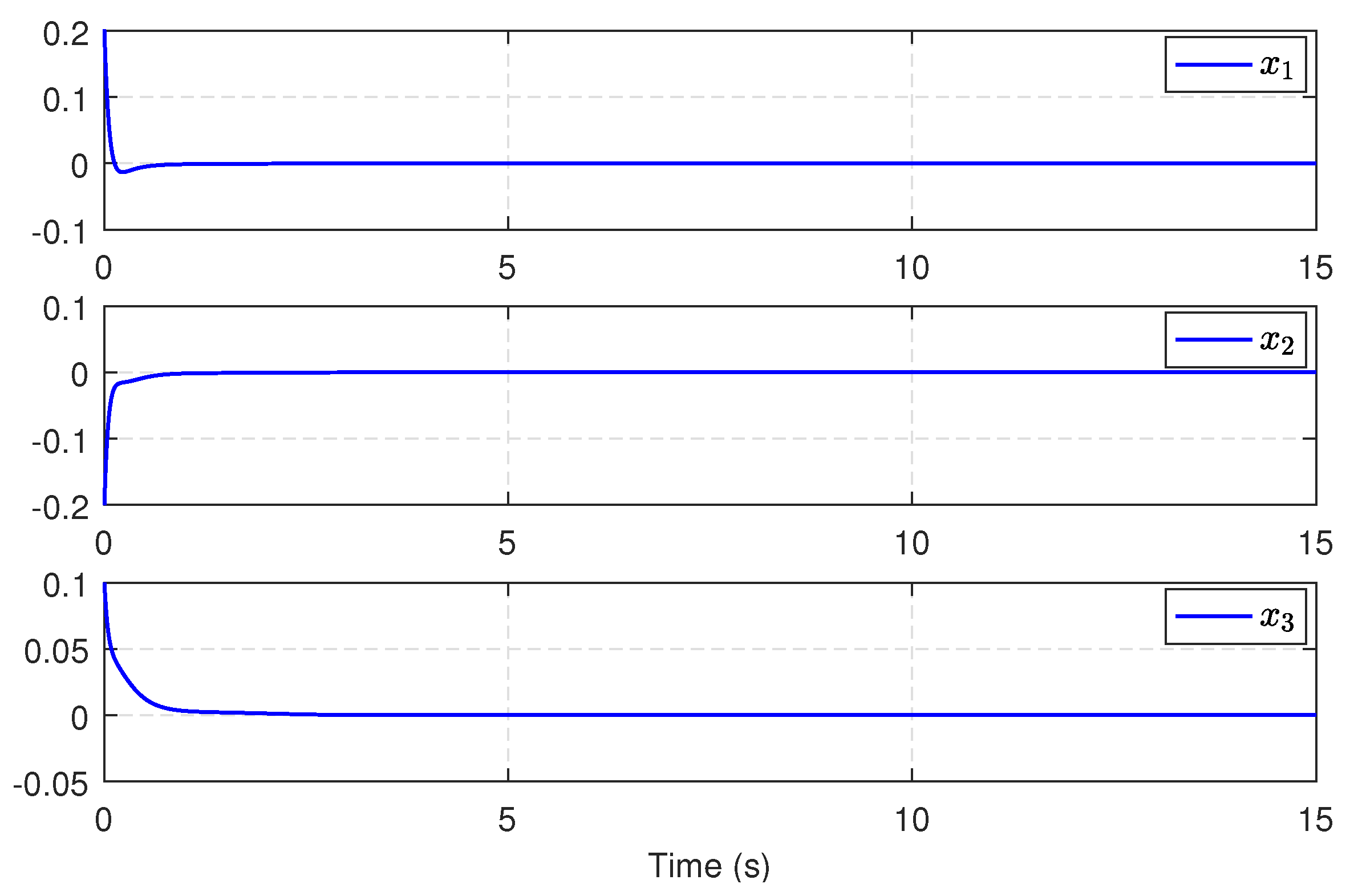
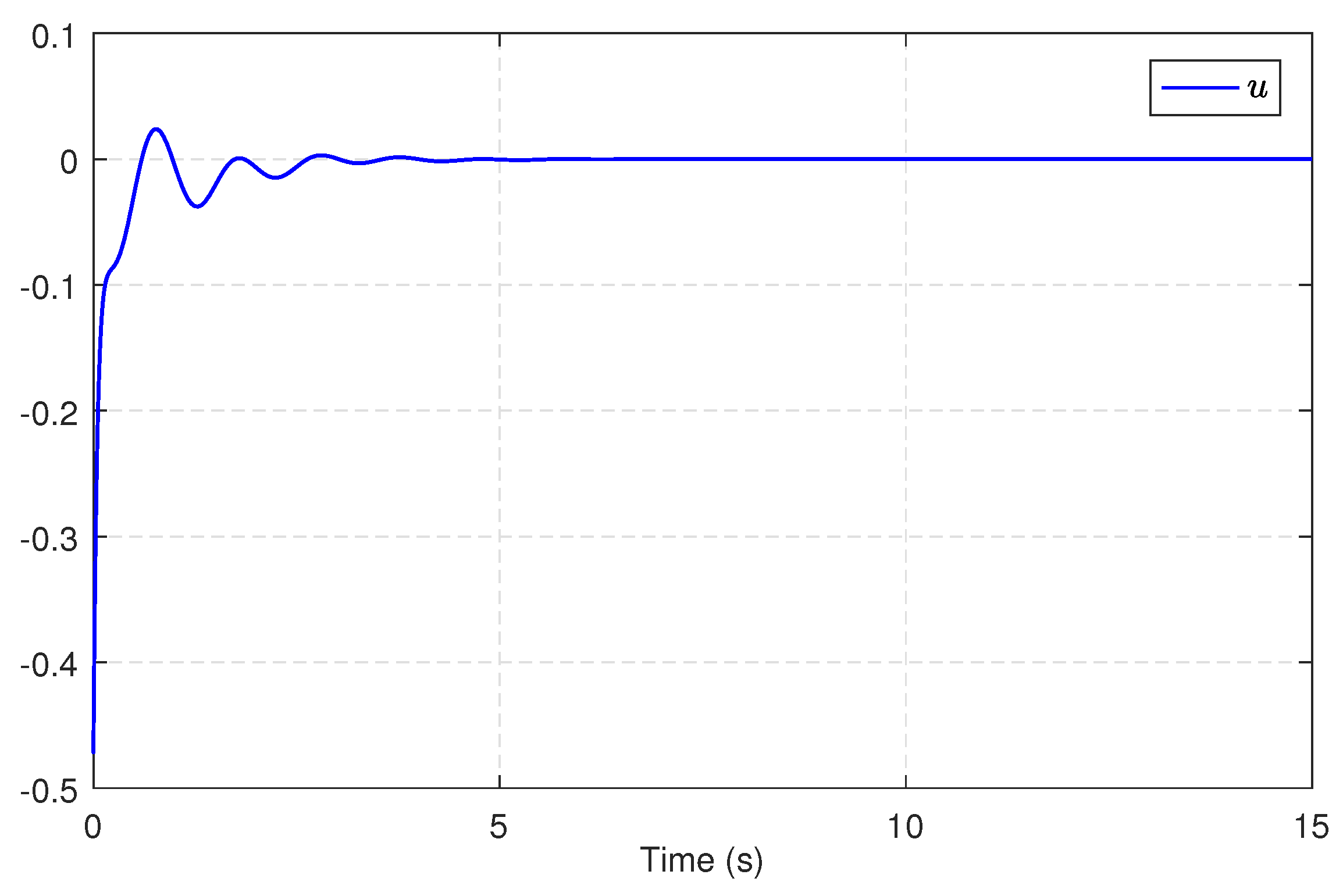
5.1. Single-Link Robot Arm
5.2. Power Plant System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ioannou, P.; Sun, J. Robust Adaptive Control; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yu, X.; Kaynak, O. Sliding-mode control with soft computing: A survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Xu, J.; Guo, Z.; Tong, H. Design and implementation of integral sliding-mode control on an underactuated two-wheeled mobile robot. IEEE Trans. Ind. Electron. 2014, 61, 3671–3681. [Google Scholar] [CrossRef]
- Chen, L.; Edwards, C.; Alwi, H. Integral sliding mode fault-tolerant control allocation for a class of affine nonlinear system. Int. J. Robust Nonlinear 2019, 29, 565–582. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral sliding mode control: Performance, modification, and improvement. IEEE Trans. Ind. Inform. 2017, 14, 3087–3096. [Google Scholar] [CrossRef]
- Errouissi, R.; Ouhrouche, M.; Chen, W.; Trzynadlowski, A. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost function. IEEE Trans. Ind. Electron. 2012, 59, 2849–2858. [Google Scholar] [CrossRef]
- Huang, J.; Ri, S.; Fukuda, T.; Wang, Y. A disturbance observer based sliding mode control for a class of underactuated robotic system with mismatched uncertainties. IEEE Trans. Autom. Control 2019, 64, 2480–2487. [Google Scholar] [CrossRef]
- Cui, R.; Chen, L.; Yang, C.; Chen, M. Extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities. IEEE Trans. Ind. Electron. 2017, 64, 6785–6795. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, X.; Chadli, M.; Xie, S.; Peng, Y. Sliding-mode control of fuzzy singularly perturbed descriptor systems. IEEE Trans. Fuzzy Syst. 2020, 29, 2349–2360. [Google Scholar] [CrossRef]
- Chen, M.; Chen, W. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int. J. Adapt. Control Signal Process 2010, 24, 51–64. [Google Scholar] [CrossRef]
- Rubagotti, M.; Estrada, A.; Castanos, F.; Ferrara, A. Integral sliding mode control for nonlinear systems with matched and unmatched perturbations. IEEE Trans. Autom. Control 2011, 56, 2699–2704. [Google Scholar] [CrossRef]
- Castanos, F.; Fridman, L. Analysis and design of integral sliding manifolds for systems with unmatched perturbations. IEEE Trans. Autom. Control 2006, 51, 853–858. [Google Scholar] [CrossRef]
- Kiumarsi, B.; Vamvoudakis, K.G.; Modares, H.; Lewis, F.L. Optimal and autonomous control using reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2042–2062. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wei, Q.; Wang, D.; Yang, X.; Li, H. Adaptive Dynamic Programming with Applications in Optimal Control; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Lewis, F.L.; Liu, D. Reinforcement Learning and Approximate Dynamic Programming for Feedback Control; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ha, M.; Wang, D.; Liu, D. Discounted iterative adaptive critic designs with novel stability analysis for tracking control. IEEE/CAA J. Autom. Sin. 2022, 9, 1262–1272. [Google Scholar] [CrossRef]
- Wei, Q.; Lewis, F.L.; Liu, D.; Song, R.; Lin, H. Discrete-time local value iteration adaptive dynamic programming: Convergence analysis. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 875–891. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, L.; Lu, J.; Wang, F.Y. Discrete-Time Self-Learning Parallel Control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 192–204. [Google Scholar] [CrossRef]
- Heydari, A.; Balakrishnan, S. Finite-horizon control-constrained nonlinear optimal control using single network adaptive critics. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wei, Q.; Wang, Z.; Zhou, T.; Wang, F. Event-triggered optimal control for discrete-time multi-player non-zero-sum games using parallel control. Inf. Sci. 2022, 584, 519–535. [Google Scholar] [CrossRef]
- Wang, D.; Ren, J.; Ha, M. Discounted linear Q-learning control with novel tracking cost and its stability. Inf. Sci. 2023, 626, 339–353. [Google Scholar] [CrossRef]
- Zhang, X.; Ni, Z.; He, H. A theoretical foundation of goal representation heuristic dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2513–2525. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, D.; Liu, D. Bounded robust control design for uncertain nonlinear systems using single-network adaptive dynamic programming. Neurocomputing 2017, 266, 128–140. [Google Scholar] [CrossRef]
- Yang, X.; Wei, Q. Adaptive critic designs for optimal event-driven control of a CSTR system. IEEE Trans. Ind. Inform. 2021, 17, 484–493. [Google Scholar] [CrossRef]
- Yang, X.; He, H.; Zhong, X. Approximate dynamic programming for nonlinear-constrained optimizations. IEEE Trans. Cybern. 2021, 51, 2419–2432. [Google Scholar] [CrossRef] [PubMed]
- Wen, G.; Niu, B. Optimized tracking control based on reinforcement learning for a class of high-order unknown nonlinear dynamic systems. Inf. Sci. 2022, 606, 368–379. [Google Scholar] [CrossRef]
- Wang, D.; Qiao, J.; Cheng, L. An approximate neuro-optimal solution of discounted guaranteed cost control design. IEEE Trans. Cybern. 2022, 52, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Xue, S.; Zhao, B.; Luo, B.; Wei, Q. Adaptive dynamic programming for control: A survey and recent advances. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 142–160. [Google Scholar] [CrossRef]
- Wang, D.; Ha, M.; Zhao, M. The intelligent critic framework for advanced optimal control. Artif. Intell. Rev. 2022, 55, 1–22. [Google Scholar] [CrossRef]
- Modares, H.; Lewis, F.L. Optimal tracking control of nonlinear partially-unknown constrained input systems using integral reinforcement learning. Automatica 2014, 50, 1780–1792. [Google Scholar] [CrossRef]
- Luo, B.; Wu, H.; Huang, T. Off-policy reinforcement learning for H∞ control design. IEEE Trans. Cybern. 2014, 45, 65–76. [Google Scholar] [CrossRef]
- Modares, H.; Lewis, F.L.; Jiang, Z. H∞ tracking control of completely unknown continuous-time systems via off-policy reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2550–2562. [Google Scholar] [CrossRef]
- Wang, D.; He, H.; Liu, D. Adaptive critic nonlinear robust control: A survey. IEEE Trans. Cybern. 2017, 47, 3429–3451. [Google Scholar] [CrossRef]
- Mitra, A.; Behera, L. Continuous-time single network adaptive critic based optimal sliding mode control for nonlinear control affine systems. In Proceedings of the 34th Chinese Control Conference, HangZhou, China, 28–30 July 2015; pp. 3300–3306. [Google Scholar]
- Fan, Q.; Yang, G. Adaptive actor-critic design-based integral sliding-mode control for partially unknown nonlinear systems with input disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Qu, Q.; Zhang, H.; Yu, R.; Liu, Y. Neural network-based H∞ sliding mode control for nonlinear systems with actuator faults and unmatched disturbances. Neurocomputing 2018, 275, 2009–2018. [Google Scholar] [CrossRef]
- Zhang, H.; Qu, Q.; Xiao, G.; Cui, Y. Optimal guaranteed cost sliding mode control for constrained-input nonlinear systems with matched and unmatched disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2112–2126. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Li, T.; Xie, X.; Zhang, H. Event-triggered integral sliding-mode control for nonlinear constrained-input systems with disturbances via adaptive dynamic programming. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 4086–4096. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhang, Z. Neural Adaptive H∞ Sliding-Mode Control for Uncertain Nonlinear Systems with Disturbances Using Adaptive Dynamic Programming. Entropy 2023, 25, 1570. https://doi.org/10.3390/e25121570
Huang Y, Zhang Z. Neural Adaptive H∞ Sliding-Mode Control for Uncertain Nonlinear Systems with Disturbances Using Adaptive Dynamic Programming. Entropy. 2023; 25(12):1570. https://doi.org/10.3390/e25121570
Chicago/Turabian StyleHuang, Yuzhu, and Zhaoyan Zhang. 2023. "Neural Adaptive H∞ Sliding-Mode Control for Uncertain Nonlinear Systems with Disturbances Using Adaptive Dynamic Programming" Entropy 25, no. 12: 1570. https://doi.org/10.3390/e25121570
APA StyleHuang, Y., & Zhang, Z. (2023). Neural Adaptive H∞ Sliding-Mode Control for Uncertain Nonlinear Systems with Disturbances Using Adaptive Dynamic Programming. Entropy, 25(12), 1570. https://doi.org/10.3390/e25121570





