Revisiting Sequential Information Bottleneck: New Implementation and Evaluation
Abstract
:1. Introduction
2. Algorithm Overview
2.1. Theoretical Foundation
- X—the list of vectors to cluster;
- Y—the vocabulary used for representing the texts;
- —the estimated joint distribution between X and Y;
- K—the number of clusters to produce;
- T—a partition of X into K clusters.
“Intuitively, in this procedure the information contained in X about Y is ‘squeezed’ through a compact ‘bottleneck’ of clusters T, that is forced to represent the ‘relevant’ part in X with respect to Y”(p. 2)
2.2. Divergence Function
2.3. Pseudo-Code
| Algorithm 1 Algorithm pseudo-code. |
Input: objects to be clustered Parameters: Output: A partition T of X into K clusters Main Loop: For random partition of X. While not For x in shuffle(X) draw x out of If then Merge x into if or then |
2.4. Sequential Clustering Algorithm
2.5. Vector Representation
2.6. Focus of This Work
3. Methods
3.1. Computation of and Associated Intuition
- = —the TF vector representing the sample x normalized by the -norm. Let , the -norm of u is defined by: ;
- = —the vector representing the centroid of cluster t, normalized by ;
- m = —the average of and weighted by and , respectively.
3.2. Optimization for Sparse Vector Representation
3.3. Caching Computations
3.4. Implementation
4. Experimental Setup
4.1. Materials
- BBC News [34] consists of 2225 articles from the BBC news website. The articles are from 2004–2005 and cover stories in five topical areas: business, entertainment, politics, sport, and tech.
- 20 News Groups [23] consists of emails sent through 20 news groups. The topics are diverse and cover tech, religion, and politics, among others.
- AG News [35] consists of pairs of titles and snippets of news articles from the AG corpus, covering four topical areas: World, Sports, Business, and Sci/Tech. The title and snippet of each article are concatenated when the data is clustered.
- DBPedia [35] consists of pairs of titles and abstracts of documents from 14 non-overlapping ontology classes such as Artist, Film, and Company. The title and abstract are concatenated when the data are clustered.
- Yahoo! Answers [35] consists of triplets of question title, question content, and best answer from the Yahoo! Answers Comprehensive Questions and Answers version dataset. The data covers the 10 largest topical categories, such as Society & Culture, Computers & Internet, and Health. The question title, content, and best answer are concatenated when the data are clustered.
4.2. Clustering Metrics
4.3. Clustering Setups
4.4. Robustness Considerations
4.5. Hardware
4.6. Code
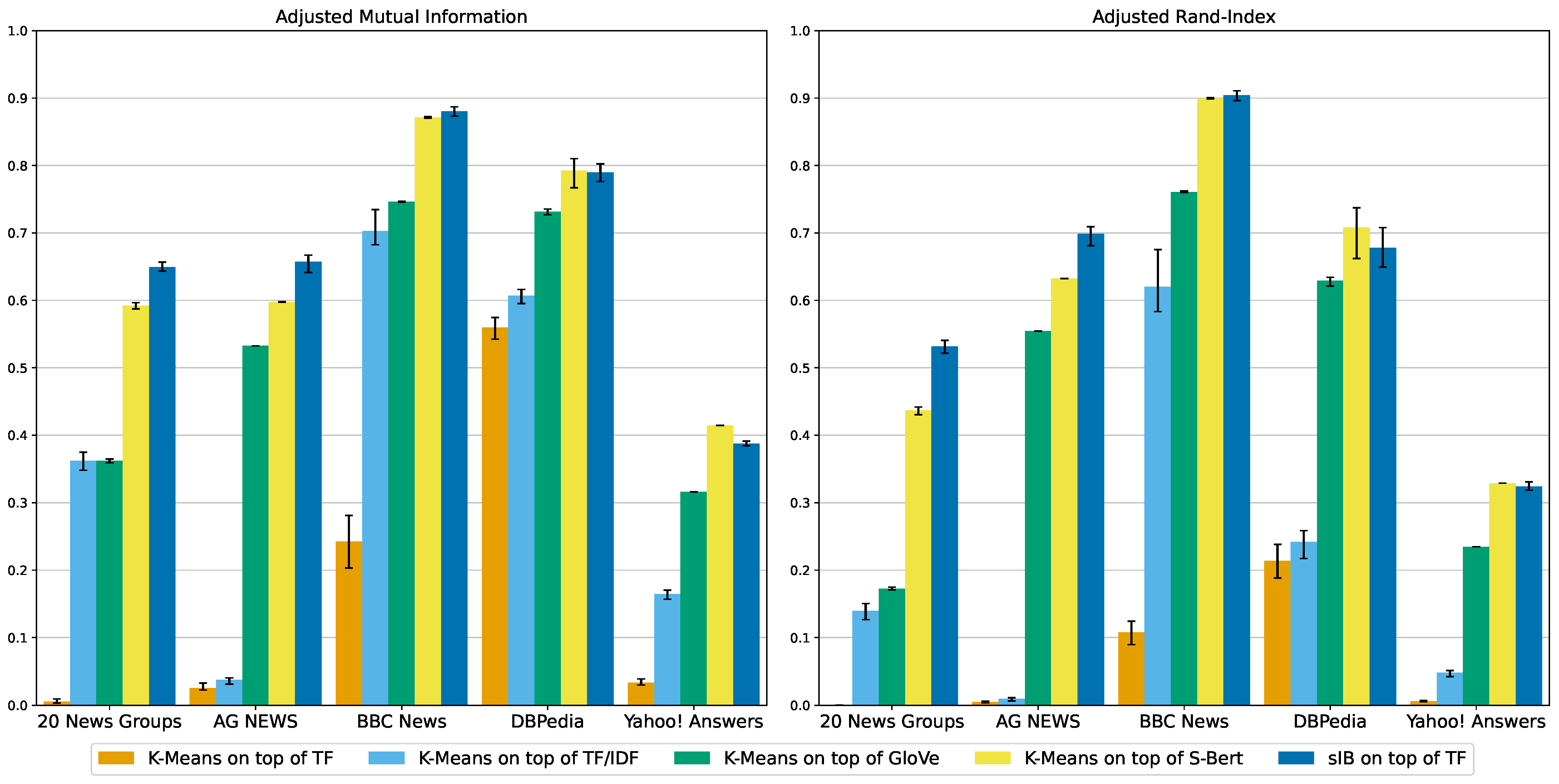
5. Results
Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Package Distribution
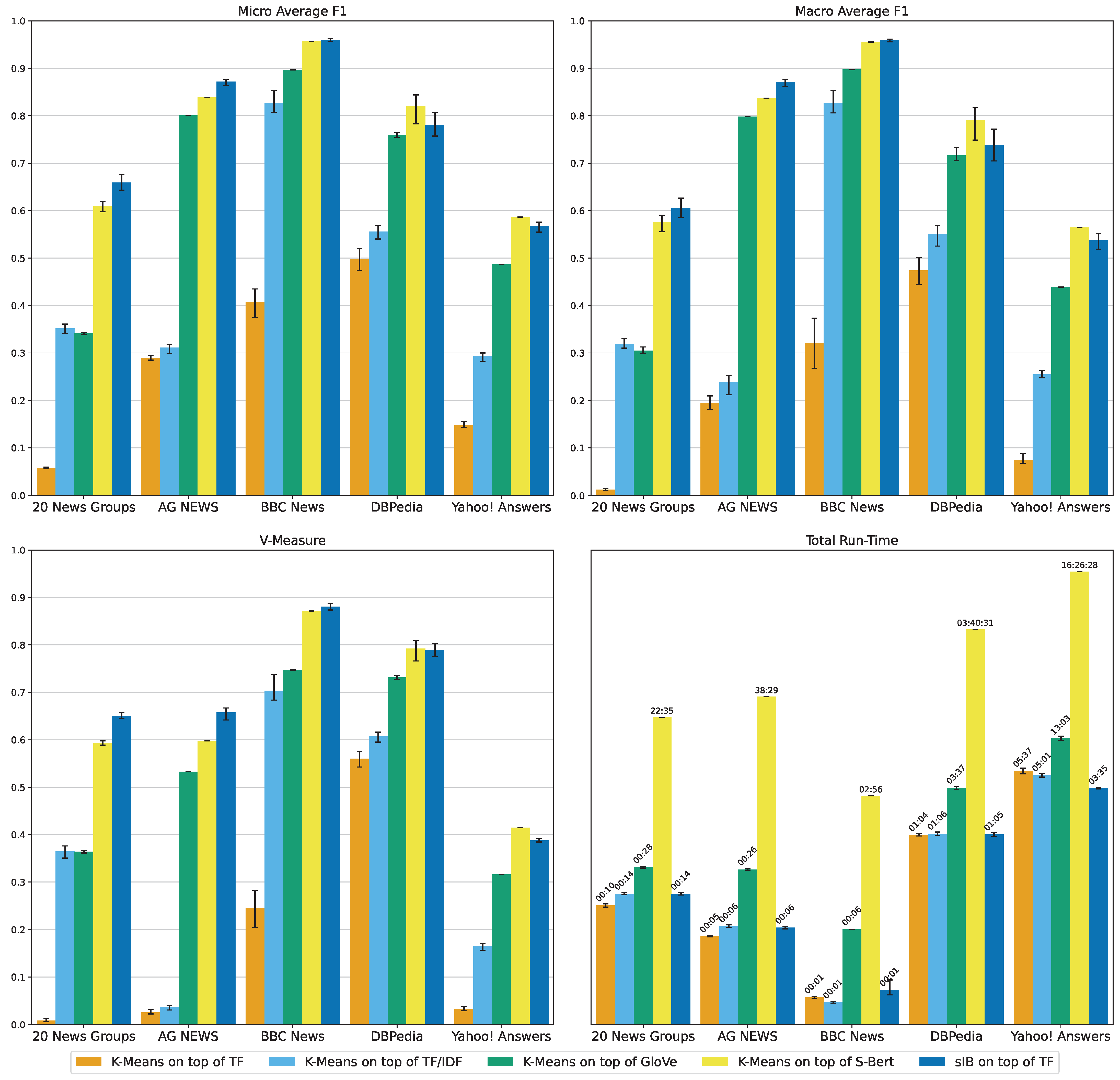
Appendix B. Illustrations of Micro-F1, Macro-F1, V-Measure and Total Run-Time
Appendix C. Comparing sIB and K-Means Parallelism Models
References
- Aggarwal, C.C.; Zhai, C. A Survey of Text Clustering Algorithms. In Mining Text Data; Aggarwal, C.C., Zhai, C., Eds.; Springer US: Boston, MA, USA, 2012; pp. 77–128. [Google Scholar] [CrossRef]
- Huang, A. Similarity measures for text document clustering. In Proceedings of the Sixth New Zealand Computer Science Research Student Conference (NZCSRSC2008), Christchurch, New Zealand, 6–9 April 2008; Volume 4, pp. 9–56. [Google Scholar]
- Abualigah, L.M.Q. Feature Selection and Enhanced Krill Herd Algorithm for Text Document Clustering, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Roy, S.; Muni, D.P.; Tack Yan, J.J.Y.; Budhiraja, N.; Ceiler, F. Clustering and Labeling IT Maintenance Tickets. In Proceedings of the Service-Oriented Computing, Banff, AB, Canada, 10–13 October 2016; Sheng, Q.Z., Stroulia, E., Tata, S., Bhiri, S., Eds.; pp. 829–845. [Google Scholar]
- Compton, J.E.; Adams, M.C. Clustering Support Tickets with Natural Language Processing: K-Means Applied to Transformer Embeddings; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Poomagal, S.; Visalakshi, P.; Hamsapriya, T. A novel method for clustering tweets in Twitter. Int. J. Web Based Commun. 2015, 11, 170–187. [Google Scholar] [CrossRef]
- Rosa, K.D.; Shah, R.; Lin, B.; Gershman, A.; Frederking, R.E. Topical Clustering of Tweets. In Proceedings of the ACM SIGIR: SWSM, Beijing, China, 28 July 2011. [Google Scholar]
- Curiskis, S.A.; Drake, B.; Osborn, T.R.; Kennedy, P.J. An evaluation of document clustering and topic modelling in two online social networks: Twitter and Reddit. Inf. Process. Manag. 2020, 57, 102034. [Google Scholar] [CrossRef]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theor. 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Salton, G.; McGill, M.J. Introduction to Modern Information Retrieval; McGraw-Hill, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar] [CrossRef]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.; Dean, J. Distributed Representations of Words and Phrases and their Compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 1421. [Google Scholar] [CrossRef]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global Vectors for Word Representation. In Proceedings of the Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Janvin, C. A Neural Probabilistic Language Model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. CoRR 2017, 30, 3058. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Wang, A.; Singh, A.; Michael, J.; Hill, F.; Levy, O.; Bowman, S.R. GLUE: A Multi-Task Benchmark and Analysis Platform for Natural Language Understanding. arXiv 2018, arXiv:1804.07461. [Google Scholar] [CrossRef]
- Wang, A.; Pruksachatkun, Y.; Nangia, N.; Singh, A.; Michael, J.; Hill, F.; Levy, O.; Bowman, S.R. SuperGLUE: A Stickier Benchmark for General-Purpose Language Understanding Systems. Adv. Neural Inf. Process. Syst. 2019, 32, 1828. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. arXiv 2019, arXiv:1908.10084. [Google Scholar] [CrossRef]
- Slonim, N.; Friedman, N.; Tishby, N. Unsupervised Document Classification Using Sequential Information Maximization. In Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR’02, Tampere, Finland, 11–15 August 2002; pp. 129–136. [Google Scholar] [CrossRef]
- Lang, K. NewsWeeder: Learning to Filter Netnews. In Proceedings of the 12th International Machine Learning Conference (ML95), Tahoe City, CA, USA, 9–12 July 1995. [Google Scholar]
- Connor, R.C.H.; Cardillo, F.A.; Moss, R.; Rabitti, F. Evaluation of Jensen-Shannon Distance over Sparse Data. In Proceedings of the SISAP, A Coruna, Spain, 2–4 October 2013. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar] [CrossRef]
- Slonim, N. The Information Bottleneck: Theory and Applications. Ph.D. Thesis, Hebrew University of Jerusalem, Jerusalem, Israel, 2002. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Slonim, N.; Tishby, N. Agglomerative Information Bottleneck. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; Solla, S., Leen, T., Müller, K., Eds.; Volume 12. [Google Scholar]
- Zhang, J.A.; Kurkoski, B.M. Low-complexity quantization of discrete memoryless channels. In Proceedings of the 2016 International Symposium on Information Theory and Its Applications (ISITA), Monterey, CA, USA, 3 October–2 November 2016; pp. 448–452. [Google Scholar]
- Chou, P. Optimal partitioning for classification and regression trees. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 340–354. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Kurkoski, B.M. On the relationship between the KL means algorithm and the information bottleneck method. In Proceedings of the SCC 2017, 11th International ITG Conference on Systems, Communications and Coding, Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Slonim, N.; Aharoni, E.; Crammer, K. Hartigan’s K-Means versus Lloyd’s K-Means: Is It Time for a Change? In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, IJCAI’13, Beijing, China, 3–9 August 2013; pp. 1677–1684. [Google Scholar]
- Greene, D.; Cunningham, P. Practical Solutions to the Problem of Diagonal Dominance in Kernel Document Clustering. In Proceedings of the 23rd International Conference on Machine Learning (ICML’06), New York, NY, USA, 25–29 June 2006; pp. 377–384. [Google Scholar]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level Convolutional Networks for Text Classification. Adv. Neural Inf. Process. Syst. 2015, 28, 456. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Meilă, M. Comparing clusterings—An information based distance. J. Multivar. Anal. 2007, 98, 873–895. [Google Scholar] [CrossRef]
- Rosenberg, A.; Hirschberg, J. V-Measure: A Conditional Entropy-Based External Cluster Evaluation Measure. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; pp. 410–420. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, Louisiana, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Spencer, N. Essentials of Multivariate Data Analysis; Taylor & Francis: Abingdon, UK, 2013; p. 95. [Google Scholar]
| Dataset | #Texts | #Words | #Classes |
|---|---|---|---|
| BBC News | 2225 | 390 | 5 |
| 20 News Groups | 18,846 | 284 | 20 |
| AG NEWS | 127,600 | 38 | 4 |
| DBPedia | 630,000 | 46 | 14 |
| Yahoo! Answers | 1,460,000 | 92 | 10 |
| Dataset | Algorithm | Embed | AMI | ARI | VM | Mic-F1 | Mac-F1 | Vector | Cluster | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| 20 News Groups | K-Means | TF | 0.01 | 0.00 | 0.01 | 0.06 | 0.01 | 00:03 | 00:07 | 00:10 |
| K-Means | TF/IDF | 0.36 | 0.14 | 0.36 | 0.35 | 0.32 | 00:03 | 00:10 | 00:14 | |
| K-Means | GloVe | 0.36 | 0.17 | 0.36 | 0.34 | 0.31 | 00:19 | 00:09 | 00:28 | |
| K-Means | S-Bert | 0.59 | 0.44 | 0.59 | 0.61 | 0.58 | 22:27 | 00:08 | 22:35 | |
| sIB | TF | 0.65 | 0.53 | 0.65 | 0.66 | 0.61 | 00:03 | 00:11 | 00:14 | |
| AG NEWS | K-Means | TF | 0.03 | 0.00 | 0.03 | 0.29 | 0.20 | 00:03 | 00:02 | 00:05 |
| K-Means | TF/IDF | 0.04 | 0.01 | 0.04 | 0.31 | 0.24 | 00:03 | 00:03 | 00:06 | |
| K-Means | GloVe | 0.53 | 0.55 | 0.53 | 0.80 | 0.80 | 00:19 | 00:07 | 00:26 | |
| K-Means | S-Bert | 0.60 | 0.63 | 0.60 | 0.84 | 0.84 | 38:18 | 00:11 | 38:29 | |
| sIB | TF | 0.66 | 0.70 | 0.66 | 0.87 | 0.87 | 00:03 | 00:03 | 00:06 | |
| BBC News | K-Means | TF | 0.24 | 0.11 | 0.24 | 0.41 | 0.32 | 00:01 | 00:00 | 00:01 |
| K-Means | TF/IDF | 0.70 | 0.62 | 0.70 | 0.83 | 0.83 | 00:00 | 00:00 | 00:01 | |
| K-Means | GloVe | 0.75 | 0.76 | 0.75 | 0.90 | 0.90 | 00:05 | 00:00 | 00:06 | |
| K-Means | S-Bert | 0.87 | 0.90 | 0.87 | 0.96 | 0.96 | 02:55 | 00:00 | 02:56 | |
| sIB | TF | 0.88 | 0.90 | 0.88 | 0.96 | 0.96 | 00:01 | 00:01 | 00:01 | |
| DBPedia | K-Means | TF | 0.56 | 0.21 | 0.56 | 0.50 | 0.47 | 00:20 | 00:43 | 01:04 |
| K-Means | TF/IDF | 0.61 | 0.24 | 0.61 | 0.56 | 0.55 | 00:20 | 00:45 | 01:06 | |
| K-Means | GloVe | 0.73 | 0.63 | 0.73 | 0.76 | 0.72 | 01:28 | 02:08 | 03:37 | |
| K-Means | S-Bert | 0.79 | 0.71 | 0.79 | 0.82 | 0.79 | 03:38:31 | 02:00 | 03:40:31 | |
| sIB | TF | 0.79 | 0.68 | 0.79 | 0.78 | 0.74 | 00:20 | 00:44 | 01:05 | |
| Yahoo! Answers | K-Means | TF | 0.03 | 0.01 | 0.03 | 0.15 | 0.08 | 01:15 | 04:22 | 05:37 |
| K-Means | TF/IDF | 0.16 | 0.05 | 0.16 | 0.29 | 0.25 | 01:16 | 03:44 | 05:01 | |
| K-Means | GloVe | 0.32 | 0.23 | 0.32 | 0.49 | 0.44 | 06:21 | 06:42 | 13:03 | |
| K-Means | S-Bert | 0.41 | 0.33 | 0.41 | 0.59 | 0.56 | 16:20:10 | 06:18 | 16:26:28 | |
| sIB | TF | 0.39 | 0.32 | 0.39 | 0.57 | 0.54 | 01:15 | 02:20 | 03:35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toledo, A.; Venezian, E.; Slonim, N. Revisiting Sequential Information Bottleneck: New Implementation and Evaluation. Entropy 2022, 24, 1132. https://doi.org/10.3390/e24081132
Toledo A, Venezian E, Slonim N. Revisiting Sequential Information Bottleneck: New Implementation and Evaluation. Entropy. 2022; 24(8):1132. https://doi.org/10.3390/e24081132
Chicago/Turabian StyleToledo, Assaf, Elad Venezian, and Noam Slonim. 2022. "Revisiting Sequential Information Bottleneck: New Implementation and Evaluation" Entropy 24, no. 8: 1132. https://doi.org/10.3390/e24081132
APA StyleToledo, A., Venezian, E., & Slonim, N. (2022). Revisiting Sequential Information Bottleneck: New Implementation and Evaluation. Entropy, 24(8), 1132. https://doi.org/10.3390/e24081132






