Probabilistic Shaping for Finite Blocklengths: Distribution Matching and Sphere Shaping
Abstract
1. Introduction
2. Preliminaries
2.1. Notation and Definitions
2.2. Discrete Constellations and Amplitude Shaping
2.3. Fundamentals of Amplitude Shaping Schemes
2.4. Shaping Architecture vs. Shaping Algorithm
3. Signaling Schemes
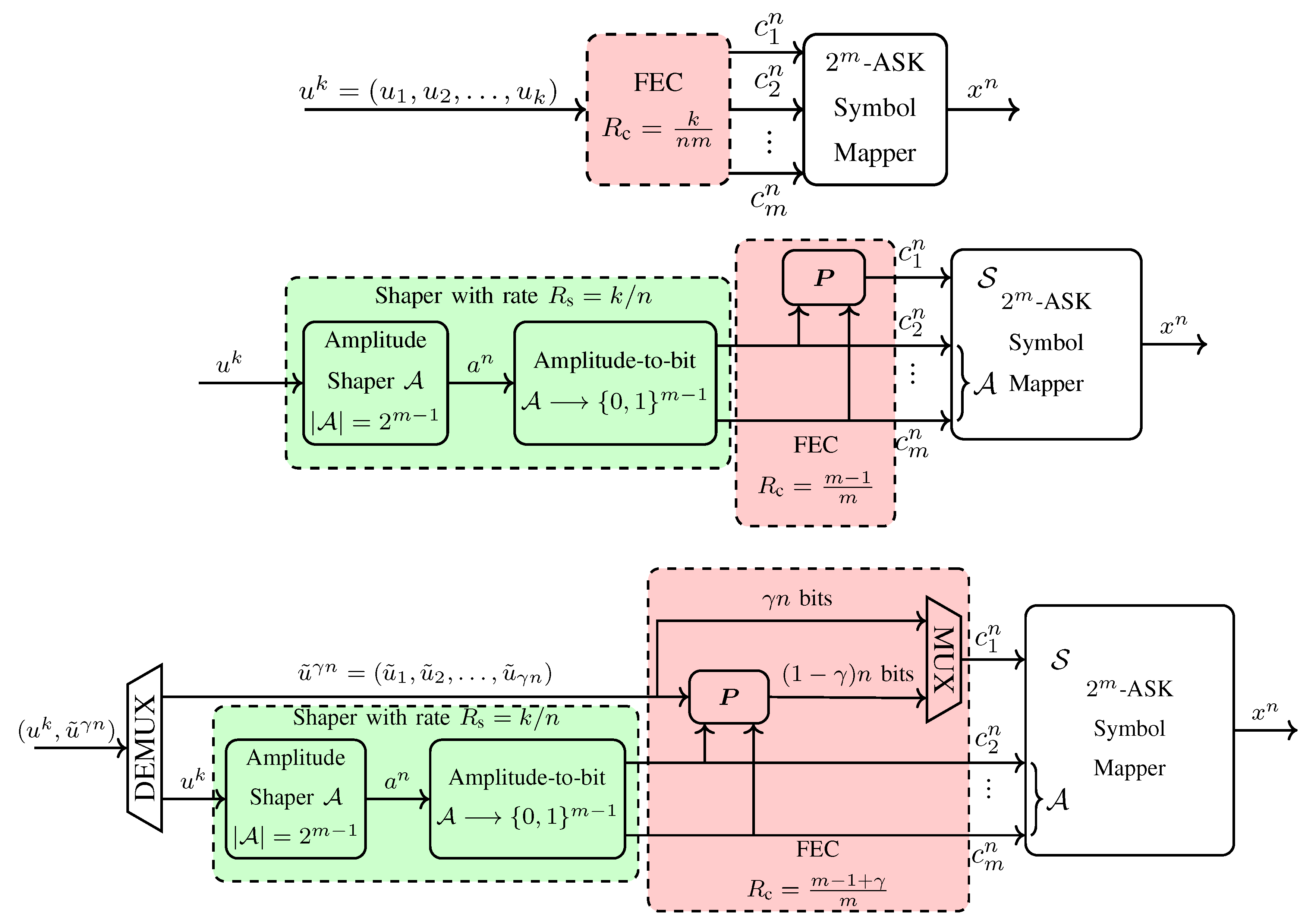
3.1. Uniform Signaling
3.2. Probabilistic Amplitude Shaping
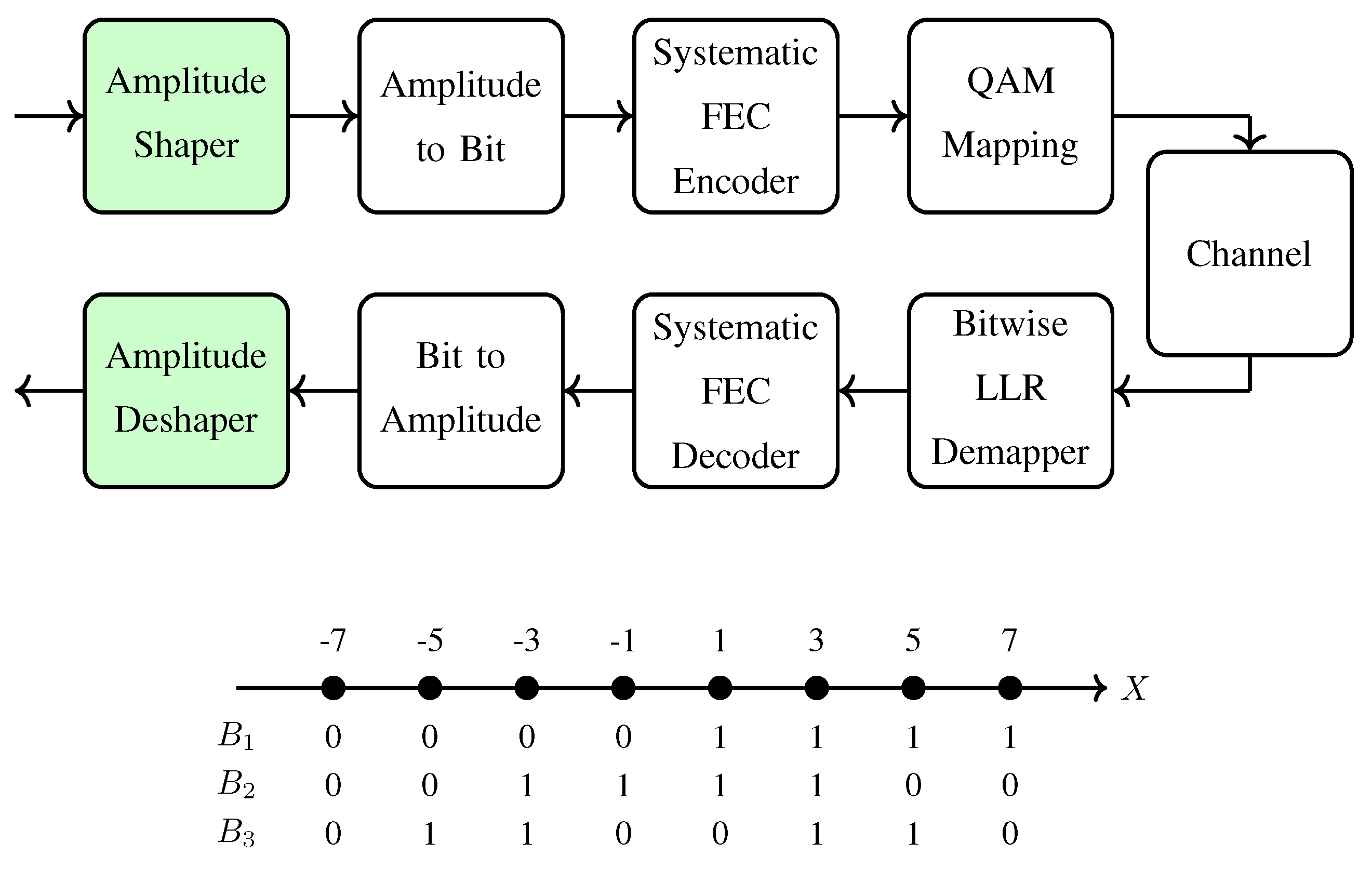
3.3. PAS Receiver
3.4. Selection of Parameters for PAS
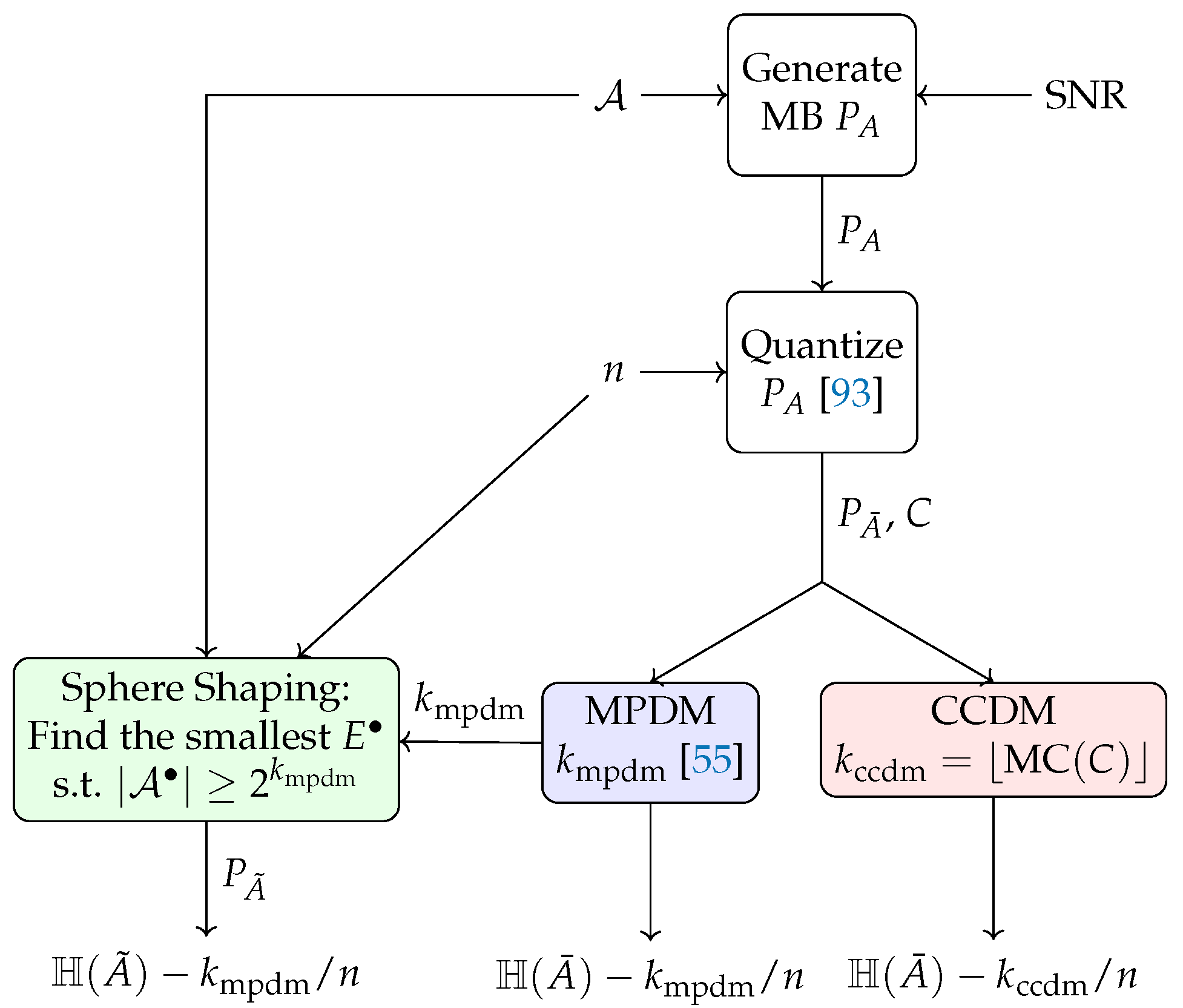
4. Distribution Matching and Sphere Shaping Architectures
4.1. Distribution Matching Architectures (Direct Method)
4.2. Sphere Shaping Architecture (Indirect Method)
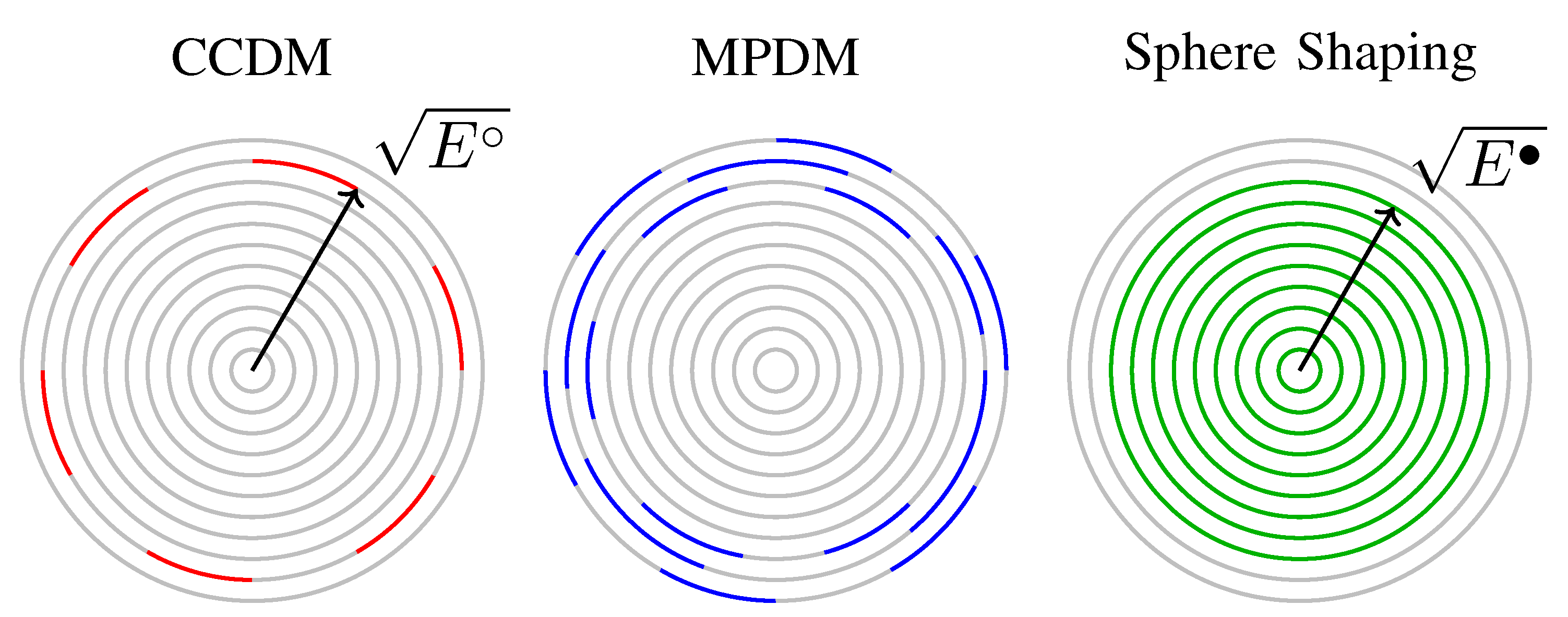
4.3. Geometric Interpretation of the Shaping Architectures
5. Performance Comparison
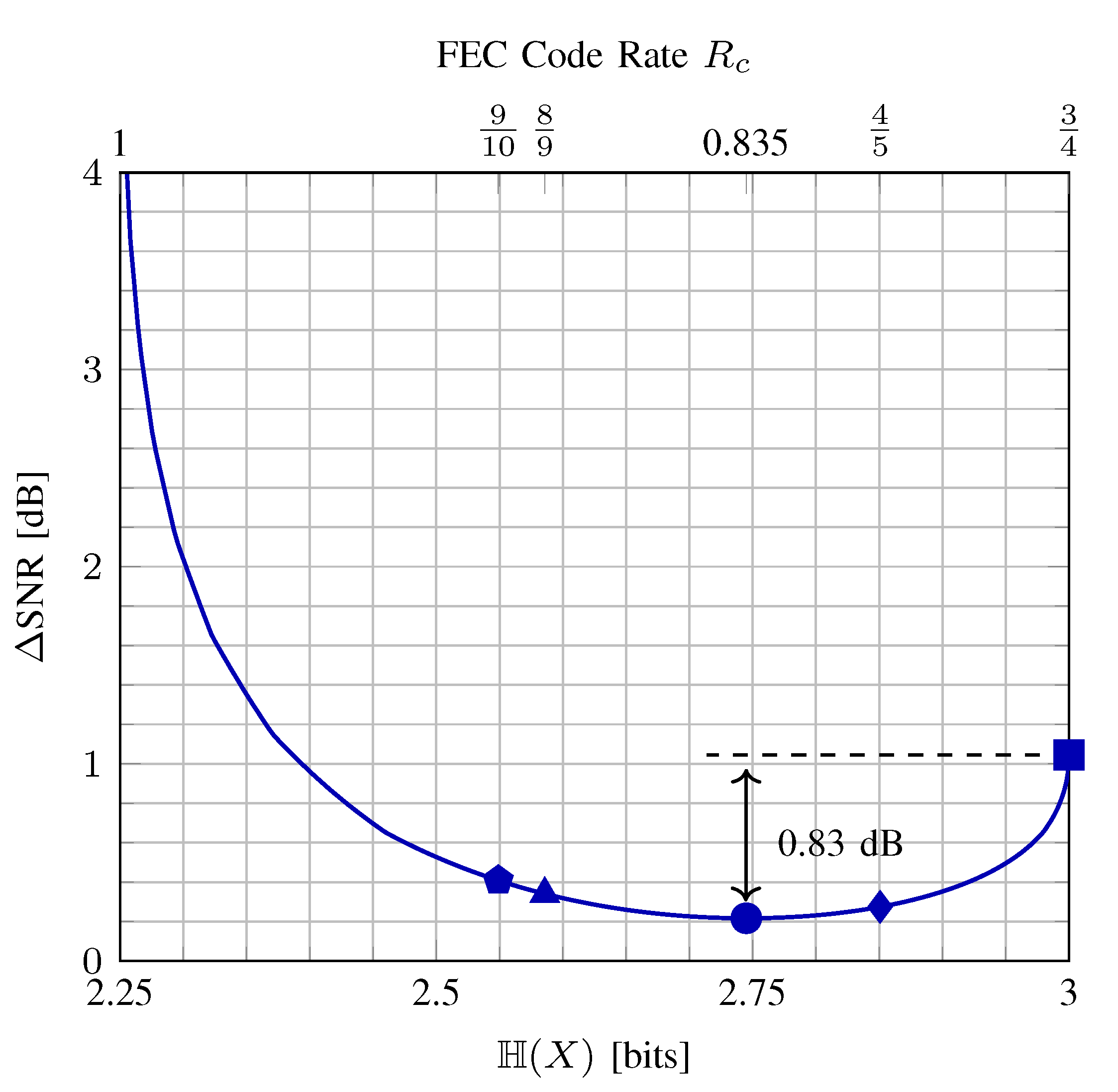
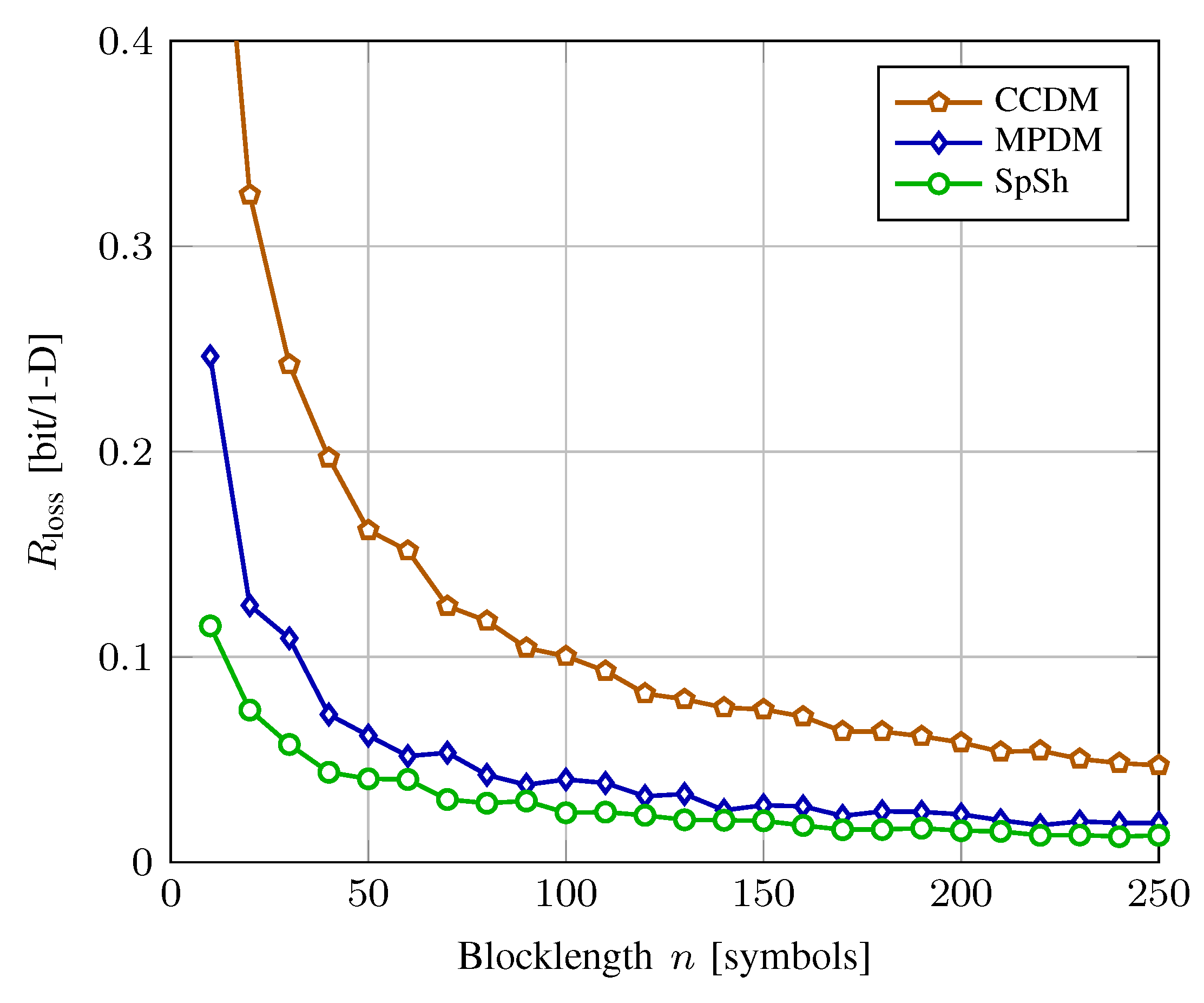
5.1. Rate Loss Analysis
5.2. Achievable Information Rates
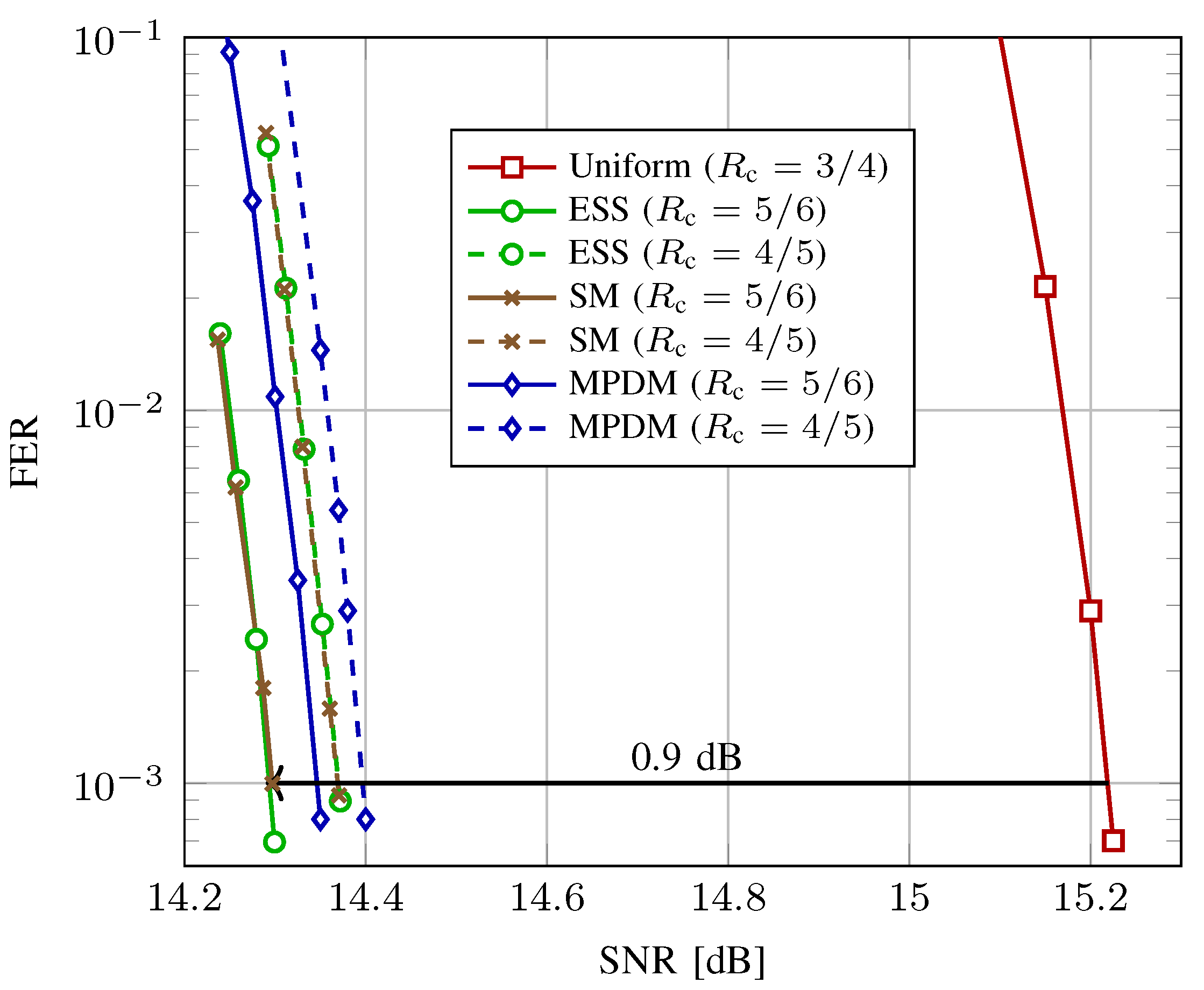
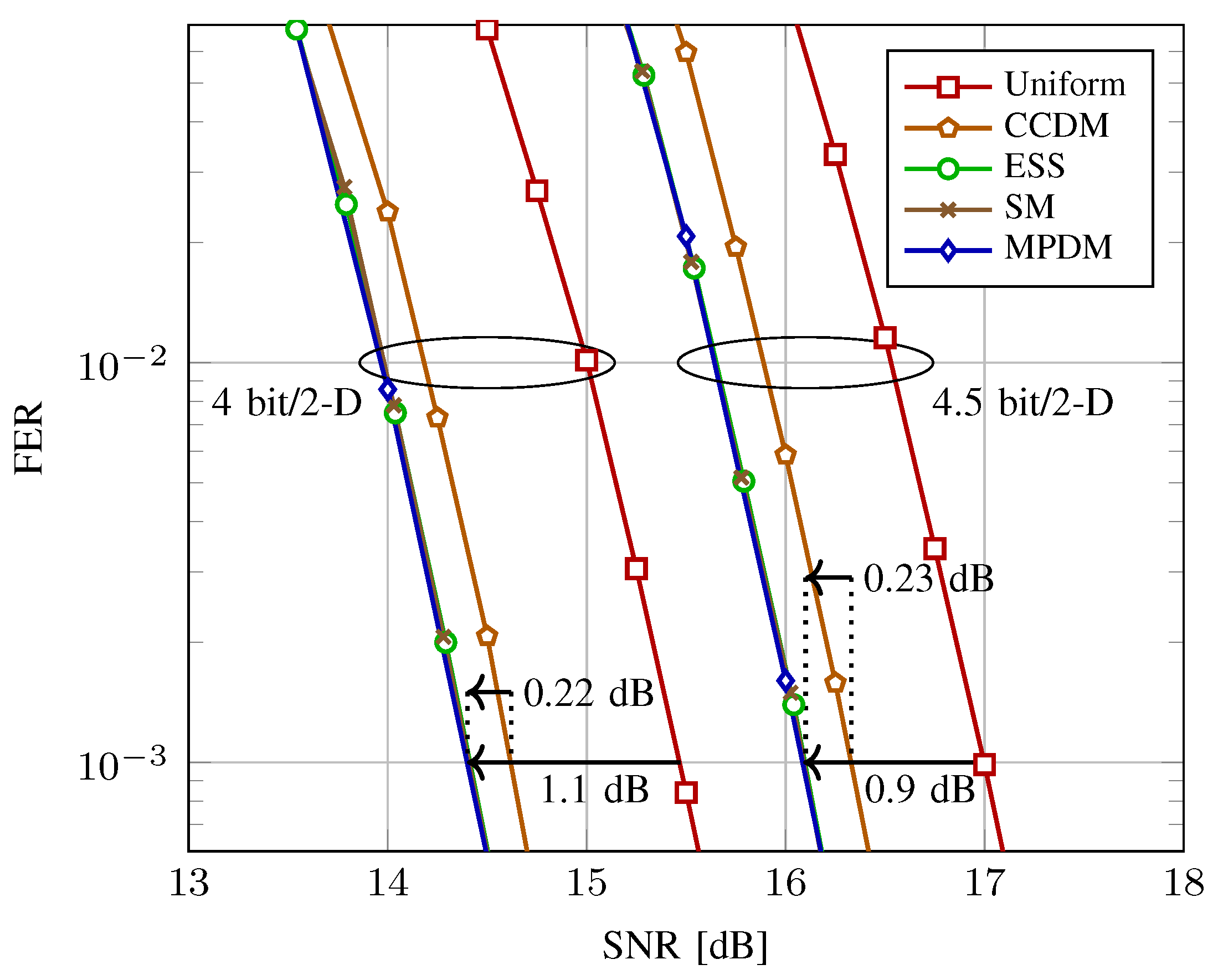
5.3. End-to-End Decoding Performance
6. Approximate Complexity Discussion
6.1. Latency
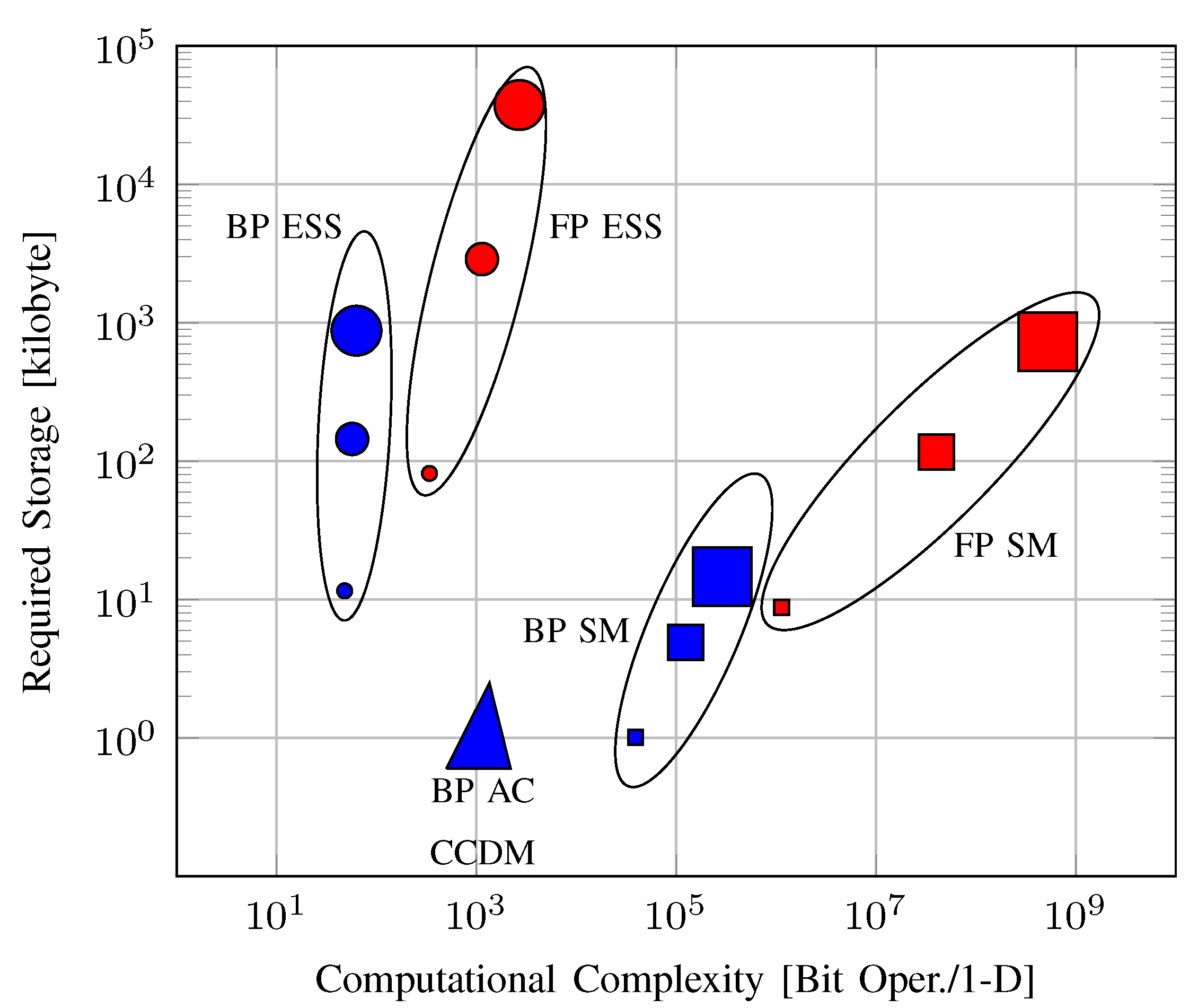
6.2. Storage Requirements
6.3. Computational Complexity
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Arithmetic coding |
| AIR | Achievable information rate |
| ASK | Amplitude-shift keying |
| AWGN | Additive white Gaussian noise |
| BC | Binomial coefficient |
| BL-DM | Bit-level distribution matching |
| BMD | Bit-metric decoding |
| BP | Bounded-precision |
| BRGC | Binary reflected Gray code |
| CCDM | Constant composition distribution matching |
| CM | Coded modulation |
| D&C | Divide and conquer |
| DEMUX | Demultiplexer |
| DM | Distribution matching |
| ESS | Enumerative sphere shaping |
| FEC | Forward error correction |
| FER | Frame error rate |
| FP | Full-precision |
| GMI | Generalized mutual information |
| GS | Geometric shaping |
| LDPC | Low-density parity-check |
| LLR | Log-likelihood ratio |
| LUT | Lookup table |
| MB | Maxwell-Boltzmann |
| MC | Multinomial coefficient |
| MI | Mutual information |
| MLC | Multilevel coding |
| MPDM | Multiset-partition distribution matching |
| MUX | Multiplexer |
| PA | Parallel-amplitude |
| PAS | Probabilistic amplitude shaping |
| PDM | Product distribution matching |
| PMF | Probability mass function |
| PS | Probabilistic shaping |
| QAM | Quadrature amplitude modulation |
| SM | Shell mapping |
| SNR | Signal-to-noise ratio |
| SpSh | Sphere shaping |
| SR | Subset ranking |
References
- Imai, H.; Hirakawa, S. A new multilevel coding method using error-correcting codes. IEEE Trans. Inf. Theory 1977, 23, 371–377. [Google Scholar] [CrossRef]
- Wachsmann, U.; Fischer, R.F.H.; Huber, J.B. Multilevel codes: Theoretical concepts and practical design rules. IEEE Trans. Inf. Theory 1999, 45, 1361–1391. [Google Scholar] [CrossRef]
- Ungerböck, G. Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory 1982, 28, 55–67. [Google Scholar] [CrossRef]
- Zehavi, E. 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun. 1992, 40, 873–884. [Google Scholar] [CrossRef]
- Caire, G.; Taricco, G.; Biglieri, E. Bit-interleaved coded modulation. IEEE Trans. Inf. Theory 1998, 44, 927–946. [Google Scholar] [CrossRef]
- Guillén i Fàbregas, A.; Martinez, A.; Caire, G. Bit-interleaved coded modulation. Found. Trends Commun. Inf. Theory 2008, 5, 1–153. [Google Scholar] [CrossRef]
- Martinez, A.; Guillén i Fàbregas, A.; Caire, G.; Willems, F.M.J. Bit-interleaved coded modulation revisited: A mismatched decoding perspective. IEEE Trans. Inf. Theory 2009, 55, 2756–2765. [Google Scholar] [CrossRef]
- Szczecinski, L.; Alvarado, A. Bit-Interleaved Coded Modulation: Fundamentals, Analysis, and Design; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Forney, G.; Gallager, R.; Lang, G.; Longstaff, F.; Qureshi, S. Efficient modulation for band-limited channels. IEEE J. Sel. Areas Commun. 1984, 2, 632–647. [Google Scholar] [CrossRef]
- Fischer, R. Precoding and Signal Shaping for Digital Transmission; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Sun, F.W.; van Tilborg, H.C.A. Approaching capacity by equiprobable signaling on the Gaussian channel. IEEE Trans. Inf. Theory 1993, 39, 1714–1716. [Google Scholar]
- Loghin, N.S.; Zöllner, J.; Mouhouche, B.; Ansorregui, D.; Kim, J.; Park, S. Non-uniform constellations for ATSC 3.0. IEEE Trans. Broadcast. 2016, 62, 197–203. [Google Scholar] [CrossRef]
- Qu, Z.; Djordjevic, I.B. Geometrically shaped 16QAM outperforming probabilistically shaped 16QAM. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Steiner, F.; Böcherer, G. Comparison of geometric and probabilistic shaping with application to ATSC 3.0. In Proceedings of the 11th International ITG Conference on Systems, Communications and Coding, Hamburg, Germany, 6–9 February 2017. [Google Scholar]
- Boutros, J.J.; Erez, U.; Wonterghem, J.V.; Shamir, G.I.; Zèmorl, G. Geometric shaping: Low-density coding of Gaussian-like constellations. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018. [Google Scholar]
- Chen, B.; Okonkwo, C.; Hafermann, H.; Alvarado, A. Increasing achievable information rates via geometric shaping. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018. [Google Scholar]
- Chen, B.; Okonkwo, C.; Lavery, D.; Alvarado, A. Geometrically-shaped 64-point constellations via achievable information rates. In Proceedings of the 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018. [Google Scholar]
- Chen, B.; Lei, Y.; Lavery, D.; Okonkwo, C.; Alvarado, A. Rate-adaptive coded modulation with geometrically-shaped constellations. In Proceedings of the Asia Communications and Photonics Conference (ACP), Hangzhou, China, 26–29 October 2018. [Google Scholar]
- Calderbank, A.R.; Ozarow, L.H. Nonequiprobable signaling on the Gaussian channel. IEEE Trans. Inf. Theory 1990, 36, 726–740. [Google Scholar] [CrossRef]
- Forney, G.D. Trellis shaping. IEEE Trans. Inf. Theory 1992, 38, 281–300. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Pasupathy, S. Optimal nonuniform signaling for Gaussian channels. IEEE Trans. Inf. Theory 1993, 39, 913–929. [Google Scholar] [CrossRef]
- Willems, F.; Wuijts, J. A pragmatic approach to shaped coded modulation. In Proceedings of the IEEE Symposium on Communications and Vehicular Technology in the Benelux, Delft, The Netherlands, 7–8 October 1993. [Google Scholar]
- Laroia, R.; Farvardin, N.; Tretter, S.A. On optimal shaping of multidimensional constellations. IEEE Trans. Inf. Theory 1994, 40, 1044–1056. [Google Scholar] [CrossRef]
- Böcherer, G.; Mathar, R. Matching dyadic distributions to channels. In Proceedings of the 2011 Data Compression Conference, Snowbird, UT, USA, 29–31 March 2011. [Google Scholar]
- Batshon, H.G.; Mazurczyk, M.V.; Cai, J.X.; Sinkin, O.V.; Paskov, M.; Davidson, C.R.; Wang, D.; Bolshtyansky, M.; Foursa, D. Coded modulation based on 56APSK with hybrid shaping for high spectral efficiency transmission. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Cai, J.X.; Batshon, H.G.; Mazurczyk, M.V.; Sinkin, O.V.; Wang, D.; Paskov, M.; Patterson, W.W.; Davidson, C.R.; Corbett, P.C.; Wolter, G.M.; et al. 70.46 Tb/s over 7600 km and 71.65 Tb/s over 6970 km transmission in C+L band using coded modulation with hybrid constellation shaping and nonlinearity compensation. J. Lightwave Technol. 2018, 36, 114–121. [Google Scholar] [CrossRef]
- Cai, J.; Batshon, H.G.; Mazurczyk, M.V.; Sinkin, O.V.; Wang, D.; Paskov, M.; Davidson, C.R.; Patterson, W.W.; Turukhin, A.; Bolshtyansky, M.A.; et al. 51.5 Tb/s capacity over 17,107 km in C+L bandwidth using single-mode fibers and nonlinearity compensation. J. Lightw. Technol. 2018, 36, 2135–2141. [Google Scholar] [CrossRef]
- Böcherer, G.; Steiner, F.; Schulte, P. Bandwidth efficient and rate-matched low-density parity-check coded modulation. IEEE Trans. Commun. 2015, 63, 4651–4665. [Google Scholar] [CrossRef]
- Sommer, D.; Fettweis, G.P. Signal shaping by non-uniform QAM for AWGN channels and applications using turbo coding. In Proceedings of the ITG Conference on Source and Channel Coding, Munich, Germany, 17–19 January 2000. [Google Scholar]
- Le Goff, S.Y. Signal constellations for bit-interleaved coded modulation. IEEE Trans. Inf. Theory 2003, 49, 307–313. [Google Scholar] [CrossRef]
- Barsoum, M.F.; Jones, C.; Fitz, M. Constellation design via capacity maximization. In Proceedings of the IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007. [Google Scholar]
- Le Goff, S.Y.; Sharif, B.S.; Jimaa, S.A. A new bit-interleaved coded modulation scheme using shaping coding. In Proceedings of the IEEE Global Telecommunications Conference, 2004. GLOBECOM ’04, Dallas, TX, USA, 29 November–3 December 2004. [Google Scholar]
- Raphaeli, D.; Gurevitz, A. Constellation shaping for pragmatic turbo-coded modulation with high spectral efficiency. IEEE Trans. Commun. 2004, 52, 341–345. [Google Scholar] [CrossRef]
- Le Goff, S.Y.; Sharif, B.S.; Jimaa, S.A. Bit-interleaved turbo-coded modulation using shaping coding. IEEE Commun. Lett. 2005, 9, 246–248. [Google Scholar] [CrossRef]
- Valenti, M.C.; Xiang, X. Constellation shaping for bit-interleaved LDPC coded APSK. IEEE Trans. Commun. 2012, 60, 2960–2970. [Google Scholar] [CrossRef][Green Version]
- Le Goff, S.Y.; Khoo, B.K.; Tsimenidis, C.C.; Sharif, B.S. Constellation shaping for bandwidth-efficient turbo-coded modulation with iterative receiver. IEEE Trans. Wirel. Commun. 2007, 6, 2223–2233. [Google Scholar] [CrossRef]
- Guillén i Fàbregas, A.; Martinez, A. Bit-interleaved coded modulation with shaping. In Proceedings of the IEEE Information Theory Workshop, Dublin, Ireland, 30 August–3 September 2010. [Google Scholar]
- Alvarado, A.; Brännström, F.; Agrell, E. High SNR bounds for the BICM capacity. In Proceedings of the IEEE Information Theory Workshop, Paraty, Brazil, 16–20 October 2011. [Google Scholar]
- Böcherer, G.; Altenbach, F.; Alvarado, A.; Corroy, S.; Mathar, R. An efficient algorithm to calculate BICM capacity. In Proceedings of the IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012. [Google Scholar]
- Peng, L.; Guillén i Fàbregas, A.; Martinez, A. Mismatched shaping schemes for bit-interleaved coded modulation. In Proceedings of the IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012. [Google Scholar]
- Peng, L. Fundamentals of Bit-Interleaved Coded Modulation and Reliable Source Transmission. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2012. [Google Scholar]
- Agrell, E.; Alvarado, A. Signal shaping for BICM at low SNR. IEEE Trans. Inf. Theory 2013, 59, 2396–2410. [Google Scholar] [CrossRef]
- Bouazza, B.S.; Djebari, A. Bit-interleaved coded modulation with iterative decoding using constellation shaping over Rayleigh fading channels. AEÜ Int. J. Electron. Commun. 2007, 61, 405–410. [Google Scholar] [CrossRef]
- Xiang, X.; Valenti, M.C. Improving DVB-S2 performance through constellation shaping and iterative demapping. In Proceedings of the MILCOM 2011 Military Communications Conference, Baltimore, MD, USA, 7–10 November 2011. [Google Scholar]
- Bliss, W.G. Circuitry for performing error correction calculations on baseband encoded data to eliminate error propagation. IBM Technol. Discl. Bull. 1981, 23, 4633–4634. [Google Scholar]
- Fan, J.L.; Cioffi, J.M. Constrained coding techniques for soft iterative decoders. In Proceedings of the IEEE Global Telecommunications Conference, Rio de Janeireo, Brazil, 5–9 December 1999. [Google Scholar]
- Prinz, T.; Yuan, P.; Böcherer, G.; Steiner, F.; İşcan, O.; Böhnke, R.; Xu, W. Polar coded probabilistic amplitude shaping for short packets. In Proceedings of the IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017. [Google Scholar]
- Gültekin, Y.C.; van Houtum, W.J.; Koppelaar, A.; Willems, F.M.J. Enumerative sphere shaping for wireless communications with short packets. IEEE Trans. Wirel. Commun. 2020, 19, 1098–1112. [Google Scholar] [CrossRef]
- Buchali, F.; Steiner, F.; Böcherer, G.; Schmalen, L.; Schulte, P.; Idler, W. Rate Adaptation and Reach Increase by Probabilistically Shaped 64-QAM: An Experimental Demonstration. J. Lightwave Technol. 2016, 34, 1599–1609. [Google Scholar] [CrossRef]
- Fehenberger, T.; Lavery, D.; Maher, R.; Alvarado, A.; Bayvel, P.; Hanik, N. Sensitivity Gains by Mismatched Probabilistic Shaping for Optical Communication Systems. IEEE Photonics Technol. Lett. 2016, 28, 786–789. [Google Scholar] [CrossRef]
- Steiner, F.; Schulte, P.; Böcherer, G. Approaching waterfilling capacity of parallel channels by higher order modulation and probabilistic amplitude shaping. In Proceedings of the 52nd Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2018. [Google Scholar]
- Schulte, P.; Böcherer, G. Constant composition distribution matching. IEEE Trans. Inf. Theory 2016, 62, 430–434. [Google Scholar] [CrossRef]
- Ramabadran, T.V. A coding scheme for m-out-of-n codes. IEEE Trans. Commun. 1990, 38, 1156–1163. [Google Scholar] [CrossRef]
- Gültekin, Y.C.; van Houtum, W.J.; Willems, F.M.J. On constellation shaping for short block lengths. In Proceedings of the 2018 Symposium on Information Theory and Signal Processing in the Benelux, Enschede, The Netherlands, 31 May–1 June 2018. [Google Scholar]
- Fehenberger, T.; Millar, D.S.; Koike-Akino, T.; Kojima, K.; Parsons, K. Multiset-partition distribution matching. IEEE Trans. Commun. 2019, 67, 1885–1893. [Google Scholar] [CrossRef]
- Sayood, K. Lossless Compression Handbook; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Pikus, M.; Xu, W. Bit-level probabilistically shaped coded modulation. IEEE Commun. Lett. 2017, 21, 1929–1932. [Google Scholar] [CrossRef]
- Fehenberger, T.; Millar, D.S.; Koike-Akino, T.; Kojima, K.; Parsons, K. Parallel-amplitude architecture and subset ranking for fast distribution Matching. IEEE Trans. Commun. 2020. [Google Scholar] [CrossRef]
- Lang, G.R.; Longstaff, F.M. A Leech lattice modem. IEEE J. Sel. Areas Commun. 1989, 7, 968–973. [Google Scholar] [CrossRef]
- Gültekin, Y.C.; van Houtum, W.J.; Şerbetli, S.; Willems, F.M.J. Constellation shaping for IEEE 802.11. In Proceedings of the IEEE 21st International Symposium on Personal, Indoor and Mobile Radio Communications, Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Amari, A.; Goossens, S.; Gültekin, Y.C.; Vassilieva, O.; Kim, I.; Ikeuchi, T.; Okonkwo, C.; Willems, F.M.J.; Alvarado, A. Introducing enumerative sphere shaping for optical communication systems with short blocklengths. J. Lightwave Technol. 2019, 37, 5926–5936. [Google Scholar] [CrossRef]
- Amari, A.; Goossens, S.; Gültekin, Y.C.; Vassilieva, O.; Kim, I.; Ikeuchi, T.; Okonkwo, C.; Willems, F.M.J.; Alvarado, A. Enumerative sphere shaping for rate adaptation and reach increase in WDM transmission systems. In Proceedings of the European Conference on Communications, Valencia, Spain, 18–21 June 2019. [Google Scholar]
- Goossens, S.; van der Heide, S.; van den Hout, M.; Amari, A.; Gültekin, Y.C.; Vassilieva, O.; Kim, I.; Willems, F.M.J.; Alvarado, A.; Okonkwo, C. First experimental demonstration of probabilistic enumerative sphere shaping in optical fiber communications. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019. [Google Scholar]
- Schulte, P.; Steiner, F. Divergence-optimal fixed-to-fixed length distribution matching with shell mapping. IEEE Wirel. Commun. Lett. 2019, 8, 620–623. [Google Scholar] [CrossRef]
- Gültekin, Y.C.; Willems, F.M.J.; van Houtum, W.J.; Şerbetli, S. Approximate Enumerative Sphere Shaping. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018. [Google Scholar]
- Yoshida, T.; Karlsson, M.; Agrell, E. Short-block-length shaping by simple mark ratio controllers for granular and wide-range spectral efficiencies. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Yoshida, T.; Karlsson, M.; Agrell, E. Low-complexity variable-length output distribution matching with periodical distribution uniformalization. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018. [Google Scholar]
- Böcherer, G.; Steiner, F.; Schulte, P. Fast probabilistic shaping implementation for long-haul fiber-optic communication systems. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Cho, J.; Winzer, P.J. Multi-rate prefix-free code distribution matching. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Cho, J. Prefix-Free Code Distribution Matching for Probabilistic Constellation Shaping. IEEE Trans. Commun. 2020, 68, 670–682. [Google Scholar] [CrossRef]
- Pikus, M.; Xu, W. Arithmetic coding based multi-composition codes for bit-level distribution matching. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019. [Google Scholar]
- Pikus, M.; Xu, W.; Kramer, G. Finite-precision implementation of arithmetic coding based distribution matchers. arXiv 2019, arXiv:1907.12066. [Google Scholar]
- Gültekin, Y.C.; van Houtum, W.J.; Koppelaar, A.; Willems, F.M. Partial Enumerative Sphere Shaping. In Proceedings of the IEEE Vehicular Technology Conference (Fall), Honolulu, HI, USA, 22–25 September 2019. [Google Scholar]
- Yoshida, T.; Karlsson, M.; Agrell, E. Hierarchical distribution matching for probabilistically shaped coded modulation. J. Lightwave Technol. 2019, 37, 1579–1589. [Google Scholar] [CrossRef]
- Civelli, S.; Secondini, M. Hierarchical distribution matching: A versatile tool for probabilistic shaping. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Millar, D.S.; Fehenberger, T.; Yoshida, T.; Koike-Akino, T.; Kojima, K.; Suzuki, N.; Parsons, K. Huffman coded sphere shaping with short length and reduced complexity. In Proceedings of the European Conference on Optical Communication, Dublin, Ireland, 22–26 September 2019. [Google Scholar]
- Digital Video Broadcasting (DVB); 2nd Generation Framing Structure, Channel Coding and Modulation Systems for Broadcasting, Interactive Services, News Gathering and Other Broadband Satellite Applications (DVB-S2); (ETSI) Standard EN 302 307, Rev. 1.2.1; European Telecommunications Standards Institute: Sophia Antipolis, France, 2009.
- IEEE Standard for Inform. Technol.-Telecommun. and Inform. Exchange Between Syst. Local and Metropolitan Area Networks-Specific Requirements-Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; Revision of IEEE Standard 802.11-2012; IEEE Standard 802.11-2016: Piscataway, NJ, USA, 2016.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Böcherer, G. Principles of Coded Modulation. Habilitation Thesis, Department of Electrical and Computer Engineering, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Khandani, A.K.; Kabal, P. Shaping multidimensional signal spaces – Part I: Optimum shaping, shell mapping. IEEE Trans. Inf. Theory 1993, 39, 1799–1808. [Google Scholar] [CrossRef]
- Tretter, S. Constellation Shaping, Nonlinear Precoding, and Trellis Coding for Voiceband Telephone Channel Modems with Emphasis on ITU-T Recommendation; Springer: New York, NY, USA, 2002. [Google Scholar]
- Vassilieva, O.; Kim, I.; Ikeuchi, T. On the fairness of the performance evaluation of probabilistically shaped QAM. In Proceedings of the European Conference on Communications (ECOC), Athens, Greece, 13–16 May 2019. [Google Scholar]
- Böcherer, G. Probabilistic signal shaping for bit-metric decoding. In Proceedings of the IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014. [Google Scholar]
- Böcherer, G. Probabilistic signal shaping for bit-metric decoding. arXiv 2014, arXiv:1401.6190. [Google Scholar]
- Kramer, G. Topics in multi-user information theory. Found. Trends Commun. Inf. Theory 2008, 4, 265–444. [Google Scholar] [CrossRef]
- Böcherer, G. Achievable rates for shaped bit-metric decoding. arXiv 2016, arXiv:1410.8075. [Google Scholar]
- Merhav, N.; Kaplan, G.; Lapidoth, A.; Shamai (Shitz), S. On information rates for mismatched decoders. IEEE Trans. Inf. Theory 1994, 40, 1953–1967. [Google Scholar] [CrossRef]
- Böcherer, G. Achievable rates for probabilistic shaping. arXiv 2018, arXiv:1707.01134. [Google Scholar]
- Amjad, R.A. Information Rates and Error Exponents for Probabilistic Amplitude Shaping. In Proceedings of the IEEE IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018. [Google Scholar]
- Gültekin, Y.C.; Alvarado, A.; Willems, F.M.J. Achievable information rates for probabilistic amplitude shaping: A minimum-randomness approach via random sign-coding arguments. arXiv 2020, arXiv:2002.10387. [Google Scholar]
- Fischer, R.F.H.; Huber, J.B.; Wachsmann, U. Multilevel coding: Aspects from information theory. In Proceedings of the IEEE Global Telecommunications Conference, London, UK, 18–28 November 1996. [Google Scholar]
- Böcherer, G.; Geiger, B.C. Optimal quantization for distribution synthesis. IEEE Trans. Inf. Theory 2016, 62, 6162–6172. [Google Scholar] [CrossRef]
- Millar, D.S.; Fehenberger, T.; Koike-Akino, T.; Kojima, K.; Parsons, K. Distribution matching for high spectral efficiency optical communication with multiset partitions. J. Lightwave Technol. 2019, 37, 517–523. [Google Scholar] [CrossRef]
- Fehenberger, T.; Millar, D.S.; Koike-Akino, T.; Kojima, K.; Parsons, K. Partition-based probabilistic shaping for fiber-optic communication systems. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Schalkwijk, J. An algorithm for source coding. IEEE Trans. Inf. Theory 1972, 18, 395–399. [Google Scholar] [CrossRef]
- Cover, T. Enumerative source encoding. IEEE Trans. Inf. Theory 1973, 19, 73–77. [Google Scholar] [CrossRef]
- Wozencraft, J.M.; Jacobs, I.M. Principles of Communication Engineering; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Gültekin, Y.C.; Willems, F.M.J. Building the optimum enumerative shaping trellis. In Proceedings of the Symposium on Information Theory in the Benelux, Bruxelles, Benelux, 28–29 May 2019; p. 34. [Google Scholar]
- Fischer, R.F.H. Calculation of shell frequency distributions obtained with shell-mapping schemes. IEEE Trans. Inf. Theory 1999, 45, 1631–1639. [Google Scholar] [CrossRef][Green Version]
- Böcherer, G.; Schulte, P.; Steiner, F. Probabilistic shaping and forward error correction for fiber-optic communication Systems. J. Lightwave Technol. 2019, 37, 230–244. [Google Scholar] [CrossRef]
- Yoshida, T.; Binkai, M.; Koshikawa, S.; Chikamori, S.; Matsuda, K.; Suzuki, N.; Karlsson, M.; Agrell, E. FPGA implementation of distribution matching and dematching. In Proceedings of the European Conference on Optical Communication, Athens, Greece, 13–16 May 2019. [Google Scholar]
- Li, J.; Zhang, A.; Zhang, C.; Huo, X.; Yang, Q.; Wang, J.; Wang, J.; Qu, W.; Wang, Y.; Zhang, J.; et al. Field trial of probabilistic-shaping-programmable real-time 200-Gb/s coherent transceivers in an intelligent core optical network. In Proceedings of the Asia Communications and Photonics Conference (ACP), Hangzhou, China, 26–29 October 2018. [Google Scholar]
- Zhang, Z.; Wang, J.; Ouyang, S.; Wang, J.; Chen, J.; Liu, X.; Chen, J.; Wang, Y.; Wang, W.; Ding, T.; et al. Real-time measurement of a probabilistic-shaped 200Gb/s DP-16QAM transceiver. Opt. Express 2019, 27, 18787–18793. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Corteselli, S.; Cho, J. FPGA implementation of prefix-free code distribution matching for probabilistic constellation shaping. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Rissanen, J.; Langdon, G.G. Arithmetic Coding. IBM J. Res. Dev. 1979, 23, 149–162. [Google Scholar] [CrossRef]
- Langdon, G.G. An Introduction to Arithmetic Coding. IBM J. Res. Dev. 1984, 28, 135–149. [Google Scholar] [CrossRef]

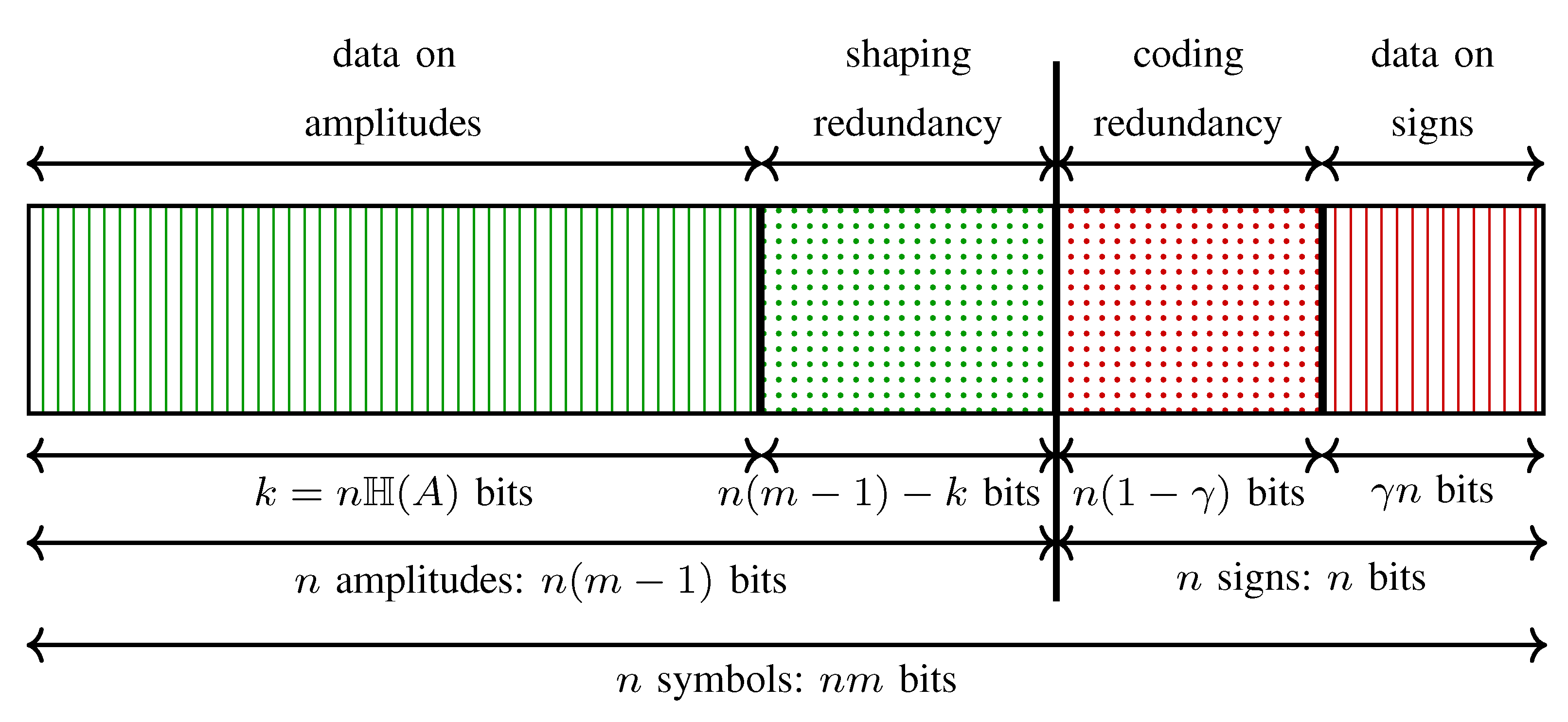

| Parameter | Formula (per n-Sequence) | Value per 1-D (Example 2) | Value per 216-D (Example 2) |
|---|---|---|---|
| Data on amp. | 1.75 | 378 | |
| Data on sign | 0.50 | 108 | |
| Shap. redundancy | 0.25 | 54 | |
| Cod. redundancy | 0.50 | 108 | |
| Redundancy | 0.75 | 162 | |
| Data, | 2.25 | 486 |
| Architecture | k | E | or | Rloss | |
|---|---|---|---|---|---|
| CCDM | 367 | 1.6991 | 11.00 | 1.7504 | 0.0513 |
| MPDM | 374 | 1.7315 | 11.00 | 1.7504 | 0.0189 |
| SpSh | 374 | 1.7315 | 10.90 | 1.7448 | 0.0133 |
| Direct Method (Distribution Matching) | Indirect Method (Energy-Efficient Signal Space) | ||||
|---|---|---|---|---|---|
| AC-CCDM [52] | SR-DM [58] | ESS [22] and (Algorithm 1 in [23]) | SM [23] | ||
| Serialism (no. of loop iter.) | |||||
| Storage Complexity | FP: BP [65]: | FP: BP [65]: | |||
| Computations (per 1-D) | divisions, multiplications and comparisons | Sh: BCs Dsh: BCs | Sh: comparisons and subtractions Dsh: additions (and L comparisons/additions per n-D for [23, Algorithm 1]) | Sh: L multiplications, comparisons and subtractions Dsh: L multiplications and additions | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gültekin, Y.C.; Fehenberger, T.; Alvarado, A.; Willems, F.M.J. Probabilistic Shaping for Finite Blocklengths: Distribution Matching and Sphere Shaping. Entropy 2020, 22, 581. https://doi.org/10.3390/e22050581
Gültekin YC, Fehenberger T, Alvarado A, Willems FMJ. Probabilistic Shaping for Finite Blocklengths: Distribution Matching and Sphere Shaping. Entropy. 2020; 22(5):581. https://doi.org/10.3390/e22050581
Chicago/Turabian StyleGültekin, Yunus Can, Tobias Fehenberger, Alex Alvarado, and Frans M. J. Willems. 2020. "Probabilistic Shaping for Finite Blocklengths: Distribution Matching and Sphere Shaping" Entropy 22, no. 5: 581. https://doi.org/10.3390/e22050581
APA StyleGültekin, Y. C., Fehenberger, T., Alvarado, A., & Willems, F. M. J. (2020). Probabilistic Shaping for Finite Blocklengths: Distribution Matching and Sphere Shaping. Entropy, 22(5), 581. https://doi.org/10.3390/e22050581





