A Dual Measure of Uncertainty: The Deng Extropy
Abstract
1. Introduction
2. The Deng Extropy
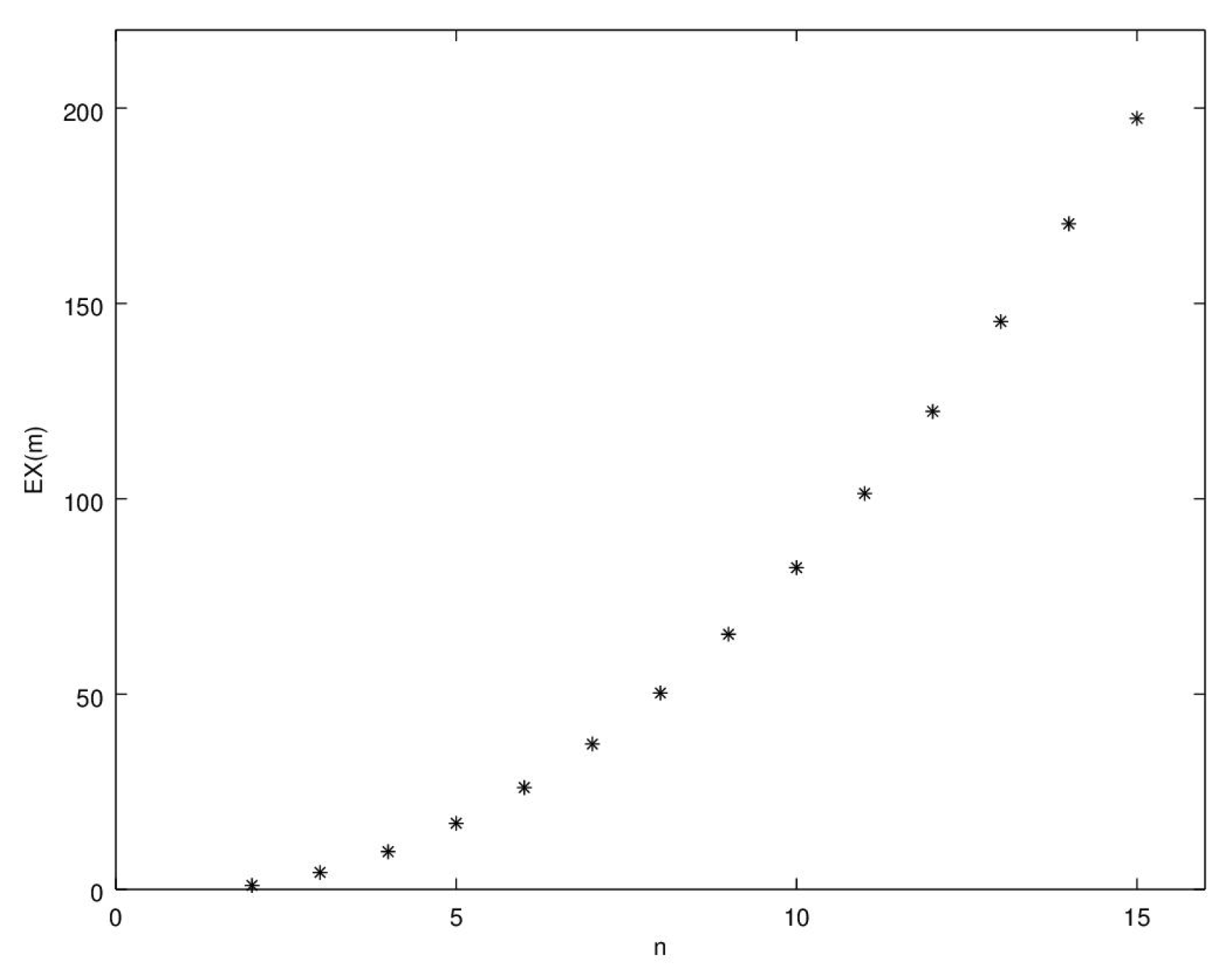
3. The Maximum Deng Extropy
4. Application to Pattern Recognition
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BPA | Basic probability assignment |
| PPT | Pignistic probability transformation |
| SL | Sepal length in cm |
| SW | Sepal width in cm |
| PL | Petal length in cm |
| PW | Petal width in cm |
| Se | Iris Setosa |
| Ve | Iris Versicolour |
| Vi | Iris Virginica |
References
- Shannon, C.E. A mathematical theory of communication. Bell Labs. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lad, F.; Sanfilippo, G.; Agrò, G. Extropy: Complementary dual of entropy. Stat. Sci. 2015, 30, 40–58. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Fu, C.; Yang, J.B.; Yang, S.L. A group evidential reasoning approach based on expert reliability. Eur. J. Oper. Res. 2015, 246, 886–893. [Google Scholar] [CrossRef]
- Yang, J.B.; Xu, D.L. Evidential reasoning rule for evidence combination. Artif. Intell. 2013, 205, 1–29. [Google Scholar] [CrossRef]
- Kabir, G.; Tesfamariam, S.; Francisque, A.; Sadiq, R. Evaluating risk of water mains failure using a Bayesian belief network model. Eur. J. Oper. Res. 2015, 240, 220–234. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Fan, X.J.; Lin, Q.L. Failure mode and effects analysis using D numbers and grey relational projection method. Expert Syst. Appl. 2014, 41, 4670–4679. [Google Scholar] [CrossRef]
- Han, Y.; Deng, Y. An enhanced fuzzy evidential DEMATEL method with its application to identify critical success factors. Soft Comput. 2018, 22, 5073–5090. [Google Scholar] [CrossRef]
- Liu, Z.; Pan, Q.; Dezert, J.; Han, J.W.; He, Y. Classifier fusion with contextual reliability evaluation. IEEE Trans. Cybern. 2018, 48, 1605–1618. [Google Scholar] [CrossRef]
- Smets, P. Data fusion in the transferable belief model. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000; Volume 1, pp. PS21–PS33. [Google Scholar]
- Balakrishnan, N.; Buono, F.; Longobardi, M. On weighted extropies. Comm. Stat. Theory Methods. (under review).
- Calì, C.; Longobardi, M.; Ahmadi, J. Some properties of cumulative Tsallis entropy. Physica A 2017, 486, 1012–1021. [Google Scholar] [CrossRef]
- Calì, C.; Longobardi, M.; Navarro, J. Properties for generalized cumulative past measures of information. Probab. Eng. Inform. Sci. 2020, 34, 92–111. [Google Scholar] [CrossRef]
- Calì, C.; Longobardi, M.; Psarrakos, G. A family of weighted distributions based on the mean inactivity time and cumulative past entropies. Ricerche Mat. 2019, 1–15. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies. J. Stat. Plann. Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
- Kamari, O.; Buono, F. On extropy of past lifetime distribution. Ricerche Mat. 2020, in press. [Google Scholar] [CrossRef]
- Longobardi, M. Cumulative measures of information and stochastic orders. Ricerche Mat. 2014, 63, 209–223. [Google Scholar] [CrossRef]
- Abellan, J. Analyzing properties of Deng entropy in the theory of evidence. Chaos Solitons Fractals 2017, 95, 195–199. [Google Scholar] [CrossRef]
- Tang, Y.; Fang, X.; Zhou, D.; Lv, X. Weighted Deng entropy and its application in uncertainty measure. In Proceedings of the 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–5. [Google Scholar]
- Wang, D.; Gao, J.; Wei, D. A New Belief Entropy Based on Deng Entropy. Entropy 2019, 21, 987. [Google Scholar] [CrossRef]
- Hohle, U. Entropy with respect to plausibility measures. In Proceedings of the 12th IEEE International Symposium on Multiple-Valued Logic, Paris, France, 25–27 May 1982; pp. 167–169. [Google Scholar]
- Yager, R.R. Entropy and specificity in a mathematical theory of evidence. Int. J. Gen. Syst. 1983, 9, 249–260. [Google Scholar] [CrossRef]
- Klir, G.J.; Ramer, A. Uncertainty in the Dempster-Shafer theory: A critical re-examination. Int. J. Gen. Syst. 1990, 18, 155–166. [Google Scholar] [CrossRef]
- Kang, B.; Deng, Y. The Maximum Deng Entropy. IEEE Access 2019, 7, 120758–120765. [Google Scholar] [CrossRef]
- Dheeru, D.; Karra Taniskidou, E. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 20 May 2020).
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An Improved Deng Entropy and Its Application in Pattern Recognition. IEEE Access 2019, 7, 18284–18292. [Google Scholar] [CrossRef]
- Kang, B.Y.; Li, Y.; Deng, Y.; Zhang, Y.J.; Deng, X.Y. Determination of basic probability assignment based on interval numbers and its application. Acta Electron. Sin. 2012, 40, 1092–1096. [Google Scholar]
- Tran, L.; Duckstein, L. Comparison of fuzzy numbers using a fuzzy distance measure. Fuzzy Sets Syst. 2002, 130, 331–341. [Google Scholar] [CrossRef]
| A | Deng Extropy | Deng Entropy |
|---|---|---|
| 28.104 | 2.6623 | |
| 27.904 | 3.9303 | |
| 27.704 | 4.9082 | |
| 27.504 | 5.7878 | |
| 27.304 | 6.6256 | |
| 27.104 | 7.4441 | |
| 26.903 | 8.2532 | |
| 26.702 | 9.0578 | |
| 26.500 | 9.8600 | |
| 26.295 | 10.661 | |
| 26.086 | 11.462 | |
| 25.866 | 12.262 | |
| 25.621 | 13.062 | |
| 25.304 | 13.862 |
| Item | SL | SW | PL | PW |
|---|---|---|---|---|
| [4.4,5.8] | [2.3,4.4] | [1.0,1.9] | [0.1,0.6] | |
| [4.9,7.0] | [2.0,3.4] | [3.0,5.1] | [1.0,1.7] | |
| [4.9,7.9] | [2.2,3.8] | [4.5,6.9] | [1.4,2.5] | |
| [4.9,5.8] | [2.3,3.4] | – | – | |
| [4.9,5.8] | [2.3,3.8] | – | – | |
| [4.9,7.0] | [2.2,3.4] | [4.5,5.1] | [1.4,1.7] | |
| [4.9,5.8] | [2.3,3.4] | – | – |
| Item | SL | SW | PL | PW | Combined BPA |
|---|---|---|---|---|---|
| 0.1098 | 0.1018 | 0.0625 | 0.1004 | 0.0059 | |
| 0.1703 | 0.1303 | 0.1839 | 0.2399 | 0.4664 | |
| 0.1257 | 0.1385 | 0.1819 | 0.3017 | 0.4656 | |
| 0.1413 | 0.1663 | 0.0000 | 0.0000 | 0.0000 | |
| 0.1413 | 0.1441 | 0.0000 | 0.0000 | 0.0000 | |
| 0.1703 | 0.1527 | 0.5719 | 0.3580 | 0.0620 | |
| 0.1413 | 0.1663 | 0.0000 | 0.0000 | 0.0000 | |
| Deng extropy | 5.2548 | 5.2806 | 5.1636 | 4.9477 |
| Item | SL | SW | PL | PW | Combined BPA |
|---|---|---|---|---|---|
| 0.0808 | 0.0730 | 0.0504 | 0.1004 | 0.0224 | |
| 0.1252 | 0.0934 | 0.1482 | 0.2399 | 0.4406 | |
| 0.0925 | 0.0993 | 0.1465 | 0.3017 | 0.4451 | |
| 0.1039 | 0.1192 | 0.0000 | 0.0000 | 0.0000 | |
| 0.1039 | 0.1033 | 0.0000 | 0.0000 | 0.0000 | |
| 0.1252 | 0.1095 | 0.4608 | 0.3580 | 0.0919 | |
| 0.3684 | 0.4023 | 0.1942 | 0.0000 | 0.0000 |
| Item | Setosa | Versicolor | Virginica | Global |
|---|---|---|---|---|
| Kang’s method | 100% | 96% | 84% | 93.33% |
| Method based on Deng extropy | 100% | 96% | 86% | 94% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buono, F.; Longobardi, M. A Dual Measure of Uncertainty: The Deng Extropy. Entropy 2020, 22, 582. https://doi.org/10.3390/e22050582
Buono F, Longobardi M. A Dual Measure of Uncertainty: The Deng Extropy. Entropy. 2020; 22(5):582. https://doi.org/10.3390/e22050582
Chicago/Turabian StyleBuono, Francesco, and Maria Longobardi. 2020. "A Dual Measure of Uncertainty: The Deng Extropy" Entropy 22, no. 5: 582. https://doi.org/10.3390/e22050582
APA StyleBuono, F., & Longobardi, M. (2020). A Dual Measure of Uncertainty: The Deng Extropy. Entropy, 22(5), 582. https://doi.org/10.3390/e22050582






