Some Useful Integral Representations for Information-Theoretic Analyses
Abstract
1. Introduction
2. Statistical Moments of Arbitrary Positive Orders
3. Applications
3.1. Moments of Guesswork
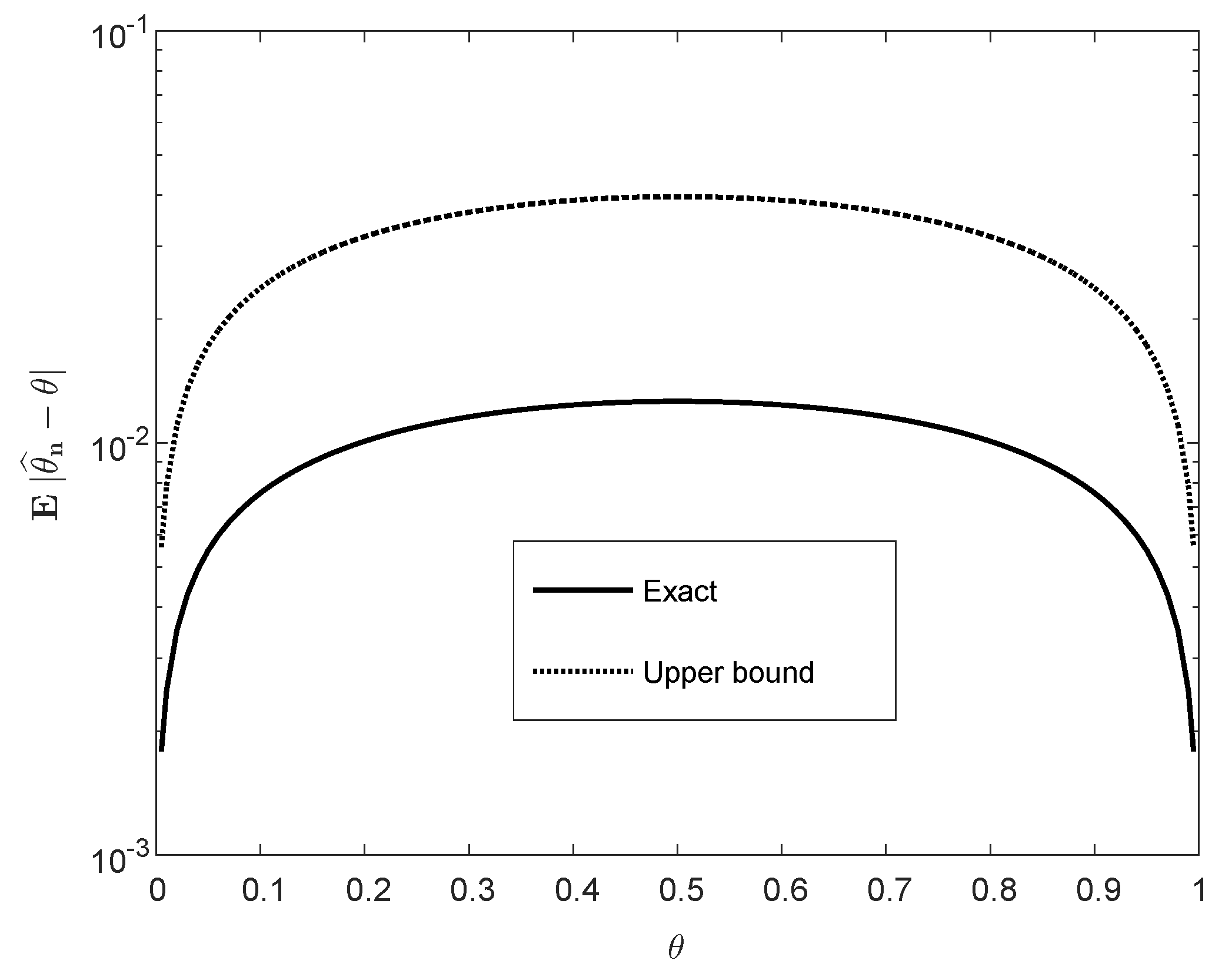
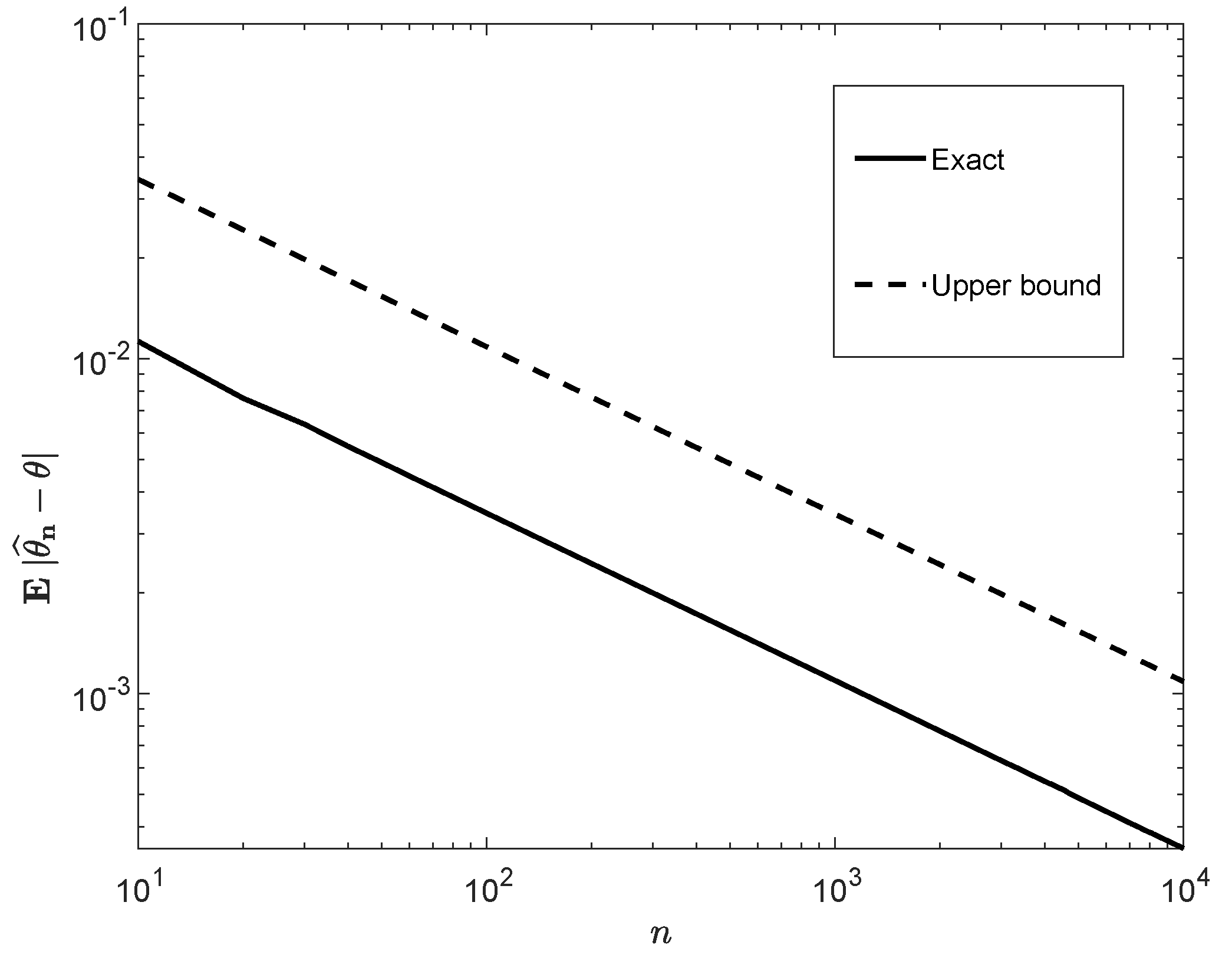
3.2. Moments of Estimation Errors
3.3. Rényi Entropy of Extended Multivariate Cauchy Distributions
- (a)
- If for some , thenwith
- (b)
- Otherwise (i.e., if ), thenwhere , and for all ,
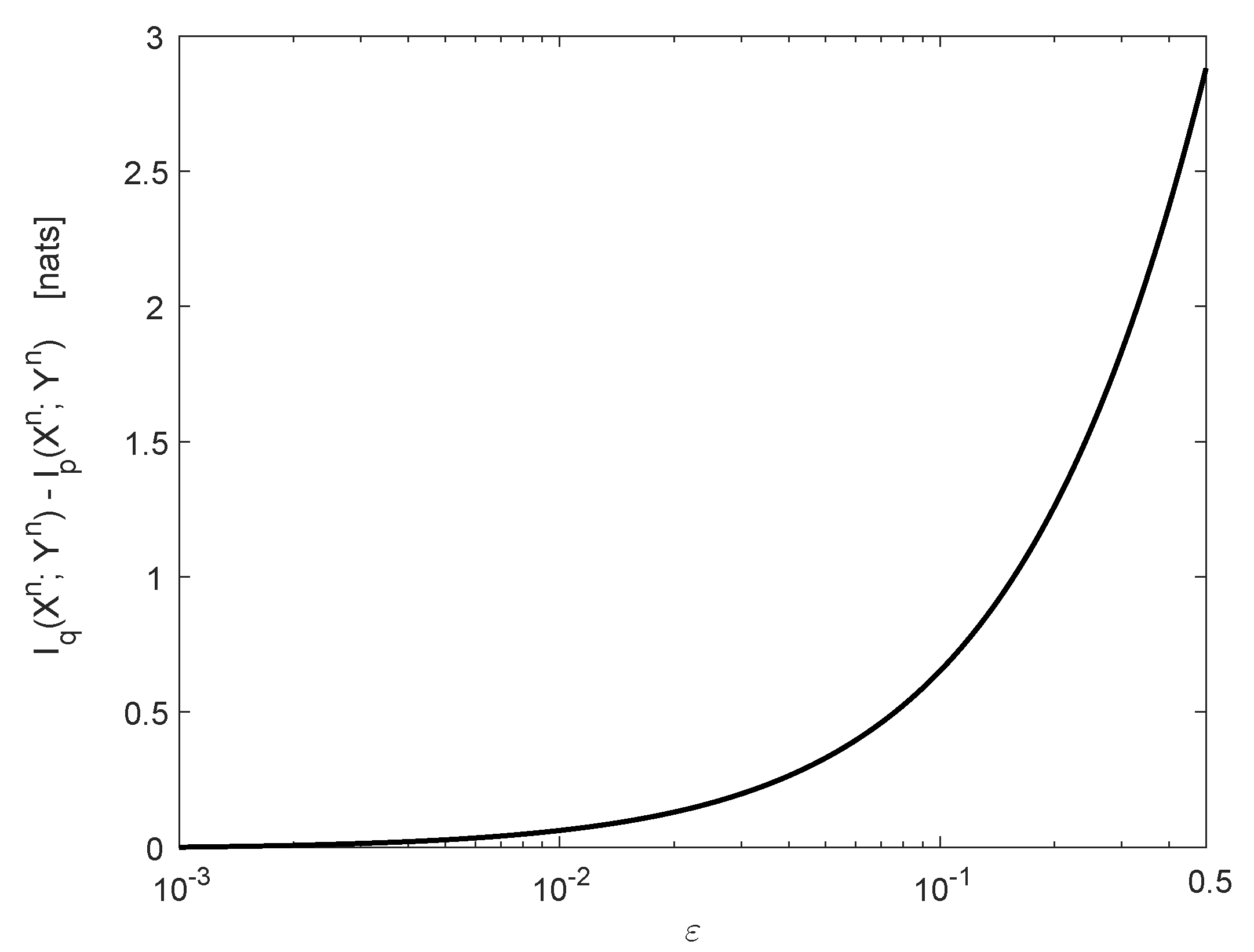
3.4. Mutual Information Calculations for Communication Channels with Jamming
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Complementary Details of the Analysis in Section 3.2
Appendix B.1. Proof of Equation (36)
Appendix B.2. Derivation of the Upper Bound in (40)
Appendix C. Complementary Details of the Analysis in Section 3.3
Appendix D. Calculations of the n-Dimensional Integrals in Section 3.4
Appendix D.1. Proof of Equations (62)–(64)
Appendix D.2. Proof of Equation (65)
Appendix D.3. Proof of Equations (67)–(73)
Appendix D.4. Specialization to a BSC with Jamming
References
- Dong, A.; Zhang, H.; Wu, D.; Yuan, D. Logarithmic expectation of the sum of exponential random variables for wireless communication performance evaluation. In 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall); IEEE: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Appledorn, C.R. The entropy of a Poisson distribution. SIAM Rev. 1988, 30, 314–317. [Google Scholar] [CrossRef]
- Knessl, C. Integral representations and asymptotic expansions for Shannon and Rényi entropies. Appl. Math. Lett. 1998, 11, 69–74. [Google Scholar] [CrossRef]
- Lapidoth, A.; Moser, S. Capacity bounds via duality with applications to multiple-antenna systems on flat fading channels. IEEE Trans. Inf. Theory 2003, 49, 2426–2467. [Google Scholar] [CrossRef]
- Martinez, A. Spectral efficiency of optical direct detection. J. Opt. Soc. Am. B 2007, 24, 739–749. [Google Scholar] [CrossRef]
- Merhav, N.; Sason, I. An integral representation of the logarithmic function with applications in information theory. Entropy 2020, 22, 51. [Google Scholar] [CrossRef]
- Rajan, A.; Tepedelenlioǧlu, C. Stochastic ordering of fading channels through the Shannon transform. IEEE Trans. Inf. Theory 2015, 61, 1619–1628. [Google Scholar] [CrossRef]
- Zadeh, P.H.; Hosseini, R. Expected logarithm of central quadratic form and its use in KL-divergence of some distributions. Entropy 2016, 18, 288. [Google Scholar] [CrossRef]
- Arikan, E. An inequality on guessing and its application to sequential decoding. IEEE Trans. Inf. Theory 1996, 42, 99–105. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Guessing subject to distortion. IEEE Trans. Inf. Theory 1998, 44, 1041–1056. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Joint source-channel coding and guessing with application to sequential decoding. IEEE Trans. Inf. Theory 1998, 44, 1756–1769. [Google Scholar] [CrossRef]
- Boztaş, S. Comments on “An inequality on guessing and its application to sequential decoding”. IEEE Trans. Inf. Theory 1997, 43, 2062–2063. [Google Scholar] [CrossRef]
- Bracher, A.; Hof, E.; Lapidoth, A. Guessing attacks on distributed-storage systems. IEEE Trans. Inf. Theory 2019, 65, 6975–6998. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A. Encoding tasks and Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 5065–5076. [Google Scholar] [CrossRef]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Courtade, T.; Verdú, S. Cumulant generating function of codeword lengths in optimal lossless compression. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2494–2498. [Google Scholar] [CrossRef]
- Courtade, T.; Verdú, S. Variable-length lossy compression and channel coding: Non-asymptotic converses via cumulant generating functions. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2499–2503. [Google Scholar] [CrossRef]
- Merhav, N. Lower bounds on exponential moments of the quadratic error in parameter estimation. IEEE Trans. Inf. Theory 2018, 64, 7636–7648. [Google Scholar] [CrossRef]
- Sason, I.; Verdú, S. Improved bounds on lossless source coding and guessing moments via Rényi measures. IEEE Trans. Inf. Theory 2018, 64, 4323–4346. [Google Scholar] [CrossRef]
- Sason, I. Tight bounds on the Rényi entropy via majorization with applications to guessing and compression. Entropy 2018, 20, 896. [Google Scholar] [CrossRef]
- Sundaresan, R. Guessing under source uncertainty. IEEE Trans. Inf. Theory 2007, 53, 269–287. [Google Scholar] [CrossRef]
- Sundaresan, R. Guessing based on length functions. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 716–719. [Google Scholar] [CrossRef]
- Mézard, M.; Montanari, A. Information, Physics, and Computation; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Esipov, S.E.; Newman, T.J. Interface growth and Burgers turbulence: The problem of random initial conditions. Phys. Rev. E 1993, 48, 1046–1050. [Google Scholar] [CrossRef]
- Song, J.; Still, S.; Rojas, R.D.H.; Castillo, I.P.; Marsili, M. Optimal work extraction and mutual information in a generalized Szilárd engine. arXiv 2019, arXiv:1910.04191. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 8th ed.; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Gzyl, H.; Tagliani, A. Stieltjes moment problem and fractional moments. Appl. Math. Comput. 2010, 216, 3307–3318. [Google Scholar] [CrossRef]
- Gzyl, H.; Tagliani, A. Determination of the distribution of total loss from the fractional moments of its exponential. Appl. Math. Comput. 2012, 219, 2124–2133. [Google Scholar] [CrossRef]
- Tagliani, A. On the proximity of distributions in terms of coinciding fractional moments. Appl. Math. Comput. 2003, 145, 501–509. [Google Scholar] [CrossRef]
- Tagliani, A. Hausdorff moment problem and fractional moments: A simplified procedure. Appl. Math. Comput. 2011, 218, 4423–4432. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; NIST and Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Hanawal, M.K.; Sundaresan, R. Guessing revisited: A large deviations approach. IEEE Trans. Inf. Theory 2011, 57, 70–78. [Google Scholar] [CrossRef]
- Merhav, N.; Cohen, A. Universal randomized guessing with application to asynchronous decentralized brute-force attacks. IEEE Trans. Inf. Theory 2020, 66, 114–129. [Google Scholar] [CrossRef]
- Salamatian, S.; Huleihel, W.; Beirami, A.; Cohen, A.; Médard, M. Why botnets work: Distributed brute-force attacks need no synchronization. IEEE Trans. Inf. Foren. Sec. 2019, 14, 2288–2299. [Google Scholar] [CrossRef]
- Carrillo, R.E.; Aysal, T.C.; Barner, K.E. A generalized Cauchy distribution framework for problems requiring robust behavior. EURASIP J. Adv. Signal Process. 2010, 2010, 312989. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F.; Ghosh, I. The generalized Cauchy family of distributions with applications. J. Stat. Distrib. App. 2016, 3, 12. [Google Scholar] [CrossRef]
- Marsiglietti, A.; Kostina, V. A lower bound on the differential entropy of log-concave random vectors with applications. Entropy 2018, 20, 185. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 8–9 August 1961; pp. 547–561. [Google Scholar]
- Berend, D.; Kontorovich, A. On the concentration of the missing mass. Electron. Commun. Probab. 2013, 18, 3. [Google Scholar] [CrossRef]
- Raginsky, M.; Sason, I. Concentration of Measure Inequalities in Information Theory, Communications and Coding. In Foundations and Trends in Communications and Information Theory, 3rd ed.; NOW Publishers: Hanover, MA, USA; Delft, The Netherlands, 2019. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merhav, N.; Sason, I. Some Useful Integral Representations for Information-Theoretic Analyses. Entropy 2020, 22, 707. https://doi.org/10.3390/e22060707
Merhav N, Sason I. Some Useful Integral Representations for Information-Theoretic Analyses. Entropy. 2020; 22(6):707. https://doi.org/10.3390/e22060707
Chicago/Turabian StyleMerhav, Neri, and Igal Sason. 2020. "Some Useful Integral Representations for Information-Theoretic Analyses" Entropy 22, no. 6: 707. https://doi.org/10.3390/e22060707
APA StyleMerhav, N., & Sason, I. (2020). Some Useful Integral Representations for Information-Theoretic Analyses. Entropy, 22(6), 707. https://doi.org/10.3390/e22060707