1. Introduction
Polar codes, proposed by Arikan in [
1], are the first error correcting codes to provably achieve the symmetric capacity with low complexity in binary-input discrete memoryless channels (B-DMCs). This result means that Shannon’s random codes, which achieve channel capacity, are replaced by a practical code with a low-complexity decoding algorithm [
1]. Due to its better performance compared to turbo and low-density parity-check (LDPC) codes at short lengths, it has been adopted as the error correcting code for control signals in the enhanced mobile broadband (eMBB) scenario of the third generation partnership project (3GPP) 5G standard [
2].
Decoding schemes of polar codes are commonly used with successive cancellation (SC) [
1] and belief propagation (BP) algorithms [
1]. SC decoding has a relatively low computational complexity and high latency, while BP decoding has a high throughput and computational complexity [
3]. In addition, both schemes perform poorly at finite lengths, e.g., hundreds to thousands of bits. SC list (SCL) decoding with concatenated a cyclic redundancy check (CRC) code was proposed later [
4], and it was proved that similar performance can be obtained as compared to turbo and LDPC codes in finite lengths. That is, polar codes have been shown to be practically available. Recently, decoders using deep learning (DL) have been proposed to replace traditional decoders of polar codes [
5,
6,
7,
8,
9,
10,
11].
DL has made a great success in computer vision [
12], machine translation [
13], speech and image recognition [
14], and many other fields. Its influence has become widespread and has reached communication systems, where analytic solutions have been preferred. There have been a number of DL approaches [
5,
15,
16] to physical layer communications. Among them, we have got a special interest in deep neural networks (DNN)-based decoding of channel codes. As a pioneering work, Gruber et al. employed feedforward deep neural networks to learn the maximum a posteriori (MAP) decoding of polar codes [
5]. That approach was extended to convolutional neural networks (CNN) and recurrent neural networks (RNN) and it was shown that better performance can be obtained by the advanced structures of DNN [
6]. Such small neural network decoders (NNDs) are used to form a decoder for longer polar codes in combination with BP processing [
7]. Nachmani et al. designed an NND called the ‘neural BP decoder’ that basically performs weighted BP decoding with variable weights [
8]. A proper training finds the weight values that compensate finite length impairments of the BP algorithm and the performance is therefore improved for high density parity check codes such as Bose, Chaudhuri, and Hocquenghem (BCH) codes. Bennatan et al. proposed a syndrome-based NND for linear block codes [
9]. For CRC-polar codes, a neural BP algorithm was proposed by Doan et al. [
10]. In [
17], Tandler et al. proposed an ordering of data for efficient training of the decoder of convolutional codes. Unlike the problems of applying general deep learning, NND has an advantage that it is very easy to generate a training data set. In addition, the NNDs are capable of one-shot decoding because the received signal is decoded only once through the hidden layers, and can approach the optimal decoding performance with low latency.
Previous studies [
5,
6,
7,
8,
9,
10,
11,
17] considered learning an NND for a specific code of fixed length and rate. However, wireless standards normally use a class of codes of multiple parameter sets, since a receiver is required to have either multiple decoders each of which is specialized to a code or a decoder which is flexible to decode many codes. For NND, a decoder is determined by the values of the weights. To support multiple codes, the same number of sets of weight values should be stored even though the NND hardware is commonly used. Because the supervised learning method [
5,
6] trains a decoder with data from a specific code and channel, a straightforward approach is to train all the decoders separately. However, we thought if codes are closely related, then decoder training can be aided by the results of the training of another decoder.
In this paper, we consider the problem of training a set of rate-compatible polar codes that are expurgated from the same mother code. Exploiting the inclusion property of rate-compatible polar codes which are defined by a single polar coding sequence as adopted in a 5G New Radio (NR) [
2], we propose an efficient decoder training method via transfer learning. We compare the complexity and performance of the proposed method with conventional separate learning. We also tackle an underfitting problem where the given model complexity is not sufficiently high to be well trained by conventional training methods. It is shown that transfer learning from low to high-rate codes can train a high-rate code decoder better than the conventional training methods.
The rest of this paper is organized as follows. In
Section 2, we briefly introduce the NND framework, basics of polar codes, and the conventional NND for polar codes. The characteristics of rate-compatible polar codes and their training data are investigated and the proposed transfer learning-based training method of NNDs for the rate-compatible polar codes is then presented in
Section 3. Performance comparison with the conventional separate learning is given in
Section 4.
Section 5 concludes the paper.
3. Training of NNDs via Transfer Learning
Since the decoding function for the NND [
5,
6] is a classification into all codewords, the number of classes (i.e., the size of the code) grows exponentially with the code dimension
K. Naturally, the training data should be sufficiently larger than the number of classes. Therefore, the training complexity is a major bottleneck for a long code although the generation of a data set is easy. This limits the training problem to only codes of a small
K. Even though the code is short, training complexity increases when we need to support rate-compatible codes.
If a set of polar codes is constructed based on expurgation that uses a single polar coding sequence [
2], a low rate code is included in a higher rate code within the family of codes. In this section, we introduce a method of generating training data using the inclusion relationship between codewords according to the code rate of polar codes. Then, we propose an efficient training method for the NNDs of multiple polar codes in the context of transfer learning. We also suggest to train a single decoder via transfer learning method to solve an underfitting problem due to low model complexity.
3.1. Inclusion Relation of Training Data
In this subsection, we investigate the inclusion relation of the polar codes defined by a single polar coding sequence. To support rate-compatibility of polar codes, multiple codes with rate
should be used. Assume without loss of generality
for
. Because the polarization is channel-sensitive, the optimal construction for
requires the optimal channel parameter
and the corresponding order
. However, to reduce the complexity of description, a unified sequence
S can be used for multiple rate-compatible codes with small performance penalty as adopted in 5G NR [
2]. Let us define such a set of codes as follows.
Definition 1. Let , be a rate-compatible set of polar codes supporting where and is the polar code of dimension defined by the unified polar coding sequence S.
It is manifest that the inclusion relation for holds because for rate-compatible polar codes based on a single polar coding sequence. Let be the submatrix of G.
Proposition 1. Polar code is linear if the frozen vector .
Proof. Assume
and for
,
which proves that
is a binary linear code with the generator matrix
. □
Proposition 2. Assume all , are linear by setting . For , we have .
Proof. For a codeword
since
. Due to (
2) for a codeword
,
where
is the zero vector of length
and there exists a permutation matrix
P satisfying the last equality. It has been proved that codeword
corresponding to message
is the codeword of
for message
. □
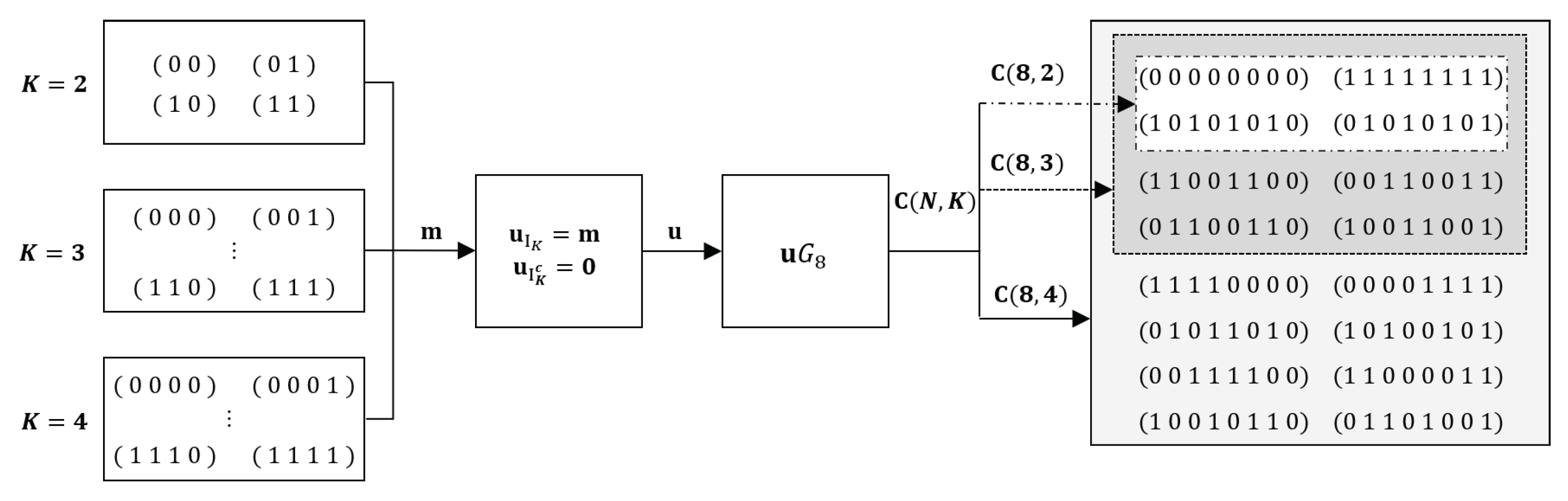
Figure 2 exhibits an example of the inclusion relationship of polar codes
, and
with generator matrix
and
. Note that
. Since
holds for
and
, data points generated for the code of dimension
can be valid data points for the code of
. The set of training data for
can be made to have an inclusion relation between the data for individual codes. The data used to train the NND for
is a valid subset of data for training the NND for
. Therefore, we apply transfer learning to train an NND for
by adopting the NND trained for
as the initial state. Transfer learning can be applied recursively to the sequence of NND training in the increasing order of rate. In the next subsection, we describe the procedure of transfer learning for training NNDs of rate-compatible polar codes in detail.
3.2. Transfer Learning for NNDs of Rate Compatible Polar Codes
Our problem is to train
NNDs where the elements in
are equally long rate-compatible polar codes as defined in
Section 3.1. A naive approach is to train them independently, but a more efficient way can be considered. Complexity of NND training is counted in the number of mini-batches. Let
be the total complexity, where
is the complexity used for training the
-NND. We set the size of the mini-batch
to 128 throughout the paper. We consider the application of transfer learning [
20,
21] for decoder training, which has been used when similar problems and solutions exist on an NN model, where a trained model can be reused to boost the training of another problem. For a given
, we pursue a more efficient training in terms of performance of the NNDs.
As noted in the previous section, each data point used to train the decoder for is a valid data point for . So we assume that the decoder for may be a good initial state of the training phase of . In other words, the learned state of an NND is transferred to the NND for a code of a higher dimension at the beginning of a training session. If transfer learning is effective, the overall complexity of the training may be reduced by this approach. In order to reduce the complexity, the training should be planned well. We train the NNDs in increasing order of rate. So we start from the code of the lowest rate and the training procedure is described in detail below.
In Algorithm 1, the training procedure of NNDs via transfer learning is described. NNDs are trained in increasing order of rate using a single NN model. The NN model used is either the MLP or the LSTM described in
Section 2.3. The NN model is initialized with random weights first. Let
-NND be the decoder for code
. The training data is generated for training of
-NND and the decoder is then trained
mini-batches. How to generate data is described in Algorithm 2. The learned state of
-NND is stored and transferred to the training of
-NND as its initial state. MSE is used for the cost function and SGD is used as the optimizer. For the training of a low rate code NND where
, redundant output nodes are labeled as
which remains neutral between 0 and 1. This procedure is repeated until the last decoder,
-NND training is finished. The entire procedure can viewed as a multi-step training of an NN toward a good
-NND, during that the state of NN is sampled as
-NND.
Each NND can be tested concurrently along with its training. A test evaluates the BER of the decoder where a bit error is counted when the message mismatches with the output truncated to the message length
. When data is generated, the
function defined in Algorithm 2 collects
data points each of which is a pair of a message
and a received signal
or the output of an AWGN channel. A message is randomly generated from the entire set of messages. The message is encoded by
and modulated with BPSK, and then sent through an AWGN channel where a Gaussian noise vector
is added to the transmitted vector
. Random sampling of the received vector is repeated without replacement
times. For the AWGN channel, the channel parameter
is chosen empirically.
| Algorithm 1 Train NNDs via transfer learning for rate-compatible polar codes. |
Input: Rate =(, code length N, numbers of mini-batches ’s, polar coding sequence S- 1:
Initialize the -NND with random weights - 2:
fori = 1 : T do - 3:
- 4:
Train -NND with mini-batches random-sampled from - 5:
Store -NND - 6:
if i < T then - 7:
Initialize -NND with -NND - 8:
end if - 9:
end for - 10:
return All NNDs
|
| Algorithm 2. |
Input: index i, code length N, polar coding sequence S, training , data size - 1:
Generate all messages of length - 2:
Empty data set - 3:
fordo - 4:
Initialize as the zero vector - 5:
Select a message randomly from - 6:
Determine the information and frozen vectors ( and ) - 7:
Make the transmitted signal (, with ) - 8:
Channel operation ( where is iid Gaussian with variance ) - 9:
Add to - 10:
end for - 11:
return
|
The benefit of transfer learning lies in the efficiency of training. In order to get a well trained set of NNDs, the total complexity should be properly distributed among the , . Faster learning due to transfer learning saves training complexity for small K so that NNDs for a larger K can be trained more. To show the advantage of the proposed learning method effectively, the uniform allocation , is considered for the conventional separate learning.
3.3. Training of Individual NND via Transfer Learning
In this subsection, we consider the training problem of a single NND with a limited model. According to previous results [
5], polar NNDs have been well trained from the MLP model when
N is 16 or smaller. Similar performance was achieved on LSTM models with a lower model complexity but higher training complexity [
6]. Assume we want to train a
-NND individually from an NN model. If the model complexity is not sufficiently high, the model might underfit even though the data size and
are large. We propose to use transfer learning to solve the underfitting problem. It will be shown that multi-step training with a proper sequential application of data sets can train the
-NND better at the same complexity. We simply run Algorithm 1 with a given total training complexity
. However, training data
’s and
are sequentially applied from a certain value of
.
4. Numerical Results
In this section, we numerically evaluate our proposed transfer learning technique for rate-compatible polar codes. The training results are compared with those of separate learning in terms of performance. We assume the BPSK modulation and the AWGN channel for all simulations. Codes with parameters
and
were used. The polar coding sequence defined in [
2] was used in the construction of such codes. As mentioned an MLP and an LSTM model is used for the corresponding NNDs. The structures of the NN models were specified in
Section 2.3. The detailed parameter setting is shown in
Table 1. A 64-32-16 MLP and an LSTM have similar complexities in terms of the number of trainable parameters. For the training, the dropout and learning rate are set to 0.1 and 0.0009, respectively. As noted, MSE is used for the loss function as in
Section 2. The SGD method with ADAM optimizer [
22] is used. The training is implemented using TensorFlow. The hyper-parameters of NN training are listed in
Table 2. Polar codes of parameter sets
,
, and
are used for training multiple MLP and LSTM-based NNDs.
We generate
training data points for each training session. The training data of the proposed method is generated at
according to Algorithm 2. We did not rigorously optimize the training
to simplify comparison. On the other hand, the separate learning generates data with the training ratio
p [
6], which is the portion of codewords used to generate training data, compared to the entire code. In this simulation, we set
. That is, the selecting from all messages in Algorithm 2 is changed from the selecting a smaller message set to
p. For each
p, we took 5 different training
points from −2.0 to 6.0 dB. We train the NND using the total of 20 training data and select the parameters that show the best test performance. We assume the complexity of training with a mini-batch of a fixed size is similar among the codes of the same length. To train the NNDs for a given set of rate-compatible codes, uniform allocation of complexity or the number of weight updates is considered. For both the proposed and separate learning methods, the numbers of weight updates are assigned as
for
and
for
. Note that we are interested in a training setting with constrained computing resources. The trained decoders are evaluated in terms of BER for the considered communication system. A test set has
data points for each
point ranging from 0 to 6 dB.
The NNDs trained by separate learning perform closely to MAP decoding for
and all rates if
are sufficiently large without training ratio adjustment (
). However, the proposed method trains the NNDs quicker.
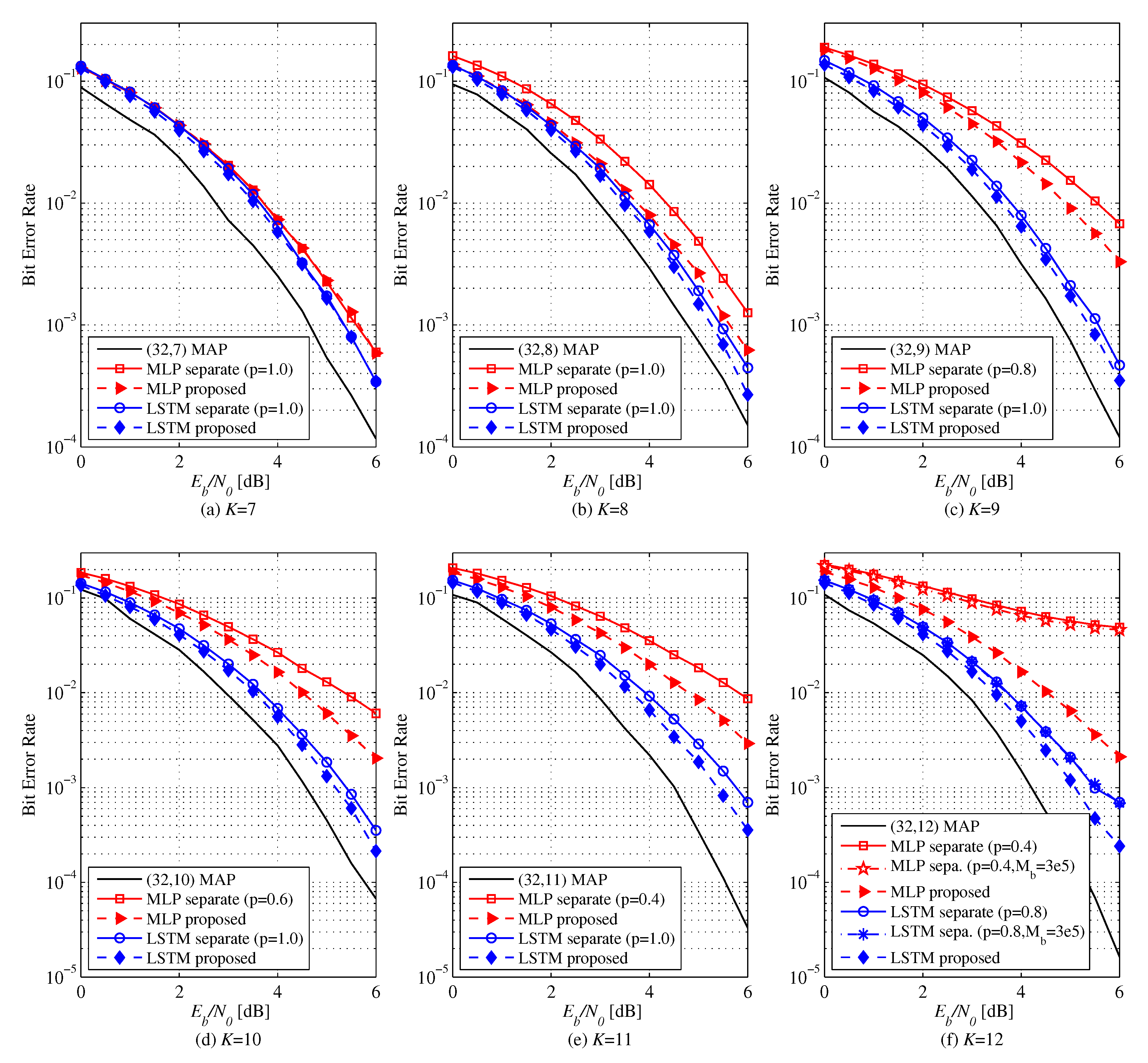
Figure 3 shows the BER of MLP and LSTM-based decoders for
polar codes. At low rates, both learning methods perform similarly. However, as the code rate increases, the proposed method shows better decoding performance than the separate leaning. Especially, when
, MLP attains a coding gain of 0.6 dB and LSTM gets 0.5 dB with the proposed learning method. Via transfer learning, good performance can be achieved with smaller
, i.e., less learning complexity, as the code rate increases. If
is increased at all code rates, the decoding performances of all NNDs come close to MAP decoder.
Figure 4 and
Figure 5 show the BER performance of different learning methods for polar codes of
. Unlike the case of
, NNDs are not trained to achieve MAP performances. The BER of the MLP and LSTM-based decoders for
is shown in
Figure 4. Separate learning can achieve a better performance with an adjustment of
p down to 0.4. while the NND underfits for
. For low rates, performances are similar between the proposed and the separate learning methods as for
. However, as the code rate increases, the proposed method outperforms the conventional one. The MLP-based decoder with proposed method achieves a performance gain of 0.5 dB for
, 0.7 dB for
, 0.9 dB for
, and 1.0 dB for
at a BER of
over the separate learning. For
, the separate learning fails to train the decoder well even for large
. On the other hand, the proposed method shows a much better error performance already at
. The performance gain of LSTM-based decoder with the proposed method is 0.2 dB for
, 0.2 dB for
, 0.3 dB for
, 0.5 dB for
, and 0.5 dB for
. For
, the performance of the separate learning does not improve as
increases even to
from
. As a result, we confirm that the proposed method mitigates the underfitting problem of the separate learning.
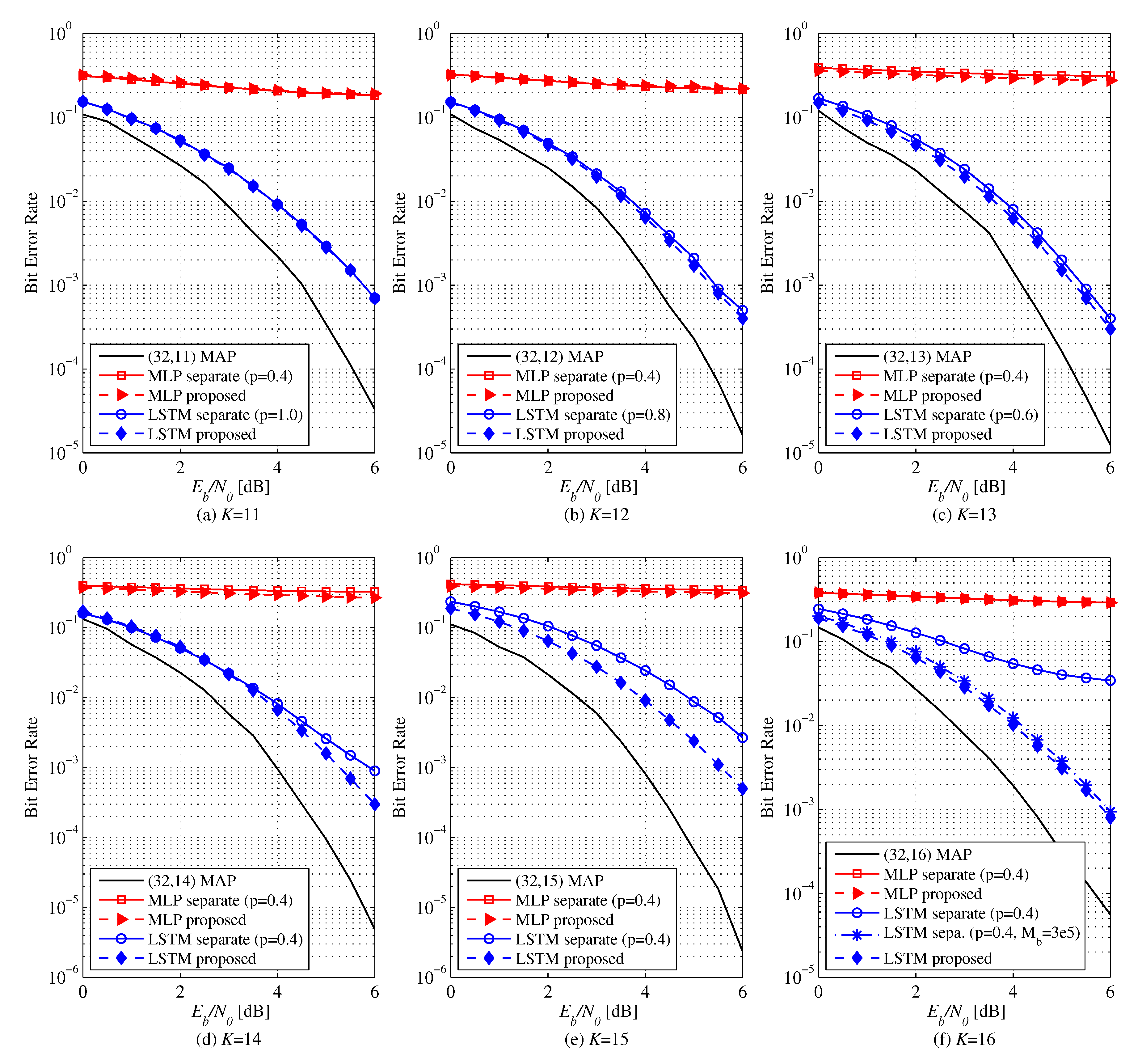
Figure 5 exhibits the BER performance of MLP and LSTM-based decoders for
. We employ a smaller 64-32-16 MLP whose number of parameters is similar to that of the LSTM-based decoder with single cell of 256 units for fair comparison. For
, there is no difference in performance of the LSTM-based decoder between the two learning methods. The proposed method performs better for
. For
, separate learning does not train the LSTM-based decoder well at rather small
although the performance eventually improves up to
. On the other hand, the proposed method trains the NND faster without showing error floor at
, already. It has been confirmed that NNDs can be trained by the proposed transfer learning method in a lower complexity than the separate learning method. As you can see, the MLP-based decoder does not learn at all for both the proposed and separate learning methods, whereas the LSTM-based decoder performs fairly well. It seems that the lower triangular structure of the generator matrix
induces a desired but hidden sequential processing that is better learnable by the LSTM model under the model complexity constraint than the MLP model.