Mutual Information as a General Measure of Structure in Interaction Networks
Abstract
1. Introduction
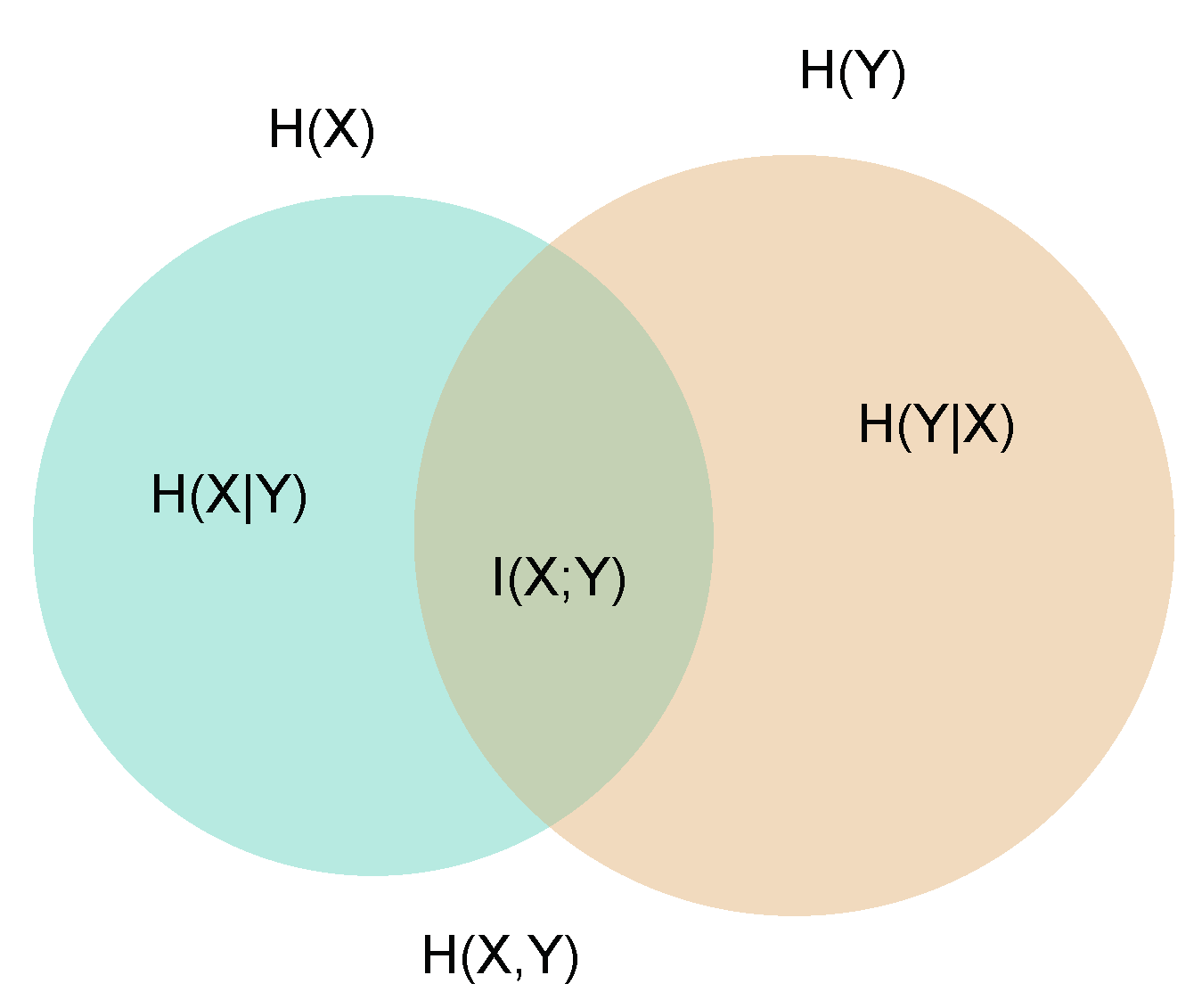
2. Mutual Information—Setting the Problem
3. Baseline Models
3.1. Uniform Networks
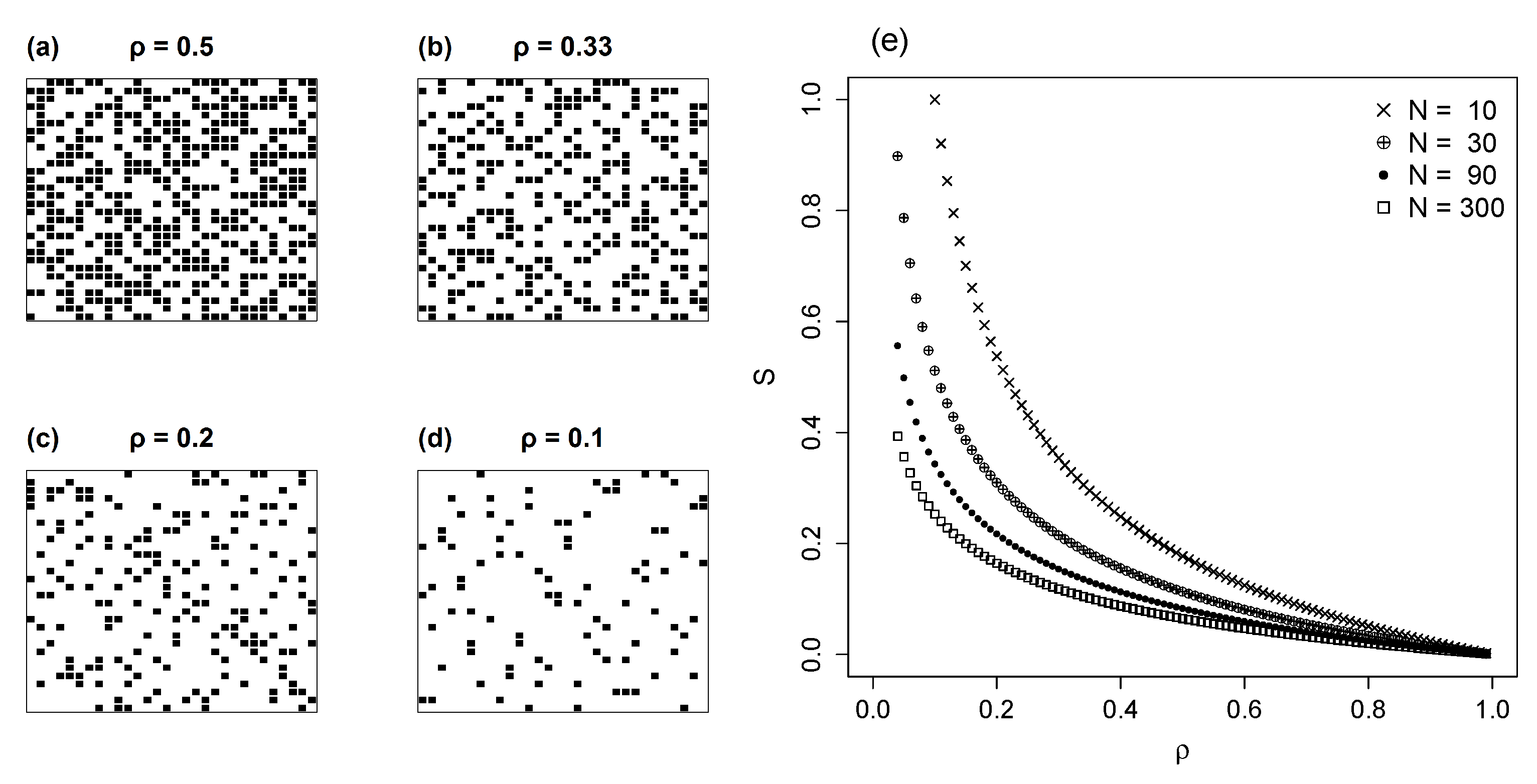
3.2. Random Networks
3.3. Matrix Shape
4. Simple Topologies
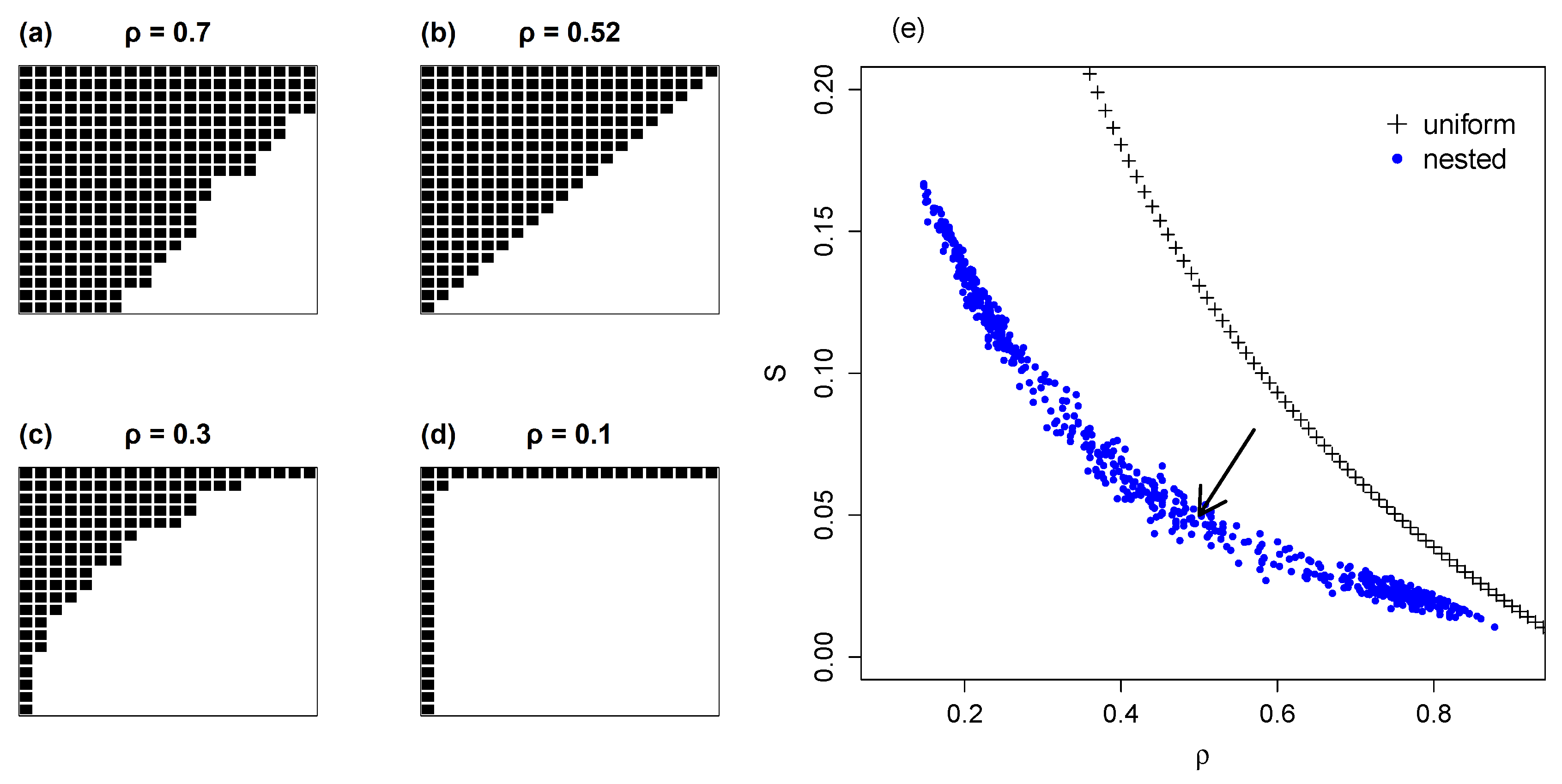
4.1. Nested Networks
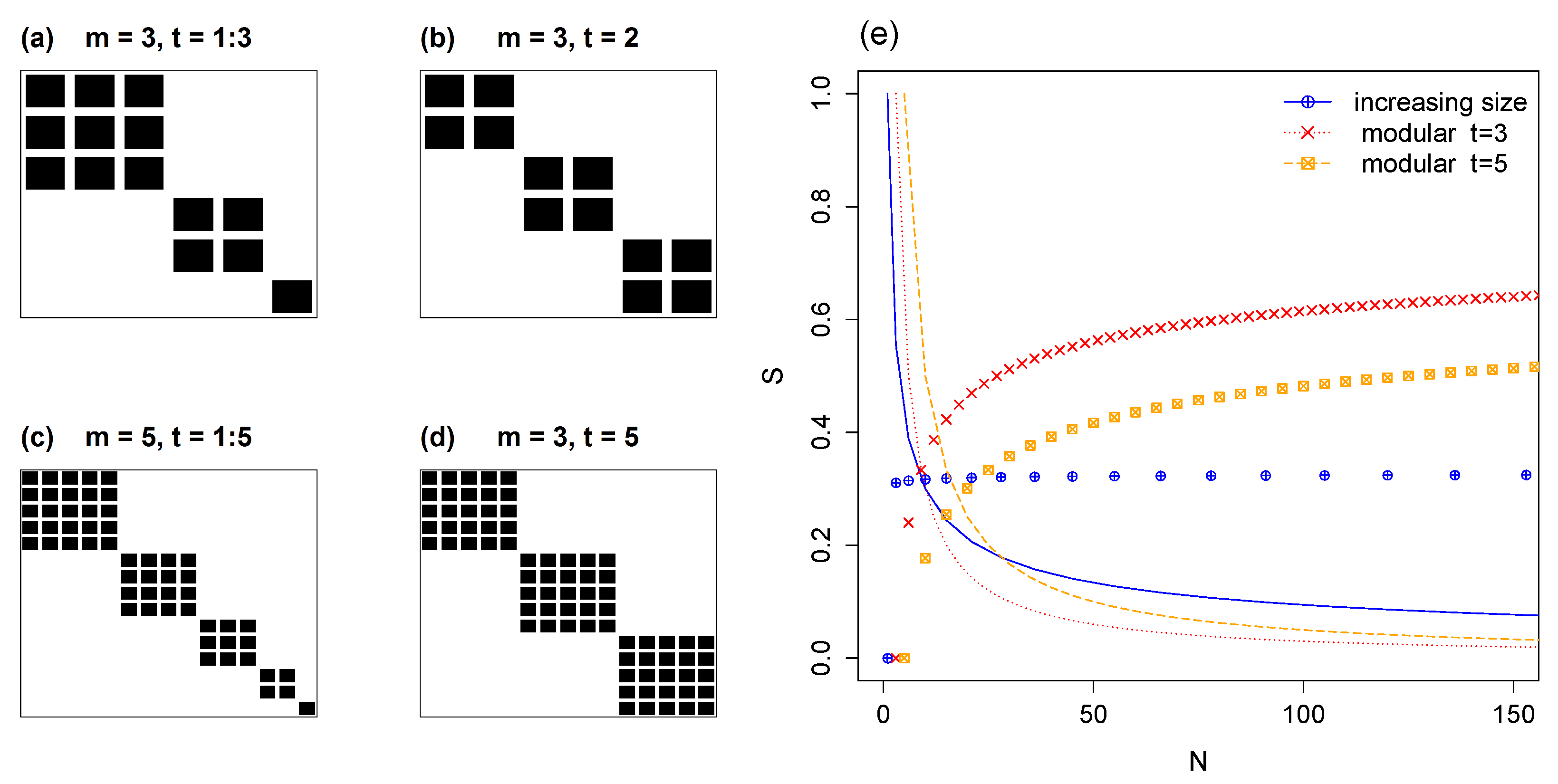
4.2. Isometric Modules
4.3. Non-Square Modular Matrices
5. Complex Topologies
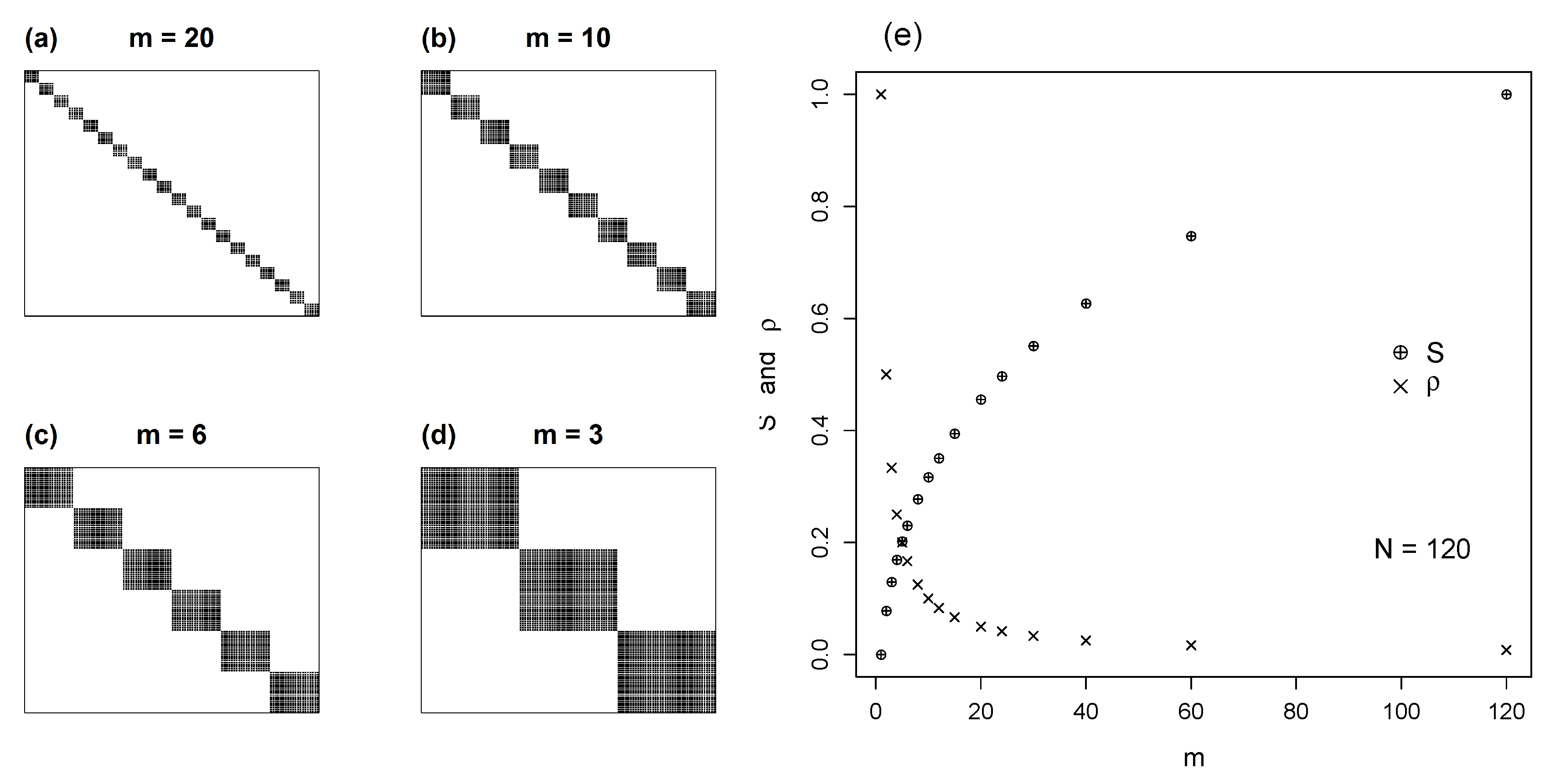
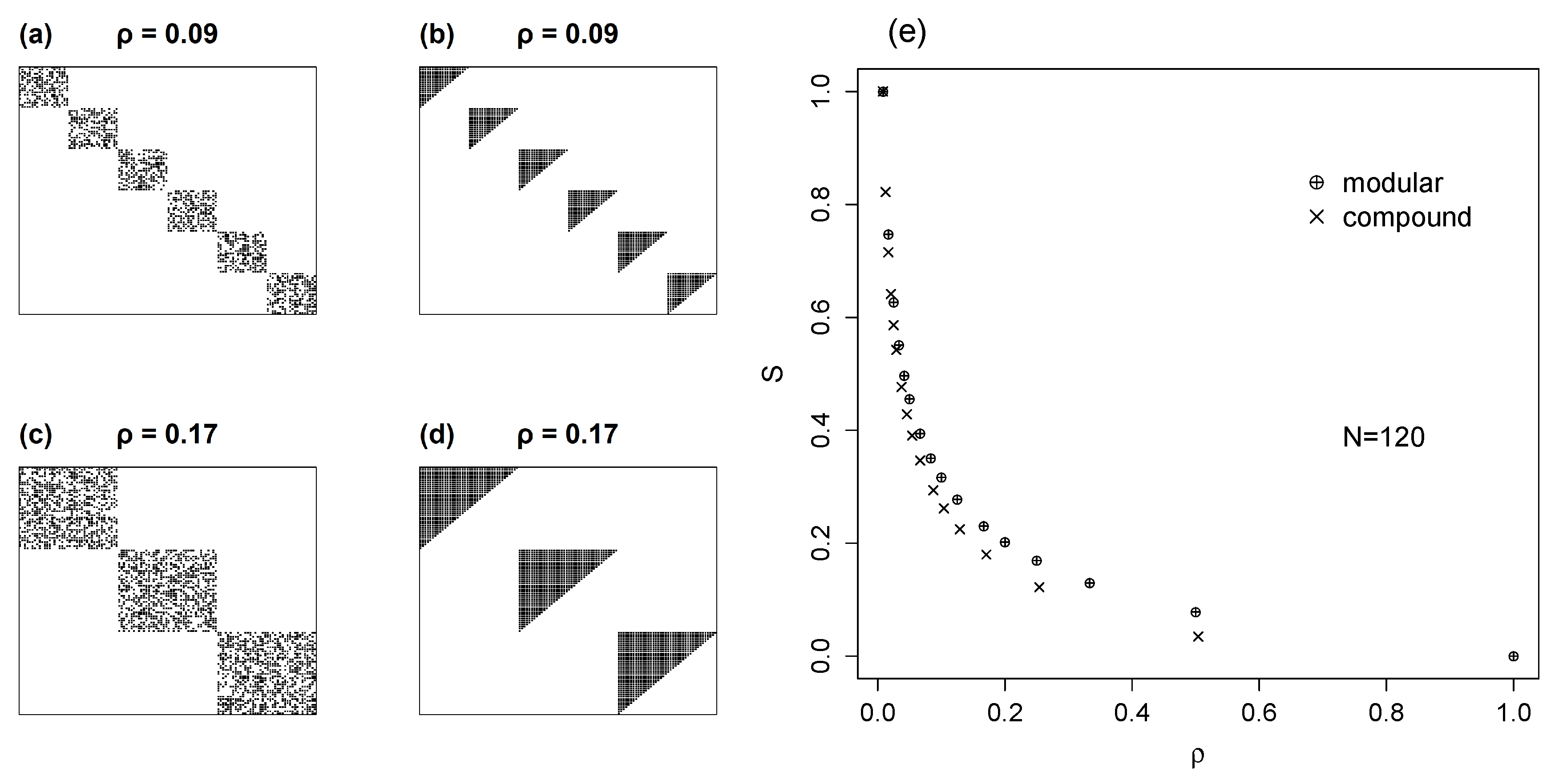
5.1. Modules of Varying Size
5.2. Compound Models with Nested Modules
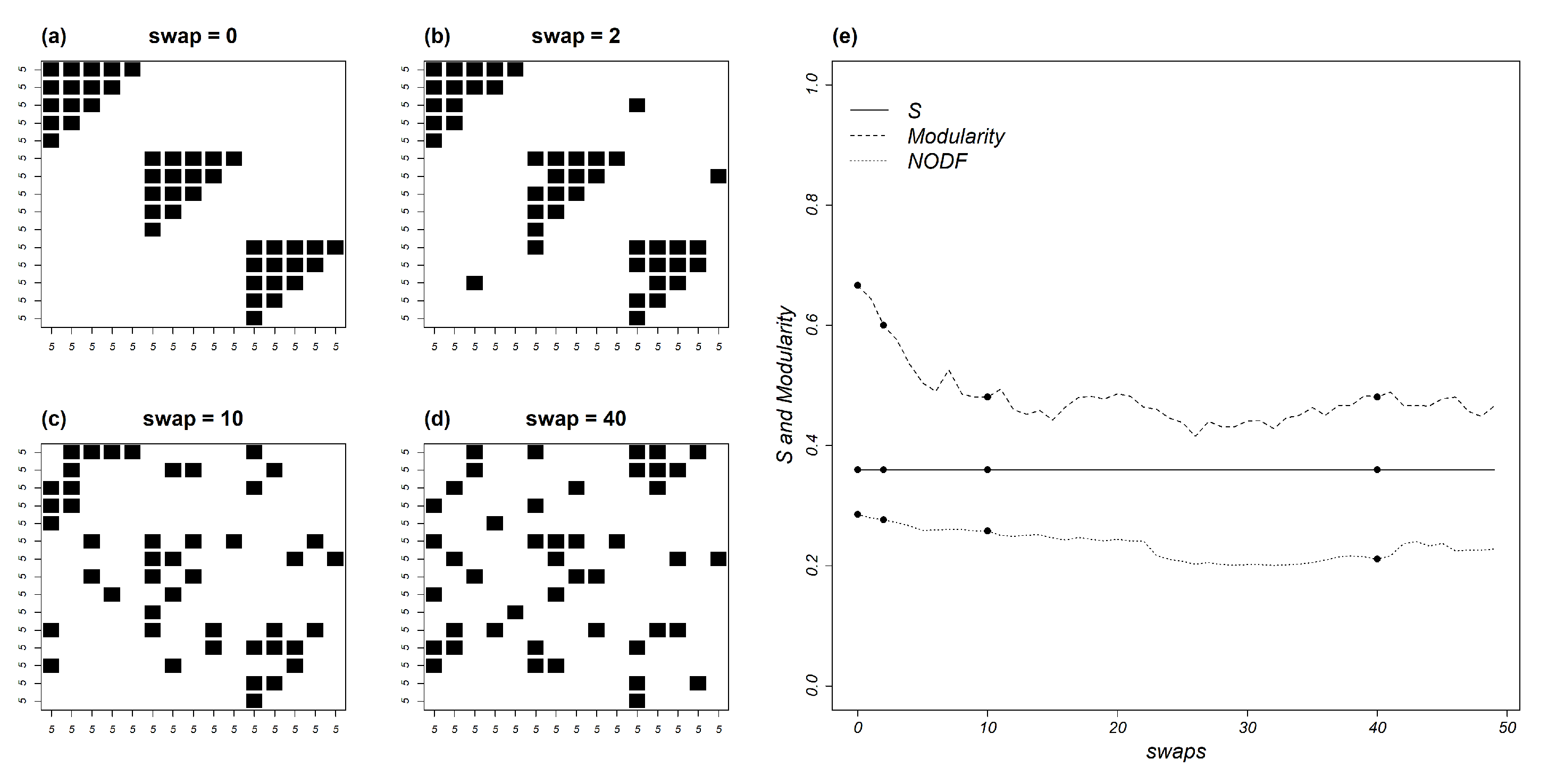
6. Does Mutual Information Vary with Topology?
7. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Hyperfactorial Function
References
- Sherwin, W.B. Entropy and information approaches to genetic diversity and its expression: Genomic geography. Entropy 2010, 12, 1765–1798. [Google Scholar] [CrossRef]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; OUP Oxford: Oxford, UK, 2011. [Google Scholar]
- Vranken, I.; Baudry, J.; Aubinet, M.; Visser, M.; Bogaert, J. A review on the use of entropy in landscape ecology: Heterogeneity, unpredictability, scale dependence and their links with thermodynamics. Landsc. Ecol. 2014, 30, 51–65. [Google Scholar] [CrossRef]
- Straka, M.J.; Caldarelli, G.; Squartini, T.; Saracco, F. From ecology to finance (and back?): A review on entropy-based null models for the analysis of bipartite networks. J. Stat. Phys. 2018, 173, 1252–1285. [Google Scholar] [CrossRef]
- Addiscott, T.M. Entropy, non-linearity and hierarchy in ecosystems. Geoderma 2010, 160, 57–63. [Google Scholar] [CrossRef]
- Ulanowicz, R.E. Information theory in ecology. Comput. Chem. 2001, 25, 393–399. [Google Scholar] [CrossRef]
- Brinck, K.; Jensen, H.J. The evolution of ecosystem ascendency in a complex systems based model. J. Theor. Biol. 2017, 428, 18–25. [Google Scholar] [CrossRef]
- Ulanowicz, R.E. The dual nature of ecosystem dynamics. Ecol. Model. 2009, 220, 1886–1892. [Google Scholar] [CrossRef]
- Rutledge, R.W.; Basore, B.L.; Mulholland, R.J. Ecological Stability: An Information Theory Viewpoint. J. Theor. Biol. 1976, 57, 355–371. [Google Scholar] [CrossRef]
- Margalef, R. Información y diversidad específica en las comunidades de organismos. Investigación Pesquera 1956, 3, 99–106. [Google Scholar]
- Margalef, R. Information theory in ecology. Gen. Syst. 1958, 3, 36–71. [Google Scholar]
- Sherwin, W.B.; Prat i Fornells, N. The introduction of entropy and information methods to ecology by Ramon Margalef. Entropy 2019, 21, 794. [Google Scholar] [CrossRef]
- MacArthur, R.H. Environmental factors affecting bird species diversity. Am. Nat. 1964, 98, 387–397. [Google Scholar] [CrossRef]
- Pielou, E. The measurement of diversity in different types of biological collections. J. Theor. Biol. 1966, 13, 131–144. [Google Scholar] [CrossRef]
- Pielou, E.C. Shannon’s formula as a measure of specific diversity: Its use and misuse. Am. Nat. 1966, 100, 463–465. [Google Scholar] [CrossRef]
- Ellison, A.M. Partitioning diversity. Ecology 2010, 91, 1962–1963. [Google Scholar] [CrossRef]
- Crist, T.O.; Veech, J.A.; Gering, J.C.; Summerville, K.S.; Boecklen, A.E.W.J. Partitioning species diversity across landscapes and regions: A hierarchical analysis of α, β, and γ diversity. Am. Nat. 2003, 162, 734–743. [Google Scholar] [CrossRef]
- Carstensen, D.W.; Trøjelsgaard, K.; Ollerton, J.; Morellato, L.P.C. Local and regional specialization in plant-pollinator networks. Oikos 2018, 127, 531–537. [Google Scholar] [CrossRef]
- van der Heijden, M.G.A.; Bardgett, R.D.; van Straalen, N.M. The unseen majority: Soil microbes as drivers of plant diversity and productivity in terrestrial ecosystems. Ecol. Lett. 2008, 11, 296–310. [Google Scholar] [CrossRef]
- Abrams, P.A. The evolution of predator-prey interactions: Theory and evidence. Annu. Rev. Ecol. Evol. Syst. 2000, 31, 79–105. [Google Scholar] [CrossRef]
- Jeger, M.J.; Spence, N.J. (Eds.) Biotic Interactions in Plant-Pathogen Associations; CABI: Wallingford, UK, 2001. [Google Scholar]
- Lafferty, K.D.; Dobson, A.P.; Kuris, A.M. Parasites dominate food web links. Proc. Natl. Acad. Sci. USA 2006, 103, 11211–11216. [Google Scholar] [CrossRef]
- Callaway, R.M.; Brooker, R.W.; Choler, P.; Kikvidze, Z.; Lortie, C.; Michalet, R.; Paolini, L.; Pugnaire, F.I.; Newingham, B.; Aschehoug, E.; et al. Positive interactions among alpine plants increase with stress. Nature 2002, 417, 844–848. [Google Scholar] [CrossRef]
- Newman, M. The structure and function of complex networks. Siam Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Proulx, S.R.; Promislow, D.E.L.; Phillips, P.C. Network thinking in ecology and evolution. Trends Ecol. Evol. 2005, 20, 345–353. [Google Scholar] [CrossRef]
- Lewinsohn, T.M.; Prado, P.I.; Jordano, P.; Bascompte, J.; Olesen, J.M. Structure in plant-animal interaction assemblages. Oikos 2006, 113, 174–184. [Google Scholar] [CrossRef]
- Dormann, C.F.; Fründ, J.; Schaefer, H.M. Identifying causes of patterns in ecological networks: Opportunities and limitations. Annu. Rev. Ecol. Evol. Syst. 2017, 48, 559–584. [Google Scholar] [CrossRef]
- Thébault, E.; Fontaine, C. Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 2010, 329, 853–856. [Google Scholar] [CrossRef]
- Zenil, H.; Soler-Toscano, F.; Dingle, K.; Louis, A.A. Correlation of automorphism group size and topological properties with program-size complexity evaluations of graphs and complex networks. Physica A 2014, 404, 341–358. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Tegnér, J. Low-algorithmic-complexity entropy-deceiving graphs. Phys. Rev. E 2017, 96, 012308. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Blüthgen, N.; Menzel, F.; Blüthgen, N. Measuring specialization in species interaction networks. BMC Ecol. 2006, 6. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Gotelli, N.J.; Ulrich, W. Statistical challenges in null model analysis. Oikos 2012, 121, 171–180. [Google Scholar] [CrossRef]
- Ulrich, W.; Gotelli, N.J. Null model analysis of species nestedness patterns. Ecology 2007, 88 7, 1824–1831. [Google Scholar] [CrossRef]
- Mello, M.A.R.; Felix, G.M.; Pinheiro, R.B.P.; Muylaert, R.L.; Geiselman, C.; Santana, S.E.; Tschapka, M.; Lotfi, N.; Rodrigues, F.A.; Stevens, R.D. Insights into the assembly rules of a continent-wide multilayer network. Nat. Ecol. Evol. 2019, 3, 1525–1532. [Google Scholar] [CrossRef]
- Pinheiro, R.B.P.; Félix, G.M.F.; Dormann, C.F.; Mello, M.A.R. A new model explaining the origin of different topologies in interaction networks. Ecology 2019, 100. [Google Scholar] [CrossRef]
- Gotelli, N.; Entsminger, G. Swap and fill algorithms in null model analysis: Rethinking the knight’s tour. Oecologia 2001, 129, 281–291. [Google Scholar] [CrossRef]
- Barber, M. Modularity and community detection in bipartite networks. Phys. Rev. E 2007, 76, 066102. [Google Scholar] [CrossRef]
- Almeida-Neto, M.; Guimarães, P.R., Jr.; Loyola, R.D.; Ulrich, W. A consistent metric for nestedness analysis in ecological systems: Reconciling concept and measurement. Oikos 2008, 117, 1227–1239. [Google Scholar] [CrossRef]
- Orlóci, L.; Anand, M.; Pillar, V.D. Biodiversity analysis: Issues, concepts, techniques. Community Ecol. 2002, 3, 217–236. [Google Scholar] [CrossRef]
- Segar, S.; Fayle, T.M.; Srivastava, D.S.; Lewinsohn, T.M.; Lewis, O.T.; Novotny, V.; Kitching, R.L.; Maunsell, S.C. The role of evolutionary processes in shaping ecological networks. Trends Ecol. Evol. 2020. [Google Scholar] [CrossRef]
- Jorge, L.R.; Prado, P.I.; Almeida-Neto, M.; Lewinsohn, T.M. An integrated framework to improve the concept of resource specialisation. Ecol. Lett. 2014, 17, 1341–1350. [Google Scholar] [CrossRef]
- Forister, M.L.; Novotny, V.; Panorska, A.K.; Baje, L.; Basset, Y.; Butterill, P.T.; Cizek, L.; Coley, P.D.; Dem, F.; Diniz, I.R.; et al. The global distribution of diet breadth in insect herbivores. Proc. Natl. Acad. Sci. USA 2015, 112, 442–447. [Google Scholar] [CrossRef] [PubMed]
- Wardhaugh, C.W.; Edwards, W.; Stork, N.E. The specialization and structure of antagonistic and mutualistic networks of beetles on rainforest canopy trees. Biol. J. Linn. Soc. 2015, 114, 287–295. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corso, G.; Ferreira, G.M.F.; Lewinsohn, T.M. Mutual Information as a General Measure of Structure in Interaction Networks. Entropy 2020, 22, 528. https://doi.org/10.3390/e22050528
Corso G, Ferreira GMF, Lewinsohn TM. Mutual Information as a General Measure of Structure in Interaction Networks. Entropy. 2020; 22(5):528. https://doi.org/10.3390/e22050528
Chicago/Turabian StyleCorso, Gilberto, Gabriel M. F. Ferreira, and Thomas M. Lewinsohn. 2020. "Mutual Information as a General Measure of Structure in Interaction Networks" Entropy 22, no. 5: 528. https://doi.org/10.3390/e22050528
APA StyleCorso, G., Ferreira, G. M. F., & Lewinsohn, T. M. (2020). Mutual Information as a General Measure of Structure in Interaction Networks. Entropy, 22(5), 528. https://doi.org/10.3390/e22050528




