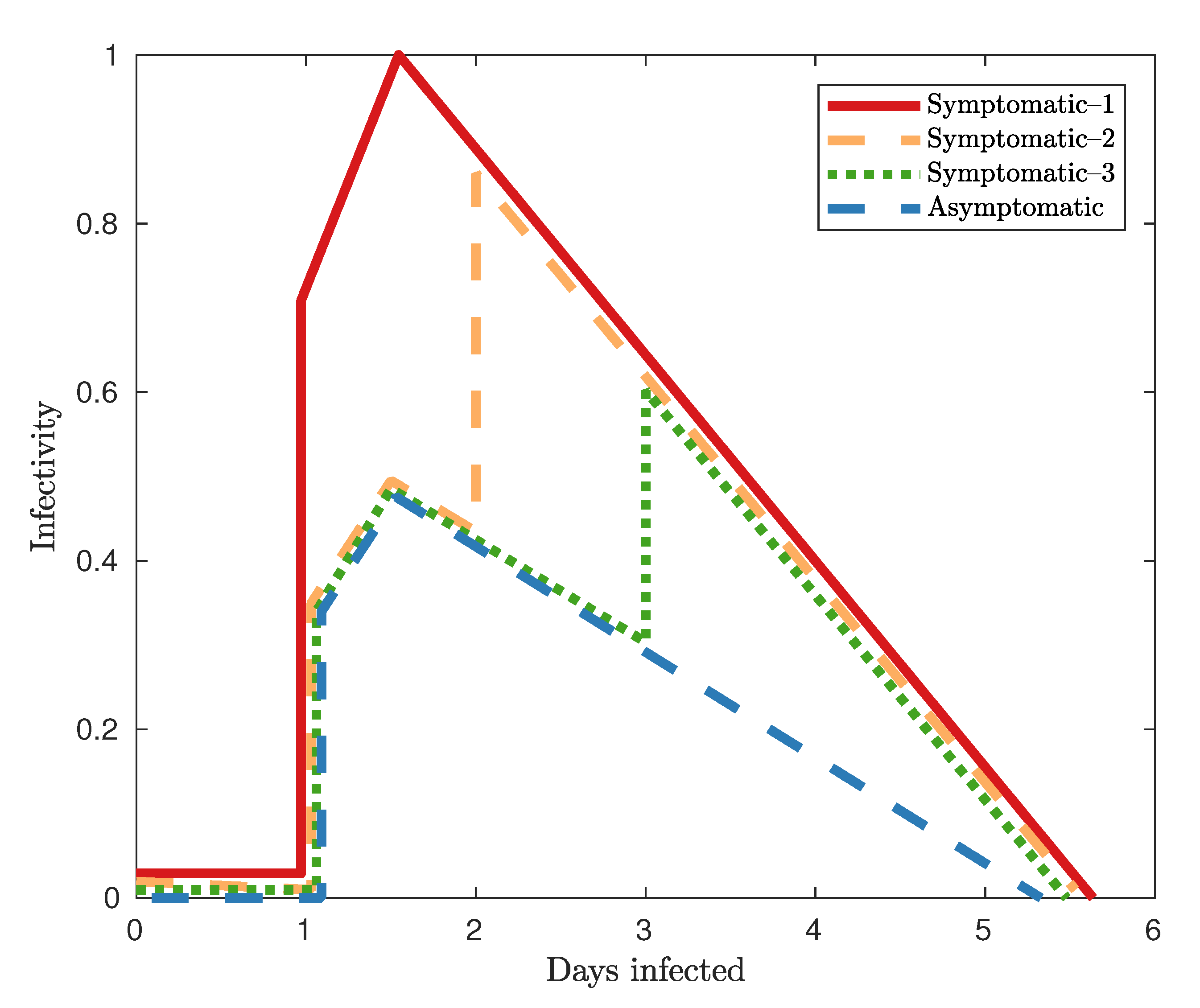
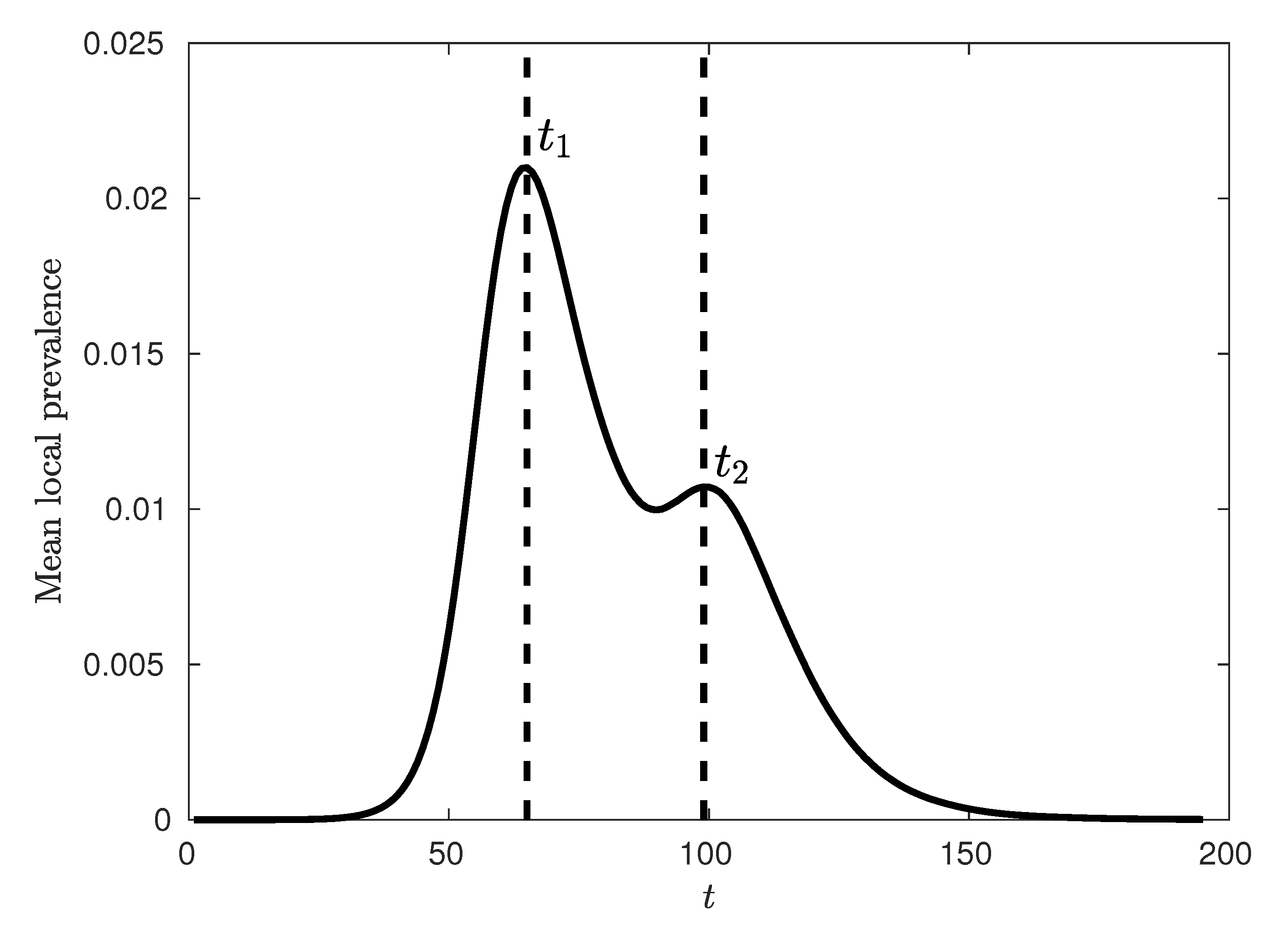
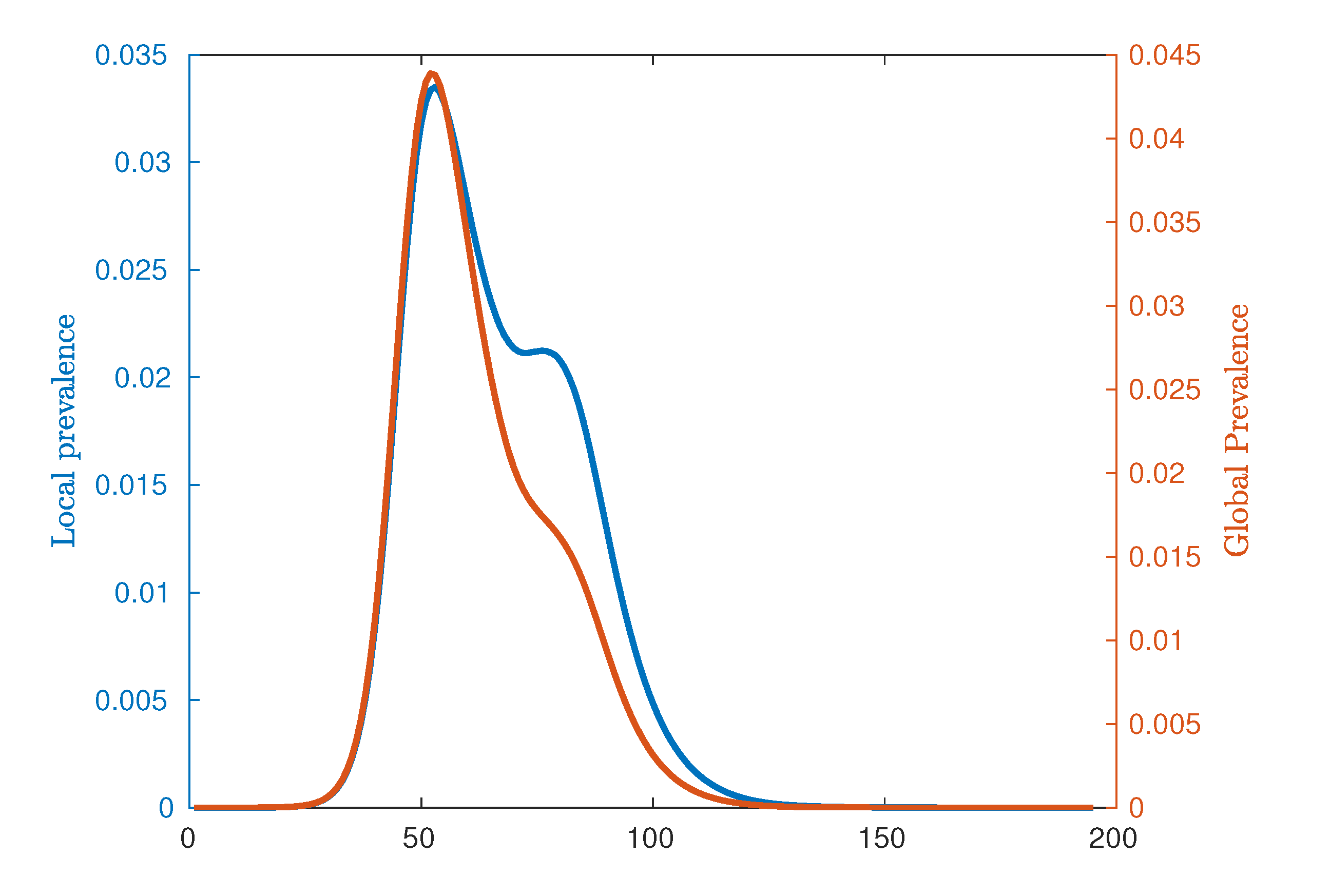
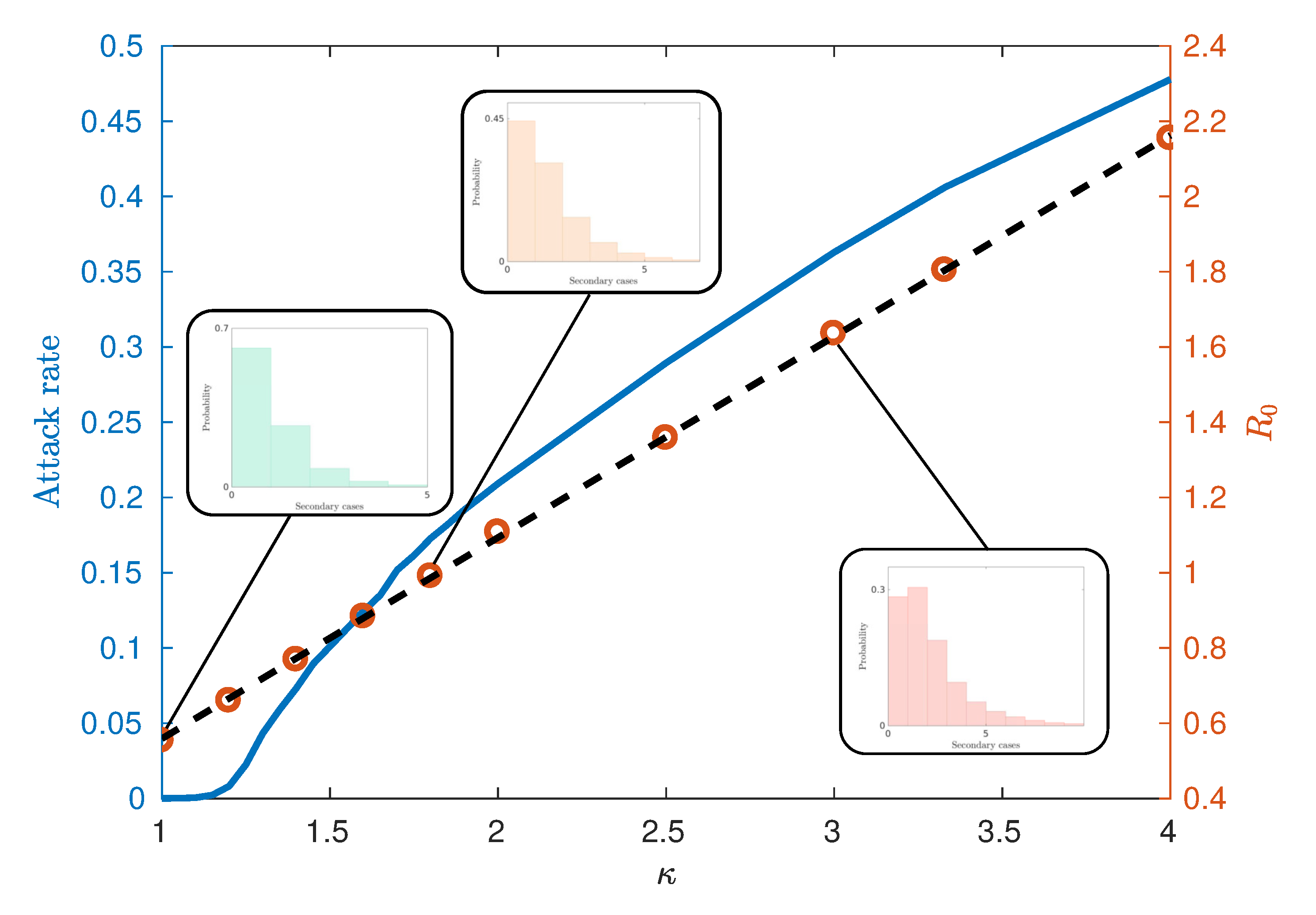
1. Introduction
A comprehensive understanding of complex spreading patterns of epidemics and pandemics is of key importance for efficient mitigation and effective response strategies, providing insights into timely and focussed interventions at national and regional levels. Understanding the spatial dispersion of these epidemic spreading patterns may provide insight into early warning and intervention strategies [
1]. Specifically, one may be able to find key spatial factors which allow understanding of epidemic spread more deeply [
2]. One feature which is of interest in this pursuit is the spatial connectivity of regions with sufficiently high levels of infection, which reflect both geographic and epidemiological features [
3]. Such spatial connectivity is not static, but rather changes over time in response to the developing epidemic, highlighting the need for a high-resolution analysis of complex epidemic diffusion patterns. In particular, several recent studies of spatiotemporal dynamics and spatial synchrony of influenza epidemics contrasted the phenomena of both hierarchical and wave-like spreads in different geographical contexts, using the notion of synchrony which is defined as the variance in the timing of the epidemic peaks across different local communities [
4,
5]. Both studies found that hierarchical spread, characterised by high synchrony across communities of similar sizes, is much more established than wave-like diffusion, which is associated with high synchrony between communities with low pairwise geographical distance. This suggests that the regional spread of a disease depends more heavily on population distribution and flow rather than the geographic distance alone. Spatial synchrony was also implicated in the bimodal pattern of influenza pandemics characterised by two distinct waves: the first wave is observed in highly-urbanised residential centres where the pandemic first reaches a nation (e.g., near international airports), whilst the second wave is observed in sparsely connected rural regions [
6].
In this paper, we aimed to investigate how the spatial patterns contribute to the connectivity at different time points corresponding to turning points in the epidemic (e.g., peaks in prevalence, appearance of the second epidemic wave, etc.). This investigation will be carried out within a large-scale agent-based model of influenza pandemics in Australia, enabling the high-resolution simulation of diverse epidemic and pandemic scenarios, and extending beyond the limited capability of canonical meta-population and mean-field approaches. Furthermore, we shall relate the spatial connectivity of simulated pandemics to epidemic thresholds and critical phenomena, using both percolation theory and model-independent information-theoretic measures.
One major challenge in epidemic modelling is a faithful recreation of the demographic features of the affected population in a way that makes the modelling results transferable to a real-world context. Agent-based models (ABM) have been demonstrated to be particularly effective in tracing epidemics under different “what-if” scenarios and comparing possible interventions [
6,
7,
8,
9,
10,
11,
12,
13]. The primary reason for this success is that these agent-based approaches allow for high-resolution population and mobility data to be effectively incorporated into simulation and analysis. As high-resolution data continue to become more easily accessible, this strength needs to be complemented by rigorous theoretic frameworks and analytic techniques. Traditional compartment-based approaches (e.g., SIR models) struggle to incorporate these high-resolution datasets as easily as ABM models, relying on assumptions of well-mixed homogeneous populations describable by just a few parameters defining their interactions [
14,
15,
16]. Instead, ABM offers scalable simulation frameworks, while providing further spatially refined data for a detailed analysis informed by percolation and information theories.
The studies of critical phenomena have already significantly contributed to computational epidemiology. Typically, this analysis focuses on a critical epidemic threshold, above which epidemics develop and persist and below which epidemics die out. This dates back to the seminal study of Kermack and McKendrick [
15] who identified the ‘threshold behaviour’ of the model. This type of analysis has been extended to many complex models and the current discourse is generally based on the basic reproductive ratio
[
14,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26], i.e., the number of secondary cases arising from a typical primary case early in the epidemic, as well as the attack rate [
7,
27,
28], i.e., the proportion of a population infected by the conclusion of an epidemic. For example, recent studies considered critical behaviour in the spatial spread of epidemics in statistical-mechanical terms, interpreting key epidemic variables, such as the reproductive ratio, thermodynamically [
29], while also identifying phase transitions related to dynamic mobility and interaction patterns [
30]. We extend this approach, by connecting an ABM of influenza pandemics in Australia, which has been validated previously, with a broader theoretical framework.
What makes this connection more interesting is the fact that Australia has a number of demographic, geographic, and ecological features which non-trivially affect socio-economic connectivity and mobility patterns [
3,
31,
32,
33,
34,
35]. In contrast to many other countries with a more even spatial population distribution, Australia comprises a relatively small number of densely populated urban centres distributed along the coastline, sparsely connected to many more low-density inland towns and rural/regional communities. This particular population distribution has been implicated in Australia’s highly bimodal epidemic curves, with modes associated with its urban, and rural communities [
6].
In this study, we present a general method identifying critical regimes in spatial connectivity during epidemics. This analysis is performed using data generated by A
ceMod, the Australian Census-Based Epidemic Model [
5], an agent-based simulation of influenza epidemics in Australia. This could, in principle, be performed with analogous real or simulated spatial data; however, as A
ceMod incorporates high-resolution population and mobility data provided by the Australian Bureau of Statistics (ABS), this allows our connectivity analysis to be applied in a real-world context. We examined the spatial extent of epidemic spreading at two key points of the simulated epidemics, while varying infectivity parameters. While the disease progression across the regions is a result of the ABM simulation, quantifying the spatial connectivity of infection using the methods of percolation theory is an important additional step, making it one of the main contributions of this study. This was achieved with the use of percolation theory to measure connectivity, alongside the use of Fisher Information as a model-independent measure pinpointing phase transitions. Specifically, we quantified the mean cluster size to which a randomly selected “infected” location belongs [
30,
36], denoted the ‘infection connectivity’ in order to identify prominent clustering patterns during these multiple epidemic peaks of an Australian epidemic. Finally, we investigated the relationship between the infection connectivity at each of the epidemic peaks and the infectiousness of the disease.
4. Results
In this section, we present an analysis of the spatial characteristics of the simulated Australian epidemics. We begin, however, with a basic analysis of common epidemic characteristics, specifically, the dependence of attack rate, the basic reproductive ratio and the timing of the urban and rural peaks on the infectiousness parameter , used in AceMod.
As infectiousness (defined here through ) increases across a population, the number of secondary cases caused by an average primary case, characterised by , also increases. Classically, the behaviour of epidemics is then characterised by two distinct regimes separated by a critical value of . Above this threshold (with higher infectiousness) small initial infections grow into epidemics whilst below this threshold (with lower infectiousness), initial infection levels decay away and epidemics do not occur. Such a critical value of then implies that there is a critical value of used in the AceMod simulations. Consequently, to characterise the behaviour generated by AceModns, we first seek to quantify the relationship between and , then, in conjunction with the attack rates, identify their critical values.
There are several methods for computing
from simulated data in the literature attempting to capture the predominant spreading behaviour in subtly different ways [
7].
Figure 4 illustrates an observed linear relationship between
and
calculated using the ‘random index case’ method [
7]. This method involves randomly selecting individuals from the population in an unbiased way, infecting them and observing the number of secondary infections produced from the single primary case. This is in contrast to other methods for calculating
such as the ‘attack rate pattern weighted index case method’ [
7], which biases the infection of individuals based on relative attack rates between communities.
Figure 4 also demonstrates the relationship between the attack rate (the proportion of the population who have been infected by the end of the epidemic) and
, from which we may estimate the critical values of
and
. We observe that for this model, the critical value
lies in the interval
, corresponding to
. Notably, this critical value differs from models which assume continuously mixing populations such as compartmental models and metapopulation models [
15,
16], where
. However, such deviations are commonly observed within other agent-based or network-based approaches with heterogeneities and imperfect mixing [
7,
8,
18]. The reasons for observing epidemics where
can be attributed to several factors. The predominant reason is the existence of super-spreaders within the highly urbanised communities and certain agent categories (see the fat-tailed distributions of
Figure 4 inset), which may be initially infected and contribute to further spread beyond a vanishing epidemic. Finally, the choice of the ‘random index case’ method used to calculate
tends to produce lower values than other methods such as the ‘attack rate pattern weighted index case’ method [
7].
Observation of A
ceMod simulation data indicates that the infectiousness of individuals controls not only the extent of the epidemic, as measured through the attack rates, but the whole evolution of its progression. Of particular interest is the
timing of the epidemic which we characterise using the mean of the urban and rural prevalence peaks,
and
(see
Figure 3). The variation of these mean peak times varying against
are shown in
Figure 5. Importantly, we point out that the A
ceMod simulator terminates after 195 days. Consequently, regions of the parameter space of
for which
indicate the lack of a significant epidemic or the inability to distinguish a second peak due to low global infection.
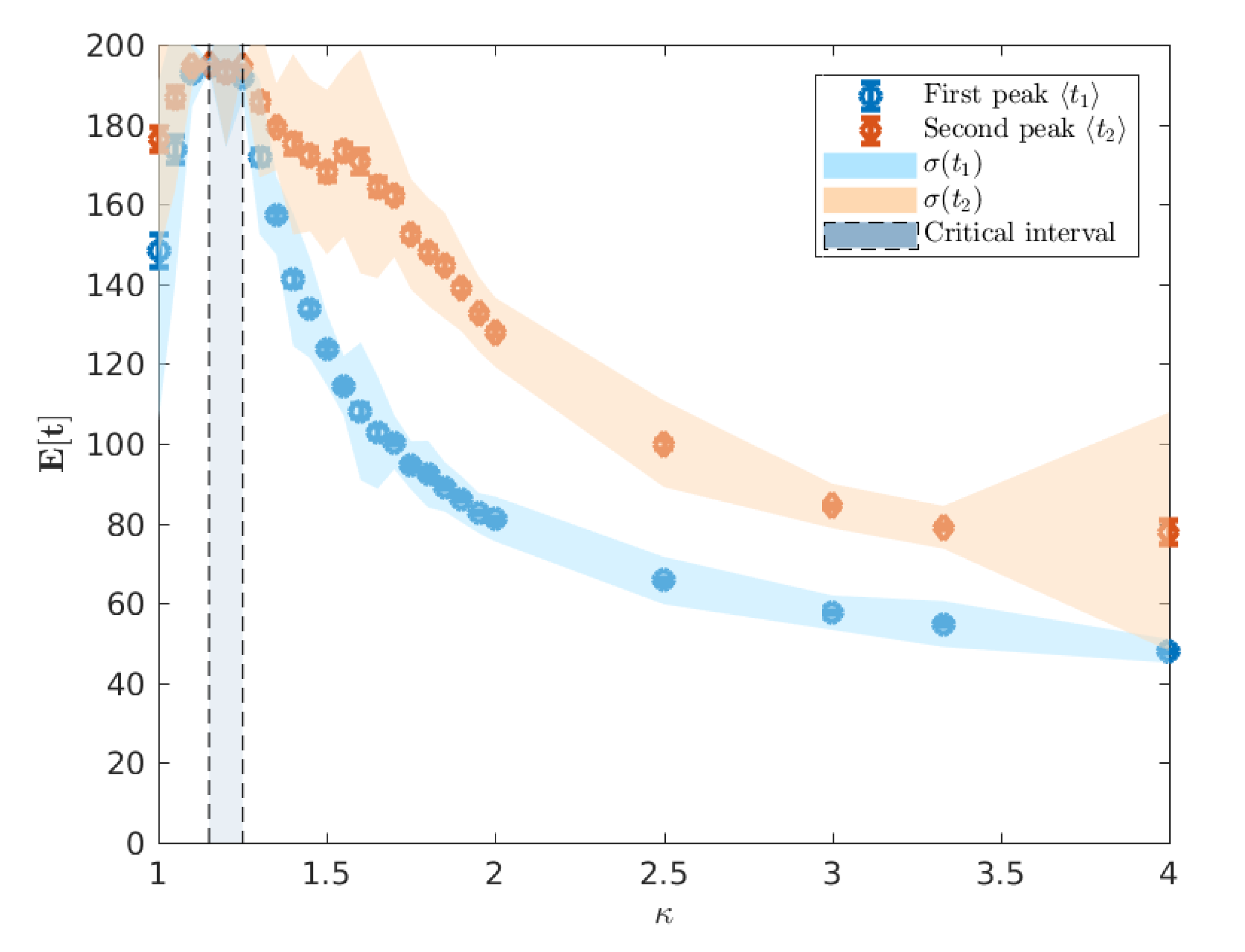
We note that for
, there is no significant epidemic such that the indicated peaks are dominated by noise. For
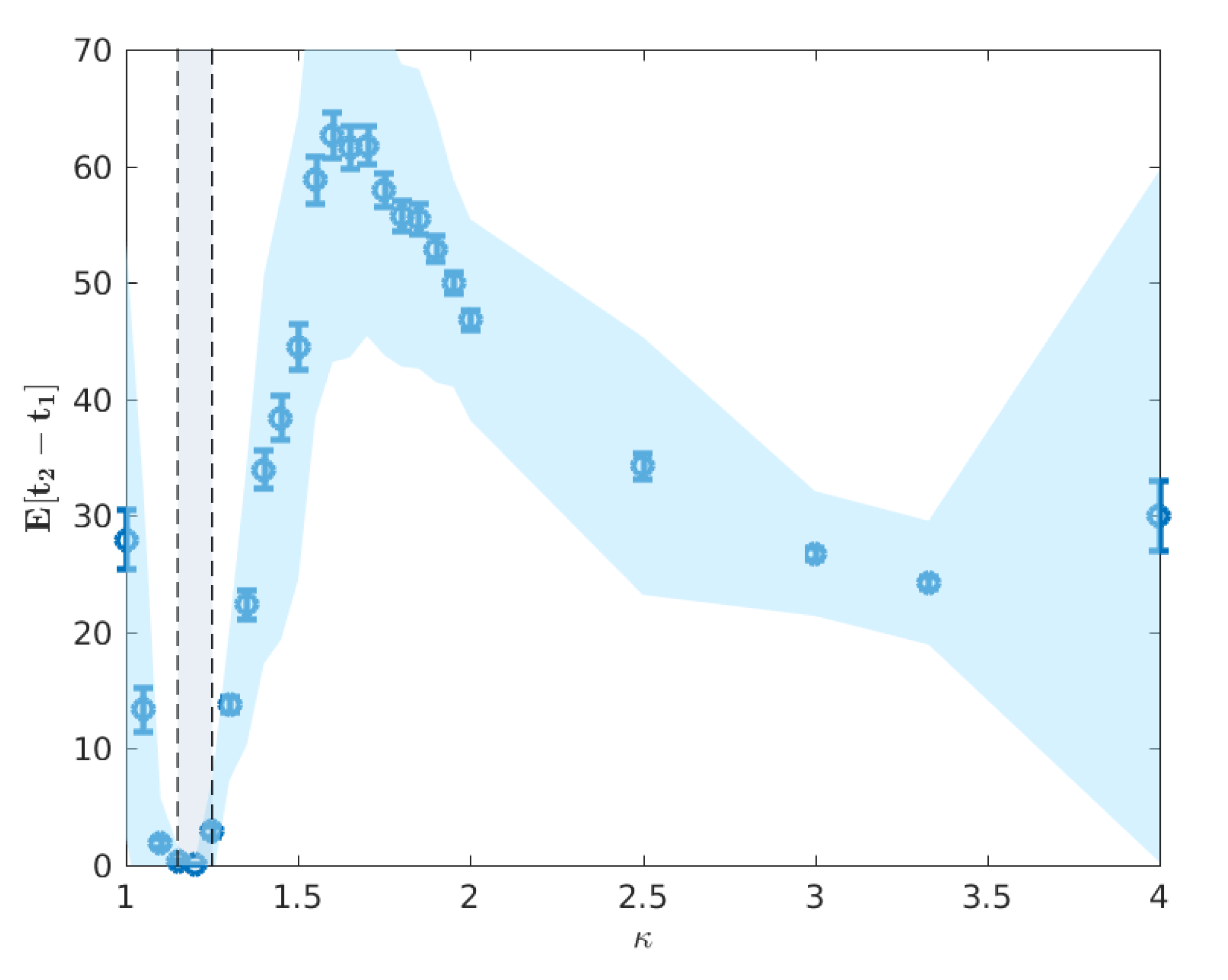
, around the critical point, the characteristic lack of clear exponential growth or decay combined with the constant seeding results in nominal peaks in both waves to occur at the time horizon for any reasonable simulation length (here limited to 195 days). More pertinently, as we increase
beyond the critical interval, the average timing of two peaks begins to decouple, as shown in
Figure 6, and we begin to observe two clearly distinguished profiles. In this post-critical phase,
, each profile monotonically decreases, indicating that the respective peak occurs earlier in time for higher values of
. In order to understand the spatial extent of Australian epidemics, we offer a characterisation in terms of the extent of spatial spread at the two key points of the epidemic: namely, the urban and rural peaks of the epidemic
and
[
6] (see
Section 2.3).
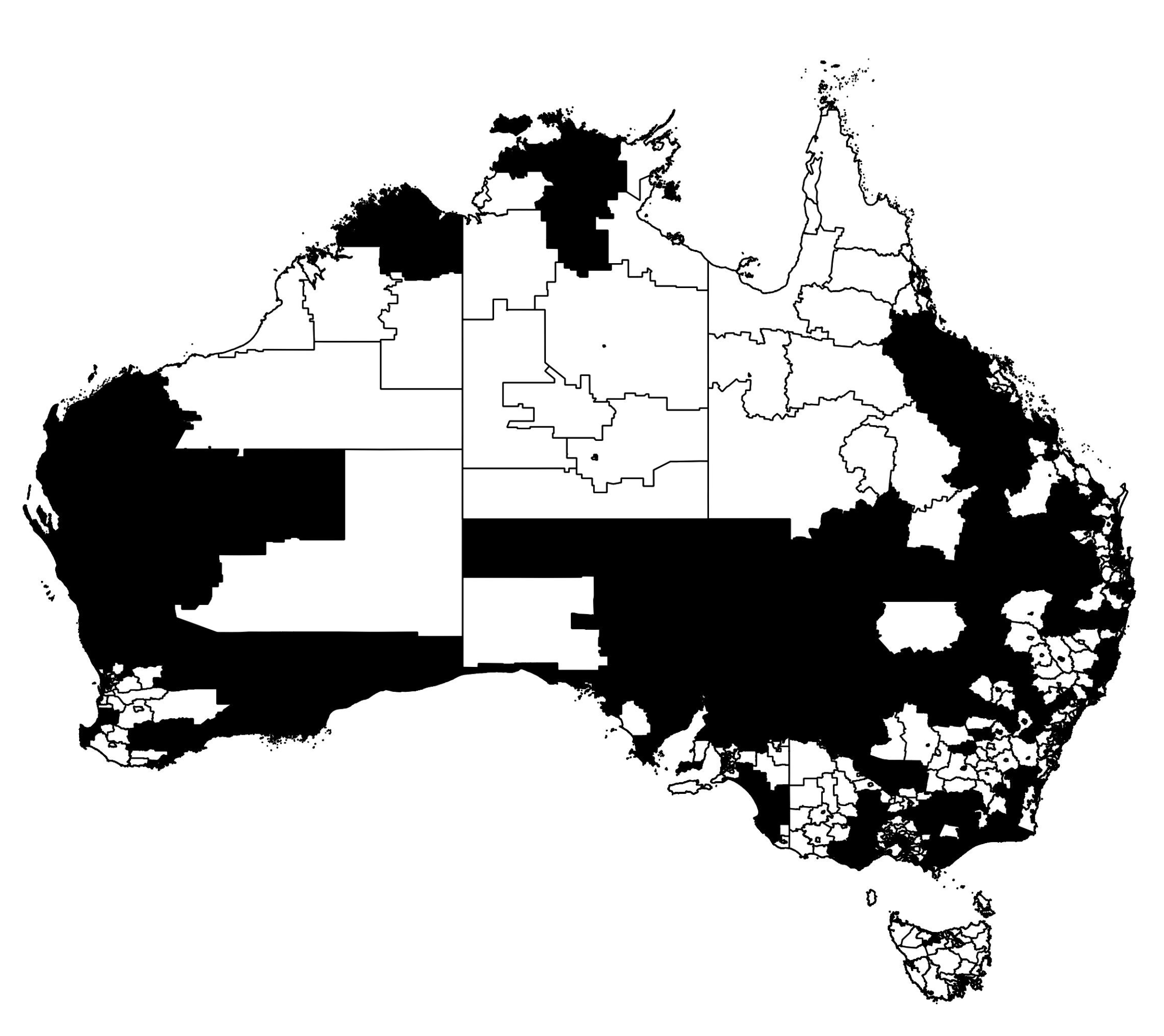
In particular, we are concerned with the spread of the epidemic across the extended spatial system, differentiating between highly connected and isolated infected communities, as commonly quantified using percolation measures. In order to utilise such measures, we thus classify each region as either strongly or weakly infected, using the mean prevalence fraction as the threshold for this distinction. The distribution of strongly and weakly infected regions at example times
and
are illustrated in
Figure 7 and
Figure 8, with black and white corresponding to strongly and weakly infected regions, respectively.
The extent to which the epidemic is well connected or isolated, across all population areas can then be characterised by the degree of clustering in the strongly infected regions. This is achieved by (i) identifying spatially contiguous regions of strongly infected locations and identifying them as clusters, (ii) recording all cluster sizes as a (normalized) number of connected regions and (iii) constructing the probability distribution
that a randomly chosen region belongs to a cluster of normalised size
. Configurations with larger clusters and thus, larger values of
, are more connected than configurations with smaller values of
. This quantitative examination can better characterise the actual spatial “infection” connectivity than a simple visual inspection: for example,
Figure 7 depicts the state which happens to be more connected than the one shown in
Figure 8.
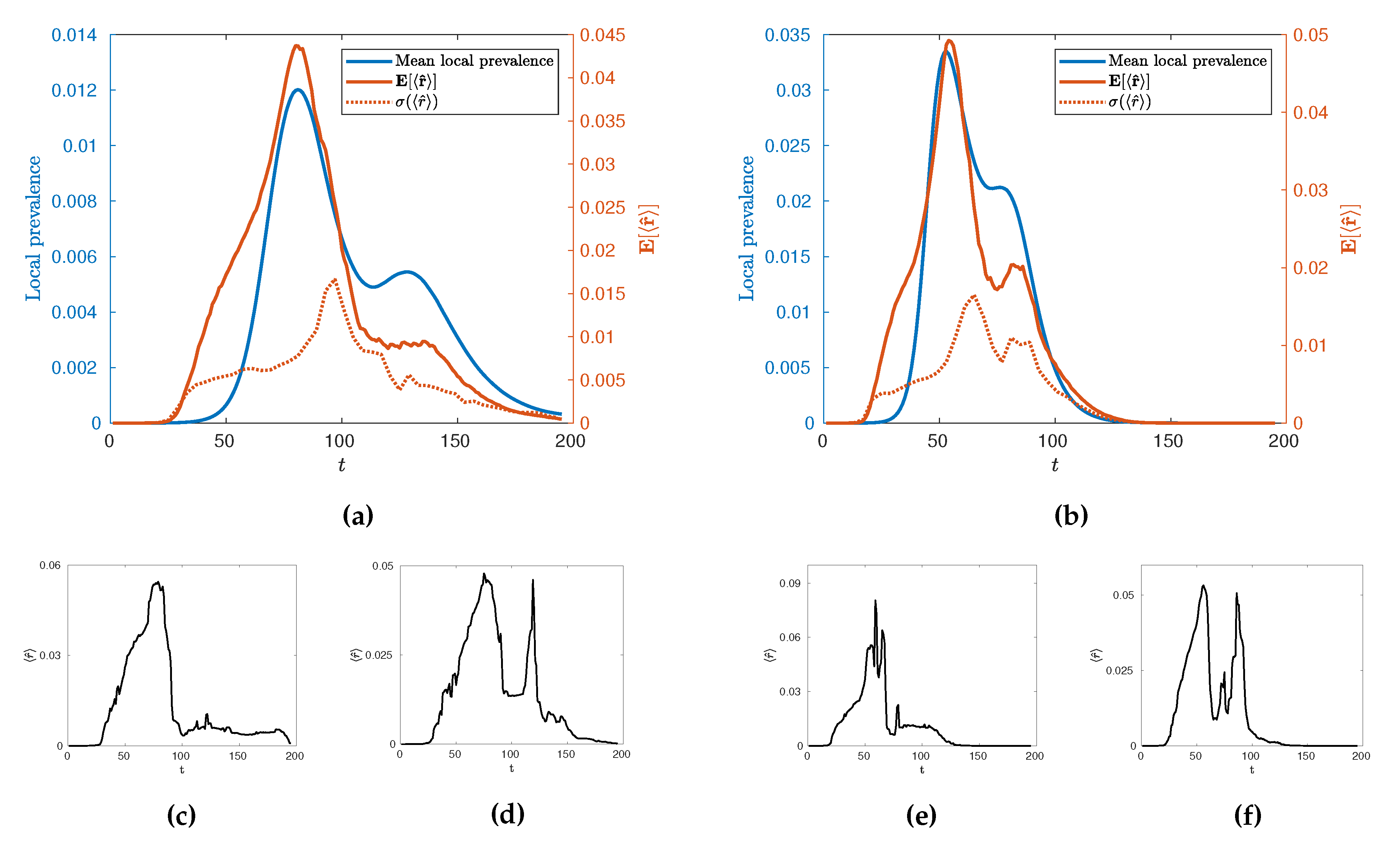
In the first instance, we may use this new measure,
, to characterise the temporal evolution of the epidemic by calculating its mean value across many realisations,
as a function of time for different values of
. Such evolution is illustrated in
Figure 9 for
and
alongside its standard deviation,
, and some illustrative individual trajectories for specific extremal realisations of epidemics. Broadly, we see an evolution with two local maxima as with the local prevalence indicating that the increases in local prevalence associated with the urban and rural waves are accompanied by an increase in spatial clustering. The height of the second peak, however, depends on the value of
with a stronger second peak occurring at higher values. Some insight into this behaviour can be gained by observing the variance of the values and individual realisations of the epidemic. In particular, we see a marked increase in variance in
after the initial urban peak, implying that this time is a crucial point in the evolution with regards to the spatial connectivity of the epidemic whereby a great number of qualitatively distinct spatial spreading behaviours become possible. This can then be observed in the example extremal realisations which all have similar rises in
leading to the urban peak, but a range of possible subsequent behaviour which may or may not include a second, rural, peak in clustering. We conjecture that this is due to an inherent sensitivity in the evolution of the epidemic in terms of timing and configuration, when the spread reaches the edge of urban populations. This implies that there are qualitatively distinct ways to spread through rural populations as opposed to the generally uniform spread through urban centres. Interestingly, as
is increased to
we see that whilst this variance peak between waves remains similar in size, the variance then subsequently increases as
increases. This suggests that the expected connectivity of the rural wave is subject to greater variations due to an increase in the number of realisations with both highly connected and highly disconnected rural waves.
The fact that increases in prevalence are associated with increases in spatial clustering immediately presents a question related to the existence of the usual phase transition at and whether it can be characterised as a percolation transition in terms of alongside its variation with more broadly. Explicitly, does the existence of a phase transition between growth and decay from infection seeding imply a percolation transition? Further, given the variation in the behaviour at the rural peak, how does the connectivity and distribution vary with at this point in the evolution of the epidemic? To answer these questions, we investigate the behaviour of , both through its mean, , and the sensitivity of its distribution through the Fisher information, as it varies with as evaluated at the urban and rural peaks of the epidemic since these capture (i) the peak in spatial connectivity and (ii) the behaviour during the rural wave.
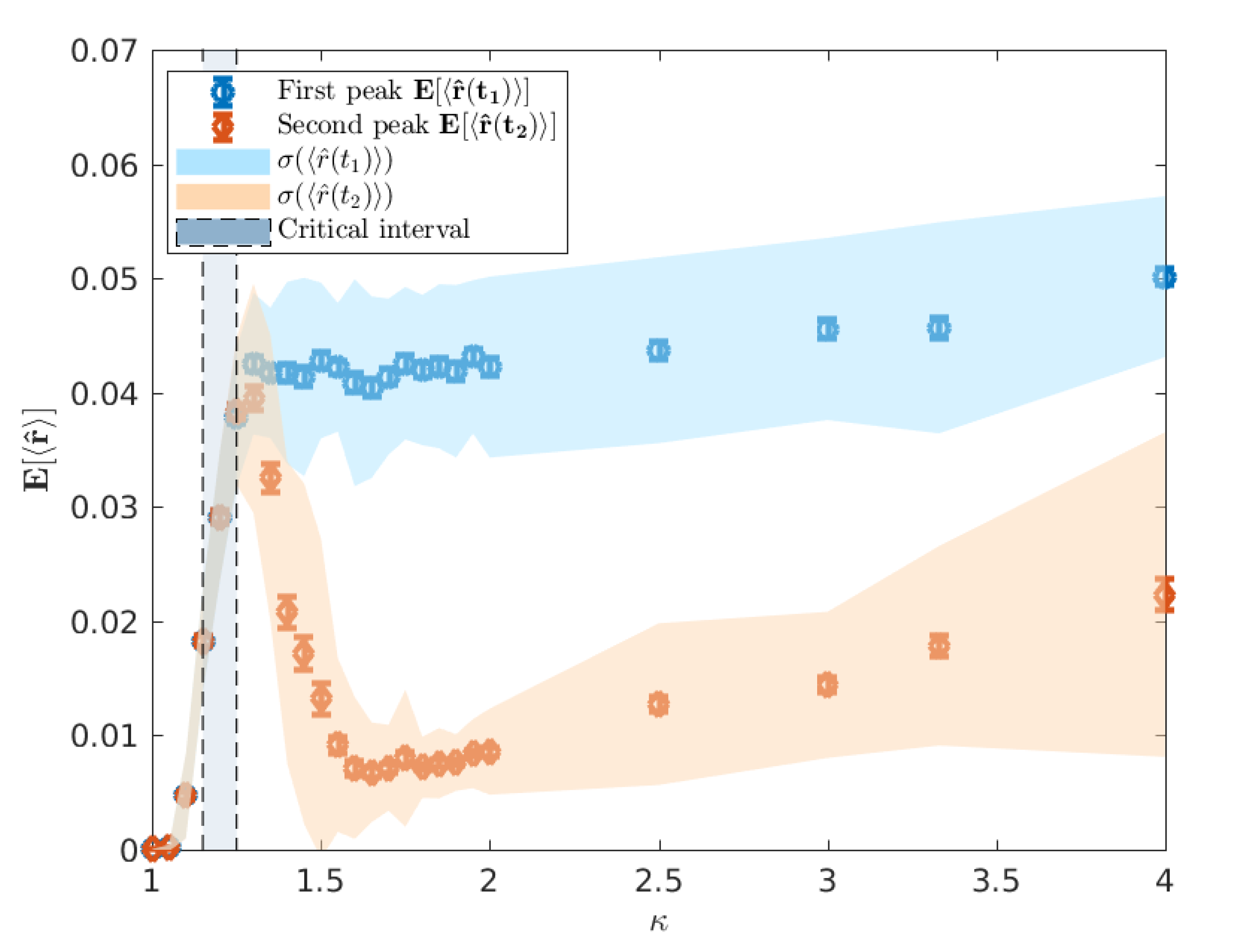
First, we plot
and
as functions of
in
Figure 10. As
increases from 1 towards the critical interval, we observe a rapid increase in
until
where
and
are indistinguishable, indicative of a percolation phase transition. However, as the peaks become increasingly distinguishable in the post-critical regime, there is a distinct difference in the relationship between
and
when measured at the urban and rural peaks.
The minimum in this profile, around
(
Figure 10), occurs when the difference in mean peak times
and
is the largest (
Figure 6). We argue that this minimal connectivity, which coincides with the maximum difference in peak times marks the minimum value of
for which the urban and rural waves of the epidemic are meaningfully separated such that all measured connectivity at
is a result of the rural wave. In contrast, below this value, the urban and rural waves are, to different extents, overlapping and thus, much of the measured connectivity at
is attributable to the urban wave. In light of this, it is interesting to note the distinct behaviour measured at
and
beyond
. Specifically, we see a reasonably constant connectivity and variance measured at
, but a distinctly increasing connectivity and variance measured at
. This supports the view implied by Figure (
Figure 9) where the onset of the urban wave is a consistent, reliable phenomenon, whereas the rural wave is a much more variable phenomenon with many more possible realisations. As
continues to increase, the relatively low probability of a large connected rural peak gets larger, but with increased variability. This is again observed in
Figure 9 where the extremal cases include realisations with no rural peak in spatial connectivity for both measured values of
.
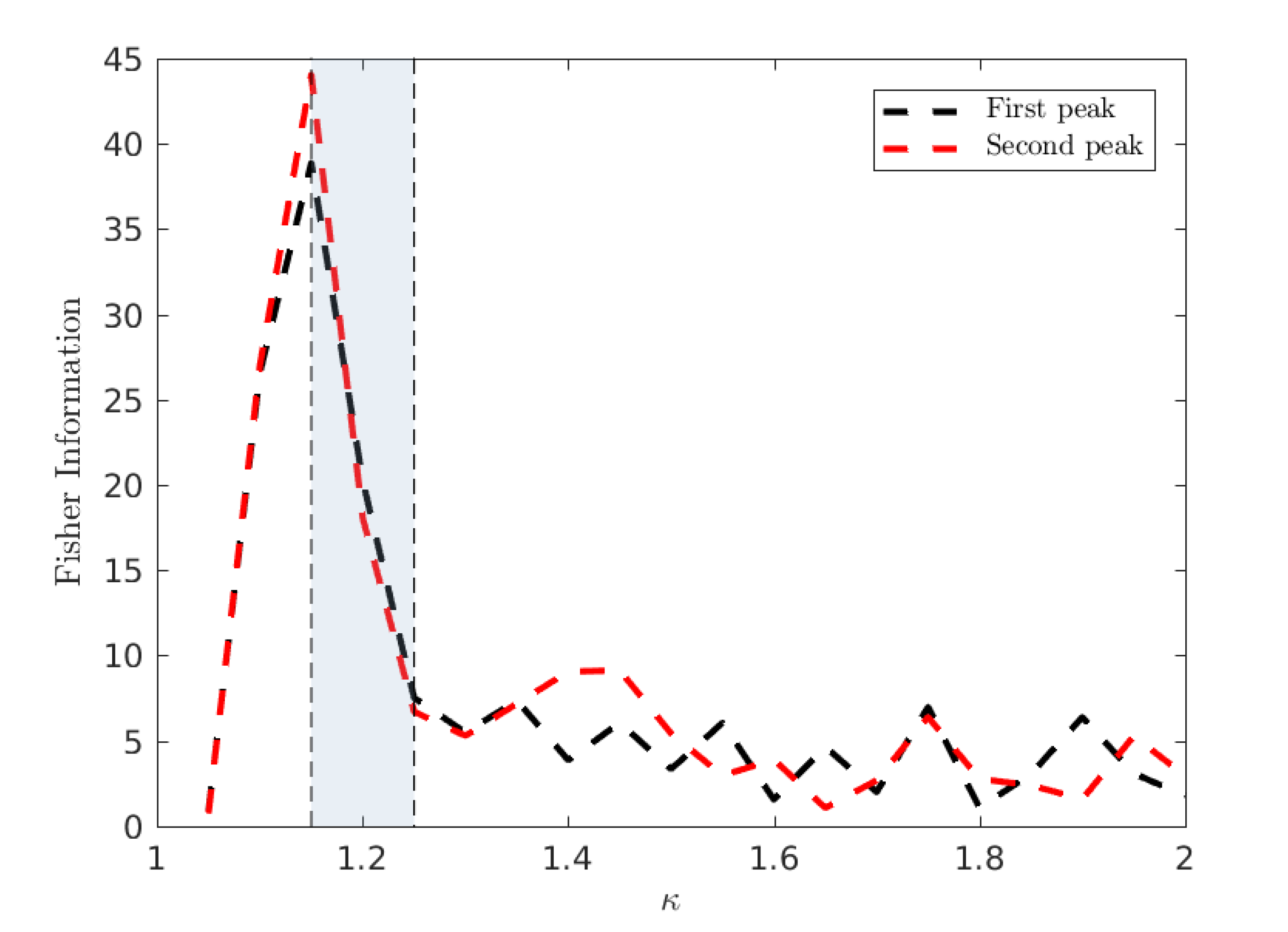
At this stage, we support the assertion of a percolation phase transition between low and high connectivity configurations using model-free measures of criticality, namely the Fisher Information. We compute the Fisher information using the probability distribution
, implicitly taking
as a statistic of the full phase space, instead of the configurational probability distribution defined in terms of the system’s Hamiltonian [
44]. In a canonical statistical physics setting, the Fisher information is proportional to the rate of change of the order parameter, being analogous to susceptibility which has a singularity diverging at the critical point. As discussed in
Section 3.2, a divergence in this Fisher information based on the statistic
implies a phase transition across the wider state space.
In order to accurately estimate the Fisher Information of
with respect to the infectivity parameter
, we follow the approach of Kallionatis et al. [
47] which uses the Freedman-Diaconis rule [
48] to determine the bin size
, where
is the interquartile range, and
n is the number of samples.
Figure 11 demonstrates the Fisher Information of
with respect to the infectivity parameter
.
We clearly observe a peak in the Fisher Information in close proximity to the critical value relating to the onset of an epidemic phase in terms of global attack rates. This implies that the epidemic transition commonly associated with (and thus ) has a specific spatial characteristic allowing it to be simultaneously understood as a percolation transition. We emphasize that this spatial percolation is observable in a realistic multi-agent heterogeneous setting, grounded in real data, complete with non-trivial and realistic transmission dynamics on a complex real-world topology of commuting and residential interactions distinct from the spatial network upon which the emergent clusters are identified.
5. Conclusions
In this paper, we studied influenza pandemics in terms of their spatial connectivity using the Australian Census-based Epidemic Model (A
ceMod), simulating influenza spread at a national level over an artificial population of
million agents, generated from the most recent 2016 Australian census data. It has been previously noted that Australian epidemics exhibit a relatively uncommon progression with characteristically bimodal epidemic curves [
6]. Moreover, these modes have been associated with two distinct waves of infection upon the relatively separate urban and rural populations. Consequently, our analysis was tailored to this phenomenon, focussing on two key time points—the stationary points in mean local prevalence associated with peak urban and rural prevalence (see
Figure 2 and
Figure 3).
A primary finding, observable in both rural and urban peaks due to their high synchrony around the critical , is the behaviour of the infection connectivity, characterised in terms of percolation measures of clustering. By measuring this degree of clustering at various levels of infectivity, we have provided evidence, through direct computation of order parameters () and model free measures of criticality (the Fisher information), that the threshold transition is accompanied by a sharp increase in connectivity indicative of a percolation transition. As far as we are aware, this is the first time such a percolation transition has been implicated in a national, large-scale agent-based model of epidemics. We note that the location of this transition in terms of is lower than is generally observed in models based on homogeneous well mixed populations. This phenomenon is explained here and in other agent-based approaches by the extreme heterogeneity of individuals which interfere with the effectiveness of an average measure such as , emphasising the importance of flexible, heterogeneous, modelling approaches such as agent-based modelling.
By examining both the statistical and individual behaviour of as both a function of time and of the infectivity, we have shown distinct clustering phenomenon associated with the urban and rural waves of the epidemic. In particular we observe the urban wave to be a consistent phenomenon with relatively constant behaviour beyond the critical point with relatively low variation in its timing and extent. However, the behaviour of the rural wave is much more nuanced. Of crucial importance is that, at all values of , the existence of a highly connected rural wave is not guaranteed, with it being a probabilistic phenomenon with relatively large variance. When the urban and rural peaks are distinguishable we see that the likelihood and extent of such a connected rural wave increases with increasing infectivity accompanied by an increase in the variance such that it is inherently less predictable than the urban wave. We conjecture that this is due to a fundamental sensitivity in the spread of the epidemic from urban to rural areas leading to a multiplicity of qualitatively distinct outcomes, though further research is needed on this issue.
Broadly, this study emphasises the importance of the bimodal, dual population behaviour of epidemics in Australia for both modelling and policy. Methodologically it also opens up interesting questions for further work, such as whether meaningful
local measures of interconnectivity can be developed and applied to such complex systems allowing researchers to investigate the spatial patterns of infection on localized populations when there is low synchrony on the national scale. Furthermore, future work may focus on the development of warnings in real time based on the unique spatial properties and bimodal nature of the epidemic similarly to [
1,
2].
Finally, we mention the methodological developments that were necessary to perform this spatial analysis. An essential step required for the percolation analysis and subsequent assessments of criticality through the Fisher information is the dimensional reduction of the prevalence in local regions to strongly and weakly infected. This allows for canonical percolation measures to be utilized and ensures that computation of the Fisher information is tractable, but naturally comes at the expense of a certain degree of resolution. However, this loss in resolution has not affected the ability to observe the percolation phase transition and identify pertinent features of the secondary (rural) wave. We emphasise that the results presented here utilize the results of the AceMod simulation package, performing post-processing on the output formed of spatial time series. Consequently, all of the analyses may be equally applied to similar spatially labelled prevalence data from any national or disease context, whether it is simulation or empirical data. We thus hope that this contribution encourages the use of spatial analysis in the study and understanding of epidemic processes which may involve heterogeneity of demographics, mobility, and disease transmission factors more generally.