Introduction to Extreme Seeking Entropy
Abstract
1. Introduction
2. Review of the Learning Systems Used
2.1. Adaptive Models
2.1.1. Linear Adaptive Filter
2.1.2. An Adaptive Filter Based on Higher Order Neural Units
2.2. Learning Algorithms
2.2.1. Normalized Least Mean Squares Algorithm
2.2.2. Generalized Normalized Gradient Descent
3. On the Evaluation of the Increments in the Adaptive Weights in Order to Estimate the Novelty in the Data
3.1. Learning Entropy: A Direct Algorithm
3.2. Error and Learning Based Novelty Detection
3.3. General Properties of A Suitable Learning Based Information Measure
4. Extreme Seeking Entropy
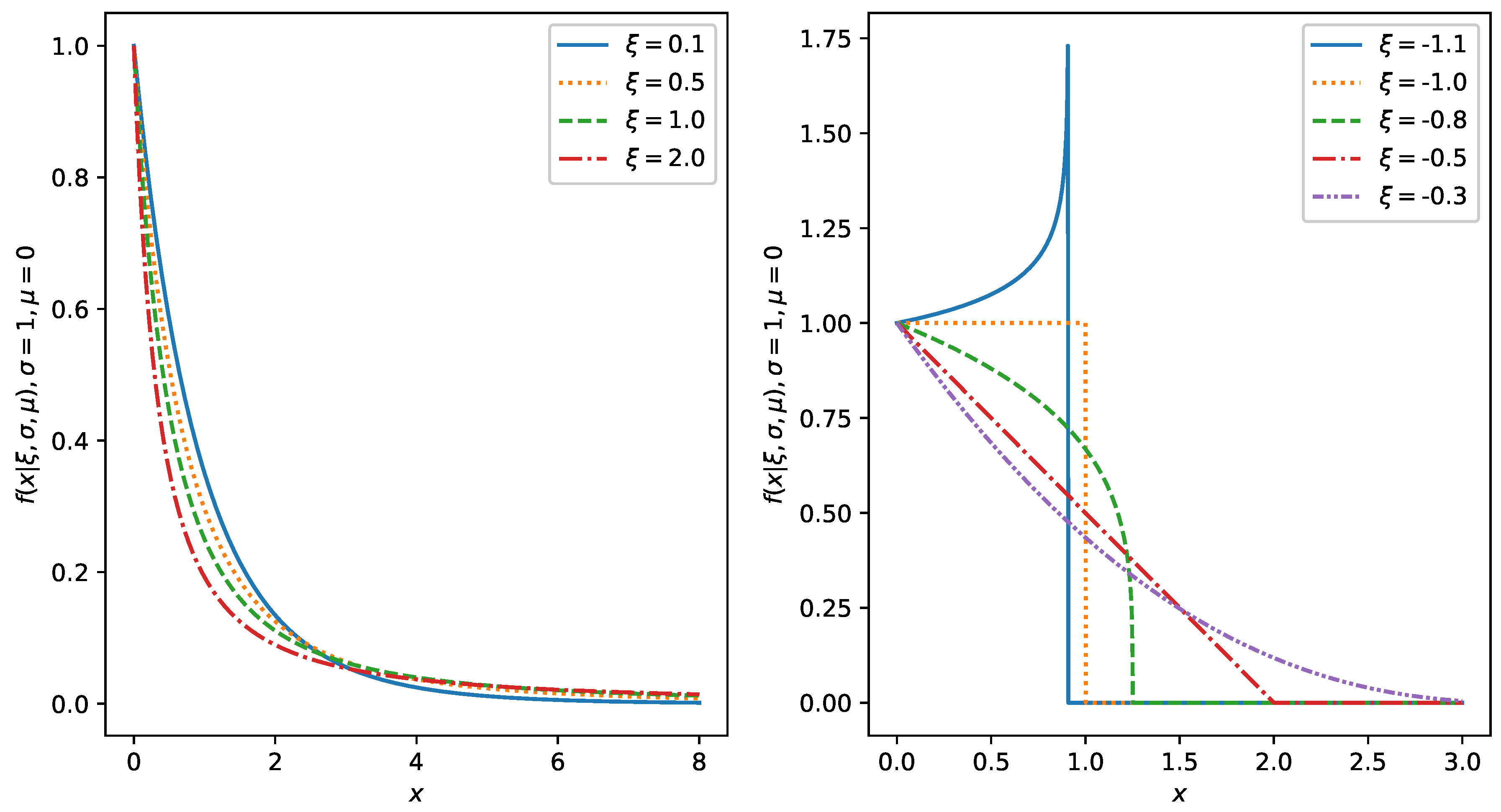
4.1. The Generalized Pareto Distribution
4.2. The Peaks over Threshold Method
4.3. Extreme Seeking Entropy Algorithm
| Algorithm 1 Extreme seeking entropy algorithm. |
|
5. Experimental Results
5.1. The Design of the Experiments
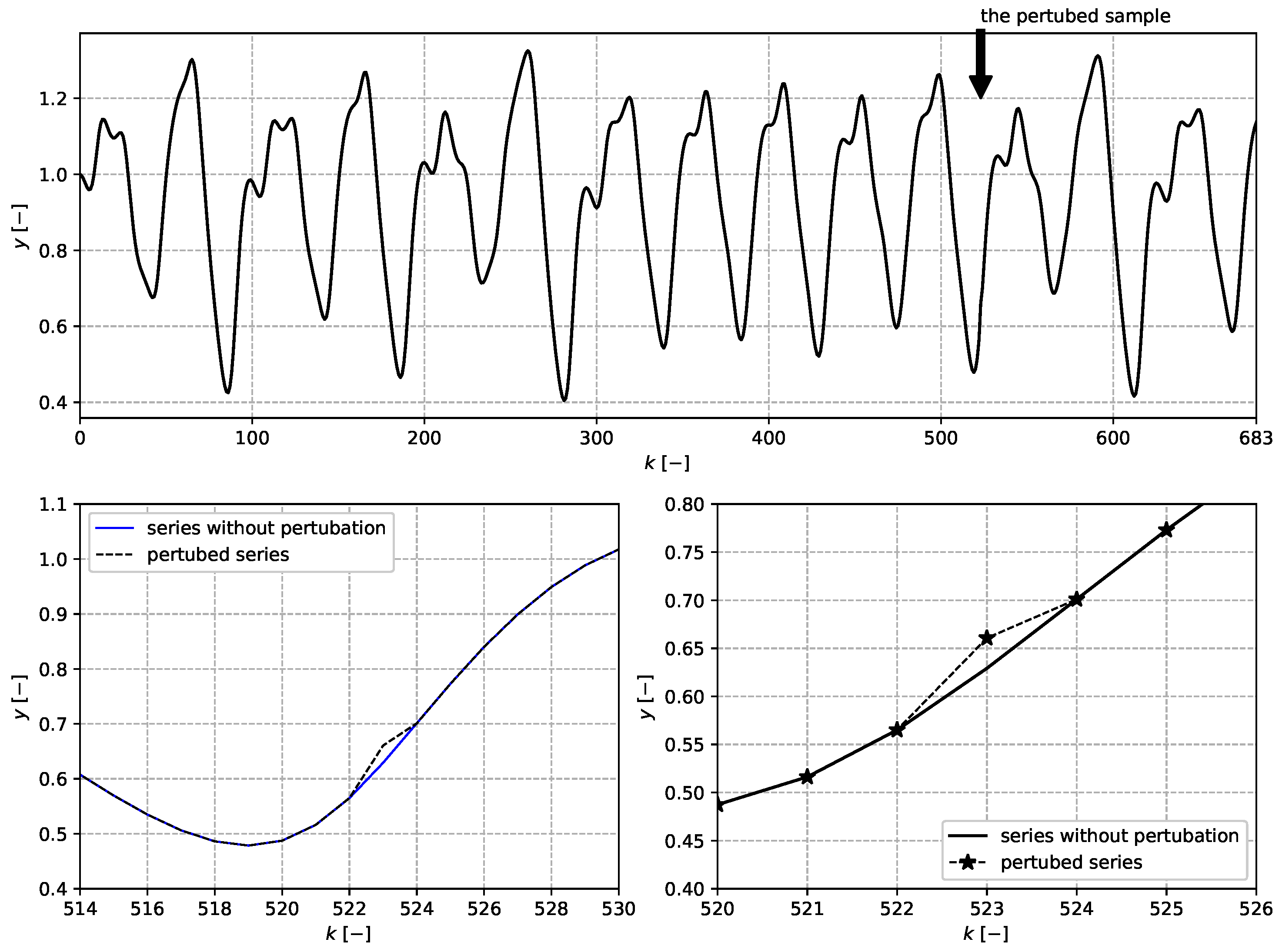
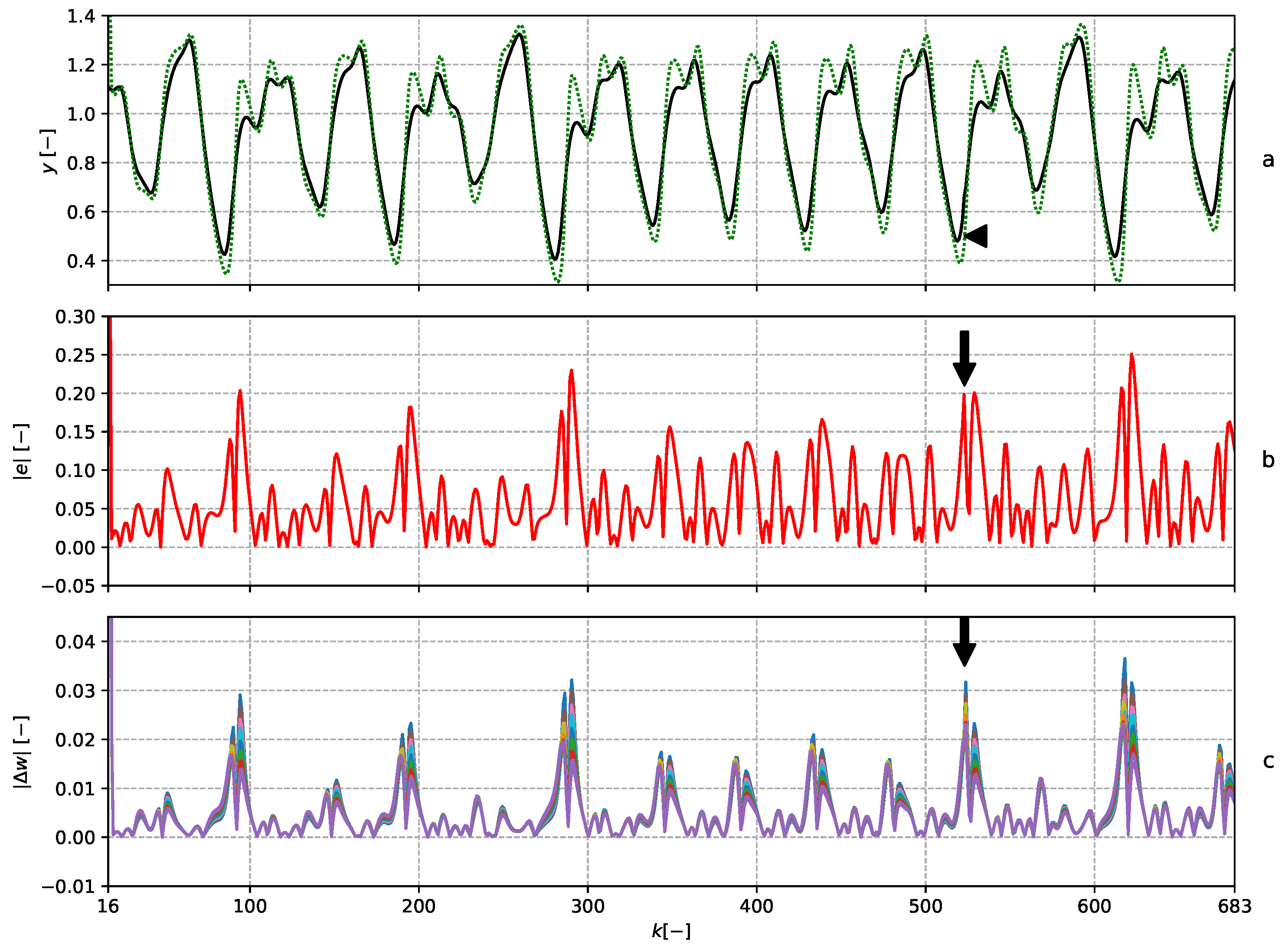
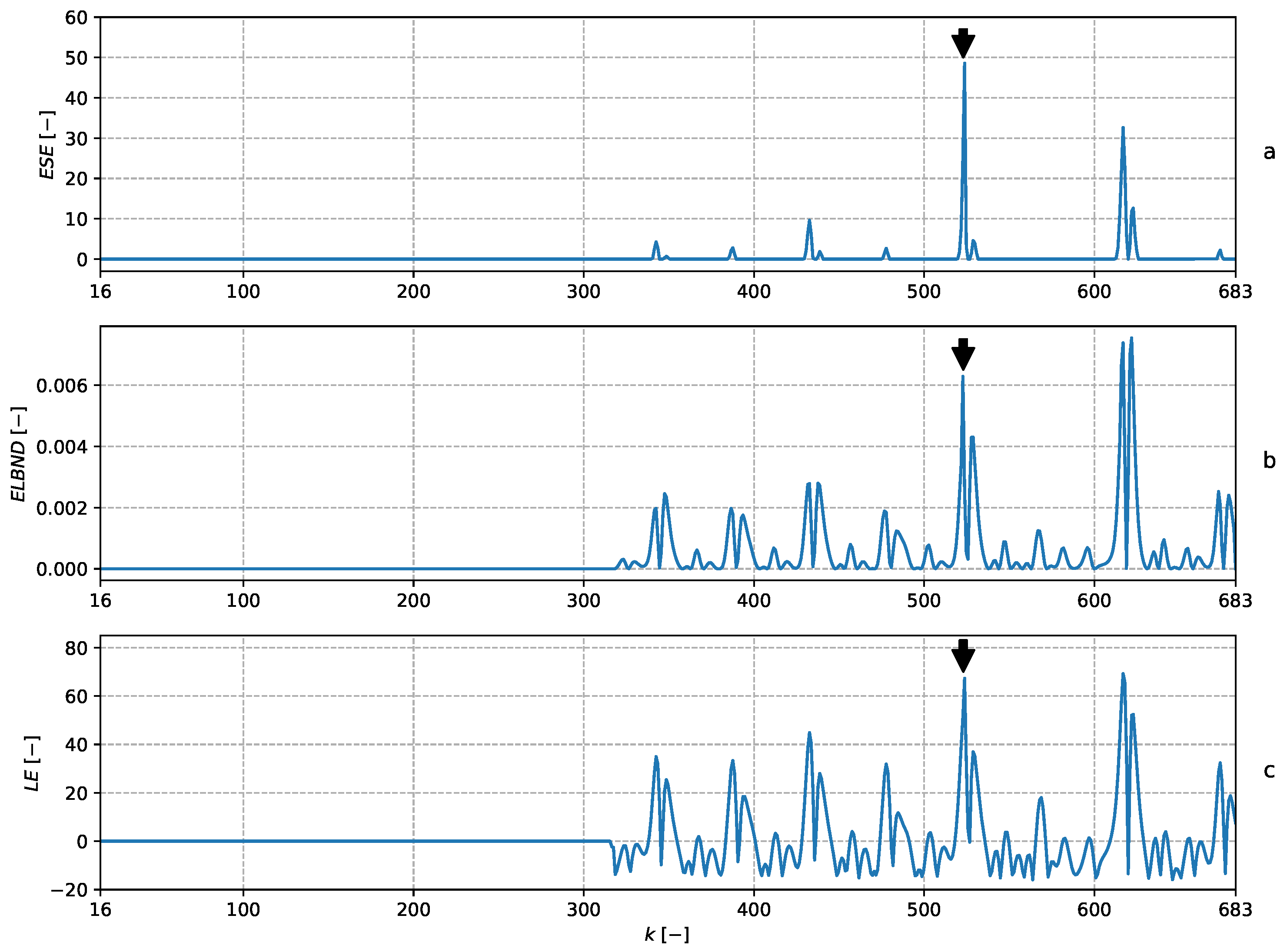
5.2. Mackey–Glass Time Series Perturbation
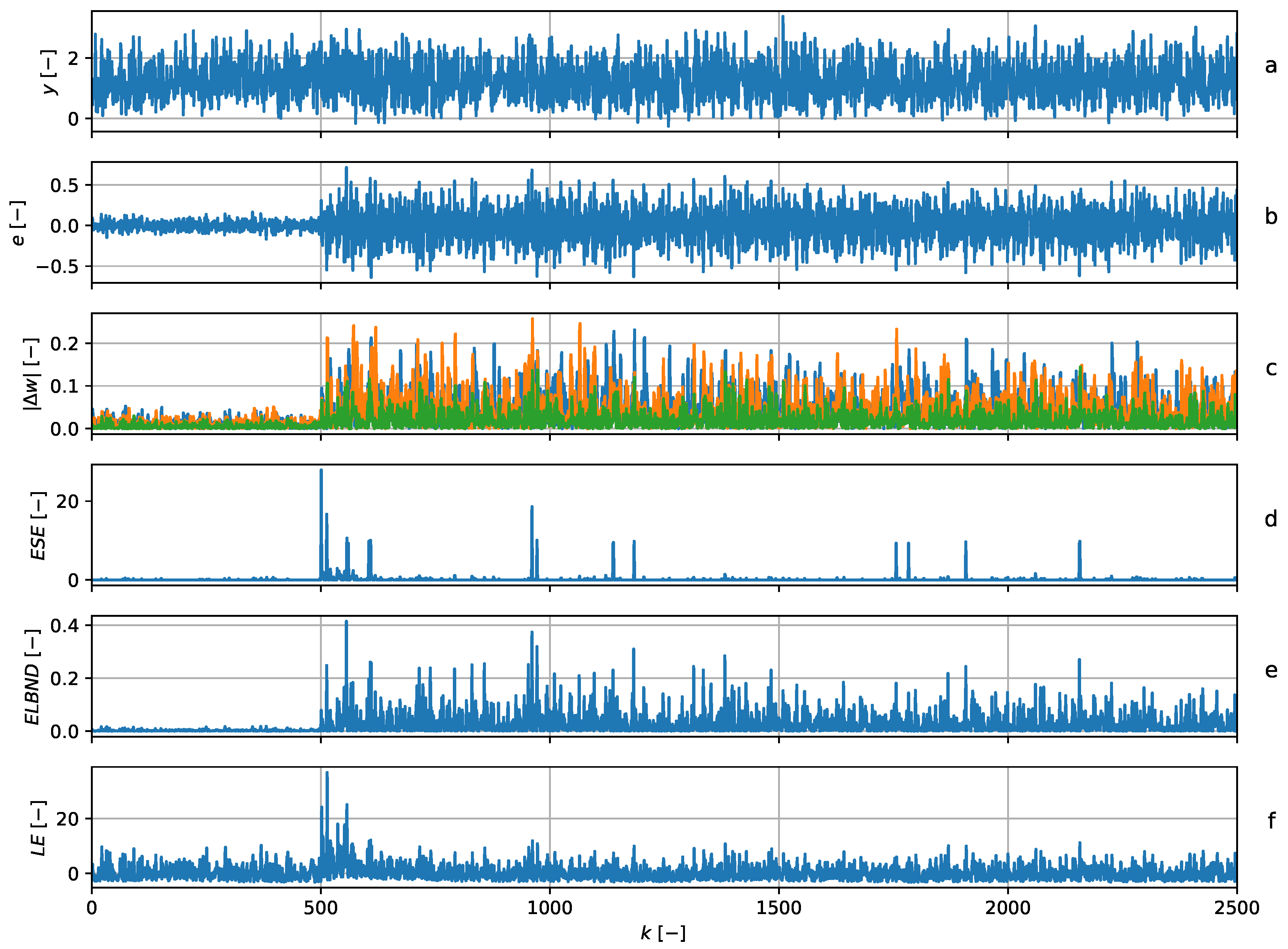
5.3. Change of the Standard Deviation of the Noise in a Random Data Stream
5.4. Step Change in the Parameters of a Signal Generator
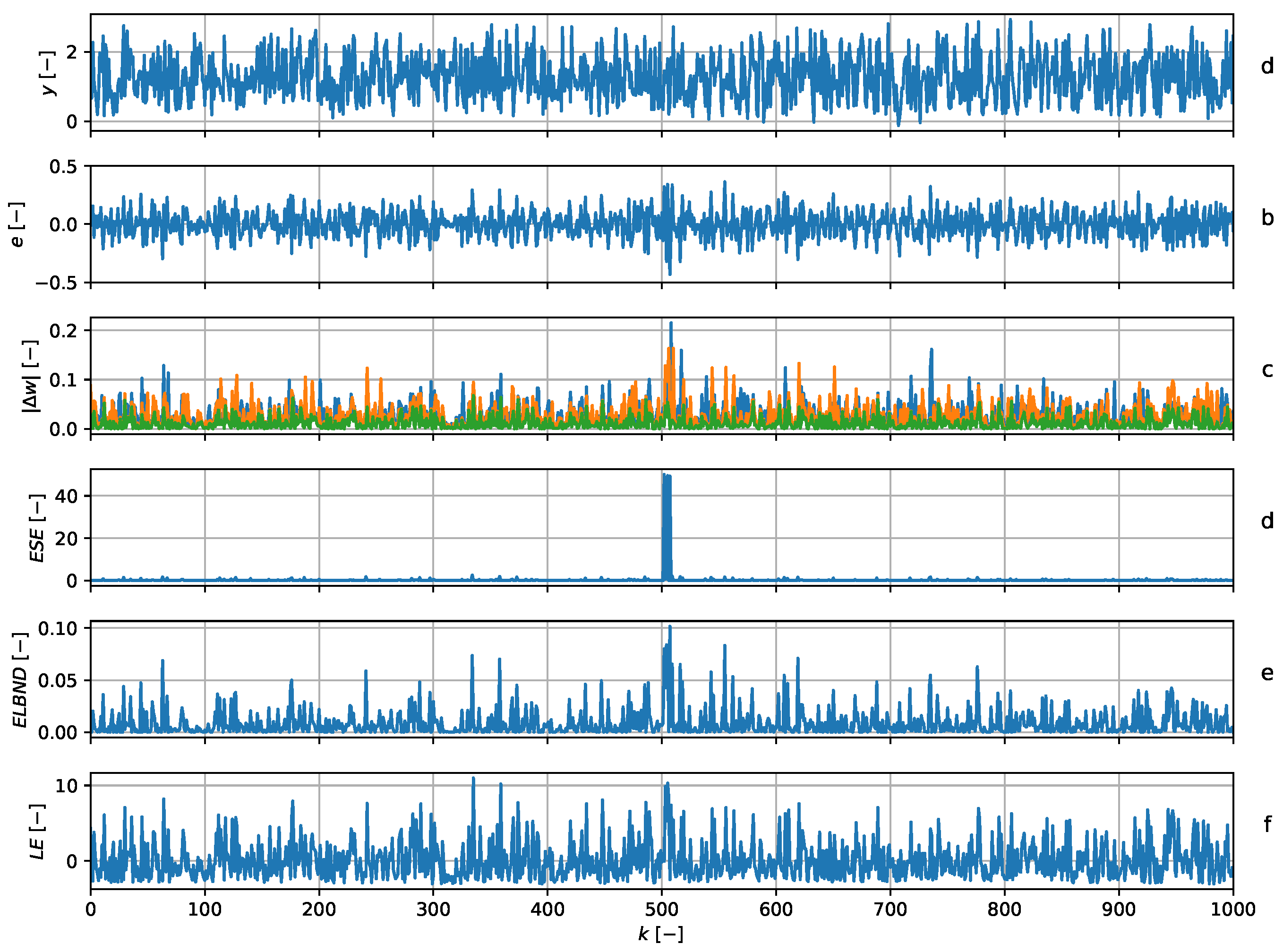
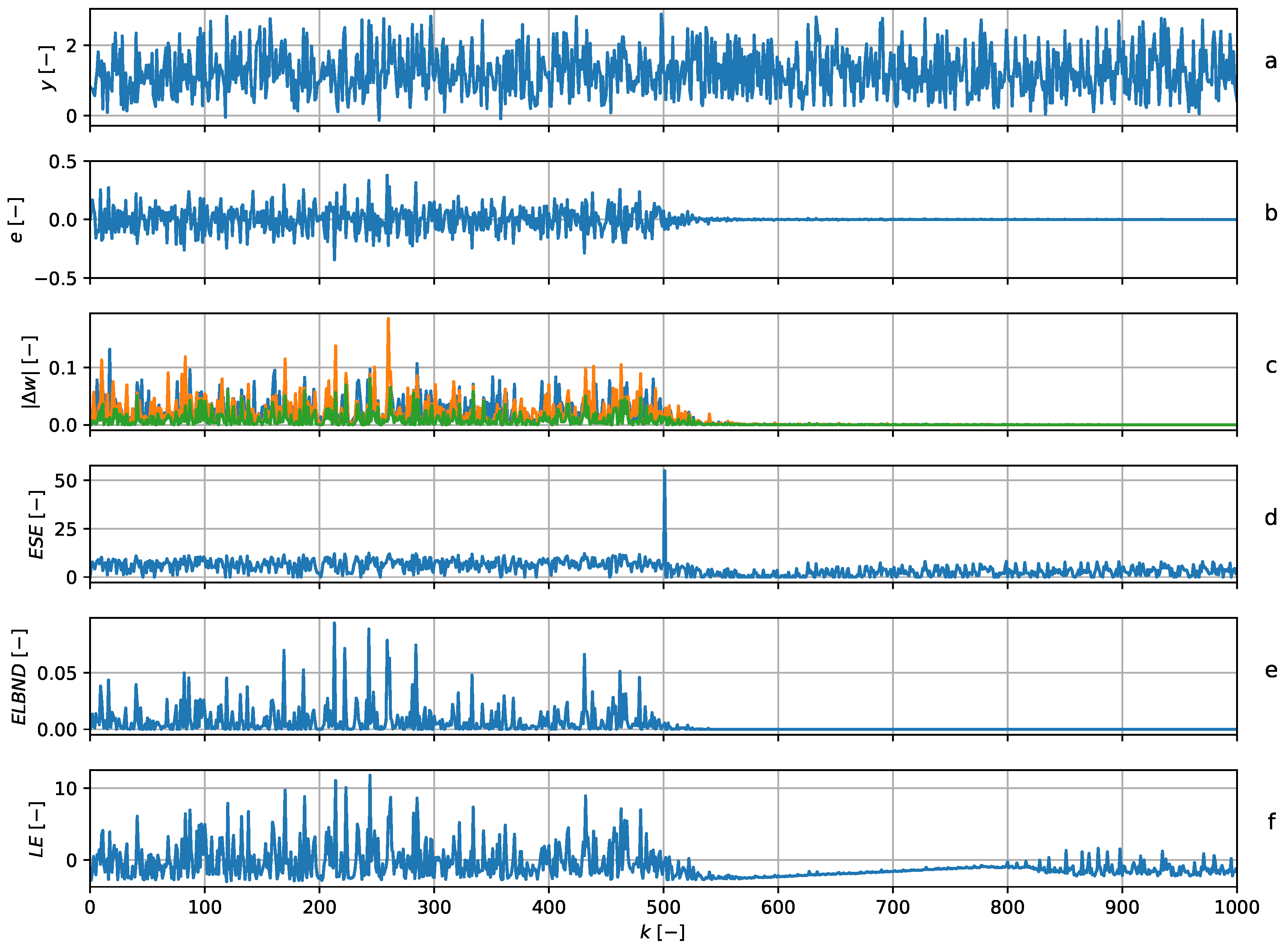
5.5. Noise Disappearance
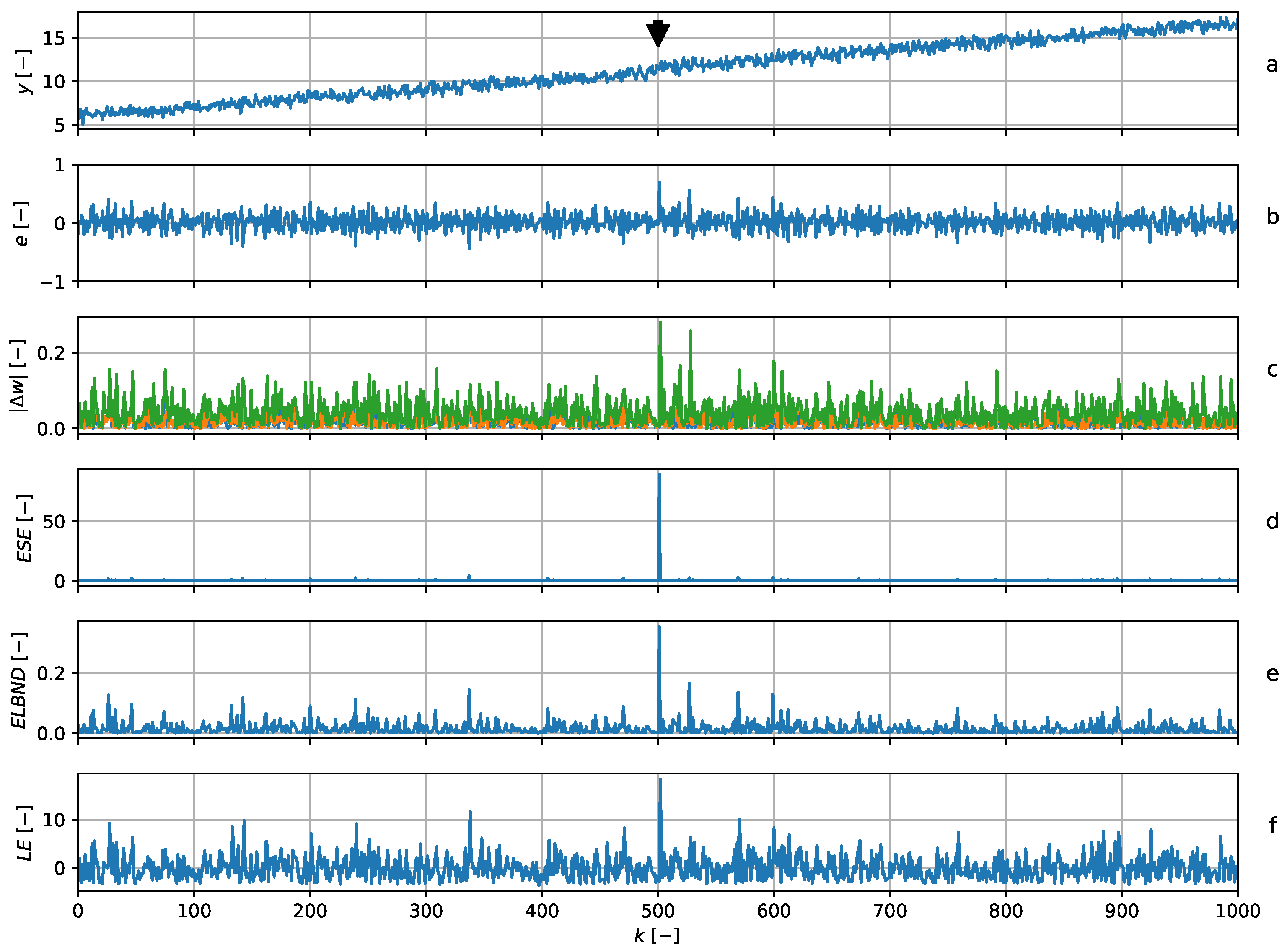
5.6. Trend Change
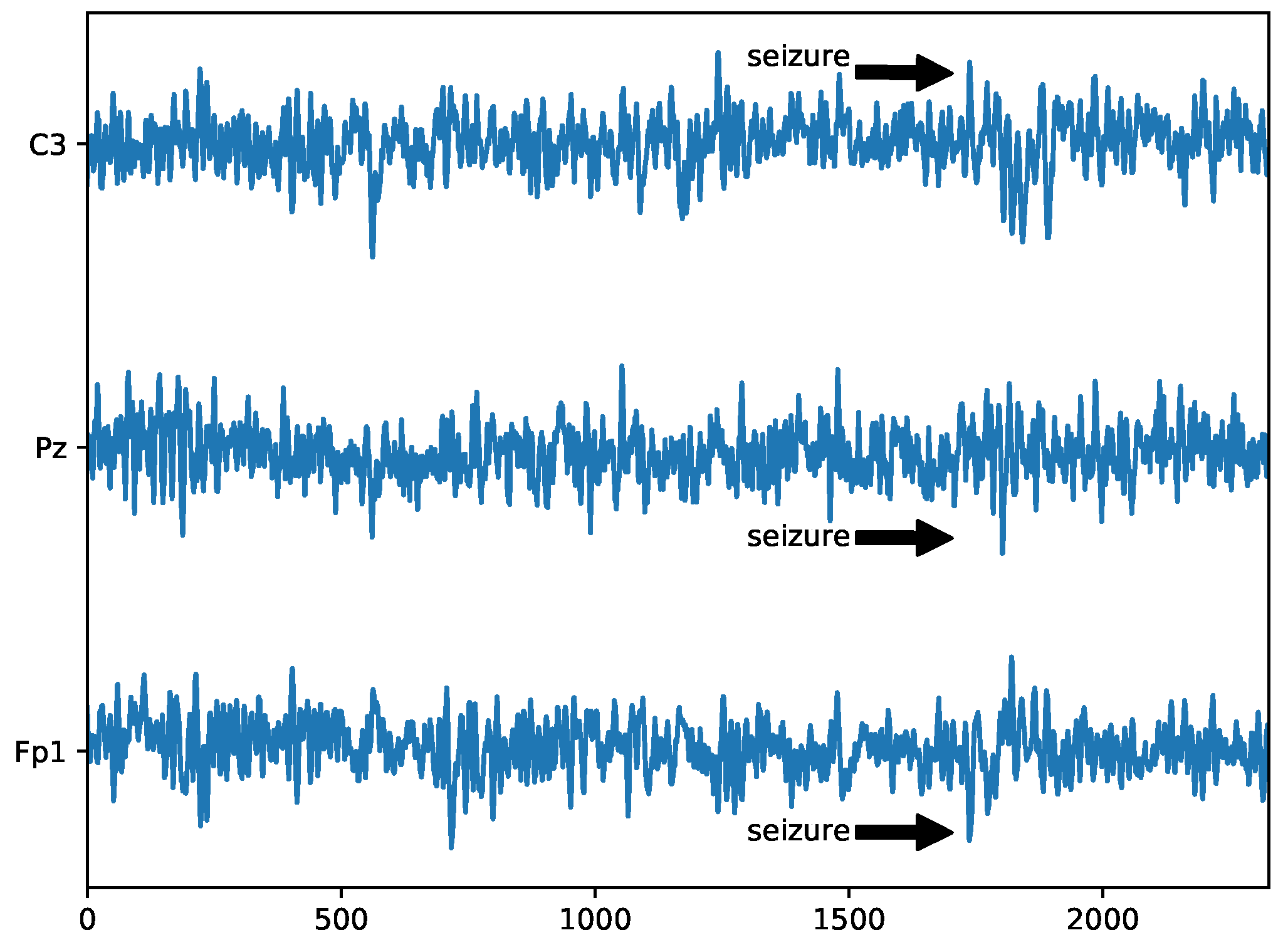
5.7. Detection of Epilepsy in Mouse EEG
6. Evaluation of the ESE Detection Rate
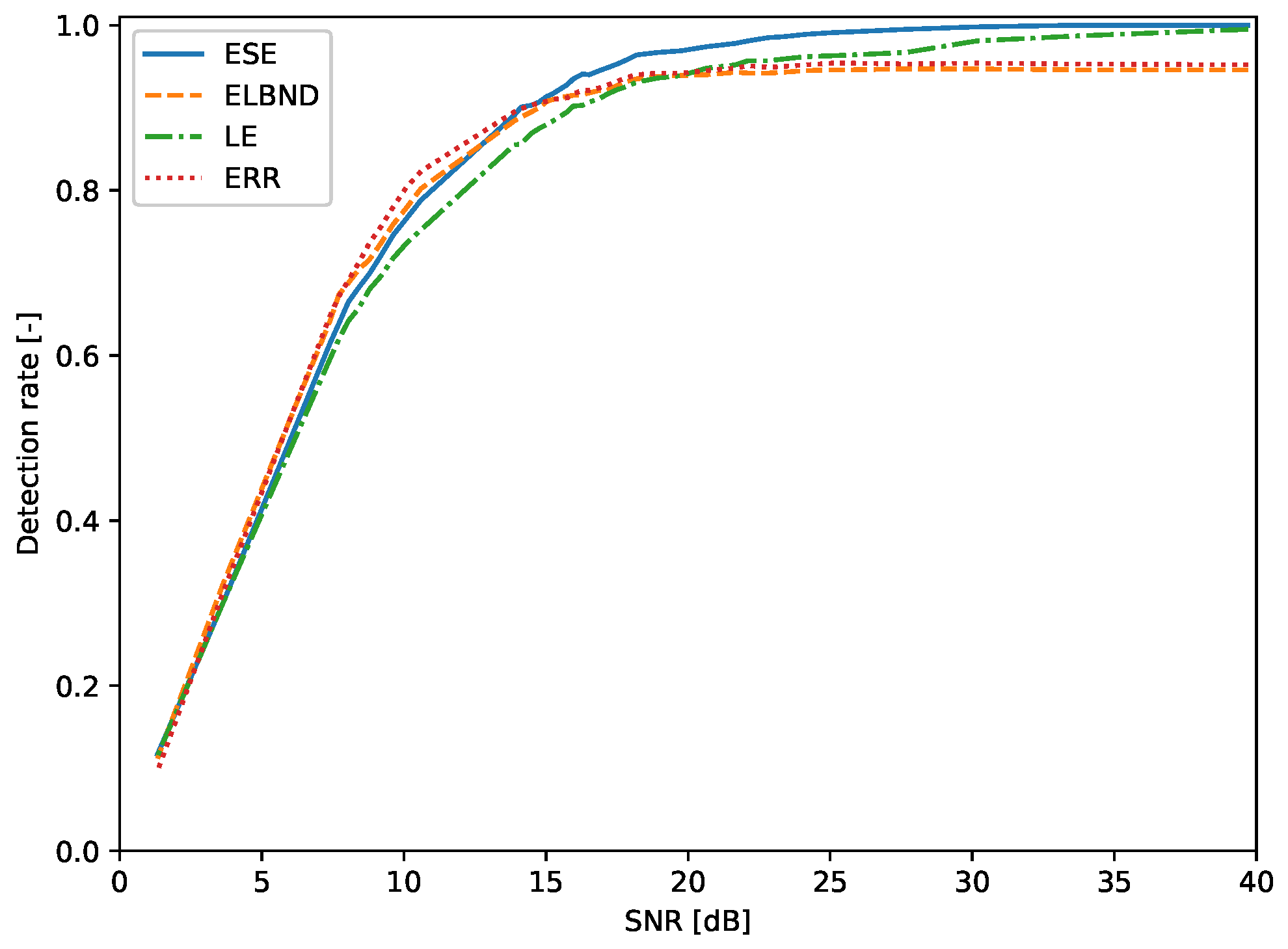
6.1. Step Change in the Parameters of a Signal Generator: Evaluation of the Detection Rate
- choose noise standard deviation
- for given noise standard deviation , perform 1000 experiments, and at the beginning of each experiment, choose new parameters , , and
- successful detection was when the global peak in ESE, LE, ELBND, or prediction error was between discrete time index and ; compute the detection rate
- compute the SNR for each experiment according to (43), and compute the average SNR for all experiments for given noise standard deviation
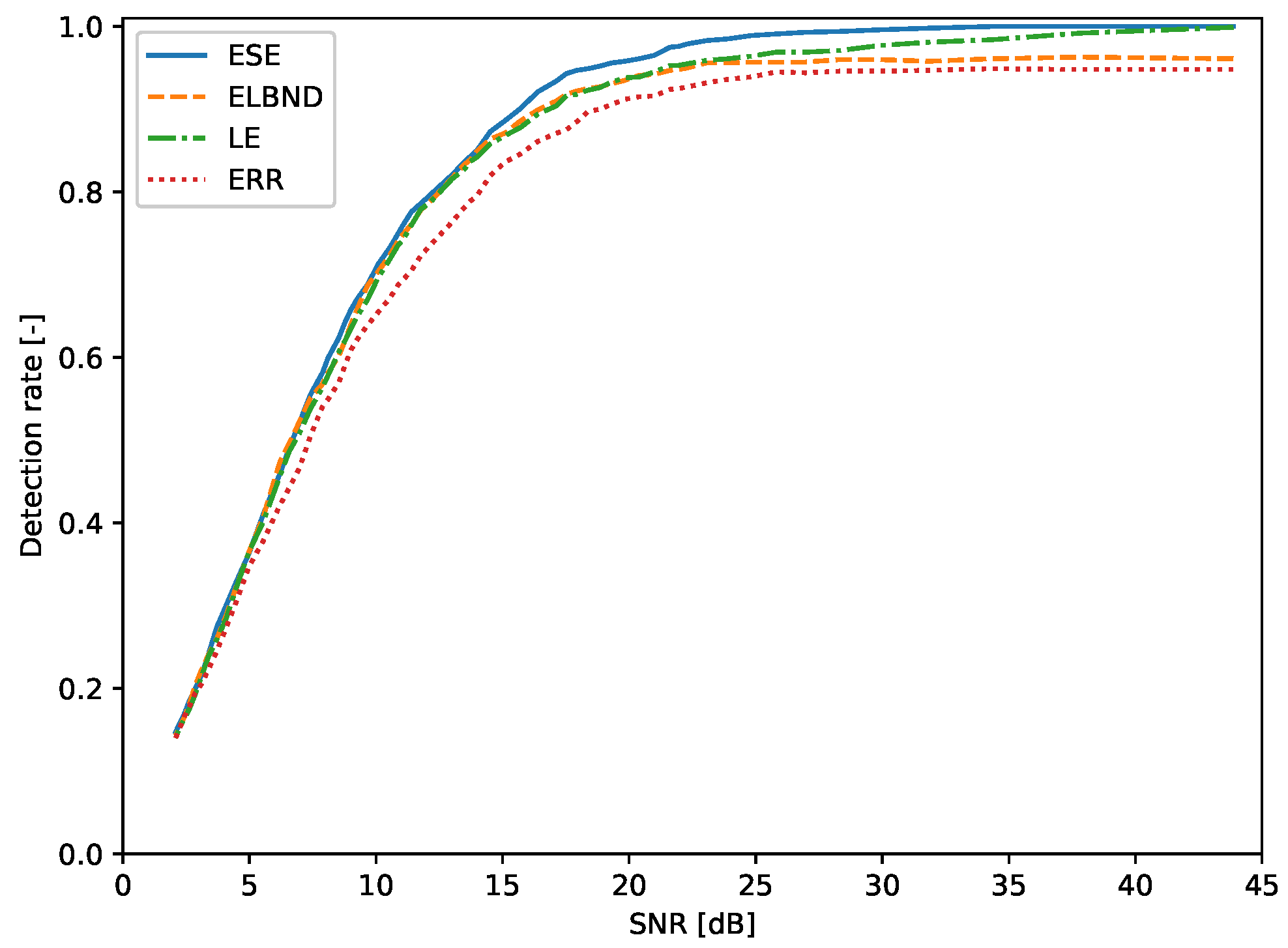
6.2. Detection of a Change in Trend: Evaluation of the Detection Rate
- choose noise standard deviation
- for given noise standard deviation , perform 1000 experiments where at , there is a change in trend
- successful detection is when the global peak in ESE, LE, ELBND, or prediction error is between discrete time index and ; compute the detection rate
- compute the SNR for each experiment according to (43), and compute the average SNR for all experiments for given noise standard deviation
7. Limitations and Further Challenges
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ND | novelty detection |
| ESE | extreme seeking entropy |
| LE | learning entropy |
| ELBND | error and learning based novelty detection |
| GEV | generalized extreme value |
| GPD | generalized Pareto distribution |
| GNGD | generalized normalized gradient descent |
| NLMS | normalized least mean squares |
| probability density function | |
| cdf | cumulative density function |
| POT | peak over threshold |
| LNU | linear neural unit |
| QNU | quadratic neural unit |
| SNR | signal-to-noise ratio |
Appendix A
| SNR (dB) | ESE (%) | ELBND (%) | LE (%) | Err (%) |
|---|---|---|---|---|
| 41.63 | 99.0 | 68.1 | 98.9 | 54.8 |
| 35.62 | 98.4 | 68.3 | 98.4 | 54.2 |
| 29.61 | 97.3 | 70.2 | 97.3 | 56.9 |
| 26.11 | 96.1 | 74.6 | 95.7 | 59.3 |
| 23.64 | 94.3 | 74.0 | 94.1 | 61.5 |
| 21.74 | 92.9 | 74.9 | 92.7 | 62.1 |
| 20.20 | 91.6 | 74.0 | 91.4 | 62.1 |
| 18.92 | 90.4 | 74.2 | 89.4 | 63.9 |
| 17.81 | 89.4 | 73.4 | 89.1 | 65.8 |
| 16.85 | 88.8 | 72.6 | 88.0 | 65.8 |
| 16.00 | 87.5 | 74.5 | 87.0 | 66.7 |
| 15.23 | 86.5 | 74.4 | 85.5 | 67.3 |
| 14.55 | 85.5 | 74.0 | 84.0 | 68.2 |
| 13.92 | 84.5 | 75.3 | 83.8 | 70.4 |
| 13.35 | 84.2 | 75.3 | 83.2 | 69.9 |
| 12.82 | 83.6 | 75.6 | 82.4 | 70.9 |
| 12.34 | 82.6 | 76.7 | 81.2 | 72.1 |
| 11.88 | 81.6 | 76.2 | 80.4 | 72.8 |
| 11.46 | 80.9 | 75.6 | 79.3 | 72.0 |
| 11.07 | 79.8 | 75.2 | 78.4 | 71.8 |
| 10.70 | 78.7 | 74.7 | 77.3 | 72.4 |
| 10.02 | 76.9 | 75.0 | 75.6 | 73.0 |
| 9.42 | 75.6 | 74.2 | 74.0 | 72.3 |
| 8.88 | 73.9 | 72.8 | 71.3 | 72.3 |
| 8.39 | 72.2 | 72.1 | 69.1 | 71.9 |
| 7.95 | 70.4 | 70.4 | 66.9 | 70.3 |
| 7.54 | 69.1 | 68.3 | 65.2 | 68.8 |
| 7.16 | 66.5 | 67.1 | 63.0 | 67.7 |
| 6.82 | 64.4 | 66.7 | 60.7 | 66.7 |
| 6.20 | 59.2 | 63.2 | 56.1 | 63.9 |
| 5.67 | 55.4 | 58.6 | 52.1 | 60.6 |
| 4.99 | 49.0 | 52.5 | 46.2 | 55.6 |
| SNR (dB) | ESE (%) | ELBND (%) | LE (%) | Err (%) |
|---|---|---|---|---|
| 39.70 | 100.0 | 94.6 | 99.5 | 95.2 |
| 33.68 | 100.0 | 94.6 | 98.7 | 95.3 |
| 30.16 | 99.8 | 94.7 | 98.1 | 95.4 |
| 27.67 | 99.5 | 94.7 | 96.7 | 95.3 |
| 25.73 | 99.2 | 94.6 | 96.4 | 95.4 |
| 25.07 | 99.1 | 94.6 | 96.3 | 95.4 |
| 24.15 | 98.9 | 94.5 | 96.2 | 95.2 |
| 23.33 | 98.6 | 94.3 | 95.9 | 95.0 |
| 22.82 | 98.5 | 94.2 | 95.7 | 94.9 |
| 22.11 | 98.1 | 94.2 | 95.7 | 95.1 |
| 21.67 | 97.8 | 94.3 | 95.2 | 94.8 |
| 20.66 | 97.4 | 94.0 | 94.8 | 94.5 |
| 19.75 | 96.9 | 93.9 | 93.9 | 94.2 |
| 18.93 | 96.7 | 93.8 | 93.6 | 94.2 |
| 18.19 | 96.4 | 93.5 | 93.1 | 94.0 |
| 17.77 | 95.7 | 93.1 | 92.5 | 93.6 |
| 17.51 | 95.3 | 92.7 | 92.2 | 93.2 |
| 17.12 | 94.8 | 92.1 | 91.6 | 92.7 |
| 16.88 | 94.5 | 92.1 | 91.1 | 92.4 |
| 16.52 | 94.0 | 91.8 | 90.7 | 92.1 |
| 16.29 | 94.1 | 91.6 | 90.3 | 92.1 |
| 15.96 | 93.5 | 91.5 | 90.2 | 91.7 |
| 15.75 | 92.8 | 91.4 | 89.5 | 91.2 |
| 15.24 | 91.7 | 91.0 | 88.4 | 91.0 |
| 15.04 | 91.4 | 90.8 | 88.0 | 90.8 |
| 14.76 | 90.7 | 90.0 | 87.5 | 90.6 |
| 14.48 | 90.3 | 89.5 | 86.9 | 90.3 |
| 14.31 | 90.2 | 89.2 | 86.3 | 90.1 |
| 14.13 | 90.1 | 88.9 | 85.6 | 89.9 |
| 13.88 | 89.1 | 88.4 | 85.5 | 89.5 |
| 10.60 | 78.8 | 80.2 | 75.2 | 82.3 |
| 10.09 | 76.6 | 77.9 | 73.6 | 80.4 |
| 9.62 | 74.6 | 75.9 | 71.8 | 78.0 |
| 9.19 | 72.1 | 73.6 | 69.6 | 75.6 |
| 8.78 | 69.9 | 71.6 | 68.0 | 73.6 |
| 8.41 | 68.2 | 70.4 | 65.7 | 71.2 |
| 8.05 | 66.5 | 68.8 | 64.2 | 69.1 |
| 7.72 | 63.9 | 67.4 | 62.0 | 67.2 |
| 7.40 | 61.5 | 64.2 | 59.6 | 64.8 |
| 3.64 | 30.1 | 32.4 | 30.1 | 31.4 |
| 1.33 | 11.7 | 11.2 | 11.5 | 9.7 |
| SNR (dB) | ESE (%) | ELBND (%) | LE (%) | Err (%) |
|---|---|---|---|---|
| 43.86 | 100.0 | 96.1 | 99.9 | 94.8 |
| 37.84 | 100.0 | 96.3 | 99.2 | 94.8 |
| 34.32 | 100.0 | 96.1 | 98.4 | 94.9 |
| 31.83 | 99.8 | 95.8 | 98.1 | 94.7 |
| 29.89 | 99.6 | 96.0 | 97.7 | 94.6 |
| 28.31 | 99.4 | 96.0 | 97.1 | 94.6 |
| 26.97 | 99.3 | 95.7 | 96.9 | 94.4 |
| 25.82 | 99.1 | 95.7 | 96.9 | 94.5 |
| 24.80 | 98.9 | 95.7 | 96.4 | 93.9 |
| 23.89 | 98.5 | 95.6 | 96.1 | 93.6 |
| 23.06 | 98.3 | 95.6 | 95.9 | 93.2 |
| 22.31 | 97.9 | 95.0 | 95.5 | 92.7 |
| 21.96 | 97.6 | 94.8 | 95.3 | 92.5 |
| 21.62 | 97.5 | 94.7 | 95.3 | 92.4 |
| 20.98 | 96.5 | 94.2 | 94.5 | 91.6 |
| 20.39 | 96.1 | 94.1 | 93.9 | 91.5 |
| 19.84 | 95.8 | 93.5 | 93.8 | 91.2 |
| 19.32 | 95.6 | 93.1 | 93.3 | 90.6 |
| 18.83 | 95.2 | 92.7 | 92.6 | 90.0 |
| 18.37 | 94.9 | 92.5 | 92.3 | 89.7 |
| 17.93 | 94.7 | 92.2 | 91.8 | 88.5 |
| 17.52 | 94.3 | 91.8 | 91.6 | 87.5 |
| 17.12 | 93.4 | 91.0 | 90.4 | 87.1 |
| 16.39 | 92.1 | 89.9 | 89.4 | 86.1 |
| 15.71 | 90.1 | 88.6 | 87.8 | 84.6 |
| 15.09 | 88.6 | 87.1 | 86.8 | 83.6 |
| 14.52 | 87.3 | 86.4 | 85.8 | 82.0 |
| 13.98 | 85.0 | 84.9 | 84.2 | 79.5 |
| 13.73 | 84.3 | 83.9 | 83.7 | 78.9 |
| 13.48 | 83.6 | 83.3 | 82.7 | 78.1 |
| 13.02 | 82.1 | 81.7 | 81.6 | 76.4 |
| 12.16 | 79.7 | 78.9 | 78.8 | 73.6 |
| 11.77 | 78.6 | 77.8 | 77.9 | 72.3 |
| 11.40 | 77.6 | 76.1 | 76.0 | 70.5 |
| 11.05 | 75.9 | 74.8 | 74.1 | 69.3 |
| 10.88 | 75.0 | 74.1 | 73.6 | 68.8 |
| 10.55 | 73.3 | 72.4 | 71.9 | 67.2 |
| 10.09 | 71.3 | 70.4 | 69.7 | 65.5 |
| 9.67 | 68.8 | 68.7 | 67.0 | 63.9 |
| 9.27 | 67.1 | 65.9 | 65.0 | 62.2 |
| 9.01 | 65.8 | 64.0 | 63.5 | 60.9 |
| 8.77 | 64.2 | 62.0 | 62.0 | 59.0 |
| 8.54 | 62.4 | 60.2 | 60.7 | 57.0 |
| 8.10 | 59.9 | 58.1 | 57.8 | 54.9 |
| 7.89 | 58.2 | 56.8 | 56.4 | 54.1 |
| 7.41 | 55.5 | 55.1 | 53.8 | 50.5 |
| 6.97 | 52.1 | 52.2 | 50.8 | 46.6 |
| 6.57 | 49.0 | 49.6 | 48.6 | 44.2 |
| 6.20 | 45.9 | 47.3 | 45.6 | 42.1 |
| 5.54 | 41.0 | 40.7 | 40.1 | 37.8 |
| 4.98 | 36.3 | 36.5 | 36.5 | 34.7 |
| 4.50 | 33.0 | 32.4 | 32.3 | 30.6 |
| 4.08 | 30.0 | 28.8 | 28.4 | 27.3 |
| 3.71 | 27.4 | 26.0 | 25.9 | 24.5 |
| 3.39 | 24.2 | 24.1 | 23.9 | 22.3 |
| 3.10 | 21.6 | 22.2 | 21.4 | 20.5 |
| 2.85 | 19.9 | 20.3 | 19.2 | 19.4 |
| 2.63 | 18.5 | 18.1 | 17.5 | 17.8 |
| 2.43 | 16.9 | 16.5 | 16.3 | 16.6 |
| 2.25 | 15.8 | 15.4 | 15.3 | 15.2 |
| 2.09 | 14.7 | 14.3 | 14.0 | 14.0 |
References
- Markou, M.; Singh, S. Novelty detection: A review—Part 1: Statistical approaches. Signal Process. 2003, 83, 2481–2497. [Google Scholar] [CrossRef]
- Clifton, D.A.; Hugueny, S.; Tarassenko, L. Novelty detection with multivariate extreme value statistics. J. Signal Process. Syst. 2011, 65, 371–389. [Google Scholar] [CrossRef]
- Hugueny, S.; Clifton, D.A.; Tarassenko, L. Probabilistic patient monitoring with multivariate, multimodal extreme value theory. In International Joint Conference on Biomedical Engineering Systems and Technologies; Springer: Berlin/Heidelberg, Germnay, 2010; pp. 199–211. [Google Scholar]
- Clifton, D.A.; Clifton, L.; Hugueny, S.; Tarassenko, L. Extending the generalised Pareto distribution for novelty detection in high-dimensional spaces. J. Signal Process. Syst. 2014, 74, 323–339. [Google Scholar] [CrossRef]
- Luca, S.; Clifton, D.A.; Vanrumste, B. One-class classification of point patterns of extremes. J. Mach. Learn. Res. 2016, 17, 6581–6601. [Google Scholar]
- Markou, M.; Singh, S. Novelty detection: A review—Part 2: Neural network based approaches. Signal Process. 2003, 83, 2499–2521. [Google Scholar] [CrossRef]
- Marsland, S. Novelty detection in learning systems. Neural Comput. Surv. 2003, 3, 157–195. [Google Scholar]
- Polycarpou, M.M.; Trunov, A.B. Learning approach to nonlinear fault diagnosis: Detectability analysis. IEEE Trans. Autom. Control 2000, 45, 806–812. [Google Scholar] [CrossRef]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Yazdanpanah, H.; Lima, M.V.; Diniz, P.S. On the robustness of set-membership adaptive filtering algorithms. EURASIP J. Adv. Signal Process. 2017, 2017, 72. [Google Scholar] [CrossRef]
- Diniz, P.S.R. Adaptive Filtering; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Gollamudi, S.; Nagaraj, S.; Kapoor, S.; Huang, Y.F. Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size. IEEE Signal Process. Lett. 1998, 5, 111–114. [Google Scholar] [CrossRef]
- Bukovsky, I. Learning Entropy: Multiscale Measure for Incremental Learning. Entropy 2013, 15, 4159–4187. [Google Scholar] [CrossRef]
- Bukovsky, I.; Kinsner, W.; Homma, N. Learning Entropy as a Learning-Based Information Concept. Entropy 2019, 21, 166. [Google Scholar] [CrossRef]
- Cejnek, M.; Bukovsky, I. Concept drift robust adaptive novelty detection for data streams. Neurocomputing 2018, 309, 46–53. [Google Scholar] [CrossRef]
- Bukovsky, I.; Kinsner, W.; Bila, J. Multiscale analysis approach for novelty detection in adaptation plot. In Proceedings of the Sensor Signal Processing for Defence (SSPD 2012), London, UK, 25–27 September 2012; pp. 1–6. [Google Scholar]
- Taoum, A.; Mourad-chehade, F.; Amoud, H. Early-warning of ARDS using novelty detection and data fusion. Comput. Biol. Med. 2018, 102, 191–199. [Google Scholar] [CrossRef] [PubMed]
- Rad, N.M.; van Laarhoven, T.; Furlanello, C.; Marchiori, E. Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders. Sensors 2018, 18, 3533. [Google Scholar] [CrossRef]
- Burlina, P.; Joshi, N.; Billings, S.; Wang, I.J.; Albayda, J. Deep embeddings for novelty detection in myopathy. Comput. Biol. Med. 2019, 105, 46–53. [Google Scholar] [CrossRef]
- Hu, L.; Hu, N.; Fan, B.; Gu, F. Application of novelty detection methods to health monitoring and typical fault diagnosis of a turbopump. J. Phys. Conf. Ser. 2012, 364, 012128. [Google Scholar] [CrossRef]
- Surace, C.; Worden, K. A novelty detection method to diagnose damage in structures: An application to an offshore platform. In The Eighth International Offshore and Polar Engineering Conference; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 1998. [Google Scholar]
- Bukovsky, I.; Homma, N.; Smetana, L.; Rodriguez, R.; Mironovova, M.; Vrana, S. Quadratic neural unit is a good compromise between linear models and neural networks for industrial applications. In Proceedings of the 9th IEEE International Conference on Cognitive Informatics (ICCI’10), Beijing, China, 7–9 July 2010; pp. 556–560. [Google Scholar] [CrossRef]
- Zhang, M. (Ed.) Artificial Higher Order Neural Networks for Modeling and Simulation; IGI Global: Hershey, PA, USA, 2013. [Google Scholar] [CrossRef][Green Version]
- Bukovsky, I.; Voracek, J.; Ichiji, K.; Noriyasu, H. Higher Order Neural Units for Efficient Adaptive Control of Weakly Nonlinear Systems. In Proceedings of the 9th International Joint Conference on Computational Intelligence; SciTePress—Science and Technology Publications: Setúbal, Portugal, 2017. [Google Scholar] [CrossRef]
- Haykin, S.S. Adaptive Filter Theory; Pearson Education India: Delhi, India, 2005. [Google Scholar]
- Mandic, D.P. A generalized normalized gradient descent algorithm. IEEE Signal Process. Lett. 2004, 11, 115–118. [Google Scholar] [CrossRef]
- Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Ma, J.; Perkins, S. Time-series novelty detection using one-class support vector machines. In Proceedings of the International Joint Conference on Neural Networks, 2003, Portland, OR, USA, 20–24 July 2003; Volume 3, pp. 1741–1745. [Google Scholar]
- Ma, J.; Perkins, S. Online novelty detection on temporal sequences. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 613–618. [Google Scholar]
- Limpert, E.; Stahel, W.A. Problems with Using the Normal Distribution—And Ways to Improve Quality and Efficiency of Data Analysis. PLoS ONE 2011, 6, e21403. [Google Scholar] [CrossRef]
- Pickands, J., III. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Balkema, A.A.; De Haan, L. Residual life time at great age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2013. [Google Scholar]
- Lee, H.J.; Roberts, S.J. On-line novelty detection using the Kalman filter and extreme value theory. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008. [Google Scholar] [CrossRef]
- Scarrott, C.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT-Stat. J. 2012, 10, 33–60. [Google Scholar]
- DuMouchel, W.H. Estimating the stable index α in order to measure tail thickness: A critique. Ann. Stat. 1983, 11, 1019–1031. [Google Scholar] [CrossRef]
- Ferreira, A.; de Haan, L.; Peng, L. On optimising the estimation of high quantiles of a probability distribution. Statistics 2003, 37, 401–434. [Google Scholar] [CrossRef]
- Loretan, M.; Phillips, P.C. Testing the covariance stationarity of heavy-tailed time series: An overview of the theory with applications to several financial datasets. J. Empir. Financ. 1994, 1, 211–248. [Google Scholar] [CrossRef]
- Spangenberg, M.; Calmettes, V.; Julien, O.; Tourneret, J.Y.; Duchateau, G. Detection of variance changes and mean value jumps in measurement noise for multipath mitigation in urban navigation. Navigation 2010, 57, 35–52. [Google Scholar] [CrossRef]
- L’Ecuyer, P. History of uniform random number generation. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 202–230. [Google Scholar]
- Maurya, M.R.; Rengaswamy, R.; Venkatasubramanian, V. Fault diagnosis using dynamic trend analysis: A review and recent developments. Eng. Appl. Artif. Intell. 2007, 20, 133–146. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Rodriguez-Bermudez, G.; Garcia-Laencina, P.J. Analysis of EEG signals using nonlinear dynamics and chaos: A review. Appl. Math. Inf. Sci. 2015, 9, 2309. [Google Scholar]
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing USA, 2006; Volume 1, Available online: https://ecs.wgtn.ac.nz/foswiki/pub/Support/ManualPagesAndDocumentation/numpybook.pdf (accessed on 11 January 2020).
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.bibsonomy.org/bibtex/21b37d2cc741af879d7958f2f7c23c420/microcuts (accessed on 11 January 2020).
- Cejnek, M. Padasip—Open source library for adaptive signal processing in language Python. In Studentská Tvůrčí činnost 2017; Department of Instrumentation and Control Engineering: Prague, Czech Rebpublic, 2017. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Mackey, M.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Likelihood moment estimation for the generalized Pareto distribution. Aust. N. Z. J. Stat. 2007, 49, 69–77. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, W.; Zhao, J.; Zhao, X. Parameter estimation for generalized Pareto distribution by generalized probability weighted moment-equations. Commun. Stat.-Simul. Comput. 2017, 46, 7761–7776. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Z.; Cheng, W.; Zhang, P. A New Parameter Estimator for the Generalized Pareto Distribution under the Peaks over Threshold Framework. Mathematics 2019, 7, 406. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrba, J.; Mareš, J. Introduction to Extreme Seeking Entropy. Entropy 2020, 22, 93. https://doi.org/10.3390/e22010093
Vrba J, Mareš J. Introduction to Extreme Seeking Entropy. Entropy. 2020; 22(1):93. https://doi.org/10.3390/e22010093
Chicago/Turabian StyleVrba, Jan, and Jan Mareš. 2020. "Introduction to Extreme Seeking Entropy" Entropy 22, no. 1: 93. https://doi.org/10.3390/e22010093
APA StyleVrba, J., & Mareš, J. (2020). Introduction to Extreme Seeking Entropy. Entropy, 22(1), 93. https://doi.org/10.3390/e22010093





