Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic
Abstract
1. Introduction
2. Unconditionally Secure Signature
2.1. Toeplitz Hash Message Authentication Code
- We map the first n elements of S into the first column of M, starting from the bottom to the top .
- We map the last elements of S into the first row of M, starting from the left to the right .
2.2. Toeplitz Group Signature
- 1.
- The set is the set of the communication participants including the signer , and the n potential receivers to . We assume that a proportion of δ participants are honest, where ;
- 2.
- is the set of possible messages of length ;
- 3.
- is the set of possible signatures of length ;
- 4.
- is a function that takes a message and outputs a signature . There are two stages for signing a message—the distribution stage and the signing stage:
- (a)
- The distribution stage:
- i.
- The sender randomly generates a bit strings . The length of every is . We use to denote the Toeplitz hash functions determined by these strings;
- ii.
- The sender securely sends to each recipient ;
- iii.
- Each receiver sends to every other receiver ;].
- (b)
- The signing stage: The signature for the message is defined as .
- 5.
- is a function that takes a message , a signature σ, and a participant and returns a Boolean value based on the validity of the signature, as verified by the participant .Formally, upon receiving a message/signature pair , where σ is a signature of the form , the receiver calculates the following test:and ifThat is, participant accepts the signature when more than of the tests are passed, where δ is the proportion of honest participants.
- Unforgeability: It is not possible for an adversary to create a valid signature with the probability higher than some negligible level;
- Transferability: If an honest receiver accepts a signature, then any other honest receiver would also accept the signature;
- Non-repudiation: It is not possible for a signer to repudiate a legitimate signature he has created with the probability higher than some negligible level.
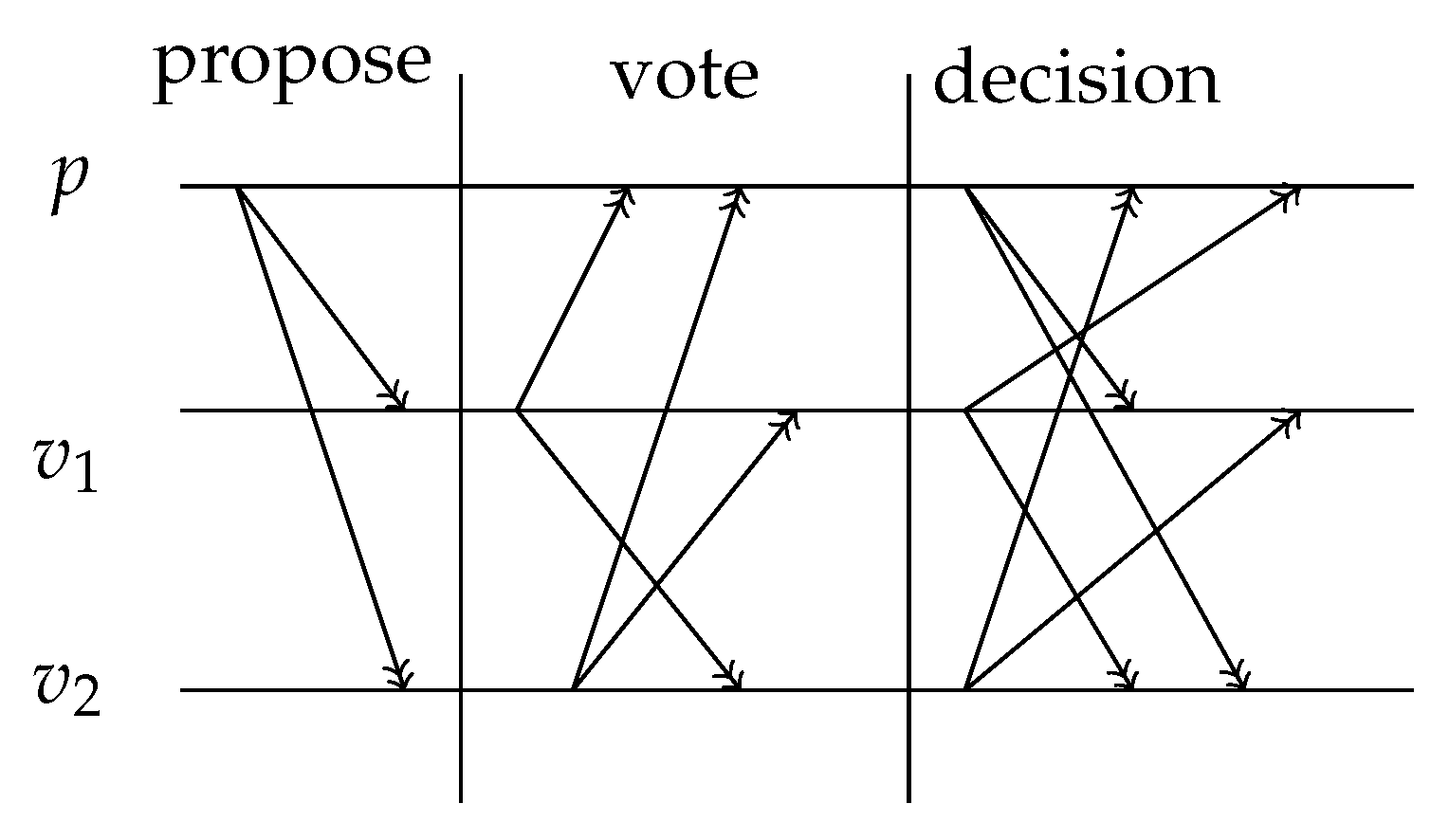
3. Quantum-Secured Consensus
3.1. The QSYAC Protocol
- The proposing phase. After checking the validity of signatures of transactions, the proposing peer generates a block proposal and sends it to voting peers. The block proposal contains an ordered list of transactions that will potentially be added to the blockchain in this round. The proposal is signed by the TGS scheme with the proposing peer being the sender and all voting peers as receivers;
- The voting phase. The proposal is sent to all voting peers. Voting peers enter the voting phase, during which they exchange votes across the network:
- (a)
- The voting peer calculates a verified proposal after it receives a proposal from the proposing peer. A verified proposal is a subset of transactions from the proposal, defined to be valid by the voting peer. The block, that is generated by a voting peer, consists of transactions from the verified proposal and the hash value (Here the hash function is a collision-resistant hash function, not a Toeplitz hash. We require the length of the hash value of this hash function to be the same as the length of hash value of the Toeplitz hash.) of the collection of those transactions;
- (b)
- The vote on the block generated by the voting peer is formed by a pair which contains the hash value of this block and the TGS of this hash value. In this TGS scheme, the voting peer is the sender and all other peers (including the proposing peer) are receivers;
- (c)
- When a peer votes for a block, it generates an order for all peers for the current round. The order is generated by a function that takes the hash value of the block as the input and returns an order for all peers as the output. An order function f is required to produce a uniformly distributed output. That is, for two orders of peers and , it holds that , where l is the length of the hash value and calculates the cardinality of a set.
- The decision phase. Votes for a block are sent to each peer in the specified order. Let the order be . Acceptance or rejection of a block is achieved by the following decision phase:
- (a)
- Let ;
- (b)
- All votes are sent to the peer ;
- (c)
- Supermajority is defined to be a number greater than of all peers in the network. When has collected a supermajority of votes for one block, this set of votes enables the creation of an accepting message for the block. broadcasts the accepting message to all peers. Every peer who receives this accepting message adds the block to its local blockchain, broadcasts the accepting message to all peers and this round ends.A rejecting message is created when Oi has not collected the supermajority of votes for any block. broadcasts the rejecting message in the same way as the accepting message. Every peer sends its vote to the peer if it receives a rejecting message or it did not receive an accepting message within a predefined waiting period.The decision procedure then continues with peer ;
- (d)
- If no accepting message is broadcast at the end the decision procedure, then this round ends with the block rejection and there is no update of the blockchain.
3.2. Evaluation: Correctness, Scalability, and Security
3.2.1. Correctness
- If is honest, then will collect a supermajority of votes, generate an accepting message, and send it to all peers. This means every honest peer will receive an accepting message and add the same block to its blockchain;
- If is dishonest, since cannot counterfeit other peers’ vote, it cannot create a rejecting message. Now, another damaged can cause it to not send any message to other peers. There are two possible situations:
- (a)
- No honest peer receives an accepting message from . Then after the pre-defined waiting period all honest peers will send their votes to . As long as is honest, then all honest peers will make the same update of their blockchain.
- (b)
- Some honest peers receive an accepting message from . Assume is an honest peer who receives an accepting message. Since will broadcast the accepting message, all honest peers will receive the accepting message.
To sum up, all honest peers will receive an accepting message and add the same block to its blockchain even if is dishonest.
3.2.2. Scalability
3.2.3. Security
4. Script Language and Smart Contracts for Logicontract
- Logical contracts are often more compact than their procedural counterparts. This is because writing procedural contracts forces the programmer to write explicitly what has to be done and how to do it; while in the logical contracts the programmer only needs to write down what has to be done, without specifying how to achieve it.
- Writing contracts in a procedural language is error prone [46] since the order of instructions affects the correctness of the resulting contract, while logical contracts can be seen as a set of specifications, and the contracts are guaranteed to be correct with respect to the specifications.
- It is easier to formally verify a logical contract than to verify a procedural contract. To verify a procedural contract, a common technique is to construct a formal calculus with rigorous semantics and translate the procedural contract to expressions of the formal calculus [41,47]. Since logic by itself is a formal calculus, the verification of logical contracts is relatively easier.
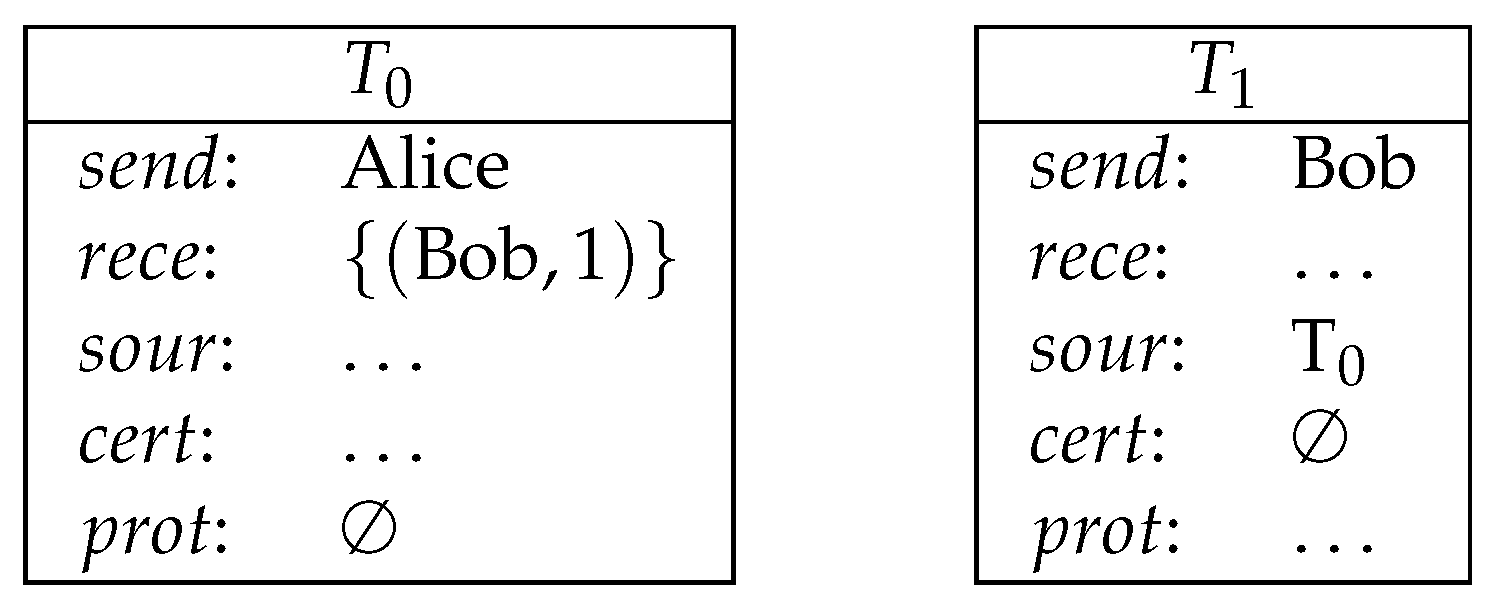
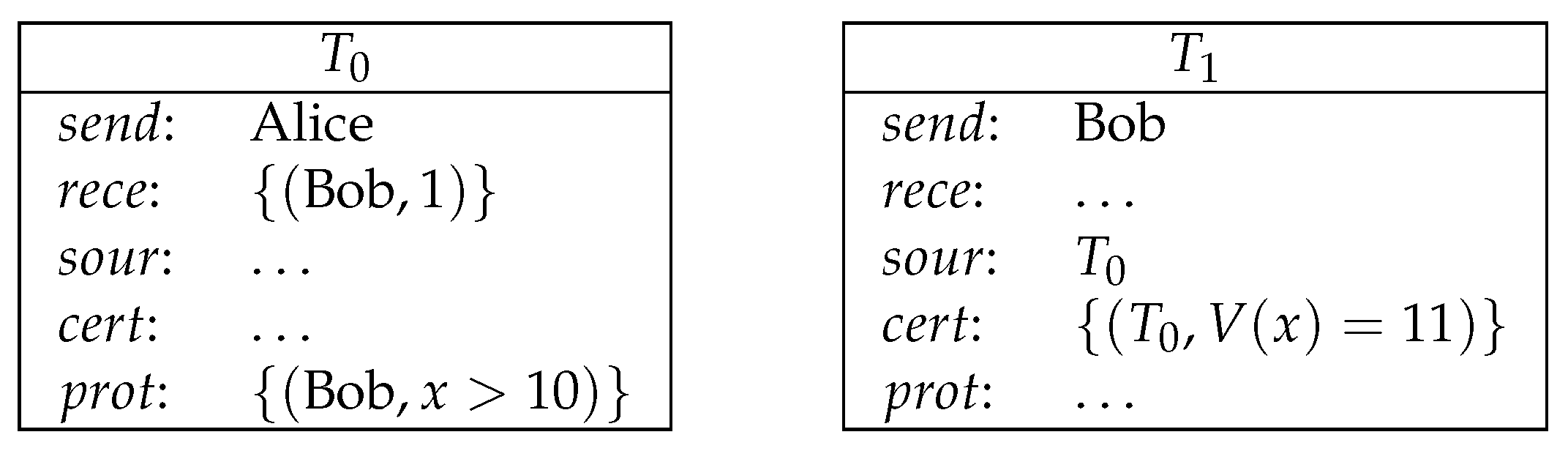
- is the sender of this transaction;
- rece is the set of receivers of this transaction and the amount of the currency they will receive. Formally, ;
- is the source, which is a list of transactions to be redeemed by T;
- is the , which is a list of formulas. The number of formulas must be the same as the number of receivers. Formally, . If a receiver wants to redeem T, then has to make true by providing appropriate certifications;
- is the certification, which is a list of valuation functions that map variables to natural numbers. The functionality of certifications is to satisfy the protection of the source transactions. The number of valuations must be the same as the number of the source transactions. Formally, .
- T is properly signed by its sender;
- The sender of T is one of the receivers in each of its source transactions;
- The certification of T evaluates the protections of all its source to be true;
- None of its source transaction has been redeemed.
5. Application: A Lottery Protocol on Logicontract
- Randomness. All tickets are equally likely to win;
- Unpredictability. No player can predict the winning ticket;
- Unforgeability. Tickets cannot be forged. Especially, it is impossible to create a winning ticket after the outcome of the random process is known;
- Verifiablity. The number and the revenue of winning tickets are publicly verifiable;
- Decentralization. The random process does not rely on a single authority.
- 6.
- Quantum resistance. Even an adversary with a realistic quantum computer cannot rig the lottery.
- 2.
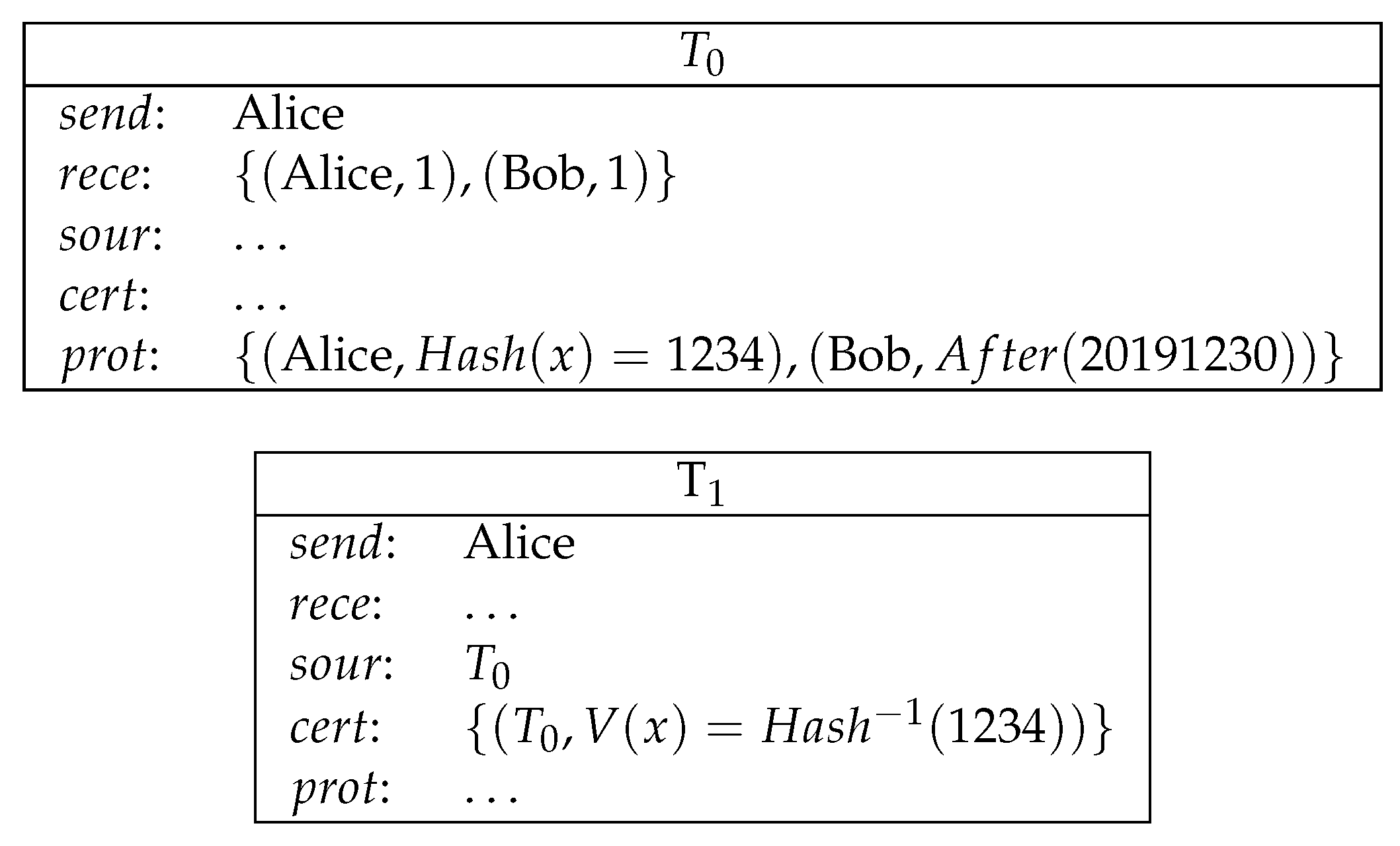
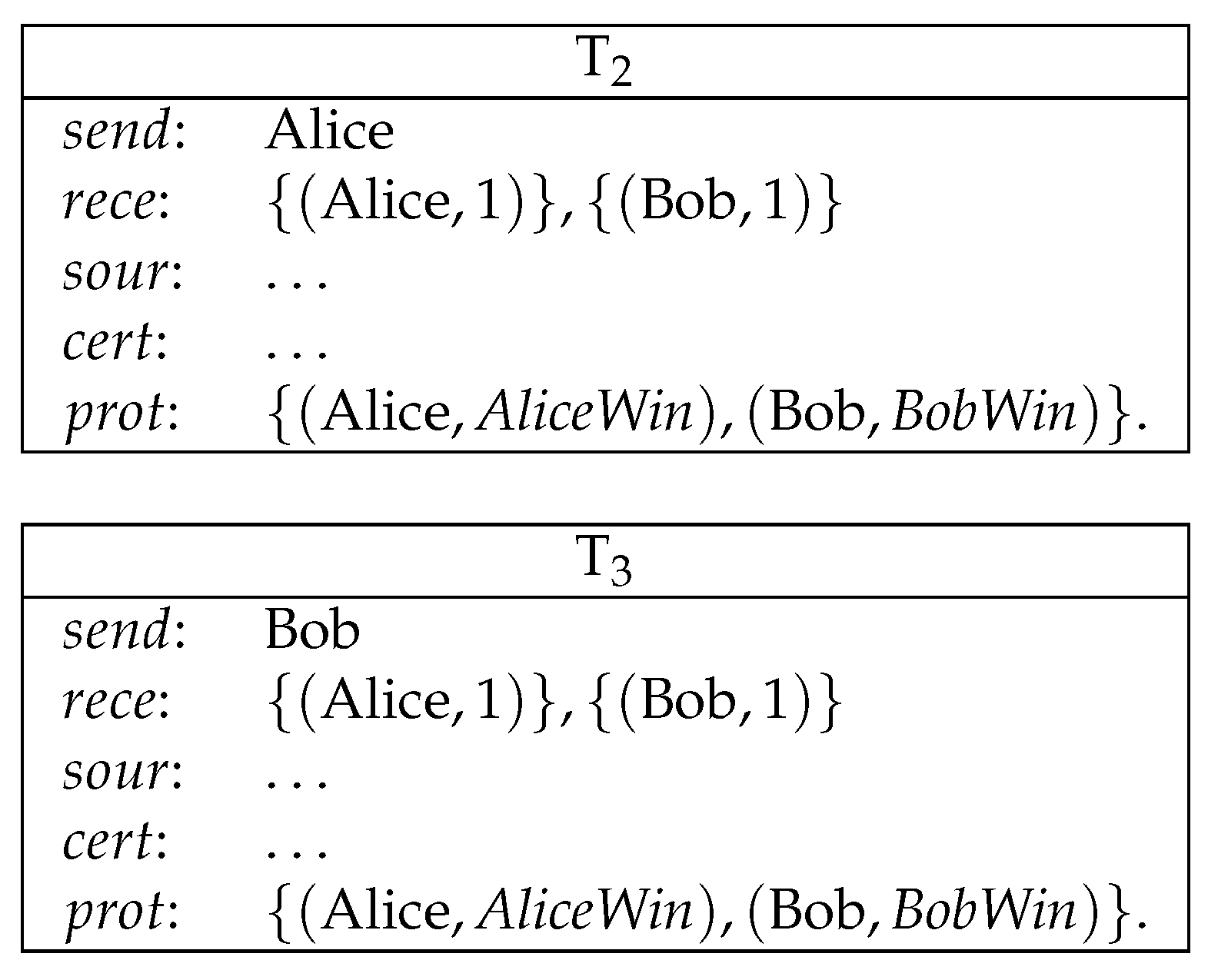
- Alice sends a conditional transfer to Alice and Bob. Bob sends a conditional transfer to Alice and Bob (see Figure 7).Here, AliceWin is specified by . BobWin is specified by .
- 3.
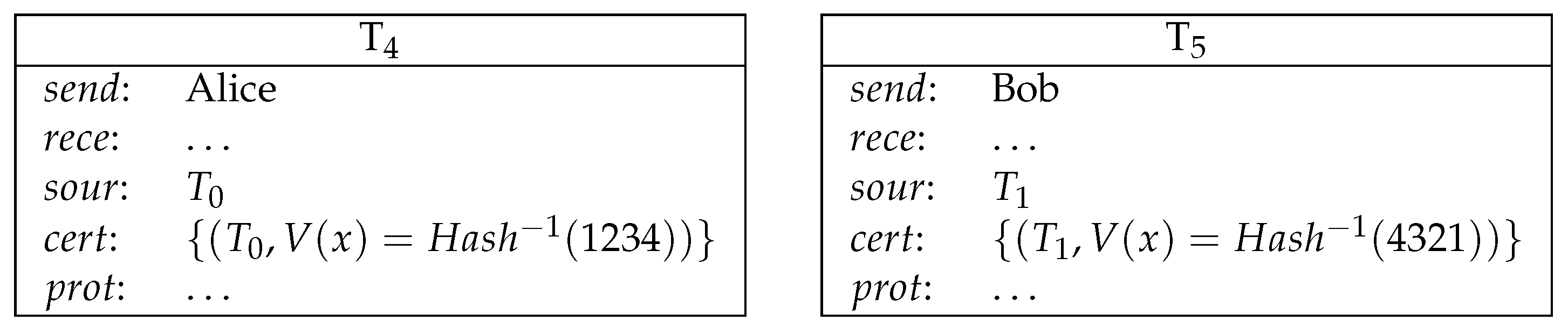
- Alice reveals her secret and gets her deposit back. Bob reveals his secret and gets his deposit back (see Figure 8).
- 4.
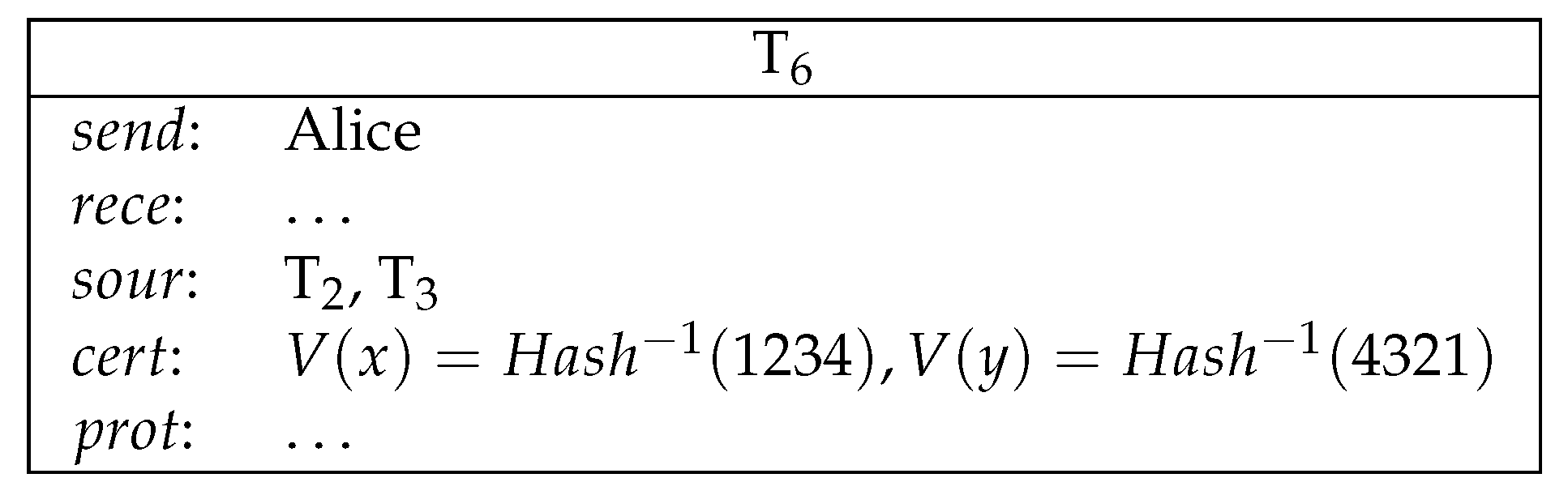
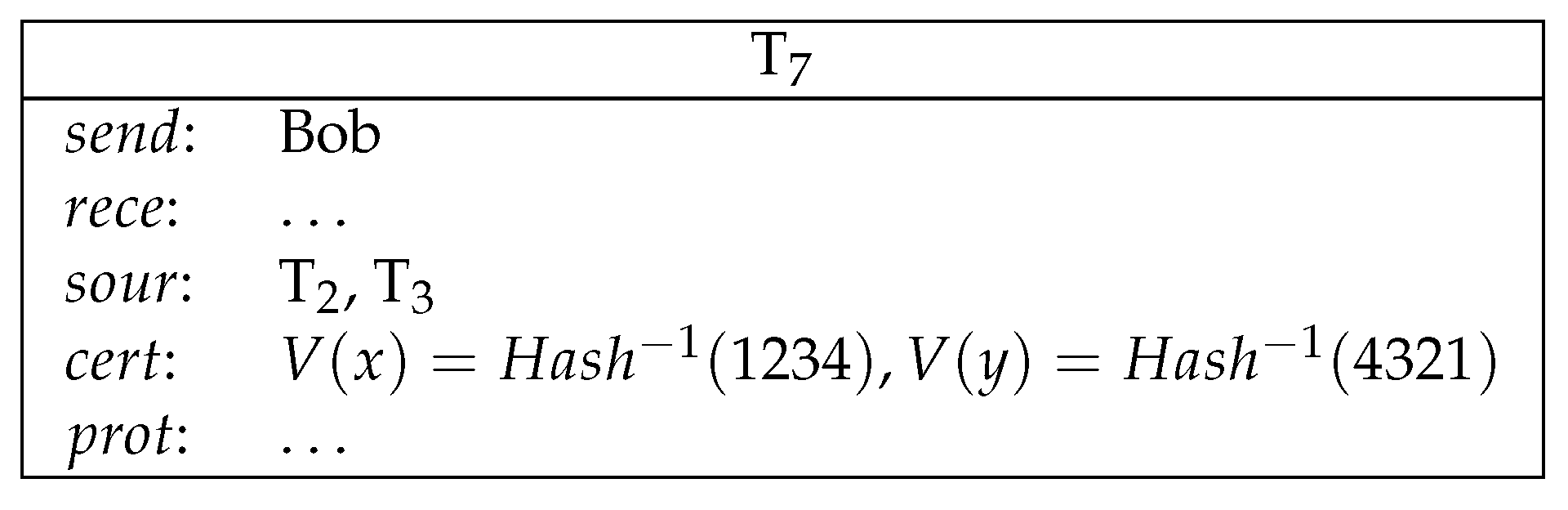
- Now both Alice and Bob’s secrets are public and the winner can be determined. The winner redeems the loser’s conditional transfer and his/her own conditional transfer. If Alice is the winner, then she redeems and (see Figure 9).If Bob is the winner, then he redeems and (see Figure 10).
6. Related Work
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 July 2019).
- Szabo, N. The Idea of Smart Contracts; The George Washington University Law School: Washington, DC, USA, 1997. [Google Scholar]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Mosca, M. Cybersecurity in an Era with Quantum Computers: Will We Be Ready? IEEE Secur. Priv. 2018, 16, 38–41. [Google Scholar] [CrossRef]
- Fedorov, A.K.; Kiktenko, E.O.; Lvovsky, A.I. Quantum computers put blockchain security at risk. Nature 2018, 563, 465–467. [Google Scholar] [CrossRef] [PubMed]
- Stewart, I.; Ilie, D.; Zamyatin1, A.; Werner, S.; Torshizi, M.; Knottenbelt, W. Committing to quantum resistance: A slow defence for Bitcoin against a fast quantum computing attack. R. Soc. Open Sci. 2018, 5, 180410. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Chen, X.; Chen, Y.; Sun, Y.; Niu, X.; Yang, Y. A Secure Cryptocurrency Scheme Based on Post-Quantum Blockchain. IEEE Access 2018, 6, 27205–27213. [Google Scholar] [CrossRef]
- Li, C.; Chen, X.; Chen, Y.; Hou, Y.; Li, J. A New Lattice-Based Signature Scheme in Post-Quantum Blockchain Network. IEEE Access 2019, 7, 2026–2033. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Pozhar, N.O.; Anufriev, M.N.; Trushechkin, A.S.; Yunusov, R.R.; Kurochkin, Y.V.; Lvovsky, A.I.; Fedorov, A.K. Quantum-secured blockchain. Quantum Sci. Technol. 2018, 3, 035004. [Google Scholar] [CrossRef]
- Aggarwal, D.; Brennen, G.; Lee, T.; Santha, M.; Tomamichel, M. Quantum Attacks on Bitcoin, and How to Protect Against Them. Ledger 2018, 3. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Q.; Kulicki, P.; Sopek, M. A Simple Voting Protocol on Quantum Blockchain. Int. J. Theor. Phys. 2019, 58, 275–281. [Google Scholar] [CrossRef]
- Pease, M.C.; Shostak, R.E.; Lamport, L. Reaching Agreement in the Presence of Faults. J. ACM 1980, 27, 228–234. [Google Scholar] [CrossRef]
- Muratov, F.; Lebedev, A.; Iushkevich, N.; Nasrulin, B.; Takemiya, M. YAC: BFT Consensus Algorithm for Blockchain. arXiv 2018, arXiv:1809.00554. [Google Scholar]
- Zou, X.; Qiu, D. Arbitrated Quantum Signature Schemes: Attacks and Security. In Frontiers in Algorithmics and Algorithmic Aspects in Information and Management; Fellows, M., Tan, X., Zhu, B., Eds.; Springer: Berlin, Germany, 2013; pp. 48–59. [Google Scholar]
- Zou, X.; Qiu, D. Attack and improvements of fair quantum blind signature schemes. Quantum Inf. Process. 2013, 12, 2071–2085. [Google Scholar] [CrossRef]
- Zou, X.; Qiu, D.; Mateus, P. Security Analyses and Improvement of Arbitrated Quantum Signature with an Untrusted Arbitrator. Int. J. Theor. Phys. 2013, 52, 3295–3305. [Google Scholar] [CrossRef]
- Zou, X.; Qiu, D.; Yu, F.; Mateus, P. Security Problems in the Quantum Signature Scheme with a Weak Arbitrator. Int. J. Theor. Phys. 2014, 53, 603–611. [Google Scholar] [CrossRef]
- Amiri, R.; Andersson, E. Unconditionally Secure Quantum Signatures. Entropy 2015, 17, 5635–5659. [Google Scholar] [CrossRef]
- Wallden, P.; Dunjko, V.; Kent, A.; Andersson, E. Quantum digital signatures with quantum-key-distribution components. Phys. Rev. A 2015, 91, 042304. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Wallden, P.; Andersson, E. Multiparty quantum signature schemes. Quantum Inf. Comput. 2016, 16, 435–464. [Google Scholar]
- Zhang, W.; Qiu, D.; Zou, X. Improvement of a quantum broadcasting multiple blind signature scheme based on quantum teleportation. Quantum Inf. Process. 2016, 15, 2499–2519. [Google Scholar] [CrossRef]
- Zhang, W.; Qiu, D.; Zou, X.; Mateus, P. Analyses and improvement of a broadcasting multiple blind signature scheme based on quantum GHZ entanglement. Quantum Inf. Process. 2017, 16, 150. [Google Scholar] [CrossRef]
- Amiri, R.; Abidin, A.; Wallden, P.; Andersson, E. Efficient Unconditionally Secure Signatures Using Universal Hashing. In Proceedings of the 16th International Conference on Applied Cryptography and Network Security (ACNS), Leuven, Belgium, 2–4 July 2018; pp. 143–162. [Google Scholar] [CrossRef]
- Carter, L.; Wegman, M.N. Universal Classes of Hash Functions. J. Comput. Syst. Sci. 1979, 18, 143–154. [Google Scholar] [CrossRef]
- Wegman, M.N.; Carter, L. New Hash Functions and Their Use in Authentication and Set Equality. J. Comput. Syst. Sci. 1981, 22, 265–279. [Google Scholar] [CrossRef]
- Brassard, G. On Computationally Secure Authentication Tags Requiring Short Secret Shared Keys. In Proceedings of the Advances in Cryptology: Proceedings of CRYPTO ’82, Santa Barbara, CA, USA, 23–25 August 1982; Chaum, D., Rivest, R.L., Sherman, A.T., Eds.; Plenum Press: New York, NY, USA, 1982; pp. 79–86. [Google Scholar]
- Desmedt, Y. Unconditionally Secure Authentication Schemes and Practical and Theoretical Consequences. In Proceedings of the Advances in Cryptology—CRYPTO ’85, Santa Barbara, CA, USA, 18–22 August 1985; Williams, H.C., Ed.; Springer: Berlin, Germany, 1985; Volume 218, pp. 42–55. [Google Scholar] [CrossRef]
- Krawczyk, H. LFSR-based Hashing and Authentication. In Proceedings of the 14th Annual International Cryptology Conference, Advances in Cryptology (CRYPTO ’94), Santa Barbara, CA, USA, 21–25 August 1994; Desmedt, Y., Ed.; Springer: Berlin, Germany, 1994; Volume 839, pp. 129–139. [Google Scholar] [CrossRef]
- Krawczyk, H. New Hash Functions For Message Authentication. In Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, Advances in Cryptology (EUROCRYPT ’95), Saint-Malo, France, 21–25 May 1995; Guillou, L.C., Quisquater, J., Eds.; Springer: Berlin, Germany, 1995; Volume 921, pp. 301–310. [Google Scholar] [CrossRef]
- Abidin, A.; Larsson, J. Direct proof of security of Wegman-Carter authentication with partially known key. Quantum Inf. Process. 2014, 13, 2155–2170. [Google Scholar] [CrossRef]
- Dianati, M.; Alléaume, R.; Gagnaire, M.; Shen, X. Architecture and protocols of the future European quantum key distribution network. Secur. Commun. Netw. 2008, 1, 57–74. [Google Scholar] [CrossRef]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.F.; et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef]
- Tajima, A.; Kondoh, T.; Ochi, T.; Fujiwara, M.; Yoshino, K.; Iizuka, H.; Sakamoto, T.; Tomita, A.; Shimamura, E.; Asami, S.; et al. Quantum key distribution network for multiple applications. Quantum Sci. Technol. 2017, 2, 034003. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Ren, J.G.; Liao, S.K.; Zhang, L.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-to-Ground Entanglement-Based Quantum Key Distribution. Phys. Rev. Lett. 2017, 119, 200501. [Google Scholar] [CrossRef]
- Razavi, M. An Introduction to Quantum Communications Networks; Morgan and Claypool Publishers: San Rafael, CA, USA, 2018. [Google Scholar]
- Nguyen, G.; Kim, K. A Survey about Consensus Algorithms Used in Blockchain. JIPS 2018, 14, 101–128. [Google Scholar] [CrossRef]
- Lamport, L.; Shostak, R.E.; Pease, M.C. The Byzantine Generals Problem. ACM Trans. Program. Lang. Syst. 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical Byzantine Fault Tolerance. In Proceedings of the Third USENIX Symposium on Operating Systems Design and Implementation (OSDI), New Orleans, LA, USA, 22–25 February 1999; Seltzer, M.I., Leach, P.J., Eds.; USENIX Association: Berkeley, CA, USA, 1999; pp. 173–186. [Google Scholar]
- Bessani, A.N.; Sousa, J.; Alchieri, E.A.P. State Machine Replication for the Masses with BFT-SMART. In Proceedings of the 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN 2014), Atlanta, GA, USA, 23–26 June 2014; pp. 355–362. [Google Scholar] [CrossRef]
- Abraham, I.; Malkhi, D.; Nayak, K.; Ren, L.; Spiegelman, A. Solida: A Blockchain Protocol Based on Reconfigurable Byzantine Consensus. In Proceedings of the 21st International Conference on Principles of Distributed Systems (OPODIS 2017), Lisbon, Portugal, 18–20 December 2017; Aspnes, J., Bessani, A., Felber, P., Leitão, J., Eds.; Schloss Dagstuhl: Wadern, Germany, 2017; Volume 95, pp. 25:1–25:19. [Google Scholar] [CrossRef]
- Atzei, N.; Bartoletti, M.; Cimoli, T.; Lande, S.; Zunino, R. SoK: Unraveling Bitcoin Smart Contracts. In Proceedings of the 7th International Conference on Principles of Security and Trust, European Joint Conferences on Theory and Practice of Software, Thessaloniki, Greece, 14–20 April 2018; Bauer, L., Küsters, R., Eds.; Springer: Berlin, Germany, 2018; Volume 10804, pp. 217–242. [Google Scholar]
- Bartoletti, M.; Cimoli, T.; Zunino, R. Fun with Bitcoin Smart Contracts. In Proceedings of the 8th International Symposium on Leveraging Applications of Formal Methods, Verification and Validation. Industrial Practice (ISoLA 2018), Limassol, Cyprus, 5–9 November 2018; Margaria, T., Steffen, B., Eds.; Springer: Berlin, Germany, 2018; Volume 11247, pp. 432–449. [Google Scholar] [CrossRef]
- Bartoletti, M.; Zunino, R. BitML: A Calculus for Bitcoin Smart Contracts. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS 2018), Toronto, ON, Canada, 15–19 October 2018; Lie, D., Mannan, M., Backes, M., Wang, X., Eds.; ACM: New York, NY, USA, 2018; pp. 83–100. [Google Scholar] [CrossRef]
- Bartoletti, M.; Cimoli, T.; Giamberardino, P.D.; Zunino, R. Vicious circles in contracts and in logic. Sci. Comput. Program. 2015, 109, 61–95. [Google Scholar] [CrossRef]
- Governatori, G.; Idelberger, F.; Milosevic, Z.; Riveret, R.; Sartor, G.; Xu, X. On legal contracts, imperative and declarative smart contracts, and blockchain systems. Artif. Intell. Law 2018, 26, 377–409. [Google Scholar] [CrossRef]
- Atzei, N.; Bartoletti, M.; Cimoli, T. A Survey of Attacks on Ethereum Smart Contracts (SoK). In Proceedings of the 6th International Conference Principles of Security and Trust (POST 2017), Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017, Uppsala, Sweden, 22–29 April 2017; Maffei, M., Ryan, M., Eds.; Springer: Berlin, Germany, 2017; Volume 10204, pp. 164–186. [Google Scholar] [CrossRef]
- Grishchenko, I.; Maffei, M.; Schneidewind, C. A Semantic Framework for the Security Analysis of Ethereum Smart Contracts. In Proceedings of the International Conference on Principles of Security and Trust, Thessaloniki, Greece, 16–19 April 2018; Bauer, L., Küsters, R., Eds.; Springer: Berlin, Germany, 2018; Volume 10804, pp. 243–269. [Google Scholar]
- Isidore, C. Americans Spend More on the Lottery than on... Available online: https://money.cnn.com/2015/02/11/news/companies/lottery-spending/ (accessed on 1 July 2019).
- Chow, S.S.M.; Hui, L.C.K.; Yiu, S.; Chow, K.P. An e-Lottery Scheme Using Verifiable Random Function. In Proceedings of the International Conference Computational Science and Its Applications (ICCSA 2005), Singapore, 9–12 May 2005; Gervasi, O., Gavrilova, M.L., Kumar, V., Laganà, A., Lee, H.P., Mun, Y., Taniar, D., Tan, C.J.K., Eds.; Springer: Berlin, Germany, 2005; Volume 3482, pp. 651–660. [Google Scholar] [CrossRef]
- Bentov, I.; Kumaresan, R. How to Use Bitcoin to Design Fair Protocols. In Proceedings of the 34th Annual Cryptology Conference in Advances in Cryptology (CRYPTO 2014), Santa Barbara, CA, USA, 17–21 August 2014; Garay, J.A., Gennaro, R., Eds.; Springer: Berlin, Germany, 2014; Volume 8617, pp. 421–439. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Dziembowski, S.; Malinowski, D.; Mazurek, L. Secure Multiparty Computations on Bitcoin. In Proceedings of the IEEE Symposium on Security and Privacy, SP 2014, Berkeley, CA, USA, 18–21 May 2014; pp. 443–458. [Google Scholar] [CrossRef]
- Bartoletti, M.; Zunino, R. Constant-Deposit Multiparty Lotteries on Bitcoin. In Proceedings of the International Workshops on Financial Cryptography and Data Security, FC, WAHC, BITCOIN, VOTING, WTSC, and TA, Sliema, Malta, 7 April 2017; Brenner, M., Rohloff, K., Bonneau, J., Miller, A., Ryan, P.Y.A., Teague, V., Bracciali, A., Sala, M., Pintore, F., Jakobsson, M., Eds.; Springer: Berlin, Germany, 2017; Volume 10323, pp. 231–247. [Google Scholar] [CrossRef]
- Grumbach, S.; Riemann, R. Distributed Random Process for a Large-Scale Peer-to-Peer Lottery. In Distributed Applications and Interoperable Systems; Chen, L.Y., Reiser, H.P., Eds.; Springer: Cham, Switzerland, 2017; pp. 34–48. [Google Scholar]
- Miller, A.; Bentov, I. Zero-Collateral Lotteries in Bitcoin and Ethereum. In Proceedings of the IEEE European Symposium on Security and Privacy Workshops (EuroS&P Workshops), Paris, France, 26–28 April 2017; pp. 4–13. [Google Scholar] [CrossRef]
- Goldenberg, L.; Vaidman, L.; Wiesner, S. Quantum Gambling. Phys. Rev. Lett. 1999, 82, 3356–3359. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Rudolph, T. Quantum Protocol for Cheat-Sensitive Weak Coin Flipping. Phys. Rev. Lett. 2002, 89, 227901. [Google Scholar] [CrossRef] [PubMed]
- Nayak, A.; Shor, P. Bit-commitment-based quantum coin flipping. Phys. Rev. A 2003, 67, 012304. [Google Scholar] [CrossRef]
- Ambainis, A.; Buhrman, H.; Dodis, Y.; Rohrig, H. Multiparty Quantum Coin Flipping. In Proceedings of the 19th IEEE Annual Conference on Computational Complexity (CCC ’04), Amherst, MA, USA, 21–24 June 2004; pp. 250–259. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Frison, J.; Huy, K.P.; Massar, S. Experimental quantum tossing of a single coin. New J. Phys. 2008, 10, 083037. [Google Scholar] [CrossRef]
- Silman, J.; Chailloux, A.; Aharon, N.; Kerenidis, I.; Pironio, S.; Massar, S. Fully Distrustful Quantum Bit Commitment and Coin Flipping. Phys. Rev. Lett. 2011, 106, 220501. [Google Scholar] [CrossRef] [PubMed]
- Hänggi, E.; Wullschleger, J. Tight Bounds for Classical and Quantum Coin Flipping. In Theory of Cryptography; Ishai, Y., Ed.; Springer: Berlin, Germany, 2011; pp. 468–485. [Google Scholar]
- Nayak, A.; Sikora, J.; Tunçel, L. A search for quantum coin-flipping protocols using optimization techniques. Math. Program. 2016, 156, 581–613. [Google Scholar] [CrossRef]
- Quantique. Available online: https://www.idquantique.com/ (accessed on 1 July 2019).


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Sopek, M.; Wang, Q.; Kulicki, P. Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic. Entropy 2019, 21, 887. https://doi.org/10.3390/e21090887
Sun X, Sopek M, Wang Q, Kulicki P. Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic. Entropy. 2019; 21(9):887. https://doi.org/10.3390/e21090887
Chicago/Turabian StyleSun, Xin, Mirek Sopek, Quanlong Wang, and Piotr Kulicki. 2019. "Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic" Entropy 21, no. 9: 887. https://doi.org/10.3390/e21090887
APA StyleSun, X., Sopek, M., Wang, Q., & Kulicki, P. (2019). Towards Quantum-Secured Permissioned Blockchain: Signature, Consensus, and Logic. Entropy, 21(9), 887. https://doi.org/10.3390/e21090887




