Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation–Projection Pursuit
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site
2.2. Crop Management
2.3. Irrigation Scheme Design
2.4. Measurements
2.5. Irrigation Scheme Decision-Making Model
3. Results and Discussion
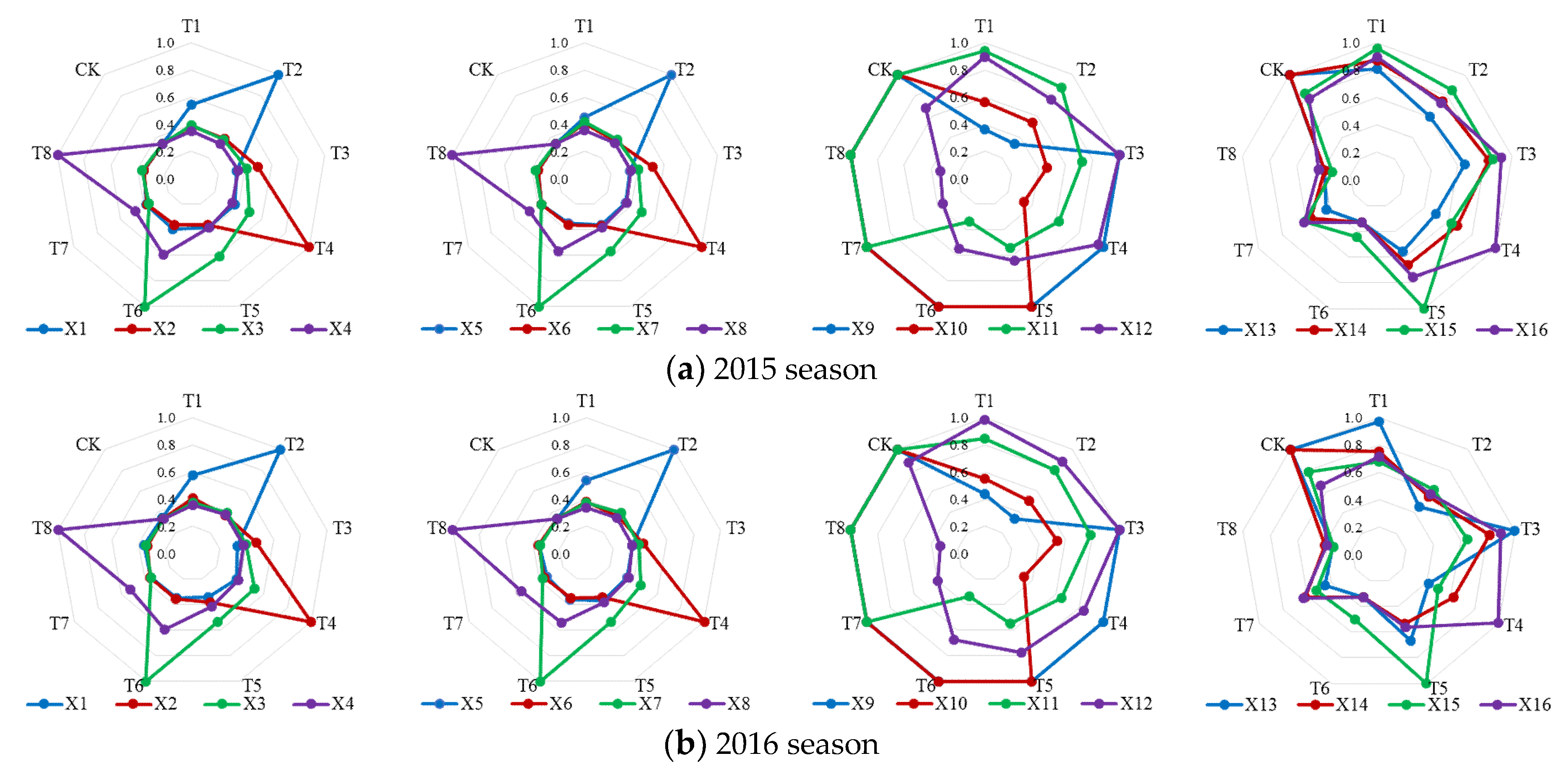
3.1. Irrigation Scheme Decision-Making Index Values
3.2. Grey Relation Coefficient of Each Decision-Making Index
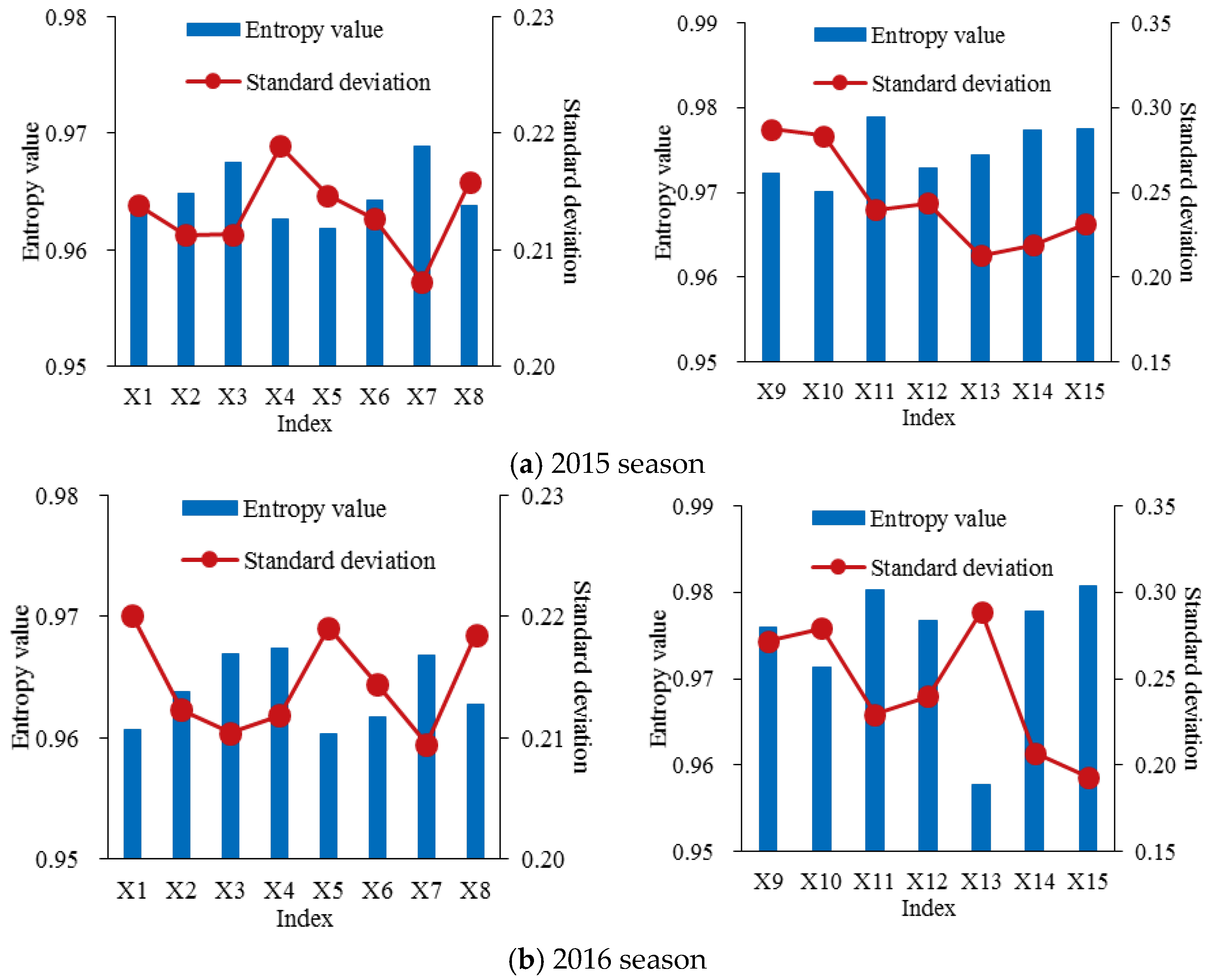
3.3. Grey Entropy Weight of Each Decision-Making Index
3.3.1. Weight of Each Decision-Making Subsystem
3.3.2. Weight of Each Decision-Making Index in the Respective Subsystem
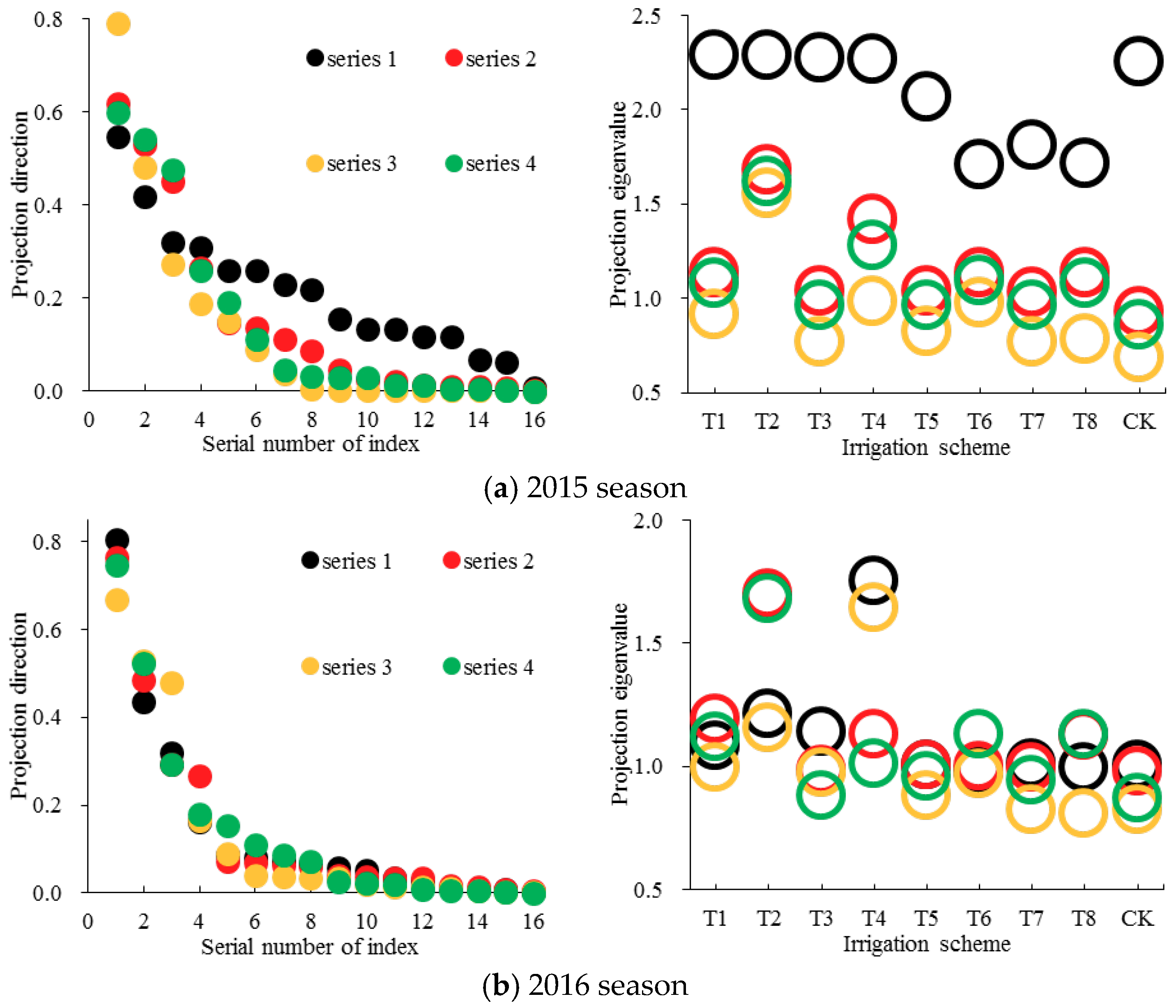
3.4. Grey Relation Projection Weight of Each Decision-Making Index
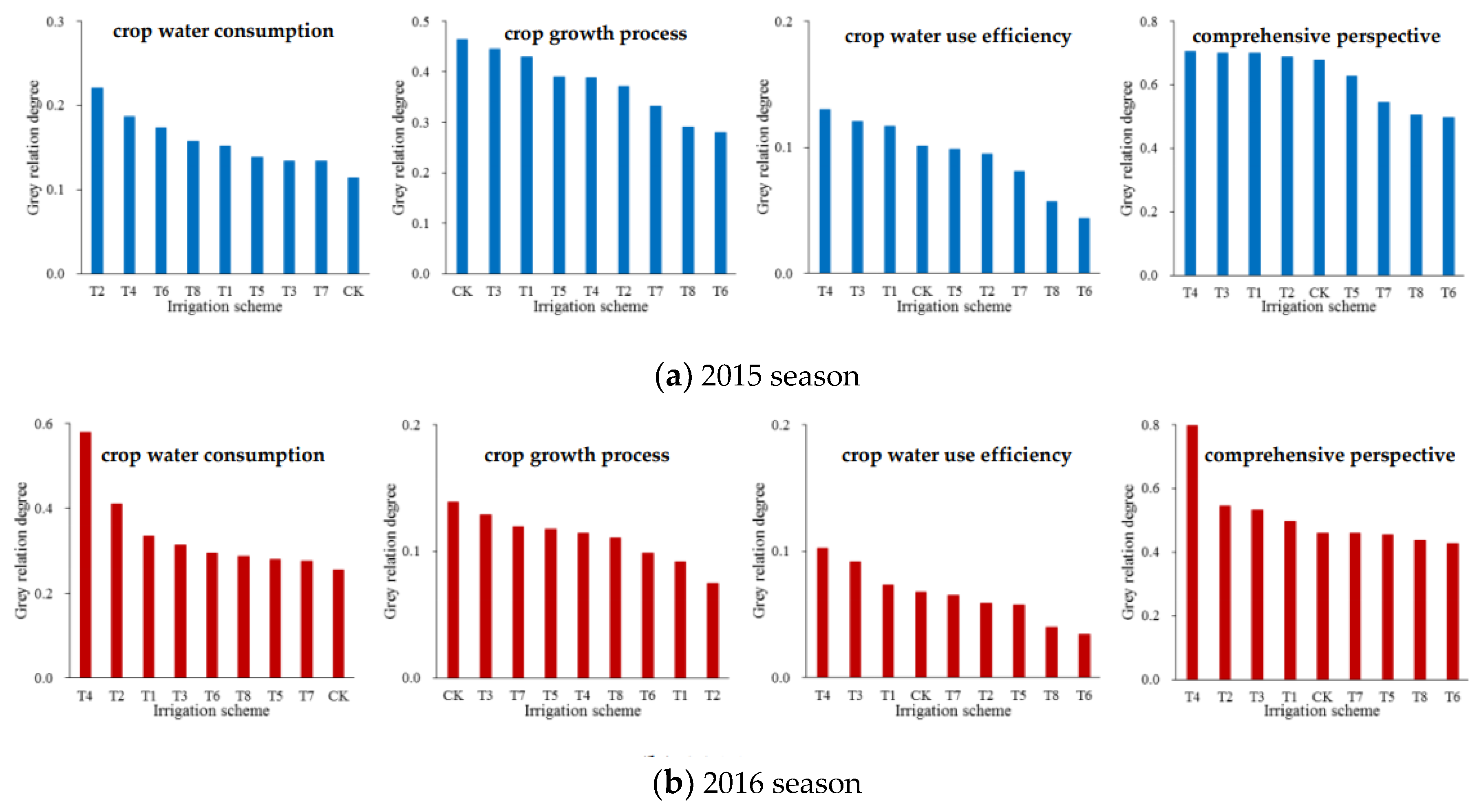
3.5. Decision-Making Results of Irrigation Scheme for Soybeans in the Huaibei Plain
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, X.B.; Jin, H.; Wang, G.H.; Herbert, S.J. Soybean yield physiology and development of high-yielding practices in Northeast China. Field Crops Res. 2008, 105, 157–171. [Google Scholar] [CrossRef]
- Wei, Z.; Paredes, P.; Liu, Y.; Chi, W.W.; Pereira, L.S. Modelling transpiration, soil evaporation and yield prediction of soybean in North China Plain. Agric. Water Manag. 2015, 147, 43–53. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, S.M.; Jin, J.L.; Ning, S.W.; Feng, P. Quantitative assessment of soybean drought loss sensitivity at different growth stages based on S-shaped damage curve. Agric. Water Manag. 2019, 213, 821–832. [Google Scholar] [CrossRef]
- Wei, Y.Q.; Jin, J.L.; Jiang, S.M.; Ning, S.W.; Cui, Y.; Zhou, Y.L. Simulated assessment of summer maize drought loss sensitivity in Huaibei Plain, China. Agronomy 2019, 9, 78. [Google Scholar] [CrossRef]
- Fontaine, M.M.; Steinemann, A.C. Assessing vulnerability to natural hazards: Impact-based method and application to drought in Washington State. Nat. Hazards Rev. 2009, 10, 11–18. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Aragues, R.; Medina, E.T.; Claveria, I.; Martinez-Cob, A.; Faci, J. Regulated deficit irrigation, soil salinization and soil sodification in a table grape vineyard drip-irrigated with moderately saline waters. Agric. Water Manag. 2014, 134, 84–93. [Google Scholar] [CrossRef] [Green Version]
- Mounzer, O.; Pedrero-Salcedo, F.; Nortes, P.A.; Bayona, J.M.; Nicolas-Nicolas, E.; Alarcon, J.J. Transient soil salinity under the combined effect of reclaimed water and regulated deficit drip irrigation of Mandarin trees. Agric. Water Manag. 2013, 120, 23–29. [Google Scholar] [CrossRef]
- Zhao, W.X.; Li, J.S.; Li, Y.F.; Yin, J.F. Effects of drip system uniformity on yield and quality of Chinese cabbage heads. Agric. Water Manag. 2012, 110, 118–128. [Google Scholar] [CrossRef]
- Chalmers, D.J.; Van den Ende, B. Productivity of peach trees: Factors affecting dry weight distribution during tree growth. Ann. Bot. 1975, 39, 423–432. [Google Scholar] [CrossRef]
- Rosadi, R.B.; Senge, M.; Ito, K.; Adomako, J.T. The effect of water stress in regulated deficit irrigation on soybean yield (Glycine max[L.] Merr.). Paddy Water Environ. 2007, 5, 163–169. [Google Scholar] [CrossRef]
- Sincik, M.; Candogan, B.N.; Demirtas, C.; Buyukcangaz, H.; Yazgan, S.; Goksoy, A.T. Deficit irrigation of soya bean [Glycine max (L.) Merr.] in a sub-humid climate. J. Agron. Crop Sci. 2008, 194, 200–205. [Google Scholar] [CrossRef]
- Dogan, E.; Kirnak, H.; Copur, O. Deficit irrigations during soybean reproductive stages and CROPGRO-soybean simulations under semi-arid climatic conditions. Field Crops Res. 2007, 103, 154–159. [Google Scholar] [CrossRef]
- Mondani, F.; Khani, K.; Honarmand, S.J.; Saeidi, M. Evaluating effects of plant growth-promoting rhizobacteria on the radiation use efficiency and yield of soybean (Glycine max) under water deficit stress condition. Agric. Water Manag. 2019, 213, 707–713. [Google Scholar] [CrossRef]
- Montoya, F.; Garcia, C.; Pintos, F.; Otero, A. Effects of irrigation regime on the growth and yield of irrigated soybean in temperate humid climatic conditions. Agric. Water Manag. 2017, 193, 30–45. [Google Scholar] [CrossRef]
- Gajic, B.; Kresovic, B.; Tapanarova, A.; Zivotic, L.; Todorovic, M. Effect of irrigation regime on yield, harvest index and water productivity of soybean grown under different precipitation conditions in a temperate environment. Agric. Water Manag. 2018, 210, 224–231. [Google Scholar] [CrossRef]
- Jha, P.K.; Kumar, S.N.; Ines, A.V.M. Responses of soybean to water stress and supplemental irrigation in upper Indo-Gangetic Plain. Field Crops Res. 2018, 219, 76–86. [Google Scholar] [CrossRef]
- Li, Q.S.; Willardson, L.S.; Deng, W.; Li, X.J.; Liu, C.J. Crop water deficit estimation and irrigation schedule in western Jilin Province. Agric. Water Manag. 2005, 71, 47–60. [Google Scholar] [CrossRef]
- Memmah, M.M.; Lescourret, F.; Yao, X.; Lavigne, C. Metaheuristics for agricultural land use optimization. A review. Agron. Sustain. Dev. 2015, 35, 975–998. [Google Scholar] [CrossRef] [Green Version]
- Singh, T.; Patnaik, A.; Chauhan, R. Optimization of tribological properties of cement kiln dust-filled brake pad using grey relation analysis. Mater. Des. 2016, 89, 1335–1342. [Google Scholar] [CrossRef]
- Lee, C.; Lee, J.W.; Ryu, S.G.; Oh, J.H. Optimum design of a large area, flexure based XY theta mask alignment stage for a 12-inch wafer using grey relation analysis. Robot. Comput.-Integr. Manuf. 2019, 58, 109–119. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.Q.; Zhang, H.Y. Stochastic multicriteria decision-making approach based on SMAA-ELECTRE with extended gray numbers. Int. Trans. Oper. Res. 2019, 26, 2032–2052. [Google Scholar] [CrossRef]
- Tseng, M.L.; Lim, M.; Wu, K.J.; Zhou, L.; Bui, D.T.D. A novel approach for enhancing green supply chain management using converged interval-valued triangular fuzzy numbers-grey relation analysis. Resour. Conserv. Recycl. 2018, 128, 122–133. [Google Scholar] [CrossRef]
- Sahoo, M.; Sahoo, S.; Dhar, A.; Pradhan, B. Effectiveness evaluation of objective and subjective weighting methods for aquifer vulnerability assessment in urban context. J. Hydrol. 2016, 541, 1303–1315. [Google Scholar] [CrossRef]
- Maruyama, T.; Kawachi, T.; Singh, V.P. Entropy-based assessment and clustering of potential water resources availability. J. Hydrol. 2005, 309, 104–113. [Google Scholar] [CrossRef]
- Lai, C.G.; Chen, X.H.; Chen, X.Y.; Wang, Z.L.; Wu, X.S.; Zhao, S.W. A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory. Nat. Hazards 2015, 77, 1243–1259. [Google Scholar] [CrossRef]
- Han, Y.P.; Ruan, B.Q.; Xie, J.C. Multi-objective and multilevel fuzzy optimization model and its application in water security evaluation. Resour. Sci. 2003, 4, 37–42. [Google Scholar]
- Cui, Y.; Feng, P.; Jin, J.L.; Liu, L. Water resources carrying capacity evaluation and diagnosis based on set pair analysis and improved the entropy weight method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef]
- Pei, W.; Fu, Q.; Liu, D.; Li, T.X.; Cheng, K.; Cui, S. Spatiotemporal analysis of the agricultural drought risk in Heilongjiang Province, China. Theor. Appl. Climatol. 2018, 133, 151–164. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, J.H.; Zhou, R.J. Interval multi-attribute decision of watershed ecological compensation schemes based on projection pursuit cluster. Water 2018, 10, 1280. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Wang, Y.Z.; Tang, G.M. Study on optimization of irrigation regime and the Jensen model parameter for rain fed crop in Huaibei District of Anhui Province. J. Nanjing Agric. Univ. 2007, 30, 124–128. [Google Scholar]
- Wang, L.Z.; Sun, J.M.; Wang, L.; Li, B.; Zhao, R.J. Breeding and application of soybean cultivar Zhonghuang 13 with wide adaptability, high yield and high protein content traits. Soybean Sci. 2019, 38, 1–6. [Google Scholar] [CrossRef]
- Xu, X.P.; Liu, H.; Tian, L.; Dong, X.B.; Shen, S.H.; Qu, L.Q. Integrated and comparative proteomics of high-oil and high-protein soybean seeds. Food Chem. 2015, 172, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Desclaux, D.; Huynh, T.; Roumet, P. Identification of soybean plant characteristics that indicate the timing of drought stress. Crop Sci. 2000, 40, 716–722. [Google Scholar] [CrossRef]
- Chen, J.L.; Kang, S.Z.; Du, T.S.; Qiu, R.J.; Guo, P.; Chen, R.Q. Quantitative response of greenhouse tomato yield and quality to water deficit at different growth stages. Agric. Water Manag. 2013, 129, 152–162. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar] [CrossRef]
- Song, G.X.; Yang, D.L. Methods for identifying and improving the consistency of fuzzy judgment matrix. Syst. Eng. 2003, 21, 110–116. [Google Scholar]
- Zhou, R.X.; Pan, Z.W.; Jin, J.L.; Li, C.H.; Ning, S.W. Forewarning model of regional water resources carrying capacity based on combination weights and entropy principles. Entropy 2017, 19, 574. [Google Scholar] [CrossRef]
- Yu, S.; Lu, H.W. An integrated model of water resources optimization allocation based on projection pursuit model - Grey wolf optimization method in a transboundary river basin. J. Hydrol. 2018, 559, 156–165. [Google Scholar] [CrossRef]
- Neri, C.; Schneider, L. The impact of the prior density on a minimum relative entropy density: A case study with SPX option data. Entropy 2014, 16, 2642–2668. [Google Scholar] [CrossRef]
- Chen, M.L.; Ning, S.W.; Cui, Y.; Jin, J.L.; Zhou, Y.L.; Wu, C.G. Quantitative assessment and diagnosis for regional agricultural drought resilience based on set pair analysis and connection entropy. Entropy 2019, 21, 373. [Google Scholar] [CrossRef]
- Li, Y.H.; Zhang, M.Z.; Xie, L.G.; Li, X.J. Calculation of rice evapotranspiration under the condition of unsufficient irrigation. J. Hydraul. Eng. 1995, 2, 64–68. [Google Scholar] [CrossRef]
- Foroud, N.; Mündel, H.H.; Saindon, G.; Entz, T. Effect of level and timing of moisture stress on soybean plant development and yield components. Irrig. Sci. 1993, 13, 149–155. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Analyzing fish condition factor index through skew-Gaussian information theory quantifiers. Fluct. Noise Lett. 2016, 15, 1650013. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, S.M.; Feng, P.; Jin, J.L.; Yuan, H.W. Winter wheat evapotranspiration estimation under drought stress during several growth stages in Huaibei Plain, China. Water 2018, 10, 1208. [Google Scholar] [CrossRef]
- Kendig, S.R.; Rupe, J.C.; Scott, H.D. Effect of irrigation and soil water stress on densities of Macrophomina phaseolina in soil and roots of two soybean cultivars. Plant Dis. 2000, 84, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Lopez, J.R.; Winter, J.M.; Elliott, J.; Ruane, A.C.; Porter, C.; Hoogenboom, G. Integrating growth stage deficit irrigation into a process based crop model. Agric. For. Meteorol. 2017, 243, 84–92. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, E.N.; Zhang, Z.X. Evaluation of high yield cultivation and regulated deficit irrigation system of soybean based on grey relation projection model. Water Sav. Irrig. 2017, 6, 38–40. [Google Scholar]
- Fu, Q.; Yang, L.Y.; Li, H.; Li, T.X.; Liu, D.; Ji, Y.; Li, M.; Zhang, Y. Study on the optimization of dry land irrigation schedule in the downstream Songhua River Basin based on the SWAT model. Water 2019, 11, 1147. [Google Scholar] [CrossRef]
- Xu, S.Q.; Song, J.; Wu, Y. Discussion of soybean water demand regulation and sprinkling irrigation pattern. Water Sav. Irrig. 2003, 3, 23–25. [Google Scholar]
- Egli, D.B.; Bruening, W.P. Water stress, photosynthesis, seed sucrose levels and seed growth in soybean. J. Agric. Sci. 2004, 142, 1–8. [Google Scholar] [CrossRef]
- Oya, T.; Nepomuceno, A.L.; Neumaier, N.; Farias, J.R.B.; Tobita, S.; Ito, O. Drought tolerance characteristics of Brazilian soybean cultivars—Evaluation and characterization of drought tolerance of various Brazilian soybean cultivars in the field. Plant Prod. Sci. 2004, 7, 129–137. [Google Scholar] [CrossRef]
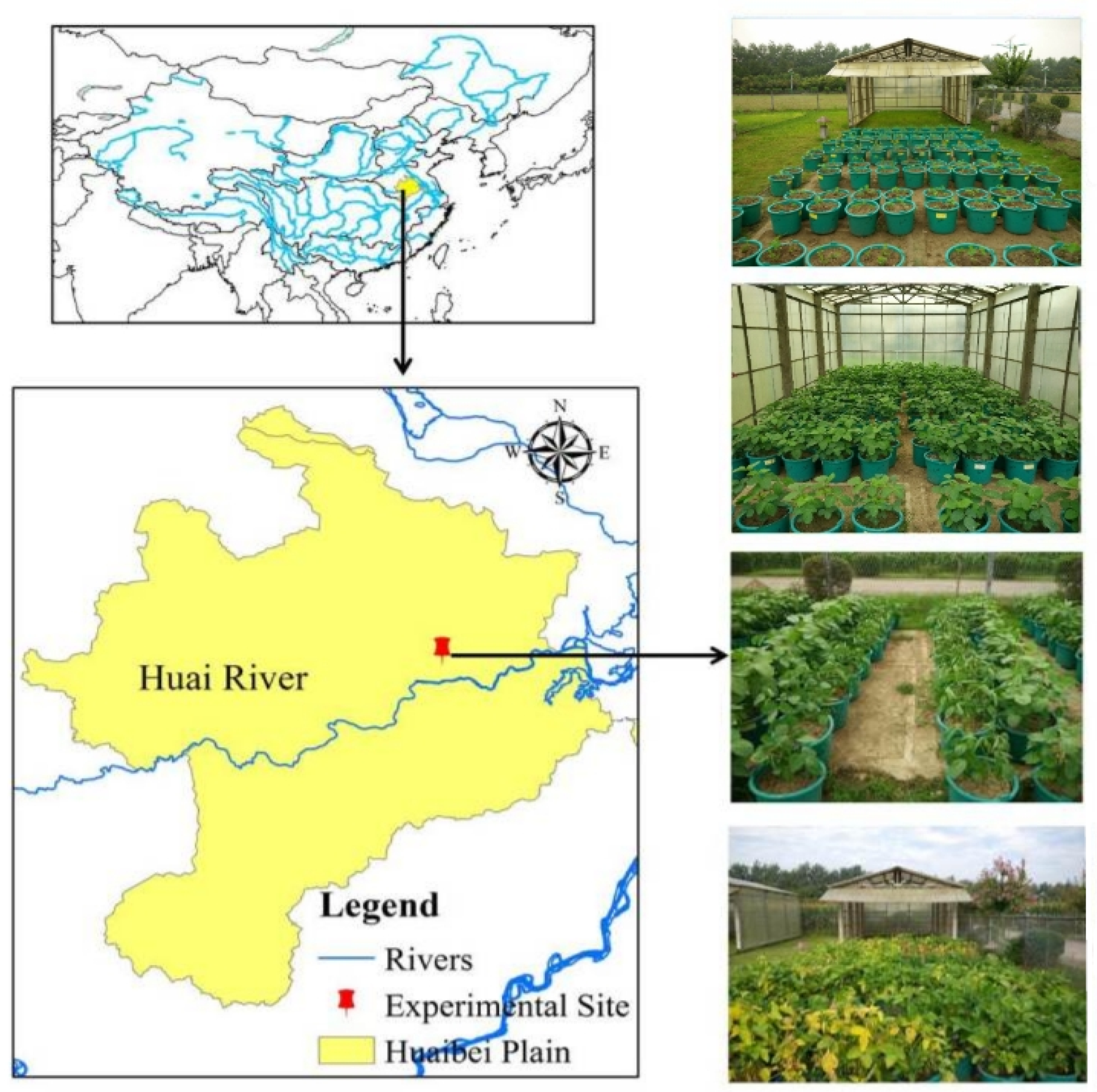
| Soil Characteristics | Value |
|---|---|
| Sand (%) | 3.45 |
| Silt (%) | 70.52 |
| Clay (%) | 26.03 |
| pH (in water solution) | 7.5 |
| Organic matter (%) | 0.85 |
| Bulk density (g/cm3) | 1.36 |
| Field capacity at −0.03 MPa (cm3/cm3) | 0.38 |
| Wilting point at −1.5 MPa (cm3/cm3) | 0.12 |
| Cultivar Parameters | Value | Seed Characteristics | Value | |
|---|---|---|---|---|
| Whole growth period (d) | 97 | Protein content (%) | 43.73 | |
| Plant height (cm) | 46.3 | Oil content (%) | 19.10 | |
| Number of nods on main stem | 13.8 | Vitamin E content (μg/g) | 181.9 ± 25.1 | |
| Number of branches per plant | 2.3 | Fatty acid (%) | 16: 0 | 11.5 ± 0.5 |
| Number of pods per plant | 40.0 | 18: 0 | 4.2 ± 0.4 | |
| Number of seeds per pod | 2.04 | 18: 1 | 25.5 ± 0.5 | |
| Weight of 100 seeds (g) | 24.0 | 18: 2 | 51.8 ± 0.8 | |
| Seed yield (t/ha) | 3.04 | 18: 3 | 7.0 ± 0.2 | |
| Description of Growth Stage | 2015 Season | 2016 Season |
|---|---|---|
| Germination stage, from sowing to seed germination | From June 20 to July 3, 14 days | From June 29 to July 14, 16 days |
| Seedling stage, from seed germination to plants with four fully expanded leaves | From July 4 to July 14, 11 days | From July 15 to July 27, 13 days |
| Branching stage, from plants with four fully expanded leaves to first flower appearance | From July 15 to August 3, 20 days | From July 28 to August 10, 14 days |
| Flowering-podding stage, from first flower appearance to the beginning of pod filling | From August 4 to August 20, 17 days | From August 11 to August 31, 21 days |
| Seed filling stage, from the beginning of pod filling to plant maturation | From August 21 to September 20, 31 days | From September 1 to September 27, 27 days |
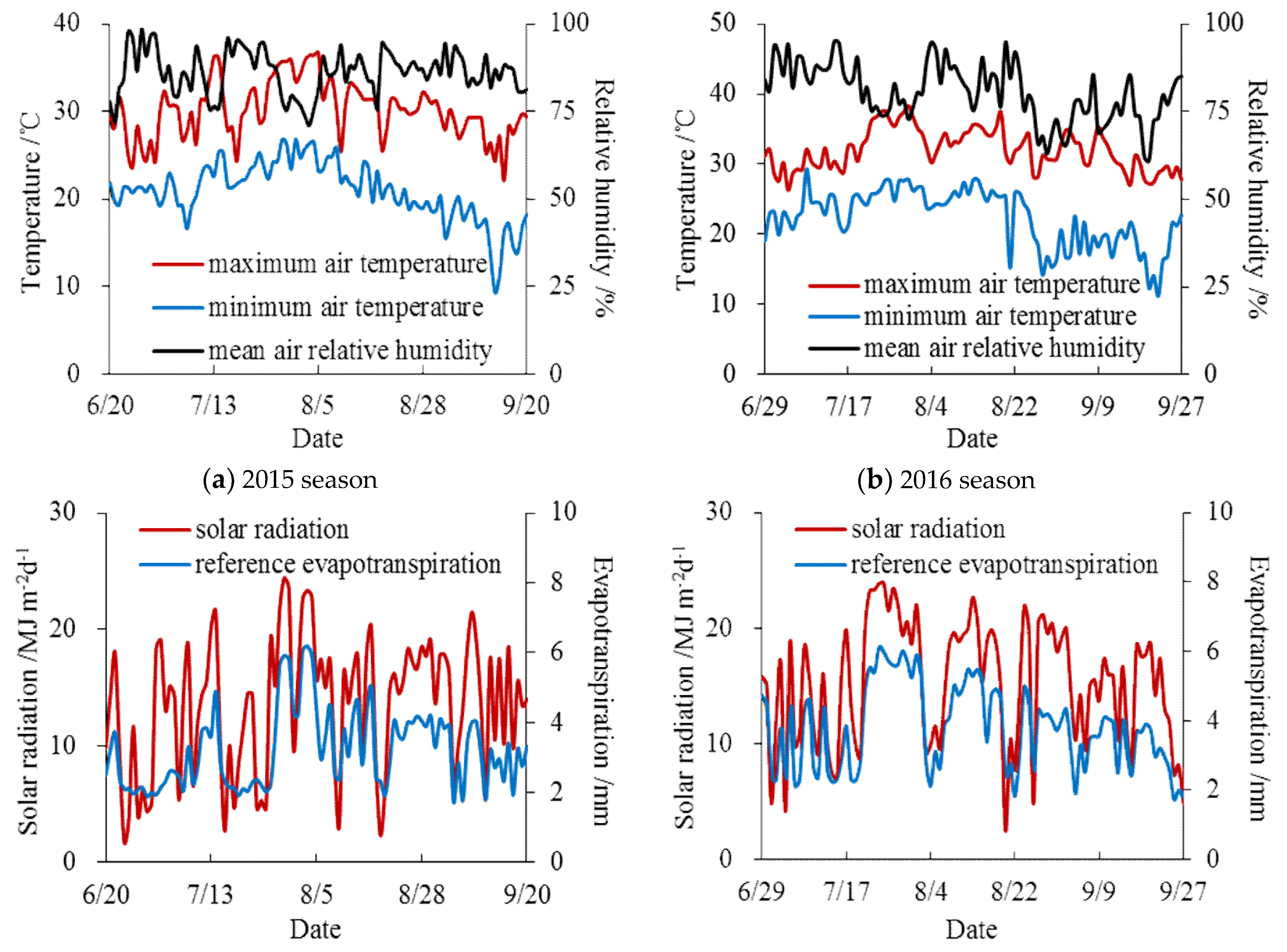
| Meteorological Element | Germination Stage | Seedling Stage | Branching Stage | Flowering-Podding Stage | Seed Filling Stage | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2015 | 2016 | 2015 | 2016 | 2015 | 2016 | 2015 | 2016 | 2015 | 2016 | |
| Maximum air temperature (°C) | 27.8 | 29.8 | 30.9 | 33.8 | 32.2 | 34.2 | 31.5 | 32.8 | 28.9 | 30.6 |
| Minimum air temperature (°C) | 20.9 | 23.3 | 21.3 | 24.7 | 24.1 | 25.7 | 22.8 | 22.7 | 17.6 | 18.4 |
| Mean air temperature (°C) | 24.0 | 26.3 | 26.0 | 29.1 | 28.0 | 29.3 | 26.7 | 27.7 | 22.9 | 24.2 |
| Mean air relative humidity (%) | 88.4 | 87.8 | 82.2 | 81.3 | 85.9 | 84.2 | 86.4 | 79.3 | 86.7 | 74.8 |
| Wind speed (m/s) | 0.9 | 1.3 | 0.9 | 1.0 | 1.0 | 1.0 | 0.9 | 1.0 | 0.6 | 0.9 |
| Sunshine duration (h) | 0.5 | 3.5 | 2.8 | 6.4 | 3.6 | 7.4 | 5.3 | 7.4 | 7.3 | 6.6 |
| Solar radiation (MJ/(m2·d)) | 9.92 | 12.30 | 14.37 | 18.03 | 13.32 | 16.48 | 13.48 | 16.73 | 15.12 | 13.95 |
| Vapor pressure deficit (kPa) | 0.36 | 0.42 | 0.63 | 0.80 | 0.58 | 0.69 | 0.50 | 0.75 | 0.37 | 0.76 |
| Reference evapotranspiration (mm/d) | 2.33 | 3.23 | 3.09 | 4.28 | 3.42 | 4.43 | 3.56 | 4.11 | 3.29 | 3.18 |
| Cropping Season | Irrigation Scheme | Seedling Stage | Branching Stage | Flowering-Podding Stage | Seed Filling Stage |
|---|---|---|---|---|---|
| 2015 and 2016 | T1 | 55% | 75% | 75% | 75% |
| T2 | 35% | 75% | 75% | 75% | |
| T3 | 75% | 55% | 75% | 75% | |
| T4 | 75% | 35% | 75% | 75% | |
| T5 | 75% | 75% | 55% | 75% | |
| T6 | 75% | 75% | 35% | 75% | |
| T7 | 75% | 75% | 75% | 55% | |
| T8 | 75% | 75% | 75% | 35% | |
| CK | 75% | 75% | 75% | 75% |
| Decision-Making System | Decision-Making Index | Index Type |
|---|---|---|
| crop water consumption subsystem | X1 soybean evapotranspiration at the seedling stage (mm) | negative |
| X2 soybean evapotranspiration at the branching stage (mm) | negative | |
| X3 soybean evapotranspiration at the flowering-podding stage (mm) | negative | |
| X4 soybean evapotranspiration at the seed filling stage (mm) | negative | |
| X5 irrigation amount at the seedling stage (mm) | negative | |
| X6 irrigation amount at the branching stage (mm) | negative | |
| X7 irrigation amount at the flowering-podding stage (mm) | negative | |
| X8 irrigation amount at the seed filling stage (mm) | negative | |
| crop growth process subsystem | X9 soybean aboveground accumulated biomass at the seedling stage (t/ha) | positive |
| X10 soybean aboveground accumulated biomass at the branching stage (t/ha) | positive | |
| X11 soybean aboveground accumulated biomass at the flowering-podding stage (t/ha) | positive | |
| X12 soybean aboveground accumulated biomass at the seed filling stage (t/ha) | positive | |
| X13 soybean aboveground biomass at harvest time (t/ha) | positive | |
| X14 soybean seed yield (t/ha) | positive | |
| X15 soybean 1000 seed weight (g) | positive | |
| crop water use efficiency subsystem | X16 soybean water use efficiency during the whole growth period (kg/m3) | positive |
| Cropping Season | Irrigation Scheme | Crop Water Consumption Decision-Making Subsystem | Crop Growth Process Decision-Making Subsystem | Crop Water Use Efficiency Decision-Making Subsystem | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | X16 | ||
| 2015 | T1 | 0.58 | 0.21 | 0.23 | 0.07 | 0.39 | 0.26 | 0.31 | 0.09 | 0.13 | 0.62 | 0.97 | 0.94 | 0.88 | 0.93 | 0.98 | 0.94 |
| T2 | 1.00 | 0.21 | 0.16 | 0.02 | 1.00 | 0.11 | 0.17 | 0.05 | 0.00 | 0.58 | 0.93 | 0.84 | 0.67 | 0.83 | 0.92 | 0.81 | |
| T3 | 0.01 | 0.50 | 0.30 | 0.07 | 0.03 | 0.53 | 0.27 | 0.07 | 1.00 | 0.42 | 0.81 | 1.00 | 0.74 | 0.89 | 0.92 | 0.96 | |
| T4 | 0.16 | 1.00 | 0.48 | 0.07 | 0.09 | 1.00 | 0.48 | 0.10 | 1.00 | 0.00 | 0.70 | 0.98 | 0.49 | 0.76 | 0.71 | 1.00 | |
| T5 | 0.18 | 0.11 | 0.67 | 0.19 | 0.11 | 0.13 | 0.62 | 0.19 | 1.00 | 1.00 | 0.58 | 0.72 | 0.60 | 0.75 | 1.00 | 0.84 | |
| T6 | 0.22 | 0.11 | 1.00 | 0.66 | 0.07 | 0.11 | 1.00 | 0.62 | 1.00 | 1.00 | 0.00 | 0.59 | 0.00 | 0.00 | 0.37 | 0.00 | |
| T7 | 0.18 | 0.17 | 0.12 | 0.45 | 0.16 | 0.15 | 0.15 | 0.44 | 1.00 | 1.00 | 1.00 | 0.11 | 0.33 | 0.61 | 0.68 | 0.69 | |
| T8 | 0.09 | 0.09 | 0.14 | 1.00 | 0.08 | 0.08 | 0.15 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.22 | 0.22 | 0.00 | 0.36 | |
| CK | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.76 | 1.00 | 1.00 | 0.89 | 0.85 | |
| 2016 | T1 | 0.63 | 0.26 | 0.17 | 0.10 | 0.57 | 0.19 | 0.16 | 0.01 | 0.36 | 0.59 | 0.91 | 0.99 | 0.98 | 0.83 | 0.76 | 0.80 |
| T2 | 1.00 | 0.15 | 0.24 | 0.15 | 1.00 | 0.10 | 0.22 | 0.05 | 0.00 | 0.52 | 0.87 | 0.94 | 0.41 | 0.60 | 0.69 | 0.63 | |
| T3 | 0.00 | 0.44 | 0.24 | 0.16 | 0.02 | 0.33 | 0.22 | 0.04 | 1.00 | 0.58 | 0.87 | 1.00 | 1.00 | 0.89 | 0.73 | 0.94 | |
| T4 | 0.16 | 1.00 | 0.54 | 0.20 | 0.06 | 1.00 | 0.41 | 0.10 | 1.00 | 0.00 | 0.73 | 0.91 | 0.30 | 0.70 | 0.49 | 1.00 | |
| T5 | 0.03 | 0.18 | 0.57 | 0.29 | 0.13 | 0.04 | 0.56 | 0.18 | 1.00 | 1.00 | 0.58 | 0.86 | 0.75 | 0.57 | 1.00 | 0.61 | |
| T6 | 0.07 | 0.09 | 1.00 | 0.66 | 0.11 | 0.05 | 1.00 | 0.57 | 1.00 | 1.00 | 0.00 | 0.76 | 0.00 | 0.00 | 0.51 | 0.00 | |
| T7 | 0.08 | 0.10 | 0.09 | 0.55 | 0.00 | 0.10 | 0.14 | 0.60 | 1.00 | 1.00 | 1.00 | 0.25 | 0.39 | 0.70 | 0.55 | 0.71 | |
| T8 | 0.12 | 0.00 | 0.06 | 1.00 | 0.08 | 0.09 | 0.05 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.03 | 0.24 | 0.00 | 0.21 | |
| CK | 0.05 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.93 | 1.00 | 1.00 | 0.87 | 0.74 | |
| Decision-Making System | Decision-Making Index | Improved Fuzzy Analytic Hierarchy Process Method | Grey Entropy Weight Method | Grey Relation–Projection Pursuit Model | Combined Weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subsystem Weight | CIC | Index Weight | CIC | Comprehensive Index Weight | 2015 | 2016 | 2015 | 2016 | |||||
| 2015 | 2016 | 2015 | 2016 | 2015 | 2016 | ||||||||
| crop water consumption subsystem | X1 | 0.334 | 0.000 | 0.127 | 0.131 | 0.004 | 0.004 | 0.043 | 0.044 | 0.174 | 0.191 | 0.116 | 0.186 |
| X2 | 0.124 | 0.125 | 0.042 | 0.042 | 0.094 | 0.644 | 0.084 | 0.335 | |||||
| X3 | 0.120 | 0.119 | 0.040 | 0.040 | 0.005 | 0.005 | 0.018 | 0.030 | |||||
| X4 | 0.130 | 0.120 | 0.043 | 0.040 | 0.018 | 0.001 | 0.038 | 0.004 | |||||
| X5 | 0.129 | 0.131 | 0.043 | 0.044 | 0.014 | 0.003 | 0.033 | 0.025 | |||||
| X6 | 0.126 | 0.128 | 0.042 | 0.043 | 0.001 | 0.102 | 0.002 | 0.135 | |||||
| X7 | 0.116 | 0.118 | 0.039 | 0.039 | 0.017 | 0.001 | 0.035 | 0.004 | |||||
| X8 | 0.126 | 0.128 | 0.042 | 0.043 | 0.004 | 0.008 | 0.017 | 0.037 | |||||
| crop growth process subsystem | X9 | 0.283 | 0.151 | 0.141 | 0.003 | 0.004 | 0.043 | 0.040 | 0.047 | 0.027 | 0.061 | 0.067 | |
| X10 | 0.157 | 0.154 | 0.044 | 0.043 | 0.013 | 0.001 | 0.033 | 0.001 | |||||
| X11 | 0.130 | 0.125 | 0.037 | 0.035 | 0.068 | 0.004 | 0.067 | 0.025 | |||||
| X12 | 0.149 | 0.139 | 0.042 | 0.039 | 0.299 | 0.001 | 0.151 | 0.011 | |||||
| X13 | 0.145 | 0.185 | 0.041 | 0.052 | 0.068 | 0.001 | 0.071 | 0.004 | |||||
| X14 | 0.133 | 0.134 | 0.038 | 0.038 | 0.052 | 0.003 | 0.060 | 0.021 | |||||
| X15 | 0.135 | 0.122 | 0.038 | 0.035 | 0.102 | 0.001 | 0.084 | 0.013 | |||||
| crop water use efficiency subsystem | X16 | 0.383 | 1.000 | 1.000 | \ | \ | 0.383 | 0.383 | 0.024 | 0.007 | 0.130 | 0.102 | |
| Cropping Season | Optimized Projection Index Function Q(y) = SzDz | Projection Direction of Each Decision-Making Index (Projection Vector y) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sz | Dz | Q | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | X16 | |
| 2015 | 0.26 | 0.44 | 0.11 | 0.42 | 0.31 | 0.07 | 0.13 | 0.12 | 0.01 | 0.13 | 0.06 | 0.22 | 0.12 | 0.26 | 0.55 | 0.26 | 0.23 | 0.32 | 0.16 |
| 2016 | 0.25 | 0.45 | 0.11 | 0.44 | 0.81 | 0.07 | 0.01 | 0.06 | 0.32 | 0.01 | 0.09 | 0.16 | 0.00 | 0.07 | 0.03 | 0.01 | 0.05 | 0.04 | 0.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Jiang, S.; Jin, J.; Feng, P.; Ning, S. Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation–Projection Pursuit. Entropy 2019, 21, 877. https://doi.org/10.3390/e21090877
Cui Y, Jiang S, Jin J, Feng P, Ning S. Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation–Projection Pursuit. Entropy. 2019; 21(9):877. https://doi.org/10.3390/e21090877
Chicago/Turabian StyleCui, Yi, Shangming Jiang, Juliang Jin, Ping Feng, and Shaowei Ning. 2019. "Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation–Projection Pursuit" Entropy 21, no. 9: 877. https://doi.org/10.3390/e21090877
APA StyleCui, Y., Jiang, S., Jin, J., Feng, P., & Ning, S. (2019). Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation–Projection Pursuit. Entropy, 21(9), 877. https://doi.org/10.3390/e21090877





