Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches
Abstract
1. Introduction
2. Some Notes on Fractional Calculus
3. Description of the Investigated MOR Techniques
3.1. Open-Loop Balancing Reduction
3.2. Implicit Model Order Reduction via Fractional Order Calculus
3.3. Fractional Order Transfer Function Fitting
4. Numerical Examples
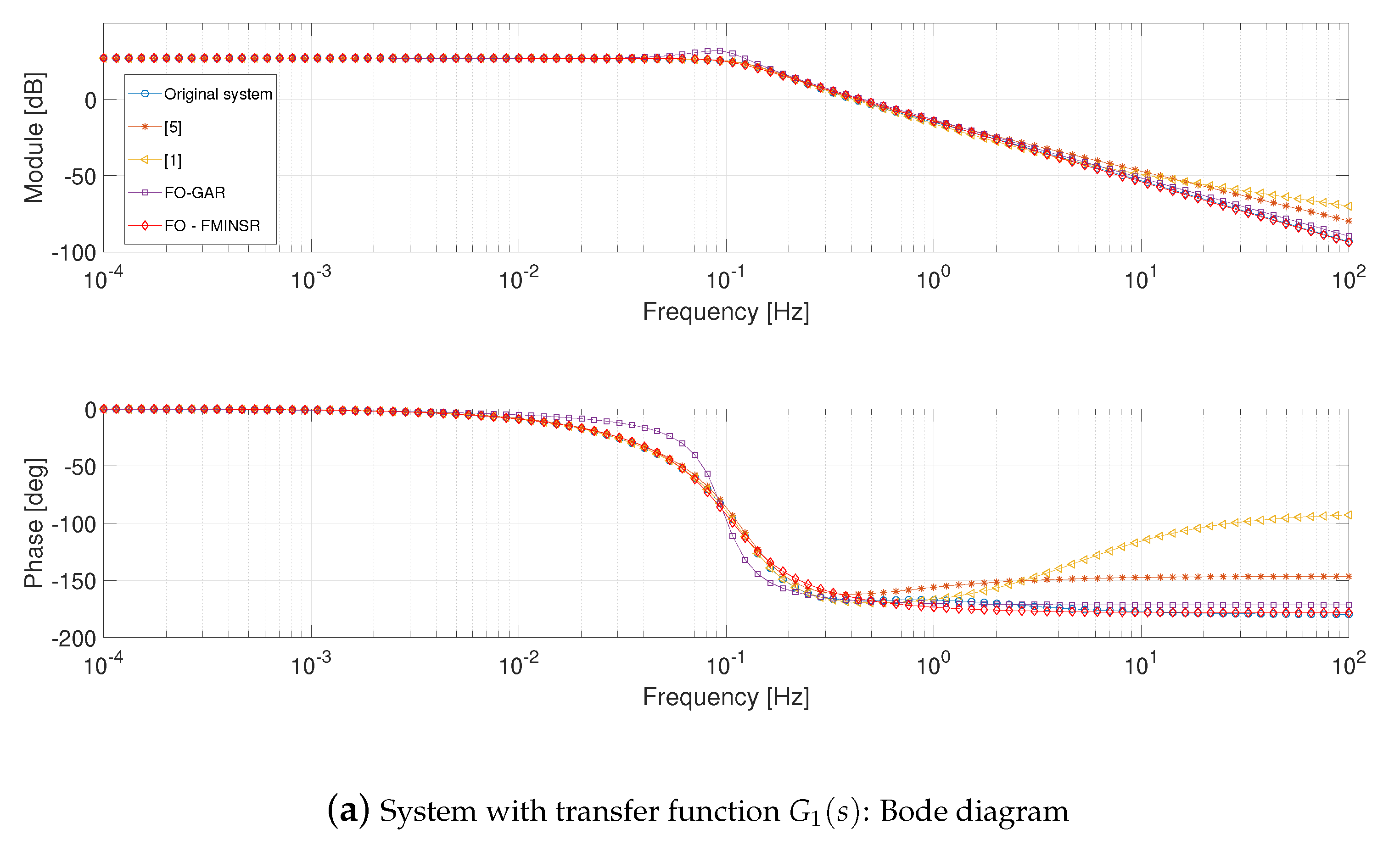
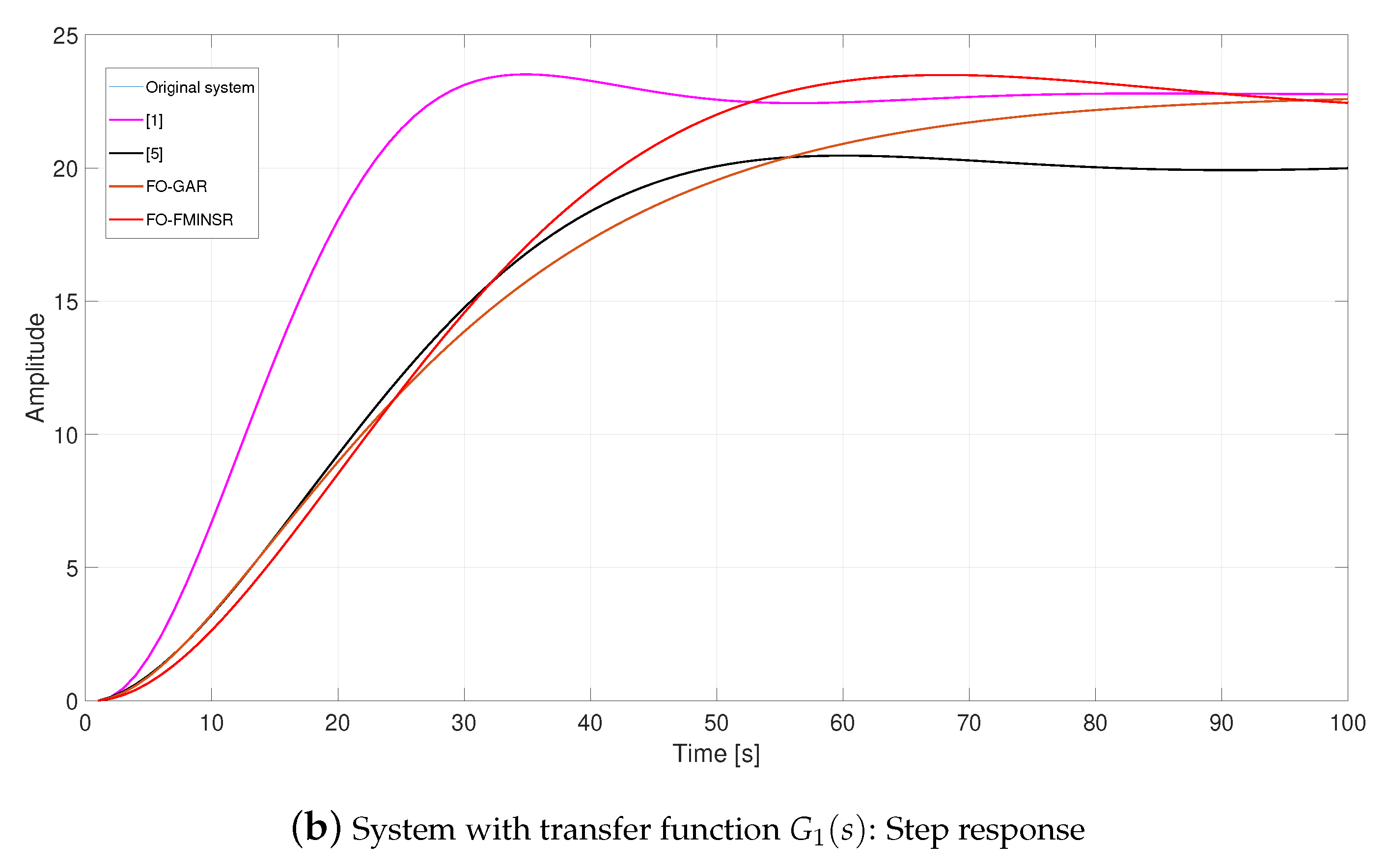
4.1. System with Transfer Function
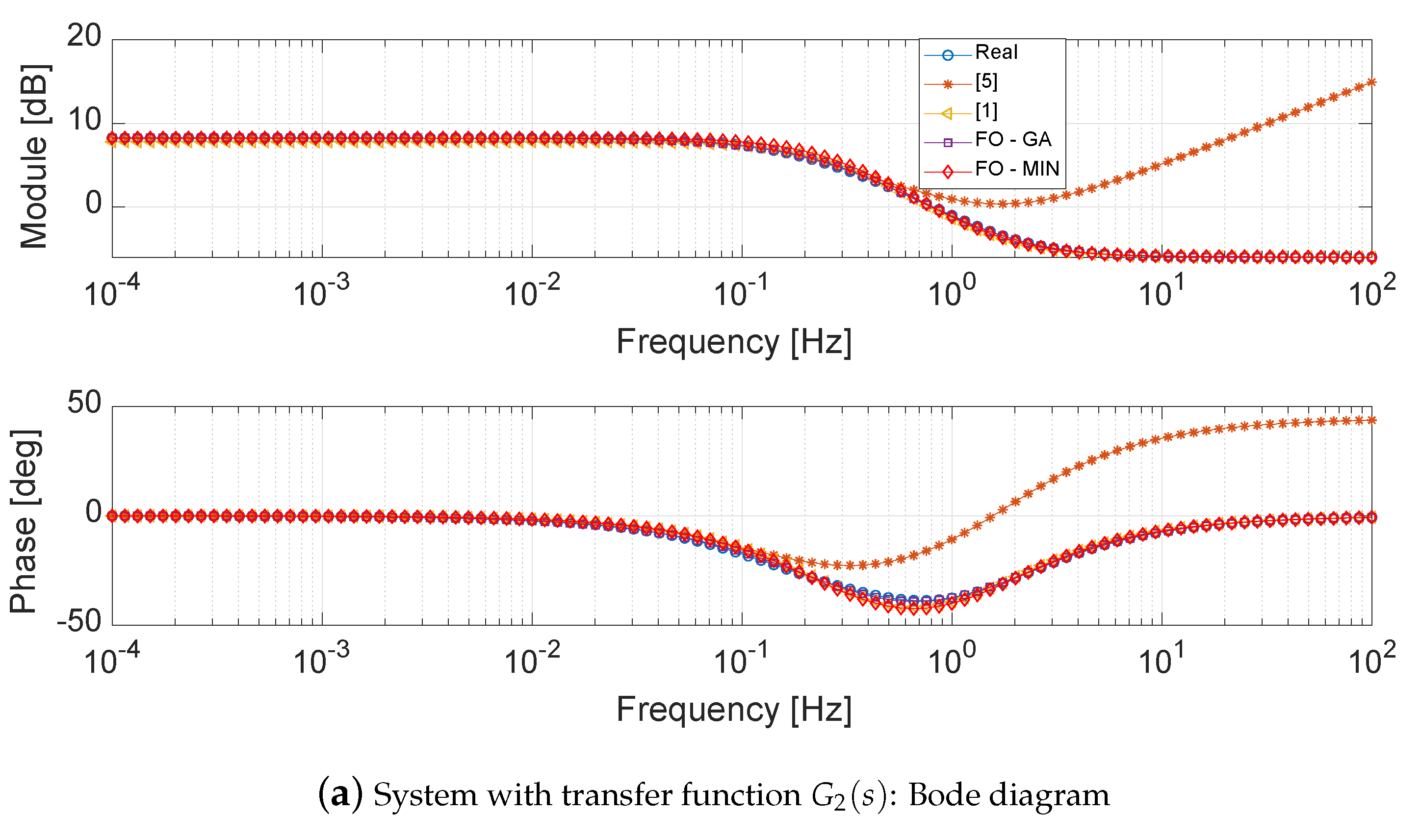
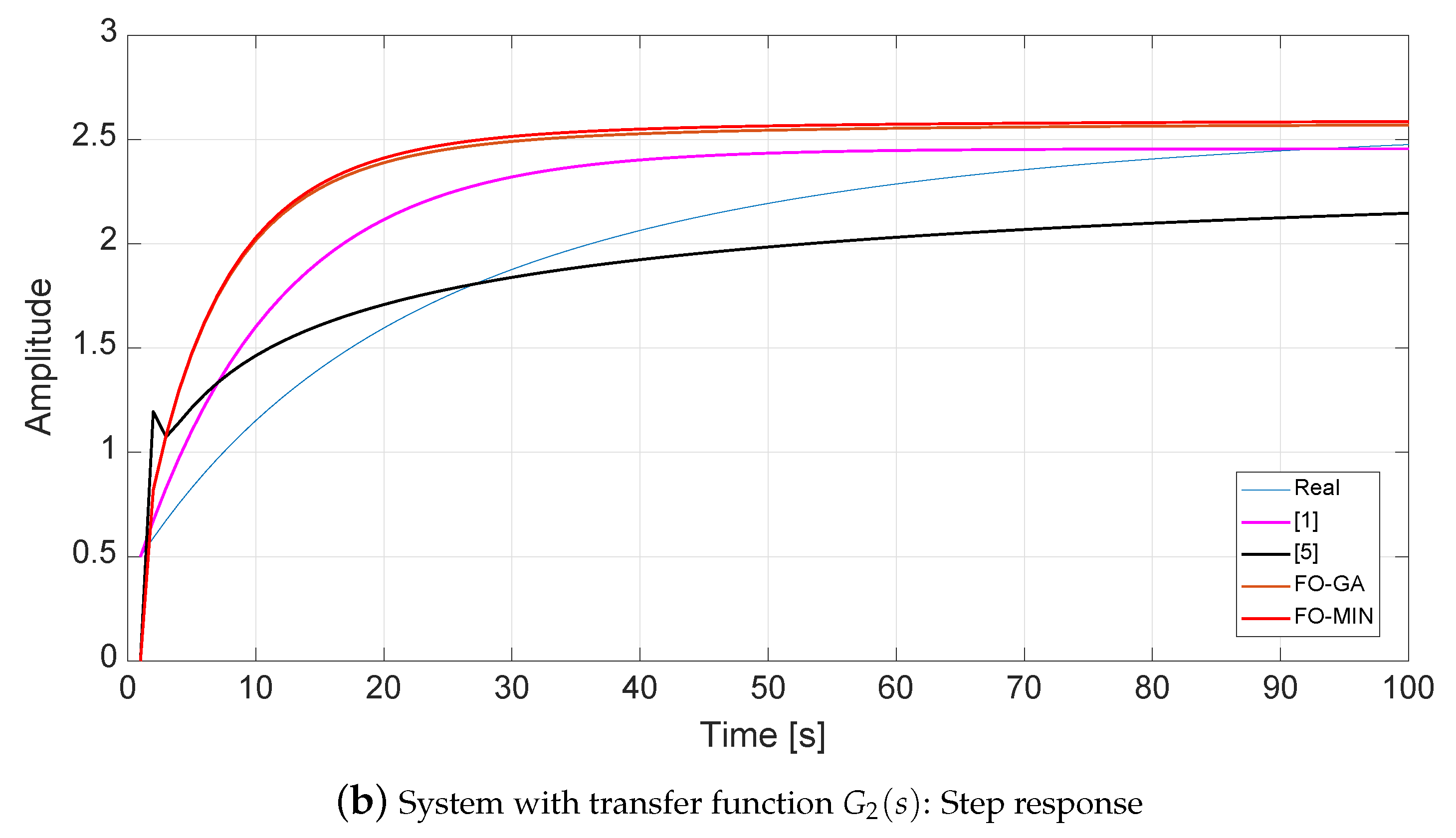
4.2. System with Transfer Function
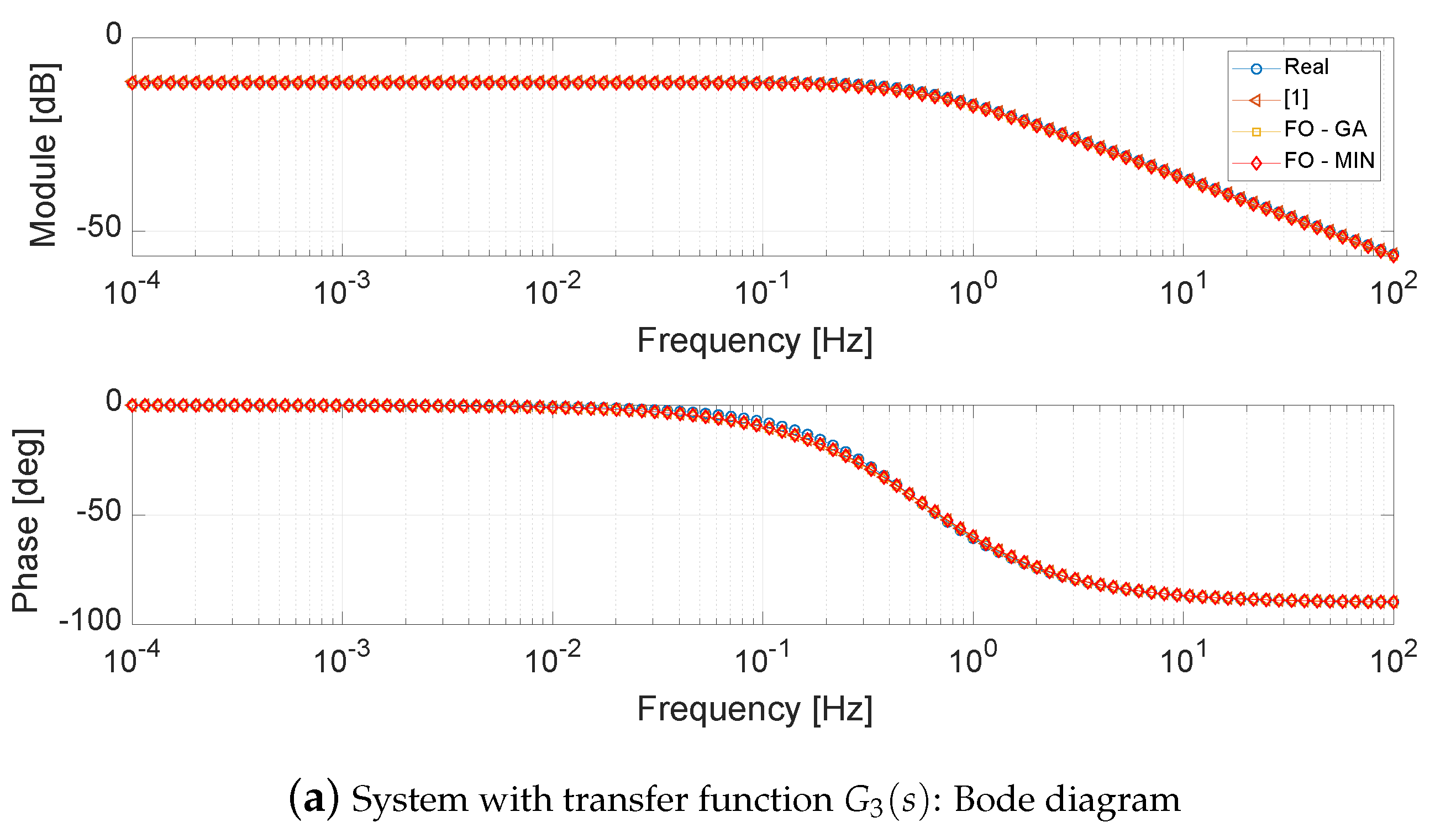
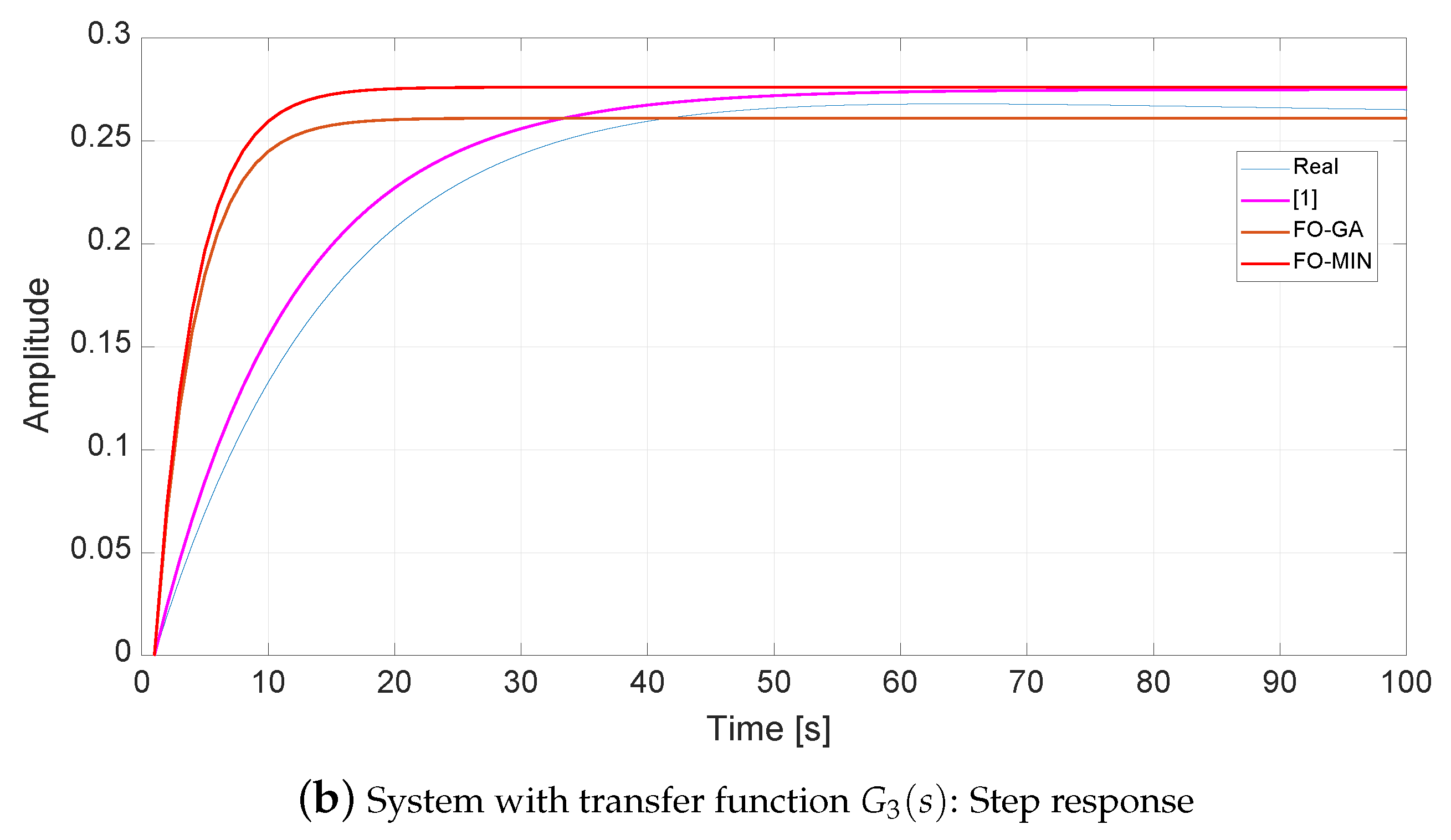
4.3. System with Transfer Function
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MOR | Model Order Reduction |
| FOC | Fractional Order Calculus |
| GA | Genetic Algorithm |
| IOTF | Integer Order Transfer Function |
| Order of Differentiation | |
| FOS | Fractional Order System |
| FOTF | Fractional Order Transfer Function |
| OLBR | Open Loop Balancing Realization |
References
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Automatic Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Das, S.; Patnaik, P.; Jha, R. Model Order Reduction of High Order LTI System using Genetic Algorithm. In Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017; pp. 73–77. [Google Scholar]
- Khaled, S. A generic model order reduction technique based on Particle Swarm Optimization (PSO) algorithm. In Proceedings of the IEEE EUROCON 2017—17th International Conference on Smart Technologies, Ohrid, Macedonia, 6–8 July 2017; pp. 193–196. [Google Scholar]
- Ahmed, A.; Khaled, S. Model order reduction using artificial neural networks. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016; pp. 89–92. [Google Scholar]
- Rachid, M.; Maamar, B.; Said, D. Approximation of high order integer systems by fractional order reduced parameter models. Math. Comput. Model. 2010, 51, 53–62. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier Science: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Ross, B. Fractional Calculus and its Applications; Springer: Berlin, Germay, 1975. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Sebah, P.; Gourdon, X. Introduction to the Gamma Functions. 2012. Available online: http://numbers.computation.free.fr/Constants/constants.html (accessed on 15 July 2019).
- Sabatier, J.; Farges, C.; Trigeassou, J.C. Fractional systems state space description: some wrong ideas and proposed solutions. J. Vib. Control 2014, 20, 1076–1084. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Pappalardo, F.; Tomasello, V. Auto-Tuning and Fractional Order Controller Implementation on Hardware in the Loop System. J. Optim. Theory Appl. 2013, 156, 141–152. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Maione, G.; Pisano, A. Integrated technology fractional order proportional- integral-derivative design. J. Vib. Control 2014, 20, 1066–1075. [Google Scholar] [CrossRef]
- De Keyser, R.; Muresan, C.; Ionescu, C. A novel auto-tuning method for fractional order PI/PD controllers. ISA Trans. 2016, 62, 268–275. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G. A numerical approach for computing stability region of FO-PID controller. J. Frankl. Inst. 2013, 350, 871–889. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G. Field programmable analog array implementation of noninteger order PIλDμ controller. J. Comput. Nonlinear Dyn. 2008, 3, 021302. [Google Scholar] [CrossRef]
- Caponetto, R.; Maione, G.; Pisano, A.; Rapaic, M.; Usai, E. Analysis and shaping of the self-sustained oscillations in relay controlled fractional-order systems. Fract. Calc. Appl. Anal. 2013, 16, 93–108. [Google Scholar] [CrossRef]
- Lino, P.; Maione, G. Design and simulation of fractional-order controllers of injection in CNG engines. IFAC Proc. Vol. 2013, 1, 582–587. [Google Scholar] [CrossRef]
- Caponetto, R.; Sapuppo, F.; Tomasello, V.; Maione, G.; Lino, P. Fractional-Order Identification and Control of Heating Processes with Non-Continuous Materials. Entropy 2016, 18, 398. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.; Torres, L.; Escobar-Jimènez, R.; Olivares-Peregrino, V. Fractional observer to estimate periodical forces. ISA Trans. 2018, 82, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mondal, D.; Biswas, K. Packaging of Single-Component Fractional Order Element. IEEE Trans. Device Mater. Reliab. 2013, 13, 73–80. [Google Scholar] [CrossRef]
- Jesus, I.; Machado, T. Development of fractional order capacitors based on electrolyte processes. Nonlinear Dyn. 2009, 56, 45–55. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Graziani, S.; Strazzeri, S. A fractional model for IPMC actuators. In Proceedings of the 2008 IEEE Instrumentation and Measurement Technology Conference, Victoria, BC, Canada, 12–15 May 2008; pp. 2103–2107. [Google Scholar]
- John, D.; Banerjee, S.; Bohannan, G.; Biswas, K. Solid-state fractional capacitor using MWCNT-epoxy nanocomposite. Appl. Phys. Lett. 2017, 110, 163504. [Google Scholar] [CrossRef]
- Buscarino, A.; Caponetto, R.; Di Pasquale, G.; Fortuna, L.; Graziani, S.; Pollicino, A. Carbon Black based capacitive Fractional Order Element towards a new electronic device. AEU—Int. J. Electron. Commun. 2018, 84, 307–312. [Google Scholar] [CrossRef]
- Said, L.; Radwan, A.; Madian, A.; Solimane, A. Fractional order oscillators based on operational transresistance amplifiers. AEU—Int. J. Electron. Commun. 2015, 69, 988–1003. [Google Scholar] [CrossRef]
- Krishna, S.; Das, S.; Biswas, K.; Goswami, B. Fabrication of a Fractional Order Capacitor With Desired Specifications: A Study on Process Identification and Characterization. IEEE Trans. Electron. Device 2011, 58, 4067–4072. [Google Scholar] [CrossRef]
- Bohannan, G. Electrical Component with Fractional Order Impedance. U.S. Patent n.20060267595, 30 November 2006. [Google Scholar]
- Vastarouchas, C.; Tsirimokou, G.; Freeborn, T.; Psychalinos, C. Emulation of an electrical-analogue of a fractional-order human respiratory mechanical impedance model using OTA topologies. AEU—Int. J. Electron. Commun. 2017, 78, 201–208. [Google Scholar] [CrossRef]
- Ionescu, C.; Machado, T.; De Keyser, R. Modeling of the lung impedance using a fractional-order ladder network with constant phase elements. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Solís-Péreza, J.; Gómez-Aguilar, J.; Torres, L.; Escobar-Jiménez, R.; Reyes-Reyes, J. Fitting of experimental data using a fractional Kalman-like observer. ISA Trans. 2019, 88, 153–169. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.M.; Machado, T. Complex Systems and Fractional Dynamics. Entropy 2018, 20, 507. [Google Scholar] [CrossRef]
- Tarasov, V.; Tarasova, V. Criterion of Existence of Power-Law Memory for Economic Processes. Entropy 2018, 20, 414. [Google Scholar] [CrossRef]
- Mata, M.; Machado, J. Entropy Analysis of Monetary Unions. Entropy 2017, 19, 6245. [Google Scholar] [CrossRef]
- Machado, J. Fractional Order Generalized Information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Karci, A. Fractional order entropy: New perspectives. Optik 2016, 27, 9172–9177. [Google Scholar] [CrossRef]
- Machado, T.; Lopes, A. Fractional Rényi entropy, Fractional Rényi entropy. Eur. Physic J. Plus 2019. [Google Scholar] [CrossRef]
- Lopes, A.; Machado, J. Entropy analysis of soccer dynamics. Entropy 2019, 21, 2. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Computing the Matrix Mittag-Leffler Function with Applications to Fractional Calculus. J. Sci. Comput. 2018, 77, 129–153. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC-Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Garrappa, R. Trapezoidal methods for fractional differential equations: Theoretical and computational aspects. Math. Comput. Simul. 2015, 110, 96–112. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: Fractional-order modeling and control toolbox for MATLAB. In Proceedings of the 18th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2011, Gliwice, Poland, 16–18 June 2011; pp. 684–689. [Google Scholar]
- Garrappa, R.; Maione, G. Model order reduction on Krylov subspaces for fractional linear systems. IFAC Proc. Vol. 2013, 46, 143–148. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Number of individuals | 3000 |
| Maximum number of generation | 150 |
| Generation gap | |
| Precision | 40 |
| System | Transfer Function |
|---|---|
| System | Method in [1] | Method in [5] | FO-GA | FO-FMINS | No. of param. |
|---|---|---|---|---|---|
| [6,6,6,6] | |||||
| [2,4,6,5] | |||||
| not applicable | [2,-,2,2] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caponetto, R.; Machado, J.T.; Murgano, E.; Xibilia, M.G. Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy 2019, 21, 876. https://doi.org/10.3390/e21090876
Caponetto R, Machado JT, Murgano E, Xibilia MG. Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy. 2019; 21(9):876. https://doi.org/10.3390/e21090876
Chicago/Turabian StyleCaponetto, Riccardo, José Tenreiro Machado, Emanuele Murgano, and Maria Gabriella Xibilia. 2019. "Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches" Entropy 21, no. 9: 876. https://doi.org/10.3390/e21090876
APA StyleCaponetto, R., Machado, J. T., Murgano, E., & Xibilia, M. G. (2019). Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy, 21(9), 876. https://doi.org/10.3390/e21090876







