Permutation Entropy and Irreversibility in Gait Kinematic Time Series from Patients with Mild Cognitive Decline and Early Alzheimer’s Dementia
Abstract
1. Introduction
2. Results
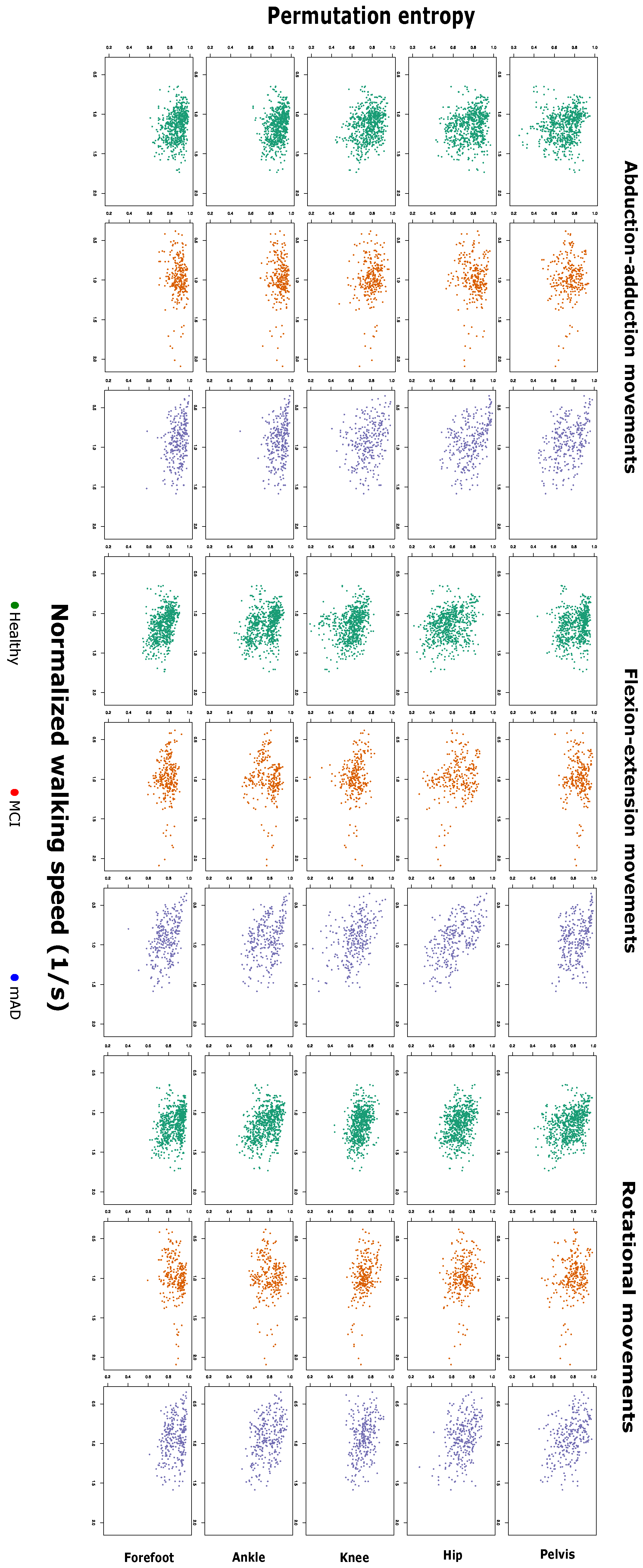
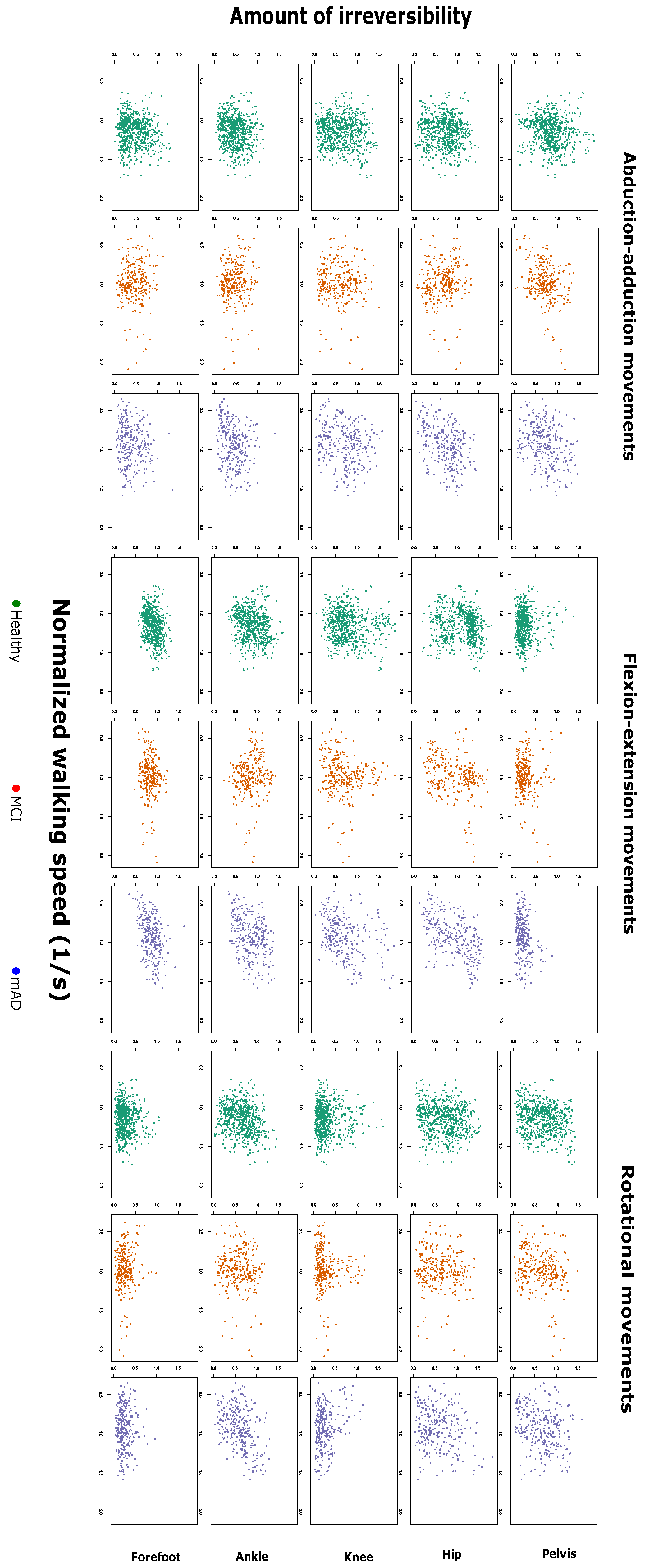
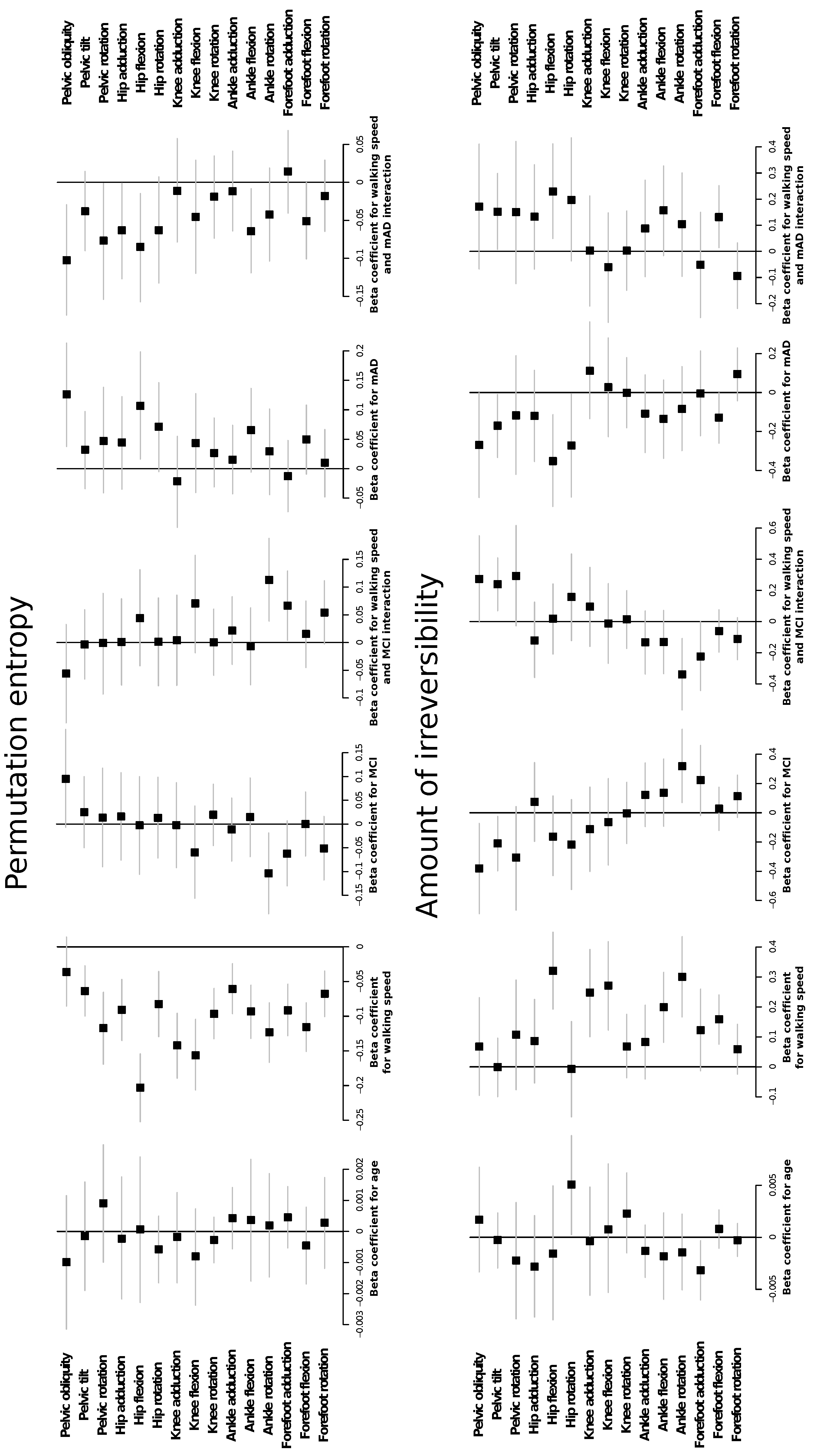
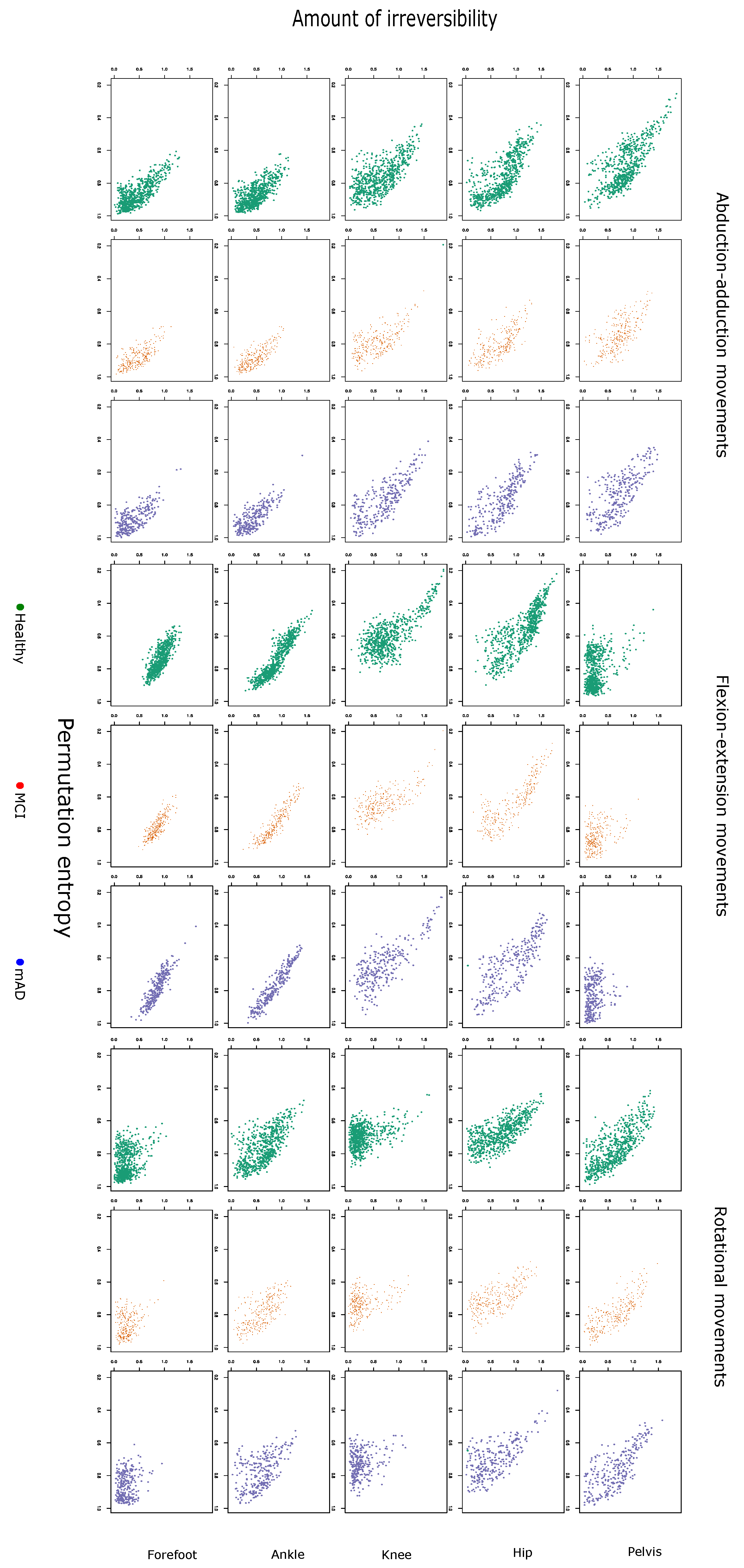
2.1. Complexity Measures are Related with Preferred Walking Speed and Cognitive Impairment
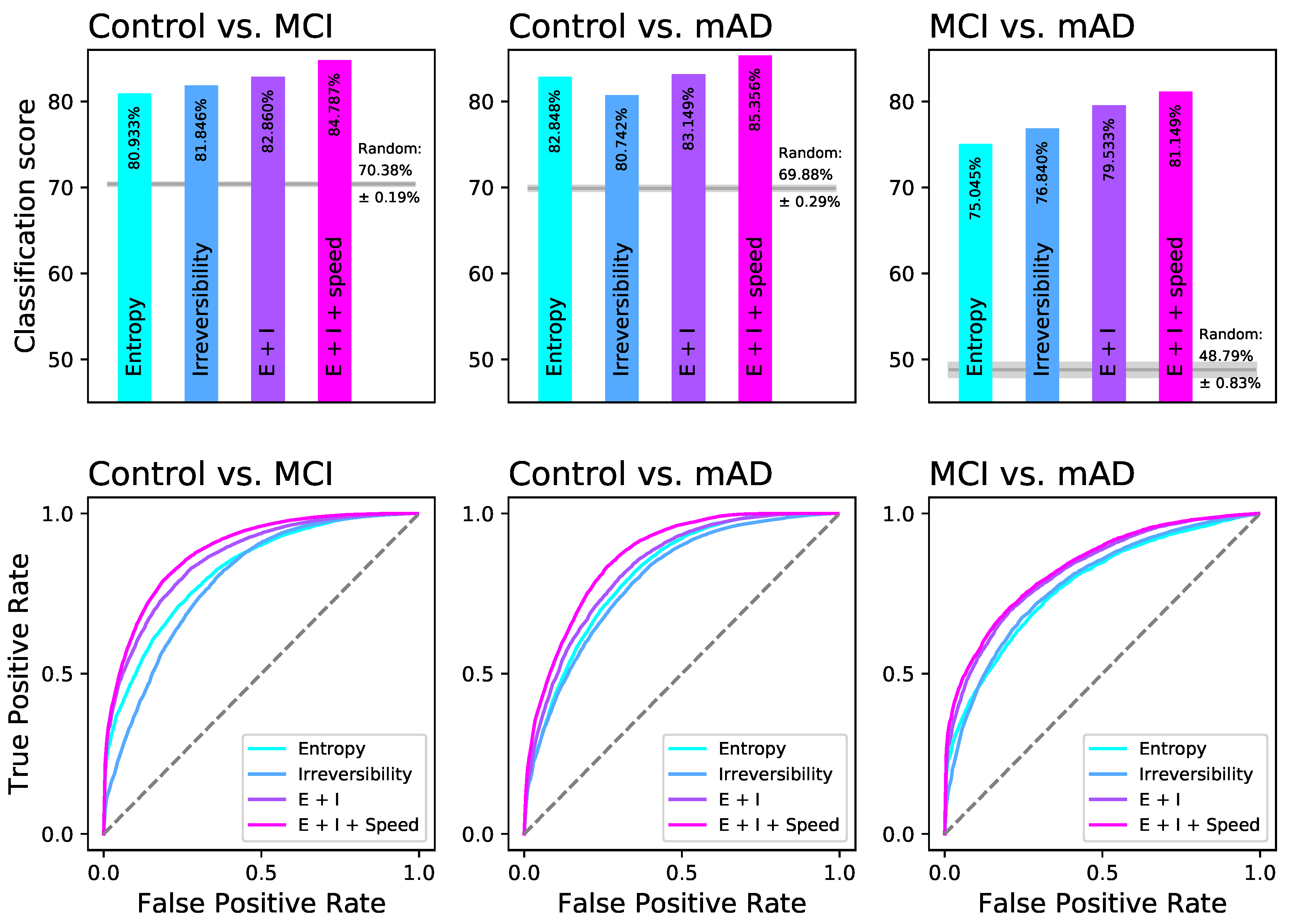
2.2. Random Forests Detect a Distinguishable Pattern between the Different Groups of Cognitive Impairment
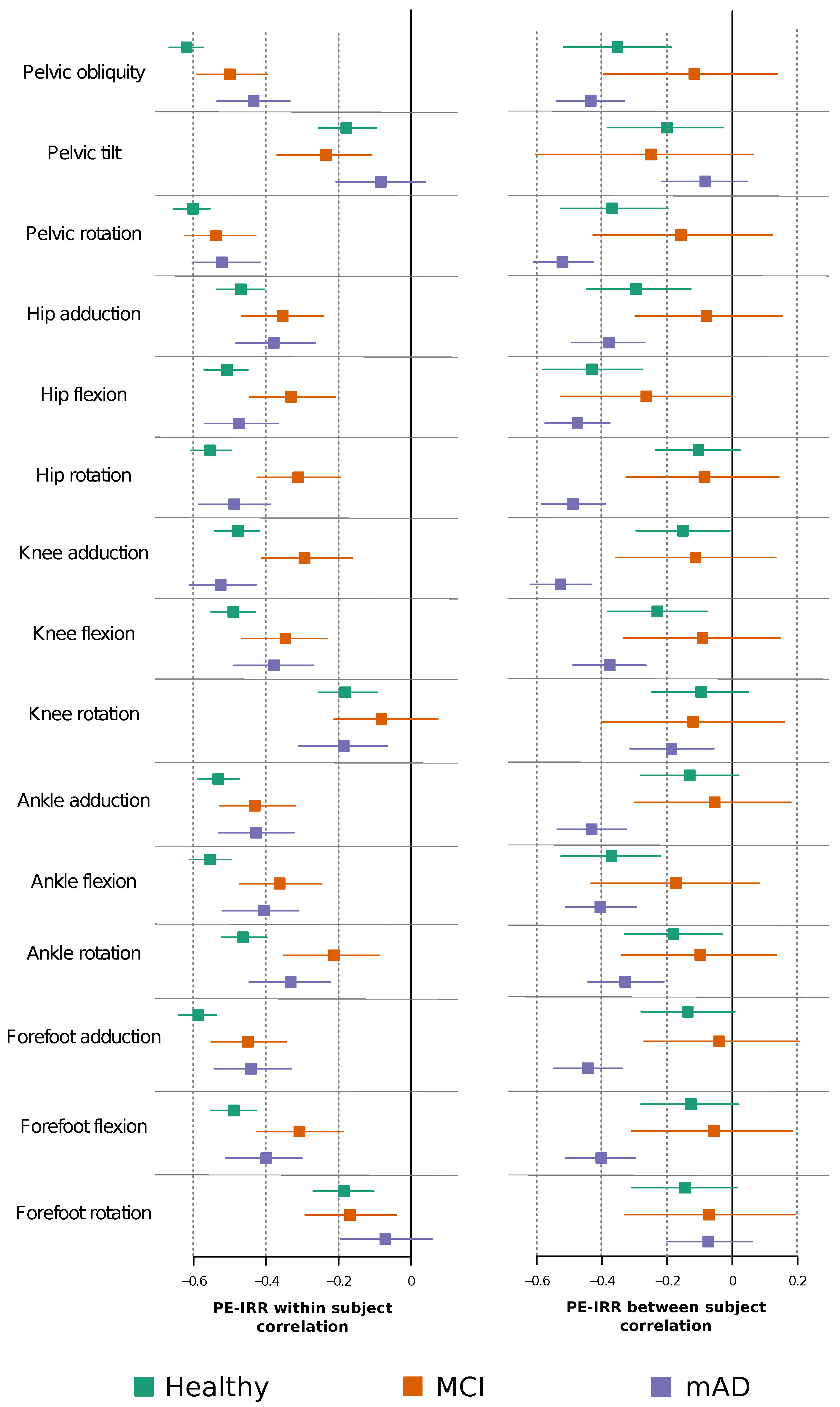
2.3. Permutation Entropy and Irreversibility Yield Complementary Information
3. Discussion
4. Materials and Methods
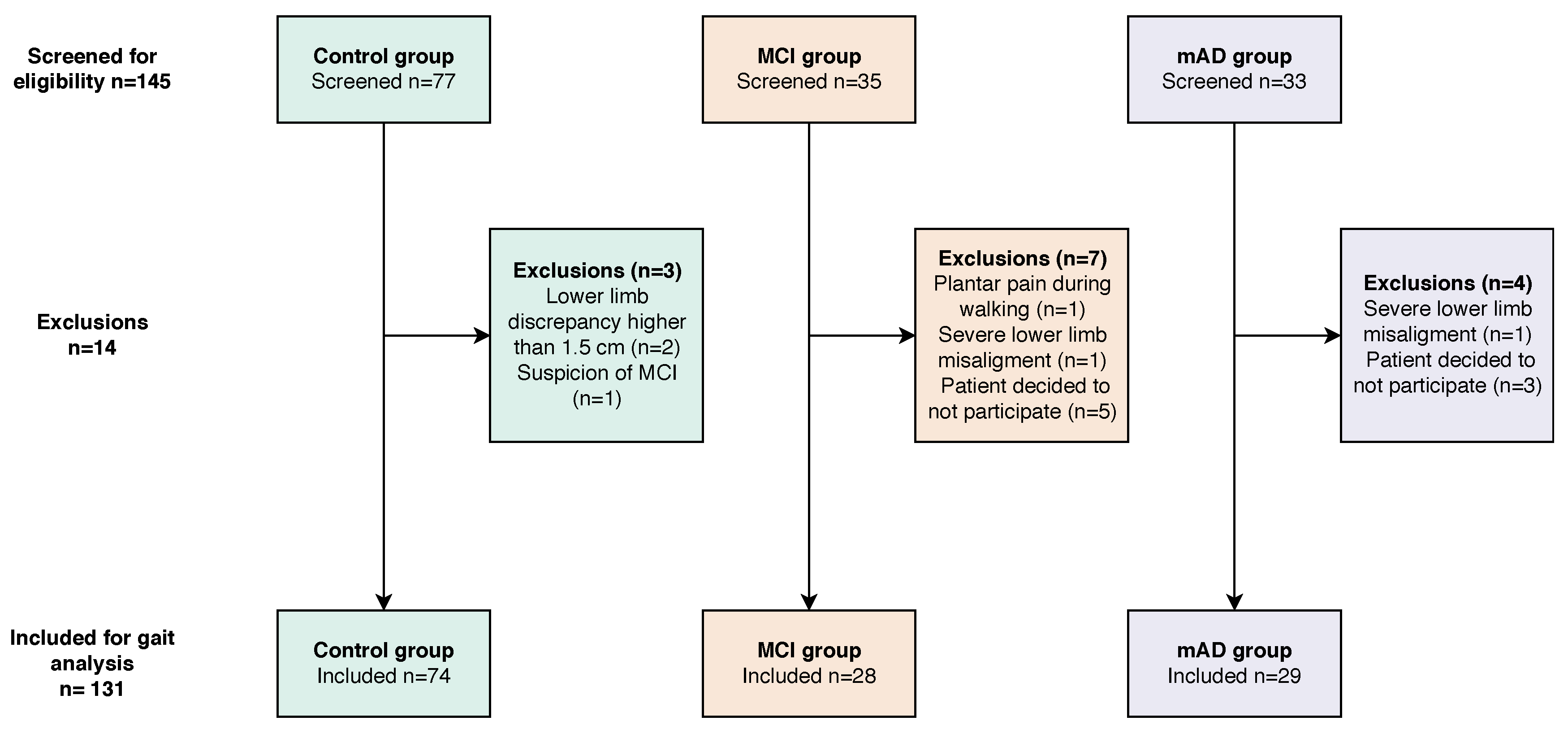
4.1. Participants
- Age lower than 75 years;
- Absence of a diagnosis of moderate or severe dementia;
- Absence of clinical suspicion of rapidly progressive dementia;
- Absence of previous stroke within six months or previous stroke without full recovery;
- Absence of an active and non-related diagnosis of a psychiatric or neurological disorder that may impair gait;
- No suspicion of rapidly progressive dementia;
- Not having history of previous stroke within six months or focal findings attributed to a previous stroke;
- No previous psychiatric or other neurological disorders that may impair clinical evaluation or gait analysis;
- Absence of a current diagnosis of an inter-current systemic neurological or cardio- respiratory disease;
- Absence of severe visual or auditory disability;
- Absence of surgical treatment in lower limbs within the previous year;
- Ability to walk seven meters without external support;
- Satisfactory family environment.
- Age between 50 years and 75 years;
- Absence of orthopaedic lesions or major surgery within the previous five years;
- Absence of cognitive complaints;
- Absence of a current diagnosis of an inter-current systemic neurologic or cardio- respiratory disease;
- Absence of severe visual or auditory disability, and
4.2. 3D Gait Analysis and Data Preprocessing
4.3. Permutation Patterns and Entropy
4.4. Irreversibility of Time Series
4.5. Effect of Cognitive Decline on Permutation Entropy and Irreversibility of Every Joint Kinematic Time Series: Univariate Study
4.6. Correlation of Permutation Entropy and Irreversibility of Every Joint Kinematic Time Series in Each Joint Time Series
4.7. Classification Tasks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s dementia |
| IGA | Instrumented gait analysis |
| IRR | Amount of irreversibility |
| IQR | Inter-Quartile Range |
| mAD | Mild Alzheimer’s dementia |
| MCI | Mild cognitive impairment |
| PE | Permutation entropy |
| RF | Random forests |
References
- Clark, C.; Trojanowski, J.Q. Neurodegenerative Dementias: Clinical Features and Pathological Mechanisms; Appleton & Lange: New York, NY, USA, 2000. [Google Scholar]
- Wimo, A.; Guerchet, M.; Ali, G.C.; Wu, Y.T.; Prina, A.M.; Winblad, B.; Jönsson, L.; Liu, Z.; Prince, M. The worldwide costs of dementia 2015 and comparisons with 2010. Alzheimer’s Dement. 2017, 13, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Arrighi, H.M.; Michels, S.; Cedarbaum, J.M. Mild cognitive impairment: Disparity of incidence and prevalence estimates. Alzheimer’s Dement. 2012, 8, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Petersen, R.C. Mild cognitive impairment as a diagnostic entity. J. Intern. Med. 2004, 256, 183–194. [Google Scholar] [CrossRef] [PubMed]
- Petersen, R.C. Mild cognitive impairment. N. Engl. J. Med. 2011, 364, 2227–2234. [Google Scholar] [CrossRef] [PubMed]
- Farias, S.T.; Mungas, D.; Reed, B.R.; Harvey, D.; DeCarli, C. Progression of mild cognitive impairment to dementia in clinic-vs community-based cohorts. Arch. Neurol. 2009, 66, 1151–1157. [Google Scholar] [CrossRef]
- Dubois, B.; Hampel, H.; Feldman, H.H.; Scheltens, P.; Aisen, P.; Andrieu, S.; Bakardjian, H.; Benali, H.; Bertram, L.; Blennow, K. Preclinical Alzheimer’s disease: Definition, natural history, and diagnostic criteria. Alzheimer’s Dement. 2016, 12, 292–323. [Google Scholar] [CrossRef]
- Dubois, B.; Feldman, H.H.; Jacova, C.; Hampel, H.; Molinuevo, J.L.; Blennow, K.; DeKosky, S.T.; Gauthier, S.; Selkoe, D.; Bateman, R. Advancing research diagnostic criteria for Alzheimer’s disease: The IWG-2 criteria. Lancet Neurol. 2014, 13, 614–629. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Mammone, N.; Bonanno, L.; Salvo, S.D.; Marino, S.; Bramanti, P.; Bramanti, A.; Morabito, F.C. Permutation disalignment index as an indirect, EEG-based, measure of brain connectivity in MCI and AD patients. Int. J. Neural Syst. 2017, 27, 1750020. [Google Scholar] [CrossRef]
- Stonnington, C.M.; Chen, Y.; Savage, C.R.; Lee, W.; Bauer, R.J., III; Sharieff, S.; Thiyyagura, P.; Alexander, G.E.; Caselli, R.J.; Locke, D.E. Predicting imminent progression to clinically significant memory decline using volumetric MRI and FDG PET. J. Alzheimer’s Dis. 2018, 63, 603–615. [Google Scholar] [CrossRef]
- Hane, F.T.; Robinson, M.; Lee, B.Y.; Bai, O.; Leonenko, Z.; Albert, M.S. Recent progress in Alzheimer’s disease research, part 3: Diagnosis and treatment. J. Alzheimer’s Dis. 2017, 57, 645–665. [Google Scholar] [CrossRef] [PubMed]
- Fodor, Z.; Sirály, E.; Horváth, A.; Salacz, P.; Hidasi, Z.; Csibri, É.; Szabó, Á.; Csukly, G. Decreased event-related beta synchronization during memory maintenance marks early cognitive decline in mild cognitive impairment. J. Alzheimer’s Dis. 2018, 63, 489–502. [Google Scholar] [CrossRef] [PubMed]
- Padovani, A.; Benussi, A.; Cantoni, V.; Dell’Era, V.; Cotelli, M.S.; Caratozzolo, S.; Turrone, R.; Rozzini, L.; Alberici, A.; Altomare, D. Diagnosis of mild cognitive impairment due to Alzheimer’s disease with transcranial magnetic stimulation. J. Alzheimer’s Dis. 2018, 65, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Henley, B.C.; Shokouhi, M.; Mahajan, A.Y.; Inan, O.T.; Hajjar, I. Cardiovascular Response to Mental Stress in Mild Cognitive Impairment and its Association with Cerebral Perfusion. J. Alzheimer’s Dis. 2018, 63, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Illán-Gala, I.; Alcolea, D.; Montal, V.; Dols-Icardo, O.; Muñoz, L.; de Luna, N.; Turón-Sans, J.; Cortés-Vicente, E.; Sánchez-Saudinós, M.B.; Subirana, A. CSF sAPPβ, YKL-40, and NfL along the ALS-FTD spectrum. Neurology 2018, 91, e1619–e1628. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.; Lord, S.; Bunce, J.; Burn, D.; Rochester, L. Gait and cognition: Mapping the global and discrete relationships in ageing and neurodegenerative disease. Neurosci. Biobehav. Rev. 2016, 64, 326–345. [Google Scholar] [CrossRef] [PubMed]
- De Cock, A.M.; Fransen, E.; Perkisas, S.; Verhoeven, V.; Beauchet, O.; Vandewoude, M.; Remmen, R. Comprehensive quantitative spatiotemporal gait analysis identifies gait characteristics for early dementia sub-typing in community dwelling older adults. Front. Neurol. 2019, 10, 313. [Google Scholar] [CrossRef] [PubMed]
- Sakurai, R.; Montero-Odasso, M. Apolipoprotein E4 allele and gait performance in mild cognitive impairment: Results from the Gait and Brain Study. J. Gerontol. Ser. A Biomed. Sci. Med Sci. 2017, 72, 1676–1682. [Google Scholar] [CrossRef]
- Persad, C.C.; Jones, J.L.; Ashton-Miller, J.A.; Alexander, N.B.; Giordani, B. Executive function and gait in older adults with cognitive impairment. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2008, 63, 1350–1355. [Google Scholar] [CrossRef]
- Maquet, D.; Lekeu, F.; Warzee, E.; Gillain, S.; Wojtasik, V.; Salmon, E.; Petermans, J.; Croisier, J.L. Gait analysis in elderly adult patients with mild cognitive impairment and patients with mild Alzheimer’s disease: Simple versus dual task: A preliminary report. Clin. Physiol. Funct. Imaging 2010, 30, 51–56. [Google Scholar] [CrossRef]
- Tian, Q.; Chastan, N.; Bair, W.N.; Resnick, S.M.; Ferrucci, L.; Studenski, S.A. The brain map of gait variability in aging, cognitive impairment and dementia: A systematic review. Neurosci. Biobehav. Rev. 2017, 74, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Allali, G.; Montembeault, M.; Saj, A.; Wong, C.H.; Cooper-Brown, L.A.; Bherer, L.; Beauchet, O. Structural Brain Volume Covariance Associated with Gait Speed in Patients with Amnestic and Non-Amnestic Mild Cognitive Impairment: A Double Dissociation. J. Alzheimer’s Dis. 2019. [Google Scholar] [CrossRef] [PubMed]
- Auyeung, T.W.; Kwok, T.; Lee, J.; Leung, P.C.; Leung, J.; Woo, J. Functional decline in cognitive impairment–The relationship between physical and cognitive function. Neuroepidemiology 2008, 31, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Beauchet, O.; Annweiler, C.; Callisaya, M.L.; De Cock, A.M.; Helbostad, J.L.; Kressig, R.W.; Srikanth, V.; Steinmetz, J.P.; Blumen, H.M.; Verghese, J. Poor gait performance and prediction of dementia: Results from a meta-analysis. J. Am. Med Dir. Assoc. 2016, 17, 482–490. [Google Scholar] [CrossRef] [PubMed]
- Peel, N.M.; Alapatt, L.J.; Jones, L.V.; Hubbard, R.E. The association between gait speed and cognitive status in community-dwelling older people: A systematic review and meta-analysis. J. Gerontol. Ser. A 2018, 74, 943–948. [Google Scholar] [CrossRef] [PubMed]
- Grande, G.; Triolo, F.; Nuara, A.; Welmer, A.K.; Fratiglioni, L.; Vetrano, D.L. Measuring gait speed to better identify prodromal dementia. Exp. Gerontol. 2019, 124. [Google Scholar] [CrossRef] [PubMed]
- Bahureksa, L.; Najafi, B.; Saleh, A.; Sabbagh, M.; Coon, D.; Mohler, M.J.; Schwenk, M. The impact of mild cognitive impairment on gait and balance: A systematic review and meta-analysis of studies using instrumented assessment. Gerontology 2017, 63, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M. Gait dynamics, fractals and falls: Finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci. 2007, 26, 555–589. [Google Scholar] [CrossRef]
- Byun, S.; Han, J.W.; Kim, T.H.; Kim, K.; Kim, T.H.; Park, J.Y.; Suh, S.W.; Seo, J.Y.; So, Y.; Lee, K.H. Gait variability can predict the risk of cognitive decline in cognitively normal older people. Dement. Geriatr. Cogn. Disord. 2018, 45, 251–261. [Google Scholar] [CrossRef]
- Ihlen, E.A.; Weiss, A.; Bourke, A.; Helbostad, J.L.; Hausdorff, J.M. The complexity of daily life walking in older adult community-dwelling fallers and non-fallers. J. Biomech. 2016, 49, 1420–1428. [Google Scholar] [CrossRef]
- Rucco, R.; Agosti, V.; Jacini, F.; Sorrentino, P.; Varriale, P.; De Stefano, M.; Milan, G.; Montella, P.; Sorrentino, G. Spatio-temporal and kinematic gait analysis in patients with Frontotemporal dementia and Alzheimer’s disease through 3D motion capture. Gait Posture 2017, 52, 312–317. [Google Scholar] [CrossRef] [PubMed]
- Shumway-Cook, A.; Woollacott, M.H. Motor Control: Translating Research into Clinical Practice; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007. [Google Scholar]
- Gage, J.R.; Schwartz, M.H.; Koop, S.E.; Novacheck, T.F. The Identification andTreatment of Gait Problems in Cerebral Palsy; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 4. [Google Scholar]
- Lai, D.T.; Begg, R.K.; Palaniswami, M. Computational intelligence in gait research: A perspective on current applications and future challenges. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 687–702. [Google Scholar] [CrossRef] [PubMed]
- Pulido-Valdeolivas, I.; Gómez-Andrés, D.; Martín-Gonzalo, J.A.; Rodríguez-Andonaegui, I.; López-López, J.; Pascual-Pascual, S.I.; Rausell, E. Gait phenotypes in paediatric hereditary spastic paraplegia revealed by dynamic time warping analysis and random forests. PLoS ONE 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Amigó, J. Permutation Complexity in Dynamical Systems: Ordinal Patterns, Permutation Entropy and All That; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zanin, M.; Rodríguez-González, A.; Menasalvas Ruiz, E.; Papo, D. Assessing Time Series Reversibility through Permutation Patterns. Entropy 2018, 20, 665. [Google Scholar]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Phys. A Stat. Mech. Appl. 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Sun, S.Q. Complexity analysis of the gait time series using fine-grained permutation entropy. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 7, pp. 3878–3879. [Google Scholar]
- Leverick, G.; Szturm, T.; Wu, C. Investigation of the suitability of utilizing permutation entropy to characterize gait dynamics. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013. [Google Scholar]
- Chen, M.S.; Jiang, B.C. Resistance training exercise program for intervention to enhance gait function in elderly chronically ill patients: Multivariate multiscale entropy for center of pressure signal analysis. Comput. Math. Methods Med. 2014, 2014. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, P.; Luo, X.; Wu, M.; Liao, L.; Yang, S.; Rangayyan, R.M. Measuring signal fluctuations in gait rhythm time series of patients with Parkinson’s disease using entropy parameters. Biomed. Signal Process. Control. 2017, 31, 265–271. [Google Scholar] [CrossRef]
- Zanin, M.; Gómez-Andrés, D.; Pulido-Valdeolivas, I.; Martín-Gonzalo, J.; López-López, J.; Pascual-Pascual, S.; Rausell, E. Characterizing normal and pathological gait through permutation entropy. Entropy 2018, 20, 77. [Google Scholar] [CrossRef]
- Orellana, J.N.; Sixto, A.S.; Torres, B.D.L.C.; Cachadina, E.S.; Martín, P.F.; de la Rosa, F.B. Multiscale time irreversibility: Is it useful in the analysis of human gait? Biomed. Signal Process. Control. 2018, 39, 431–434. [Google Scholar] [CrossRef]
- McKhann, G.M.; Knopman, D.S.; Chertkow, H.; Hyman, B.T.; Jack, C.R., Jr.; Kawas, C.H.; Klunk, W.E.; Koroshetz, W.J.; Manly, J.J.; Mayeux, R. The diagnosis of dementia due to Alzheimer’s disease: Recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimer’s Dement. 2011, 7, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Hughes, C.P.; Berg, L.; Danziger, W.; Coben, L.A.; Martin, R.L. A new clinical scale for the staging of dementia. Br. J. Psychiatry 1982, 140, 566–572. [Google Scholar] [CrossRef] [PubMed]
- Blessed, G.; Tomlinson, B.E.; Roth, M. The association between quantitative measures of dementia and of senile change in the cerebral grey matter of elderly subjects. Br. J. Psychiatry 1968, 114, 797–811. [Google Scholar] [CrossRef] [PubMed]
- Folstein, M.F.; Robins, L.N.; Helzer, J.E. The mini-mental state examination. Arch. Gen. Psychiatry 1983, 40, 812. [Google Scholar] [CrossRef]
- Lobo, A.; Saz, P.; Marcos, G.; Día, J.L.; de la Cámara, C.; Ventura, T.; Morales Asín, F.; Fernando Pascual, L.; Montañés, J.; Aznar, S. Revalidación y normalización del Mini-Examen Cognoscitivo (primera versión en castellano del Mini-Mental Status Examination) en la población general geriátrica. Med. Clin. 1999, 112, 767–774. [Google Scholar]
- Wechsler, D. Wechsler Adult Intelligence Scale—Fourth Edition (WAIS–IV); NCS Pearson: San Antonio, TX, USA, 2008; Volume 22, p. 498. [Google Scholar]
- Peña-Casanova, J. Programa Integrado de Exploración Neuropsicológica: Test Barcelona Revisado; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Buschke, H. Cued recall in amnesia. J. Clin. Exp. Neuropsychol. 1984, 6, 433–440. [Google Scholar] [CrossRef]
- Peña-Casanova, J.; Gramunt-Fombuena, N.; Quiñones-Úbeda, S.; Sánchez-Benavides, G.; Aguilar, M.; Badenes, D.; Molinuevo, J.L.; Robles, A.; Barquero, M.S.; Payno, M. Spanish multicenter normative studies (NEURONORMA Project): Norms for the Rey–Osterrieth complex figure (copy and memory), and free and cued selective reminding test. Arch. Clin. Neuropsychol. 2009, 24, 371–393. [Google Scholar] [CrossRef]
- Battersby, W.S.; Bender, M.B.; Pollack, M.; Kahn, R.L. Unilateral spatial agnosia (inattention) in patients with cerebral lesions. Brain 1956, 79, 68–93. [Google Scholar] [CrossRef]
- Rey, A. L’examen psychologique dans les cas d’encéphalopathie traumatique. (Les problems.). Arch. Psychol. 1941, 28, 215–285. [Google Scholar]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A. True and false forbidden patterns in deterministic and random dynamics. EPL 2007, 79, 50001. [Google Scholar] [CrossRef]
- Lawrance, A. Directionality and reversibility in time series. Int. Stat. Rev. 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Stone, L.; Landan, G.; May, R.M. Detecting time’s arrow: A method for identifying nonlinearity and deterministic chaos in time-series data. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1996, 263, 1509–1513. [Google Scholar]
- Puglisi, A.; Villamaina, D. Irreversible effects of memory. EPL 2009, 88, 30004. [Google Scholar] [CrossRef]
- Yao, W.; Wang, J. Equalities-involved permutation relative entropy in quantifying time irreversibility of heartbeats. arXiv 2018, arXiv:1801.02665. [Google Scholar]
- Yao, W.; Yao, W.; Wang, J.; Dai, J. Quantifying time irreversibility using probabilistic differences between symmetric permutations. Phys. Lett. A 2019, 383, 738–743. [Google Scholar] [CrossRef]
- Hadfield, J. MCMC Methods for Multi-Response Generalized Linear Mixed Models: The MCMCglmm R Package. J. Stat. Softw, Artic. 2010, 33, 1–22. [Google Scholar]
- Dingemanse, N.J.; Dochtermann, N.A. Quantifying individual variation in behaviour: Mixed-effect modelling approaches. J. Anim. Ecol. 2013, 82, 39–54. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| Healthy Subjects (n = 74) | Mild Cognitive Decline (n = 28) | Mild Alzheimer’s Dementia (n = 29) | p-Value | |
|---|---|---|---|---|
| Age (years) [median (Q1–Q3)] | 63.2 (11.2) | 69.1 (5.2) | 67.8 (5.49) | |
| Female [n (%)] | 42 (53%) | 16 (57%) | 17 (59%) | 1 |
| Body mass index (kg/m) [median (Q1–Q3)] | 26.91 (24.13–30.83) | 27.72 (23.13–31,25) | 26.04 (24.02–28.3) | |
| MMSE [median (Q1–Q3)] | 30 (29–30) | 25.5 (22–27) | 20 (18–23) | <0.001 |
| Education level [n (%)] | ||||
| No studies | 3 (4.1%) | 1 (3.6%) | 2 (6.9%) | |
| Basic studies | 51 (68.9%) | 23 (82.1%) | 22 (75.9%) | |
| Intermediate studies | 8 (10.8%) | 2 (7.1%) | 2 (6.9%) | |
| University studies | 12 (16.2%) | 2 (7.1%) | 3 (10.3%) | |
| Time with cognitive complaints [median (IQR)] | - | 12 (6–24.25) | 13 (7–24) | |
| Knee osteoarthritis * [n (%)] | 0 (0%) | 0 (0%) | 1 (3.4%) | |
| Hip osteoarthritis * [n (%)] | 0 (0%) | 0 (0%) | 1 (3.4%) | |
| Normalised walking speed (s) [median (Q1–Q3)] | 1.13 (1.03–1.28) | 0.99 (0.86) | 0.94 (0.77–1.09) | <0.001 |
| Cadence (steps/s) [median (Q1–Q3)] | 1.63 (1.53–1.75) | 1.5 (1.43–1.66) | 1.5 (1.39–1.59) | |
| Stance time (% gait cycle) [median (Q1–Q3)] | 65 (64.1–66) | 67.1 (65.7–69.1) | 66.9 (66–70.4) | <0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Gonzalo, J.-A.; Pulido-Valdeolivas, I.; Wang, Y.; Wang, T.; Chiclana-Actis, G.; Algarra-Lucas, M.d.C.; Palmí-Cortés, I.; Fernández Travieso, J.; Torrecillas-Narváez, M.D.; Miralles-Martinez, A.A.; et al. Permutation Entropy and Irreversibility in Gait Kinematic Time Series from Patients with Mild Cognitive Decline and Early Alzheimer’s Dementia. Entropy 2019, 21, 868. https://doi.org/10.3390/e21090868
Martín-Gonzalo J-A, Pulido-Valdeolivas I, Wang Y, Wang T, Chiclana-Actis G, Algarra-Lucas MdC, Palmí-Cortés I, Fernández Travieso J, Torrecillas-Narváez MD, Miralles-Martinez AA, et al. Permutation Entropy and Irreversibility in Gait Kinematic Time Series from Patients with Mild Cognitive Decline and Early Alzheimer’s Dementia. Entropy. 2019; 21(9):868. https://doi.org/10.3390/e21090868
Chicago/Turabian StyleMartín-Gonzalo, Juan-Andrés, Irene Pulido-Valdeolivas, Yu Wang, Ting Wang, Guadalupe Chiclana-Actis, Maria del Carmen Algarra-Lucas, Itziar Palmí-Cortés, Jorge Fernández Travieso, Maria Dolores Torrecillas-Narváez, Ambrosio A. Miralles-Martinez, and et al. 2019. "Permutation Entropy and Irreversibility in Gait Kinematic Time Series from Patients with Mild Cognitive Decline and Early Alzheimer’s Dementia" Entropy 21, no. 9: 868. https://doi.org/10.3390/e21090868
APA StyleMartín-Gonzalo, J.-A., Pulido-Valdeolivas, I., Wang, Y., Wang, T., Chiclana-Actis, G., Algarra-Lucas, M. d. C., Palmí-Cortés, I., Fernández Travieso, J., Torrecillas-Narváez, M. D., Miralles-Martinez, A. A., Rausell, E., Gómez-Andrés, D., & Zanin, M. (2019). Permutation Entropy and Irreversibility in Gait Kinematic Time Series from Patients with Mild Cognitive Decline and Early Alzheimer’s Dementia. Entropy, 21(9), 868. https://doi.org/10.3390/e21090868






