Topological Information Data Analysis
Abstract
“When you use the word information, you should rather use the word form”–René Thom
| Contents | ||
| 1 | Introduction | 2 |
| 1.1 | Information Decompositions and Multivariate Statistical Dependencies | 2 |
| 1.2 | The Approach by Information Topology | 3 |
| 2 | Theory: Homological Nature of Entropy and Information Functions | 6 |
| 3 | Results | 8 |
| 3.1 | Entropy and Mutual-Information Decompositions | 8 |
| 3.2 | The Independence Criterion | 11 |
| 3.3 | Information Coordinates | 12 |
| 3.4 | Mutual-Information Negativity and Links | 16 |
| 4 | Experimental Validation: Unsupervised Classification of Cell Types and Gene Modules | 18 |
| 4.1 | Gene Expression Dataset | 18 |
| 4.2 | Ik Positivity and General Correlations, Negativity and Clusters | 18 |
| 4.3 | Cell Type Classification | 20 |
| 4.3.1 | Example of Cell Type Classification with a Low Sample Size m = 41, Dimension n = 20, and Graining N = 9. | 20 |
| 4.3.2 | Total Correlations (Multi-Information) vs. Mutual-Information | 22 |
| 5 | Discussion | 23 |
| 5.1 | Topological and Statistical Information Decompositions | 23 |
| 5.2 | Mutual-Information Positivity and Negativity | 23 |
| 5.3 | Total Correlations (Multi-Information) | 24 |
| 5.4 | Beyond Pairwise Statistical Dependences: Combinatorial Information Storage | 24 |
| 6 | Materials and Methods | 25 |
| 6.1 | The Dataset: Quantified Genetic Expression in Two Cell Types | 25 |
| 6.2 | Probability Estimation | 26 |
| 6.3 | Computation of k-Entropy, k-Information Landscapes and Paths | 28 |
| 6.4 | Estimation of the Undersampling Dimension | 28 |
| 6.4.1 | Statistical Result | 28 |
| 6.4.2 | Computational Result | 29 |
| 6.5 | k-Dependence Test | 30 |
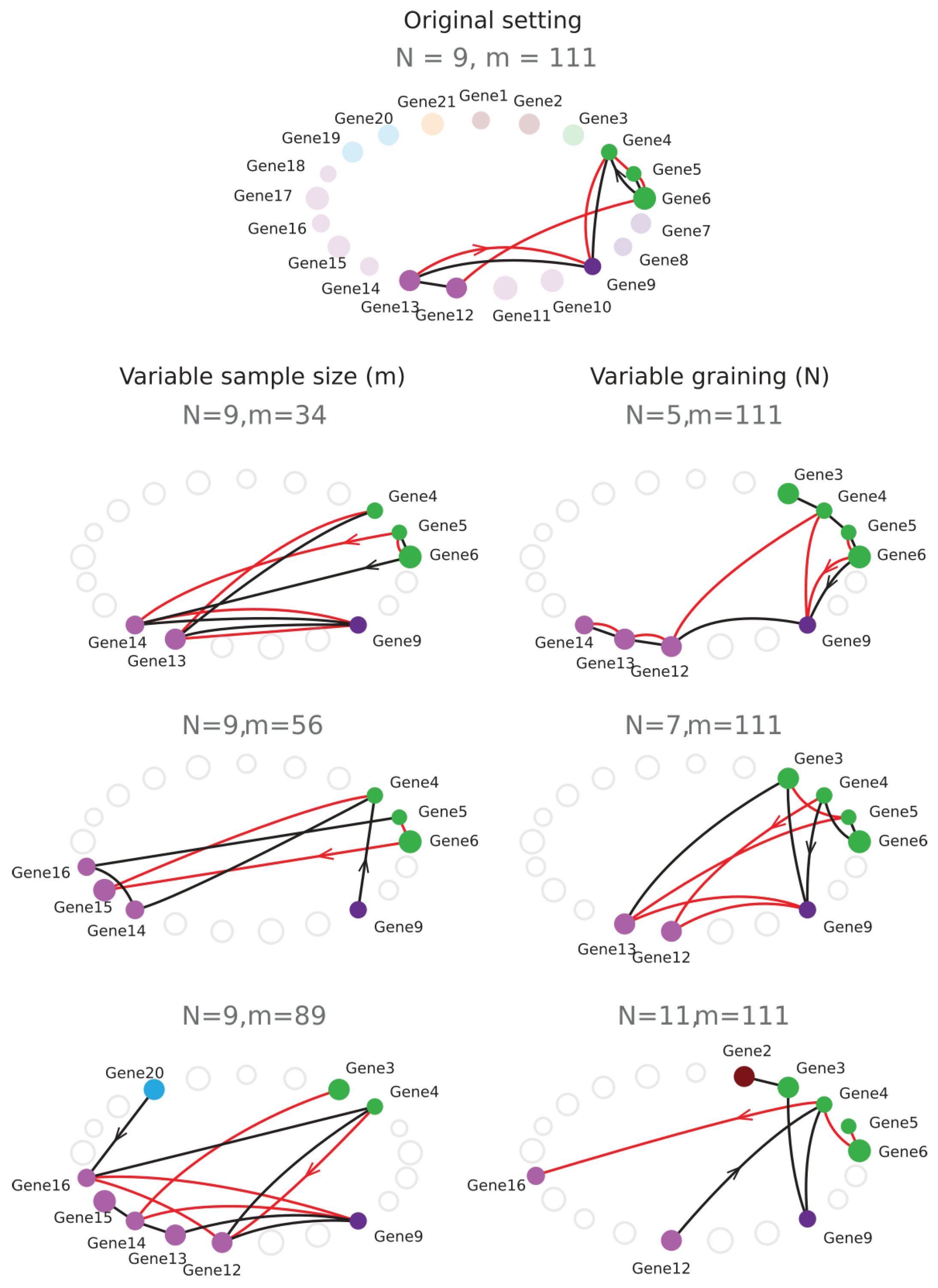
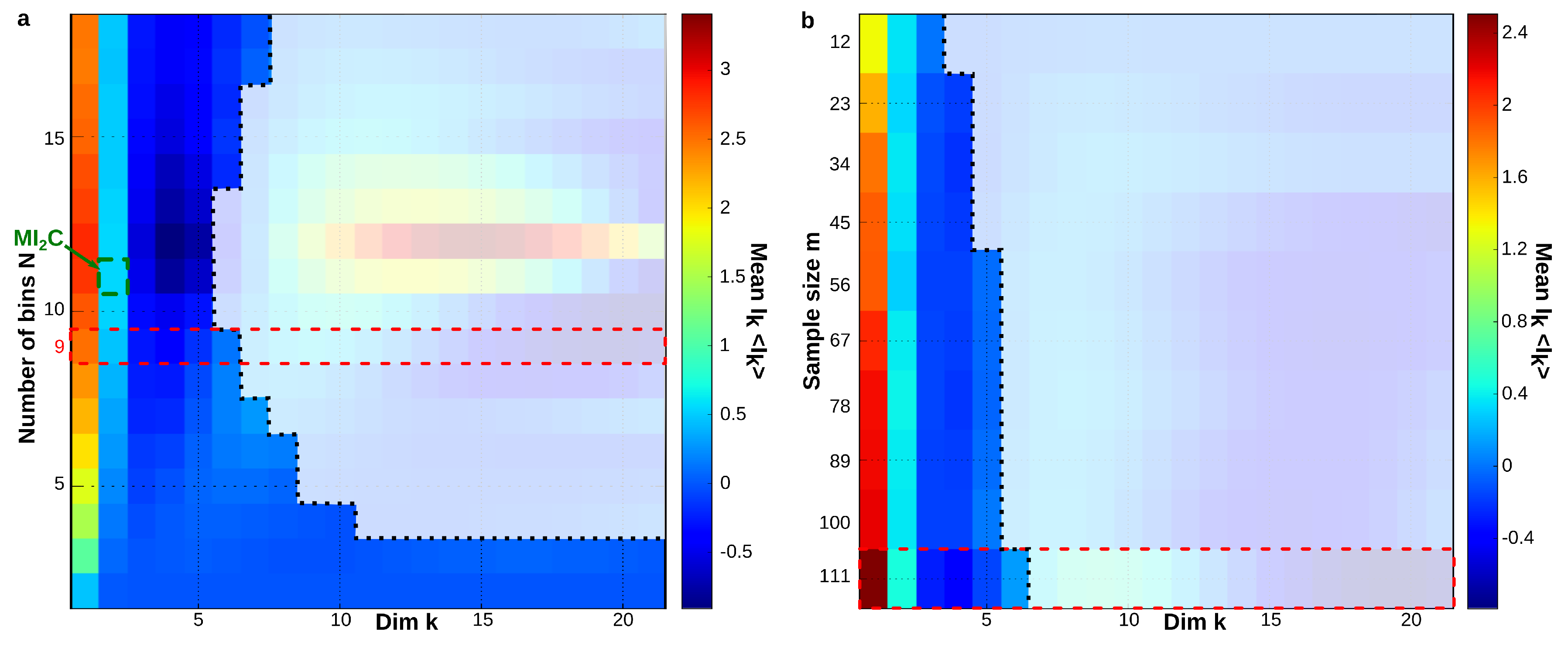
| 6.6 | Sampling Size and Graining Landscapes—Stability of Minimum Energy Complex Estimation | 32 |
| A | Appendix: Bayes Free Energy and Information Quantities | 34 |
| A.1 | Parametric Modelling | 34 |
| A.2 | Bethe Approximation | 35 |
| References | 35 |
1. Introduction
1.1. Information Decompositions and Multivariate Statistical Dependencies
1.2. The Approach by Information Topology
2. Theory: Homological Nature of Entropy and Information Functions
3. Results
3.1. Entropy and Mutual-Information Decompositions
3.2. The Independence Criterion
3.3. Information Coordinates
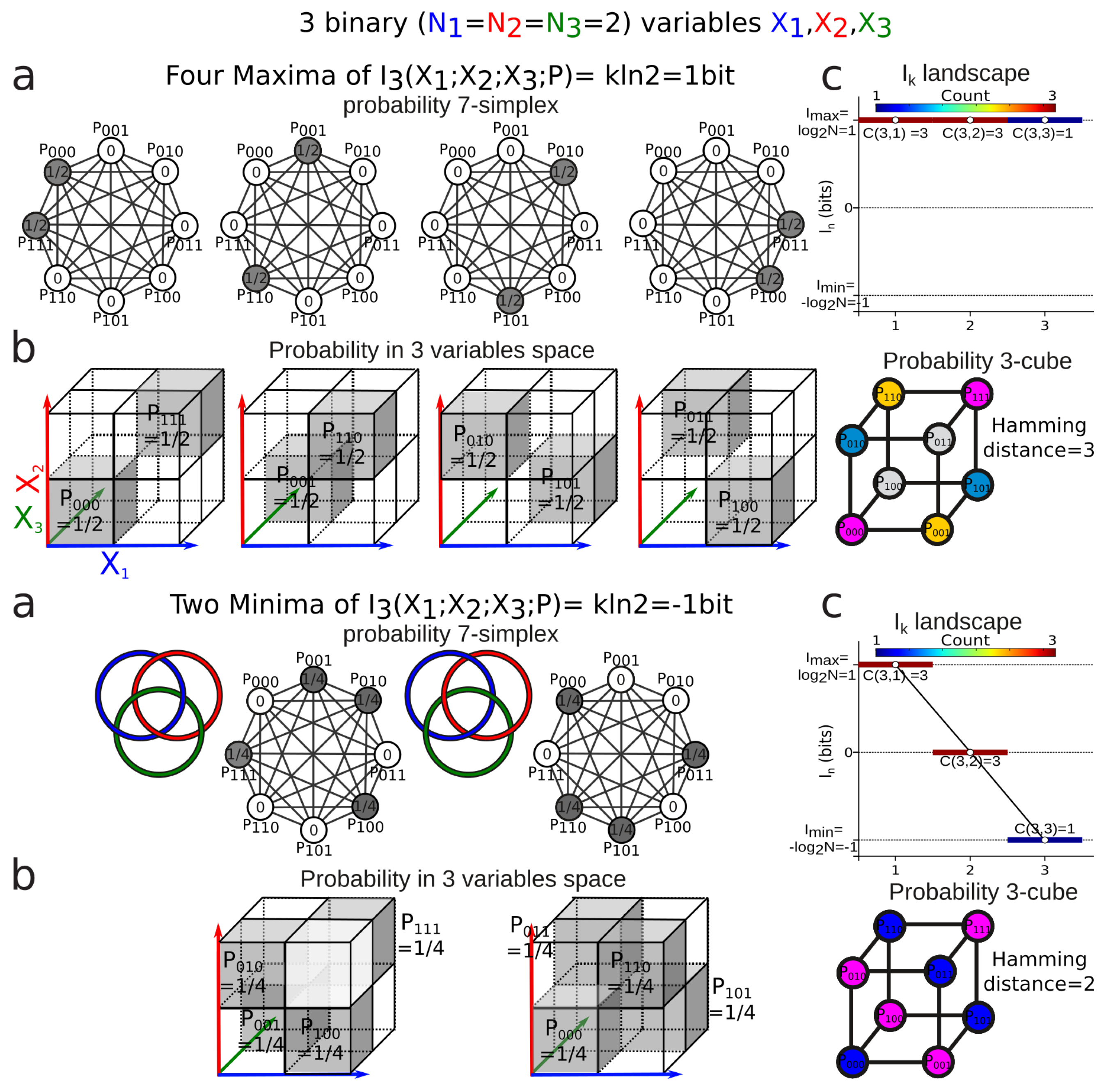
3.4. Mutual-Information Negativity and Links
- (1)
- when two variables are independent from the information of the three is negative or zero;
- (2)
- when two variables are conditionally independent with respect to the third, the information of the three is positive or zero.
4. Experimental Validation: Unsupervised Classification of Cell Types and Gene Modules
4.1. Gene Expression Dataset
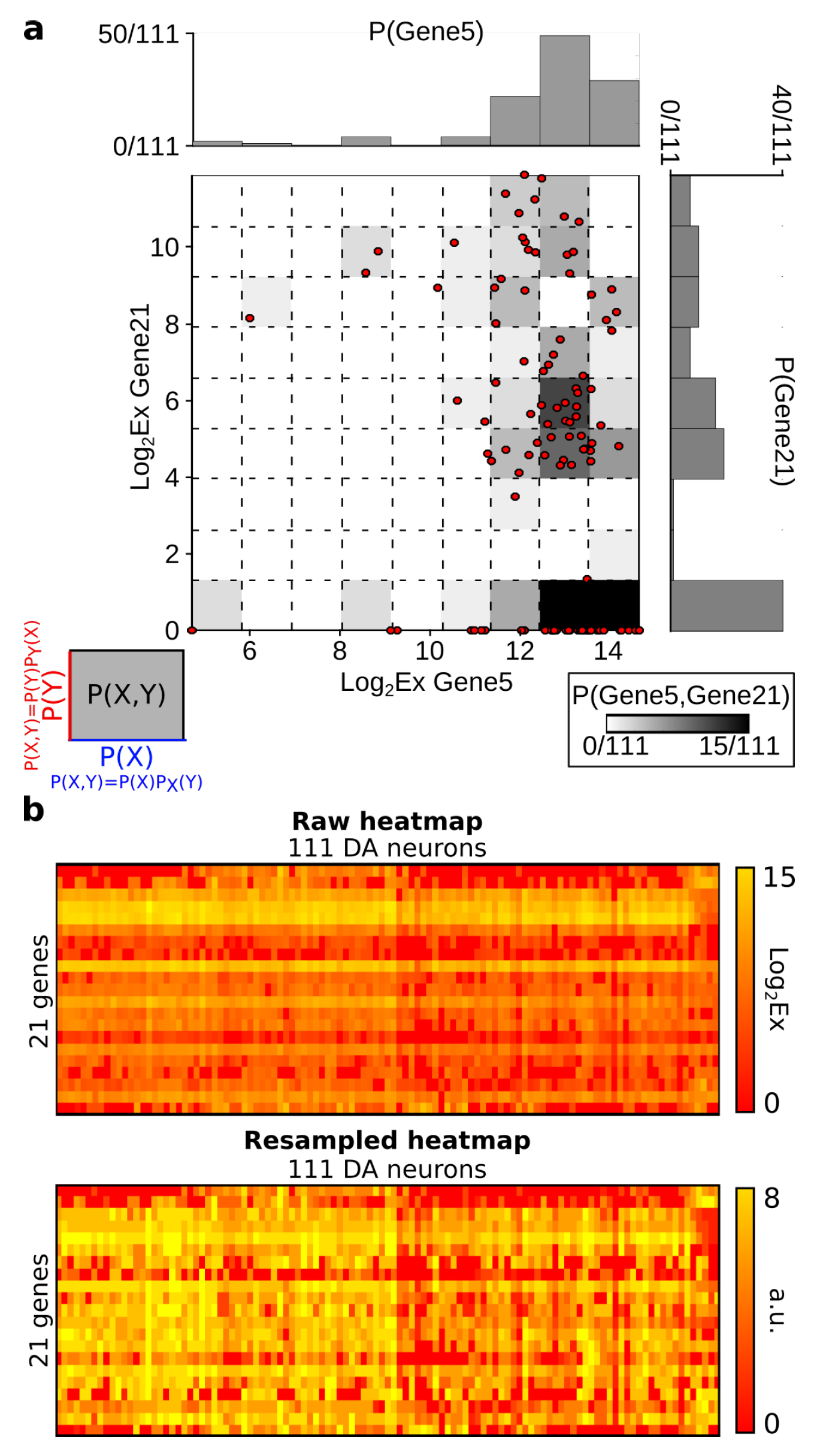
- The analysis with genes as variables: in this case, the “Heat maps” correspond to matrices D (presented in the Section 6.2) together with the labels (population A or population B) of the cells. The data analysis consists of the unsupervised classification of gene modules (presented in Section 4.2).
- The analysis with cells (neurons) as variables: in this case, the “Heat maps” correspond to the transposed matrices (presented in Section 4.3.1) together with the labels (population A or population B) of the cells. The data analysis consists of the unsupervised classification of cell types.
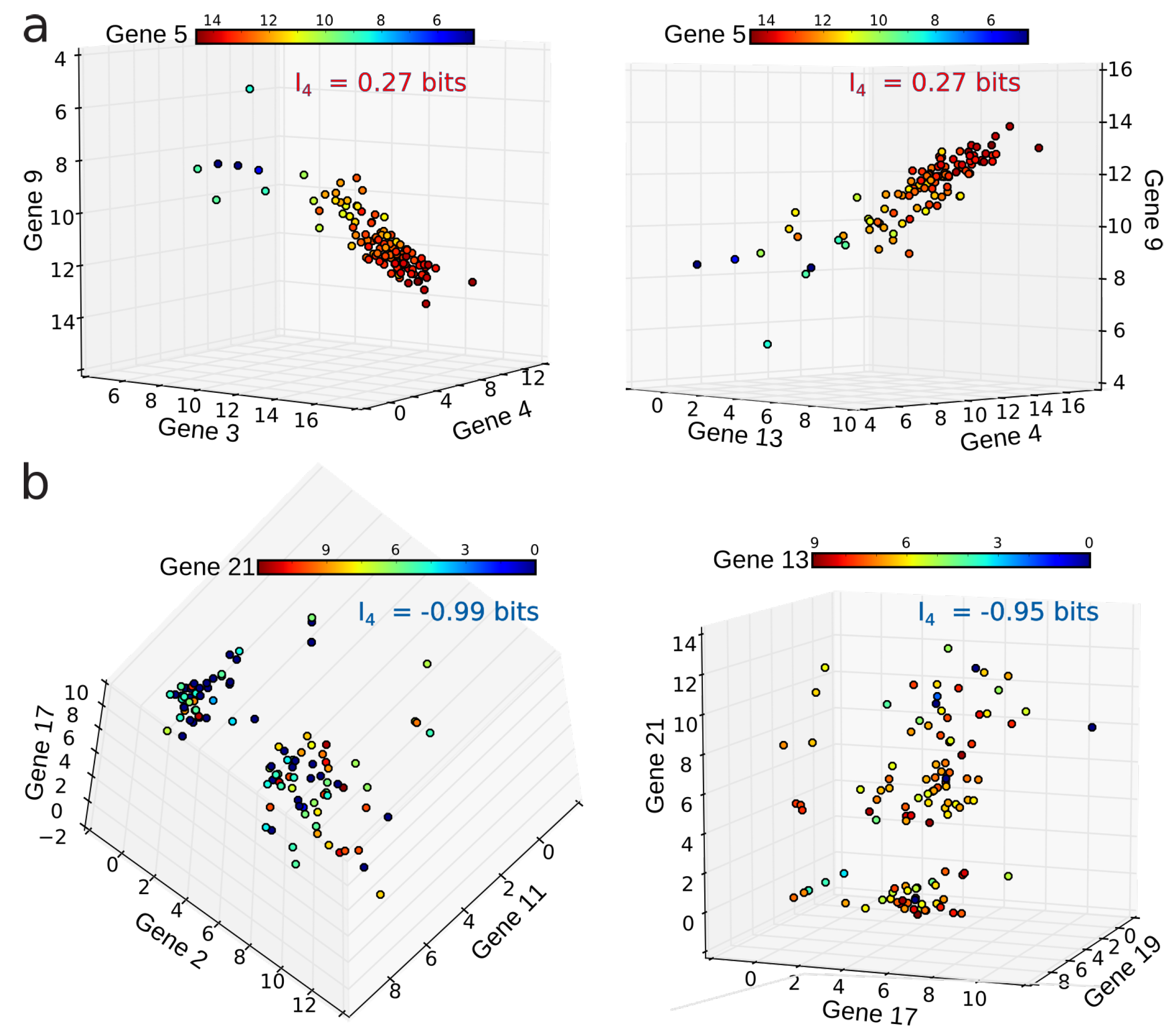
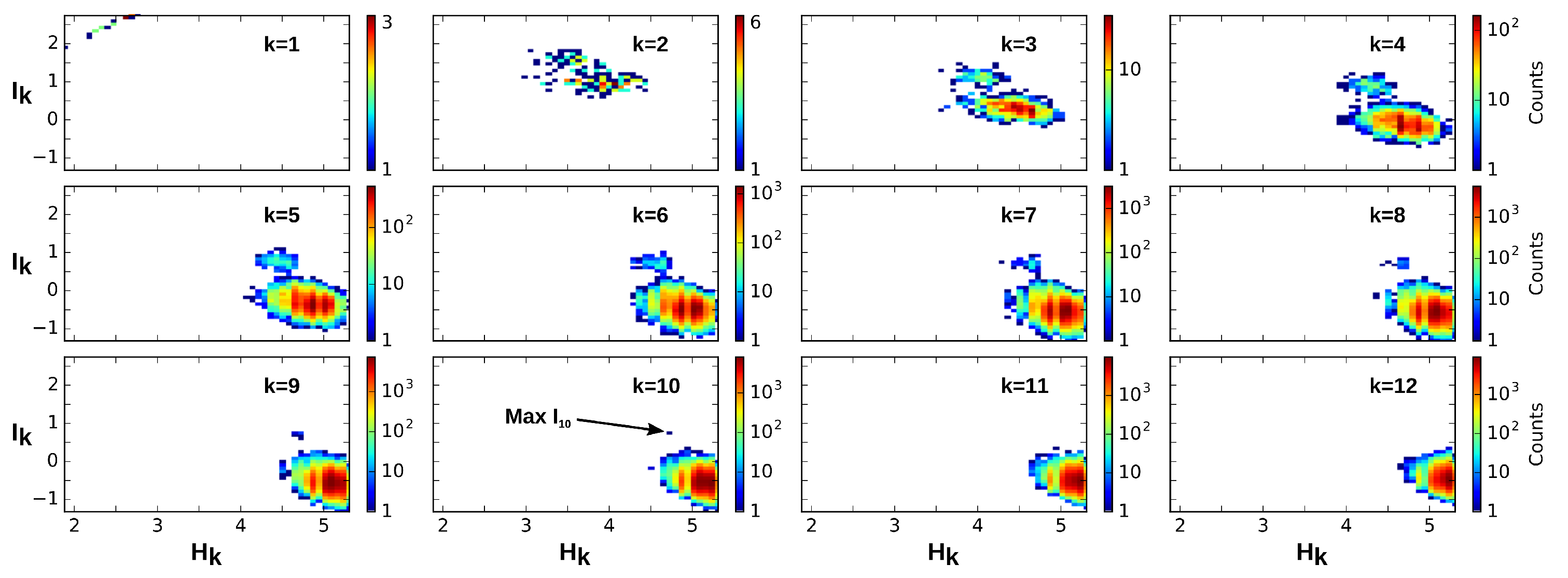
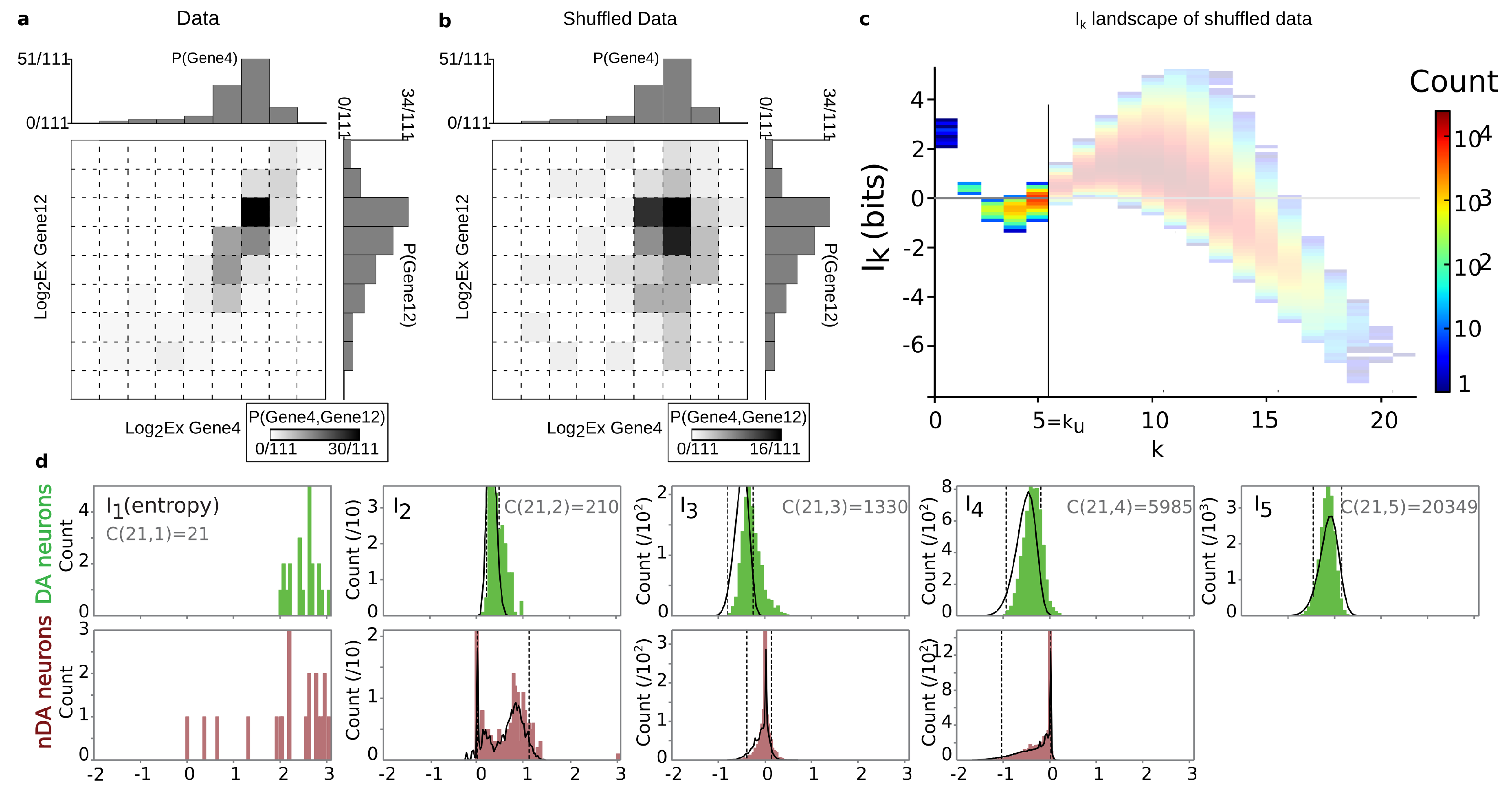
4.2. Positivity and General Correlations, Negativity and Clusters
4.3. Cell Type Classification
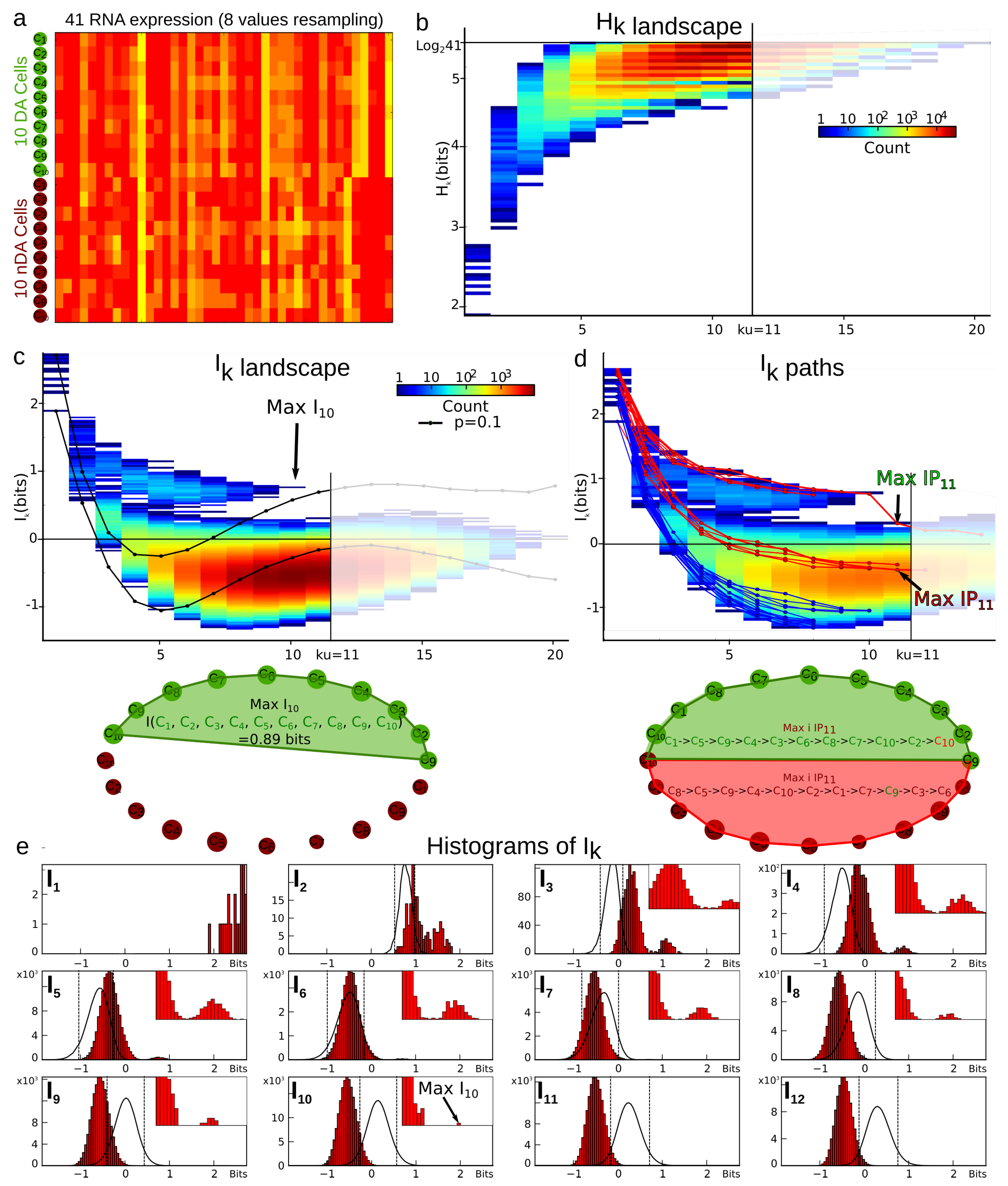
4.3.1. Example of Cell Type Classification with a Low Sample Size , Dimension , and Graining .
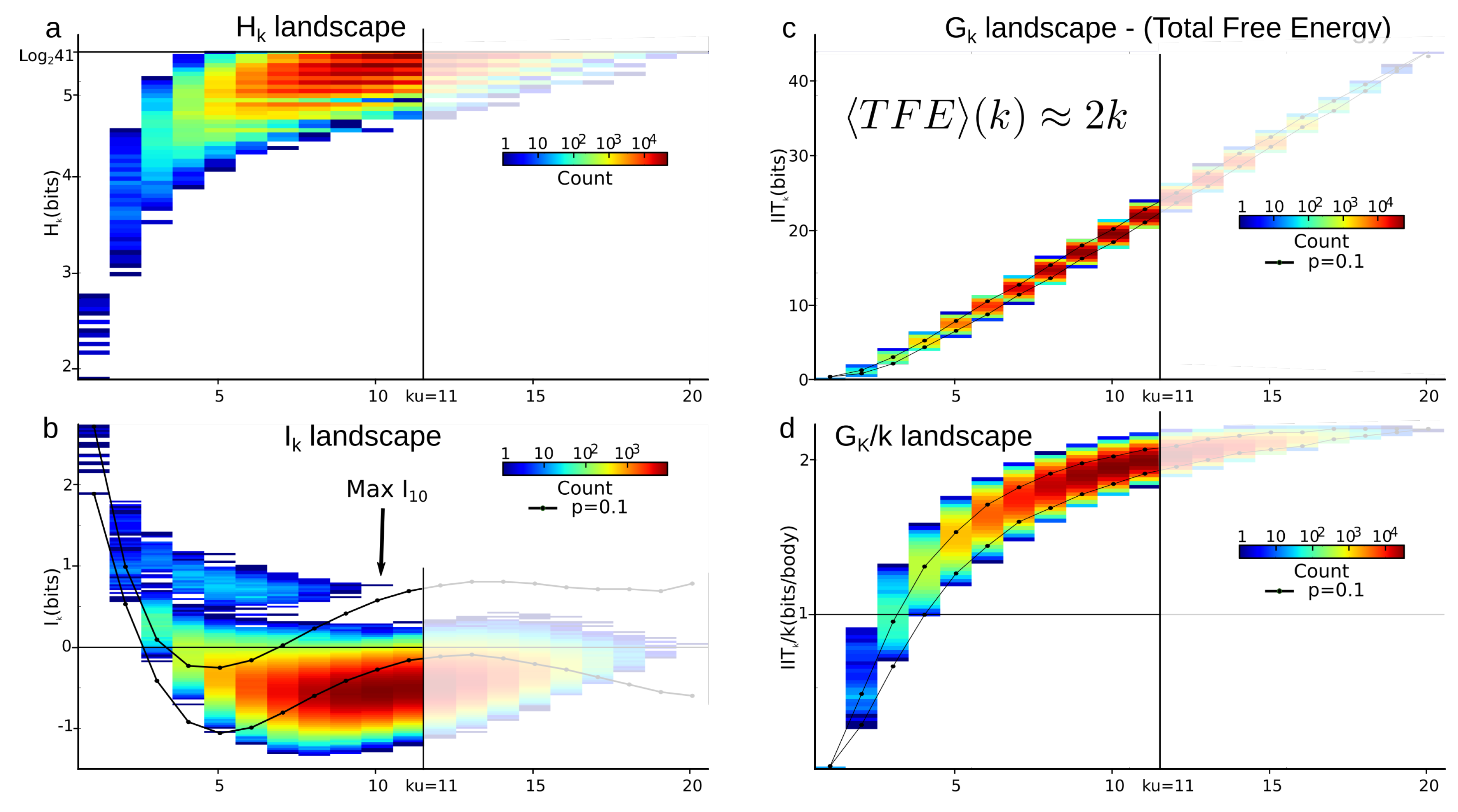
4.3.2. Total Correlations (Multi-Information) vs. Mutual-Information
5. Discussion
5.1. Topological and Statistical Information Decompositions
5.2. Mutual-Information Positivity and Negativity
5.3. Total Correlations (Multi-Information)
5.4. Beyond Pairwise Statistical Dependences: Combinatorial Information Storage
6. Materials and Methods
6.1. The Dataset: Quantified Genetic Expression in Two Cell Types
6.2. Probability Estimation
6.3. Computation of k-Entropy, k-Information Landscapes and Paths
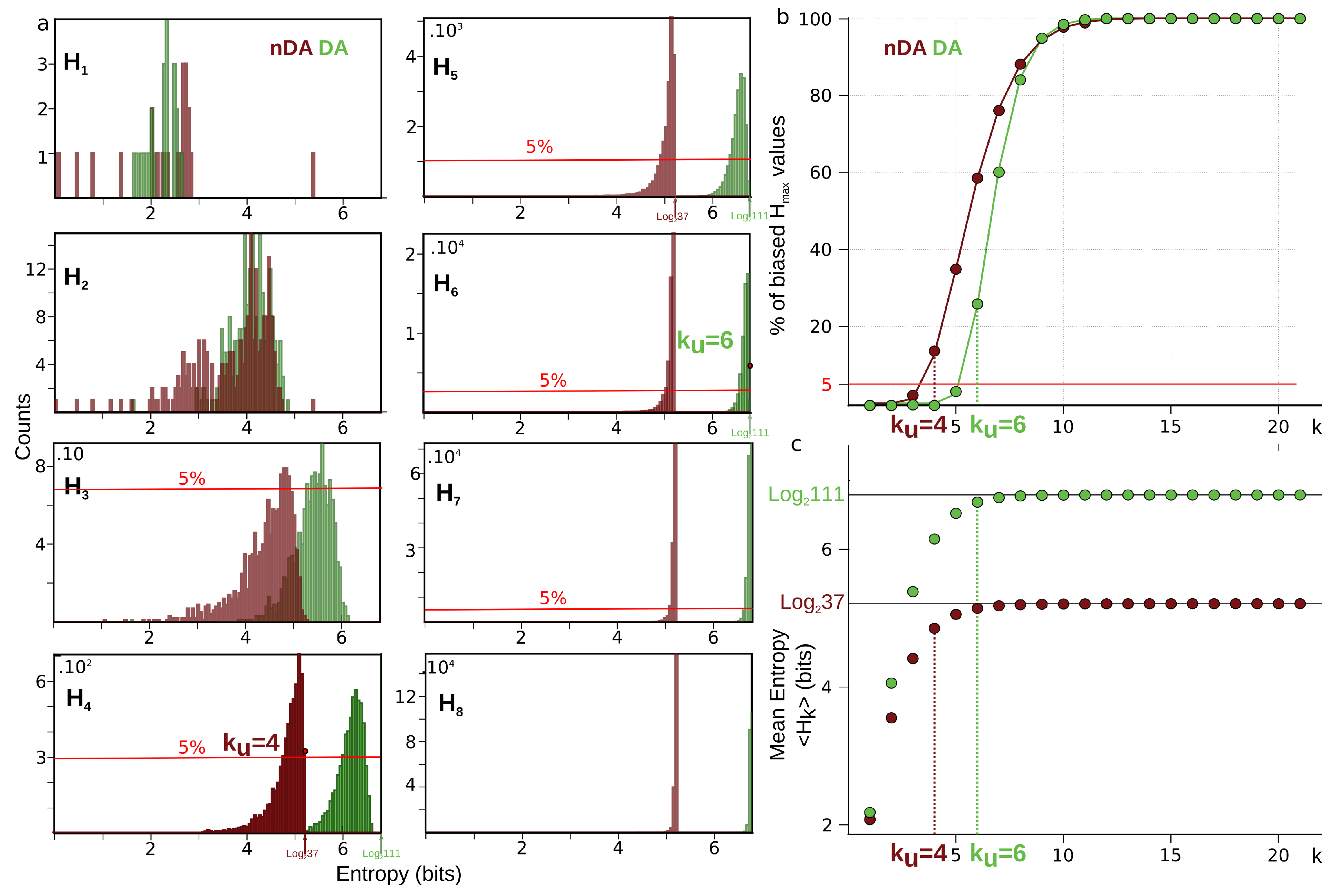
6.4. Estimation of the Undersampling Dimension
6.4.1. Statistical Result
6.4.2. Computational Result
- When , there is a single box and and we have . The case where is identical. This fixes the lower bound of our analysis in order not to be trivial; we need and .
- When are such that only one data point falls into a box, m of the values of atomic probabilities are and are null as a consequence of Equation (71), and hence we have .
6.5. k-Dependence Test
6.6. Sampling Size and Graining Landscapes—Stability of Minimum Energy Complex Estimation
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| iid | independent identically distributed |
| DA | Dopaminergic neuron |
| nDA | non Dopaminergic neuron |
| Multivariate k-joint Entropy | |
| Multivariate k-Mutual-Information | |
| Multivariate k-Total-Correlation or k-Multi-Information | |
| Maximal 2-Mutual-Information Coefficient |
Appendix A. Appendix: Bayes Free Energy and Information Quantities
Appendix A.1. Parametric Modelling
Appendix A.2. Bethe Approximation
References
- Baudot, P.; Bennequin, D. The Homological Nature of Entropy. Entropy 2015, 17, 3253–3318. [Google Scholar] [CrossRef]
- Vigneaux, J. The structure of information: From probability to homology. arXiv 2017, arXiv:1709.07807. [Google Scholar]
- Vigneaux, J.P. Topology of Statistical Systems. A Cohomological Approach to Information Theory. Ph.D. Thesis, Paris 7 Diderot University, Paris, France, 2019. [Google Scholar]
- Tapia, M.; Baudot, P.; Formizano-Treziny, C.; Dufour, M.; Temporal, S.; Lasserre, M.; Marqueze-Pouey, B.; Gabert, J.; Kobayashi, K.; Goaillard, J.-M. Neurotransmitter identity and electrophysiological phenotype are genetically coupled in midbrain dopaminergic neurons. Sci. Rep. 2018, 8, 13637. [Google Scholar] [CrossRef]
- Gibbs, J. Elementary Principles in Statistical Mechanics; Dover Edition (1960 Reprint); Charles Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C. A lattice theory of information. Trans. IRE Prof. Group Inform. Theory 1953, 1, 105–107. [Google Scholar] [CrossRef]
- McGill, W. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Fano, R. Transmission of Information: A Statistical Theory of Communication; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Hu, K.T. On the Amount of Information. Theory Probab. Appl. 1962, 7, 439–447. [Google Scholar]
- Han, T.S. Linear dependence structure of the entropy space. Inf. Control 1975, 29, 337–368. [Google Scholar] [CrossRef]
- Han, T.S. Nonnegative entropy measures of multivariate symmetric correlations. IEEE Inf. Control 1978, 36, 133–156. [Google Scholar] [CrossRef]
- Matsuda, H. Information theoretic characterization of frustrated systems. Phys. Stat. Mech. Its Appl. 2001, 294, 180–190. [Google Scholar] [CrossRef]
- Bell, A. The co-information lattice. In Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation, Nara, Japan, 1–4 April 2003. [Google Scholar]
- Brenner, N.; Strong, S.; Koberle, R.; Bialek, W. Synergy in a Neural Code. Neural Comput. 2000, 12, 1531–1552. [Google Scholar] [CrossRef]
- Watkinson, J.; Liang, K.; Wang, X.; Zheng, T.; Anastassiou, D. Inference of Regulatory Gene Interactions from Expression Data Using Three-Way Mutual Information. Chall. Syst. Biol. Ann. N. Y. Acad. Sci. 2009, 1158, 302–313. [Google Scholar] [CrossRef]
- Kim, H.; Watkinson, J.; Varadan, V.; Anastassiou, D. Multi-cancer computational analysis reveals invasion-associated variant of desmoplastic reaction involving INHBA, THBS2 and COL11A1. BMC Med. Genom. 2010, 3, 51. [Google Scholar] [CrossRef]
- Watanabe, S. Information theoretical analysis of multivariate correlation. Ibm J. Res. Dev. 1960, 4, 66–81. [Google Scholar] [CrossRef]
- Tononi, G.; Edelman, G. Consciousness and Complexity. Science 1998, 282, 1846–1851. [Google Scholar] [CrossRef]
- Tononi, G.; Edelman, G.; Sporns, O. Complexity and coherency: Integrating information in the brain. Trends Cogn. Sci. 1998, 2, 474–484. [Google Scholar] [CrossRef]
- Studeny, M.; Vejnarova, J. The multiinformation function as a tool for measuring stochastic dependence. In Learning in Graphical Models; Jordan, M.I., Ed.; MIT Press: Cambridge, UK, 1999; pp. 261–296. [Google Scholar]
- Schneidman, E.; Bialek, W.; Berry, M.n. Synergy, redundancy, and independence in population codes. J. Neurosci. 2003, 23, 11539–11553. [Google Scholar] [CrossRef]
- Slonim, N.; Atwal, G.; Tkacik, G.; Bialek, W. Information-based clustering. Proc. Natl. Acad. Sci. USA 2005, 102, 18297–18302. [Google Scholar] [CrossRef]
- Brenner, N.; Bialek, W.; de Ruyter van Steveninck, R. Adaptive Rescaling Maximizes Information Transmission. Neuron 2000, 26, 695–702. [Google Scholar] [CrossRef]
- Laughlin, S. A simple coding procedure enhances the neuron’s information capacity. Z. Naturforsch 1981, 36, 910–912. [Google Scholar] [CrossRef]
- Margolin, A.; Wang, K.; Califano, A.; Nemenman, I. Multivariate dependence and genetic networks inference. IET Syst. Biol. 2010, 4, 428–440. [Google Scholar] [CrossRef]
- Williams, P.; Beer, R. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515v1. [Google Scholar]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information Decomposition and Synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Wibral, M.; Finn, C.; Wollstadt, P.; Lizier, J.; Priesemann, V. Quantifying Information Modification in Developing Neural Networks via Partial Information Decomposition. Entropy 2017, 19, 494. [Google Scholar] [CrossRef]
- Kay, J.; Ince, R.; Dering, B.; Phillips, W. Partial and Entropic Information Decompositions of a Neuronal Modulatory Interaction. Entropy 2017, 19, 560. [Google Scholar] [CrossRef]
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. In Proceedings of the IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014. [Google Scholar]
- Abdallah, S.A.; Plumbley, M.D. Predictive Information, Multiinformation and Binding Information; Technical Report; Queen Mary, University of London: London, UK, 2010. [Google Scholar]
- Valverde-Albacete, F.; Pelaez-Moreno, C. Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle. Entropy 2018, 20, 498. [Google Scholar] [CrossRef]
- Valverde-Albacete, F.; Pelaez-Moreno, C. The evaluation of data sources using multivariate entropy tools. Expert Syst. Appl. 2017, 78, 145–157. [Google Scholar] [CrossRef]
- Baudot, P. The Poincaré-Boltzmann Machine: From Statistical Physics to Machine Learning and back. arXiv 2019, arXiv:1907.06486. [Google Scholar]
- Khinchin, A. Mathematical Foundations of Information Theory; Translated by R. A. Silverman and M.D. Friedman from Two Russian Articles in Uspekhi Matematicheskikh Nauk, 7 (1953): 320 and 9 (1956): 1775; Dover: New York, NY, USA, 1957. [Google Scholar]
- Artin, M.; Grothendieck, A.; Verdier, J. Theorie des Topos et Cohomologie Etale des Schemas—(SGA 4) Vol I,II,III; Seminaire de Geometrie Algebrique du Bois Marie 1963–1964. Berlin, coll. e Lecture Notes in Mathematics; Springer: New York, NY, USA, 1972. [Google Scholar]
- Rota, G. On the Foundations of Combinatorial Theory I. Theory of Moebius Functions. Z. Wahrseheinlichkeitstheorie 1964, 2, 340–368. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley Series in Telecommunication; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Kellerer, H. Masstheoretische Marginalprobleme. Math. Ann. 1964, 153, 168–198. [Google Scholar] [CrossRef]
- Matus, F. Discrete marginal problem for complex measures. Kybernetika 1988, 24, 39–46. [Google Scholar]
- Reshef, D.; Reshef, Y.; Finucane, H.; Grossman, S.; McVean, G.; Turnbaugh, P.; Lander, E.; Mitzenmacher, M.; Sabeti, P. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518. [Google Scholar] [CrossRef]
- Tapia, M.; Baudot, P.; Dufour, M.; Formizano-Treziny, C.; Temporal, S.; Lasserre, M.; Kobayashi, K.; Goaillard, J.M. Information topology of gene expression profile in dopaminergic neurons. BioArXiv 2017, 168740. [Google Scholar] [CrossRef]
- Dawkins, R. Selfish Gene, 1st ed.; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Pethel, S.; Hahs, D. Exact Test of Independence Using Mutual Information. Entropy 2014, 16, 2839–2849. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.; Seth, A.K. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Grundbegriffe der Wahrscheinlichkeitsrechnung; English translation (1950): Foundations of the theory of probability; Springer: Berlin, Germany; Chelsea, MA, USA, 1933. [Google Scholar]
- Loday, J.L.; Valette, B. Algebr. Operads; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tkacik, G.; Marre, O.; Amodei, D.; Schneidman, E.; Bialek, W.; Berry, M.J., II. Searching for collective behavior in a large network of sensory neurons. PLoS Comput. Biol. 2014, 10, e1003408. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M., 2nd; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef]
- Merchan, L.; Nemenman, I. On the Sufficiency of Pairwise Interactions in Maximum Entropy Models of Networks. J. Stat. Phys. 2016, 162, 1294–1308. [Google Scholar] [CrossRef]
- Humplik, J.; Tkacik, G. Probabilistic models for neural populations that naturally capture global coupling and criticality. PLoS Comput. Biol. 2017, 13, e1005763. [Google Scholar] [CrossRef]
- Atick, J. Could information theory provide an ecological theory of sensory processing. Netw. Comput. Neural Syst. 1992, 3, 213–251. [Google Scholar] [CrossRef]
- Baudot, P. Natural Computation: Much ado about Nothing? An Intracellular Study of Visual Coding in Natural Condition. Master’s Thesis, Paris 6 University, Paris, France, 2006. [Google Scholar]
- Yedidia, J.; Freeamn, W.; Weiss, Y. Understanding belief propagation and its generalizations. Destin. Lect. Conf. Artif. Intell. 2001, 8, 236–239. [Google Scholar]
- Reimann, M.; Nolte, M.; Scolamiero, M.; Turner, K.; Perin, R.; Chindemi, G.; Dłotko, P.; Levi, R.; Hess, K.; Markram, H. Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function. Front. Comput. Neurosci. 2017, 12, 48. [Google Scholar] [CrossRef]
- Gibbs, J. A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces. Trans. Conn. Acad. 1873, 2, 382–404. [Google Scholar]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Shipman, J. Tkinter Reference: A GUI for Python; New Mexico Tech Computer Center: Socorro, NM, USA, 2010. [Google Scholar]
- Hunter, J. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 22–30. [Google Scholar] [CrossRef]
- Van Der Walt, S.; Colbert, C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Hagberg, A.; Schult, D.; Swart, P. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; pp. 11–15. [Google Scholar]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Strong, S.; de Ruyter van Steveninck, R.; Bialek, W.; Koberle, R. On the application of information theory to neural spike trains. Pac. Symp. Biocomput. 1998, 1998, 621–632. [Google Scholar]
- Nemenman, I.; Bialek, W.; de Ruyter van Steveninck, R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef]
- Borel, E. La mechanique statistique et l’irreversibilite. J. Phys. Theor. Appl. 1913, 3, 189–196. [Google Scholar] [CrossRef]
- Scott, D. Multivariate Density Estimation. Theory, Practice and Visualization; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Epstein, C.; Carlsson, G.; Edelsbrunner, H. Topological data analysis. Inverse Probl. 2011, 27, 120201. [Google Scholar]
- Baudot, P.; Tapia, M.; Goaillard, J. Topological Information Data Analysis: Poincare-Shannon Machine and Statistical Physic of Finite Heterogeneous Systems. Preprints 2018, 2018040157. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Verhagen, J.; Grasman, R.; Wagenmakers, E.J. A Tutorial on Fisher Information. J. Math. Psychol. 2017, 80, 44–55. [Google Scholar] [CrossRef]
- Mori, R. New Understanding of the Bethe Approximation and the Replica Method. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.-M. Topological Information Data Analysis. Entropy 2019, 21, 869. https://doi.org/10.3390/e21090869
Baudot P, Tapia M, Bennequin D, Goaillard J-M. Topological Information Data Analysis. Entropy. 2019; 21(9):869. https://doi.org/10.3390/e21090869
Chicago/Turabian StyleBaudot, Pierre, Monica Tapia, Daniel Bennequin, and Jean-Marc Goaillard. 2019. "Topological Information Data Analysis" Entropy 21, no. 9: 869. https://doi.org/10.3390/e21090869
APA StyleBaudot, P., Tapia, M., Bennequin, D., & Goaillard, J.-M. (2019). Topological Information Data Analysis. Entropy, 21(9), 869. https://doi.org/10.3390/e21090869



