Entropy Exchange and Thermodynamic Properties of the Single Ion Cooling Process
Abstract
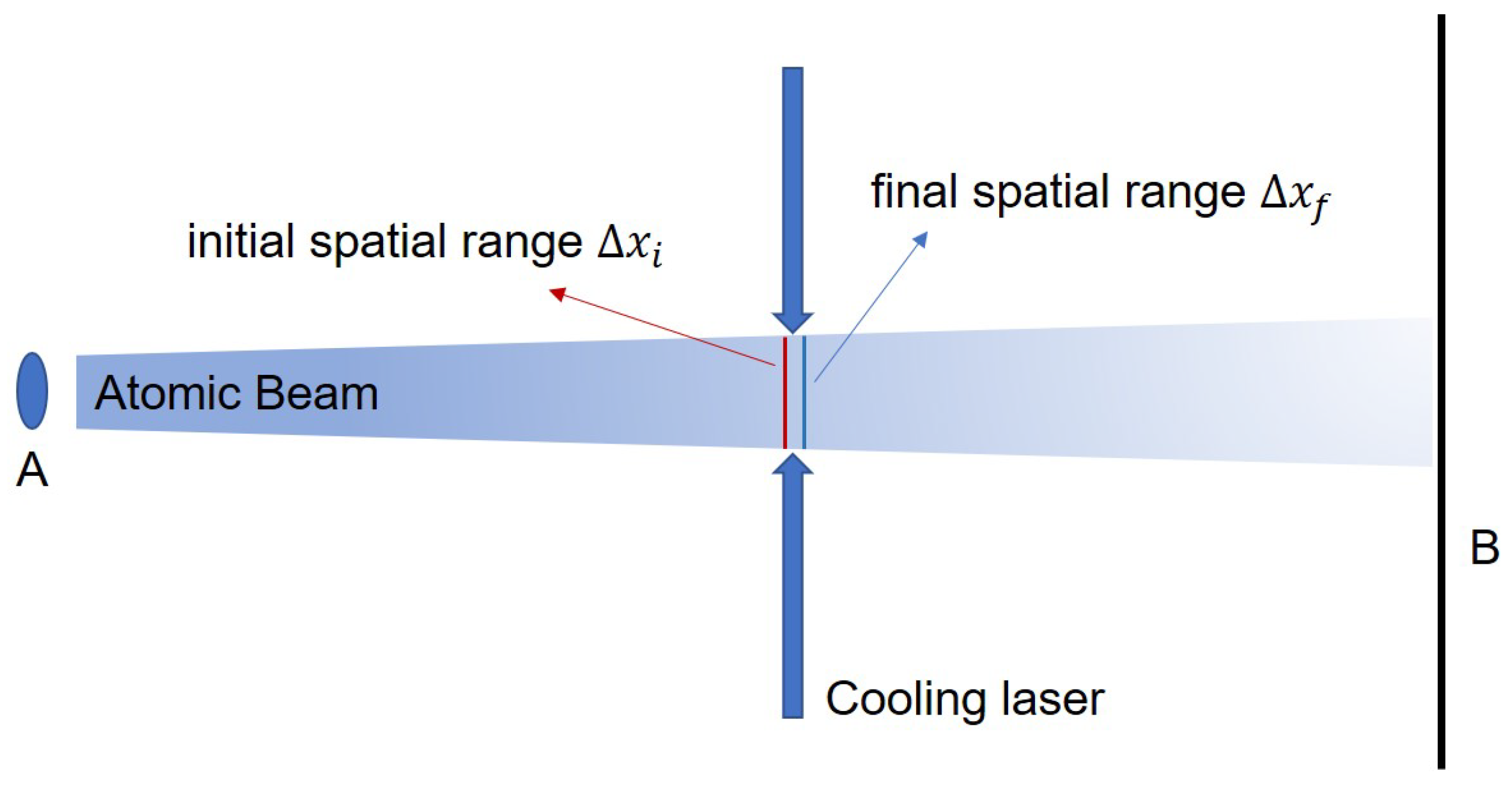
1. Introduction
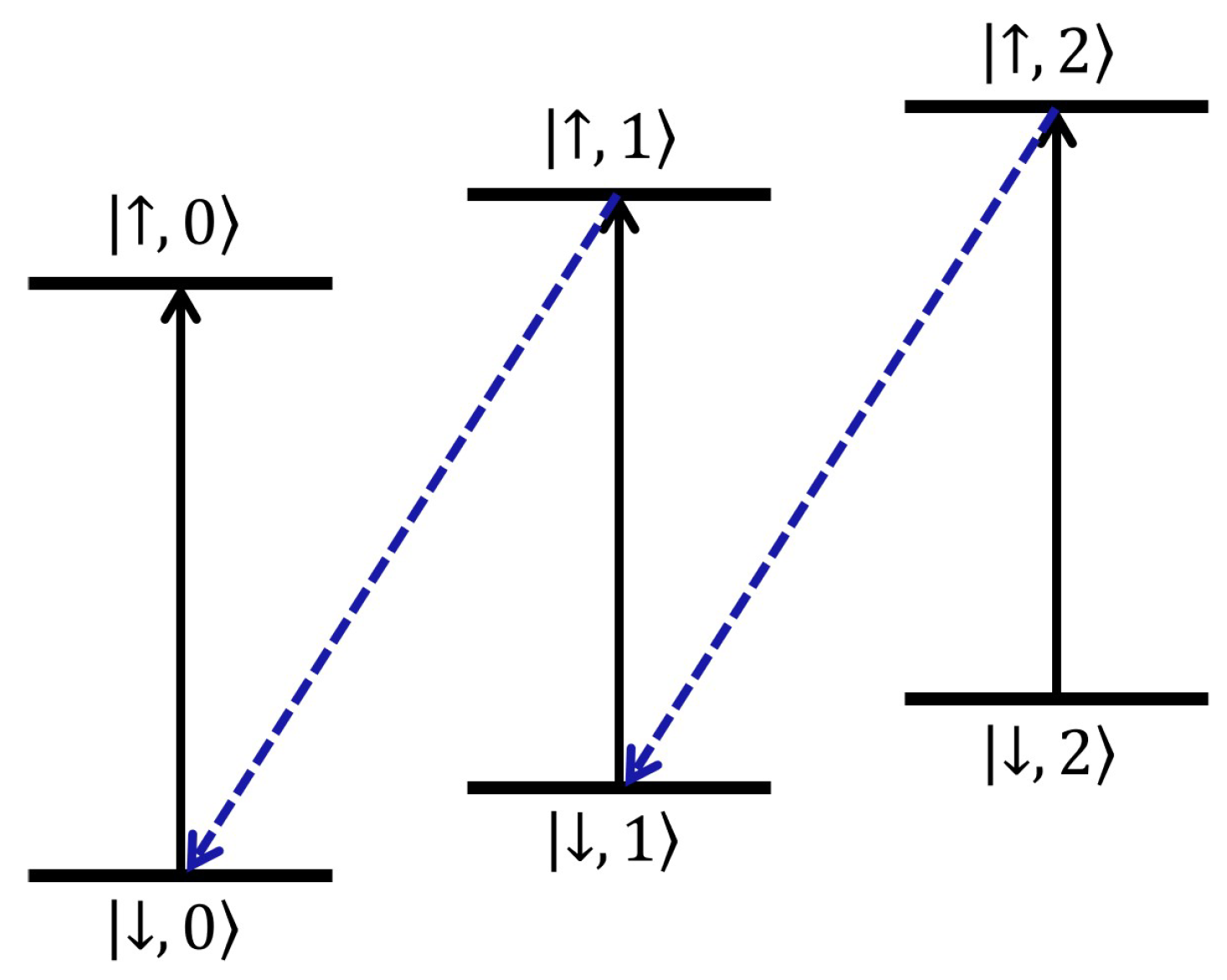
2. Calculation and Results
3. Conclusions and Discussions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Brandao, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Peña, F.J.; Negrete, O.; Barrios, G.A.; Zambrano, D.; González, A.; Nuñez, A.S.; Orellana, P.; Vargas, P. Magnetic otto engine for an electron in a quantum dot: Classical and quantum approach. Entropy 2019, 21, 512. [Google Scholar] [CrossRef]
- Barrios, G.A.; Peña, F.J.P.; Albarrán-Aarriagada, F.; Vargas, P.; Retamal, J.C. Quantum mechanical engine for the quantum rabi model. Entropy 2018, 20, 767. [Google Scholar] [CrossRef]
- Cherubim, C.; Brito, F.; Deffner, S. Non-thermal quantum engine in transmon qubits. Entropy 2019, 21, 545. [Google Scholar] [CrossRef]
- Niedenzu, W.; Mukherjee, V.; Ghosh, A.; Kofman, A.; Kurizki, G. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018, 9, 165. [Google Scholar] [CrossRef]
- Mu noz, E.; Pe na, F. Quantum heat engine in the relativistic limit: the case of a dirac particle. Phys. Rev. E 2012, 86, 061108. [Google Scholar] [CrossRef]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidtkaler, F.; Singer, K. A single-atom heat engine. Science 2015, 352, 325. [Google Scholar] [CrossRef] [PubMed]
- Abah, O.; Rossnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-ion heat engine at maximum power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Beau, M.; Jaramillo, J.D.; del Campo, A. Scaling-up quantum heat engines efficiently via shortcuts to adiabaticity. Entropy 2016, 18, 168. [Google Scholar] [CrossRef]
- Fialko, O.; Hallwood, D.W. Isolated quantum heat engine. Phys. Rev. Lett. 2012, 108, 085303. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, R.; Levy, A. Quantum heat engines and refrigerators: Continuous devices. Ann. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Bariani, F.; Meystre, P. Quantum optomechanical heat engine. Phys. Rev. Lett. 2014, 112, 150602. [Google Scholar] [CrossRef] [PubMed]
- Wineland, D.J.; Dehmelt, H.G. Principles of the stored ion calorimeter. J. Appl. Phys. 1975, 46, 919–930. [Google Scholar] [CrossRef]
- Hansch, T.W.; Schawlow, A.L. Cooling of gases by laser radiation. Opt. Commun. 1975, 13, 68–69. [Google Scholar] [CrossRef]
- Dalibard, J.; Cohentannoudji, C. Laser cooling below the doppler limit by polarization gradients: Simple theoretical models. J. Opt. Soc. Am. B-opt. Phys. 1989, 6, 2023–2045. [Google Scholar] [CrossRef]
- Wineland, D.J.; Dalibard, J.; Cohentannoudji, C. Sisyphus cooling of a bound atom. J. Opt. Soc. Am. B Opt. Phys. 1992, 9, 32–42. [Google Scholar] [CrossRef]
- Shang, S.Q.; Sheehy, B.; van der Straten, P.; Metcalf, H. Velocity-selective magnetic-resonance laser cooling. Phys. Rev. Lett. 1990, 65, 317–320. [Google Scholar] [CrossRef] [PubMed]
- Diedrich, F.; Bergquist, J.C.; Itano, W.M.; Wineland, D.J. Laser cooling to the zero-point energy of motion. Phys. Rev. Lett. 1989, 62, 403–406. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Jefferts, S.R.; Itano, W.M.; Wineland, D.J.; Gould, P.L. Resolved-sideband raman cooling of a bound atom to the 3d zero-point energy. Phys. Rev. Lett. 1995, 75, 4011–4014. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E. Electromagnetically induced transparency. Quantum Electron. Laser Sci. Conf. 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Gupta, R.; Xie, C.; Padua, S.; Batelaan, H.; Metcalf, H. Bichromatic laser cooling in a three-level system. Phys. Rev. Lett. 1993, 71, 3087. [Google Scholar] [CrossRef] [PubMed]
- Metcalf, H. Entropy exchange in laser cooling. Phys. Rev. A 2008, 77, 061401. [Google Scholar] [CrossRef]
- Christopher, C.; Brian, A.; Harold, M. Laser cooling without spontaneous emission. Phys. Rev. Lett. 2015, 114, 043002. [Google Scholar]
- Yatsenko, L.; Metcalf, H. Dressed-atom description of the bichromatic force. Phys. Rev. A 2004, 70, 5412–5418. [Google Scholar] [CrossRef]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D.J. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281–324. [Google Scholar] [CrossRef]
- Chen, X.; Ruschhaupt, A.; Schmidt, S.; Del, C.A.; Guéryodelin, D.; Muga, J.G. Fast optimal frictionless atom cooling in harmonic traps: shortcut to adiabaticity. Phys. Rev. Lett. 2010, 104, 063002. [Google Scholar] [CrossRef] [PubMed]
- Um, M.; Zhang, J.; Lv, D.; Lu, Y.; An, S.; Zhang, J.N.; Nha, H.; Kim, M.S.; Kim, K. Phonon arithmetic in a trapped ion system. Nat. Commun. 2016, 7, 11410. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Gueryodelin, D.; Muga, J.G. Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar] [CrossRef] [PubMed]
- Muga, J.G.; Chen, X.; Ibáñez, S.; Lizuain, I.; Ruschhaupt, A. Transitionless quantum drivings for the harmonic oscillator. J. Phys. B 2010, 43, 085509. [Google Scholar] [CrossRef]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Modern Phys. 1998, 70, 1003–1025. [Google Scholar] [CrossRef]
- Alessandro, Z.; Silvia, V.; Marco, B. Quantum-to-classical transition with single-photon-added coherent states of light. Science 2004, 306, 660–662. [Google Scholar]
- Lindblad, G. Entropy, information and quantum measurements. Commun. Math. Phys. 1973, 33, 305–322. [Google Scholar] [CrossRef]
- Foot, C.J. Atomic Physics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, J.-G.; Wu, C.-W.; Wu, W.; Chen, P.-X. Entropy Exchange and Thermodynamic Properties of the Single Ion Cooling Process. Entropy 2019, 21, 650. https://doi.org/10.3390/e21070650
Miao J-G, Wu C-W, Wu W, Chen P-X. Entropy Exchange and Thermodynamic Properties of the Single Ion Cooling Process. Entropy. 2019; 21(7):650. https://doi.org/10.3390/e21070650
Chicago/Turabian StyleMiao, Jian-Guo, Chun-Wang Wu, Wei Wu, and Ping-Xing Chen. 2019. "Entropy Exchange and Thermodynamic Properties of the Single Ion Cooling Process" Entropy 21, no. 7: 650. https://doi.org/10.3390/e21070650
APA StyleMiao, J.-G., Wu, C.-W., Wu, W., & Chen, P.-X. (2019). Entropy Exchange and Thermodynamic Properties of the Single Ion Cooling Process. Entropy, 21(7), 650. https://doi.org/10.3390/e21070650




