An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments
Abstract
1. Introduction
2. Measures for the Probabilistic Sensitivity Analysis
2.1. The Moment-Based Sensitivity Measure
2.2. The Reliability-Based Sensitivity Measure
3. An Entropy-Based Approach for the Reliability-Based Sensitivity Analysis
3.1. A Brief Summary on the Multiplicative Dimensional Reduction Method
3.2. Fractional Moments and the MaxEnt Distribution
3.3. The Proposed M-DRM Approach for the Moment-Based Sensitivity Index
3.4. The Proposed Approach for the Reliability-Based Sensitivity Analysis
4. Numerical Examples
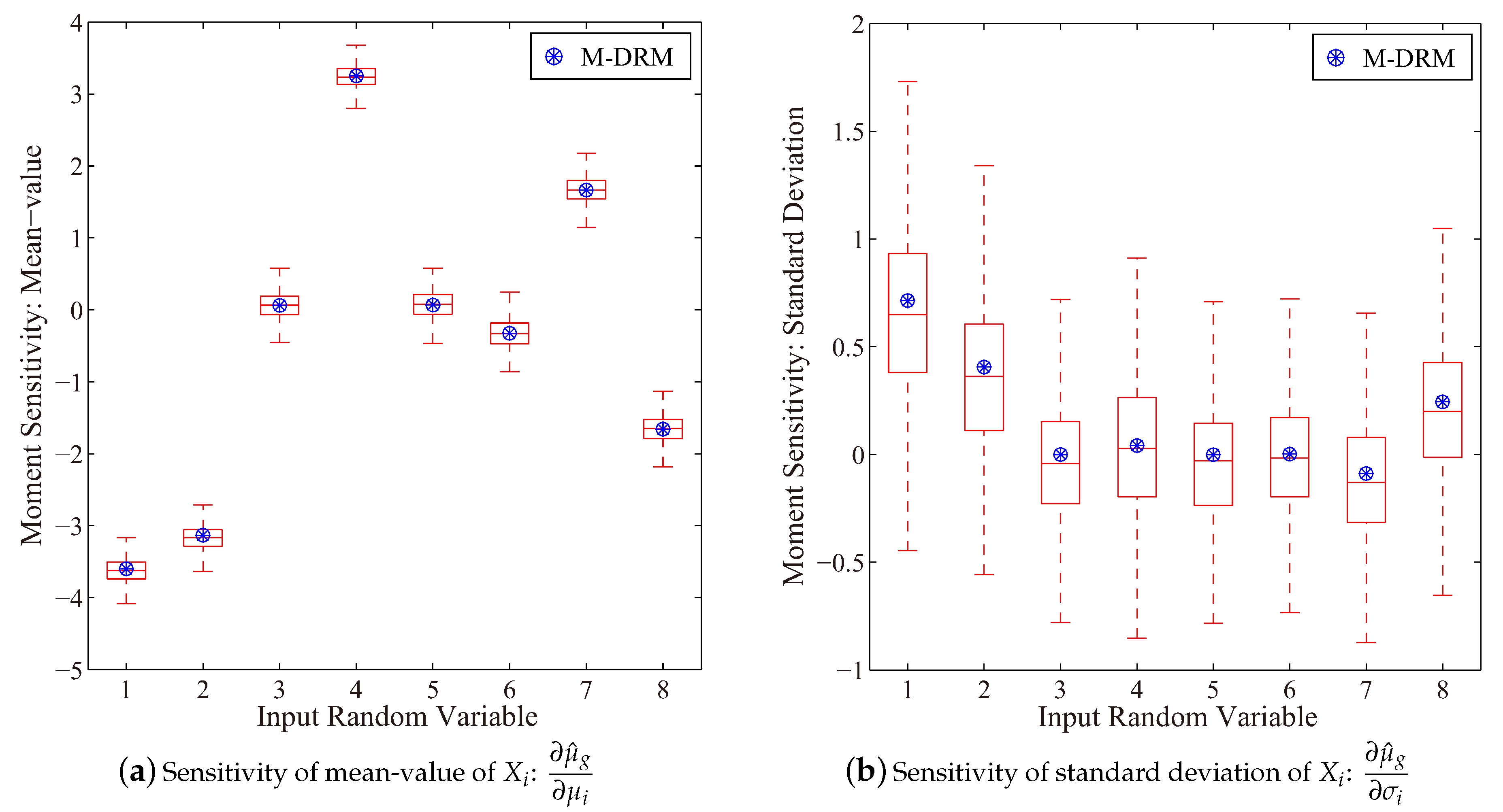
4.1. Reliability-Based Sensitivity Analysis A Cantilever Tube Structure
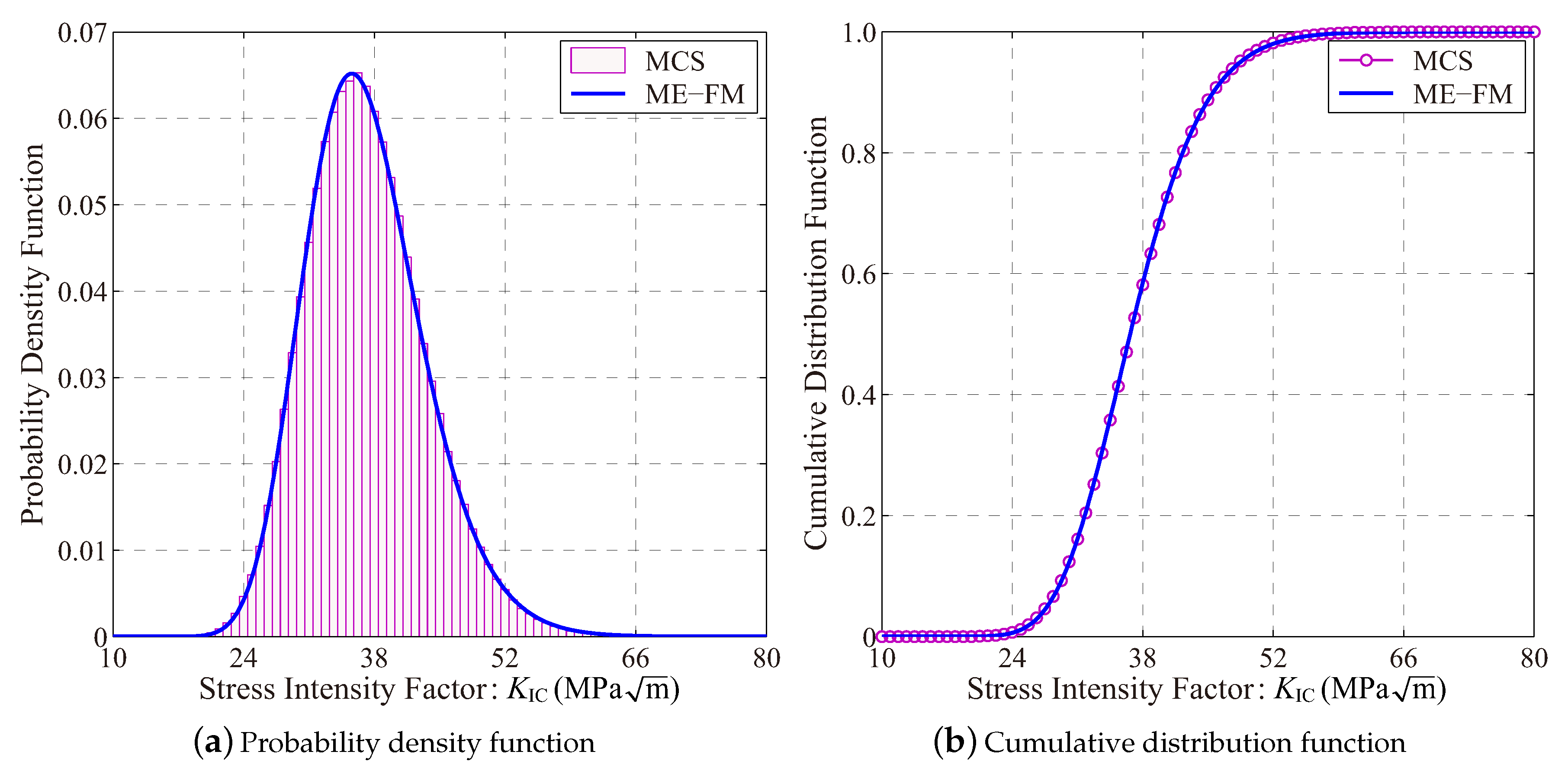
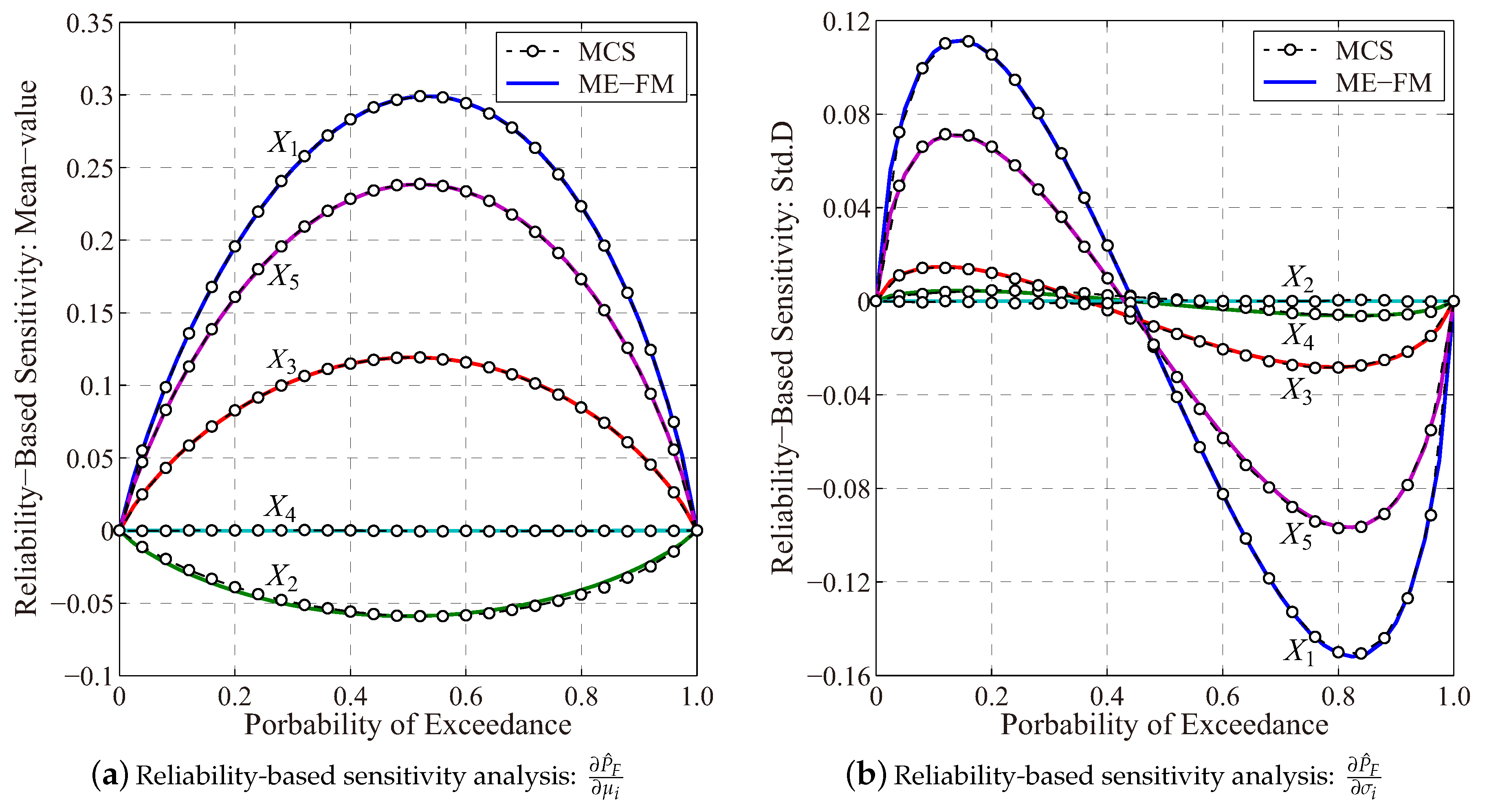
4.2. Reliability-Based Sensitivity Analysis of a Cracked Membrane
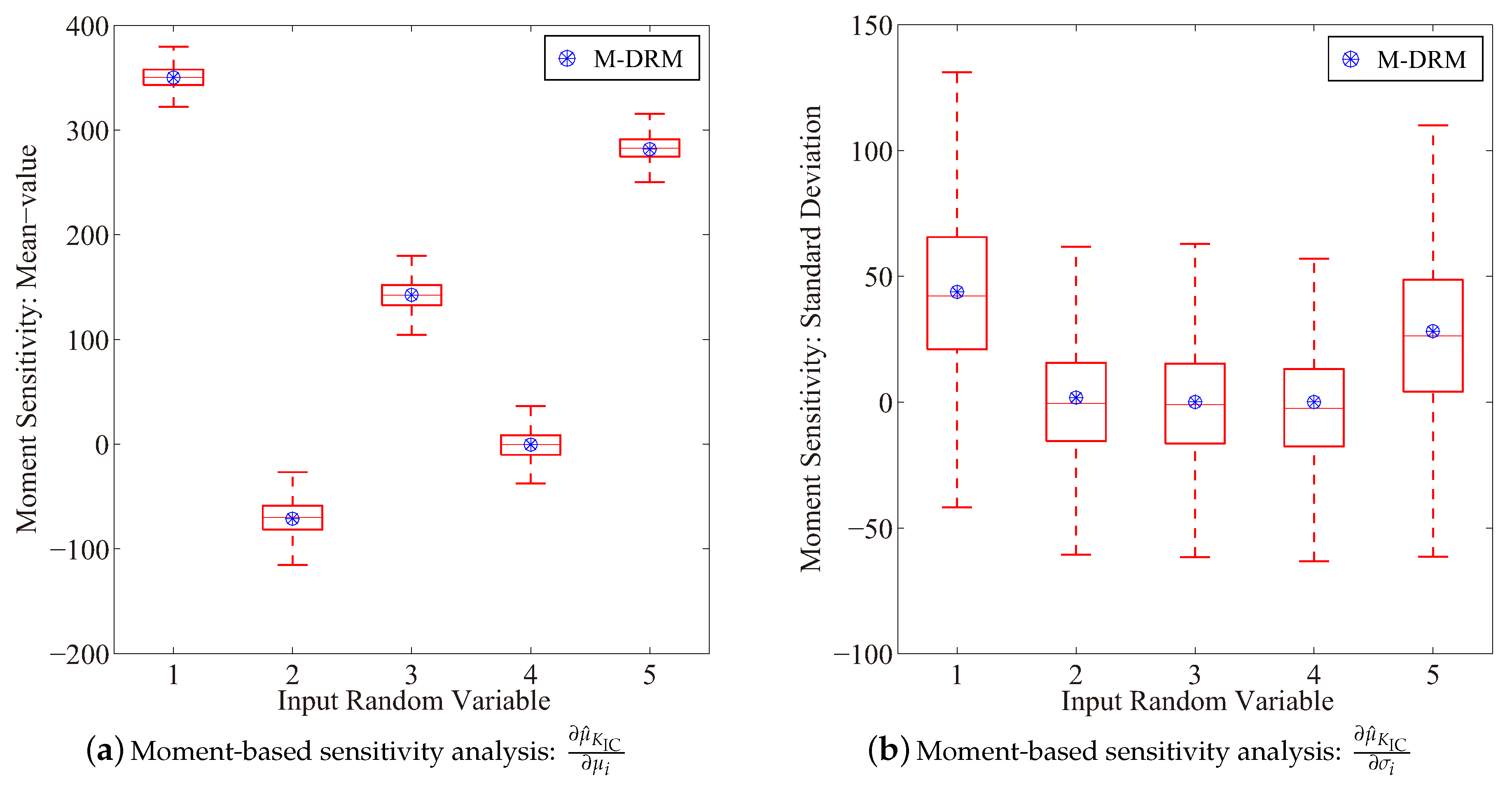
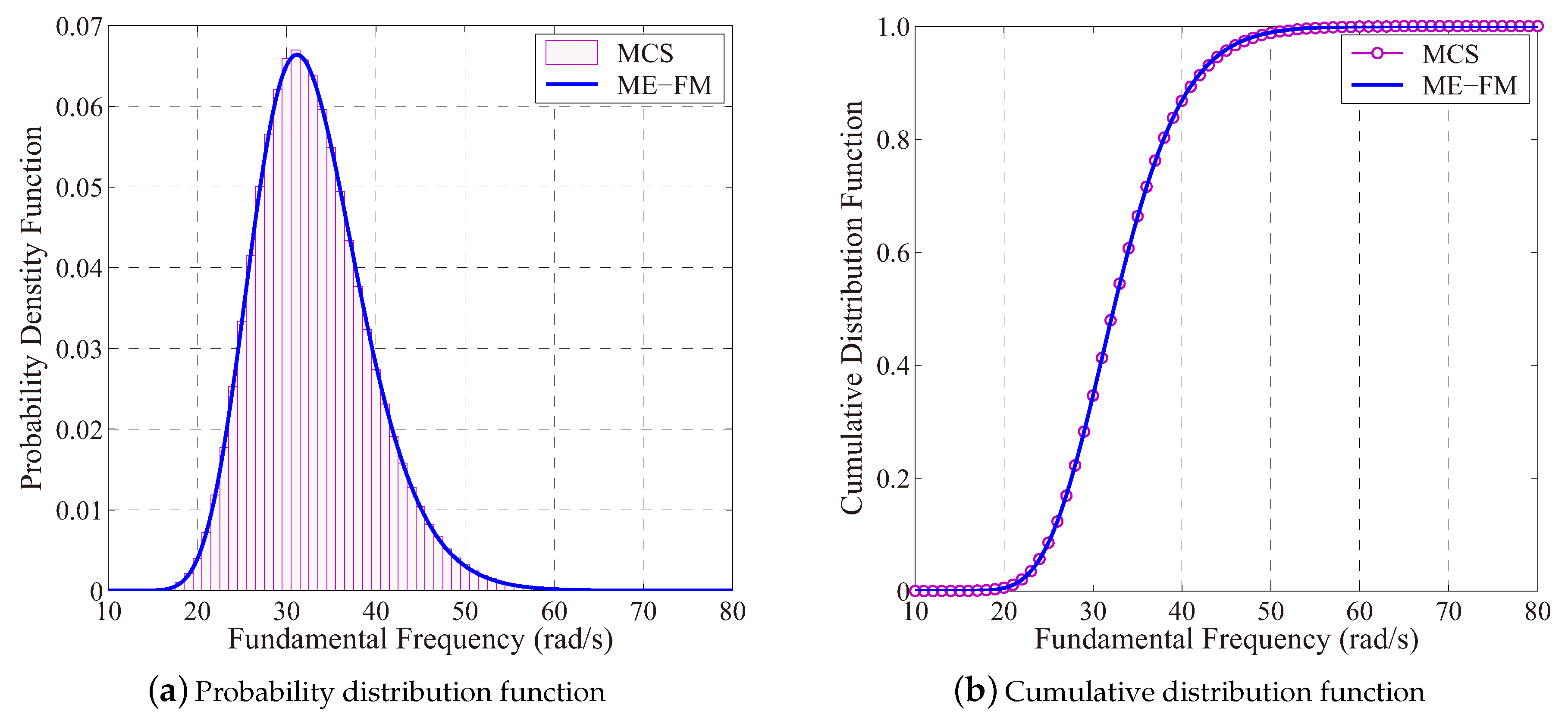
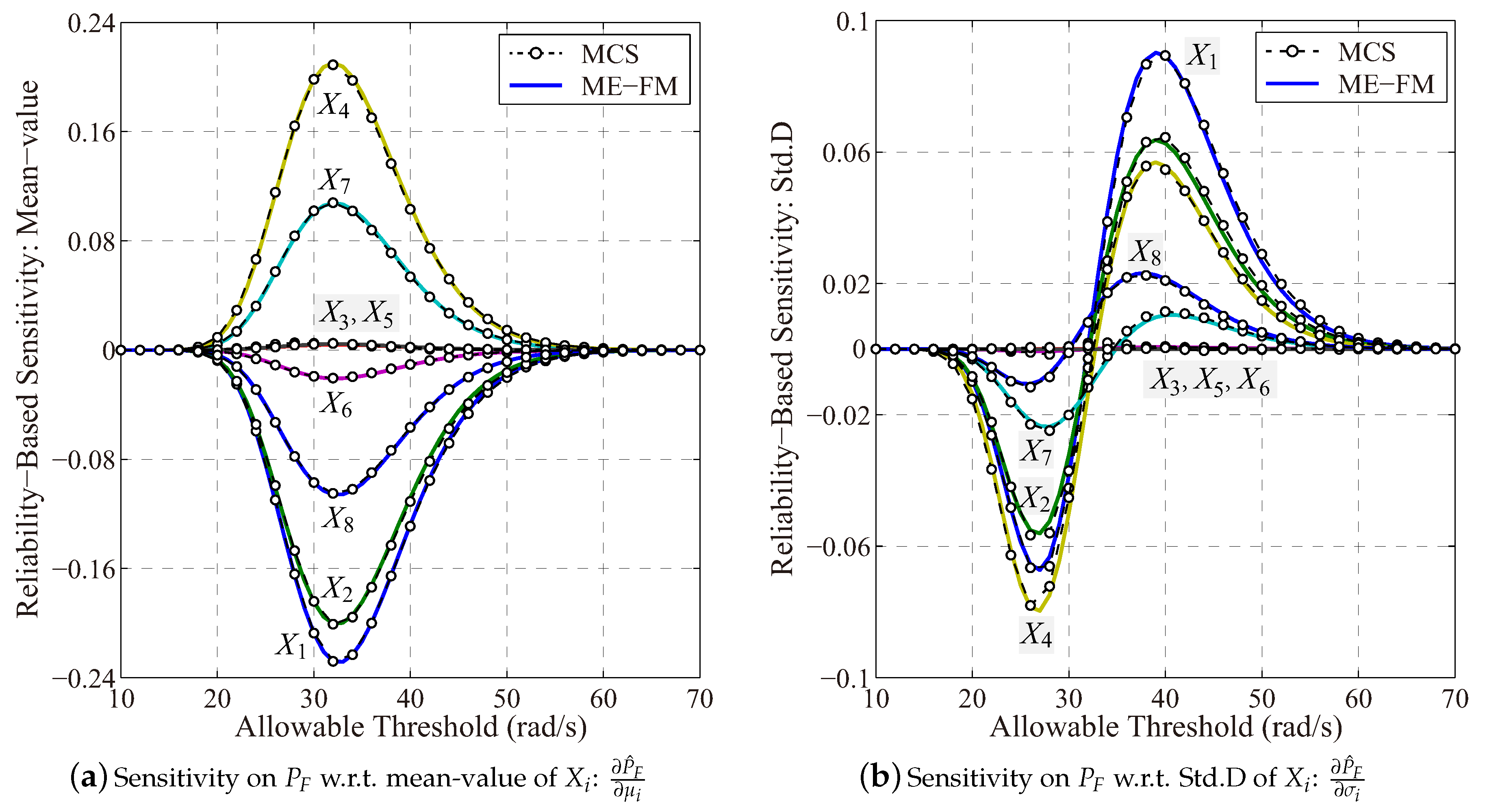
4.3. Probabilistic Sensitivity Analysis for Fundamental Natural Frequency of a Vehicle Frame
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Kernel Function of Random Variables
Appendix A.1. The Normal Random Variable
Appendix A.2. The Lognormal Random Variable
Appendix A.3. The Weibull Random Variable
References
- Ditlevsen, O.; Madsen, H. Structural Reliability Methods; John Wiley & Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Madsen, H.; Krenk, S.; Lind, N. Methods of Structural Safety; Dover publications Mineola: New York, NY, USA, 2006. [Google Scholar]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Cui, L.; Lü, Z.; Zhao, X. Moment-independent importance measure of basic random variable and its probability density evolution solution. Sci. China Technol. Sci. 2010, 53, 1138–1145. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Liu, P. Structural reliability under incomplete probability information. J. Eng. Mech.-ASCE 1986, 112, 85–104. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second-moment code format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar]
- Karamchandani, A.; Cornell, C. Sensitivity estimation within first and second order reliability methods. Struct. Saf. 1992, 11, 95–107. [Google Scholar] [CrossRef]
- Liu, P.L.; Der Kiureghian, A. Optimization algorithms for structural reliability. Struct. Saf. 1991, 9, 161–177. [Google Scholar] [CrossRef]
- Bucher, C.G.; Bourgund, U. A fast and efficient response surface approach for structural reliability problems. Struct. Saf. 1990, 7, 57–66. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Huang, X. A sparse surrogate model for structural reliability analysis based on the generalized polynomial chaos expansion. Proc. Inst. Mech. Eng. O J. Risk Reliab. 2019, 233, 487–502. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Sørensen, J.D. REIF: A novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis. Reliab. Eng. Syst. Saf. 2019, 185, 440–454. [Google Scholar] [CrossRef]
- Deng, J.; Gu, D.; Li, X.; Yue, Z.Q. Structural reliability analysis for implicit performance functions using artificial neural network. Struct. Saf. 2005, 27, 25–48. [Google Scholar] [CrossRef]
- Deng, J. Structural reliability analysis for implicit performance function using radial basis function network. Int. J. Solids Struct. 2006, 43, 3255–3291. [Google Scholar] [CrossRef]
- Xu, H.; Rahman, S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics. Int. J. Numer. Methods Eng. 2004, 61, 1992–2019. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E. Sensitivity Analysis; John Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Lee, I.; Choi, K.; Zhao, L. Sampling-based RBDO using the stochastic sensitivity analysis and Dynamic Kriging method. Struct. Multidiscipl. Optim. 2011, 44, 299–317. [Google Scholar] [CrossRef]
- Guo, J.; Du, X. Reliability sensitivity analysis with random and interval variables. Int. J. Numer. Methods Eng. 2009, 78, 1585–1617. [Google Scholar] [CrossRef]
- Song, S.; Lu, Z. Reliability sensitivity analysis based on subset simulation and importance sampling. J. Theor. App. Mech. 2008, 40, 654–662. [Google Scholar]
- Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Wu, Y.; Mohanty, S. Variable screening and ranking using sampling-based sensitivity measures. Reliab. Eng. Syst. Saf. 2006, 91, 634–647. [Google Scholar] [CrossRef]
- Rahman, S. Stochastic sensitivity analysis by dimensional decomposition and score functions. Probab. Eng. Mech. 2009, 24, 278–287. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. The score function approach for sensitivity analysis of computer simulation models. Math. Comput. Simul. 1986, 28, 351–379. [Google Scholar] [CrossRef]
- Chowdhury, R.; Rao, B.N.; Prasad, A.M. Stochastic sensitivity analysis using HDMR and score function. Sadhana 2009, 34, 967–986. [Google Scholar] [CrossRef][Green Version]
- Wu, Y. Computational methods for efficient structural reliability and reliability sensitivity analysis. AIAA J. 1994, 32, 1717–1723. [Google Scholar] [CrossRef]
- Melchers, R.; Ahammed, M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput. Struct. 2004, 82, 55–61. [Google Scholar] [CrossRef]
- Millwater, H. Universal properties of kernel functions for probabilistic sensitivity analysis. Probab. Eng. Mech. 2009, 24, 89–99. [Google Scholar] [CrossRef]
- Ahammed, M.; Melchers, R.E. Gradient and parameter sensitivity estimation for systems evaluated using Monte Carlo analysis. Reliab. Eng. Syst. Saf. 2006, 91, 594–601. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method. Struct. Saf. 2013, 43, 28–40. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D. An effective approximation for variance-based global sensitivity analysis. Reliab. Eng. Syst. Saf. 2014, 121, 164–174. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D.; Zhang, Y. Computationally efficient reliability analysis of mechanisms based on a multiplicative dimensional reduction method. J. Mech. Des. 2014, 136, 061006. [Google Scholar] [CrossRef]
- Zhang, X. Efficient Computational Methods for Structural Reliability and Global Sensitivity Analyses. Ph.D. thesis, University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Davis, P.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Inverardi, P.; Tagliani, A. Maximum entropy density estimation from fractional moments. Commun. Stat. Theory Methods 2003, 32, 327–345. [Google Scholar] [CrossRef]
- Zhang, X.; He, W.; Zhang, Y.; Pandey, M.D. An effective approach for probabilistic lifetime modelling based on the principle of maximum entropy with fractional moments. Appl. Math. Model. 2017, 51, 626–642. [Google Scholar] [CrossRef]
- Deng, J.; Pandey, M. Using partial probability weighted moments and partial maximum entropy to estimate quantiles from censored samples. Probab. Eng. Mech. 2009, 24, 407–417. [Google Scholar] [CrossRef]
- Deng, J.; Pandey, M. Estimation of minimum cross-entropy quantile function using fractional probability weighted moments. Probab. Eng. Mech. 2009, 24, 43–50. [Google Scholar] [CrossRef]
- Kang, H.Y.; Kwak, B.M. Application of maximum entropy principle for reliability-based design optimization. Struct. Multidiscipl. Optim. 2009, 38, 331–346. [Google Scholar] [CrossRef]
- Huang, B.; Du, X. A robust design method using variable transformation and Gauss–Hermite integration. Int. J. Numer. Methods Eng. 2006, 66, 1841–1858. [Google Scholar] [CrossRef]
- Wu, Y.T.; Millwater, H.; Cruse, T. Advanced probabilistic structural analysis method for implicit performance functions. AIAA J. 1990, 28, 1663–1669. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.; Irwin, G. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME Press: New York, NY, USA, 2000. [Google Scholar]
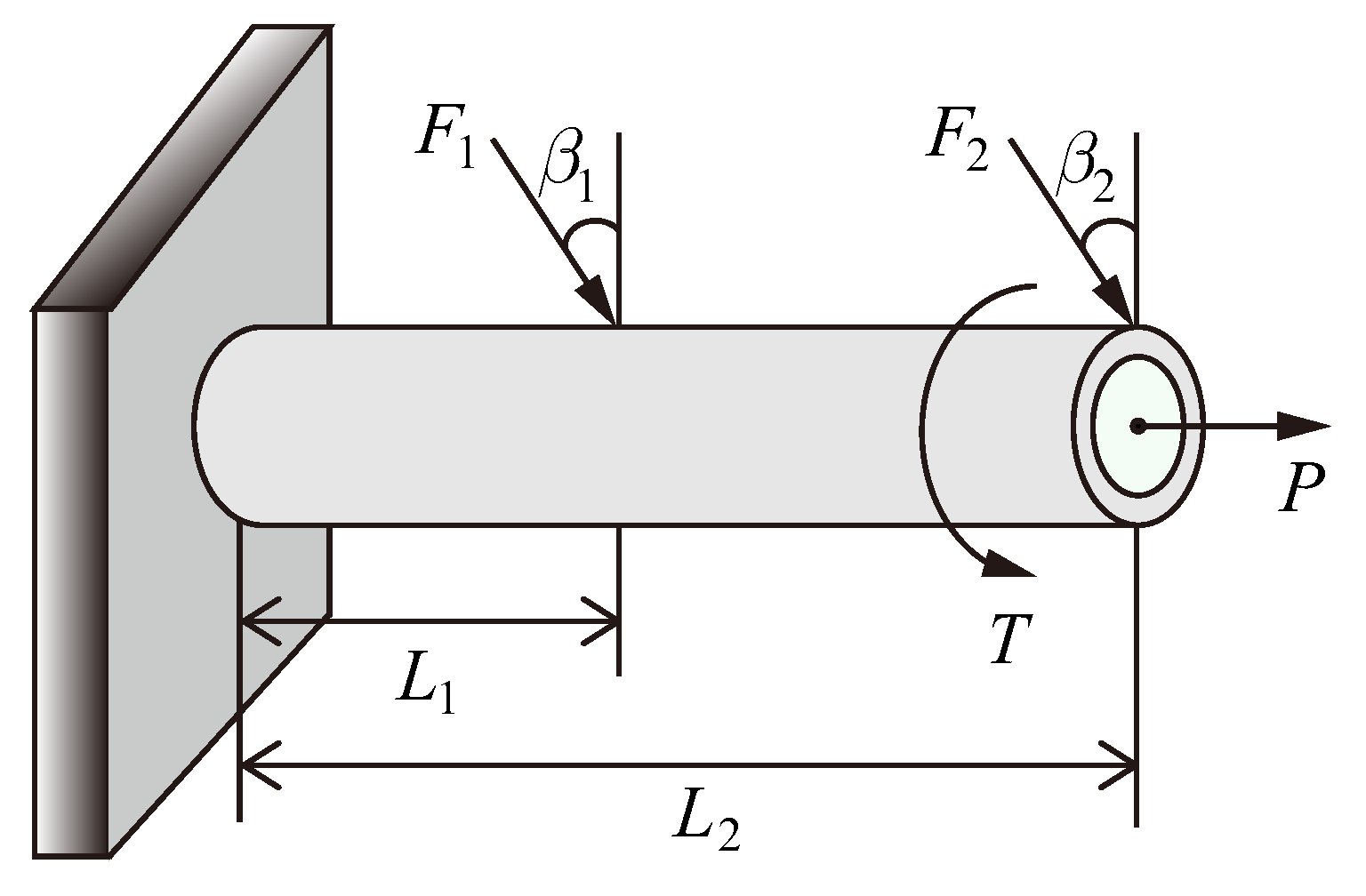
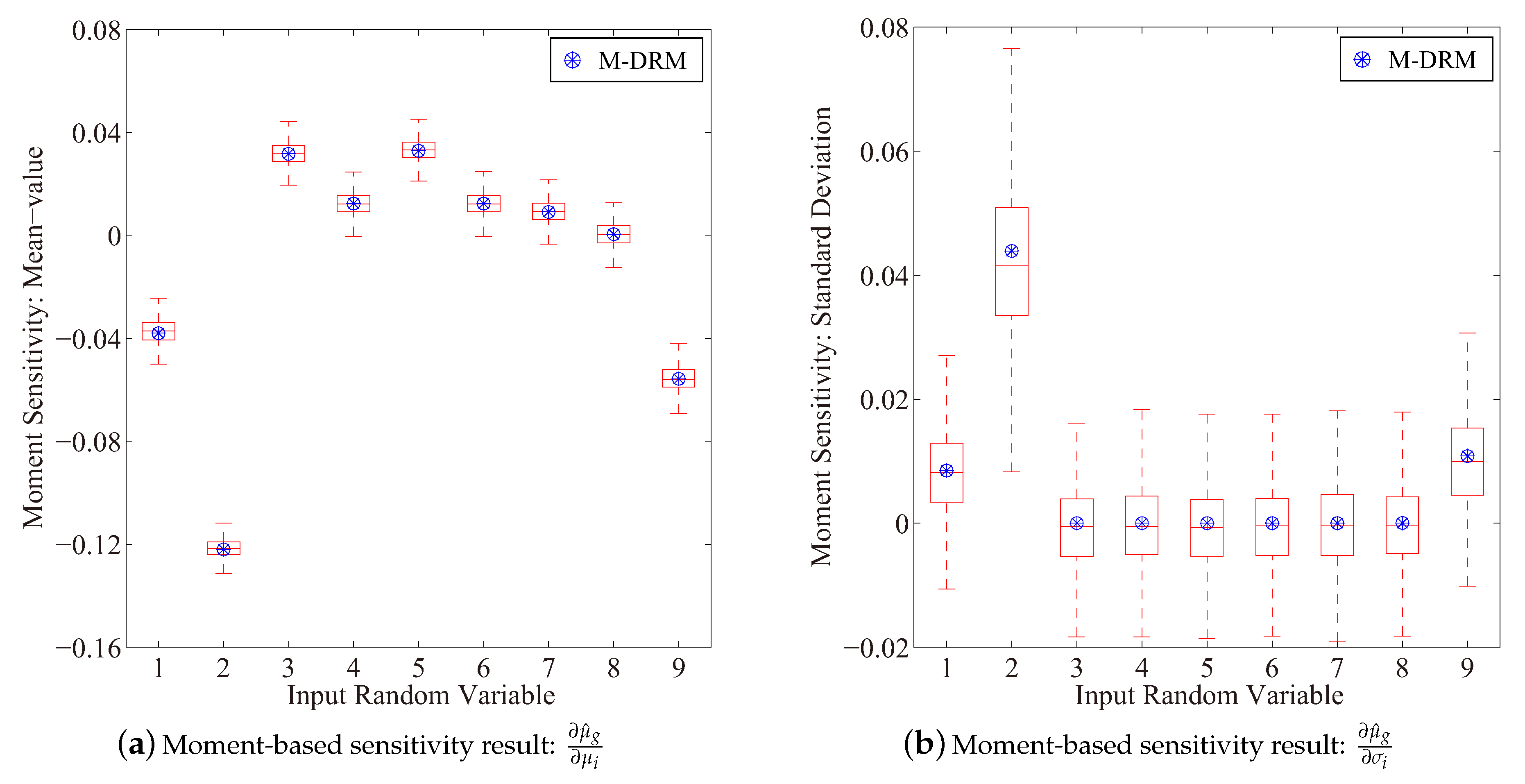

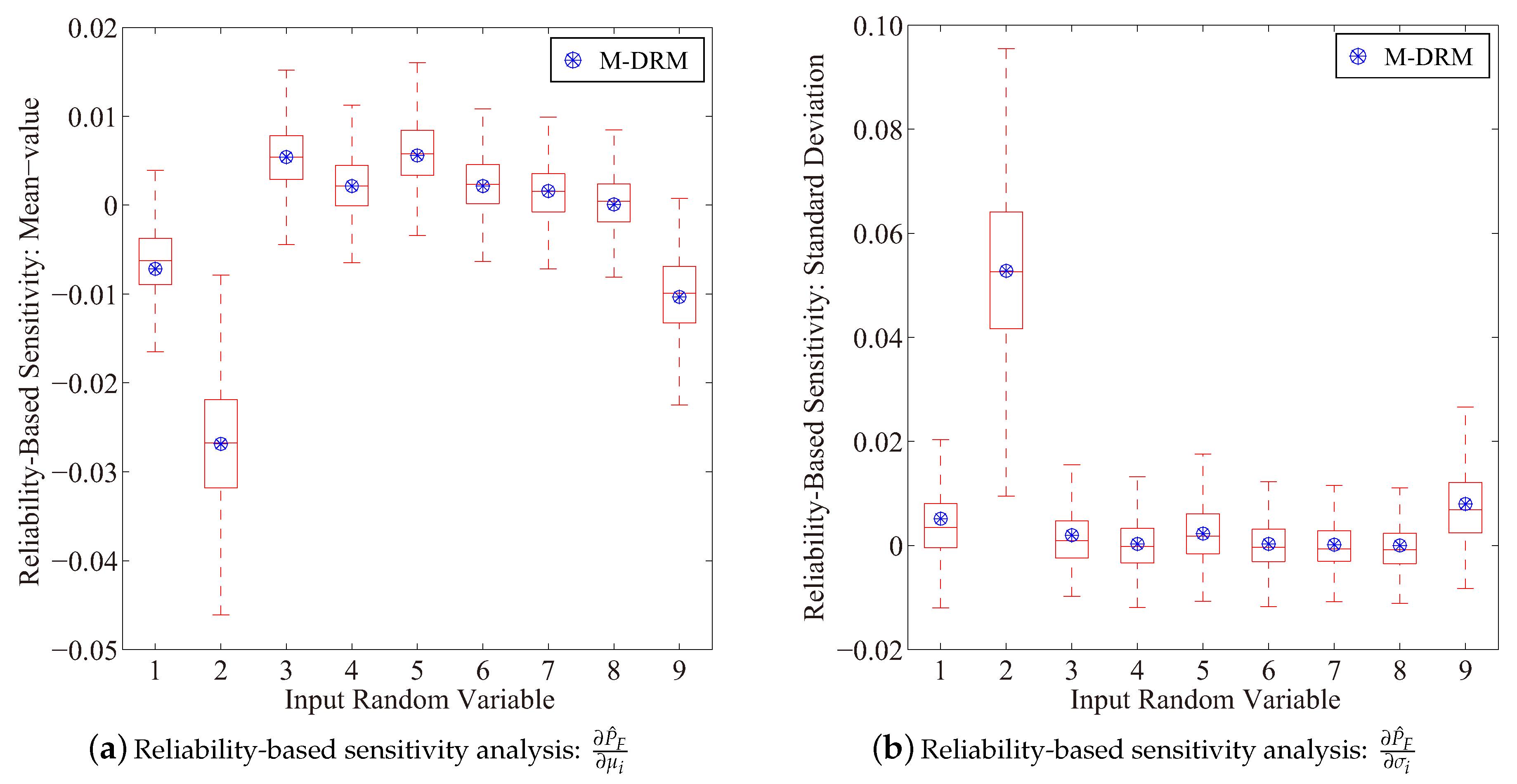
| Variable | Symbol | Unite | Distribution | Mean | COV |
|---|---|---|---|---|---|
| t | mm | Normal | 0.10 | ||
| d | mm | Normal | 0.10 | ||
| mm | Normal | 0.10 | |||
| mm | Normal | 0.10 | |||
| kN | Lognormal | 0.10 | |||
| kN | Lognormal | 0.10 | |||
| P | kN | Lognormal | 0.10 | ||
| T | kN | Lognormal | 0.10 | ||
| MPa | Lognormal | 0.10 |
| Entropy | k | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| Moment | MCS | ||||
| M-DRM |
| Name | Variable | Symbol | Distribution | Mean | COV |
|---|---|---|---|---|---|
| Initial temperature | Lognormal | 0.10 | |||
| Amphibian temperature | T | Lognormal | 0.10 | ||
| The size of crack | a | Lognormal | 10 mm | 0.10 | |
| Width | B | Normal | 200 mm | 0.10 | |
| Young’s modules | E | Lognormal | 210 GPa | 0.10 | |
| Thermal expansion Coef. | c | – | Deterministic | — |
| Entropy | k | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| Moment | MCS | ||||
| M-DRM |
| Random Variable | Symbol | Unit | Distribution | Mean | COV | |
|---|---|---|---|---|---|---|
| Geometric dimension | L | mm | Normal | 3600 | ||
| W | mm | Normal | 750 | 0.10 | ||
| w | mm | Normal | 90 | 0.10 | ||
| t | mm | Normal | 6 | 0.10 | ||
| H | mm | Normal | 200 | 0.10 | ||
| Material property | – | Lognormal | 0.10 | |||
| E | MPa | Lognormal | ||||
| kg/m | Lognormal | |||||
| Entropy | k | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| Moment | MCS | ||||
| M-DRM |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, J.; Yan, Y.; Pandey, M. An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments. Entropy 2019, 21, 649. https://doi.org/10.3390/e21070649
Zhang X, Liu J, Yan Y, Pandey M. An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments. Entropy. 2019; 21(7):649. https://doi.org/10.3390/e21070649
Chicago/Turabian StyleZhang, Xufang, Jiankai Liu, Ying Yan, and Mahesh Pandey. 2019. "An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments" Entropy 21, no. 7: 649. https://doi.org/10.3390/e21070649
APA StyleZhang, X., Liu, J., Yan, Y., & Pandey, M. (2019). An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments. Entropy, 21(7), 649. https://doi.org/10.3390/e21070649





