On the Performance of Interleavers for Quantum Turbo Codes
Abstract
1. Introduction
2. Classical Interleavers for Quantum Turbo Codes
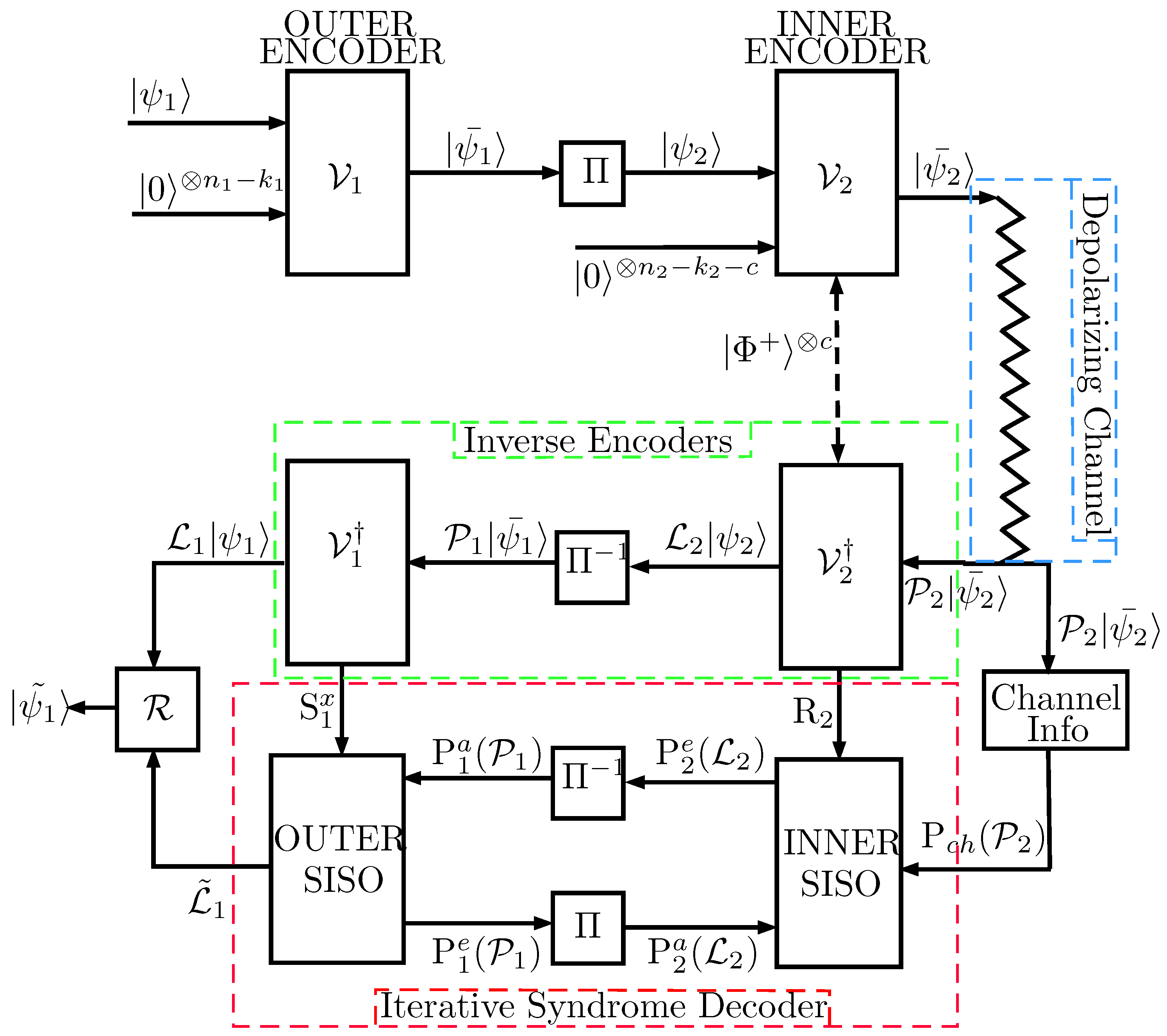
2.1. System Model
2.2. Classical Interleavers for QTCs
2.3. Considered Classical Interleavers
- Factorize the length of the interleaver , where usually.
- For to do
3. Results and Discussions
- S-random interleaver with parameter ,
- Welch-Costas interleaver with parameter and
- JPL interleaver.
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| QECC | Quantum Error Correction Code |
| QCC | Quantum Convolutional Code |
| QTC | Quantum Turbo Code |
| QIRCC | Quntum IrRegular Convolutional Code |
| QURC | Quantum Unity Rate Code |
| EXIT | EXtrinsic Information Transfer |
| EPR | Einstein-Podoslky-Rosen |
| SISO | Soft-Input Soft-Output |
| JPL | Jet Propulsion Laboratory |
| CCSDS | Consultative Committee for Space Data Systems |
| WER | Word Error Rate |
| EA | Entanglement-Assisted |
References
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. In Proceedings of the IEEE International Conference on Communications (ICC ’93), Geneva, Switzerland, 23–26 May 1993; pp. 1064–1070. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Poulin, D.; Tillich, J.; Ollivier, H. Quantum Serial Turbo Codes. IEEE Trans. Inf. Theory 2009, 55, 2776–2798. [Google Scholar] [CrossRef]
- Babar, Z.; Chandra, D.; Nguyen, H.V.; Botsinis, P.; Alanis, D.; Ng, S.X.; Hanzo, L. Duality of Quantum and Classical Error Correction Codes: Design Principles amp; Examples. IEEE Commun. Surv. Tutor. 2018, 21, 970–1010. [Google Scholar] [CrossRef]
- Brun, T.; Devetak, I.; Hsieh, M.H. Correcting Quantum Errors with Entanglement. Science 2006, 314, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Wilde, M.M.; Hsieh, M.; Babar, Z. Entanglement-Assisted Quantum Turbo Codes. IEEE Trans. Inf. Theory 2014, 60, 1203–1222. [Google Scholar] [CrossRef]
- Babar, Z.; Ng, S.X.; Hanzo, L. EXIT-Chart-Aided Near-Capacity Quantum Turbo Code Design. IEEE Trans. Veh. Technol. 2015, 64, 866–875. [Google Scholar] [CrossRef]
- Babar, Z.; Botsinis, P.; Alanis, D.; Ng, S.X.; Hanzo, L. The Road From Classical to Quantum Codes: A Hashing Bound Approaching Design Procedure. IEEE Access 2015, 3, 146–176. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Babar, Z.; Alanis, D.; Botsinis, P.; Chandra, D.; Ng, S.X.; Hanzo, L. EXIT-Chart Aided Quantum Code Design Improves the Normalised Throughput of Realistic Quantum Devices. IEEE Access 2016, 4, 10194–10209. [Google Scholar] [CrossRef]
- Babar, Z.; Nguyen, H.V.; Botsinis, P.; Alanis, D.; Chandra, D.; Ng, S.X.; Hanzo, L. Serially Concatenated Unity-Rate Codes Improve Quantum Codes Without Coding-Rate Reduction. IEEE Commun. Lett. 2016, 20, 1916–1919. [Google Scholar] [CrossRef]
- Koutsouvelis, K.V.; Dimakis, C.E. A Low Complexity Algorithm for Generating Turbo Code s-Random Interleavers. Wirel. Pers. Commun. 2008, 46, 365–370. [Google Scholar] [CrossRef]
- Saul, L.S.; Francisco, G. A comparative study for turbo code interleavers designed for short frame size and relatively high SNR channel. In Proceedings of the 2011 5th International Conference on Signal Processing and Communication Systems (ICSPCS), Honolulu, HI, USA, 12–14 December 2011; pp. 1–4. [Google Scholar]
- Sadjadpour, H.R.; Sloane, N.J.A.; Salehi, M.; Nebe, G. Interleaver design for turbo codes. IEEE J. Sel. Areas Commun. 2001, 19, 831–837. [Google Scholar] [CrossRef]
- Andrews, K.S.; Heegard, C.; Kozen, D. Interleaver design methods for turbo codes. In Proceedings of the 1998 IEEE International Symposium on Information Theory, Cambridge, MA, USA, 16–21 August 1998; p. 420. [Google Scholar]
- Kovaci, M.; Balta, H.G.; Nafornita, M.M. The performances of interleavers used in turbo codes. In Proceedings of the 2005 International Symposium on Signals, Circuits and Systems, Iasi, Romania, 14–15 July 2005; pp. 363–366. [Google Scholar]
- Vafi, S.; Wysocki, T. Performance of convolutional interleavers with different spacing parameters in turbo codes. In Proceedings of the 2005 Australian Communications Theory Workshop, Brisbane, Australia, 2–4 Febuary 2005; pp. 8–12. [Google Scholar]
- Heegard, C.; Wicker, S.B. Turbo Coding; Kluwer Academic Publishers: Norwell, MA, USA, 1999. [Google Scholar]
- Popovski, P.; Kocarev, L.; Risteski, A. Design of flexible-length S-random interleaver for turbo codes. IEEE Commun. Lett. 2004, 8, 461–463. [Google Scholar] [CrossRef]
- Consultative Committee for Space Data Systems (CCSDS). Telemetry Channel Coding. 2002. Available online: https://public.ccsds.org/Pubs/101x0b6s.pdf (accessed on 13 May 2019).
- Jeruchim, M. Techniques for Estimating the Bit Error Rate in the Simulation of Digital Communication Systems. IEEE J. Sel. Areas Commun. 1984, 2, 153–170. [Google Scholar] [CrossRef]

| Config. | Encoder | R | E | m | Seed Transformation |
|---|---|---|---|---|---|
| EXIT-optimized | Outer | 0 | 3 | ||
| Inner | 3 |
| Name | Spread (S) | Dispersion () |
|---|---|---|
| Random [17] | 1 | ≈0.81 |
| S-random | 25 | |
| Welch-Costas | 1 | 1 |
| JPL | 16 |
| Name | Parameters | Storage Requirements |
|---|---|---|
| Random [17] | N | |
| S-random | N | |
| Welch-Costas | N, | 2 |
| JPL | N, , | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etxezarreta Martinez, J.; Crespo, P.M.; Garcia-Frías, J. On the Performance of Interleavers for Quantum Turbo Codes. Entropy 2019, 21, 633. https://doi.org/10.3390/e21070633
Etxezarreta Martinez J, Crespo PM, Garcia-Frías J. On the Performance of Interleavers for Quantum Turbo Codes. Entropy. 2019; 21(7):633. https://doi.org/10.3390/e21070633
Chicago/Turabian StyleEtxezarreta Martinez, Josu, Pedro M. Crespo, and Javier Garcia-Frías. 2019. "On the Performance of Interleavers for Quantum Turbo Codes" Entropy 21, no. 7: 633. https://doi.org/10.3390/e21070633
APA StyleEtxezarreta Martinez, J., Crespo, P. M., & Garcia-Frías, J. (2019). On the Performance of Interleavers for Quantum Turbo Codes. Entropy, 21(7), 633. https://doi.org/10.3390/e21070633






