Model Selection for Non-Negative Tensor Factorization with Minimum Description Length
Abstract
1. Introduction
1.1. Motivation
1.2. Contribution
- (A-a)
- Tensor slice based approach: It is not appropriate to employ the MDL principle directly to NTF because the number of elements in factor matrices is too much smaller than that in a data tensor, hence the model complexity might be ignored inappropriately. We call this problem the imbalance problem. Our key idea to resolve this problem is that we first slice the data tensor into multiple tensor slices, namely matrices, then select the rank for each tensor slice, and finally select the largest rank of tensor slices as the best rank of the data tensor. We call this methodology the tensor slice based approach.
- (A-b)
- NML-based code-length calculation: When the goodness of a model is measured in terms of its code-length, the selection of a coding method is important. We specifically utilize the normalized maximum likelihood (NML) code-lengths [12] to encode the results of factorization. This is due to the facts (1) the NML code-length has optimality under the Shtarkov’s minimax regret [13], and (2) it achieves Rissanen’s lower bound on code-length [10].
- (B-a)
- Accuracy for estimating true rank: When the true rank that generates the data is known, we measure the goodness of any rank estimation method in terms of its estimation accuracy.
- (B-b)
- Accuracy for completing missing values: When the true rank is unknown, we measure the goodness of any rank estimation method in terms of accuracy of competing missing values.
2. Related Work
3. Proposed Method
| Algorithm 1 Rank Selection with Tensor Slices |
|
4. Comparison Method: MDL2stage
5. Experiments
5.1. Comparison Methods
5.2. Experiments on Synthetic Data
5.3. Experiments on Real Data
5.3.1. On-Line Retail Data Set
5.3.2. Web Access Data Set
5.3.3. App Usage Data Set
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NTF | Non-negative Tensor Factorization |
| MDL | Minimum Description Length |
| NML | Normalized Maximum Likelihood |
| NMF | Non-negative Matrix Factorization |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| CV | Cross Validation |
References
- Kiers, H.A.L. Towards a standardized notation and terminology in multiway analysis. J. Chemom. 2000, 14, 105–122. [Google Scholar] [CrossRef]
- Welling, M.; Weber, M. Positive tensor factorization. Pattern Recognit. Lett. 2001, 22, 1255–1261. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by nonnegative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Shashua, A.; Hazan, T. Non-negative tensor factorization with applications to statistics and computer vision. In Proceedings of the 22nd International Conference on Machine Learning (ICML ’05), Bonn, Germany, 7–11 August 2005; pp. 792–799. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Choi, S.; Plemmons, R.; Amari, S.-i. Non-Negative Tensor Factorization using Alpha and Beta Divergences. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP ’07), Honolulu, HI, USA, 15–20 April 2007; Volmue 3, pp. 1393–1396. [Google Scholar]
- Barker, T.; Virtanen, T. Semi-supervised non-negative tensor factorisation of modulation spectrograms for monaural speech separation. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 3556–3561. [Google Scholar]
- Rissanen, J. Modeling By Shortest Data Description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Rissanen, J. Optimal Estimation of Parameters; Cambridge University Press: London, UK, 2012. [Google Scholar]
- Yamanishi, K. A learning criterion for stochastic rules. Mach. Learn. 1992, 9, 165–203. [Google Scholar] [CrossRef]
- Rissanen, J. Fisher information and stochastic complexity. IEEE Trans. Inf. Theor. 1996, 42, 40–47. [Google Scholar] [CrossRef]
- Shtarkov, Y. Universal sequential coding of single messages. Problemy Peredachi Informatsii 1987, 23, 3–17. [Google Scholar]
- Kirbiz, S.; Günsel, B. A multiresolution non-negative tensor factorization approach for single channel sound source separation. Signal Process. 2014, 105, 56–69. [Google Scholar] [CrossRef]
- Goutte, C.; Amini, M.R. Probabilistic tensor factorization and model selection. In Proceedings of the Advances in Neural Information Processing Systems 23 (NIPS 2010), Hyatt Regency, BC, Canada, 6–11 December 2010; pp. 1–4. [Google Scholar]
- Owen, A.B.; Perry, P.O. Bi-cross-validation of the SVD and the nonnegative matrix factorization. Ann. Appl. Stat. 2009, 3, 564–594. [Google Scholar] [CrossRef]
- Ito, Y.; Oeda, S.; Yamanishi, K. Rank Selection for Non-negative Matrix Factorization with Normalized Maximum Likelihood Coding. In Proceedings of the 2016 SIAM International Conference on Data Mining (SDM 2016), Miami, FL, USA, 5–7 May 2016; pp. 720–728. [Google Scholar]
- Hoffman, M.D.; Blei, D.M.; Cook, P.R. Bayesian Nonparametric Matrix Factorization for Recorded Music. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 439–446. [Google Scholar]
- Tanaka, S.; Kawamura, Y.; Kawakita, M.; Murata, N.; Takeuchi, J. MDL Criterion for NMF with Application to Botnet Detection. In Proceedings of the International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October; Springer: Berlin, Germany, 2016; pp. 570–578. [Google Scholar]
- Squires, S.; Prügel-Bennett, A.; Niranjan, M. Rank Selection in Nonnegative Matrix Factorization using Minimum Description Length. Neural Comput. 2017, 29, 2164–2176. [Google Scholar] [CrossRef] [PubMed]
- Fanaee-T, H.; Gama, J. SimTensor: A synthetic tensor data generator. arXiv 2016, arXiv:1612.03772. [Google Scholar]
- Chen, D.; Sain, S.L.; Guo, K. Data mining for the online retail industry: A case study of RFM model-based customer segmentation using data mining. J. Database Market. Custom. Strateg. Manag. 2012, 19, 197–208. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository, University of California, Irvine, School of Information and Computer Sciences. 2019. Available online: http://archive.ics.uci.edu/ml (accessed on 27 June 2019).
- Yamanishi, K.; Wu, T.; Sugawara, S.; Okada, M. The decomposed normalized maximum likelihood code-length criterion for selecting hierarchical latent variable models. Data Min. Knowl. Discov. 2019, 33, 1017–1058. [Google Scholar] [CrossRef]
| True Rank | 15 | 20 | 25 | 30 | 35 | 40 |
|---|---|---|---|---|---|---|
| Proposed | 0.11 | 0.45 | 0.94 | 0.88 | 0.81 | 0.92 |
| MDL2stage | 0.92 | 0.74 | 0.61 | 0.47 | 0.37 | 0.28 |
| AIC1 | 0 | 0 | 0 | 0 | 0 | 0 |
| AIC2 | 0 | 0 | 0 | 0 | 0 | 0 |
| BIC1 | 0.54 | 0.72 | 0.87 | 0.76 | 0.63 | 0.72 |
| BIC2 | 0.84 | 0.66 | 0.4 | 0.29 | 0.1 | 0.08 |
| CV | 0.95 | 0.86 | 0.73 | 0.65 | 0.62 | 0.71 |
| Rank and Error | AVE R | STDDEV | Error |
|---|---|---|---|
| Proposed | 36.8 | 2.39 | |
| MDL2stage | 548.1 | 23.26 | 36.52 × |
| AIC1 | 472 | 145.26 | 39.38 × |
| AIC2 | 546.1 | 22.09 | 38.89 × |
| BIC1 | 7.2 | 1.55 | 5.27 × |
| BIC2 | 3 | 0 | 5.42 × |
| Rank and Score | AVE R | STDDEV | Male at Night | Female at Day | Male at Day | Female at Night |
|---|---|---|---|---|---|---|
| Proposed | 82.4 | 15.23 | 0.642 | 0.823 | 0.685 | 0.947 |
| MDL2stage | 194.4 | 25.40 | 0.598 | 0.666 | 0.745 | 0.745 |
| AIC1 | 155.9 | 21.05 | 0.612 | 0.683 | 0.564 | 0.607 |
| AIC2 | 196.7 | 23.71 | 0.599 | 0.679 | 0.577 | 0.794 |
| BIC1 | 13.9 | 1.52 | 0.160 | 0.197 | 0.140 | 0.201 |
| BIC2 | 35.0 | 6.09 | 0.471 | 0.566 | 0.446 | 0.324 |
| Randomly generated vectors | 0.070 | −0.022 | 0.004 | −0.004 | ||
| Specified generated patterns | 0.365 | 0.298 | 0.302 | 0.256 | ||
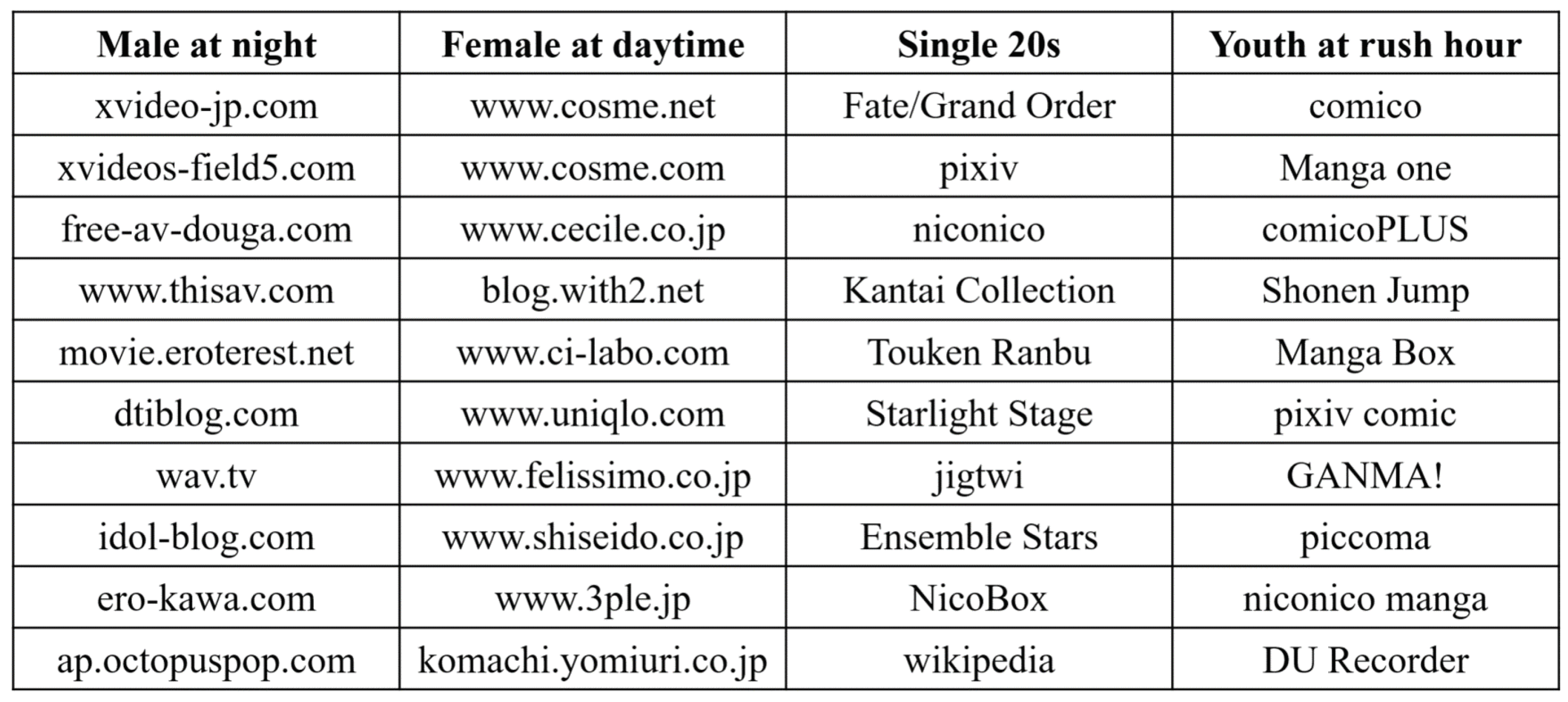
| Rank and Score | AVE R | STDDEV | Single 20s | Youth at Rush Hour |
|---|---|---|---|---|
| Proposed | 61.8 | 10.25 | 0.990 | 0.849 |
| MDL2stage | 147.6 | 22.27 | 0.939 | 0.722 |
| AIC1 | 97.4 | 15.15 | 0.963 | 0.732 |
| AIC2 | 148.5 | 19.72 | 0.939 | 0.723 |
| BIC1 | 14.5 | 3.44 | 0.467 | 0.602 |
| BIC2 | 26.7 | 8.93 | 0.617 | 0.686 |
| Randomly generated vectors | −0.109 | 0.300 | ||
| Specified generated patterns | 0.498 | 0.655 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Matsushima, S.; Yamanishi, K. Model Selection for Non-Negative Tensor Factorization with Minimum Description Length. Entropy 2019, 21, 632. https://doi.org/10.3390/e21070632
Fu Y, Matsushima S, Yamanishi K. Model Selection for Non-Negative Tensor Factorization with Minimum Description Length. Entropy. 2019; 21(7):632. https://doi.org/10.3390/e21070632
Chicago/Turabian StyleFu, Yunhui, Shin Matsushima, and Kenji Yamanishi. 2019. "Model Selection for Non-Negative Tensor Factorization with Minimum Description Length" Entropy 21, no. 7: 632. https://doi.org/10.3390/e21070632
APA StyleFu, Y., Matsushima, S., & Yamanishi, K. (2019). Model Selection for Non-Negative Tensor Factorization with Minimum Description Length. Entropy, 21(7), 632. https://doi.org/10.3390/e21070632





