Learning Using Concave and Convex Kernels: Applications in Predicting Quality of Sleep and Level of Fatigue in Fibromyalgia
Abstract
1. Introduction
2. Dataset
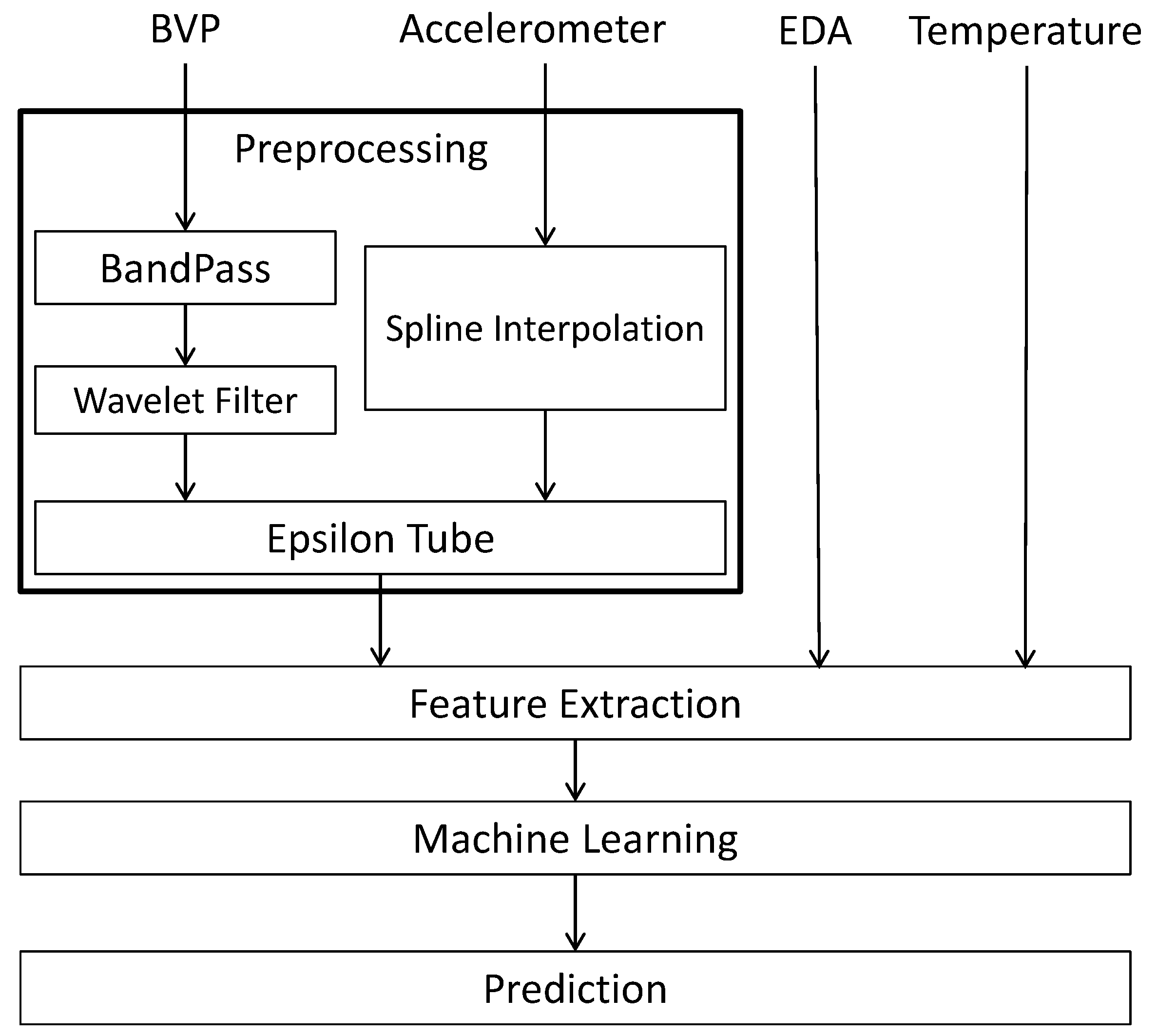
3. Signal Processing: Preprocessing, Filtering, and Feature Extraction
3.1. Preprocessing
3.2. Feature Extraction
- Denoised (filtered) BVP signal, i.e., the output of the Epsilon Tube algorithm, with sampling frequency of 64 Hz.
- Low-band, mid-band, and high-band pass filters applied to the denoised BVP signal.
- Interpolated accelerometer signal, from 32 HZ to 64 Hz.
- Tube sizes from the Epsilon Tube filtering method, another output of the Epsilon Tube algorithm that has the time-varying tube size signal.
- Temperature signal, with sampling frequency of 4 Hz.
- EDA signal, with sampling frequency of 4 Hz.
- The calculated breaths per minute (BPM) signal based on the denoised BVP signal.
- The calculated HRV signal based on the denoised BVP signal.
4. Machine Learning: Learning Using Concave and Convex Kernels
4.1. Notation
4.2. Classification Using a Similarity Function
- for all ;
- for all ;
- if is non-zero and .
4.3. Choosing the Similarity Function
- One or more of the features is prone to large errors —The value of is close to 0 even if and only differ significantly in a few of the features. This choice of is therefore very sensitive to small subsets of bad features.
- The curse of dimensionality—For the training data to properly represent the probability distribution function underlying the data, the number of training vectors should be exponential in n, the number of features. In practice, it usually is much smaller. Thus, if is a test vector in class , there may not be a training vector in for which is not small.
4.4. Choosing the Parameters
4.5. Reweighting the Classes
5. Experiments
5.1. UCI Machine Learning Repository
5.2. Fibromyalgia Dataset
5.2.1. Results with Conventional Machine Learning Methods
5.2.2. Results with Our Machine Learning Method: Machine Learning Using Concave and Convex Kernels
6. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LUCCK | Learning Using Concave and Convex Kernels |
| BVP | Blood Volume Pulse |
| EDA | Electrodermal Activity |
| ANS | Autonomic Nervous System |
| HRV | Heart Rate Variability |
| FFT | Fast Fourier transform |
| BPM | Breaths Per Minute |
| AUROC | Area Under Receiver Operating Characteristic Curve |
Appendix A Classification as Maximum a Posteriori Estimation
Appendix B. Examples
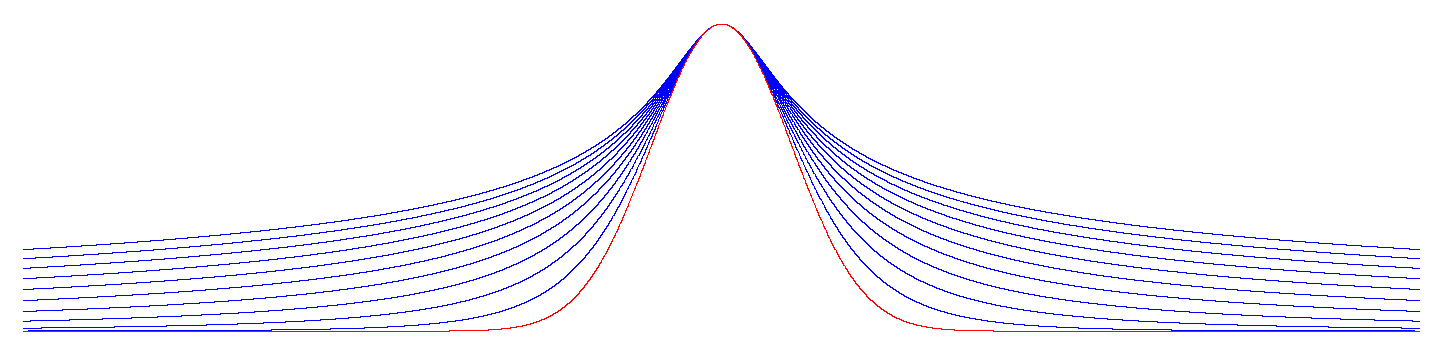
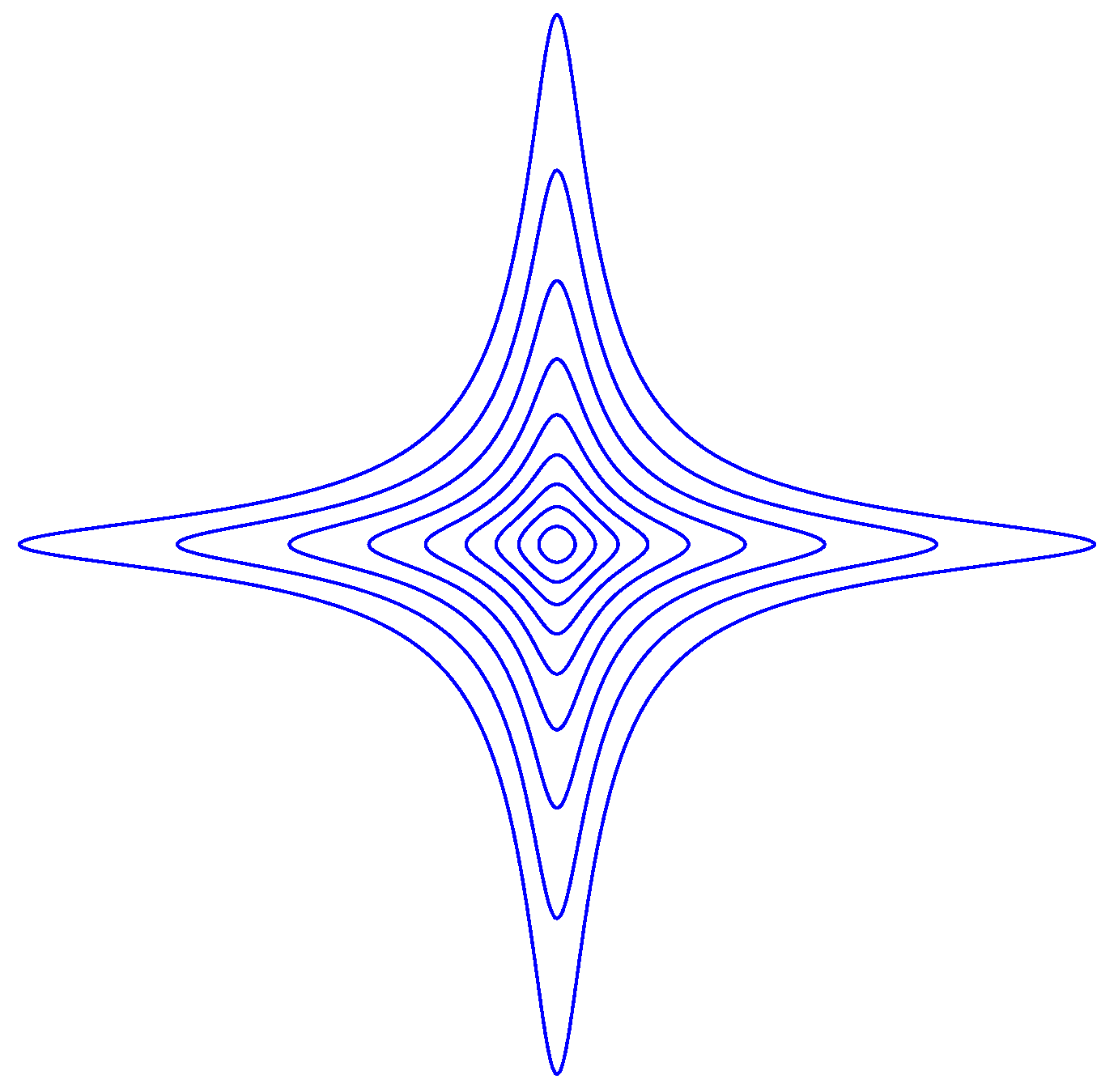
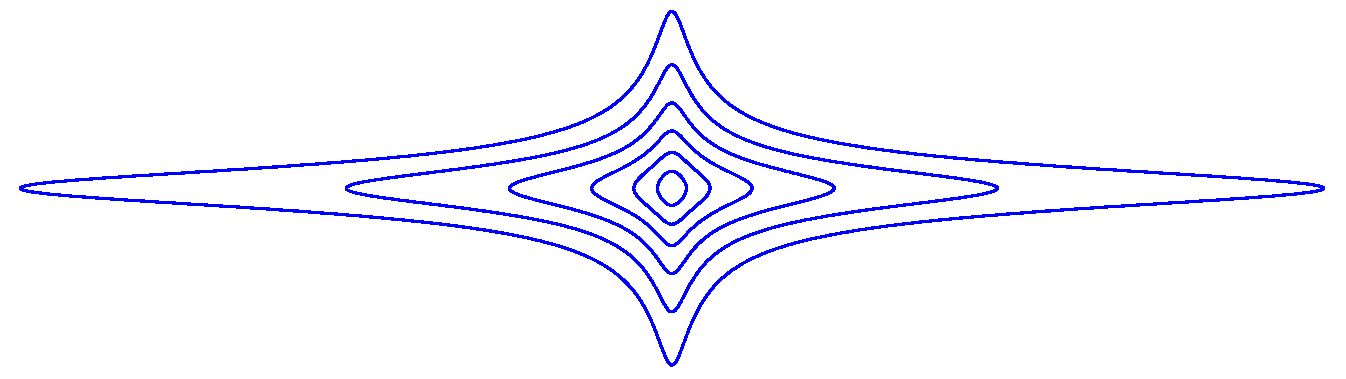
References
- Moldofsky, H. The significance of dysfunctions of the sleeping/waking brain to the pathogenesis and treatment of fibromyalgia syndrome. Rheumatic Dis. Clin. 2009, 35, 275–283. [Google Scholar] [CrossRef]
- Moldofsky, H. The significance of the sleeping–waking brain for the understanding of widespread musculoskeletal pain and fatigue in fibromyalgia syndrome and allied syndromes. Joint Bone Spine 2008, 75, 397–402. [Google Scholar] [CrossRef] [PubMed]
- Horne, J.; Shackell, B. Alpha-like EEG activity in non-REM sleep and the fibromyalgia (fibrositis) syndrome. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 271–276. [Google Scholar] [CrossRef]
- Burns, J.W.; Crofford, L.J.; Chervin, R.D. Sleep stage dynamics in fibromyalgia patients and controls. Sleep Med. 2008, 9, 689–696. [Google Scholar] [CrossRef]
- Belt, N.; Kronholm, E.; Kauppi, M. Sleep problems in fibromyalgia and rheumatoid arthritis compared with the general population. Clin. Expe. Rheumatol. 2009, 27, 35. [Google Scholar]
- Landis, C.A.; Lentz, M.J.; Rothermel, J.; Buchwald, D.; Shaver, J.L. Decreased sleep spindles and spindle activity in midlife women with fibromyalgia and pain. Sleep 2004, 27, 741–750. [Google Scholar] [CrossRef]
- Stuifbergen, A.K.; Phillips, L.; Carter, P.; Morrison, J.; Todd, A. Subjective and objective sleep difficulties in women with fibromyalgia syndrome. J. Am. Acad. Nurse Pract. 2010, 22, 548–556. [Google Scholar] [CrossRef] [PubMed]
- Theadom, A.; Cropley, M.; Parmar, P.; Barker-Collo, S.; Starkey, N.; Jones, K.; Feigin, V.L.; BIONIC Research Group. Sleep difficulties one year following mild traumatic brain injury in a population-based study. Sleep Med. 2015, 16, 926–932. [Google Scholar] [CrossRef]
- Buskila, D.; Neumann, L.; Odes, L.R.; Schleifer, E.; Depsames, R.; Abu-Shakra, M. The prevalence of musculoskeletal pain and fibromyalgia in patients hospitalized on internal medicine wards. Semin. Arthritis Rheum. 2001, 30, 411–417. [Google Scholar] [CrossRef] [PubMed]
- Theadom, A.; Cropley, M.; Humphrey, K.L. Exploring the role of sleep and coping in quality of life in fibromyalgia. J. Psychosom. Res. 2007, 62, 145–151. [Google Scholar] [CrossRef]
- Theadom, A.; Cropley, M. This constant being woken up is the worst thing–experiences of sleep in fibromyalgia syndrome. Disabil. Rehabil 2010, 32, 1939–1947. [Google Scholar] [CrossRef] [PubMed]
- Stone, K.C.; Taylor, D.J.; McCrae, C.S.; Kalsekar, A.; Lichstein, K.L. Nonrestorative sleep. Sleep Med. Rev. 2008, 12, 275–288. [Google Scholar] [CrossRef]
- Harding, S.M. Sleep in fibromyalgia patients: Subjective and objective findings. Am. J. Med. Sci. 1998, 315, 367–376. [Google Scholar] [PubMed]
- Landis, C.A.; Frey, C.A.; Lentz, M.J.; Rothermel, J.; Buchwald, D.; Shaver, J.L. Self-reported sleep quality and fatigue correlates with actigraphy in midlife women with fibromyalgia. Nurs. Res. 2003, 52, 140–147. [Google Scholar] [CrossRef]
- Fogelberg, D.J.; Hoffman, J.M.; Dikmen, S.; Temkin, N.R.; Bell, K.R. Association of sleep and co-occurring psychological conditions at 1 year after traumatic brain injury. Arch. Phys. Med Rehabil. 2012, 93, 1313–1318. [Google Scholar] [CrossRef]
- Towns, S.J.; Silva, M.A.; Belanger, H.G. Subjective sleep quality and postconcussion symptoms following mild traumatic brain injury. Brain Injury 2015, 29, 1337–1341. [Google Scholar] [CrossRef] [PubMed]
- Trinder, J.; Kleiman, J.; Carrington, M.; Smith, S.; Breen, S.; Tan, N.; Kim, Y. Autonomic activity during human sleep as a function of time and sleep stage. J. Sleep Res. 2001, 10, 253–264. [Google Scholar] [CrossRef]
- Baharav, A.; Kotagal, S.; Gibbons, V.; Rubin, B.; Pratt, G.; Karin, J.; Akselrod, S. Fluctuations in autonomic nervous activity during sleep displayed by power spectrum analysis of heart rate variability. Neurology 1995, 45, 1183–1187. [Google Scholar] [CrossRef]
- Sano, A.; Picard, R.W.; Stickgold, R. Quantitative analysis of wrist electrodermal activity during sleep. Int. J. Psychophysiol. 2014, 94, 382–389. [Google Scholar] [CrossRef]
- Sano, A.; Picard, R.W. Comparison of sleep-wake classification using electroencephalogram and wrist-worn multi-modal sensor data. In Proceedings of the 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; Volume 2014, p. 930. [Google Scholar]
- Sano, A.; Picard, R.W. Recognition of sleep dependent memory consolidation with multi-modal sensor data. In Proceedings of the 2013 IEEE International Conference on Body Sensor Networks, Cambridge, MA, USA, 6–9 May 2013; pp. 1–4. [Google Scholar]
- Sano, A.; Picard, R.W. Toward a taxonomy of autonomic sleep patterns with electrodermal activity. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011. [Google Scholar]
- Lötsch, J.; Ultsch, A. Machine learning in pain research. Pain 2018, 159, 623. [Google Scholar] [CrossRef] [PubMed]
- Robinson, M.E.; O’Shea, A.M.; Craggs, J.G.; Price, D.D.; Letzen, J.E.; Staud, R. Comparison of machine classification algorithms for fibromyalgia: Neuroimages versus self-report. J. Pain 2015, 16, 472–477. [Google Scholar] [CrossRef]
- Sevel, L.; Letzen, J.; Boissoneault, J.; O’Shea, A.; Robinson, M.; Staud, R. (337) MRI based classification of chronic fatigue, fibromyalgia patients and healthy controls using machine learning algorithms: A comparison study. J. Pain 2016, 17, S60. [Google Scholar] [CrossRef]
- López-Solà, M.; Woo, C.W.; Pujol, J.; Deus, J.; Harrison, B.J.; Monfort, J.; Wager, T.D. Towards a neurophysiological signature for fibromyalgia. Pain 2017, 158, 34. [Google Scholar] [CrossRef] [PubMed]
- Sundermann, B.; Burgmer, M.; Pogatzki-Zahn, E.; Gaubitz, M.; Stüber, C.; Wessolleck, E.; Heuft, G.; Pfleiderer, B. Diagnostic classification based on functional connectivity in chronic pain: model optimization in fibromyalgia and rheumatoid arthritis. Acad. Radiol. 2014, 21, 369–377. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Zapirain, B.; Garcia-Chimeno, Y.; Rogers, H. Machine Learning Techniques for Automatic Classification of Patients with Fibromyalgia and Arthritis. Int. J. Comput. Trends Technol. 2015, 25, 149–152. [Google Scholar] [CrossRef]
- Lukkahatai, N.; Walitt, B.; Deandrés-Galiana, E.J.; Fernández-Martínez, J.L.; Saligan, L.N. A predictive algorithm to identify genes that discriminate individuals with fibromyalgia syndrome diagnosis from healthy controls. J. Pain Res. 2018, 11, 2981. [Google Scholar] [CrossRef]
- Ansari, S.; Ward, K.; Najarian, K. Epsilon-tube filtering: Reduction of high-amplitude motion artifacts from impedance plethysmography signal. IEEE J. Biomed. Health Inf. 2015, 19, 406–417. [Google Scholar] [CrossRef] [PubMed]
- Frank, E.; Hall, M.; Holmes, G.; Kirkby, R.; Pfahringer, B.; Witten, I.H.; Trigg, L. Weka-a machine learning workbench for data mining. In Data Mining and Knowledge Discovery Handbook; Springer: Boston, MA, USA, 2009; pp. 1269–1277. [Google Scholar]
- Tarvainen, M.P.; Niskanen, J.P.; Lipponen, J.A.; Ranta-Aho, P.O.; Karjalainen, P.A. Kubios HRV–heart rate variability analysis software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef] [PubMed]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Dudani, S.A. The distance-weighted k-nearest-neighbor rule. IEEE Trans. Sys. Man Cybern. 1976, 4, 325–327. [Google Scholar] [CrossRef]
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When is “nearest neighbor” meaningful? In International Conference on Database Theory; Springer: Berlin/Heidelberg, Germany, 1999; pp. 217–235. [Google Scholar]
- Hechenbichler, K.; Schliep, K. Weighted k-nearest-neighbor Techniques and Ordinal Classification. 2004. Available online: https://epub.ub.uni-muenchen.de/1769/ (accessed on 24 April 2019).
- Mitchell, T. Machine Learning; McGraw-Hill International, Ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://ergodicity.net/2013/07/ (accessed on 24 April 2019).
- Apkarian, A.V.; Hashmi, J.A.; Baliki, M.N. Pain and the brain: specificity and plasticity of the brain in clinical chronic pain. Pain 2011, 152, S49. [Google Scholar] [CrossRef] [PubMed]
- Wartolowska, K. How neuroimaging can help us to visualise and quantify pain? Eur. J. Pain Suppl. 2011, 5, 323–327. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
| Detail Coefficients Level | Threshold |
|---|---|
| 8 | 94.38 |
| 7 | 147.8 |
| 6 | 303.1 |
| 5 | 329.9 |
| 4 | 90.16 |
| 3 | 30.67 |
| 2 | 0 |
| 1 | 0 |
| Signals | Features |
|---|---|
| Denoised BVP | Mean, Standard deviation, Variance, Power, Median, Frequency with the highest peak, |
| Amplitude of the frequency with highest peak, FFT power, Mean of FFT amplitudes, | |
| Mean of the FFT frequencies, Median of FFT amplitudes (11 features) | |
| Low-band denoised | Mean, Standard deviation, Variance, Power, Median, Frequency with the highest peak, |
| BVP | Amplitude of the frequency with highest peak, FFT power, Mean of FFT amplitudes, |
| Mean of the FFT frequencies, Median of FFT amplitudes (11 features) | |
| Mid-band denoised | Mean, Standard deviation, Variance, Power, Median, Frequency with the highest peak, |
| BVP | Amplitude of the frequency with highest peak, FFT power, Mean of FFT amplitudes, |
| Mean of the FFT frequencies, Median of FFT amplitudes (11 features) | |
| High-band denoised | Mean, Standard deviation, Variance, Power, Median, Frequency with the highest peak, |
| BVP | Amplitude of the frequency with highest peak, FFT power, Mean of FFT amplitudes, |
| Mean of the FFT frequencies, Median of FFT amplitudes (11 features) | |
| Tube size | Mean, Standard Deviation, Variance, Power (4 features) |
| Interpolated | Mean, Standard Deviation, Variance, Power (4 features) |
| accelerometer | |
| Temperature signal | Mean, Standard Deviation, Variance, Power (4 features) |
| EDA signal | Mean, Standard Deviation, Variance, Power (4 features) |
| BPM signal | Maximum, Minimum, Range, Mean, Standard deviation, Power (6 features) |
| HRV | The Kubios Standard HRV feature set [32] (25 features) |
| Dataset | Method | Accuracy (%) | Time (s) |
|---|---|---|---|
| Sonar (208 samples) | LUCCK | 87.42 | 1.5082 |
| 3-NN | 81.66 | 0.0178 | |
| 5-NN | 81.05 | 0.0178 | |
| Adaboost | 82.19 | 1.0239 | |
| SVM | 81.00 | 0.0398 | |
| Random Forest (10) | 78.14 | 0.1252 | |
| Random Forest (100) | 83.39 | 1.1286 | |
| LDA | 74.90 | 0.0343 | |
| Glass (214 samples) | LUCCK | 82.56 | 0.3500 |
| 3-NN | 68.72 | 0.0161 | |
| 5-NN | 67.04 | 0.0162 | |
| Adaboost | 50.82 | 0.5572 | |
| SVM | 35.57 | 0.0342 | |
| Random Forest (10) | 75.31 | 0.1062 | |
| Random Forest (100) | 79.24 | 0.9319 | |
| LDA | 63.28 | 0.0155 | |
| Iris (150 samples) | LUCCK | 95.93 | 0.1508 |
| 3-NN | 96.09 | 0.0135 | |
| 5-NN | 96.54 | 0.0135 | |
| Adaboost | 93.82 | 0.4912 | |
| SVM | 96.52 | 0.0143 | |
| Random Forest (10) | 94.81 | 0.0889 | |
| Random Forest (100) | 95.29 | 0.7686 | |
| LDA | 98.00 | 0.0122 | |
| E. coli (336 samples) | LUCCK | 87.61 | 0.5937 |
| 3-NN | 85.08 | 0.0190 | |
| 5-NN | 86.43 | 0.0193 | |
| Adaboost | 74.13 | 0.6058 | |
| SVM | 87.53 | 0.0448 | |
| Random Forest (10) | 84.56 | 0.1075 | |
| Random Forest (100) | 87.34 | 0.9265 | |
| LDA | 81.46 | 0.0182 |
| Method | Accuracy (%) | Time (s) |
|---|---|---|
| LUCCK | 88.38 ± 5.55 | 0.6507 |
| 3-NN | 82.89 ± 11.27 | 0.0166 |
| 5-NN | 82.77 ± 12.29 | 0.0167 |
| Adaboost | 75.24 ± 18.18 | 0.6695 |
| SVM | 75.16 ± 27.15 | 0.0333 |
| Random Forest (10) | 83.21 ± 8.65 | 0.1070 |
| Random Forest (100) | 86.32 ± 6.84 | 0.9389 |
| LDA | 79.41 ± 14.49 | 0.0201 |
| Method | Sleep | Fatigue | ||
|---|---|---|---|---|
| Accuracy (%) | AUROC | Accuracy (%) | AUROC | |
| AdaBoost - Decision Stump | 62.07 | 0.63 | 46.64 | 0.55 |
| AdaBoost - Random Forest | 59.97 | 0.65 | 51.24 | 0.55 |
| K-Nearest Neighbor | 60.55 | 0.55 | 51.88 | 0.53 |
| Weighted K-Nearest Neighbor | 65.27 | 0.62 | 68.05 | 0.51 |
| Neural Network | 63.47 | 0.64 | 54.80 | 0.59 |
| Random Forest | 63.32 | 0.63 | 52.46 | 0.57 |
| Support Vector Machine | 64.47 | 0.50 | 55.94 | 0.50 |
| LUCCK | 66.95 | 0.66 | 87.59 | 0.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabeti, E.; Gryak, J.; Derksen, H.; Biwer, C.; Ansari, S.; Isenstein, H.; Kratz, A.; Najarian, K. Learning Using Concave and Convex Kernels: Applications in Predicting Quality of Sleep and Level of Fatigue in Fibromyalgia. Entropy 2019, 21, 442. https://doi.org/10.3390/e21050442
Sabeti E, Gryak J, Derksen H, Biwer C, Ansari S, Isenstein H, Kratz A, Najarian K. Learning Using Concave and Convex Kernels: Applications in Predicting Quality of Sleep and Level of Fatigue in Fibromyalgia. Entropy. 2019; 21(5):442. https://doi.org/10.3390/e21050442
Chicago/Turabian StyleSabeti, Elyas, Jonathan Gryak, Harm Derksen, Craig Biwer, Sardar Ansari, Howard Isenstein, Anna Kratz, and Kayvan Najarian. 2019. "Learning Using Concave and Convex Kernels: Applications in Predicting Quality of Sleep and Level of Fatigue in Fibromyalgia" Entropy 21, no. 5: 442. https://doi.org/10.3390/e21050442
APA StyleSabeti, E., Gryak, J., Derksen, H., Biwer, C., Ansari, S., Isenstein, H., Kratz, A., & Najarian, K. (2019). Learning Using Concave and Convex Kernels: Applications in Predicting Quality of Sleep and Level of Fatigue in Fibromyalgia. Entropy, 21(5), 442. https://doi.org/10.3390/e21050442





