Thermodynamic Analysis of Time Evolving Networks
Abstract
1. Introduction
Related Literature
2. Thermodynamic Framework for Time-Evolving Complex Networks
2.1. Initial Considerations
2.2. Approximate von Neumann Entropy for Undirected Graphs
2.3. Internal Energy and Temperature
2.3.1. Undirected Edges
2.3.2. Directed Edges
2.4. Section Summary
3. Experiments and Evaluations
3.1. Thermodynamic Measures for Analysing Network Evolution
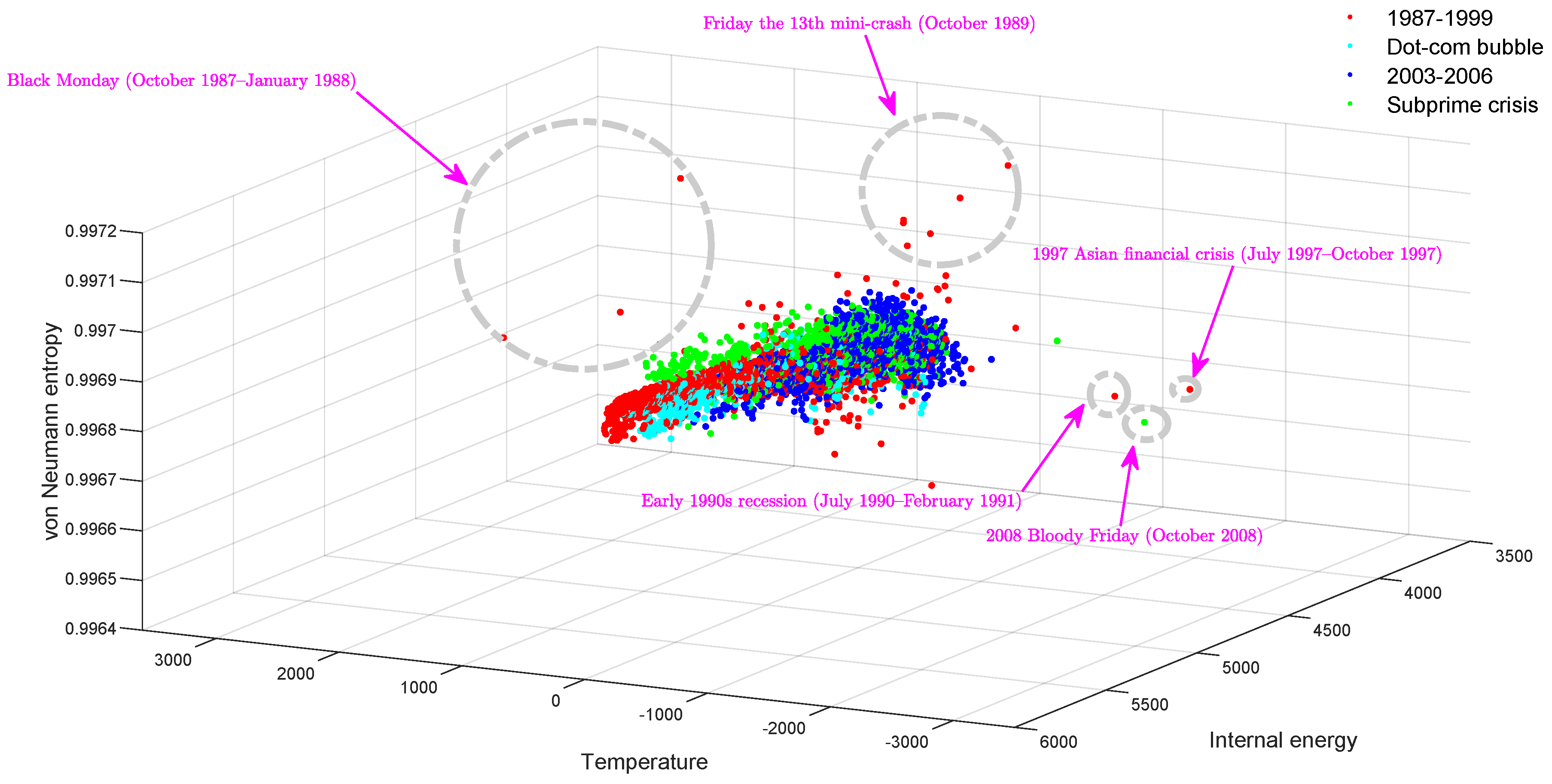
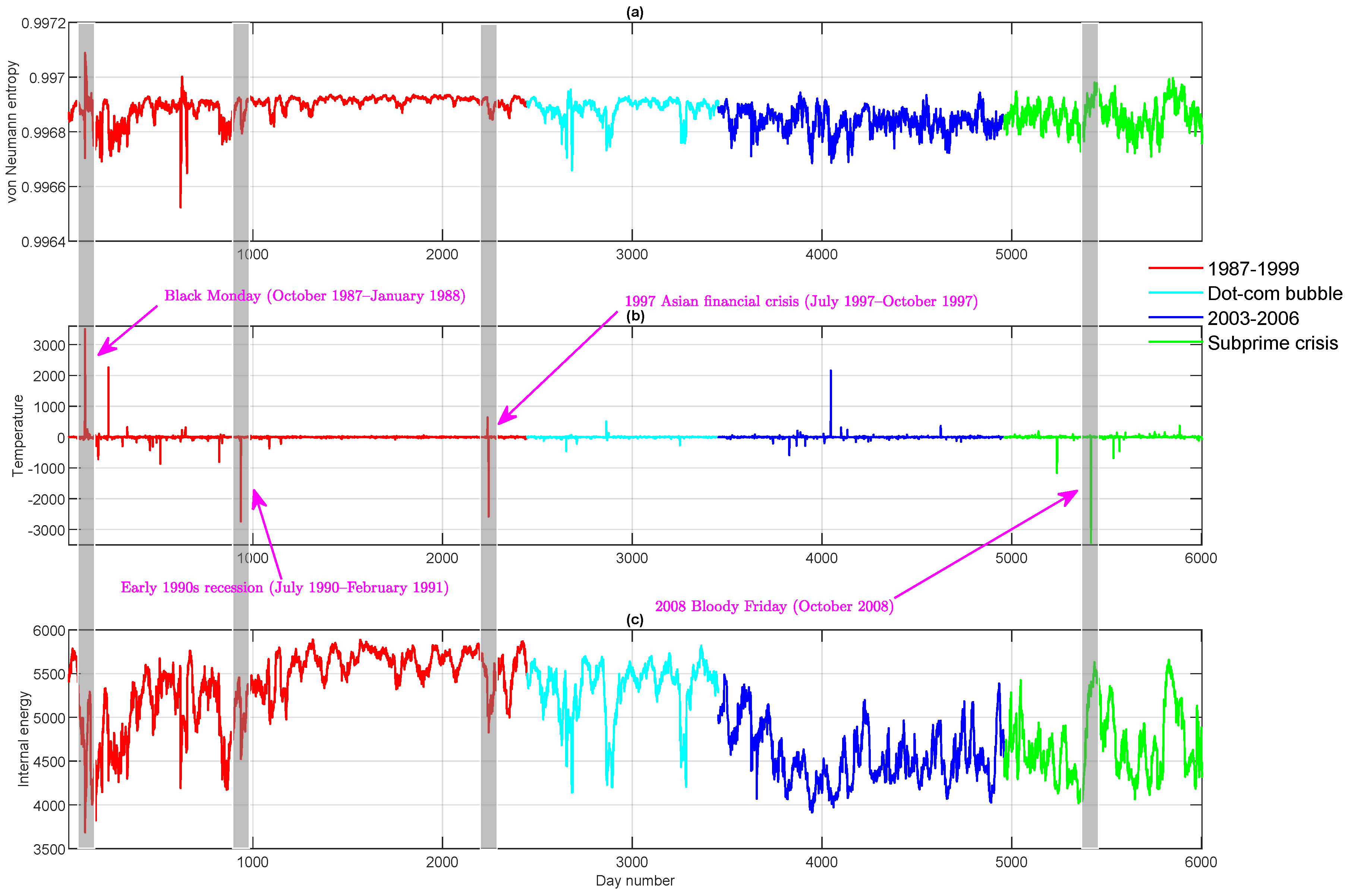
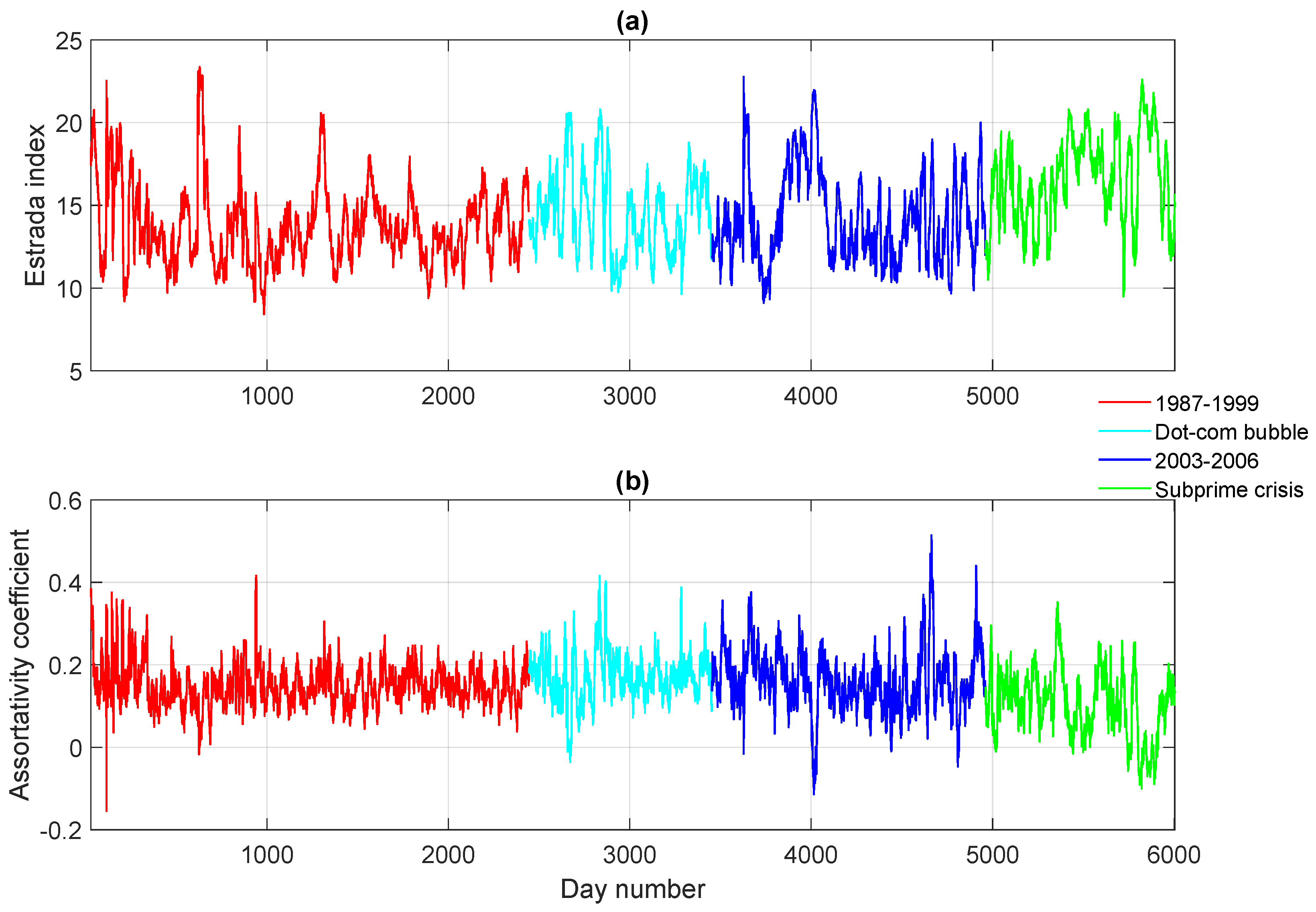
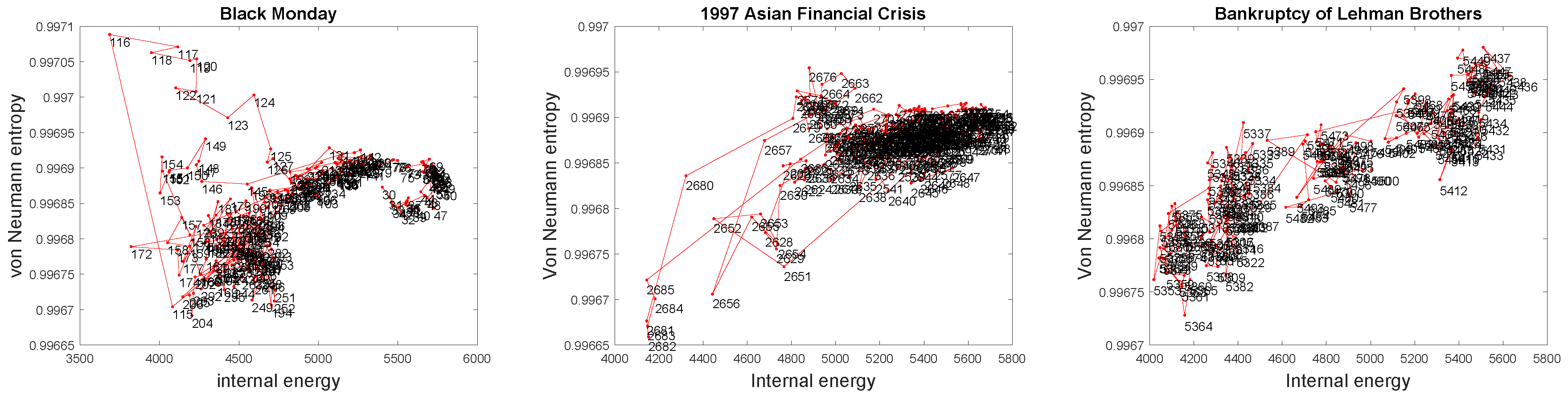
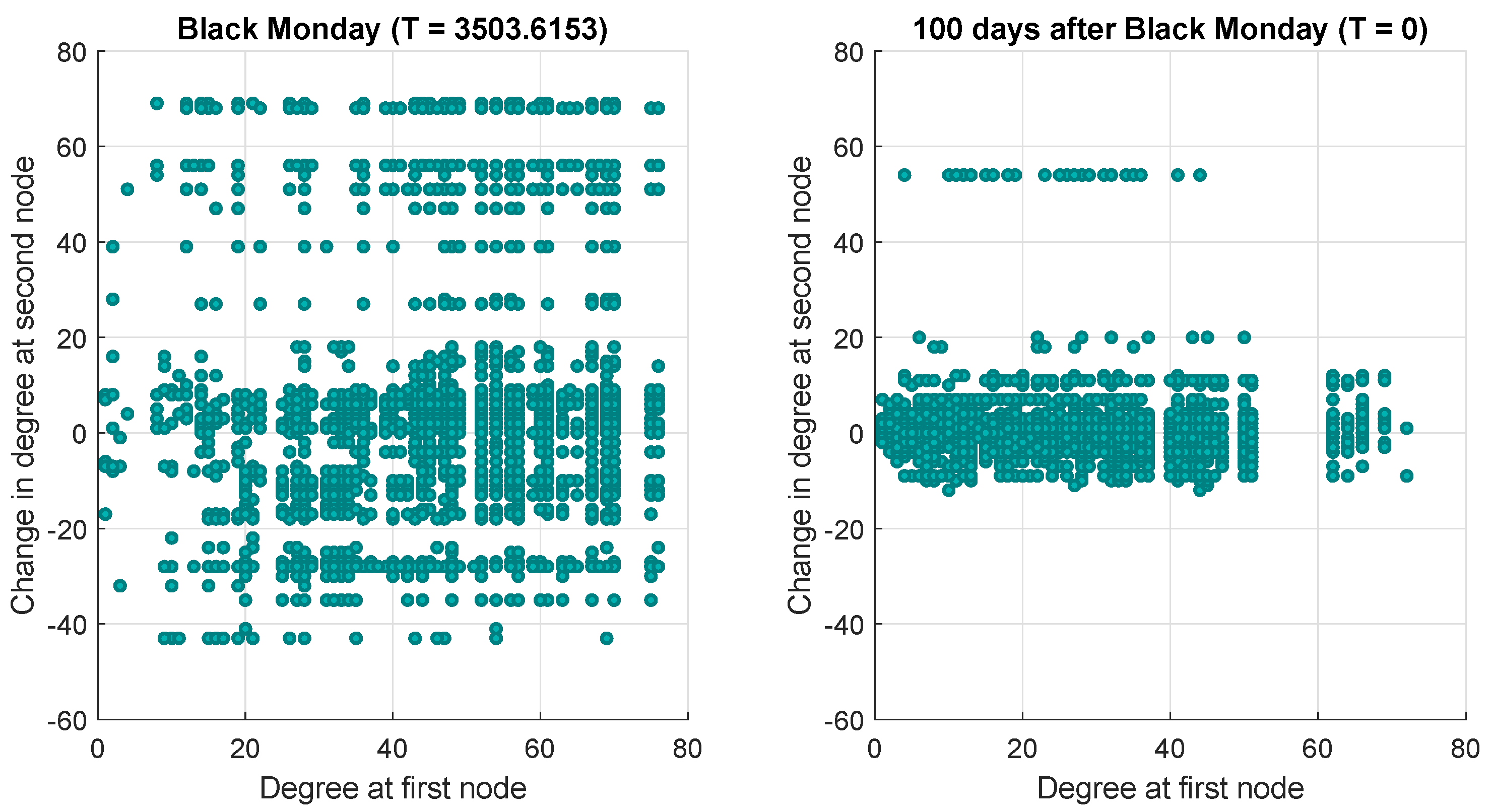
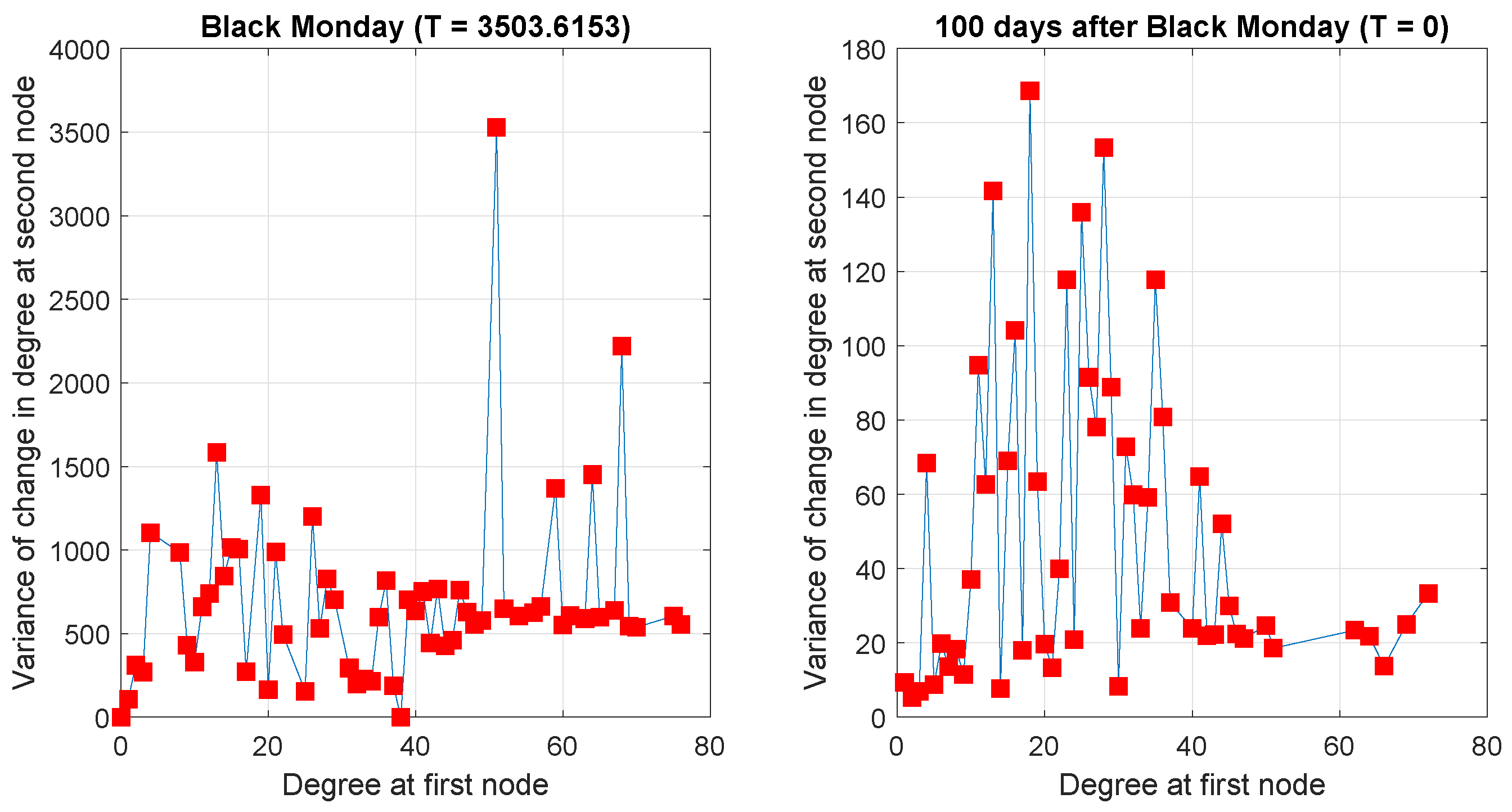
3.1.1. Financial Networks
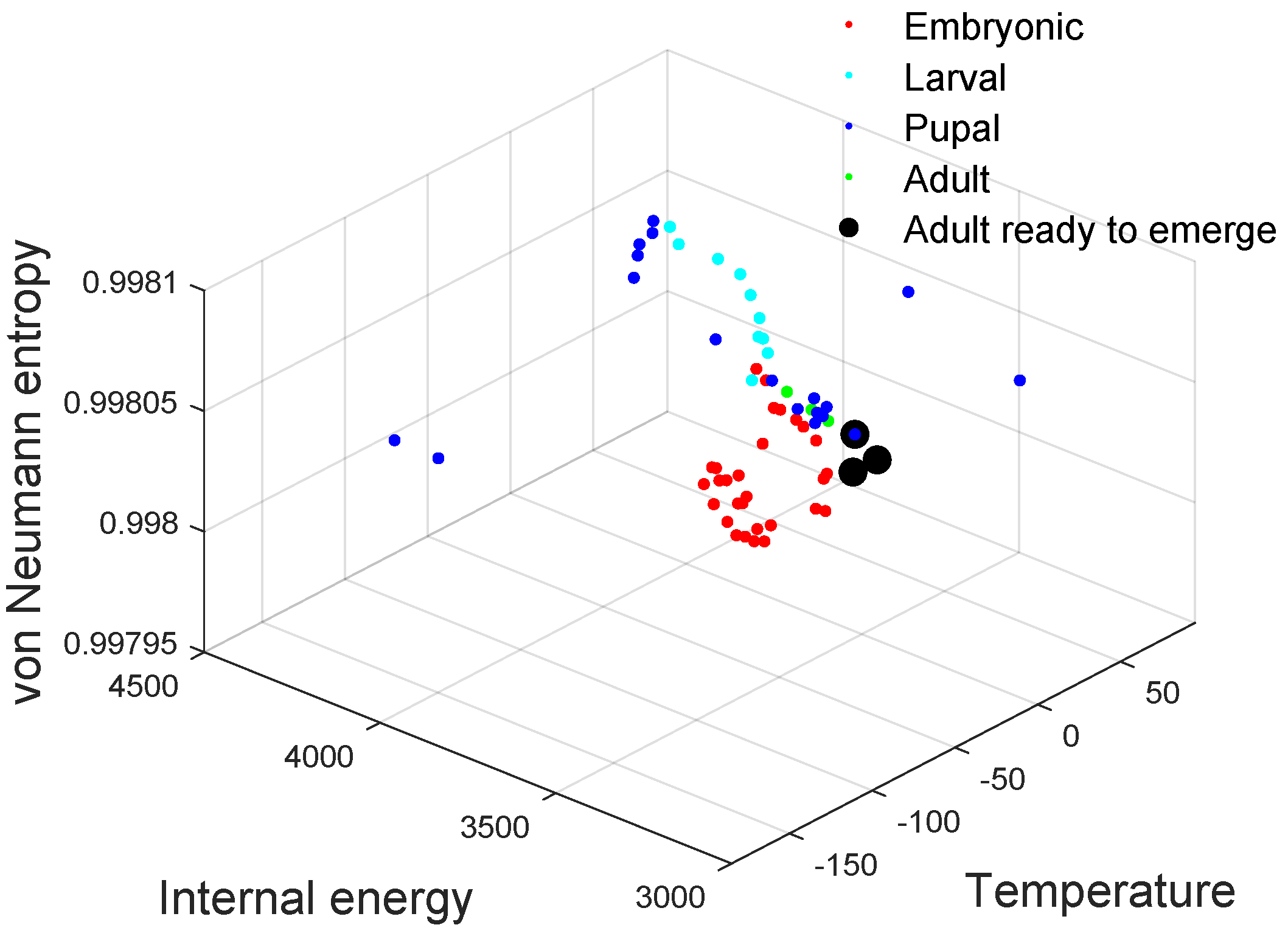
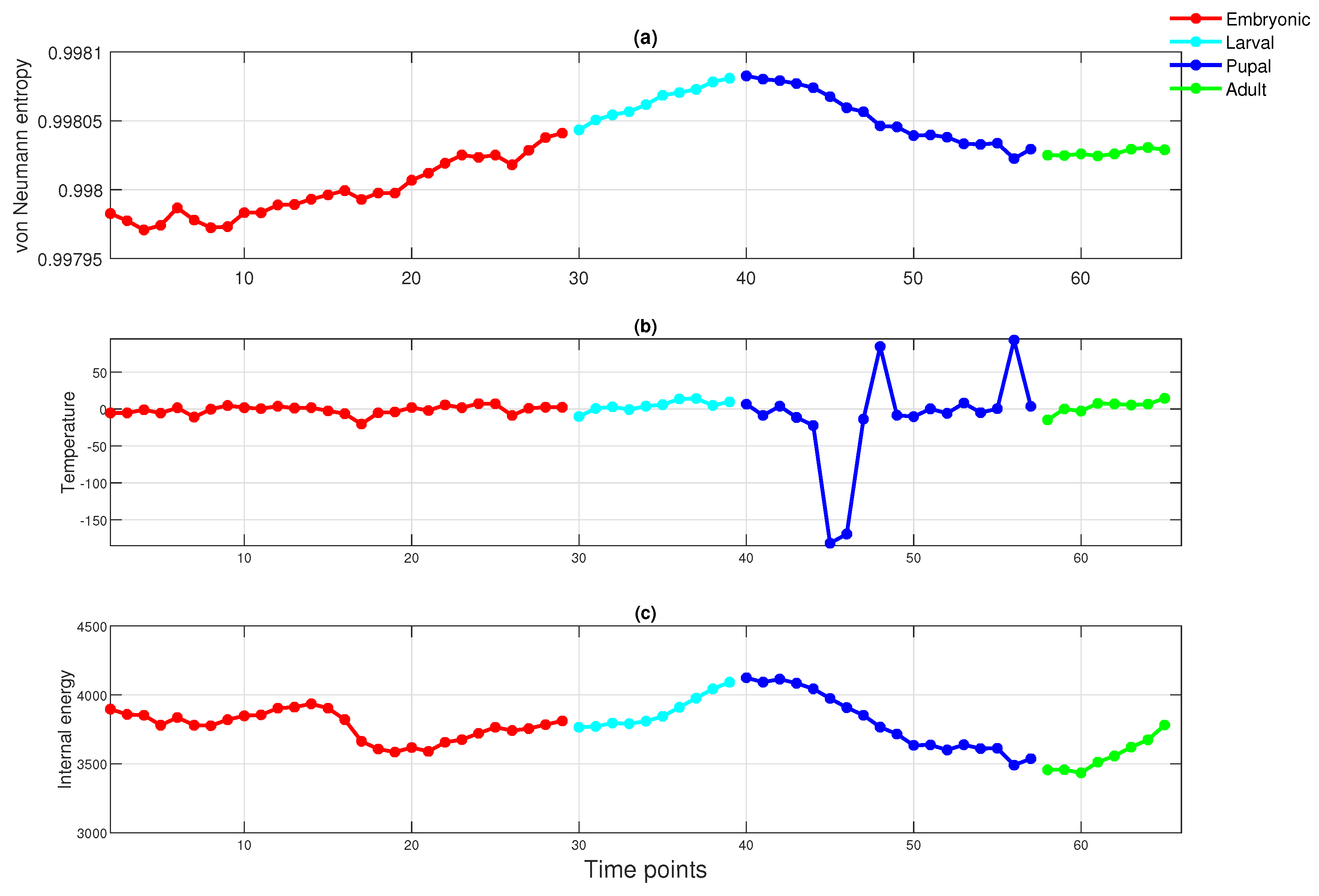
3.1.2. Gene Regulatory Network
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Van der Hofstad, R. Random Graphs and Complex Networks; Eindhoven University of Technology: Eindhoven, The Netherlands, 2010. [Google Scholar]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80, 045102. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Newman, M. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Feldman, D.; Crutchfield, J. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Dehmer, M.; Mowshowitz, A.; Emmert-Streib, F. Advances in Network Complexity; Wiley-Blackwell: Hoboken, NJ, USA, 2013. [Google Scholar]
- Anand, K.; Bianconi, G.; Severini, S. Shannon and von Neumann entropy of random networks with heterogeneous expected degree. Phys. Rev. E 2011, 83, 036109. [Google Scholar] [CrossRef] [PubMed]
- Anand, K.; Krioukov, D.; Bianconi, G. Entropy distribution and condensation in random networks with a given degree distribution. Phys. Rev. E 2014, 89, 062807. [Google Scholar] [CrossRef] [PubMed]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bianconi, G. The entropy of randomized network ensembles. Europhys. Lett. 2008, 81, 28005. [Google Scholar] [CrossRef]
- Mikulecky, D.C. Network thermodynamics and complexity: A transition to relational systems theory. Comput. Chem. 2001, 25, 369–391. [Google Scholar] [CrossRef]
- Delvenne, J.C.; Libert, A.S. Centrality measures and thermodynamic formalism for complex networks. Phys. Rev. E 2011, 83, 046117. [Google Scholar] [CrossRef] [PubMed]
- Fronczak, A.; Fronczak, P.; Holyst, J.A. Thermodynamic forces, flows, and Onsager coefficients in complex networks. Phys. Rev. E 2007, 76, 061106. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Hatano, N. Statistical-mechanical approach to subgraph centrality in complex networks. Chem. Phys. Lett. 2007, 439, 247–251. [Google Scholar] [CrossRef]
- Minello, G.; Torsello, A.; Hancock, E.R. Quantum thermodynamics of time evolving networks. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 1536–1541. [Google Scholar]
- Ye, C.; Torsello, A.; Wilson, R.C.; Hancock, E.R. Thermodynamics of Time Evolving Networks. In Graph-Based Representations in Pattern Recognition; Liu, C.L., Luo, B., Kropatsch, W.G., Cheng, J., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 315–324. [Google Scholar]
- Holme, P.; Edling, C.R.; Liljeros, F. Structure and time evolution of an Internet dating community. Soc. Netw. 2004, 26, 155–174. [Google Scholar] [CrossRef]
- Kumar, R.; Novak, J.; Tomkins, A. Structure and evolution of online social networks. In Proceedings of the Twelfth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 611–617. [Google Scholar]
- Palla, G.; Barabási, A.L.; Vicsek, T. Quantifying social group evolution. Nature 2007, 446, 664–667. [Google Scholar] [CrossRef] [PubMed]
- Peel, L.; Clauset, A. Detecting change points in the large-scale structure of evolving networks. In Proceedings of the 29th International Conference on Artificial Intelligence (AAAI), Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Chung, F. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Passerini, F.; Severini, S. The Von Neumann Entropy of Networks. Int. J. Agent Technol. Syst. 2008, 1, 58–67. [Google Scholar] [CrossRef]
- Han, L.; Escolano, F.; Hancock, E.R.; Wilson, R.C. Graph Characterizations from Von Neumann Entropy. Pattern Recognit. Lett. 2012, 33, 1958–1967. [Google Scholar] [CrossRef]
- Ye, C.; Wilson, R.C.; Comin, C.H.; da F. Costa, L.; Hancock, E.R. Approximate von Neumann entropy for directed graphs. Phys. Rev. E 2014, 89, 052804. [Google Scholar] [CrossRef] [PubMed]
- Gorban, A.N.; Smirnova, E.V.; Tyukina, T.A. Correlations, risk and crisis: From physiology to finance. Phys. A Stat. Mech. Appl. 2010, 389, 3193–3217. [Google Scholar] [CrossRef]
- Mojtahedi, M.; Skupin, A.; Zhou, J.; Castaño, I.G.; Leong-Quong, R.Y.Y.; Chang, H.; Trachana, K.; Giuliani, A.; Huang, S. Cell Fate Decision as High-Dimensional Critical State Transition. PLoS Biol. 2016, 14, e2000640. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.N.; Comin, C.H.; Peron, T.K.D.; Rodrigues, F.A.; Ye, C.; Wilson, R.C.; Hancock, E.R.; da F. Costa, L. On the Modular Dynamics of Financial Market Networks. arXiv, 2015; arXiv:1501.05040. [Google Scholar]
- Battiston, S.; Caldarelli, G. Systemic Risk in Financial Networks. J. Financ. Manag. Mark. Inst. 2013, 1, 129–154. [Google Scholar]
- Bonanno, G.; Caldarelli, G.; Lillo, F.; Miccichè, S.; Vandewalle, N.; Mantegna, R.N. Networks of equities in financial markets. Eur. Phys. J. B 2004, 38, 363–372. [Google Scholar] [CrossRef]
- Caldarelli, G.; Battiston, S.; Garlaschelli, D.; Catanzaro, M. Emergence of Complexity in Financial Networks. In Complex Networks; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 650, pp. 399–423. [Google Scholar]
- Peron, T.K.D.; Rodrigues, F.A. Collective behavior in financial markets. Europhys. Lett. 2011, 96, 48004. [Google Scholar] [CrossRef]
- Arbeitman, M.N.; Furlong, E.E.; Imam, F.; Johnson, E.; Null, B.H.; Baker, B.S.; Krasnow, M.A.; Scott, M.P.; Davis, R.W.; White, K.P. Gene expression during the life cycle of Drosophila melanogaster. Science 2002, 297, 2270–2275. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Kolar, M.; Xing, E.P. KELLER: Estimating time-varying interactions between genes. Bioinformatics 2009, 25, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. Characterization of 3D molecular structure. Chem. Phys. Lett. 2000, 319, 713–718. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Wilson, R.C.; Rossi, L.; Torsello, A.; Hancock, E.R. Thermodynamic Analysis of Time Evolving Networks. Entropy 2018, 20, 759. https://doi.org/10.3390/e20100759
Ye C, Wilson RC, Rossi L, Torsello A, Hancock ER. Thermodynamic Analysis of Time Evolving Networks. Entropy. 2018; 20(10):759. https://doi.org/10.3390/e20100759
Chicago/Turabian StyleYe, Cheng, Richard C. Wilson, Luca Rossi, Andrea Torsello, and Edwin R. Hancock. 2018. "Thermodynamic Analysis of Time Evolving Networks" Entropy 20, no. 10: 759. https://doi.org/10.3390/e20100759
APA StyleYe, C., Wilson, R. C., Rossi, L., Torsello, A., & Hancock, E. R. (2018). Thermodynamic Analysis of Time Evolving Networks. Entropy, 20(10), 759. https://doi.org/10.3390/e20100759




